Параметрические уравнения: Теория параметрических уравнений, задачи

Теория параметрических уравнений, задачи

Уравнение, которое кроме неизвестной величины содержит также другую дополнительную величину, которая может принимать различные значения из некоторой области, называется параметрическим. Эта дополнительная величина в уравнении называется параметр . На самом деле с каждым параметрическим уравнением может быть написано множество уравнений. Мы рассмотрим модуль параметрического уравнения и решение простых параметрических уравнений.

---

Задача 1 Решите уравнения в отношении к $x$
A) $x + a = 7$
B) $2x + 8a = 4$
C) $x + a = 2a – x$
D) $ax = 5$
E) $a – x = x + b$
F) $ax = 3a$

Решение:

A) $x + a = 7 \Leftrightarrow x = 7 – a$, то есть решение к данному уравнению найдено.
Для различных значений параметров, решения есть $x = 7 – a$

B) $2x + 8a = 4 \Leftrightarrow 2x = 4 — 8a \Leftrightarrow x = 2 – 4a$

C) $x + a = 2a – x \Leftrightarrow x + x = 2a – a \Leftrightarrow 2x = a \Leftrightarrow x = \frac{a}{2}$

D) $ax = 5$, когда а отличается от 0 мы можем разделить обе части на a и мы получим $x = 5$
Если $a = 0$, мы получим уравнение, такое как $0. 2}$ является решением уравнения.

---

Задача $4$ Для каких значений $x$ следующие выражения имеют равные значения :
A) $5x + a$ и $3ax + 4$
B) $2x — 2$ и $4x + 5a$

Решение:

Чтобы получить одинаковые значения мы должны найти решения уравнений
$5x + a = 3ax + 4$ и $2x – 2 = 4x + 5a$

A) $5x + a = 3ax + 4 \Leftrightarrow$
$5x — 3ax = 4 – a \Leftrightarrow$
$(5 — 3a)x = 4 – a$
Если $5 — 3a \neq 0$, т.e. $a \neq \frac{5}{3}$, решения есть $x = \frac{4-a}{5-3a}$
Если $5 — 3a = 0$, т.e. $a = \frac{5}{3}$, уравнение принимает вид $0\cdot x = 4 – \frac{5}{3} \Leftrightarrow$
$0\cdot x = \frac{7}{3}$, что не имеет решения

B) $2x — 2 = 4x + 5a \Leftrightarrow$
$-2 — 5a = 4x — 2x \Leftrightarrow$

$2x = — 2 — 5a \Leftrightarrow$
$x = -\frac{2+5a}{2}$

---

Задача 5 Решите параметрическое уравнение:
A) $|ax + 2| = 4$
B) $|2x + 1| = 3a$
C) $|ax + 2a| = 3$

Решение:

A) $|ax + 2| = 4 \Leftrightarrow ax + 2 = 4$ или $ax + 2 = -4 \Leftrightarrow$
$ax = 2$ или $ax = — 6$
Если $a \neq 0$, уравнения примут вид $x = \frac{2}{a}$ or $x = -\frac{6}{a}$
Если $a = 0$, уравнения не имею решения

B) Если $a Если $a > 0$, это эквивалентно $2x + 1 = 3a$
или $2x + 1 = -3a \Leftrightarrow 2x = 3a — 1 \Leftrightarrow x = \frac{3a-1}{2}$ or
$2x = -3a — 1 \Leftrightarrow x = \frac{3a-1}{2} = -\frac{3a-1}{2}$

C) $|ax + 2a| = 3 \Leftrightarrow ax + 2a = 3$ или $ax + 2a = — 3$,
и мы находим $ax = 3 — 2a$ или $ax = -3 — 2a$
Если a = 0, тогда нет решений, если $a \neq 0$
решениями есть: $x = \frac{3-2a}{a}$ и $x = -\frac{3+2a}{a}$

---

Задача 6 Решите уравнение $2 – x = 2b – 2ax$, где a и b являются действительными параметрами.

Найдите, для каких значениях a уравнение имеет в качестве решения натуральное число, если $b = 7$

Решение:

Представим данное уравнение в следующем виде: $(2a — 1)x = 2(b — 1)$
Возможны следующие варианты:
Если $2a — 1 \neq 0$, т.e. $a \neq \frac{1}{2}$, уравнение имеет единственное решение
$x = \frac{2(b-1)}{2a-1}$
Если $a = \frac{1}{2}$ и $b = 1$, уравнение получает вид $0\cdot x = 0$ и любое $x$ является решением
Если $a = \frac{1}{2}$ и $b \neq 1$, мы получаем $0\cdot x = 2(b — 1)$, где $2(b — 1) \neq 0$
В этом случае уравнение не имеет решения.
Если $b = 7$ и $a \neq \frac{1}{2}$ является единственным решением
$x = \frac{2(7-1)}{2a-1} = \frac{12}{2a-1}$
Если a целое число, тогда $2a — 1$ также есть целым числом и решением есть
$x = \frac{12}{2a-1}$ является натуральным числом когда

$2a — 1$ есть положительным делителем для числа $12$.
Чтобы a было целым числом, делитель числа $12$ должен быть нечетным. Но только $1$ и $3$ являются положительными нечетными числами, на которые делится12
Поэтому $2a — 1 = 3 \Leftrightarrow a = 2$ или $2a — 1 = 1 \Leftrightarrow$
$a = 1 a = 2$ или $2a — 1 = 1 \Leftrightarrow a = 1$

---

Задача 7 Решите уравнение $|ax — 2 – a| = 4$, где a является параметром. Найдите, для каких значениях а корнями уравнения являются целые отрицательные числа.

Решение:

Из определения модуля мы получаем
$|ax — 2 – x| = 4 \Leftrightarrow ax — 2 – x = 4$ или $ax — 2 – x = — 4$
Из первого равенства мы получаем $x(a — 1) — 2 = 4 \Leftrightarrow$
$(a — 1)x = 4 + 2 \Leftrightarrow (a — 1)x = 6$
Из второго равенства мы получаем $(a — 1)x = -2$
Если $a — 1 = 0$, т.e. $a = 1$, последнее уравнение не имеет решения.

Если $a \neq 1$ мы находим, что $x = \frac{6}{a-1}$ или $x = -\frac{2}{a-1}$
Чтобы эти корни были целыми отрицательными числами, должно выполняться следующее:
Для первого равенство $a — 1$ должно быть отрицательным делителем 6, и для второго — положительным делителям 2
Тогда $a — 1 = -1; -2; -3; — 6$ или $a — 1 = 1; 2$
Мы получаем $a — 1 = -1 \Leftrightarrow a = 0; a — 1 = -2 \Leftrightarrow$
$a = -1; a — 1 = -3 \Leftrightarrow a = -2; a — 1 = -6 \Leftrightarrow a = -5$
или $a — 1 = 1 \Leftrightarrow a = 2; a — 1 = 2 \Leftrightarrow a = 3$
Тогда $a = -5; -2; -1; 0; 2; 3$ являются решениями задачи.

---

Задача 8 Решите уравнение:
A) $3ax – a = 1 – x$, где a это параметр;
B) $2ax + b = 2 + x$, где a и b являются параметрами

Решение:

A) $3ax + x = 1 + a \Leftrightarrow (3a + 1)x = 1 + a$.

Если $3a + 1 \neq 0$, т.e. $a \neq -11 /3 /3$ , решение есть
$x = \frac{1+a}{3a+1}$
Если $a = -\frac{1}{3}$ уравнение принимает вид $0\cdot x = \frac{1.1}{3}$, что не имеет решения.

B) $2ax – x = 2 – b \Leftrightarrow (2a — 1)x = 2 – b$
Если $2a — 1 \neq 0$, т.e. $a \neq \frac{1}{2}, x = \frac{2-b}{2a-1}$ является решением.
Если $a = \frac{1}{2}$ уравнение принимает вид $0.x = 2 – b$
Тогда, если $b = 2$, любое x является решением, если $b \neq 2$, уравнение не имеет решения.

---

Задача 9 Дано уравнение $6(kx — 6) + 24 = 5kx$ , где к — целое число. Найдите, для каких значений k уравнение:
A) имеет корень $-\frac{4}{3}$
B) не имеет решения;
C) имеет корень как натуральное число.

Решение:

Перепишем уравнение в виде $6kx — 36 + 24 = 5kx \Leftrightarrow kx = 12$

A) Если $x = -\frac{4}{3}$, для k мы получим уравнение $-\frac{4}{3k} = 12 \Leftrightarrow k = — 9$

B) Уравнение $kx = 12$ не имеет решения, когда $k = 0$

C) Когда $k \neq 0$ является корнем $x = \frac{12}{k}$ и это натуральное число, если k есть целым положительным числом, на которое делится 12, т. e. $k = 1, 2, 3, 4, 6, 12$

---

Задача 10 Решите уравнение:
A) $2ax + 1 = x + a$, где a является параметром;
B) $2ax + 1 = x + b$, где a и b являются параметрами.

Решение:

A) $2ax + 1 = x + a \Leftrightarrow 2ax – x = a — 1 \Leftrightarrow$
$(2a — 1)x = a — 1$
Если $2a — 1 \neq 0$, т.e. $a \neq \frac{1}{2}$, единственным решением уравнения является
$x = \frac{a-1}{2a-1}$
Если $2a — 1 = 0$, т.e. $a = \frac{1}{2}$, уравнение принимает вид
$0.x = \frac{1}{2}- 1 \Leftrightarrow 0.x = -\frac{1}{2}$, что не имеет решения

B) $2ax + 1 = x + b \Leftrightarrow$
$2ax – x = b — 1 \Leftrightarrow$

$(2a — 1)x = b — 1$
Если $2a — 1 \neq 0$, т.e. $a \neq \frac{1}{2}$, решением является
$x = \frac{b-1}{2a-1}$
Если $a = \frac{1}{2}$, уравнения эквивалентно $0.x = b — 1$
Если b = 1 любое x является решением, если $b \neq 1$ тогда нет решения.

---

Задача 11 Дано уравнение $3(ax — 4) + 4 = 2ax$, где параметром является целым числом. Найдите, для каких значений a уравнение в качестве корней имеет:
А) $\left(-\frac{2}{3}\right)$
B) целое число
C) натуральное число

Решение:

A) Если $x = -\frac{2}{3}$ есть решением уравнения, тогда должно быть истинным
$3\left[a\left(-\frac{2}{3}\right) — 4\right] + 4 = 2a\left(-\frac{2}{3}\right) \Leftrightarrow$
$-2a — 12 + 4 = -\frac{4a}{3} \Leftrightarrow$
$\frac{4a}{3} — 2a = 8 \Leftrightarrow \frac{4a-6a}{3} = 8 \Leftrightarrow$
$-\frac{2a}{3} = 8 \Leftrightarrow a = -12$

B) $3(ax — 4) + 4 = 2ax \Leftrightarrow 3ax — 2ax = 12 — 4 \Leftrightarrow ax = 8$
Если $a \neq 0$ решением является $x = \frac{8}{a}$, это целое число, если а является делимым числа $8$.
Поэтому; $±2; ±4; ±8$
Если $a=0$, уравнение не имеет решения

C) Чтобы получить натуральное (целое положительное) число для этого решения $x=\frac{8}{a}$ число должно равняться: $a=1, 2, 4, 8$

---

Задача 12 Дано уравнение $2 – x = 2b – 2ax$, где $a$ и $b$ — параметры. Найдите, для каких значений a уравнение имеет решения в виде натурального числа, если $b = 7$

Решение:

В уравнение мы подставляем $b = 7$ и получаем $2 – x = 2.7 — 2ax \Leftrightarrow$
$2ax – x = 14 – 2 \Leftrightarrow (2a — 1)x = 12$
Если $2a -1 \neq 0$, т.e. $a \neq \frac{1}{2}$, уравнение примет вид
$x = \frac{12}{2a-1}$ и это будет натуральное число, если знаменатель $2a — 1$ есть положительным делимым $12$ и кроме того, чтобы оно было целым числом, необходимо, чтобы $2a — 1$ было нечетным числом.

Поэтому $2a — 1$ может быть $1$ или $3$
Из $2a — 1 = 1 \Leftrightarrow 2a = 2 \Leftrightarrow a = 1$ и $2a — 1 = 3$
$\Leftrightarrow 2a = 4 \Leftrightarrow a = 2$

---

Задача 13 Дана функция $f(x) = (3a — 1)x — 2a + 1$, где a — параметр. Найдите, для каких значений a график функции:
А) пересекает ось абсцисс;
B) пересекает ось абсцисс

Решение:

Чтобы график функции пересёк ось абсцисс, необходимо, чтобы
$(3a — 1)\cdot x -2a + 1 = 0$ имело решения и не имело решения для непересечения оси абсцисс.
С уравнения мы получаем $(3a — 1)x = 2a — 1$
Если $3a — 1 \neq 0$, т.e. $a \neq \frac{1}{3}$, уравнение имеет решения
$x = \frac{2a-1}{3a-1}$, поэтому график функции пересекает ось абсцисс.

Если $a = \frac{1}{3}$, мы получаем $0.x = \frac{2}{3} — 1 \Leftrightarrow 0.x = -\frac{1}{3}$, что не имеет решения.
Поэтому, если $a = \frac{1}{3}$, график функций не пересекает ось абсцисс.

---

Задача 14 Решите параметрическое уравнение:
A) $|x -2| = a$
B) $|ax -1| = 3$
C) $|ax — 1| = a — 2$

Решение:

A) Если $a 0$ мы получаем:
$|x — 2| = a \Leftrightarrow x — 2 = a$ или $x — 2 = -a$
Из $x — 2 = a \Rightarrow x = a + 2$, и из
$x — 2 = -a \Rightarrow x = 2 – a$
Если $a = 0$, тогда $x — 2 = 0$ или $x = 2$

B) $|ax — 1| = 3 \Leftrightarrow ax — 1 = 3$ или $ax — 1 = -3$
откуда $ax = 4$ или $ax = — 2$
Если $a \neq 0$ решения: $x = \frac{4}{a}$ or $x = -\frac{2}{a}$
Если $a = 0$, здесь нет решения

C) Если $a — 2 Если $a — 2 > 0$, т. 2 — 4x – 0 \Leftrightarrow x(x — 4) = 0 \Leftrightarrow$
$x = 0$ или $x = 4$
С условием, что $х> 3$, поэтому только $x = 4$ есть решением. Для второго уравнения мы получаем
$ax – x = 1 — 2a \Leftrightarrow (a — 1)x = 1 — 2a$
Если $a — 1 = 0$, здесь нет решения (Почему?), если $a — 1 \neq 0$, i.e. $a \neq 1$, решением есть
$x = \frac{1-2a}{a-1}$ Эти два уравнения будут равны, если $4 = \frac{1-2a}{a-1} \Leftrightarrow$ $4(a — 1) = 1 — 2a \Leftrightarrow 4a + 2a = 1 + 4 \Leftrightarrow 6a = 5 \Leftrightarrow a = \frac{5}{6}$

описание, примеры, решение задач, уравнение прямой в параметрическом виде

Одним из подпунктов темы «Уравнение прямой на плоскости» является вопрос составления параметрических уравнений прямой на плоскости в прямоугольной системе координат. В статье ниже рассматривается принцип составления подобных уравнений при определенных известных данных. Покажем, как от параметрических уравнений переходить к уравнениям иного вида; разберем решение типовых задач.

Вывод параметрических уравнений прямой на плоскости

Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.

Допустим, нам задана прямоугольная система координат Oxy. А также заданы прямая а с указанием лежащей на ней точки М1(x1, y1) и направляющий вектор заданной прямой a→= (ax, ay). Дадим описание заданной прямой a, используя уравнения.

Используем произвольную точку М (x, y) и получим вектор М1М→; вычислим его координаты по координатам точек начала и конца: M1M→=(x-x1, y-y1). Опишем полученное: прямая задана множеством точек М (x, y), проходит через точку М1(x1, y1) и имеет направляющий вектор a→= (ax, ay). Указанное множество задает прямую только тогда, когда векторы M1M→=(x-x1, y-y1) и a→= (ax, ay) являются коллинеарными.

Существует необходимое и достаточное условие коллинеарности векторов, которое в данном случае для векторов M1M→=(x-x1, y-y1) и a→= (ax, ay) возможно записать в виде уравнения:

M1M→=λ·a→, где λ – некоторое действительное число.

Определение 1

Уравнение M1M→=λ·a→ называют векторно-параметрическим уравнением прямой.

В координатной форме оно имеет вид:

M1M→=λ·a→⇔x-x1=λ·axy-y1=λ·ay⇔x=x1+ax·λy=y1+ay·λ

Уравнения полученной системы x=x1+ax·λy=y1+ay·λ носят название параметрических уравнений прямой на плоскости в прямоугольной системе координат. Суть названия в следующем: координаты всех точек прямой возможно определить по параметрическим уравнениям на плоскости вида x=x1+ax·λy=y1+ay·λ при переборе всех действительных значений параметра λ

Составление параметрических уравнений прямой на плоскости

Согласно вышесказанному, параметрические уравнения прямой на плоскости x=x1+ax·λy=y1+ay·λ определяют прямую линию, которая задана в прямоугольной системе координат, проходит через точку М1(x1, y1) и имеет направляющий вектор a→= (ax, ay). Следовательно, если заданы координаты некоторой точки прямой и координаты ее направляющего вектора, то возможно сразу записать параметрические уравнения заданной прямой.

Пример 1

Необходимо составить параметрические уравнения прямой на плоскости в прямоугольной системе координат, если заданы принадлежащая ей точка М1(2, 3) и ее направляющий вектор a→= (3, 1).

Решение

На основе исходных данных получим: x1 = 2, y1 = 3, ax = 3, ay = 1. Параметрические уравнения будут иметь вид:

x=x1+ax·λy=y1+ay·λ⇔x=2+3·λy=3+1·λ⇔x=2+3·λy=3+λ

Наглядно проиллюстрируем:

Ответ:x=2+3·λy=3+λ

Необходимо отметить: если вектор a→=(ax, ay) служит направляющим вектором прямой а, а точки М1(x1, y1) и М2(x2, y2) принадлежат этой прямой, то ее возможно определить, задав параметрическими уравнениями вида: x=x1+ax·λy=y1+ay·λ, а также и таким вариантом: x=x2+ax·λy=y2+ay·λ.

К примеру, нам заданы направляющий вектор прямой a→= (2, -1), а также точки М1(1, -2) и М2 (3, -3), принадлежащие этой прямой. Тогда прямую определяют параметрические уравнения: x=1+2·λy=-2-λ или x=3+2·λy=-3-λ .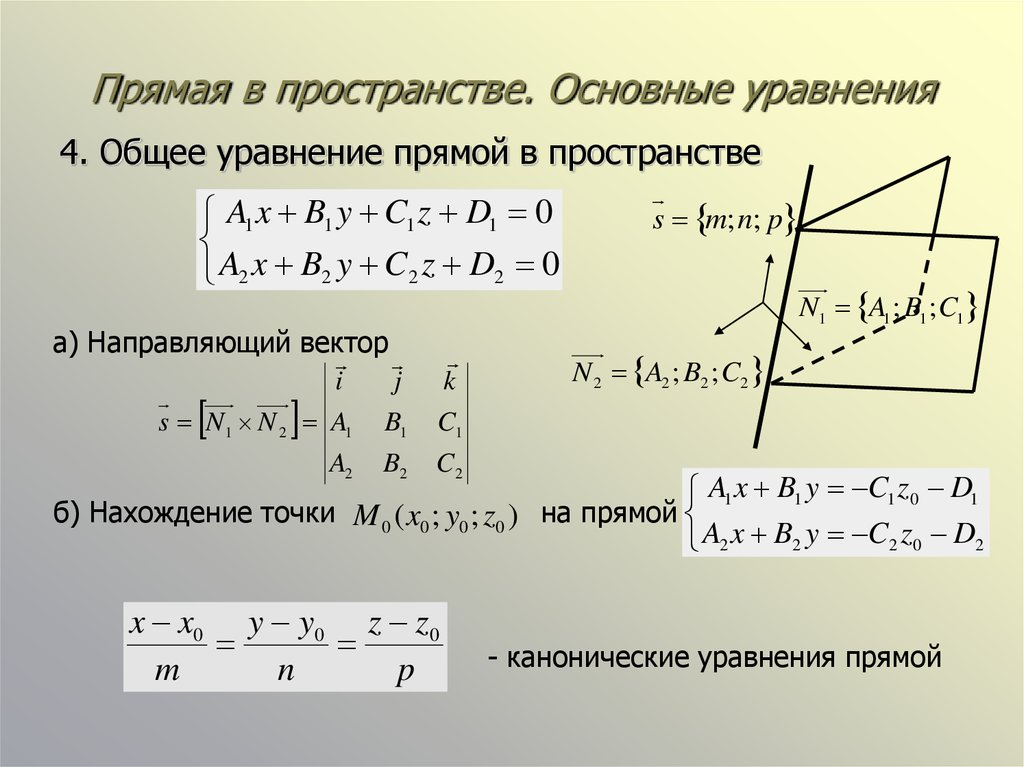

Следует обратить внимание и на такой факт: если a→= (ax, ay) — направляющий вектор прямой a, то ее направляющим вектором будет и любой из векторов μ·a→=(μ·ax, μ·ay), где μ ϵ R, μ≠0 .

Таким образом, прямая а на плоскости в прямоугольной системе координат может быть определена параметрическими уравнениями: x=x1+μ·ax·λy=y1+μ·ay·λ при любом значении μ, отличном от нуля.

Допустим, прямая а задана параметрическими уравнениями x=3+2·λy=-2-5·λ. Тогда a→= (2, -5) — направляющий вектор этой прямой. А также любой из векторов μ·a→=(μ·2, μ·-5)=2μ, -5μ, μ∈R, μ≠0 станет направляющим вектором для заданной прямой. Для наглядности рассмотрим конкретный вектор -2 · a→= (-4, 10), ему соответствует значение μ = -2. В таком случае заданную прямую можно также определить параметрическими уравнениями x=3-4·λy=-2+10·λ.

Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно

В решении некоторых задач применение параметрических уравнений является не самым оптимальным вариантом, тогда возникает необходимость перевода параметрических уравнений прямой в уравнения прямой другого вида. Рассмотрим, как же это сделать.

Параметрическим уравнениям прямой вида x=x1+ax·λy=y1+ay·λ будет соответствовать каноническое уравнение прямой на плоскости x-x1ax=y-y1ay.

Разрешим каждое из параметрических уравнений относительно параметра λ, приравняем правые части полученных равенств и получим каноническое уравнение заданной прямой:

x=x1+ax·λy=y1+ay·λ⇔λ=x-x1axλ=y-y1ay⇔x-x1ax=y-y1ay

При этом не должно смущать, если ax или ay будут равны нулю.

Пример 2

Необходимо осуществить переход от параметрических уравнений прямой x=3y=-2-4·λ к каноническому уравнению.

Решение

Запишем заданные параметрические уравнения в следующем виде: x=3+0·λy=-2-4·λ

Выразим параметр λ в каждом из уравнений: x=3+0·λy=-2-4·λ⇔λ=x-30λ=y+2-4

Приравняем правые части системы уравнений и получим требуемое каноническое уравнение прямой на плоскости:

x-30=y+2-4

Ответ: x-30=y+2-4

В случае, когда необходимо записать уравнение прямой вида Ax+By+C=0, при этом заданы параметрические уравнения прямой на плоскости, необходимо сначала осуществить переход к каноническому уравнению, а затем к общему уравнению прямой. Запишем всю последовательность действий:

x=x1+ax·λy=y1+ay·λ⇔λ=x-x1axλ=y-y1ay⇔x-x1ax=y-y1ay⇔⇔ay·(x-x1)=ax·(y-y1)⇔Ax+By+C=0

Пример 3

Необходимо записать общее уравнение прямой, если заданы определяющие ее параметрические уравнения: x=-1+2·λy=-3·λ

Решение

Для начала осуществим переход к каноническому уравнению:

x=-1+2·λy=-3·λ⇔λ=x+12λ=y-3⇔x+12=y-3

Полученная пропорция идентична равенству -3 · (x + 1) = 2 · y. Раскроем скобки и получим общее уравнение прямой: -3·x+1=2·y⇔3x+2y+3=0.

Ответ: 3x+2y+3=0

Следуя вышеуказанной логике действий, для получения уравнения прямой с угловым коэффициентом, уравнения прямой в отрезках или нормального уравнения прямой необходимо получить общее уравнение прямой, а от него осуществлять дальнейший переход.

Теперь рассмотрим обратное действие: запись параметрических уравнений прямой при другом заданном виде уравнений этой прямой.

Самый простой переход: от канонического уравнения к параметрическим. Пусть задано каноническое уравнение вида: x-x1ax=y-y1ay . Каждое из отношений этого равенства примем равным параметру λ:

x-x1ax=y-y1ay=λ⇔λ=x-x1axλ=y-y1ay

Разрешим полученные уравнения относительно переменных x и y:

x=x1+ax·λy=y1+ay·λ

Пример 4

Необходимо записать параметрические уравнения прямой, если известно каноническое уравнение прямой на плоскости: x-25=y-22

Решение

Приравняем части известного уравнения к параметру λ: x-25=y-22=λ . Из полученного равенства получим параметрические уравнения прямой: x-25=y-22=λ⇔λ=x-25λ=y-25⇔x=2+5·λy=2+2·λ

Ответ: x=2+5·λy=2+2·λ

Когда необходимо осуществить переход к параметрическим уравнениям от заданного общего уравнения прямой, уравнения прямой с угловым коэффициентом или уравнения прямой в отрезках, необходимо исходное уравнение привести к каноническому, а после осуществлять переход к параметрическим уравнениям.

Пример 5

Необходимо записать параметрические уравнения прямой при известном общем уравнении этой прямой: 4x-3y-3=0 .

Решение 

Заданное общее уравнение преобразуем в уравнение канонического вида:

4x-3y-3=0⇔4x=3y+3⇔⇔4x=3y+13⇔x3=y+134

Приравняем обе части равенства к параметру λ и получим требуемые параметрические уравнения прямой:

x3=y+134=λ⇔x3=λy+134=λ⇔x=3·λy=-13+4·λ

Ответ: x=3·λy=-13+4·λ

Примеры и задачи с параметрическими уравнениями прямой на плоскости

Рассмотрим чаще всего встречаемые типы задач с использованием параметрических уравнений прямой на плоскости в прямоугольной системе координат.

1. В задачах первого типа заданы координаты точек, принадлежащих или нет прямой, описанной параметрическими уравнениями.

Решение таких задач опирается на следующий факт: числа (x, y), определяемые из параметрических уравнений x=x1+ax·λy=y1+ay·λ при некотором действительном значении λ, являются координатами точки, принадлежащей прямой, которая описывается этими параметрическими уравнениями.

Пример 6

Необходимо определить координаты точки, которая лежит на прямой, заданной параметрическими уравнениямиx=2-16·λy=-1+2·λ при λ = 3.

Решение 

Подставим в заданные параметрические уравнения известное значение λ = 3 и осуществим вычисление искомых координат: x=2-16·3y=-1+2·3⇔x=112y=5

Ответ: 112, 5

Также возможна следующая задача: пусть задана некоторая точка M0 (x0, y0) на плоскости в прямоугольной системе координат и нужно определить, принадлежит ли эта точка прямой, описываемой параметрическими уравнениями x=x1+ax·λy=y1+ay·λ.

Чтобы решить подобную задачу, необходимо подставить координаты заданной точки в известные параметрические уравнения прямой. Если будет определено, что возможно такое значение параметра λ = λ0, при котором будут верными оба параметрических уравнения, тогда заданная точка является принадлежащей заданной прямой.

Пример 7

Заданы точки М0(4, -2) и N0(-2, 1). Необходимо определить, являются ли они принадлежащими прямой, определенной параметрическими уравнениями x=2·λy=-1-12·λ.

Решение

Подставим координаты точки М0(4, -2) в заданные параметрические уравнения:

4=2·λ-2=-1-12·λ⇔λ=2λ=2⇔λ=2

Делаем вывод, что точка М0 принадлежит заданной прямой, т. к. соответствует значению λ = 2.

Далее по аналогии проверим заданную точку N0(-2, 1), подставив ее координаты в заданные параметрические уравнения:

-2=2·λ1=-1-12·λ⇔λ=-1λ=-4

Очевидно, что не существует такого параметра λ, которому будет соответствовать точка N0. Другими словами, заданная прямая не проходит через точку N0(-2, 1).

Ответ: точка М0 принадлежит заданной прямой; точка N0 не принадлежит заданной прямой.

2. В задачах второго типа требуется составить параметрические уравнения прямой на плоскости в прямоугольной системе координат. Самый простой пример такой задачи (при известных координатах точки прямой и направляющего вектора) был рассмотрен выше. Теперь разберем примеры, в которых сначала нужно найти координаты направляющего вектора, а потом записать параметрические уравнения.

Пример 8

Задана точка M112, 23. Необходимо составить параметрические уравнения прямой, проходящей через эту точку и параллельной прямой x2=y-3-1.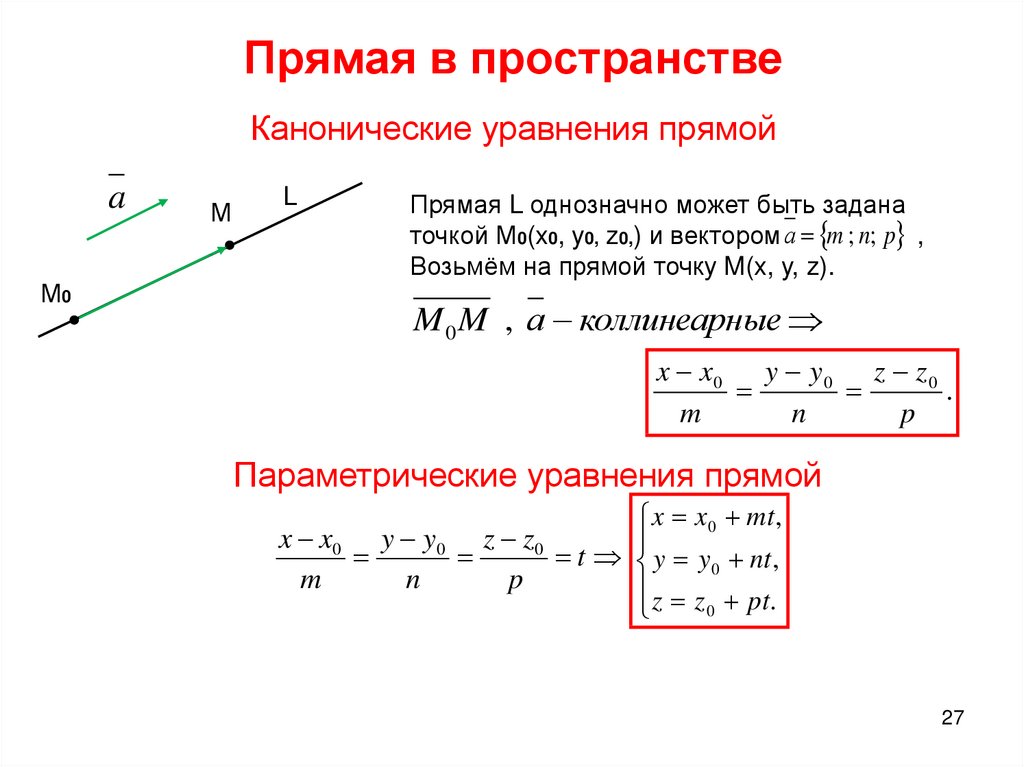

Решение

По условию задачи прямая, уравнение которой нам предстоит опередить, параллельна прямой x2=y-3-1. Тогда в качестве направляющего вектора прямой, проходящей через заданную точку, возможно использовать направляющий вектор прямой x2=y-3-1, который запишем в виде: a→=(2, -1). Теперь известны все необходимые данные для того, чтобы составить искомые параметрические уравнения:

x=x1+ax·λy=y1+ay·λ⇔x=12+2·λy=23+(-1)·λ⇔x=12+x·λy=23-λ

Ответ: x=12+x·λy=23-λ.

Пример 9

Задана точка М1(0, -7). Необходимо записать параметрические уравнения прямой, проходящей через эту точку перпендикулярно прямой 3x – 2y – 5 = 0.

Решение

В качестве направляющего вектора прямой, уравнение которой надо составить, возможно взять нормальный вектор прямой 3x – 2y – 5 = 0. Его координаты (3, -2). Запишем требуемые параметрические уравнения прямой:

x=x1+ax·λy=y1+ay·λ⇔x=0+3·λy=-7+(-2)·λ⇔x=3·λy=-7-2·λ

Ответ: x=3·λy=-7-2·λ

3. В задачах третьего типа требуется осуществить переход от параметрических уравнений заданной прямой к прочим видам уравнений, которые ее определяют. Решение подобных примеров мы рассматривали выше, приведем еще один.

Пример 10

Дана прямая на плоскости в прямоугольной системе координат, определяемая параметрическими уравнениями x=1-34·λy=-1+λ. Необходимо найти координаты какого-либо нормального вектора этой прямой.

Решение

Чтобы определить искомые координаты нормального вектора, осуществим переход от параметрических уравнений к общему уравнению:

x=1-34·λy=-1+λ⇔λ=x-1-34λ=y+11⇔x-1-34=y+11⇔⇔1·x-1=-34·y+1⇔x+34y-14=0

Коэффициенты переменных x и y дают нам требуемые координаты нормального вектора. Таким образом, нормальный вектор прямой x=1-34·λy=-1+λ имеет координаты 1, 34.

Ответ: 1, 34.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

параметрических уравнений | Алгебра и тригонометрия

Цели обучения

В этом разделе вы:

• Параметризация кривой.
• Удалите параметр.
• Найдите уравнение прямоугольной формы для параметрически заданной кривой.
• Найдите параметрические уравнения для кривых, заданных прямоугольными уравнениями.

Рассмотрим путь, по которому следует луна, вращаясь вокруг планеты, которая одновременно вращается вокруг солнца, как показано на (рис.). В любой момент Луна находится в определенном месте относительно планеты. Но как написать и решить уравнение для положения Луны, когда расстояние от планеты, скорость обращения Луны вокруг планеты и скорость вращения вокруг Солнца неизвестны? Мы можем решать только для одной переменной за раз.

. t\right)\,[/latex] где [latex]t[/latex] — независимая переменная времени. Мы можем использовать эти параметрические уравнения в ряде приложений, когда ищем не только конкретное положение, но и направление движения. Когда мы прослеживаем последовательные значения [латекс]\,t,\,[/латекс], ориентация кривой становится ясной. Это одно из основных преимуществ использования параметрических уравнений: мы можем отслеживать движение объекта по пути в зависимости от времени. Мы начнем этот раздел с рассмотрения основных компонентов параметрических уравнений и того, что означает параметризация кривой. Затем мы научимся исключать параметр, переводить уравнения кривой, заданной параметрически, в уравнения прямоугольной формы и находить параметрические уравнения кривых, заданных уравнениями прямоугольной формы.

Параметризация кривой

Когда объект движется по кривой — или по криволинейной траектории — в заданном направлении и в заданное время, положение объекта на плоскости задается координатой x- и y- координата. Однако и [латекс]\,x\,[/латекс] и [латекс]\,у\,[/латекс]
меняются со временем и поэтому являются функциями времени. По этой причине мы добавляем еще одну переменную, параметр, от которого обе [латекс]\,х\,[/латекс] и [латекс]\,у\,[/латекс] являются зависимыми функциями. В примере в начале раздела параметром является время,[латекс]\,t.\,[/латекс][латекс]\,х\,[/латекс]положение луны в момент времени,[латекс]\ ,t,\,[/latex]представляется как функция[latex]\,x\left(t\right),\,[/latex] и [latex]\,y\,[/latex]позиция луна в момент времени,[латекс]\,т,\,[/латекс]представляется как функция[латекс]\,у\влево(т\вправо).\,[/латекс]Вместе,[латекс]\, x\left(t\right)\,[/latex] и [latex]\,y\left(t\right)\,[/latex] называются параметрическими уравнениями и порождают упорядоченную пару[latex]\,\ влево(x\влево(t\вправо),\,y\влево(t\вправо)\вправо).\,[/latex]Параметрические уравнения в первую очередь описывают движение и направление.

При параметризации кривой мы переводим одно уравнение с двумя переменными, например [латекс]\,х\,[/латекс] и [латекс]\,у ,[/латекс] в эквивалентную пару уравнений с тремя переменными,[латекс]\,х,у,\,[/латекс]и[латекс]\,t.\,[/латекс] Одна из причин, по которой мы параметризуем кривую, заключается в том, что параметрические уравнения дают больше информации: в частности, направление движения объекта во времени. {2}}.\,[/latex]Если построить график[latex]\,{y}_{1}\,[/latex] и [латекс]\,{у}_{2}\,[/латекс] вместе, график не пройдет тест вертикальной линии, как показано на (рис.). Таким образом, уравнение для графика окружности не является функцией.

Рисунок 2.

Однако, если бы мы построили график каждого уравнения отдельно, каждое из них прошло бы тест вертикальной линии и, следовательно, представляло бы функцию. В некоторых случаях концепция разбиения уравнения окружности на две функции аналогична концепции создания параметрических уравнений, поскольку мы используем две функции для создания не-функции. Это станет яснее по мере продвижения вперед.

Параметрические уравнения

Предположим, [латекс]\,t\,[/латекс]является числом на интервале,[латекс]\,I.\,[/латекс]Набор упорядоченных пар,[латекс]\, \left(x\left(t\right),\,\,y\left(t\right)\right),\,[/latex],где[латекс]\,x=f\left(t\right) \,[/latex] и [latex]\,y=g\left(t\right),[/latex] образует плоскую кривую на основе параметра[latex]\,t. \,[/latex]Уравнения [latex]\,x=f\left(t\right)\,[/latex] и [latex]\,y=g\left(t\right)\,[/latex] являются параметрическими уравнениями. 9{3}-2 года.[/latex]

Показать решение

Поиск параметрических уравнений, моделирующих заданные критерии ,\left(3,\,-1\right)\,[/latex] в одной плоскости за четыре секунды. Координаты измеряются в метрах. Найдите параметрические уравнения для положения объекта.

Показать раствор

Анализ

Опять же, мы видим, что на (Рисунок)(c), когда параметр представляет время, мы можем указать движение объекта по пути с помощью стрелок.

Исключение параметра

Во многих случаях у нас может быть пара параметрических уравнений, но окажется, что проще нарисовать кривую, если уравнение включает только две переменные, такие как [латекс]\,х\,[/латекс ]and[latex]\,y.\,[/latex]Исключение параметра — это метод, который может облегчить построение графика некоторых кривых. Однако если нас интересует отображение уравнения по времени, то необходимо будет указать и ориентацию кривой. Существуют различные методы исключения параметра[latex]\,t\,[/latex] из набора параметрических уравнений; не каждый метод работает для каждого типа уравнения. Здесь мы рассмотрим методы для наиболее распространенных типов уравнений.

Исключение параметра из полиномиальных, экспоненциальных и логарифмических уравнений

Для полиномиальных, экспоненциальных или логарифмических уравнений, выраженных в виде двух параметрических уравнений, мы выбираем уравнение, которым легче всего манипулировать, и решаем для[латекс]\,t.\, [/latex]Подставляем полученное выражение для[latex]\,t\,[/latex]
во второе уравнение. Это дает одно уравнение в [латекс]\,х\,[/латекс]и[латекс]\,у.\,[/латекс]

Исключение параметра в многочленах 9{2}+1\,[/latex] и [latex]\,y\left(t\right)=2+t,\,[/latex] исключают параметр и записывают параметрические уравнения в виде декартова уравнения.

Показать раствор

Анализ

Это уравнение для параболы, в котором в прямоугольных терминах [латекс]\,х\,[/латекс]зависит от[латекс]\,у.\,[/латекс]От кривой вершина at[latex]\,\left(1,2\right),\,[/latex]граф заметает вправо. См. (Рисунок). В этом разделе мы рассматриваем системы уравнений, заданные функциями [латекс]\,х\влево(т\вправо)\,[/латекс] и [латекс]\,у\влево(т\вправо),\,[ /latex]где[latex]\,t\,[/latex] — независимая переменная времени. Обратите внимание, что и [латекс]\,x\,[/латекс] и [латекс]\,у\,[/латекс] являются функциями времени; так что в целом [латекс]\,у\,[/латекс] не является функцией [латекс]\,х.[/латекс] 9{t},\,\,t>0.\,[/latex]

Показать решение

Анализ

График параметрического уравнения показан на (Рисунок) (a) . Домен ограничен [latex]\,t>0.\,[/latex]Декартово уравнение,[latex]\,y=\frac{3}{x}\,[/latex] показано на (рис. ) (b) и имеет только одно ограничение на домен,[latex]\,x\ne 0. {2}\,[/латекс]в[латекс]\,х>2.[/латекс] 9{2}\hfill \\ y\left(t\right)=\mathrm{ln}\,t\,\,\,\,\,\,\,\,t>0\hfill \end{массив} \end{array}[/latex]

Показать решение

Исключение параметра из тригонометрических уравнений

Исключение параметра из тригонометрических уравнений представляет собой простую замену. Мы можем использовать несколько известных тригонометрических тождеств и теорему Пифагора.

Сначала используем тождества:

[латекс]\begin{array}{l}x\left(t\right)=a\mathrm{cos}\,t\\ y\left(t\right) =b\mathrm{sin}\,t\end{массив}[/latex] 9{2}=1[/latex]

Исключение параметра из пары тригонометрических параметрических уравнений

Исключение параметра из заданной пары тригонометрических уравнений где[latex]\,0\le t\le 2\pi \, [/latex] и нарисуйте график.

[латекс]\begin{array}{l}x\left(t\right)=4\mathrm{cos}\,t\\ y\left(t\right)=3\mathrm{sin}\, t\end{массив}[/latex]

Показать решение

Анализ

Применяя общие уравнения для конических сечений (введенные в аналитической геометрии, мы можем определить [латекс]\,\frac{{x}^{2}}{16}+\frac{{y}^{2 }}{9}=1\,[/latex]в виде эллипса с центром в [латексе]\,\слева(0,0\справа). \,[/латекс]Обратите внимание, что когда[латекс]\,t=0\,[/ латекс]координаты [латекс]\,\влево(4,0\вправо),\,[/латекс] и когда [латекс]\,t=\frac{\pi }{2}\,[/латекс] координаты:[латекс]\,\влево(0,3\вправо).\,[/латекс] Это показывает ориентацию кривой с увеличением значений [латекс]\,t.[/латекс]

Попробуйте

Исключите параметр из заданной пары параметрических уравнений и запишите в виде декартова уравнения: [латекс]\,х\влево(т\вправо)=2\mathrm{cos}\,t\,[/латекс]и[ латекс]\,у\влево(т\вправо)=3\mathrm{sin}\,t.[/латекс]

Показать решение

Нахождение декартовых уравнений из кривых, заданных параметрически

Когда нам дается набор параметрических уравнений и нам нужно найти эквивалентное декартово уравнение, мы, по сути, «исключаем параметр». Однако существуют различные методы, которые мы можем использовать, чтобы переписать набор параметрических уравнений в виде декартова уравнения. Самый простой способ — задать одно уравнение равным параметру, например [латекс]\,x\left(t\right)=t. \,[/latex]В этом случае [латекс]\,y\left( t\right)\,[/latex] может быть любым выражением. Например, рассмотрим следующую пару уравнений. 9{6}.[/latex]

Показать решение

Нахождение параметрических уравнений для кривых, заданных прямоугольными уравнениями

Хотя мы только что показали, что существует только один способ интерпретировать набор параметрических уравнений как прямоугольное уравнение, существует множество способов интерпретировать прямоугольное уравнение как набор параметрических уравнений. уравнения. Любая стратегия, которую мы можем использовать для нахождения параметрических уравнений, действительна, если она приводит к эквивалентности. Другими словами, если мы выберем выражение для представления[латекс]\,х,\,[/латекс], а затем подставим его в [латекс]\,у\,[/латекс]уравнение, и получим тот же график над той же областью, что и прямоугольное уравнение, то система параметрических уравнений верна. Если область определения становится ограниченной в наборе параметрических уравнений, а функция не допускает тех же значений для [латекс]\,х\,[/латекс], что и область определения прямоугольного уравнения, то графики будут другими. 9{2}+1.[/latex]

Показать решение

Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с параметрическими уравнениями.

• Введение в параметрические уравнения
• Преобразование параметрических уравнений в прямоугольную форму

Ключевые понятия

• Параметризация кривой включает преобразование прямоугольного уравнения с двумя переменными, [латекс]\,х\,[/латекс]и[латекс]\,у,\,[/латекс]в два уравнения по трем переменные, x , y и t . Часто больше информации получают из набора параметрических уравнений. См. (Рисунок), (Рисунок) и (Рисунок).
• Иногда уравнения проще представить в виде графика, если они записаны в прямоугольной форме. Путем исключения [латекс]\,t,\,[/латекс] получается уравнение в [латекс]\,х\,[/латекс] и [латекс]\,у\,[/латекс] .
• Чтобы исключить [латекс]\,t,\,[/латекс], решите одно из уравнений для [латекс]\,t,\,[/латекс] и подставьте это выражение во второе уравнение. См. (Рисунок), (Рисунок), (Рисунок) и (Рисунок).
• Нахождение уравнения прямоугольной формы для кривой, заданной параметрически, в основном то же самое, что удаление параметра. Найдите [латекс]\,t\,[/латекс] в одном из уравнений и подставьте это выражение во второе уравнение. См. (Рисунок).
• Существует бесконечное количество способов выбрать набор параметрических уравнений для кривой, определяемой как прямоугольное уравнение.
• Найдите выражение для [латекс]\,х\,[/латекс]такое, чтобы область определения набора параметрических уравнений оставалась такой же, как исходное прямоугольное уравнение. См. (Рисунок).

Раздел Упражнения

Вербальные

Что такое система параметрических уравнений?

Показать раствор

Примерами третьего параметра являются время, длина, скорость и масштаб. Объясните, когда время используется в качестве параметра.

Объясните, как исключить параметр, учитывая набор параметрических уравнений.

Показать раствор

В чем преимущество записи системы параметрических уравнений в виде декартова уравнения?

Какие преимущества дает использование параметрических уравнений?

Показать решение

Почему существует множество наборов параметрических уравнений для представления декартовой функции?

Алгебраический

В следующих упражнениях исключите параметр[latex]\,t\,[/latex], чтобы переписать параметрическое уравнение как декартово уравнение.

[латекс]\{\begin{array}{l}x(t)=5-t\hfill \\ y(t)=8-2t\hfill \end{array}[/latex]

Показать решение

[латекс] \{\ begin {массив} {l} x (t) = 6-3t \ hfill \\ y (t) = 10-t \ hfill \ end {массив} [/latex] 9{3}-2\end{массив}[/latex]

Показать решение

Для следующих упражнений перепишите параметрическое уравнение как декартово уравнение, построив таблицу [latex]x\text{-}y[/latex].

[латекс] \{\ begin {массив} {l} x (t) = 2t-1 \\ y (t) = t + 4 \ end {массив} [/ латекс]

[латекс] \ {\ begin{array}{l}x(t)=4-t\\ y(t)=3t+2\end{array}[/latex]

Показать решение

[латекс] \{\ begin {массив} {l} x (t) = 2t-1 \\ y (t) = 5t \ end {массив} [/ латекс]

[латекс] \ {\ begin { array}{l}x(t)=4t-1\\ y(t)=4t+2\end{массив}[/latex] 9{2}+3[/latex]

[latex]y\left(x\right)=2\mathrm{sin}\,x+1[/latex]

Показать решение

[латекс]x\влево(у\вправо)=3\mathrm{log}\влево(у\вправо)+у[/латекс]

[латекс]x\влево(у\вправо)=\sqrt{ y}+2y[/latex]

Показать решение

Для следующих упражнений параметризуйте (запишите параметрические уравнения) каждое декартово уравнение, используя [латекс]x\left(t\right)=a\mathrm{cos}\,t[/latex] и [латекс]\, y\left(t\right)=b\mathrm{sin}\,t.\,[/latex]Определите кривую. 9{2}=10[/latex]

Показать решение

Параметризовать строку от[латекс]\,\влево(3,0\вправо)\,[/латекс]до[латекс]\,\влево(-2,-5\вправо)\,[/латекс]так что линия находится в [латекс]\,\влево(3,0\вправо)\,[/латекс]в[латекс]\,t=0,\,[/латекс]и в [латекс]\,\влево (-2,-5\right)\,[/latex]at[latex]\,t=1. [/latex]

Параметризовать строку из[latex]\,\left(-1,0\right) \,[/латекс]в[латекс]\,\влево(3,-2\вправо)\,[/латекс]так, чтобы линия была в [латекс]\,\влево(-1,0\вправо)\ ,[/латекс]в[латекс]\,t=0,\,[/латекс]и в[латекс]\,\влево(3,-2\вправо)\,[/латекс]в[латекс]\, т=1.[/латекс]

Показать решение

Параметризовать линию от [латекс]\,\left(-1,5\right)\,[/latex]до [латекс]\,\left(2,3\right)[/latex] так, чтобы линия находится в[латекс]\,\влево(-1,5\вправо)\,[/латекс]в[латекс]\,t=0,\,[/латекс]и в[латекс]\,\влево(2 ,3\right)\,[/latex]at[latex]\,t=1.[/latex]

Параметризовать строку из[latex]\,\left(4,1\right)\,[/latex ]в[латекс]\,\влево(6,-2\вправо)\,[/латекс]так, чтобы линия была в [латекс]\,\влево(4,1\вправо)\,[/латекс]в [латекс]\,t=0,\,[/латекс]и at[латекс]\,\left(6,-2\right)\,[/latex]at[латекс]\,t=1.[/ латекс] 9{2}-4x+4.[/latex]

Показать решение

Глоссарий

параметр

переменная, часто представляющая время, от которого зависят [латекс]\,х\,[/латекс] и [латекс]\,у\,[/латекс]

8.

3 — Параметрические уравнения 8.3 — Параметрические уравнения

В прошлом мы работали с прямоугольными уравнениями, то есть уравнениями, включающими только x и y, чтобы их можно было изобразить в декартовой (прямоугольной) системе координат.

У нас также был пример зависимости высоты свободно падающего тела от времени в секундах t. Эта функция была квадратичной функцией. Если предмет не упал или не был брошен прямо в воздух, также будет горизонтальная составляющая его положения. Горизонтальная составляющая – это простая функция расстояния (d=rt).

Путь падающего предмета

y(t) = -16t ² — v ₀ t + y ₀

x(t) = r t

v

0551 0

= начальная вертикальная скорость

y ₀ = начальная высота

r = горизонтальная скорость

t = время в секундах

Обратите внимание, что обе эти функции, вертикальная высота и горизонтальное расстояние является функцией времени. Итак, чтобы полностью для описания пути объекта нам понадобятся два уравнения. Один для вертикальной составляющей и один для горизонтальной составная часть. Обе эти функции являются функциями третья переменная, t.

Это дает нам параметрические уравнения. Параметр просто независимая переменная в функции.

Рисование плоской кривой

Плоская кривая получается, когда упорядоченные пары ( x(t), y(t) ) отображаются для всех значений t на некотором интервал.

Один из способов нарисовать плоскую кривую — составить таблицу значений. Параметр t имеет несколько значения, перечисленные для него, и соответствующие значения для x(t) и y(t) вычисляются. Затем заказал наносятся пары, а между нанесенными парами рисуется кривая.

Ориентация или направление

При построении плоской кривой «направление увеличения t» или «ориентация» Кривая обозначена маленькими стрелками, указывающими, в каком направлении кривая движется, когда значение параметр t увеличивается.

Графический калькулятор

Графический калькулятор отлично справляется с построением графиков параметрических уравнений. Ты должен, однако скажите калькулятору, что вы хотите отображать параметрические уравнения, а не обычные функции. Для этого переведите калькулятор в параметрический режим, нажав [MODE] и выбрав опцию [PAR]. Обязательно верните калькулятор обратно в [FUN] для функционального режима. когда вы закончите с параметрическими уравнениями. Пока вы находитесь в меню режима, вы можете установите ваш калькулятор в режим [RADIAN] вместо режима [DEGREE]. Они используются для тригонометрические функции, которые мы не будем использовать, но они влияют на то, как клавиши масштабирования работай.

После настройки калькулятора для параметрического режима обратите внимание, что при нажатии клавиши Y= вы не больше есть у ₁ =. Теперь у вас есть пара уравнений, x и y, которые являются функциями от t. Просто введите параметрические уравнения для x и y. Обратите внимание, что ключ, который вы использовали для X также отмечен буквой T. В параметрическом режиме вместо X автоматически появляется буква T.

Настройки окна

Теперь у вас будет три дополнительных окна, которых раньше не было. Tmin, Tmax и Tstep. Tmin — наименьшее значение параметра, которое вы хотите использовать. Если у вас нет веская причина не делать этого (например, домен говорит t >= 0), обязательно используйте отрицательный значения для Tмин. Tmax — это наибольшее значение параметра, который вы хотите использовать. Если у вас нет веских причин не делать этого, используйте положительное значение для Tmax. Другими словами, убедитесь, что T может взять на себя оба положительные и отрицательные значения. Tstep — это изменение T, и оно должно быть разумным. для диапазона значений T вы указали.

TMin = -5, TMax = 5 и TStep = 0,1 обычно являются хорошими начальными значениями. Если вы обнаружите, что график не отображается, вы май необходимость чтобы изменить эти значения.

Внимание! Стандарт масштабирования сбросит настройки на T. Если вы сделаете стандарт масштабирования, ваш T будет находиться в диапазоне от 0 до 2 pi (в радиан) на pi/24 и от 0 до 360 (в режиме градусов) на 7,5. Ни один из них не содержит отрицательных значений и может не отображать все график.

Направление увеличения t — это направление, в котором калькулятор рисует кривую дюймов. Укажите это стрелками направления вдоль кривой.

Исключение параметра

Другой способ создания эскиза плоской кривой — удаление параметра. Шаги по устранению параметр прост.

1. Решите одно из параметрических уравнений для t.
2. Подставить t в другое параметрическое уравнение.

На шаге 1 вы должны найти t в более простом уравнении. Легче решить не всегда означает меньший показатель. Если у вас есть t ² и t ³ , решить для t в t ³ (по возможности). При выполнении таким образом, вы избегаете ситуации плюс/минус, когда берете квадратный корень из t.

Не всегда может потребоваться полное определение t. Это ценно когда один из членов появляется в других уравнениях.

Пример 1

Удалите параметр из x = 3t ² — 4 и y = 2t.

Определенно, функцию y проще решить для t, и когда вы это сделаете, вы получаете t = y/2.

Подставьте это в уравнение x для t, и вы получите x = 3(y/2) ² — 4. Упростите, чтобы получить x = 3/4 y ² — 4.

Пример 2

Рассмотрим систему уравнений x = e ^t и y = e ^3t .

Если бы вам нужно было решить эту проблему, используя шаги, перечисленные выше, вы бы взяли x = e ^t уравнение и решить его для t, чтобы получить t = ln x. Затем замените это в уравнение y = e ^3t , чтобы получить y = e ^{3ln x} . С использованием свойства логарифмов, вы бы переместили 3 в показатель степени x а затем функции e и ln меняются местами, оставляя вас с y = х ³ .

No related posts.