Паскаль задачи с решением: Готовые решения задач на языке Pascal

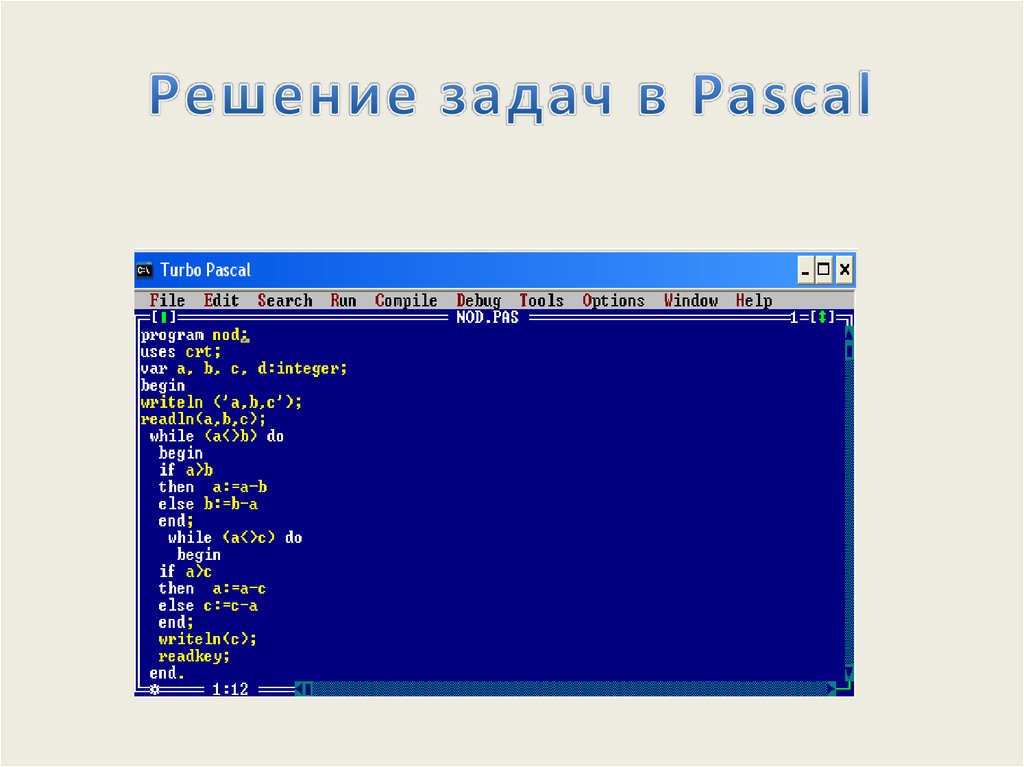
Алгоритмы задач на Паскале , Делфи. — Решение задач на Паскале , Делфи, Лазарусе

Алгоритмы задач на Паскале , Делфи. — Решение задач на Паскале , Делфи, Лазарусе

Перейти к содержимому

Глава 1. Линейные алгоритмы
Задача № 1. Вывести на экран сообщение «Hello World!»
Задача № 2. Вывести на экран три числа в порядке, обратном вводу
Задача № 3. Вывести на экран квадрат введенного числа
Задача № 4. Получить реверсную запись трехзначного числа
Задача № 5. Посчитать количество единичных битов числа
Глава 2. Условные операторы
Задача № 6. Вывести на экран наибольшее из двух чисел
Задача № 7. Вывести на экран наибольшее из трех чисел
Задача № 8. Вывести название дня недели по его номеру
Задача № 9. Проверить, является ли четырехзначное число палиндромом
Задача № 10. Проверить, является ли четырехзначное число счастливым билетом
Задача № 11. Проверить, является ли двоичное представление числа палиндромом
Задача № 12.

Решить квадратное уравнение
Глава 3. Циклы
Задача № 13. Вывести на экран все натуральные числа до заданного
Задача № 14. Найти наибольший нетривиальный делитель натурального числа
Задача № 15. Найти наименьший нетривиальный делитель натурального числа
Задача № 16. Подсчитать общее число делителей натурального числа
Задача № 17. Проверить, является ли заданное натуральное число простым
Задача № 18. Вывести на экран все простые числа до заданного
Задача № 19. Вывести на экран первых n простых чисел
Задача № 20. Проверить, является ли заданное натуральное число совершенным
Задача № 21. Проверить, являются ли два натуральных числа дружественными
Задача № 22. Найти наибольший общий делитель двух натуральных чисел
Задача № 23. Найти наименьшее общее кратное двух натуральных чисел
Задача № 24. Вычислить x в степени n
Задача № 25. Вычислить xn по алгоритму быстрого возведения в степень
Задача № 26. Решить квадратное уравнение заданного вида с параметром
Задача № 27. 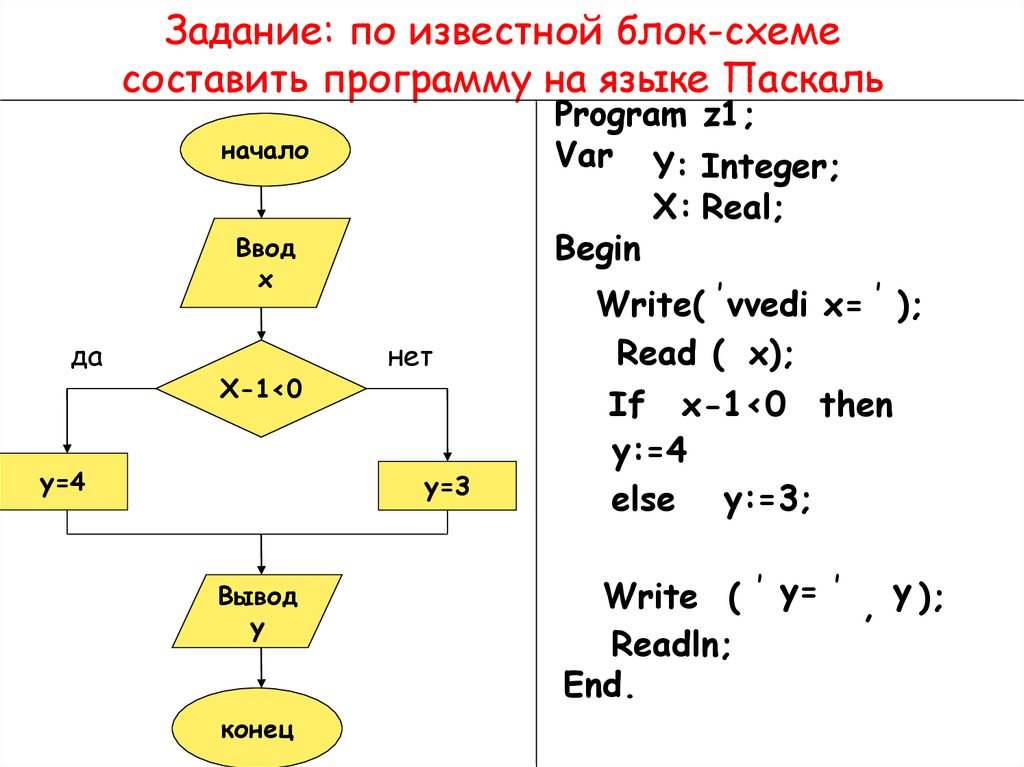Вычислить значение многочлена в точке
Задача № 28. Вычислить факториал
Задача № 29. Вычислить число сочетаний из n по k
Задача № 30. Вывести таблицу квадратов и кубов всех натуральных чисел до n
Задача № 31. Сформировать реверсную запись заданного числа
Задача № 32. Проверить монотонность последовательности цифр числа
Задача № 33. Получить каноническое разложение числа на простые сомножители
Задача № 34. Сформировать число из двух заданных чередованием разрядов
Задача № 35. Вывести на экран x, записанное в системе счисления с основанием n
Задача № 36. Найти наименьший нетривиальный делитель двух заданных чисел
Задача № 37. Проверить, является ли натуральное число счастливым билетом
Задача № 38. Проверить, является ли натуральное число палиндромом
Задача № 39. Проверить, является ли натуральное число степенью двойки
Задача № 40. Вывести на экран произведение четных элементов заданной последовательности натуральных чисел
Задача № 41. Вывести на экран произведение двузначных элементов последовательности натуральных чисел, которые делятся на заданное число
Задача № 42. Найти количество простых членов последовательности
Задача № 43. Проверить, начинается ли каждый из членов последовательности с десятичной цифры, на которую оканчивается предыдущий
Задача № 44. Проверить, является ли последовательность пилообразной
Задача № 45. Проверить, является ли последовательность строго монотонной
Задача № 46. Вывести на экран n-ное число Фибоначчи
Задача № 47. Вывести на экран сумму чисел Фибоначчи до n-ного включительно
Задача № 48. Вывести на экран все числа Фибоначчи до n-ного включительно
Задача № 49. Проверить баланс круглых скобок в символьном выражении
Задача № 50. Вычислить экспоненту с заданной точностью

Базовые задачи на языке Pascal — Школа N61 г.Ульяновска

Сервисы | МинПрос УО | Учебные предметы | Домашнее задание | Программирование | ГИА (ЕГЭ) | Я. Лицей ZooM |

 

• Электронный учебник по языку Pascal
• Основные МАТЕМАТИЧЕСКИЕ функции языка Pascal
• Процедуры и функции языка Pascal для работы со СТРОКАМИ
• Решение 50 типовых задач на Pascal, Душистов
• Программирование для начинающих: Задачи на Pascal

Задача 1
Условие задачи	Программа должна вывести фразу «Bee-Coder».
Применяемые команды, операции, функции:	writeln

Задача 2
Условие задачи	Программа должна вывести фразу, которую пользователь ввел с клавиатуры.
Используемые типы данных	String
Применяемые команды, операции, функции:	readln, writeln

Задача 3
Условие задачи	На любое введенное число пользователя, особенно отрицательное, программа должна вывести его абсолютное значение
Применяемые команды, операции, функции:	readln, writeln, abs

Задача 4
Условие задачи	Программа должна вывести квадрат числа, введенного с клавиатуры пользователем.
Применяемые команды, операции, функции:	readln, writeln, sqr

Задача 5
Условие задачи	Программа должна вывести корень числа, введенного с клавиатуры пользователем.
Применяемые команды, операции, функции:	readln, writeln, sqrt

Тригономические функции ожидают результат в радианах. Для перевода градусов в радианы нужно градусы умножить на число Пи и поделить на 180 градусов. В языке Pascal число Пи так прямо и пишется — Pi.

Задача 6
Условие задачи	Программа должна вывести синус числа, введенного с клавиатуры пользователем.
Применяемые команды, операции, функции:	readln, writeln, sin
Пример программы решающей задачу №6.

Задача 7
Условие задачи	Программа должна вывести косинус числа, введенного с клавиатуры пользователем.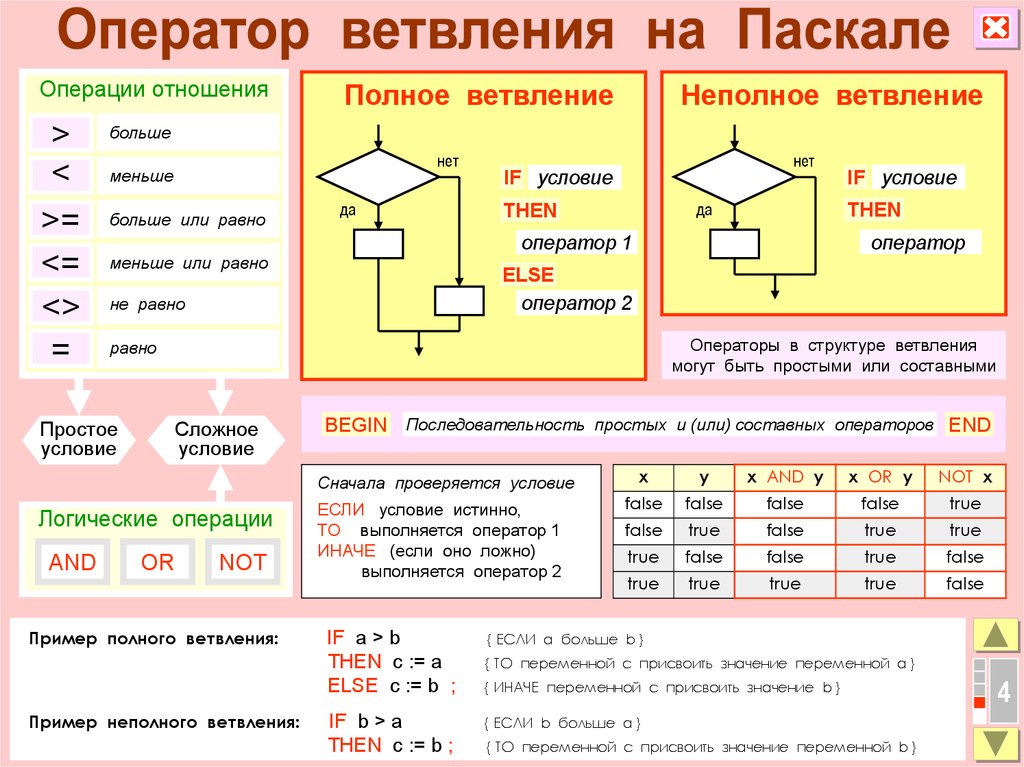
Применяемые команды, операции, функции:	readln, writeln, cos

Задача 8
Условие задачи	Программа должна вывести арктангенс числа, введенного с клавиатуры пользователем.
Применяемые команды, операции, функции:	readln, writeln, arctan

Задача 9
Условие задачи	Программа должна вывести тангенс числа, введенного с клавиатуры пользователем.
Применяемые команды, операции, функции:	readln, writeln, sin, cos

Задача 10
Условие задачи	Программа должна вывести значение экспоненты — число e (e ~ 2. 7182818284590452…) возведенное в степень X. Число X вводится с клавиатуры пользователем.
Применяемые команды, операции, функции:	readln, writeln, exp

Задача 11
Условие задачи	Программа должна вывести число, равное натуральному логарифму от числа X. Число X вводится с клавиатуры пользователем.
Применяемые команды, операции, функции:	readln, writeln, Ln

Задача 12
Условие задачи	Программа должна вывести число, на единицу большее, введенного с клавиатуры пользователем (не используя знаки операций и присвоения).
Применяемые команды, операции, функции:	readln, writeln, inc

Задача 13
Условие задачи	Программа должна вывести число, на единицу меньшее, введенного с клавиатуры пользователем (не используя знаки операций и присвоения).
Применяемые команды, операции, функции:	readln, writeln, dec

Задача 14
Условие задачи	Программа должна вывести случайное число от 0 до 200. Попробуйте выполнить программу несколько раз подряд. Меняется ли случайное число? Попробуйте в программе добавить строчки получения и вывода случайного числа. Попробуйте выполнить программу несколько раз подряд. Меняется ли случайное число?
Применяемые команды, операции, функции:	readln, writeln, random

Задача 15
Условие задачи	Программа должна вывести случайное число от 0 до 200. В код предыдущей программы добавьте новую команду. Попробуйте выполнить программу несколько раз подряд. Меняется ли случайное число?
Применяемые команды, операции, функции:	readln, writeln, random, randomize

Задача 16
Условие задачи	Программа должна вывести случайное число от 100 до 200.
Применяемые команды, операции, функции:	readln, writeln, random, randomize

Задача 17
Условие задачи	Программа должна вывести длину строки введенной пользователем клавиатуры.
Применяемые команды, операции, функции:	readln, writeln, Length

Задача 18
Условие задачи	Программа должна вывести символ по коду, введенному пользователем с клавиатуры.
Применяемые команды, операции, функции:	readln, writeln, chr

Задача 19
Условие задачи	Программа должна вывести цифровой код по символу, введенному пользователем с клавиатуры.
Применяемые команды, операции, функции:	readln, writeln, ord

Задача 20
Условие задачи	Пользователь вводит поочередно две строки. Программа проверяет, является ли первая строка подстрокой второй (является ли первая строка в составе второй). Если да, то вывести с какой позиции первая строка входит во вторую. если нет, то вывести — «Нет совпадений».
Применяемые команды, операции, функции:	readln, writeln, pos

Задача 21
Условие задачи	Программа запрашивает у пользователя 3 слова/строки. Необходимо объединить эти 3 слова/строки без использования знаков операций и присвоения. Программа должна вывести объединенную строку.
Применяемые команды, операции, функции:	readln, writeln, concat

Задача 22
Условие задачи	Программа запрашивает длинное/сложное слово у пользователя. Далее программа вырезает из этого слова с 3-го по 7-ой символ и выводит полученную подстроку на экран.
Применяемые команды, операции, функции:	readln, writeln, copy

Задача 23
Условие задачи	Программа запрашивает длинное/сложное слово или фразу у пользователя. Далее программа вырезает из этого слова или фразы с 5-го по 10-ой символ и выводит оставшуются полученную строку на экран.
Применяемые команды, операции, функции:	readln, writeln, delete

Задача 24
Условие задачи	Программа запрашивает в первой строке фразу у пользователя, далее во второй строке программа запрашивает ещё одно слово. Затем программа вставляет слово из втолрой строки во фразу из первой с 7-го символа и выводит полученную строку на экран.
Применяемые команды, операции, функции:	readln, writeln, insert

• http://uom.mv.ru:3000/
• ГосВэб
• ГосВэб
• Группа Школы 61 ВКонтакте
• Школьный клуб «Гелиос»
• Программирование

Принцип Паскаля — проблемы и решения

от Александра Сан -Лохат

1. Известно:

Площадь ₁ = 10 см ²

Область ₂ = 100 CM ^{2 2}

Сила 2 (F ₂ ) = 100 Newton

Разыскивается: Force 1 (F ₁ )

Решение:

P = F / A

P =

P = 37 давление , F = force , A = area

P ₁ = F ₁ / A ₁
P ₂ = F ₂ / a ₂

P ₁ = P ₂
F ₁ / A ₁ = F ₂ / A ₂

F ₁ /10 CM ^{2   = 100 Н/100 см 2}

F ₁ /10 = 1 N

F ₁ = (10) (1 N)

F ₁ = 10 Newton

[IRP]

2. Если область a ₁ = 0,001 м ² и площадь A ₂ = 0,1 м ² , внешняя входная сила F ₁ = 100 Н, тогда внешняя выходная сила F ₂ ?

Известно:

Площадь А ₁ = 0,001 м ²

Площадь А ₂ = 0,1 м ²

Внешнее входное силу F ₁ = 100 Newton

Разыскивается : Внешний выходной сигнал (F ₂ )

Решение:

P ₁ . = P ₂
F ₁ / A ₁ = F ₂ / A ₂

100 N / 0,001 M ² = F ₂ / 0,1 M ²

100 N / 0,001 = Ф ₂ / 0,1

100 000 n = F ₂ / 0,1

F ₂ = (0,1) (100 000 N)

F ₂ = 10 000 N

[IRP]

3. Вес автомобиля = 16 000 Н. внешняя входная сила F…

Известно:

Масса автомобиля (w) = 16 000 Н

Площадь B (A _B ) = 4000 см ² = 40 10 20 2000 / 10,0012 10 м ² = 0,4 м ²

Площадь A (A _A ) = 50 см ² = 50/1000000 м ² = 0,005 M ²

Разыскивается: FIRCH F

Решение:

F / A _A = W / A _B

F / F / F / F / F / F / F / F / F / F / F / F / F / F / F / F / F / F / F / F / F / A 0,005 М ² = 16 000 Н / 0,4 м ²

F / 0,005 = 16 000 Н / 0,4

F / 0,005 = 40 000 N

F = (40 000 Н) (0,005)

F = 200

4.

Площадь А составляет 60 см ² и площадь В составляет 4 200 см ² , определить внешнюю входную силу F.

Известно :

Площадь A (A _A ) = 60 см ²

см 2

Вес w (W) = 3500 Newton

Разыскивается: F ₁

Решение:

Сила F, рассчитанное с использованием уравнения Принципа Паскаля:

F ₁ / a _{999. 1} = Ф ₂ / А ₂

F ₁ /60 см ² = 3500 Н / 4200 см ²

F ₁ /60 = 35 N / 42

F ₁ = (60) (35). / 42

F ₁ = 2100 / 42

F ₁ = 50 ньютонов

5. Гидравлический подъемник имеет большое поперечное сечение и малое поперечное сечение. Большая площадь поперечного сечения в 20 раз больше малой площади поперечного сечения. Если на малое сечение приложена входная сила 25 Н, то определить выходную силу.

Известно:

Небольшая площадь поперечного сечения (A ₁ ) = A

Большая площадь поперечного сечения (A ₂ ) = 20A

Входная сила (F ₁ ) = 25 N

Требуется: Выходная сила (F ₂ )

Решение:

:

• Состояние Принцип Паскаля
• Описать применение принципа Паскаля
• Вывод соотношений между силами в гидравлической системе

В 1653 году французский философ и ученый Блез Паскаль опубликовал свой «Трактат о равновесии жидкостей» , в котором обсуждал принципы статических жидкостей. Статическая жидкость – это жидкость, которая не находится в движении. Когда жидкость не течет, говорят, что она находится в статическом равновесии. Если жидкостью является вода, мы говорим, что она находится в гидростатическом равновесии. Для жидкости, находящейся в статическом равновесии, результирующая сила, действующая на любую часть жидкости, должна быть равна нулю; иначе жидкость начнет течь.

Наблюдения Паскаля, подтвержденные экспериментально, составляют основу гидравлики, одного из самых важных достижений современной механики. Паскаль заметил, что изменение давления, приложенного к замкнутой жидкости, без уменьшения передается по всей жидкости и на стенки ее сосуда. Из-за этого мы часто знаем о давлении больше, чем о других физических величинах жидкости. Более того, принцип Паскаля подразумевает, что полное давление в жидкости равно сумме давлений различных источников. Хорошим примером является жидкость на глубине, зависит от глубины жидкости и давления атмосферы.

Принцип Паскаля

Принцип Паскаля (также известный как закон Паскаля) гласит, что когда изменение давления воздействует на замкнутую жидкость, оно без уменьшения передается всем частям жидкости и стенкам ее сосуда.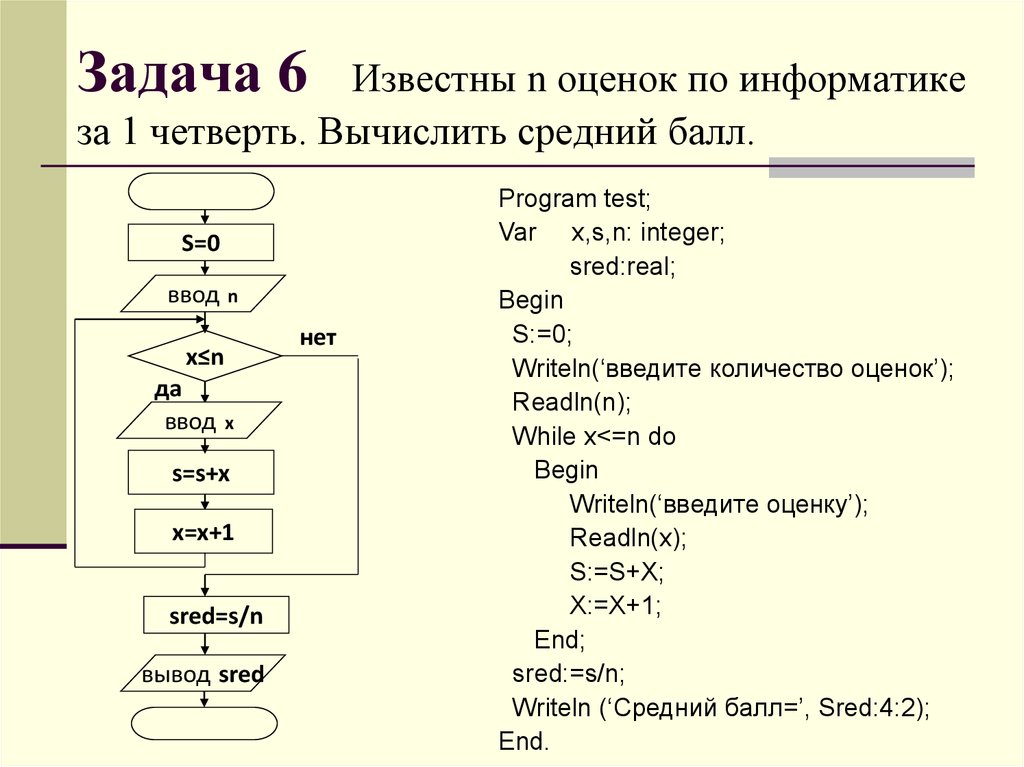 В замкнутой жидкости, поскольку атомы жидкости могут свободно перемещаться, они передают давление на все части жидкости и на стенки сосуда. Любое изменение давления передается в неизменном виде.

Обратите внимание, что этот принцип не утверждает, что давление одинаково во всех точках жидкости, что неверно, поскольку давление в жидкости вблизи Земли меняется с высотой. Скорее, этот принцип относится к изменить по давлению. Предположим, вы поместили немного воды в цилиндрический сосуд высотой х и площадью поперечного сечения х , который имеет подвижный поршень массой м (рис. 14.15). Добавление веса Mg в верхнюю часть поршня увеличивает давление в верхней части на Mg / A , так как дополнительный вес действует и на площадь A крышки:

Δptop=MgA.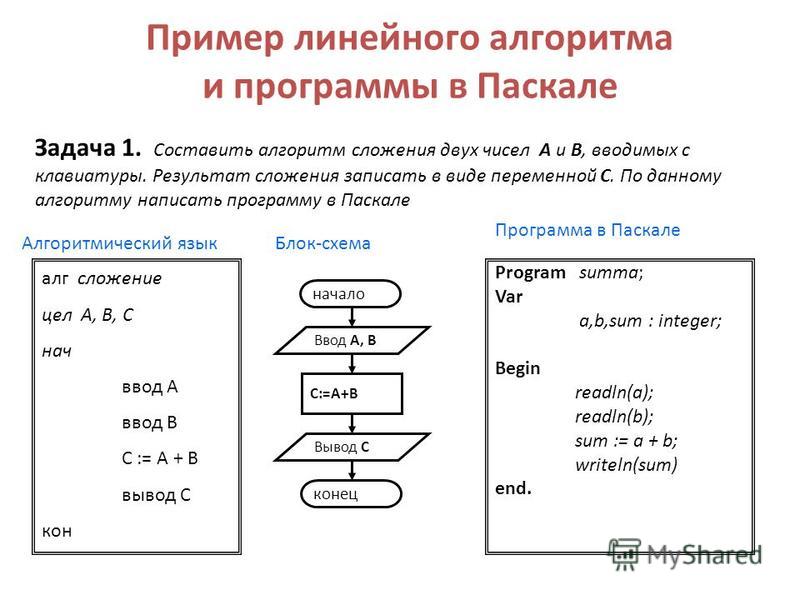 Δptop=MgA.

Рисунок 14.15 Давление в жидкости изменяется при сжатии жидкости. а) Давление в верхнем слое жидкости отличается от давления в нижнем слое. (b) Увеличение давления за счет добавления веса к поршню везде одинаково, например, ptop new-ptop=pbottom new-pbottomptop new-ptop=pbottom new-pbottom.

По закону Паскаля давление во всех точках воды изменяется на одну и ту же величину, Мг / А . Таким образом, давление на дне также увеличивается на Mg / A . Давление на дне сосуда равно сумме атмосферного давления, давления жидкости и давления массы. Изменение давления на дне сосуда из-за массы равно

Δpдно=MgA.Δpдно=MgA.

Поскольку изменения давления везде одинаковы в жидкости, нам больше не нужны нижние индексы для обозначения изменения давления вверху или внизу:

Δp=Δptop=Δpbottom=Δpвезде. Δp=Δptop=Δpbottom=Δpвезде.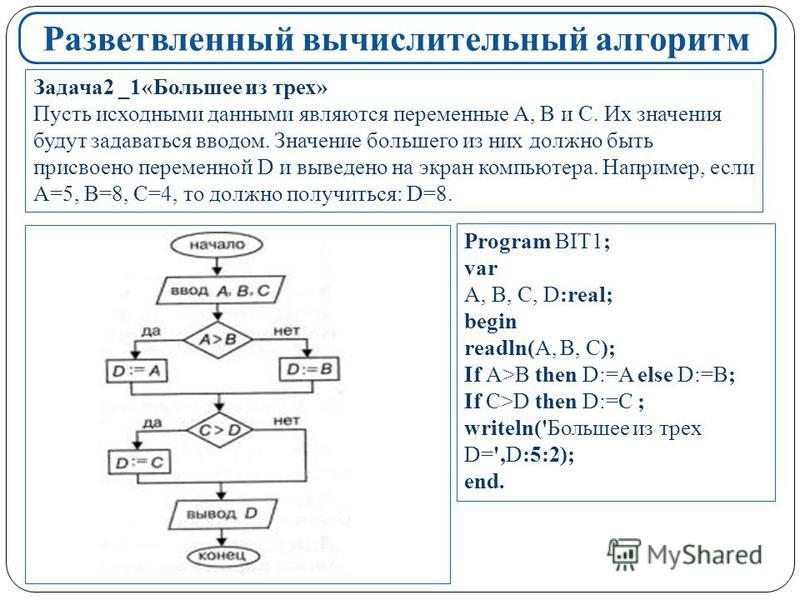

Интерактивный

Бочка Паскаля — отличная демонстрация принципа Паскаля. Посмотрите симуляцию эксперимента Паскаля 1646 года, в котором он продемонстрировал эффекты изменения давления в жидкости.

Применение принципа Паскаля и гидравлических систем

Гидравлические системы используются для управления автомобильными тормозами, гидравлическими домкратами и многими другими механическими системами (рис. 14.16).

Рисунок 14.16 Типичная гидравлическая система с двумя заполненными жидкостью цилиндрами, закрытыми поршнями и соединенными трубкой, называемой гидравлической линией. Направленная вниз сила F→1F→1, действующая на левый поршень, создает изменение давления, которое без уменьшения передается всем частям замкнутой жидкости. Это приводит к тому, что восходящая сила F→2F→2 на правом поршне больше, чем F→1F→1, потому что правый поршень имеет большую площадь поверхности.

Мы можем вывести соотношение между силами в этой простой гидравлической системе, применив принцип Паскаля. Прежде всего обратите внимание, что два поршня в системе находятся на одной высоте, поэтому нет разницы в давлении из-за разницы в глубине. Давление из-за того, что F1F1 действует на площадь A1A1, равно просто

.

p1=F1A1, как определено p=FA.p1=F1A1, как определено p=FA.

Согласно принципу Паскаля, это давление без уменьшения передается по всей жидкости и всем стенкам сосуда. Таким образом, на другом поршне ощущается давление p2p2, равное p1p1. То есть p1=p2.p1=p2. Однако, поскольку p2=F2/A2,p2=F2/A2, мы видим, что

F1A1=F2A2.F1A1=F2A2.

14.12

Это уравнение связывает отношение силы к площади в любой гидравлической системе при условии, что поршни находятся на одной и той же высоте по вертикали и что трением в системе можно пренебречь.

Гидравлические системы могут увеличивать или уменьшать прилагаемое к ним усилие. Чтобы увеличить силу, давление прикладывается к большей площади. Например, если к левому цилиндру на рис.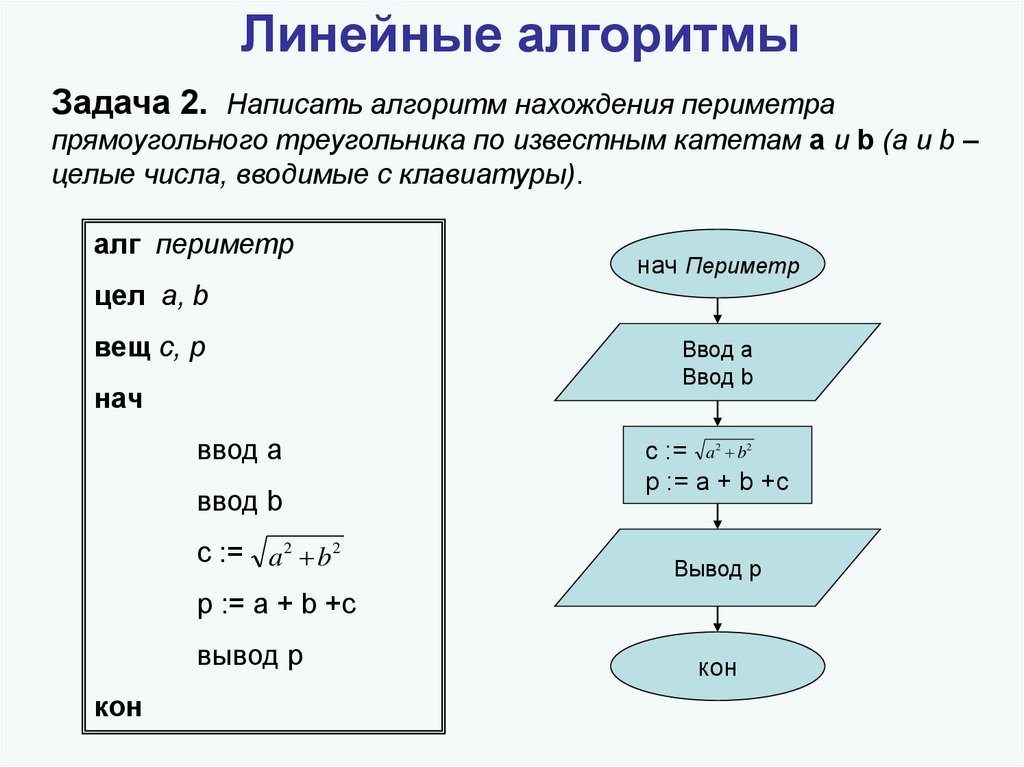 14.16 приложена сила 100 Н, а площадь правого цилиндра в пять раз больше, то выходная сила равна 500 Н. Гидравлические системы аналогичны простым рычагам, но имеют преимущество. что давление может быть направлено по извилистым изогнутым линиям сразу в несколько мест.

Гидравлический домкрат является такой гидравлической системой. Гидравлический домкрат используется для подъема тяжелых грузов, таких как те, которые автомеханики используют для подъема автомобиля. Он состоит из несжимаемой жидкости в U-образной трубке, снабженной подвижным поршнем с каждой стороны. Одна сторона U-образной трубки уже другой. Небольшая сила, приложенная к небольшой площади, может уравновесить гораздо большую силу с другой стороны на большей площади (рис. 14.17).

Рисунок 14.17 (a) Гидравлический домкрат работает за счет приложения сил (F1,F2)(F1,F2) к несжимаемой жидкости в U-образной трубе с использованием подвижного поршня (A1,A2)(A1,A2) с каждой стороны трубы. . (b) Гидравлические домкраты обычно используются автомеханиками для подъема транспортных средств, чтобы можно было выполнять ремонт и техническое обслуживание. (кредит b: модификация работы Джейн Уитни)

Из принципа Паскаля можно показать, что сила, необходимая для подъема автомобиля, меньше веса автомобиля:

Ф1=А1А2Ф2, Ф1=А1А2Ф2,

, где F1F1 — сила, приложенная для подъема автомобиля, A1A1 — площадь поперечного сечения меньшего поршня, A2A2 — площадь поперечного сечения большего поршня, а F2F2 — вес автомобиля.

Пример 14.3

Расчет силы на колесных цилиндрах: Паскаль нажимает на тормоза

Рассмотрим гидравлическую систему автомобиля, показанную на рис. 14.18. Предположим, что к педали тормоза приложено усилие 100 Н, которое действует на педальный цилиндр (выполняющий роль «главного» цилиндра) через рычаг. На цилиндр педали действует сила 500 Н. Давление, создаваемое в педальном цилиндре, передается на четыре колесных цилиндра. Педальный цилиндр имеет диаметр 0,500 см, а каждый колесный цилиндр имеет диаметр 2,50 см. Рассчитайте величину силы F2F2, создаваемой на каждом колесном цилиндре.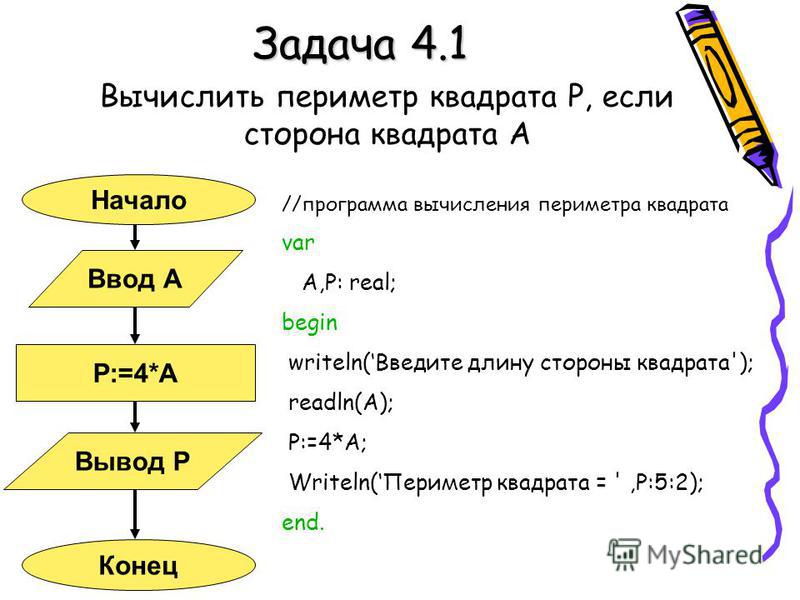

Рисунок 14.18 Гидравлические тормоза используют принцип Паскаля. Водитель нажимает на педаль тормоза, прилагая усилие, которое увеличивается простым рычагом и снова гидравлической системой. Каждый из одинаковых колесных цилиндров получает одинаковое давление и, следовательно, создает одинаковую выходную силу F2F2. Площади круглого поперечного сечения педального и колесного цилиндров обозначены A1A1 и A2A2 соответственно.

Стратегия

Нам дана сила F1F1, приложенная к педальному цилиндру. Площади поперечного сечения A1A1 и A2A2 можно рассчитать по их заданным диаметрам. Тогда мы можем использовать следующее соотношение, чтобы найти силу F2F2:

F1A1=F2A2.F1A1=F2A2.

Обработайте это алгебраически, чтобы получить F2F2 с одной стороны и заменить известные значения.

Решение

Принцип Паскаля, применяемый к гидравлическим системам, записывается как см)2(0,250см)2×500Н=1,25×104Н.

No related posts.