Перевести в дробь 0 2: Б) Выразите обыкновенной дробью: 0,2 кг, 0,6 кг, 0,25 кг, 0,375 кг

4.3.2 Перевод правильных дробей из системы с основанием p  10 в десятичную систему счисления

Единица разряда с номером (–k) у дроби в системе счисления с основанием p = 2^s в десятичной системе счисления равна десятичному числу (2)^–ks = (0,5)^ks. Поэтому перевод дроби, имеющей запись A_p = 0,_–1 …_–k в системе счисления с основанием p = 2^s, в десятичную систему счисления производят по формуле:

A₁₀ = _–1(0,5)^s + … + _–k(0,5)^ks.

Пример 9. Перевести в десятичную систему счисления восьмеричную дробь 0,26₈.

Решение. С учетом того, что 8 = 2³, s = 3 получим:

А₁₀ = 2  (0,5)

³ + 6  (0,5)⁶ = 2  0,125 + 6  0,015625 = 0,25+  0,09375 = 0,34375₁₀.

Ответ:0,26₈ = 0,34375₁₀.

Если основание p не равно степени 2, то перевод дроби в десятичную систему проще осуществлять по следующему общему правилу. Вначале дробную часть представляют в виде единой обыкновенной дроби m/n. Выполняя деление m на n в десятичной системе (любым способом), получаем искомую десятичную дробь. Если она конечна, то найдено точное решение задачи.

Если полученная дробь бесконечная и задана точность, с которой она должна быть определена (число k знаков после запятой), то оставляем (

k + 1) знак в записи дроби, округляем ее, отбрасываем последний знак и получаем искомый ответ.

Если для бесконечной десятичной дроби требуется найти точное выражение, то по ее записи вначале определяют предпериод (постоянную часть после запятой) и период (повторяющуюся часть после предпериода). Точная запись дроби состоит из предпериода и периода, взятого в круглые скобки.

Пример 10. Найти с точностью до 6 знаков после запятой приближенное значение в десятичной системе счисления семеричной (p = 7) дроби 0,165₇.

Решение. Вначале переводим заданную дробь в обыкновенную форму:

0,165₇ = 1 (1 / 7) + 6 (1 / 7)² + 5 

(1 / 7)³ = 96 / 343.

Выполняя деление до седьмого знака после запятой, получим:

96 / 343 = 0,2798833… .

Округляя последний знак, получим искомую приближенную десятичную дробь:

0,2798833  0,279883.

Ответ:cточностью до6знаков после запятой0,165₇  0,279883₁₀.

Пример 11. Для шестеричной (p = 6) дроби 0,31₆ найти в десятичной системе счисления:

1) точное выражение,

2) приближенное значение с точностью до 5 знаков после запятой.

Решение. Вначале переводим заданную дробь в обыкновенную форму:

0,31₆ = 3

 (1 / 6) + 1 (1 / 6)² = 19 / 36.

Выполняя деление, выделяя предпериод и период, получим искомое точное выражение 1) в периодической форме:

19 / 36 = 0,52777777… = 0,52(7).

Приближенное выражение 2) получим, округляя полученную бесконечную дробь до 5 знака после запятой: 0,52777777…  0,52778.

Ответ:1)0,52(7)₁₀, 2) 0,52778₁₀.

4.3.3 Перевод правильных дробей из системы счисления с основанием p = 2^s в двоичную систему счисления

Рассмотрим также “быстрые” правила перевода дробей. Для осуществления данного перевода из основания

p = 2^s в двоичную систему все величины, стоящие в разрядах дроби, заменяют их двоичными записями длины s (со всеми незначащими нулями). Если исходная дробь является периодической, то длина ее периода в двоичной системе счисления может сократиться. Незначащие нули справа в итоговом двоичном представлении можно убрать.

Пример 12. Перевести в двоичную систему счисления правильную конечную дробь, представленную в восьмеричной системе счисления: 0,3076₈.

Решение. 8 = 2³, s = 3. Представляя по очереди цифры дроби их двоичными записями длины s = 3, получим: 3₈ = 011₂, 0₈ = 000₂, 7₈ = 111₂, 6

8 = 110₂.

Соединяя полученные двоичные выражения и отбрасывая незначащий нуль справа, получим искомое выражение.

Ответ:0,3076₈ = 0,01100011111₂.

Пример 13. Перевести в двоичную систему счисления правильную периодическую дробь, представленную в шестнадцатеричной системе счисления: 0,В58(А)₁₆.

Решение. 16 = 2⁴, s = 4. Представляя по очереди цифры постоянной части и периода дроби их двоичными записями длины s = 4, получим:

В₁₆ = 1011₂, 5₁₆ = 0101₂, 8₁₆ = 1000₂,

А₁₆ = 1010₂.

Соединяя полученные двоичные записи, с учетом того, что период в двоичной системе счисления распадается на две одинаковые части, получим: 0,101101011000(10)₂

Ответ:0,В58(А)₁₆ = 0,101101011000(10)₂.

4.3.4 Перевод правильных дробей из двоичной системы счисления в систему с основанием p = 2^s

Перевод производится следующим образом. Начиная со старших разрядов двоичной записи (после запятой), все цифры дроби группируются по s и заменяются цифрами в системе счисления с основанием p = 2^s. Если исходная двоичная дробь является конечной и в последней группе меньше, чем

s знаков, ее справа дополняют незначащими нулями до s цифр. Если исходная двоичная дробь является периодической, ее период повторяется до тех пор, пока не определится период в новой системе счисления.

Пример 14. Перевести в четверичную систему счисления правильную конечную двоичную дробь 0,110110011₂.

Решение. 4 = 2², s = 2. Разбивая дробную часть слева направо по два знака и дополняя в последней группе единицу справа незначащим нулем, переводим полученные в группах двузначные двоичные числа в четверичную систему счисления:

11₂ = 3₄, 01₂ = 1₄, 10₂ = 2₄, 01₂ = 1₄, 10₂ = 2₄.

Записывая слитно полученные цифры дроби, получим: 0,31212₄.

Ответ:0,110110011₂ = 0,31212₄.

Пример 15. Перевести в шестнадцатеричную систему счисления правильную периодическую двоичную дробь 0,110110(011)₂.

Решение. 16 = 2⁴, s = 4.

Разбиваем дробную часть слева направо на группы по 4 знака и переводим двоичные числа в шестнадцатеричную систему счисления. Начиная со второй группы, в них входят цифры из периодов. Их выделим курсивом, начало и конец каждого периода дополнительно показаны скобками. Разбиение на группы и перевод чисел продолжаем до тех пор, пока не получим период в шестнадцатеричной системе счисления, который начинается с группы цифр, образованных периодом двоичного числа:

1101₂ = D₁₆; 10(01₂ = 9₁₆; 1)(011)₂ = В₁₆; (011)(0₂ = 6₁₆; 11)(01₂ = D₁₆; 1)(011)₂ = В₁₆.

Период шестнадцатеричной дроби равен (В6D) Записывая слитно полученные цифры основной части дроби и периодическую часть, получим: 0,D9(В6D)₁₆.

Ответ:0,110110(011)₂ = 

0,D9(В6D)₁₆.

4.3.5 Перевод правильных дробей из системы счисления с основанием p = 2^s в систему с другим основанием, равным степени 2

В общем случае перевод проще производить через двоичную систему счисления. При переводе из шестнадцатеричной системы счисления в четверичную можно использовать связь 4² = 16 и переводить непосредственно пары цифр четверичной записи, отсчитываемые от запятой, в шестнадцатеричные цифры и обратно. В случае периодической дроби период исходной дроби переводится до тех пор, пока не будет найден период искомой дроби.

Пример 16. Перевести в восьмеричную систему счисления правильную периодическую шестнадцатеричную дробь 0,8А9(5Е)₁₆.

Решение. Сначала, используя правило 4.3.3, переводим шестнадцатеричную дробь 0,8А9(5Е)₁₆ в двоичную систему счисления:

8₁₆ = 000₂; А₁₆ = 1010₂; 9₁₆ = 1001₂; 5₁₆ = 0101₂; Е₁₆ = 1110₂;

0,8А9(5Е)₁₆ = 0,100010101001(01011110)₂.

Затем по правилу 4.3.4 переводим полученную двоичную дробь в восьмеричную систему счисления (курсивом выделены цифры, которые взяты из периода, начало и конец каждого периода показаны скобками):

100₂ = 4₈; 010₂ = 2₈; 101₂ = 5₈; 001₂ = 1₈; (010₂ = 2₈; 111₂ = 7₈; 10)(0₂ = 4₈; 101₂ = 5₈; 111₂ = 7₈; 0)(01₂ = 1₈; 011₂ = 3₈; 110)₂ = 6₈; (010₂ = 2₈.

Период восьмеричной дроби найден и равен (27457136). Записывая слитно полученные цифры основной части дроби и периодическую часть, получим: 0,4251(27457136)₈.

Ответ:0,8А9(5Е)₁₆ = 0,4251(27457136)₈.

Пример 17. Перевести в шестнадцатеричную систему счисления из четверичной правильную периодическую дробь 0,2031223(21303)₄.

Решение. По упрощенному способу перевода из системы счисления с основанием p = 4 в шестнадцатеричную систему счисления (правило 4.3.5) сначала переводим пары цифр постоянной части дроби, отсчитывая их от запятой, затем переводим цифры из периода столько раз, чтобы определить период в искомой шестнадцатеричной записи (курсивом выделены цифры, которые взяты из периода, начало и конец каждого периода показаны скобками):

20₄ = 8₁₆; 31₄ = D₁₆; 22₄ = A₁₆; 3(2₄ = E₁₆; 13₄ = 7₁₆; 03)₄ = 3₁₆; (21₄ = 9₁₆; 30₄ = C₁₆; 3)(2₄ = E₁₆.

Период восьмеричной дроби найден и равен (E739C). Записывая слитно полученные цифры основной части дроби и периодическую часть, получим: 0,8DA(E739C)₁₆.

Ответ:0,2031223(21303)₄ = 0,8DA(E739C)₁₆.

Число, содержащее целую и дробную части, называют смешанным. Для его перевода из одной системы в другую отдельно переводят целую часть, отдельно – дробную.

Пример 18. Перевести в шестнадцатеричную систему счисления из десятичной смешанное число 7069,2089₁₀. Ответ дать с точностью до 5 знаков после запятой.

Решение. 1. Сначала по правилу 4.2.2 переводим целую часть числа из десятичной системы счисления в шестнадцатеричную путем последовательного деления десятичной записи на 16. При этом остатки от деления на каждом шаге и самое последнее частное образуют искомую шестнадцатеричную запись числа в обратном порядке.

7069  16

7056  441  16

13 432  27  16

9 16  1

11

Переводя значения в разрядах в шестнадцатеричную систему счисления и записывая их в обратном порядке, получим: 7069₁₀ = 1B9D₁₆.

2. Затем по правилу 2.2.1 переводим дробную часть десятичной записи в шестнадцатеричную систему счисления путем последовательного умножения исходной дроби на 16. Поскольку необходимо найти 6 знаков после запятой, умножение выполняем 6 раз.

0,2089 0,3424 0,4784 0,6544 0,4704 0,5264

 16  16  16  16  16  16

3,3424 5,4784 7,6544 10,4704 7,5264 8,4224

Переводя значения в разрядах в шестнадцатеричную систему счисления и выполняя округление, получим: 0,2089₁₀  0,357А78₁₆  0,357А8₁₆.

Объединяя целую и дробную части, получим: 1B9D,357А8₁₆.

Ответ:7069,2089₁₀  1B9D,357А8₁₆.

Вопросы для проверки знаний.

1. Какие дроби называют правильными?

2. Какие дроби называют обыкновенными?

3. Какие дроби называют рациональными, а какие ‑ иррациональными?

4. Что называют предпериодом записи рациональной дроби в позиционной системе счисления?

5. Что называют периодом дроби в позиционной системе счисления и как его выделяют в записи?

6. Чем отличаются записи рациональных дробей от записей иррациональных дробей в позиционных системах счисления?

7. Может ли иррациональная дробь иметь конечную запись?

8. Что называют смешанным числом?

Практические задания.

1. Перевести дробь 0,32₁₀ в систему счисления с основанием 3 с точностью до 5 знаков после запятой.

2. Перевести дробь 0,7₉ в десятичную систему счисления

3. Перевести дробь 0,46₇ в десятичную систему счисления. Ответ дать с точностью до 6 знаков после запятой.

Дневник Балдура Вильям Рекуотер #10 — Игры на DTF

169 просмотров

Что же, у нас появилась новая цель, лагерь бандитов в захудалом лесу, где нам, возможно разъяснят что всё-таки происходит на Побережье Меча с железом. А пока, нас снова увлекла дорога. Жители шахтёрского городка, после всех событий, сшили мне новую мантию, сапоги, и вручили красивый, инкрустированный камнем посох. Он довольно тяжелый, с красивыми рисунками нашей компании на древке, а камень похож на бриллиант, только чуть больше. Он может поднимать небольшие предметы в воздух, и освещать дорогу ночью. После всей этой резни, мы сдружились, и теперь весело болтаем о всяких мелочах по дороге, шутим, иногда смеемся. Наш путь довольно долгий, он проходит по нескольким долинам и лесным чащам. Иногда мне кажется, что здесь ничего кроме леса нет. Дорога на удивление шла спокойно, иногда мы выходили на чистую дорогу, но чаще, пробирались сквозь густую, лесную чащу, которая встречала нас из раза в раз одинаково. Я даже заскучал, и на протяжении пары дней не знал чем заняться, пока наконец мне не пришло в голову порадовать Имоен. Ведь я знал, что это лишь небольшая передышка перед ещё большим боем, и такие дни мы должны проводить вместе. Так что я начал действовать.

Кое-как я насобирал небольшой букет лесных цветов, ромашек, пион, пары роз. Завернул в не самый красивый пергамент завалявшейся у меня в сумке, и перевязал всё это обычной веревкой. На мой взгляд вышло довольно убого, и я ругал себя, ведь мог сделать это куда лучше пока мы лежали в городе. Помимо букета, я еле-еле упросил Джахейру приготовить нам небольшую порцию сидра, взяв с нее обет молчания, а Рассада заболтал на пару крупных рыбин, водившееся в изобилии недалеко в речке, где мы разбили лагерь. Мне потребовалось всё мужество, чтобы заговорить с Дорном. Он сделал для нас небольшой стол из поваленного дерева и два стула из его крупных веток. Всё проделанное было его мечом. Он делал всё это, потому что был в некоторой степени благодарен мне за тот бой, а после, сказал чтобы с такими просьбами я к нему больше не подходил, ведь подобные вещи недостойные настоящего воина и не для этого он становился сильнее и бла-бла-бла.

Когда всё приготовления были закончены, я оценил проделанною работу. Мы с Имоен будем сидеть и подножья небольшого холма возле реки, за столом с жареной рыбой, и несколькими кружками сидра. Место было красивое, тихое, нарушали приватность лишь забредшие кролики или лани, пришедшие напиться воды. Когда я нашел Имоен, она, как всегда, была далеко впереди отряда для разветки, то нашел ее сидевшую на земле. Она упиралась руками в землю, глубоко дыша, конечно она заметила меня за долго моего появления, и изобразила приятное удивление, хотя по началу забеспокоилась, думая что что-то случилось. Я заверил ее что все нормально, и поманил к себе. При виде букета, наспех сколоченного мной, она разрыдалась и крепко обняла меня. Мы стояли так долго, просто молчали и вдыхали запахи леса, ее волосы пахли свежей травой. Она, полагая что на этом всё и закончиться хотела было поцеловать меня, но и тут я ее оборвал, сказав что впереди нас ждёт сюрприз. Когда мы с ней вернулись в лагерь, никого не было, и мы без задержки прошли к тому месту, что я готовил с друзьями. Я знал что они не ушли далеко, а лишь наблюдают с почтительного расстояния. Дальше было только лучше, мы ели, смеялись, вспоминали старые моменты из такой далекой жизни в замке. Сидр оказался отвратительным, хотя Имоен он даже очень понравился. Когда мы сидели за столом, я про себя заметил насколько Имоен живая, как она часто жестикулирует когда, рассказывает про что-то. Ее улыбчивые глаза смотрели с нежностью и восторгом на меня, а неподстриженные волосы, заплетенные в несколько длинных кос придавали особой женственности каждому повороты головы. Так продолжалось до поздней ночи, пока вся рыба не была съедена, а истории не рассказаны.

Мы оба лежали на влажной траве, взирая на звездное небо, огромные созвездия подмигивали нам, а мошкара вокруг впивалась в нас с невероятной силой, но ничего не могло нам испортить настроение.

• Скажи, Вильям, что это было в пещере? — Ее глаза смотрели на меня, пытаясь найти ответ, я был настолько заворожён этим взглядом, что не сразу сообразил что мы начали говорить.

• Я…я не знаю, некая сила, но не обычная магия. Я просто попросил, нет, я хотел, и оно пришло. — Говоря это, я невольно вспомнил всю боль обрушившеюся на меня тогда, по телу сразу пробежала слабая дрожь, как если бы я замерз.

• Я не многое увидела, лишь несколько секунд…но ты показался тогда чем-то…не человеческим. — Что она хотела узнать от меня? На такие вопросы я и сам не знал ответы.

• Пока не знаю как контролировать эту силу, возможно мы найдём ответы в путешествии, возможно нет, в любом случае я рад, что она у меня, раз я смог вас спасти, смогу и снова. — Сейчас я лгал, я не думал что у меня выйдет возвать к ней еще раз намеренно. Мне так не хотелось продолжать эту тему, я хотел наслаждаться вечером. — Послушай, может поговорим об этом в другой раз? Такие вечера редкость, давай запомним его? — Она улыбнулась и кивнула мне, а потом крепко поцеловала, от чего я потерял голову.

Следующее три дня я провел, как бы странно не звучала, пытаясь нащупать ту самую связь в пещере. Я решил тогда что обуздаю ее, и неважно насколько сложно это будет. Но ничего не выходило к каким бы способам я не прибегал бы. Возможно всё было в критической ситуации, когда от смерти меня отделял один хороший удар. Для начала я медитировал, некоторые из библиотекарей в замке промышляли таким, а я глумился над ними. Но, во-первых, я не знал как делать правильно, что для этого нужно. И каждый раз закрывая глаза, пытаясь успокоить свои мысли, мне постоянно что-то мешало, какое-то зудящее чувство, будто через стену от меня забивают гвоздь, но звук был глухой. Я мог, например думать о Имоен, детстве или других мелочах, но как только прикасался, как я думал к той силе, звук становился громче, причиняя боль. Меня здорово напугал тот факт, что в моём сознании есть места, куда я не могу добраться, но я списал всё на усталость и неопытность в таких делах. Возможно стоит поискать лекаря, или целителя. После пары неудачных медиаций, ко мне подошел Дорн. Он сказал что слышит исходящий о меня шепот, но не знает кто его издаёт, я объяснил ему чего я пытаюсь добиться, на что он нахмурился и выдвинул свою теорию.

• Скорее всего, ты вместилище чего-то большего, когда мы встретились, я ощутил дремлющую мощь внутри тебя, она древняя и опасная, наверное передалась от предка. Советую тебе однажды отдаться ей, и если не умрёшь, тогда обретешь власть над ней, таков закон силы.

Что ещё мог сказать Чёрный страж простому магу? Но я не отчаиваюсь, думаю такие вещи не сразу открывают все свои тайны. Раны уже затянулись, тело заново слушается. Вновь я перечитываю книгу заклинаний, практикуюсь на деревьях, ловлю неодобрительный взгляд Джахейры и продолжаю. Нам остался день до лагеря бандитов. В этот раз я буду готов к любым неожиданностям. Забавно, я даже немного предвкушаю будущую схватку, смотрю как Рассад в очередной раз разминается, а Дорн повторяет взмах мечом и во мне крепнет уверенность.

Дневник Врат Балдура Вильям Рекуотер # 9 Шахты Нашкеля Глава 2

Поддержать автора золотым — 5168742293492295

Ух ребята, даже не знаю ждал ли кто-то это вот всё, в последние недели писать совсем не хотелось. Поймал себя в очень плохом состоянии духа. Но по чуть-чуть выбираюсь из состояния анабиоза. Эта штука всё-таки задумывалась как большая работа на многие месяца чисто по фану. Никаких особых целей я не преследовал. Надеюсь у вас с вдохновением лучше! Дальше текста, к сожалению, или к счастью будут больше, так как публиковать такие маленькие огрызки мне не нравиться.

3-7-дробные слова в словах — Googlesuche Произведенный результат в словах равен трем седьмым.

Калькулятор дробей — вычисление 3/7 ?

Как сказать 3 4 по-английски?

Как написать дробь 3/8 в слове?

Как написать 3/7 словами — Калькулятор дробей

thefractioncalculator.com › WriteFractionsInWords

Дробь типа 3/7 означает, что 3 делится на 7, поэтому можно сказать: три разделить на семь. Другой распространенный способ написания и произнесения 3/7: три на семь. Однако …

Как писать дроби в словах | Наука

sciencing.com › Математика › Арифметика › Дроби

13.03.2018 · В словесной форме дробь 3/10 будет записана как три десятых. … Например, вы бы написали 11/7 как одиннадцать седьмых, а 61/3 как …

Урок 2 — Запись дробей в виде слов — (5-й класс математики) — YouTube

www.youtube. com › часы

03.04.2016 · Это всего несколько минут полного курса. Все уроки и другие предметы можно получить по адресу: http://www …
Dauer: 4:01
Прислан: 03.04.2016

В. Как вводить дроби в Microsoft Word? — Ответы библиотеки

libanswers.walsh.edu › faq

Перейдите на вкладку меню «Вид» в MS Word и выберите «Панели инструментов», затем … Все еще не могу написать дробь 3/16, 7/32 или 15/64 маленькими буквами. печатать как дробь …

Как печатать дроби в Microsoft Word | Советы по написанию Proofed

proofed.com › советы по написанию › как печатать дроби-i…

01.08.2020 · Ввод дробей как обычного текста в одну строку. · Использование предварительно отформатированных дробных символов. · Создание дроби с использованием косой черты деления дроби …

[PDF] Выражение дробей словами

www.nflcacademy.com › загрузки › дроби-словами-1

1-10 93 86 79 71 64 57 50 43 36 29. 11-14 71 2 0. пр.). 1). 2). 3) … Напишите заштрихованную сумму в словесной форме. Выражение дробей словами.

ii. Написание дробей в словесной форме — Математика мистера Мэнли — Сайты Google

site. google.com › site › mrmanleysmath › ii-writing…

две четверти, три четверти, две восьмых, шесть восьмых, девять десятых. Как вы думаете, почему в конце каждого примера, показанного здесь, стоит буква «s» …

3 × 2 7 × 2 = 614 Вот полный список дробей, эквивалентных 37. 37 10. Наименее приветливые 7 словечек. В разделе «Уравнения» выберите «Автоматически преобразовывать …»

Напишите следующие дроби словами. (i) 27 (ii) 310 (iii) 1528 — Toppr

www.toppr.com › задавайте › вопрос › пишите далее…

(i)72​=Two−Seventh (ii)103 ​=три-десятый (iii)2815​=пятнадцать-двадцать восьмой. Этот ответ был полезен? голос «за» 0. голос «против» 0. Подобные вопросы отмечены звездами …

Ähnlichesuchanfragen

7/2 прописью

5/6 дробь прописью

Преобразователь дробей в пропись

5/8 прописью

3/9 прописью

3 10 40 прописью

3/8 6 прописью

4/5 прописью

Конвертер двоичных дробей

Создано Davide Borchia

Отзыв от Anna Szczepanek, PhD и Rijk de Wet

Последнее обновление: 03 ноября 2022 г. 7

Binary 901 представительство

Что такое двоичная дробь?

Как преобразовать дроби в двоичные

Преобразование двоичных дробей в десятичные

Ограничения двоичных дробей

Как использовать наш преобразователь двоичных дробей?

Помимо нулей и единиц

Часто задаваемые вопросы

Преобразование целых чисел в двоичные числа очень просто; как насчет преобразования десятичной части? Узнайте, как это сделать, с помощью нашего конвертера двоичных дробей.

Узнайте больше о своем компьютере вместе с нами. Здесь мы научим вас:

• Что такое двоичная дробь .
• Где мы используем двоичные дроби.
• Ограничения компьютера и влияние на округление.
• Как преобразовать десятичную дробь в двоичную дробь и наоборот.
• Как пользоваться нашим конвертером двоичных дробей — это просто, поверьте нам!

Двоичное представление

Компьютеры мыслят единицами и нулями — это двоичный код, и он повсюду.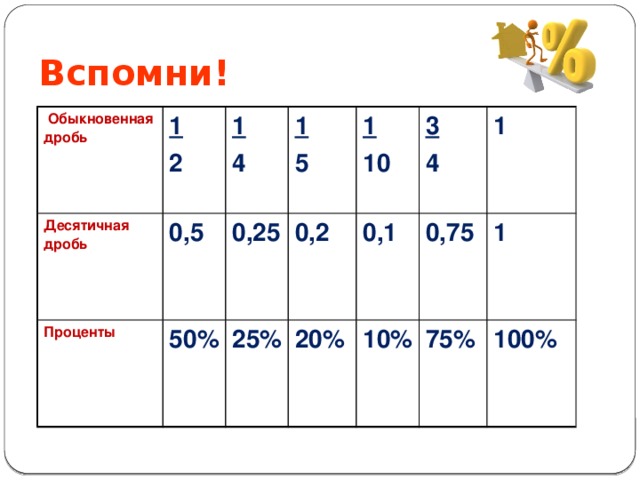 Загляните за этот преобразователь, и вы увидите много таких цифр!

Преобразование целых чисел с основанием 10 (десятичное) в основание 2 (двоичное) выполняется легко и не приводит к ошибкам. То же самое верно, когда вы рассматриваете число, записанное в позиционной записи (когда вы указываете позицию цифры в числе). Мы не можем сказать то же самое о десятичных числах, как если бы вы написали их на листе бумаги, например, 0,420.420,42 и 0,33333333…0,33333333…0,33333333….

💡 Если вы хотите научиться конвертировать целые числа от основания 101010 до основания 222, перейдите к нашему десятично-двоичному калькулятору! Вы просите другие базы? Мы вас поняли: попробуйте конвертер из двоичного кода в шестнадцатеричный или из двоичного в восьмеричный. Омни есть все!

Что такое двоичная дробь?

Взять десятичную часть нецелого числа. Это правильная дробь — ее значение меньше единицы. Когда знаменатель представляет собой степень числа десять (101010, 100100100, 100010001000,. ..), мы говорим о десятичных дробях .

1371000=0,137\frac{137}{1000}=0,1371000137​=0,137

Представление таких значений в базе 2 дает нам двоичных дробей !

Как преобразовать дроби в двоичные числа

Преобразование десятичной дроби в двоичную не так сложно. Возьмем любую десятичную дробь: мы выбрали 0,29120,29120,2912. Убедитесь, что целая часть равна 000.

Теперь умножьте на два и посмотрите, что получится.

0,2912×2=0,58240,2912\times 2 = 0,58240,2912×2=0,5824

Целая часть осталась 000: это первый элемент двоичной дроби, 0,0…0,0…0,0… , Повторите шаг; на этот раз мы увидим нечто иное.

0,5824×2=1,16480,5824\умножить на 2 =1,16480,5824×2=1,1648

Целая часть теперь равна 111: второй элемент нашей двоичной дроби будет 111: 0,01…0,01…0,01….

Удалите целую часть (вычтите 111) и повторите шаги снова и очередной раз; ваша бинарная фракция будет расти!

0,1684 × 2 = 0,3368 → 0,0100,3368 × 2 = 0,6736 → 0,01000,6736 × 2 = 1,3472 → 0,01001–10,3472 × 2 = 0,6944 → 0,0100100. 6944 × 2 = 1,388888888 → 0,6944 → 0,0100100,6944 × 2 = 1,38888888 → 0,6944 → 0,0100100,6944 × 2 = 1,3888888 → 0,6944 → 0,0100100,6944 × 2,388888 → 0,6944 → 0,0100100,6944 × 2 = 0,6944 → 0,0100100, стрелка вправо \textcolor{красный}{0,010}\\ \footnotesize 0,3368\times 2=0,6736 \rightarrow \textcolor{red}{0,0100}\\ \footnotesize 0,6736\times 2=1,3472 \rightarrow \textcolor{red}{0,01001} \\ \textcolor{синий}{-1}\\ \размер сноски 0,3472\умножить на 2 = 0,6944 \rightarrow \textcolor{red}{0,010010} \\ \footnotesize 0,6944\times 2 = 1,3888 \rightarrow \textcolor{red}{0,0100101} \\0,1684×2=0,3368→0,0100,3368×2=0,6736→0,01000,6736×2=1,3472→0,01001−10,3472×4=0,694 0,0100100,6944×2=1,3888→0,0100101

Подождите!

0,3888 × 2 = 0,7776 → 0,010010100,7776 × 2 = 1,5552 → 0,010010101110,5552 × 2 = 1,1104 → 0,01001010111104 × 2 = 0,2208 → 0,0100101011011011111104 × 2 = 0,2208 → 0,01001010101101111111110, }\\ \footnotesize 0,7776\times 2=1,5552 \rightarrow \textcolor{red}{0,010010101}\\ \textcolor{синий}{-1}\\ \footnotesize 0,5552\times 2=1,1104 \rightarrow \textcolor{red}{0,0100101011} \\ \textcolor{синий}{-1}\\ \footnotesize 0. 1104\times 2 = 0.2208 \rightarrow \textcolor{red}{0.01001010110} \\0.3888×2=0.7776→0.010010100.7776×2=1.5552→0.010010101−10.5552×2=1.1104→0.0100101011−10.1104×2=0.2208→ 0,01001010110

Это не остановить! Почему бинарная дробь все еще растет? Давайте рассмотрим причину в следующем разделе.

Преобразование двоичной дроби в десятичную

Теперь, когда вы знаете, как преобразовать десятичную дробь в двоичную, давайте научимся наоборот. Возьмите двоичную дробь, любую двоичную дробь! Вы думали о 0.01101010.01101010.0110101? Отлично — мы тоже. 😆

Правило этого преобразования состоит в том, что каждая позиция цифры соответствует отрицательной степени двойки 95}=\tfrac{1}{32}1→20=11​0,1→2−1=211​=21​0,01→2−2=221​=41​0,001→2−3=231​=81​ 0,0001→2−4=241​=161​0,00001→2−5=251​=321​

🙋 Мы включили 0-ю степень двойки, которая равна 111, только для лучшего понимания этого позиционного преобразования. Не забудьте ограничить свои преобразования числами меньше 111!

Возьмите свою двоичную дробь и перепишите ее, умножив каждую цифру на соответствующую степень числа 2. 7} \end{align*}0.0110101→0×201​+0×211​++ 0×241​+1×251​+​1×221​+1×231​0×261​+1×271​​

Преобразование дробей в их десятичные эквиваленты:

0×1+0×0,5+1×0,25++1×0,125+0×0,0625++1×0,03125+0×0,015625++1×0,0078125=0,4140625\footnotesize 0\!\раз\! 1+0\!\раз\! 0,5+1\!\раз\! 0,25+\\ \размер сноски +1\!\раз\! 0,125+0\!\раз\! 0,0625+\\ \размер сноски +1\!\раз\! 0,03125+0\!\раз\! 0,015625+\\ \размер сноски +1\!\раз\! 0,0078125 = 0,41406250×1+0×0,5+1×0,25++1×0,125+0×0,0625++1×0,03125+0×0,015625++1×0,0078125=0,4140625

Вот и все — мы преобразовали десятичную дробь дробь в двоичную дробь!

0,01101012=0,4140625100,0110101_{2}=0,4140625_{10}0,01101012​=0,414062510​

Ограничения двоичных дробей

Двоичные дроби не могут точно представлять каждое десятичное число. Для десятичных дробей с конечным числом десятичных цифр ( рациональных ) вполне возможно иметь бесконечно длинное двоичное представление. Такое преобразование приводит к ошибке с величиной ошибки в зависимости от количества цифр представления 9n}=1n=1∑∞​2n1​=1

Это геометрический ряд, который сходится к 111. Удаляя элементы ad hoc , вы можете получить каждое число от 000 до 111; однако реальная проблема здесь заключается в том, чтобы решить, какие вклады мы должны стереть.

Поскольку компьютеры имеют ограниченный объем памяти — они могут вычислять только определенное количество цифр — некоторые элементы, позволяющие точно представлять десятичную дробь, могут быть опущены.

Рассмотрим дробь 15\frac{1}{5}51​ в представлении из 888 цифр.

(15)10=0,2010\left(\tfrac{1}{5}\right)_{10}=0,20_{10}(51​)10​=0,2010​

Это конечная дробь: ошибка в 8-значном представлении равна нулю.

Найдите его бинарное представление , вы знаете как это сделать, но на этот раз мы вам поможем!

0,2000×2=0,4000→00,4000×2=0,8000→00,8000×2=1,6000→1−10,6000×2=1,2000→1−10,2000×2=0,4000→00,2000\times 2=0,4000{red}{rightarrow \textcolor\rightarrow 0}\\ 0,4000\умножить на 2=0,8000\стрелка вправо \textcolor{красный}{0}\\ 0,8000\умножить на 2=1,6000\стрелка вправо \textcolor{красный}{1}\\ \textcolor{синий}{-1}\\ 0,6000\умножить на 2=1,2000\стрелка вправо \textcolor{красный}{1}\\ \textcolor{синий}{-1}\\ 0,2000\times 2 = 0,4000\rightarrow \textcolor{red}{0}0,2000×2=0,4000→00,4000×2=0,8000→00,8000×2=1,6000→1−10,6000×2=1,2000→1−10,2000×2=0,4000→ 0

Последний шаг такой же, как и первый, поэтому, если мы продолжим, мы получим повторяющуюся последовательность 001100110011s:

0,210=0,001100110011… 20,2_{10}=0,001100110011\ldots_{\ 2} 0,210 = 0,0011001111111111111111111111111111 2

Давайте усечь его на восьмой цифре:

0. 210≃0.0011001120.2_ {10} \ simeq0.00110011_ {2} 0,210 ≃0.001100119

.20.2, хотя мы начали с этого:

0,001100112=0,19921875100,00110011_{2}=0,19{-8}7,15⋅10−8: очень мало, но все же присутствует.

Двоичное представление десятичной дроби точно только , если 222 является единственным простым делителем знаменателя: 1/21/21/2, 3/83/83/8 и 1013/10241013/10241013/ 1024 все имеют точные представления, с другой стороны, 1/51/51/5 или 1/101/101/10 всегда имеют ошибку.

Как пользоваться нашим конвертером двоичных дробей?

Вы можете использовать наши конвертеры двоичных дробей для преобразования десятичной дроби в двоичную и из двоичной дроби в десятичную. Не забудьте выбрать правильный!

Выберите необходимое количество цифр в вашем представлении. Вы не сможете вставить больше этого числа. Результатом будет усеченное и не округленное!

Вот пример: выберите из двоичного в десятичное , выберите 4 цифры и введите 0. 10100.10100.1010. Результат 0,6250,6250,625 или 5/85/85/8.

Вы заметили, что его знаменатель имеет единственный простой делитель, 222? Вводя такое число, мы неявно предполагали, что это 9.0140 конечная двоичная дробь!

🙋 Если вам нужно количество цифр, отличное от того, которое предусмотрено по умолчанию, перейдите в расширенный режим и вставьте нужное значение. Не забудьте обновить калькулятор, если хотите снова использовать значения по умолчанию! 😀

Помимо нулей и единиц

Мы надеемся, что наш преобразователь двоичных дробей помог вам в изучении этой не очень простой темы. 🤞

У нас есть много других двоичных калькуляторов: попробуйте наш двоичный арифметический калькулятор или специальные инструменты:

• Калькулятор двоичного умножения;
• Калькулятор двоичного сложения.

Часто задаваемые вопросы

Все ли дроби можно преобразовать в двоичные?

Не все дроби могут быть точно преобразованы в двоичные: только если знаменатель является степенью 2 , двоичная дробь будет конечной. Во всех остальных случаях будет ошибка в представлении. Величина ошибки зависит от количества цифр, используемых для ее представления.

Как преобразовать дроби в двоичные?

Возьмите десятичную дробь и начните умножать на два десятичную часть. Каждый раз, когда результат на меньше, чем 1 , добавляйте 0 к двоичному представлению. Если результат больше или равен 1 , добавьте 1 к двоичному представлению и вычтите 1 из результата умножения. Продолжайте умножать, пока результат не будет 0 или вы не достигнете желаемого количества цифр.

Узнайте больше о том, как представлять дроби в двоичном формате, на omnicalculator.com.

Как представить 0,5 в двоичном формате?

Умножить 0,5 на 2 : 0,5 × 2 = 1,0 . Так как результат равен 1 , добавьте 1 к двоичной дроби: 0,1 .