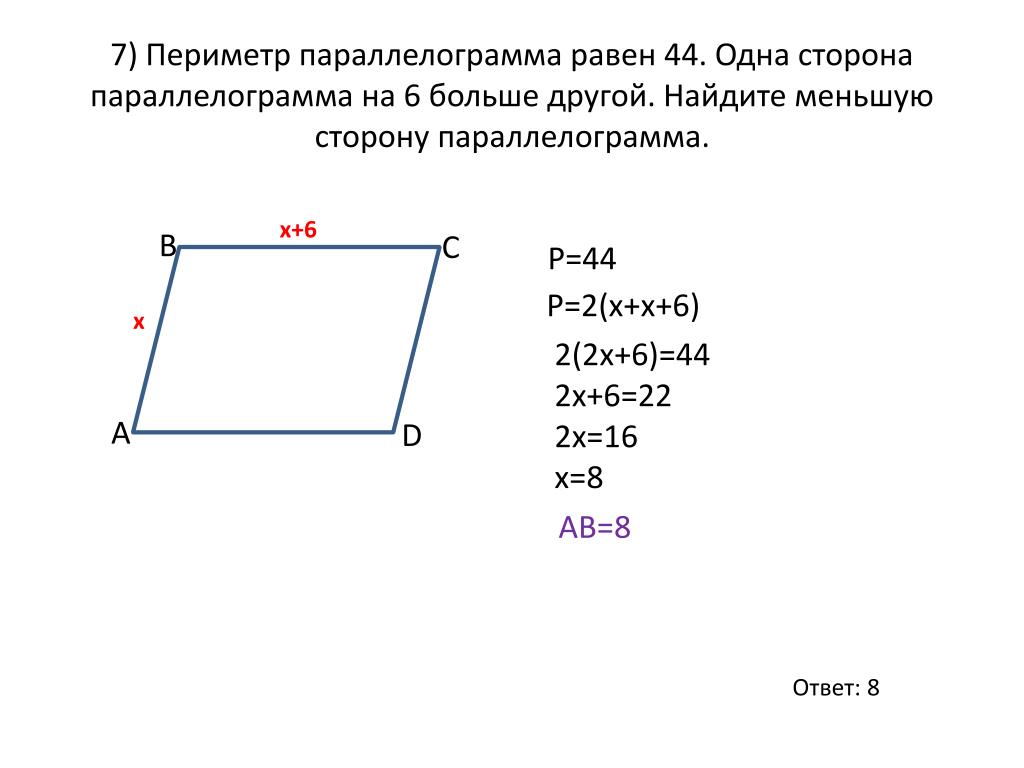
Периметр параллелограмма вычислим по формуле
\(\ P_{A B C D}=2(a+b) \)
Для данной задачи она запишется следующим образом:
\(\ P_{A B C D}=2(A B+A D) \)
Подставляя значения AB=1 и AD=2, получим:
\(\ P_{A B C D}=2 \cdot(1+2)=6_{(\mathrm{см})} \)
\(\ P_{A B C D}=6 \mathrm{см} \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Периметр трапеции Периметр окружности Периметр круга Периметр треугольника
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПодпишись на рассылку, чтобы не пропустить информацию об акциях
Периметр параллелограмма Калькулятор | Вычислить Периметр параллелограмма
✖Длинный край параллелограмма — это длина самой длинной пары параллельных сторон в параллелограмме. | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% | |
✖Короткое ребро параллелограмма — это длина самой короткой пары параллельных ребер в параллелограмме. | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
|
✖Периметр параллелограмма — это общая длина всех граничных линий параллелограмма. |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
⎘ копия |
👎
Формула
сбросить
👍
Периметр параллелограмма Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Преобразование входов в базовый блок
Длинный край параллелограмма: 12 метр —> 12 метр Конверсия не требуется
Короткий край параллелограмма: 7 метр —> 7 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
38 метр —> Конверсия не требуется
< 2 Периметр параллелограмма Калькуляторы
Периметр параллелограмма формула
Периметр параллелограмма = 2*Длинный край параллелограмма+2*Короткий край параллелограмма
P = 2*eLong+2*eShort
Что такое периметр параллелограмма?
Параллелограмм – это четырехугольник, у которого две пары противоположных сторон параллельны. Периметр параллелограмма равен сумме длин всех 4 сторон. Периметр параллелограмма — это полное расстояние вне геометрической формы.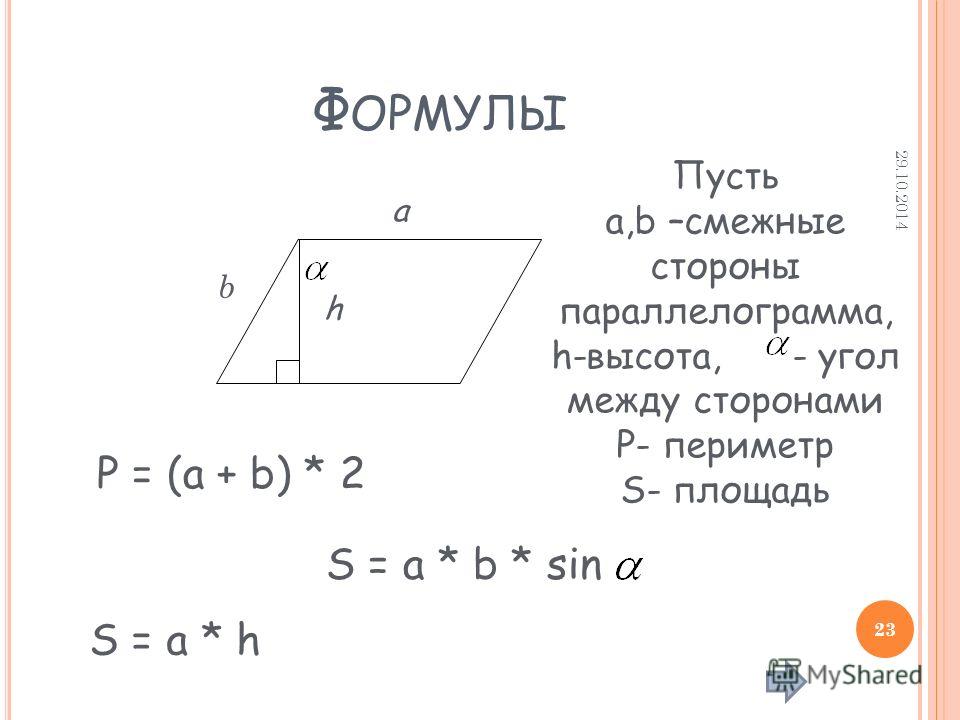 Противоположные стороны параллелограмма равны, поэтому периметр равен удвоенной сумме двух параллельных сторон, скажем, a и b.
Противоположные стороны параллелограмма равны, поэтому периметр равен удвоенной сумме двух параллельных сторон, скажем, a и b.
Share
Copied!
Площадь и периметр параллелограмма – формулы и примеры
Периметр параллелограмма представляет собой длину контура параллелограмма. С другой стороны, площадь является мерой двумерного пространства, занимаемого фигурой. Мы можем найти периметр параллелограмма, сложив длины его четырех сторон, и мы можем найти площадь, умножив длину его основания на его высоту.
В этой статье мы узнаем все о периметре и площади параллелограмма. Мы изучим его формулы и применим их для решения некоторых практических задач.
ГЕОМЕТРИЯ
Актуально для …
Изучение периметра и площади параллелограмма.
См. примеры
Содержание
ГЕОМЕТРИЯ
Актуально для …
Изучение периметра и площади параллелограмма.
См. примеры
Как найти периметр параллелограмма?
Чтобы найти периметр параллелограмма, нужно сложить длины всех его сторон. Учитывая, что противоположные стороны параллелограмма имеют одинаковую длину, мы можем составить следующую формулу:
$latex p=a+b+a+b$
$latex p=2a+2b$
| $latex p=2(a+b)$ |
Вычислить периметр a параллелограмм с основанием и высотой
Чтобы вычислить периметр параллелограмма, используя его основание и высоту, нам нужен угол между его высотой и его боковой стороной, как показано на рисунке ниже.
В параллелограмме противоположные стороны параллельны и равны, а периметр параллелограмма определяется как удвоенное произведение основания и высоты на косинус угла:
| $латекс p=2(b+h~\cos(\theta))$ |
где $латекс\тета$ — это угол между высотой и боковой стороной параллелограмма.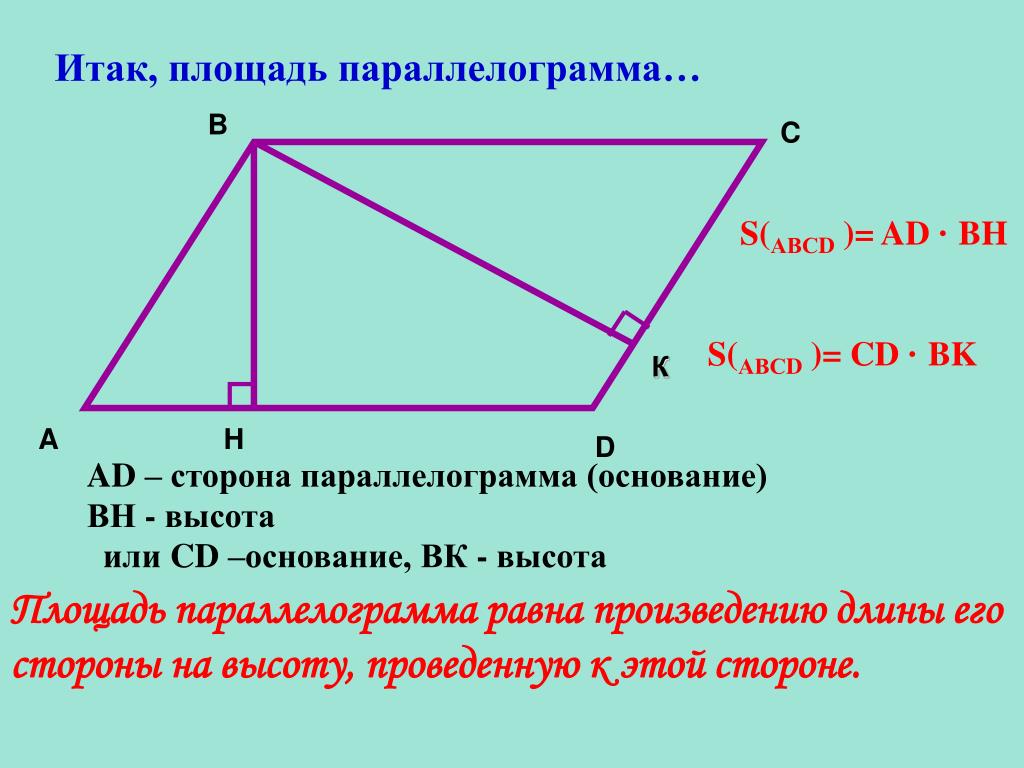
Как найти площадь параллелограмма?
Чтобы вычислить площадь параллелограмма, мы можем умножить длину основания на его высоту. Надо учитывать, что основание и высота параллелограмма перпендикулярны друг другу, а боковая сторона параллелограмма не перпендикулярна основанию.
Например, на диаграмме ниже мы видим, что высота параллелограмма отличается от его боковой стороны:
Следовательно, мы можем использовать следующую формулу, чтобы найти площадь параллелограмма:
| $ латекс A=bh$ |
, где b — длина основания, а h — высота.
Вычислить площадь параллелограмма без учета высоты
Мы можем вычислить площадь параллелограмма без учета его высоты, если нам известны длины его сторон и угол между сторонами. Поэтому используем следующую формулу:
| $latex A=ab\sin(x)$ |
где a и b — длины сторон параллелограмма, а x — угол между сторонами.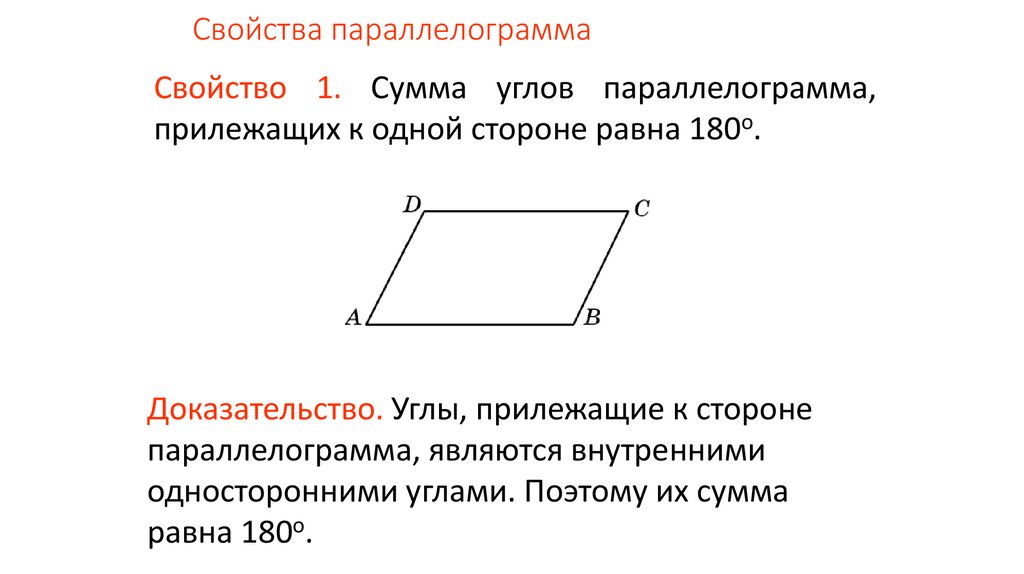
Вычисление площади параллелограмма с помощью диагоналей
Мы можем вычислить площадь параллелограмма, зная длины диагоналей и угол пересечения диагоналей. Затем используем следующую формулу:
| $latex A=\frac{d_{1}\times d_{2}\sin(y)}{2}$ |
где $latex d_{1}, ~d_{2}$ длины диагоналей и y угол пересечения диагоналей.
Периметр и площадь параллелограмма – Примеры с ответами
ПРИМЕР 1Найдите периметр параллелограмма, длина сторон которого 8 дюймов и 12 дюймов.
Решение
У нас есть следующие длины:
- Сторона 1, $латекс a=8$ в
- Сторона 2, $латекс b=12$ в
Применяя формулу для периметра с этими значениями, получаем:
$латекс p=2(a+b)$
$латекс p=2(8+12)$
$латекс p=2(20 )$
$latex p=40$
Периметр параллелограмма равен 40 дюймам.
ПРИМЕР 2 высота 11 футов.
Решение
У нас есть следующее:
- Основание, $латекс b=12$ футов
- Высота, $латекс h=11$ футов
Используя формулу для площади с этими длинами, мы имеем:
$латекс A=bh$
$латекс A=(12)(11)$
$латекс A=132$
Площадь параллелограмм равен 132 футам².
ПРИМЕР 3Найдите периметр параллелограмма, длина сторон которого 15 ярдов и 17 ярдов.
Решение
У нас есть следующее:
- Сторона 1, $латекс a=15$ ярдов
- Сторона 2, $латекс b=17$ ярдов
Используя формулу для периметра с этими значениями, мы имеем:
$латекс p=2(a+b)$
$латекс p=2(15+17)$
$латекс p=2(32 )$
$latex p=64$
Периметр параллелограмма равен 64 ярдам.
Найдите площадь параллелограмма с основанием 15 дюймов и высотой 20 дюймов.
Решение
У нас есть следующие длины:
- База, $латекс b=15$ в
- Высота, $латекс h=20$ в
Используя формулу для площади с этими длинами, мы имеем:
$латекс A=bh$
$латекс A=(15)(20)$
$латекс A=300$
Площадь параллелограмм равен 300 дм².
Если периметр параллелограмма равен 90 дюймам, а одна сторона равна 21 дюйму, то какой длины другая сторона?
Решение
У нас есть следующее:
- Периметр, $латекс p=90$ в
- Сторона 1, $латекс a=21$ в
В этом случае мы знаем периметр и хотим найти длину другой стороны параллелограмма. Поэтому воспользуемся формулой формулы и найдем недостающую сторону:
$латекс p=2(a+b)$
$латекс 90=2(21+b)$
$латекс 90=42+ 2b$
$латекс 2b=48$
$латекс b=24$
Длина другой стороны равна 24 дюймам.
ПРИМЕР 6Какова площадь параллелограмма, длина сторон которого равна 14 футам и 12 футам, а угол между ними равен 60°?
Решение
У нас есть следующее:
- Сторона 1, $латекс a=14$ футов
- Сторона 2, $латекс b=12$ футов
- Угол, $латекс x=60°$
Используя вторую формулу площади параллелограмма, имеем:
$латекс A=ab\sin(x)$
$латекс A=(14)(12)\sin(60°)$
$латекс A=(168)(0,866)$
$латекс A =145,5$
Площадь параллелограмма равна 145,5 фут².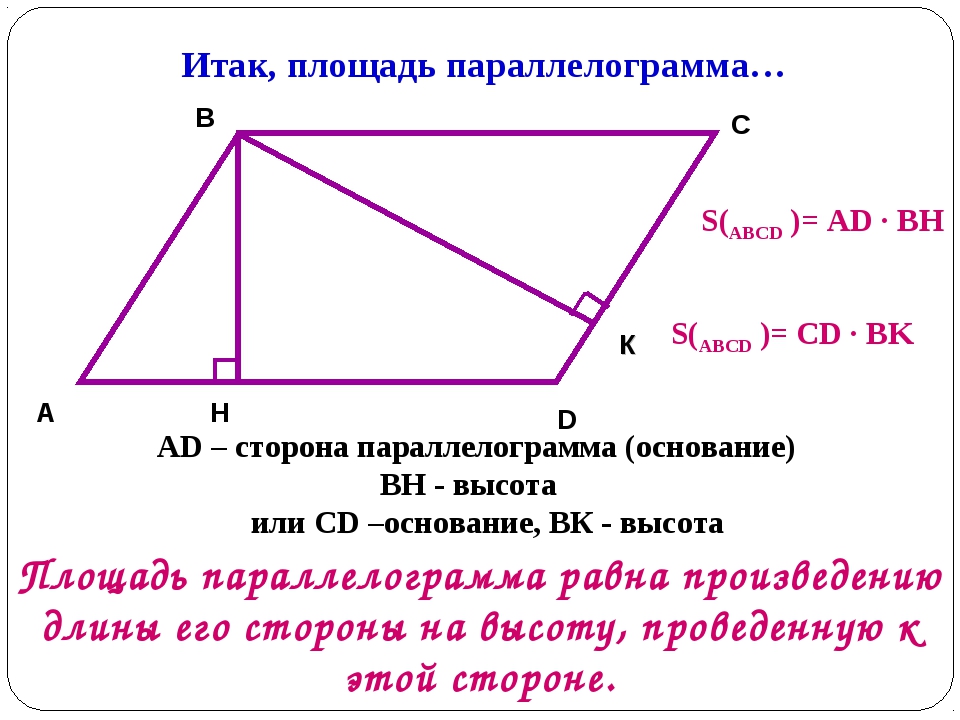
Найдите периметр параллелограмма, имеющего высоту 10 футов и основание 12 футов, если угол между высотой и боковой стороной равен 60°.
Решение
У нас есть следующее:
- Высота, $латекс h=10$ футов
- Основание, $латекс b=12$ футов
- Угол, $латекс\тета=60°$
Воспользуемся второй формулой для периметра и получим:
$latex p=2(b+h~\cos(\theta))$
$latex p=2(12+10~\cos( 60°))$
$латекс p=2(12+10(0,5))$
$латекс p=2(12+5)$
$латекс p=2(17)$
$латекс p =34$
Периметр параллелограмма равен 34 футам.дюймы. Чему равна его площадь, если угол пересечения диагоналей равен 30°?
Решение
У нас есть следующее:
- Диагональ 1, $латекс d_{1}=10$ в
- Диагональ 2, $латекс d_{2}=9$ в
- Угол, $латекс y=30°$
Используя третью формулу для площади с заданной информацией, мы имеем:
$$A=\frac{d_{1}\times d_{2}\sin(y)}{2}$$
$ $A=\frac{10\times 9\sin(30°)}{2}$$
$$A=\frac{(90)(0,5)}{2}$$
$$A=\frac{45}{2}$$
$latex A=22,5$
Площадь параллелограмма равна 22,5 дюйма².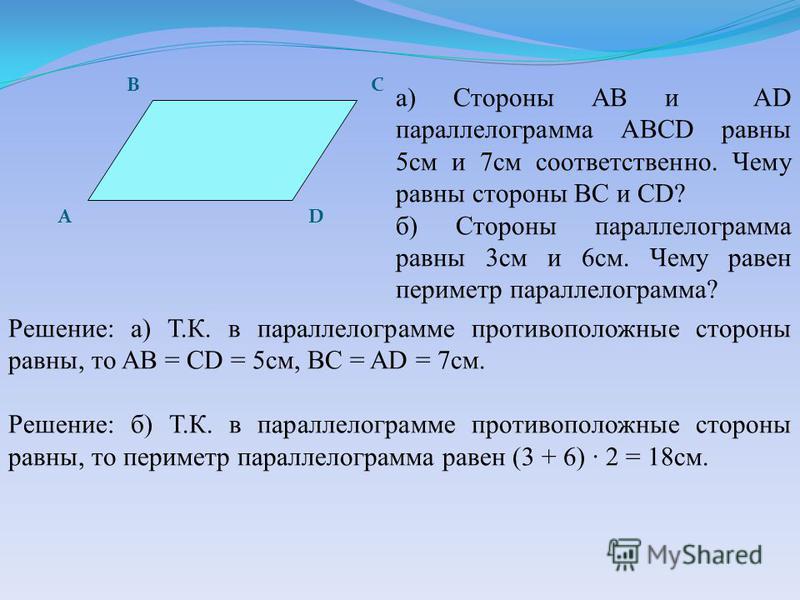
Найдите периметр параллелограмма, имеющего высоту 20 ярдов и основание 15 ярдов, если угол между высотой и боковой стороной равен 60°.
Решение
У нас есть следующее:
- Высота, $латекс h=20$ ярдов
- Основание, $латекс b=15$ ярдов
- Угол, $latex \theta=60°$
Мы используем эти значения во второй формуле периметра и имеем:
$latex p=2(b+h~\cos(\theta))$
$latex p=2(15+20~\cos( 60°))$
$латекс p=2(15+20(0,5))$
$латекс p=2(15+10)$
$латекс p=2(25)$
$латекс p =50$
Периметр параллелограмма равен 50 ярдам.
ПРИМЕР 10Площадь параллелограмма равна 182 дюймам². Если его высота 13 дюймов, какова длина его основания?
Решение
У нас есть следующие значения:
- Площадь, $латекс A=182$ дюймов²
- Высота, $латекс h=13$ в
Используем формулу площади с заданной информацией и вычисляем основание основание 14 дюймов в длину.
Периметр и площадь параллелограмма – практические задачи
Найдите периметр параллелограмма, длина сторон которого 11 дюймов и 19 дюймов.2}$
Чему равен периметр параллелограмма, высота которого 8 дюймов, основание 12 дюймов, а угол между высотой и боковой стороной равен 60°?
Выберите ответ
$латекс p=20$ в
$латекс p=32$ в
$латекс p=36$ в
$latex p=40$ in
Найдите площадь параллелограмма, диагонали которого имеют длины 13 ярдов и 15 ярдов, а угол между диагоналями равен 30°. 92}$
См. также
Хотите узнать больше о периметрах и площадях геометрических фигур? Взгляните на эти страницы:
- Периметр и площадь равностороннего треугольника – формулы и примеры
- Периметр и площадь пятиугольника – формулы и примеры
- Периметр и площадь шестиугольника – формулы и примеры
- Периметр и площадь восьмиугольника – формулы и примеры
Периметр параллелограмма, формула с одной стороной и диагоналями- Unacademy
Длина непрерывной линии, образованной границей параллелограмма, является периметром параллелограмма.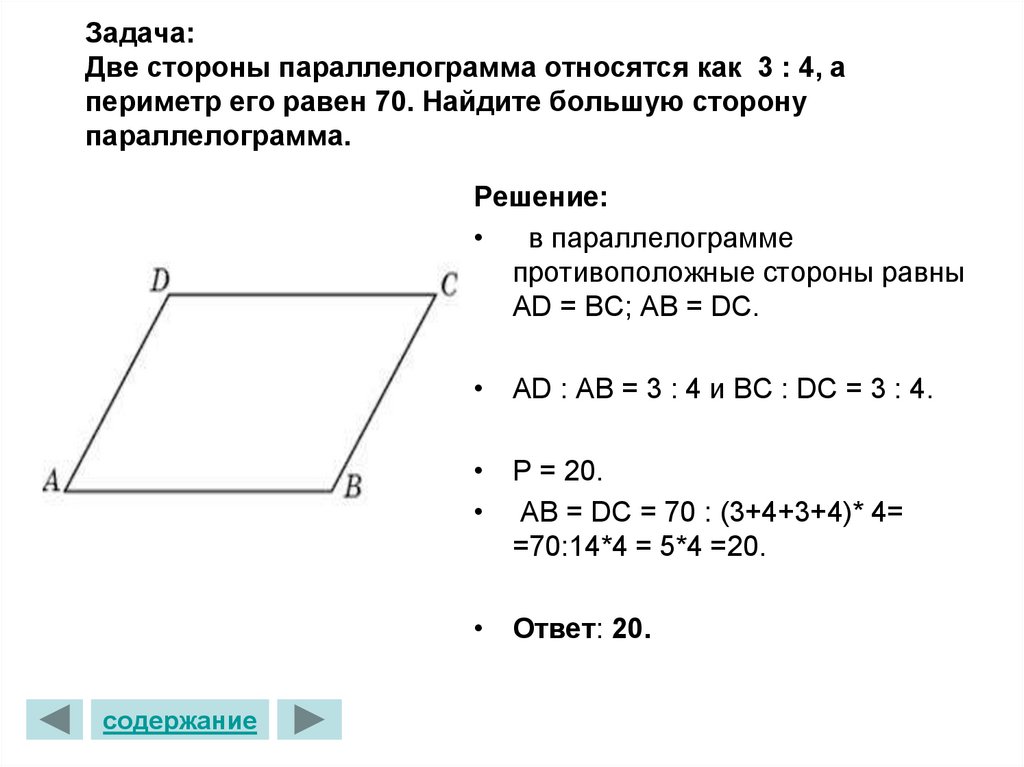 Каждая из его сторон имеет единицу, которая совпадает с ее единицей. Четырехугольник представляет собой замкнутую фигуру, состоящую из четырех отрезков, соединенных вместе. Если противоположные стороны четырехугольника параллельны и имеют одинаковую длину, то такой четырехугольник называется параллелограммом. Параллелограмм может быть представлен фигурами ромб, прямоугольник и квадрат.
Каждая из его сторон имеет единицу, которая совпадает с ее единицей. Четырехугольник представляет собой замкнутую фигуру, состоящую из четырех отрезков, соединенных вместе. Если противоположные стороны четырехугольника параллельны и имеют одинаковую длину, то такой четырехугольник называется параллелограммом. Параллелограмм может быть представлен фигурами ромб, прямоугольник и квадрат.
Ниже приведены некоторые характеристики параллелограмма:
- Проще говоря, мы можем сказать, что периметр параллелограмма равен сумме четырех сторон параллелограмма.
- Противоборствующие стороны находятся в равных условиях.
- Диаметрально противоположные углы равны.
- Диагонали разрезают друг друга пополам.
- Каждая пара смежных углов является дополнительной по отношению к другой.
Формула периметра параллелограмма
В следующих ситуациях можно определить периметр параллелограмма:
- Когда известны положения двух соседних сторон.

- Всякий раз, когда известна длина одной стороны и диагоналей.
- Когда известны основание, высота и угол, задача может быть решена.
Ниже приведены формулы периметра для расчета периметра параллелограмма в каждой из следующих ситуаций:
- Когда параллелограмм имеет две смежные стороны, уравнение P = 2 (a + b), где a и b смежные стороны параллелограмма.
- P = 2a + √(2×2 + 2y2 – 4a2), где a – сторона параллелограмма, а x и y – диагонали параллелограмма соответственно.
- Его можно записать как P = (2a + 2h)/sinθ, где a обозначает сторону параллелограмма, h обозначает высоту параллелограмма, а sinθ обозначает его угол.
Формула периметра параллелограмма со сторонами
Периметр параллелограмма равен сумме длин всех его сторон. В случае параллелограмма мы уже знаем, что противоположные стороны равны. Подумайте о параллелограмме с парой смежных сторон, которые одинаковы (тогда другая пара смежных сторон будет такой же, но они будут отличаться друг от друга).
Подумайте о параллелограмме с парой смежных сторон, которые одинаковы (тогда другая пара смежных сторон будет такой же, но они будут отличаться друг от друга).
Итак, периметр параллелограмма равен a + b + a + b (или) 2a + 2b (или) 2 (a + b). И эквивалентно Периметр (P) параллелограмма со сторонами a и b определяется следующим образом:
P равно двум единицам 2(a + b).
Периметр формулы параллелограмма с одной стороной и диагоналями
Рассмотрим следующий параллелограмм: параллелограмм со сторонами a и b и диагоналями x и y. Предположим, что сторона «а», диагонали «х» и «у» и диагонали «х» и «у» известны, но значение стороны «b» неизвестно, и нам нужно определить периметр параллелограмма.
В случае треугольника ABD применяется закон косинусов.
x2 = a2 + b2 – 2ab cos(угол BAD)
В случае треугольника ADC используется правило косинуса.
Если y2 равно a2 + b2 – 2ab cos(угол ADC), то
Объединяя два предыдущих уравнения,
сумма x2 и y2 равна 2a2 + 2b2 – 2ab (cos[угол BAD] + cos [угол АЦП])… (1)
Мы уже знаем, что любые два смежных угла параллелограмма являются дополнительными (это свойство параллелограмма). Так
Так
180° равно сумме углов BAD и ADC.
Угол между BAD и ADC составляет 180°.
Используя формулу косинуса для обеих сторон,
cos(угол BAD) = cos (180° – угол ADC) = – cos ADC
Используя это вместо (1),
x2 + y2 = 2a2 + 2b2 – 2ab (- cos[угловой АЦП] + cos[угловой АЦП]).
x2 + y2 = 2a2 + 2b2 – 2ab (0)
x2 + y2 = 2a2 + 2b2
Теперь мы знаем, каково отношение между сторонами и диагоналями площади параллелограмма. Теперь мы решим это для «b», потому что нам не предоставлена длина «b».
2b2 = x2 + y2 – 2b2
b2 = (x2 + y2 – 2a2) / 2
b = √[(x2 + y2 – 2a2) / 2]
Теперь мы знаем длины сторон параллелограмма ( ‘a’ и ‘b’), и мы можем использовать формулу из предыдущего раздела, чтобы определить длину его периметра (P).
P равно 2a плюс 2b.
P = 2a + 2√[(x2 + y2 – 2a2) / 2]
Уравнение P = 2a + √[2(x2 + y2 – 2a2)]
P = 2a + √(2×2 + 2y2 – 4a2)
Периметр параллелограмма с основанием, высотой и углом
Рассмотрим параллелограмм, в котором одна из сторон обозначена буквой «а», соответствующая высота обозначена буквой «h», а один из углов при вершине обозначен буквой «а», как показано на рисунке ниже. Предположим, что неизвестная сторона параллелограмма представлена буквой «b». Мы начнем с определения значения b, а затем вычислим периметр.
Предположим, что неизвестная сторона параллелограмма представлена буквой «b». Мы начнем с определения значения b, а затем вычислим периметр.
Когда функция sin применяется к треугольнику BEC,
sin θ = h/b
b = h /sin θ
В результате периметр параллелограмма (P) будет следующим:
P равно 2a плюс 2b.
P = 2a + 2h / sin θ
В этом случае не обязательно указывать конкретный угол параллелограмма. Неважно, под каким углом находится вершина, потому что любые два смежных угла параллелограмма являются дополнительными и sin θ = sin (180° – θ), где θ — угол.
Заключение
Периметр круга равен сумме длин всех четырех сторон. Общее расстояние за пределами геометрической формы параллелограмма известно как периметр параллелограмма. Длина непрерывной линии, образованной границей параллелограмма, является периметром параллелограмма. Четырехугольник представляет собой замкнутую фигуру, состоящую из четырех отрезков, соединенных вместе.

 ⓘ Длинный край параллелограмма [eLong]
ⓘ Длинный край параллелограмма [eLong]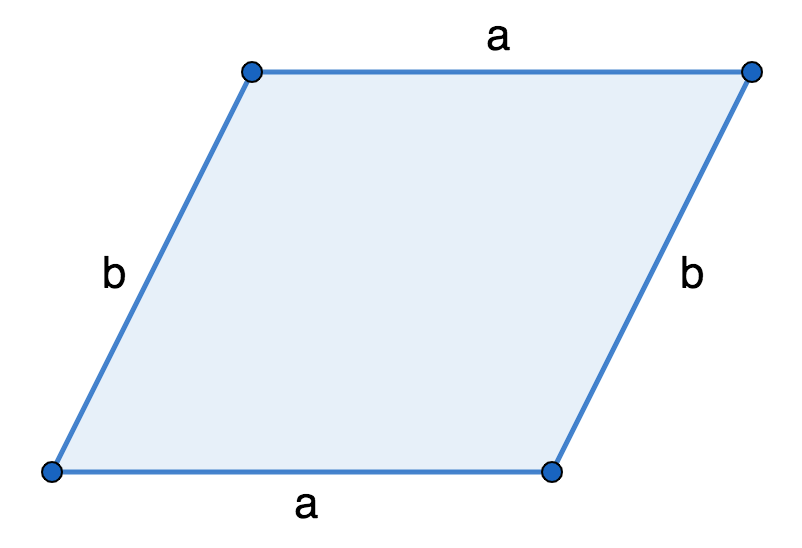
 ⓘ Периметр параллелограмма [P]
ⓘ Периметр параллелограмма [P]