Найти длину высоты параллелепипеда опущенной из вершины на основание: Аналитическая геометрия | ELiS ПГНИУ

8. Векторная алгебра

Если известны координаты точек и, то координаты вектора

Разложение этого вектора по ортам :

Длина вектора находится по формуле а направляющие косинусы равныОрт вектора

Пример 8. Даны точки

Разложить вектор по ортами найти его длину, направляющие косинусы, орт вектора. Найдем координаты векторов:

и

Вектор

Контрольные варианты к задаче 8. Даны точки А, В и С. Разложить вектор по ортамНайти длину, направляющие косинусы и орт вектора.

1.		2.
3.	.	4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.
19.		20.
21.		22.
23.		24.
25.		26.
27.		28.
29.		30.

Задача 9. Если даны векторы то.

Тогда; проекция векторана направление вектора, условие перпендикулярности ненулевых векторов выглядит следующим образом:

Условие коллинеарности векторов: .

Пример 9. Даны вершины треугольника Найти угол при вершине А и проекцию векторана сторону АС. С

Внутренний угол при вершине А образован векторами,

А В

Тогда

Проекция на направление вектора:

1. Даны векторы иНайти

2. Найти косинус угла, образованного вектором и осьюOZ.

3. Даны векторы и .Найти косинус угла между диагоналями параллелограмма, построенного на векторах .

4. Даны векторы и . Вычислить

5. Найти косинус угла, образованного вектором и осью ОУ.

6. Даны векторы и .Найти косинус угла, образованного вектором и осью ОХ.

7. Даны векторы и .Найти

8. Вычислить проекцию вектора на ось вектора .

9. Определить угол между диагоналями параллелограмма, построенного на векторах и .

10. Определить, при каком значении m векторы иперпендикулярны.

11. Определить, при каком значении векторы и взаимно перпендикулярны.

12. Даны вершины треугольника: . Определить внутренний угол при вершине В.

13. Даны вершины треугольника: . Определить внутренний угол при вершине А.

14. Найти вектор , коллинеарный векторуи удовлетворяющий условию

15. Даны две точки иВычислить проекцию вектора на ось вектора

16. Даны векторы: и . Вычислить

17. Найти острый угол между диагоналями параллелограмма, построенного на векторах , .

18. Даны три вектора: ,,. Найти

19. Даны три вектора: ,,. Найти

20. Найти острый угол между диагоналями параллелограмма, построенного на векторах и

21. Даны три вектора: ,,. Вычислить

22. Найти вектор , зная, что он перпендикулярен векторами

и удовлетворяет условию

23. Найти вектор , коллинеарный векторуи удовлетворяющий условию

24. Даны вершины треугольника: Определить внешний угол при вершине А.

25. Даны вершины треугольника: Определить внешний угол при вершине А.

26. Дан вектор и точкииНайти

27. В треугольнике с вершинами Определить внутренний угол при вершине А.

28. Даны векторы иНайти проекцию векторана направление вектора

29. Даны вершины треугольника: Найти проекцию векторана сторону

30. Даны векторы Найти проекцию вектора на вектор

Задача 10. Площадь параллелограмма, построенного на векторах

можно найти по формуле а площадь треугольника, построенного

на этих векторах:

Пример 10. Даны вершины треугольника Найти его площадь и длину высоты, опущенной из вершины С.

. Находим векторы

Векторное произведение

Так как гдедлина высоты, опущенной из вершины С на сторону АВ,.

Контрольные варианты к задаче 10

1. В параллелограмме ABCD даны векторы иНайти площадь параллелограмма, построенного на диагоналях параллелограмма

ABCD.

2. Даны три вершины параллелограмма ,,. Найти длину высоты, опущенной из вершины С (через площадь

параллелограмма).

3. Найти площадь треугольника с вершинами , ,

(средствами векторной алгебры).

4. Найти площадь треугольника с вершинами , ,(средствами векторной алгебры).

5. Даны три вершины треугольника: ,,. Найти его высоту, приняв ВС за основание (через площадь треугольника).

6. На векторах ипостроен параллелограмм. Найти

площадь параллелограмма, сторонами которого являются диагонали данного параллелограмма.

7. Даны векторы и. Найти векторперпендикулярный к векторамесли модуль векторачисленно равен площади треугольника, построенного на векторахи тройка векторовлевая.

8. Даны точки ,, Найти площадь параллелограмма, построенного на векторах и ().

9. На векторах ипостроен параллелограмм. Найти высоту, опущенную на основание(через площадь).

10. В треугольнике ABC, где ,найти длину высоты, опущенной на сторонуAB (через площадь треугольника; средствами векторной алгебры).

11. На векторах ипостроен параллелограмм. Найти площадь параллелограмма, построенного на диагоналях данного параллелограмма.

12. В треугольнике с вершинами , и точка E делит сторону АВ пополам. Найти площадь треугольника АСЕ (средствами векторной алгебры).

13. Найти площадь параллелограмма со сторонами если

14. Найти площадь треугольника со сторонами если,

и

15. Дан треугольник с вершинами , и . Вычислить площадь треугольника и высоту, опущенную из вершины А (средствами векторной алгебры).

16. Даны векторы иНайти вектор, который пер-

пендикулярен векторам , если длина его численно равна площади треуго-

льника, построенного на векторах , и тройка векторовправая.

17. Даны точки ,и . Вычислить площадь треугольника и высоту, опущенную из вершины С (средствами векторной алгебры).

18. В треугольнике с вершинами , и точка E делит сторону АВ пополам. Найти площадь треугольника ВСЕ (средствами векторной алгебры).

19. Даны точки ,и . Найти площадь параллелограмма, построенного на векторах и

20. Даны три вершины треугольника: ,,. Вычислить его высоту, опущенную из вершины В (через площадь, средствами векторной алгебры).

21. Дан треугольник с вершинами , и . Найти его высоту, опущенную из вершины А (через площадь, средствами векторной алгебры).

22. Даны векторы иВычислить площадь треугольника, построенного на векторах

23. Даны векторы иВычислить площадь треугольника, построенного на векторах

24. Найти площадь параллелограмма, построенного на векторах где

25. В треугольнике с вершинами , и точка E делит сторону АВ пополам. Найти площадь треугольника АСЕ (средствами векторной алгебры).

26. Даны векторы иНайти вектор, который перпендикулярен векторамесли модуль векторачисленно равен площади треугольника, построенного на векторах, и тройка векторовлевая.

27. Даны точки , и . Найти длину высоты треугольника АВС, опущенной из вершины С (через площадь, средствами векторной алгебры).

28. Даны три вершины параллелограмма ,и. Найти длину высоты, опущенной из вершины С (через площадь, средствами векторной алгебры).

29. На векторах ипостроен параллелограмм. Найти площадь параллелограмма, построенного на его диагоналях.

30. Даны векторы ,иВычислить площадь треугольника, построенного на векторах

Задача 11. Если даны координаты , то смешанное произведение векторов вычисляют по формуле

.

Объемы параллелепипеда и тетраэдра (треугольной пирамиды), построенных на векторах находятся с помощью смешанного произведения векторов:

,

Если > 0, то тройка векторов — правая.

Если < 0, то тройка левая.

Если = 0, то векторы компланарны.

Пример 11. Дан параллелепипед построенный на векторахиНайти высоту, проведенную из вершинына граньABCD.

Объем равен произведению площади основания на высоту:

находится также по формуле , поэтому

.

Вычислим векторное произведение =

Тогда

к основанию, к боковой стороне

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel. ru Математика Геометрия Свойства высоты равнобедренного треугольника

В данной публикации мы рассмотрим основные свойства высоты равнобедренного треугольника, а также разберем примеры решения задач по данной теме.

Примечание: треугольник называется равнобедренным, если две его стороны равны (боковые). Третья сторона называется основанием.

• Свойства высоты в равнобедренном треугольнике
  • Свойство 1
  • Свойство 2
  • Свойство 3
• Пример задачи

Свойства высоты в равнобедренном треугольнике

Свойство 1

В равнобедренном треугольнике две высоты, проведенные к боковым сторонам, равны.

AE = CD

Обратная формулировка: Если в треугольнике две высоты равны, значит он является равнобедренным.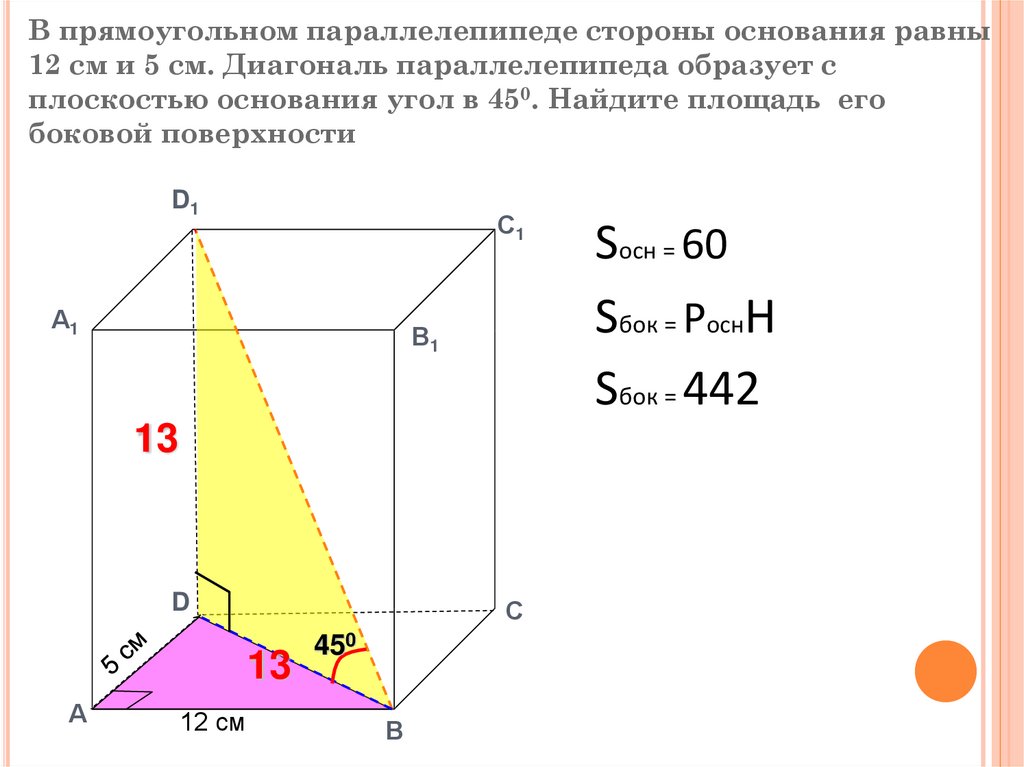

Свойство 2

В равнобедренном треугольнике высота, опущенная на основание, одновременно является и биссектрисой, и медианой, и серединным перпендикуляром.

• BD – высота, проведенная к основанию AC;
• BD – медиана, следовательно, AD = DC;
• BD – биссектриса, следовательно, угол α равен углу β.
• BD – серединный перпендикуляр к стороне AC.

Свойство 3

Если известны стороны/углы равнобедренного треугольника, то:

1. Длина высоты h_a, опущенной на основание a, вычисляется по формуле:

• a – основание;
• b – боковая сторона.

2. Длина высоты h_b, проведенной к боковой стороне b, равняется:

p – это полупериметр треугольника, рассчитывается таким образом:

3. Высоту к боковой стороне можно найти через синус угла и длину стороны треугольника:

Примечание: к равнобедренному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.

Пример задачи

Задача 1
Дан равнобедренный треугольник, основание которого равно 15 см, а боковая сторона – 12 см. Найдите длину высоты, опущенной к основанию.

Решение
Воспользуемся первой формулой, представленной в Свойстве 3:

Задача 2
Найдите высоту, проведенную к боковой стороне равнобедренного треугольника длиной 13 см. Основание фигуры равняется 10 см.

Решение
Для начала вычислим полупериметр треугольника:

Теперь применим соответствующую формулу для нахождения высоты (представлена в Свойстве 3):

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Математика, 6 класс, Площадь поверхности и объем, Анализ формулы треугольника

Обзор

Учащиеся находят площадь треугольника, складывая треугольник и копию треугольника так, чтобы получился параллелограмм с тем же основанием и высотой, что и у треугольника.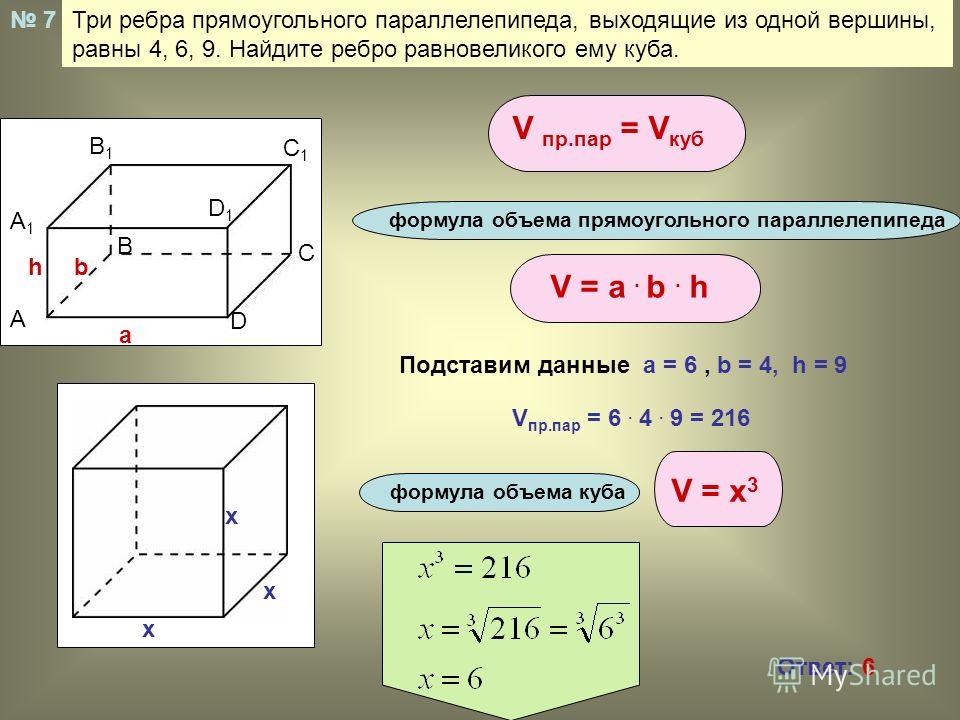 Учащиеся также создают несколько примеров треугольников и ищут отношения между мерами основания, высоты и площади. Эти действия приводят учащихся к разработке и пониманию формулы площади треугольника.

Чтобы найти площадь треугольника, нужно знать длину основания и соответствующую ему высоту. Основанием треугольника может быть любая из трех сторон. Высота — это расстояние по перпендикуляру от вершины, противоположной основанию, до линии, содержащей основание. Высота может быть найдена внутри или снаружи треугольника, или это может быть длина одной из сторон.

Из треугольника и его копии можно составить параллелограмм с тем же основанием и высотой, что и у треугольника. Площадь исходного треугольника равна половине площади параллелограмма. Потому что формула площади параллелограмма равна 9.0009 A = bh , формула площади треугольника: A = 12 bh .

• Разработайте и изучите формулу площади треугольника.

Пусть учащиеся поработают в парах, чтобы обсудить утверждения.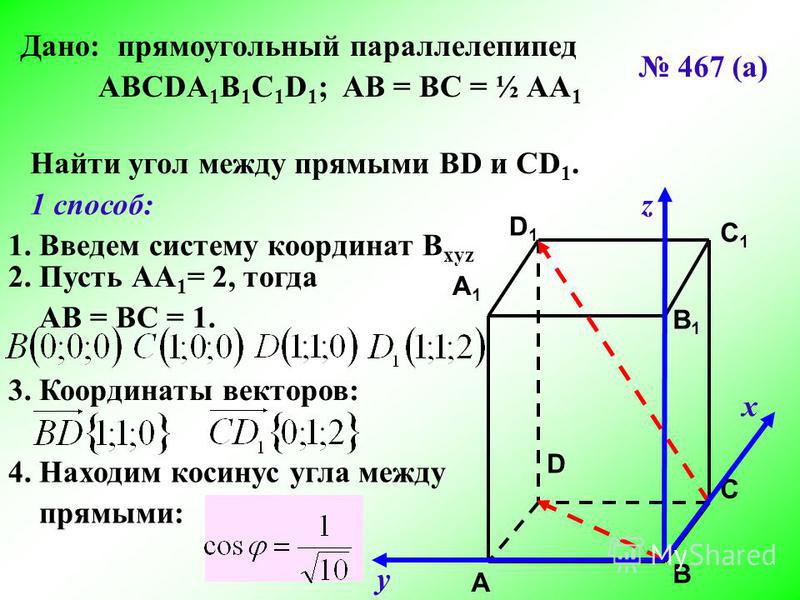

ELL: У учащихся могут возникнуть трудности с определением перпендикулярной высоты треугольника, особенно когда высота должна быть указана за пределами треугольника. Используйте края каталожной карточки, чтобы помочь учащимся лучше понять, как определить перпендикулярную высоту. Смоделируйте эту деятельность для учащихся. Каталожная карточка выравнивается с основанием, а затем сдвигается влево (или вправо) до тех пор, пока вершина, противоположная основанию, не коснется каталожной карточки. Это ясно показывает, что высота перпендикулярна основанию.

Предложите учащимся посмотреть на треугольники. Убедитесь, что они понимают, что такое основание и высота треугольника. Укажите, что высота может быть внутри треугольника, вне треугольника или одной из сторон треугольника.

Открытие

Обсудите следующие утверждения.

• Основанием треугольника может быть любая из трех сторон.
• Высота треугольника — это расстояние по перпендикуляру от основания до вершины, противоположной основанию.
• Как показано на диаграмме, высота может быть внутри или снаружи треугольника, или она может быть одной из сторон.

Партнеры должны обсудить, как они могут составить из треугольника и его копии параллелограмм. Учащиеся должны понимать, что площадь каждого треугольника равна половине площади параллелограмма, составленного из двух треугольников одинакового размера. Так как площадь параллелограмма A = bh , площадь треугольника равна A = 12b ч .

SWD: Некоторые учащиеся могут не сразу понять, как расположить треугольники в параллелограмм. Если учащиеся борются до отчаяния, смоделируйте, как использовать два треугольника для создания небольшого параллелограмма. Позвольте учащимся использовать вырезки из бумаги, если это необходимо.

Открытие

Можете ли вы взять любой треугольник, скопировать его, а затем соединить два треугольника так, чтобы они образовали параллелограмм?

Попробуйте с треугольниками, как на рисунке.

• Что ваши результаты говорят вам о площади треугольника?
• Напишите формулу площади треугольника.

Обсудить математическую миссию. Учащиеся изучают формулу площади треугольника.

SWD: Некоторым учащимся может быть сложно запомнить, какие формулы соответствуют каждой форме. Предложите учащимся создать для себя ресурсы, на которые они будут ссылаться в течение всего раздела (например, карточки для заметок, цифровые стикеры, якорные диаграммы, свой блокнот), которые включают имя фигуры, формулу площади и изображение, представляющее фигуру.

Открытие

Исследуйте формулу площади треугольника.

Пусть партнеры ответят на вопросы и вместе поработают над презентацией.

SWD: Назначьте учащимся бетонные длины для основания и высоты. Если учащиеся используют вырезки в дополнение к интерактиву, попросите их пометить вырезы получившимися областями. Это поможет им понять взаимосвязь между площадями треугольников и общей суммой площадей как площадью исходного многоугольника.

Математическая практика 7: Ищите и используйте структуру.

Определите учащихся, которые понимают, как операции в формуле влияют на ответ (т. е. увеличение коэффициента увеличивает произведение, уменьшение коэффициента уменьшает произведение или сохранение одинаковых коэффициентов не меняет произведение).

Математическое занятие 8: Ищите и выражайте регулярность в повторяющихся рассуждениях.

Следите за учащимися, которые в результате повторных попыток пришли к выводу, что если одна переменная постоянна, а другая увеличивается (или уменьшается), то площадь также увеличивается (или уменьшается).

Ищите учащихся, которые в результате повторных испытаний пришли к выводу, что если обе переменные остаются постоянными, площадь также остается постоянной.

Студенту трудно начать.

• Опишите задание своими словами своему партнеру.
• Что означает сохранение постоянной высоты или основания?
• Помните, что если вершина перемещается параллельно основанию, то она остается на том же расстоянии от основания.
• Как можно переместить вершину параллельно основанию?

Студент изменяет переменную только одним способом, просто увеличивая (или уменьшая) ее значение.

• Можно ли уменьшить (или увеличить) высоту? Что происходит?

Студент работает бессистемно.

• Можете ли вы организовать информацию о основании, высоте и площади в виде таблицы?
• Посмотрите на значения в строках вашей таблицы. Как они связаны?

Ученик нашел правильное решение.

• Как вы пришли к такому выводу?
• Объясните, как интерактивный треугольник помог вам прийти к заключению.

• Если оставить высоту и основание постоянными и переместить вершину параллельно основанию, площадь останется неизменной.
• Если оставить базу неизменной и увеличить (или уменьшить) высоту, то площадь также увеличится (или уменьшится).
• Факты могут быть разными.

Рабочее время

Формула площади треугольника равна
площадь = 12 • основание • высота, или A = 12 bh

Используйте интерактивный треугольник для изучения площади треугольника. Перемещайте вершины треугольника и исследуйте, что происходит с областью.

• Что произойдет, если оставить высоту и основание постоянными и переместить вершину параллельно основанию?
• Что произойдет, если оставить базу неизменной, а высоту изменить?
• Попробуйте узнать еще один интересный факт о треугольнике и его площади, которым вы можете поделиться с классом.

ИНТЕРАКТИВ: Треугольник

Подсказка:

• Как знание формулы площади параллелограмма помогает понять формулу площади треугольника?
• Есть две переменные, основание и высота, которые определяют площадь треугольника. Треугольник также имеет размеры углов и длины сторон для двух «неосновных» сторон. Попробуйте поэкспериментировать со всеми этими мерами.

Пока учащиеся работают над задачами, ищите примеры, которыми можно поделиться в обсуждении «Способы мышления»:

• Учащиеся, которые понимают, что если высота и основание постоянны, а вершина движется по параллельной линии, площадь остается постоянной
• Учащиеся, которые понимают, что если одна переменная постоянна, увеличение (или уменьшение) другой переменной также увеличивается ( или уменьшается) площадь
• Учащиеся, которые признают, что если основание (или высота) увеличивается (или уменьшается) в несколько раз, то площадь увеличивается (или уменьшается) во столько же раз
• Учащиеся, которые не видят зависимости между высотой , основание и площадь
• Учащиеся, узнающие взаимосвязь между формулой площади параллелограмма и площадью треугольника

Ответы

• При скольжении вершины треугольника по прямой площадь остается неизменной.
• Возможный ответ: Основание треугольника всегда одинаково. Поскольку вершина остается на линии, параллельной основанию, высота всегда будет одинаковой. Поскольку площадь треугольника зависит только от основания и высоты, площадь не изменится.

Рабочее время

• Выберите один из своих выводов о том, что происходит с площадью треугольника при изменении одной или нескольких переменных.
• Будьте готовы продемонстрировать свой вывод с помощью интерактивного треугольника и подкрепить свое мышление математически.

Предположим, что основание треугольника лежит на одной из двух параллельных прямых, а вершина, противоположная основанию, лежит на другой параллельной прямой.

• Если сдвинуть вершину вдоль линии, как вы думаете, что произойдет с площадью треугольника? Используйте интерактивный треугольник, чтобы проверить свой прогноз.
• Объясните свои результаты.

ИНТЕРАКТИВ: Треугольник

Предложите учащимся поделиться своей работой. Обязательно покажите работы студентов, у которых возникли проблемы, и тех, кто сделал неверные выводы, так как всем учащимся будет полезно обсуждение. Используйте интерактивный треугольник для проверки утверждений, созданных учащимися.

Предложите учащимся, решившим задачу-вызов, поделиться своим мнением. Попросите учащихся критически оценить, имеют ли смысл их рассуждения.

ELL: Как и в других дискуссиях, поощряйте учащихся, изучающих английский язык, использовать изученную академическую лексику. Вводите новую лексику по мере необходимости. По мере участия в обсуждении обязательно следите за знанием темы.

Performance Task

• Делайте заметки о выводах ваших одноклассников относительно того, что происходит с площадью треугольника, когда вы меняете одну или несколько переменных.

Подсказка:

В присутствии одноклассников задавайте вопросы, например:

• Что вас удивило при исследовании площади треугольника?
• Насколько ваши выводы о площади треугольника соотносятся с выводами других докладчиков?

Предложите учащимся самостоятельно решить эту задачу.

Когда вы просматриваете ответы на задачу, предложите учащимся поделиться своими методами решения. Определите следующие способы мышления и исправьте любые неправильные представления:

• Учащиеся, которые правильно используют формулы площади для вычисления площадей
• Учащиеся, которые не используют формулу площади трапеции для первой фигуры, а вместо этого находят площадь треугольника и площадь прямоугольника и складывают две площади
• [общая ошибка] Учащиеся, использующие основание 5 дюймов вместо 15 дюймов при вычислении площади трапеции (т. е. не прибавить 5 дюймов + 10 дюймов, чтобы найти длину большего основания)

• Площадь трапеции составляет 100  в ² .

Время работы

• Найдите площадь этой трапеции.

Предложите учащимся самостоятельно решить эту задачу.

Когда вы просматриваете ответы на эти задачи, предложите учащимся поделиться своими методами решения.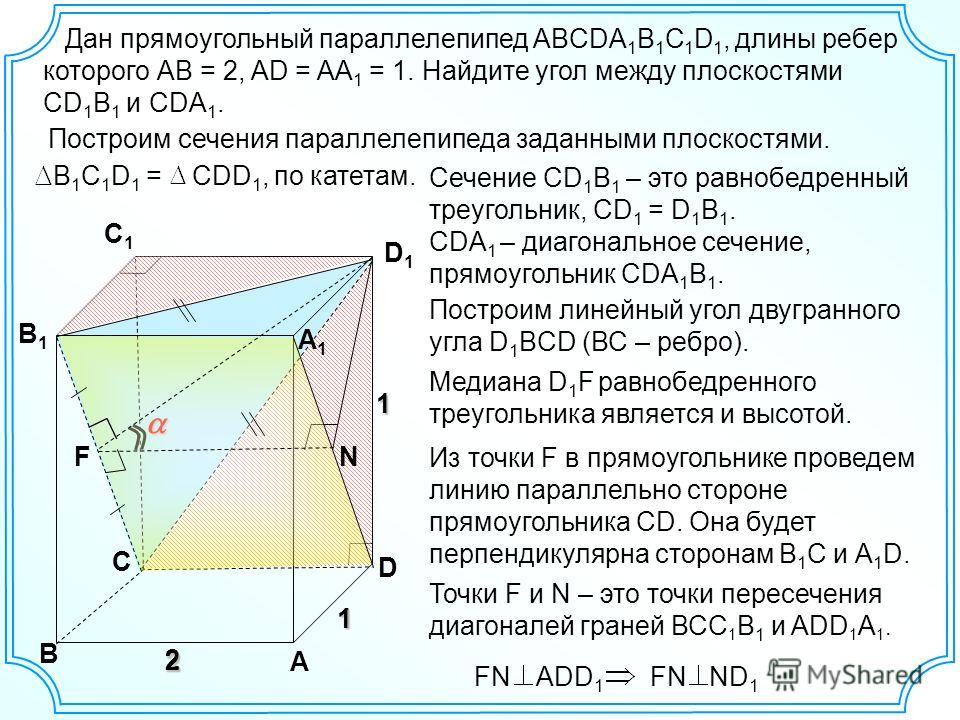 Определите следующие способы мышления и исправьте любые неправильные представления:

• [распространенная ошибка] Учащиеся, которые не используют правильное основание для нахождения площади треугольника
• Учащиеся, которые не обозначают свои ответы квадратными единицами измерения

• Площадь треугольника 17,2961 см ² .

Рабочее время

• Найдите площадь этого треугольника.

Пусть пары тихо обсудят, как они могут найти площадь параллелограмма, трапеции и треугольника, если знают формулу площади прямоугольника.

Пока учащиеся работают вместе, прислушивайтесь к учащимся, у которых все еще могут быть неправильные представления, чтобы вы могли обсудить их в ходе обсуждения в классе.

Через несколько минут обсудите резюме всем классом. Просмотрите следующие пункты:

• Части параллелограмма можно перемещать, чтобы получился прямоугольник. Как только вы сформировали прямоугольник, вы можете найти его площадь. Формула площади параллелограмма: A = bh , где b — основание, а h — высота.

• Вы можете сделать копию трапеции, сложить две трапеции вместе, чтобы получить параллелограмм, найти площадь параллелограмма и взять половину этой площади, чтобы получить площадь исходной трапеции. Формула площади трапеции равна 9.0009 A = 12( b 1 + b 2) h , где b 1 — одно основание, b 2 — другое основание, а h — высота.

• Вы можете скопировать треугольник и соединить треугольник и его копию, чтобы получился параллелограмм. Площадь треугольника равна половине площади параллелограмма. Формула площади треугольника: A = 12 bh .
  ELL: Напишите ключевые моменты на плакате, чтобы учащиеся могли обращаться к ним на протяжении всего модуля. При работе с ELL предоставьте дополнительные материалы, такие как графические органайзеры, чтобы проиллюстрировать новые понятия и словарный запас, необходимые для изучения математики. Предложите учащимся записать всю информацию в свои тетради.

Формирующее оценивание

Прочитать и обсудить

• Площадь прямоугольника равна произведению его основания на высоту.
  A = bh
• Площадь параллелограмма равна произведению его основания на высоту.
  A = bh
• Площадь трапеции равна половине произведения суммы оснований на высоту.
  А = 12( б 1 + б 2) h
• Площадь треугольника равна половине произведения основания на высоту.
  A = 12 bh

Подсказка:

Можете ли вы:

• Вычислить площадь треугольника, параллелограмма или трапеции, зная значения оснований и высоты?
• Вычислить высоту треугольника, параллелограмма или трапеции, зная значения основания(ей) и площади?

Пусть каждый учащийся напишет краткое размышление перед окончанием урока. Просмотрите размышления, чтобы узнать, как учащиеся помнят формулу площади треугольника.

Рабочее время

Напишите размышления об идеях, обсуждавшихся сегодня в классе. Используйте приведенный ниже образец предложения, если он окажется вам полезным.

Насколько я помню, формула площади треугольника – это …

ACT Math Help

Студенты, нуждающиеся в помощи ACT Math, получат большую пользу от нашей интерактивной программы. Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по ACT Math. Имея под рукой обязательные концепции обучения и соответствующие практические вопросы, вы мгновенно получите много помощи по ACT Math. Получите помощь сегодня с нашей обширной коллекцией необходимой информации ACT Math.

По мере того, как колледжи становятся все более избирательными, вступительные тесты, такие как ACT, становятся все более важными. Математическая часть ACT, проверенная в нескольких разделах, направлена ​​на то, чтобы понять, как учащиеся старших классов справляются с различными навыками алгебры, геометрии и предварительного исчисления. При надлежащем изучении математический раздел ACT становится более простым. Кроме того, поскольку у большинства учащихся первоначальные проблемы с выполнением разделов в указанные сроки, свободное владение материалом полезно для повышения эффективности. Нужны ли вам лучшие репетиторы по математике ACT в Атланте, репетиторы английского языка ACT в Хьюстоне или лучшие репетиторы по математике ACT в Сан-Франциско, работа с профессионалом может вывести ваше обучение на новый уровень.

Учащиеся, сдающие ACT, должны понимать большое количество тем, в том числе:

Предварительная алгебра: Темы в этом разделе включают числовые ряды, десятичные дроби, дроби, квадратные корни, показатели степени, научное представление, пропорции, абсолютное значение и начальное значение. вероятность. Эти навыки имеют решающее значение для понимания, поскольку они составляют основу знаний, необходимых в дальнейшем.

Алгебра: вычисление алгебраических выражений посредством подстановки, выражения факториальных отношений и решения квадратных уравнений.

Координатная геометрия: распознавание и определение линий, плоскостей, сегментов, многочленов, окружностей и других кривых; неравенства; определение уклона; и нахождение середины параллельных и перпендикулярных прямых и отрезков.

Плоская геометрия: Параллельные и перпендикулярные линии составляют основу плоской геометрии. Учащихся просят понять взаимосвязь между различными углами, определяемыми пересечением параллельных прямых. Кроме того, учащиеся узнают, как изображать треугольники, прямоугольники и другие геометрические фигуры в системе координат и использовать такие процессы, как перенос, вращение и отражение, для перемещения этих фигур. Наконец, учащиеся изучают основы корректуры двух столбцов и абзацев. Доказательство конгруэнтности и подобия между треугольниками является основной конечной точкой планиметрии, поскольку аспекты системы координат, параллельных линий и пересекающихся линий требуют объединения в одну задачу.

Тригонометрия: Понимание прямых углов и тригонометрических функций, таких как синус, косинус и тангенс, проверяется в разделе тригонометрии. Студентов часто просят найти значение неизвестной переменной, для чего требуются базовые знания функций тригонометрии.

Успех в математическом разделе ACT часто требует визуализации проблемы. Для учащихся, начинающих подготовку к ACT, это часто сложные наборы навыков, на формирование которых требуется время. Начиная с практических моделей, таких как деревянные блоки различной формы, или используя цветную плотную бумагу для обозначения частей формы или линии, вы можете создать визуальное представление, на основе которого можно построить необходимую информацию. Вы также можете воспользоваться репетиторством по математике ACT или бесплатной цифровой книгой для подготовки к ACT, предлагаемой репетиторами Varsity Tutors.

Тем не менее, основным средством достижения успеха в математическом разделе ACT является свободное время для изучения и решения практических задач. Студенты должны планировать просмотр заблаговременно и просматривать содержание, прежде чем пытаться решить большое количество практических задач.