Периметр треугольника 5 класс: Как найти периметр треугольника 🔺 формула нахождения

Содержание

Мерзляк 5 класс — § 14. Треугольник и его виды

Ответы к учебнику для 5 класса. А. Г. Мерзляк
Переход на главную страницу сайта

Вопросы к параграфу

1. Какие бывают виды треугольников в зависимости от вида их углов?

остроугольные — все из углы острые;
прямоугольные — один из углов треугольника прямой — равен 90°;
тупоугольные — один из углов треугольника тупой.

2. Какой треугольник называют остроугольным? Прямоугольным? Тупоугольным?

Остроугольные прямоугольники — это треугольники, у которых все углы острые (< 90°).
Прямоугольные треугольники — это прямоугольники, у которых один из углов прямой (= 90°).
Тупоугольные треугольники — это треугольники, у которых один из углов тупой (> 90°).

3. Какие бывают виды треугольников в зависимости от количества равных сторон?

равнобедренные треугольники — 2 стороны равны;

равносторонние треугольники — 3 стороны равны.

4. Какой треугольник называют равнобедренным? Равносторонним? Разносторонним?

Равнобедренный треугольник — это треугольник, у которого две стороны равны.
Равносторонний треугольник — это треугольник, у которого три стороны равны.
Разносторонний треугольник — это треугольник, у которого все стороны имеют различную длину.

5. Как называют стороны равнобедренного треугольника?

равные стороны равнобедренного треугольника называют боковыми сторонами;
отличающуюся по длине сторону равнобедренного треугольника называют основанием.

6. По какой формуле вычисляют периметр равностороннего треугольника? — Периметр равностороннего треугольника равен произведению числа 3 и длины его стороны : P = 3a.

Решаем устно

1. Чему равен периметр восьмиугольника, каждая сторона которого равна 4 см?

8 • 4 = 32 (см) — периметр восьмиугольника.

Ответ: 32 см.

2. Вычислите сумму 27 + 16 + 33 + 24.

27 + 16 + 33 + 24 = (27 + 33) = (16 + 24) = 60 + 40 = 100

Ответ: 100.

3. Каких чисел не хватает в цепочке вычислений?

4. На трёх кустах расцвело 15 роз. Когда на одном из этих кустов распустились ещё 3 розы, то на всех кустах роз стало поровну. Сколько роз было на каждом кусте вначале?

1) Мы знаем, что вначале на всех кустах было 15 роз, но потом на одной розе распустилось ещё 3 цветка:

15 + 3 = 18 (цветов) — стало на всех кустах в конце.

2) Мы знаем, что в конце на каждом из трёх кустов роз было поровну:

18 : 3 = 6 (цветов) — было на каждом кусте в конце.

3) Мы знаем, что на одном из кустов роз вначале было на 3 меньше:

6 — 3 = 3 (цветка) — было на одном из кустов вначале.

4) Мы знаем, что количество роз на остальных кустах не изменилось, то есть было и осталось по 6 цветков.

Ответ: 6, 6 и 3 розы.

Упражнения

338. Определите вид треугольника, изображённого на рисунке 121, в зависимости от вида его углов и количества равных сторон.

а) треугольник ABC — это разносторонний остроугольный треугольник;
б) треугольник MNK — это разносторонний прямоугольный треугольник;
в) треугольник PEF — это равнобедренный остроугольный треугольник;
г) треугольник QSR — это равнобедренный тупоугольный треугольник;
д) треугольник OTR — это разносторонний тупоугольный треугольник;
е) треугольник DAB — это равнобедренный прямоугольный треугольник.

339. Начертите:

RTQ — разносторонний остроугольный треугольник;
JLD — равнобедренный прямоугольный треугольник;
POS — равнобедренный тупоугольный треугольник.

340. Начертите:

ABC — разносторонний прямоугольный треугольник;
MNK — разносторонний тупоугольный треугольник;
EFH — равнобедренный остроугольный треугольник.

341. Найдите периметр треугольника со сторонами 16 см, 22 см и 28 см.

Периметр треугольника равен сумме длин все его сторон.

P = 16 + 22 + 28 = 66 (см)

Ответ: P = 66 см.

342. Найдите периметр треугольника со сторонами 14 см, 17 см и 17 см.

Периметр треугольника равен сумме длин все его сторон.

P = 14 + 17 + 17 = 48 (см)

Ответ: P = 48 см.

343. Начертите произвольный треугольник, измерьте его стороны и углы, найдите периметр и сумму углов этого треугольника.

Начертим произвольный треугольник ABC.

При помощи линейки измерим длины его сторон:

AB = 4,2 см
BC = 3,2 см
AC = 4,6 см

При помощи транспортира измерим его углы:

∠A = 42º
∠B = 74º
∠C = 64º

Найдём периметр треугольника ABC:

P = AB + BC + AC =4,2 + 3,2 + 4,6 = 12 (см)

∠A + ∠B + ∠C = 42º + 74º + 64º = 180º

Ответ: в треугольнике ABC: AB = 4,2 см, BC = 3,2 см, AC = 4,6 см, ∠A = 42º, ∠B = 74º, ∠C = 64º, периметр P = 12 см, сумма углов равна 180º.

344. Одна сторона треугольника равна 24 см, вторая сторона — на 18 см больше первой, а третья сторона — в 2 раза меньше второй. Найдите периметр треугольника.

1) 24 + 18 = 42 (см) — длина второй стороны треугольника.

2) 42 : 2 = 21 (см) — длина третьей стороны треугольника.

3) 24 + 42 + 21 = 87 (см) — периметр треугольника.

Ответ: P = 87 см.

345. Одна сторона треугольника равна 12 см, вторая сторона в 3 раза больше первой, а третья — на 8 см меньше второй. Найдите периметр треугольника.

1) 12 • 3 = 36 (см) — длина второй стороны треугольника.

2) 36 — 8 = 28 (см) — длина третьей стороны треугольника.

3) 12 + 36 + 28 = 78 (см) — периметр треугольника.

Ответ: P = 78 см.

346. 1) Найдите периметр равнобедренного треугольника, основание которого равно 13 см, а боковая сторона — 8 см.

У равнобедренного треугольника боковые стороны равны. Значит у данного треугольника дву стороны по 8 см и одна сторона (основание) — 13 см.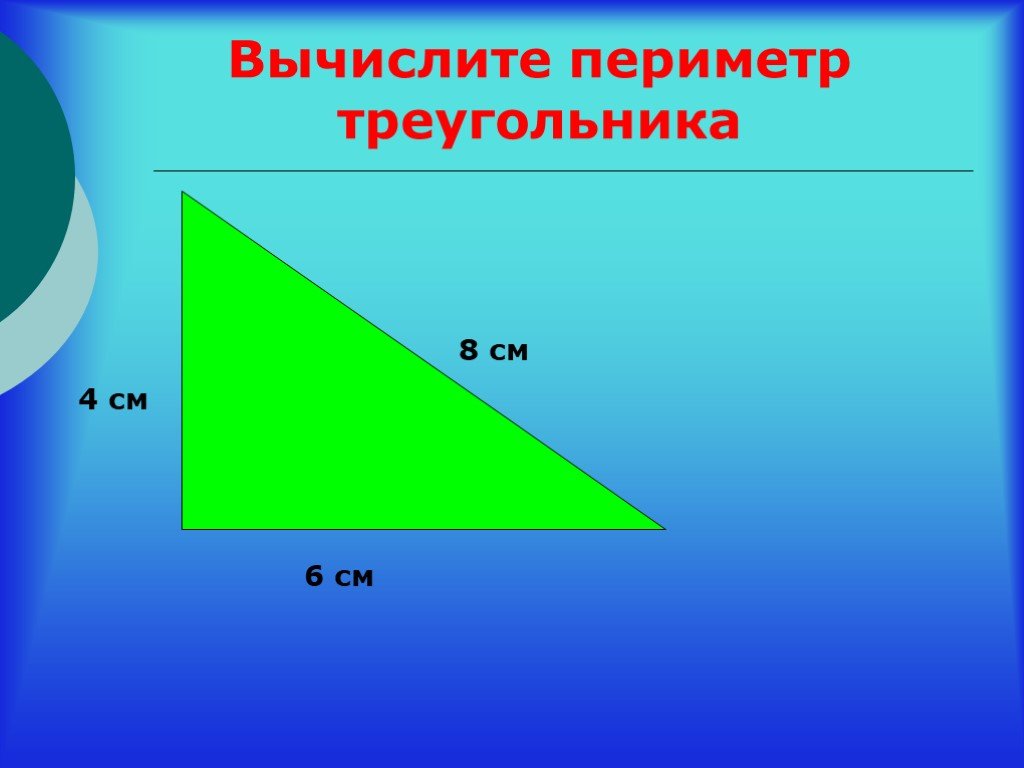 Найдём периметр:

8 + 8 + 13 = 29 (см) — периметр треугольника.

Ответ: 29 см.

2) Периметр равнобедренного треугольника равен 39 см, а основание — 15 см. Найдите боковые стороны треугольника.

Мы знаем, тто периметр треугольника — это сумма длин всех его сторон. Также мы знаем, что боковые стороны равнобедренного треугольника равны. Найдем длину боковой стороны:

(39 — 15) : 2 = 24 : 2 = 12 (см) — длина боковой стороны.

Ответ: Каждая из двух боковых сторон этого равнобедренного треугольника равна 12 см.

347. Периметр равнобедренного треугольника равен 28 см, а боковая сторона — 10 см. Найдите основание треугольника.

Мы знаем, тто периметр треугольника — это сумма длин всех его сторон. Также мы знаем, что боковые стороны равнобедренного треугольника равны. Найдем длину основания:

28 — 10 • 2 = 28 — 20 = 8 (см) — длина основания.

Ответ: 8 см.

348. Периметр треугольника равен p см, одна сторона — 22 см, вторая сторона — b см. Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если р = 72, b = 26.

Пусть третья сторона равна с см. Составим выражения для нахождения длины третьей стороны треугольника:

с = p — 22 — b (см)

При р = 72, b = 26:

с = 72 — 22 — 26 = 50 — 26 = 24 (см).

Ответ: с = p — 22 — b, с = 24 см.

349. Периметр треугольника равен 97 см, одна сторона — а см, вторая — b см. Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если а = 32, b = 26.

Пусть третья сторона равна с см. Составим выражения для нахождения длины третьей стороны треугольника:

с = 97 — а — b (см)

При а = 32, b = 26:

с = 97 — 32 — 26 = 65 — 26 = 39 (см).

Ответ: с = 97 — а — b, с = 39 см.

350. С помощью линейки и транспортира постройте треугольник ABC и укажите его вид, если:

1) две стороны равны 3 см и 6 см, а угол между ними — 40° — разносторонний тупоугольный треугольник (тупым является угол B).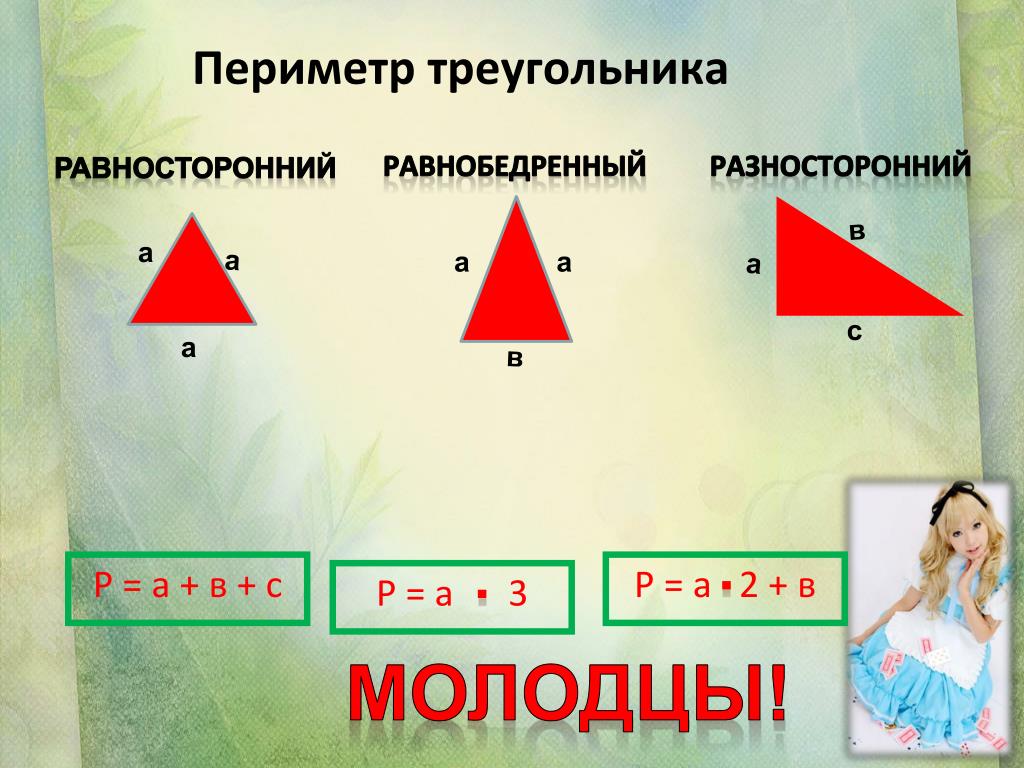

2) две стороны равны 2 см 5 мм и 5 см, а угол между ними — 130°

— разносторонний тупоугольный треугольник (тупым является угол А).

3) две стороны равны по 3 см 5 мм, а угол между ними — 54° — равнобедренный остроугольный треугольник

4) сторона АВ равна 4 см, а углы САВ и СВА соответственно равны 30° и 70° — разносторонний остроугольный треугольник.

5) сторона АВ равна 2 см 5 мм, а углы САВ и СВА соответственно равны 100° и 20° — разносторонний тупоугольный треугольник.

6) сторона ВС равна 5 см, а углы ABC и ВСА соответственно равны 30° и 60° — разносторонний прямоугольный треугольник.

7) сторона ВС равна 5 см 5 мм, а углы ABC и ВСА равны по 45° — равнобедренный прямоугольный треугольник.

8) сторона АС равна 5 см 5 мм, а углы ВАС и ВСА равны по 60°

351. С помощью линейки и транспортира постройте треугольник ABC и укажите его вид, если:

1) две стороны равны 3 см и 4 см, а угол между ними — 90° — разносторонний прямоугольный треугольник.

2) две стороны равны по 4 см 5 мм, а угол между ними — 60° — равносторонний остроугольный треугольник.

3) сторона АС равна 6 см, а углы ВАС и ВСА соответственно равны 90° и 45° — равнобедренный прямоугольный треугольник.

4) сторона АВ равна 4 см 5 мм, а углы САВ и СВА соответственно равны 35° — равнобедренный тупоугольный треугольник.

352. Постройте треугольник, стороны которого содержат четыре точки, изображённые на рисунке 122.

353. Сколько треугольников изображено на рисунке 123?

а) Изображено 7 треугольников (4 маленьких и 3 больших).
б) Изображено 20 треугольников(12 маленьких, 6 средних и 2 больших).

Упражнения для повторения

354. Запишите все углы, изображённые на рисунке 124, и укажите вид каждого угла.

∠ABC — развёрнутый угол
∠ABM — острый угол
∠ABK — тупой угол
∠MBK — прямой угол
∠MBC — тупой угол
∠KBC — острый угол

355. Миша делал домашнее задание по математике с 16 ч 48 мин до 17 ч 16 мин, а Дима — с 17 ч 53 мин до 18 ч 20 мин. Кто из мальчиков дольше делал задание и на сколько минут?

1) 17 ч 16 мин — 16 ч 48 мин = 16 ч 76 мин — 16 ч 48 мин = 28 мин — делал задание Миша.

2) 18 ч 20 мин — 17 ч 53 мин = 17 ч 80 мин — 17 ч 53 мин = 27 мин — делал задание Дима.

3) 28 мин — 27 мин = 1 мин — делал дольше Миша, чем Дима.

Ответ: Миа делал домашнее задание на 1 минуту дольше, чем Дима.

356. Решите уравнение:

357. Вместо звёздочек поставьте цифры так, чтобы действие было выполнено правильно:

Задача от мудрой совы

358. Каждый учащийся гимназии изучает по крайней мере один из двух иностранных языков. Английский язык изучают 328 учеников, французский язык — 246 учеников, а английский и французский одновременно — 109 учеников. Сколько всего учеников учится в гимназии?

1) 328 — 109 = 219 (учеников) — изучает только английский язык.

2) 246 — 109 = 137 (учеников) — изучает только французский язык.

3) 219 + 109 + 137 = 465 (учеников) — всего в гимназии.

Ответ: 465 учеников.

Ответы к учебнику для 5 класса. А. Г. Мерзляк
Переход на главную страницу сайта

урок по теме «Треугольники и их виды» 5 класс | План-конспект урока по математике (5 класс):

Слайд 1

Девиз урока: «Учиться можно весело… Чтобы переваривать знания, надо поглощать их с аппетитом». Анатоль Франс

Слайд 2

Метапредмет – Изменение и развитие Знаешь ли ты? В истории математики известен такой случай. Однажды в Германии в конце XVIII в., для того чтобы заставить учеников поработать, учитель дал им задание – сложить все числа от 1 до 100. К аково же было его удивление, когда уже через несколько минут один из учеников сказал ответ: сумма равна 5050. Э тот ученик, Карл Фридрих Гаусс, впоследствии стал великим математиком. ИНТЕРЕСНО! Прозвенел звонок! Начинается урок!

Слайд 4

Задание на внимание целеполагание На рисунке изображены равносторонние треугольники.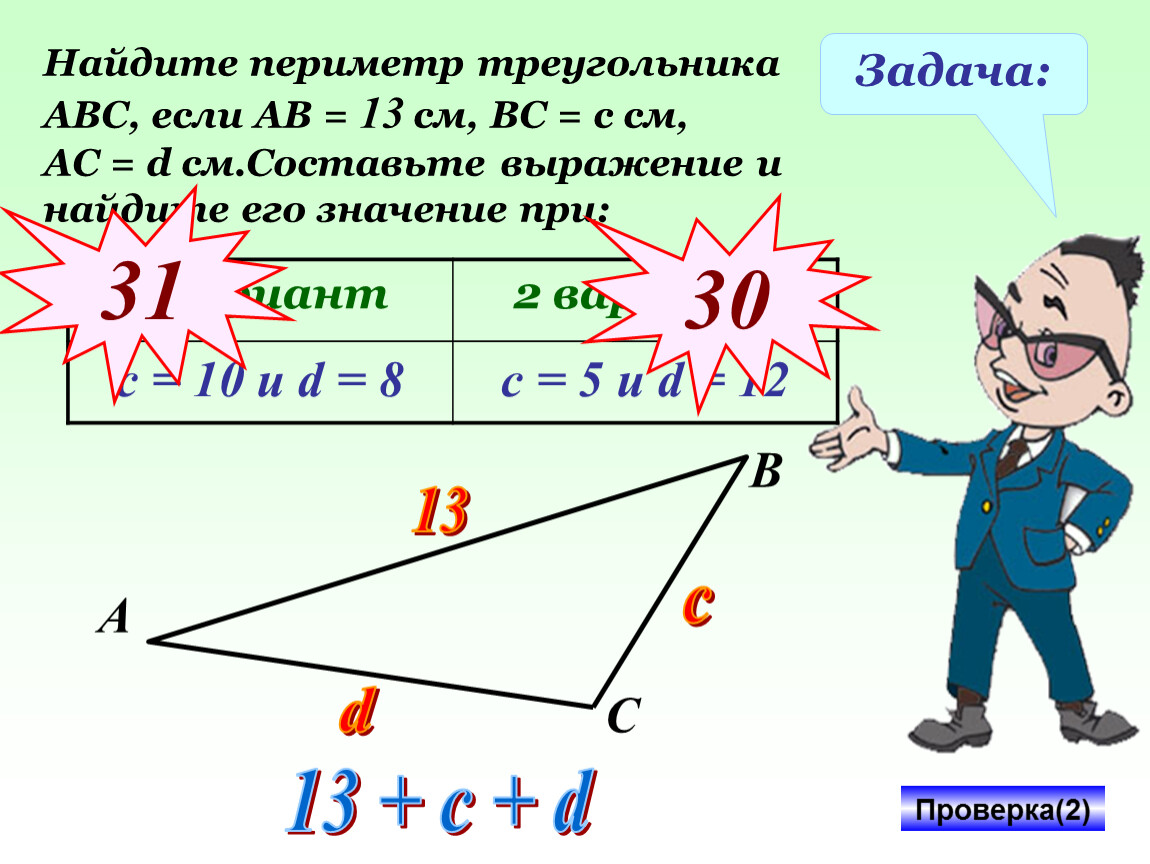 Сколько треугольников вы видите? устно № 1 Часто знает и дошкольник, Что такое треугольник, А уж вам-то как не знать! Но совсем другое дело – Быстро, точно и умело Треугольники считать. Например, на картинке этой Сколько разных? Рассмотри! Все внимательно исследуй И по краю, и внутри! На рисунке изображено 13 треугольников .

Слайд 5

ТРЕУГОЛЬНИКИ И ИХ ВИДЫ Тема урока: 18.01 Целеполагание. Вхождение в тему

Слайд 6

Треугольники и их виды Определение треугольника, элементы треугольника Виды треугольников Сумма углов треугольника Периметр треугольника Узнать … … Освоить……. Закрепить……. Проверить……. Оценить…… Цели и задачи урока

Слайд 7

Ключевое слово урока целеполагание

Слайд 8

Выбрать среди геометрических фигур треугольники. Сколько углов имеет треугольник? Сколько сторон имеет треугольник? Как найти периметр треугольника? 1 2 3 4 5 6

Слайд 12

Анализ результатов проверочной работы Вхождение в тему урока и создание условий для осознанного восприятия нового материала. Наши итоги 1 2 3 3 12 4 6 5 Характерные ошибки… Как исправить… Над чем поработать дома с родителями…

Слайд 13

Классификация треугольников по сторонам равнобедренный разносторонний равносторонний

Слайд 14

Классификация треугольников по сторонам Организация и самоорганизация учащихся. Организация обратной связи

Слайд 15

Классификация треугольников по углам тупоугольный прямоугольный остроугольный

Слайд 16

Классификация треугольников по углам Организация и самоорганизация учащихся. Организация обратной связи

Слайд 17

Определить вид треугольника по градусной мере его углов Задание: соединить стрелочкой левый и правый столбики а) 45 0 , 45 0 , 90 0 б) 25 0 , 75 0 , 80 0 в) 120 0 , 30 0 , 30 0 г) 60 0 , 60 0 , 60 0

Слайд 18

Классификация треугольников по углам Организация и самоорганизация учащихся. Организация обратной связи Примеры треугольников

Слайд 19

Виды треугольников Практикум Определите вид треугольника, углы которого равны: УЧЕБНИК № 4 06 ? тупоугольный а) 24 о , 137 о , 19 о ; ? прямоугольный б) 40 о , 50 о , 90 о ; ? остроугольный в) 35 о , 60 о , 85 о ;

Слайд 20

Чертим треугольники Практикум а) Начертите на нелинованной бумаге прямоугольный треугольник, у которого стороны, образующие прямой угол, равны 3 см и 4 см.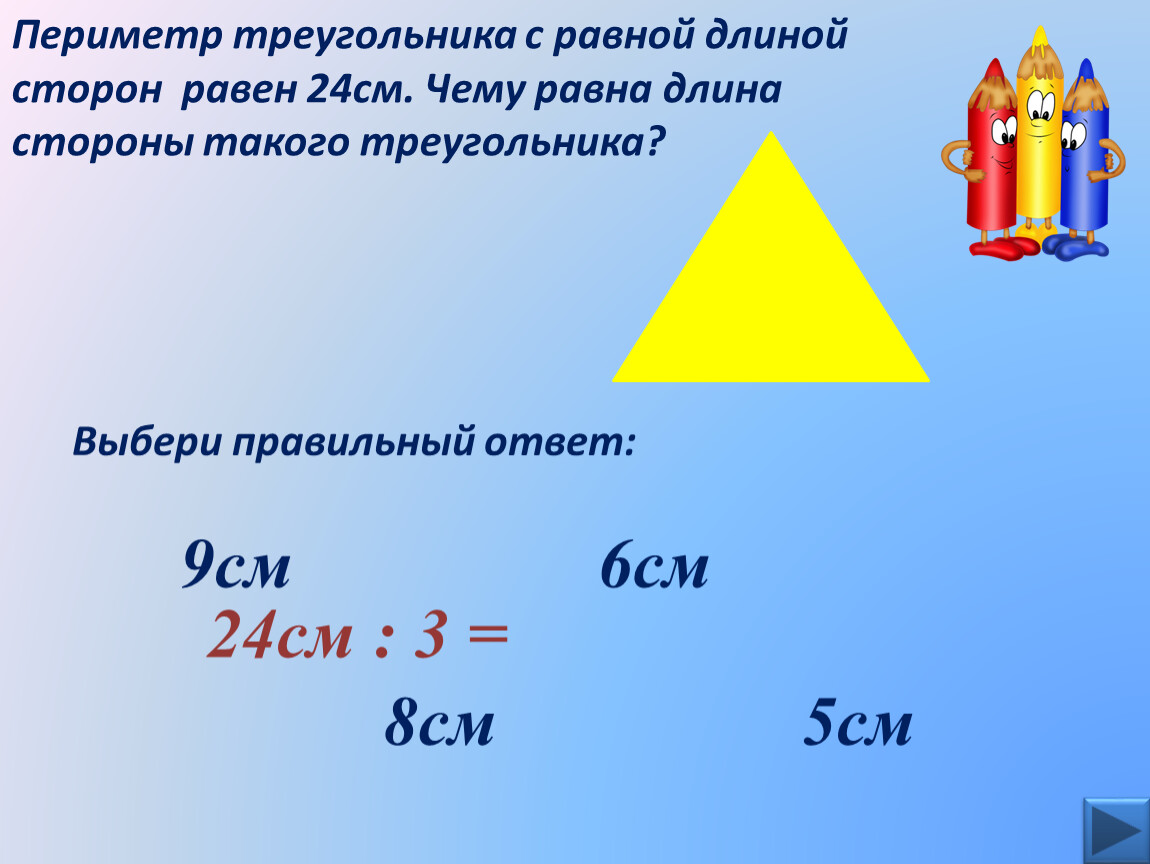 Обозначьте его. Измерьте сторону, противолежащую прямому углу. УЧЕБНИК № 4 10 построение АВ = 5 см А В С 4 см 3 см 5 см

Слайд 21

Периметр треугольника Практикум а) Проволоку длиной 15 см согнули так, что получился равносторонний треугольник. Чему равен периметр этого треугольника? Чему равна его сторона? УЧЕБНИК № 528 периметр 15 см сторона 15 : 3 = 5 (см)

Слайд 22

Периметр треугольника Практикум Вычислите периметр: УЧЕБНИК № 41 7 периметр 25 + 45 + 45 = 115 (мм) б) равнобедренного треугольника с основанием 25 мм и боковыми сторонами, равными 45 мм.

Слайд 23

Периметр треугольника Проверка полученных результатов. Коррекция. В равнобедренном треугольнике периметр равен 36 см, а основание равно 10 см. найдите длину боковой стороны. УЧЕБНИК № 41 8 решение (36 – 10) : 2 = 13 (см)

Слайд 24

Обсуждаем домашнее задание Вхождение в тему урока и создание условий для осознанного восприятия нового материала. б) Взяли проволоку длиной 17 см и из нее согнули треугольник, две стороны которого равны 5 см и 6 см. Ч то вы можете сказать об этом треугольнике? УЧЕБНИК № 4 16 ? Равнобедренный, т.к. 17 – (5 + 6) = 6 (см). Вычислите периметр равностороннего треугольника со стороной 8 см. УЧЕБНИК № 4 1 7 ? Р = 8 + 8 + 8 = 24 (см) б) В равнобедренном треугольнике периметр равен 21 см, а боковая сторона равна 6 см. найдите длину основания. УЧЕБНИК № 4 1 8 ? 2 ∙ 6 = 12 (см) 21 – 12= 9(см)

Слайд 25

Египетская цивилизация Подведение итогов, рефлексия, домашнее задание. Египетские пирамиды — величайшие архитектурные памятники Древнего Египта, среди которых одно из «семи чудес света» — пирамида Хеопса. Что представляют собой боковые грани этих пирамид? Где в жизни вы встречали подобные фигуры?

Слайд 26

Подведем итоги Подведение итогов, рефлексия сегодня я узнал… было интересно… было трудно… я выполнял задания… я понял, что… теперь я могу… я почувствовал, что … я приобрел… я научился… у меня получилось … я смог… я попробую… меня удивило… урок дал мне для жизни… мне захотелось…

Слайд 27

Подведение итогов, рефлексия, домашнее задание. Задачное множество Домашнее задание п.7.1, №п.7.1, №523, 534, выполнить задания на сайте » Учи.ру » — ГЕОМЕТРИЯ. Треугольники

Слайд 28

Существует ли треугольник с углами: а) 30 о , 60 о , 90 о ; б) 46 о , 160 о , 4 о ? 2) Найдите периметр треугольника, имеющего стороны 2 см 5 мм, 3 см, 4 см 7мм. 3) Может ли в треугольнике быть: а) два тупых угла; б) тупой и прямой углы? 4) Определите вид треугольника, а) если углы равны 40 0 , 50 0 , 90 0 ; б) если стороны равны 3 см, 5см, 3см? 5) В каком треугольнике сумма углов больше: в остроугольном или тупоугольном треугольнике? Проверка: а) да; б) нет. 2) 10 см 2 мм. а) нет; б) нет. 4) а) прямоугольный; б) равнобедренный. 5) Одинакова. Оценка: 8 верных ответов – 5 7,6 верных ответов – 4 4, 5 верных ответа — 3

Периметр треугольника: определение, формула, примеры, часто задаваемые вопросы

Что такое периметр треугольника?

Периметр треугольника равен сумме всех его сторон. Другими словами, периметр треугольника — это общая длина его границы.

Треугольник — это многоугольник, замкнутая двумерная фигура с тремя сторонами, тремя углами и тремя вершинами. Его периметр вычисляется путем сложения длин всех сторон. Периметр двумерной формы измеряется в линейных единицах измерения, таких как дюймы, футы, ярды и т. д.

Родственные игры

Периметр треугольника: определение

Периметр треугольника можно определить как сумму всех сторон треугольника.

Треугольник имеет три стороны.

Периметр треугольника $=$ Сумма трех сторон треугольника. Давай выясним.

Пусть a, b и c — длины трех сторон треугольника.

Периметр треугольника $= a + b + c$

Как найти периметр треугольника

Шаг 1: Запишите длины всех трех сторон данного треугольника. Убедитесь, что длины указаны в одних и тех же единицах измерения.

Шаг 2: Добавьте длины трех сторон.

Шаг 3: Сумма представляет собой периметр данного треугольника. Присвойте периметру ту же единицу, что и длину сторон. 9\circ)$ известен как равносторонний треугольник.

Рассмотрим равносторонний треугольник ABC, длина каждой стороны которого равна a единиц.

Периметр равностороннего треугольника $= a + a + a = 3a$

Итак, как найти периметр треугольника с тремя равными сторонами? Просто умножьте длину стороны на 3!

Периметр равнобедренного треугольника

Треугольник с двумя равными сторонами известен как равнобедренный треугольник.

Так как две стороны треугольника равны, мы имеем $a = b$ 92}$

Периметр равнобедренного прямоугольного треугольника

Прямоугольный треугольник, в котором основание и высота (два катета) имеют одинаковую длину, называется равнобедренным прямоугольным треугольником.

Применение периметра треугольника

Взгляните на треугольный парк. Предположим, нам нужно обнести его забором по внешней границе, нам нужно найти длину забора, необходимого для покрытия парка. Как мы это делаем? Необходимую длину забора можно рассчитать, найдя общую длину границы (периметра) треугольника.

Решенные примеры на периметр треугольника

1. Найдите периметр равностороннего треугольника со стороной 6 дюймов.

Решение:

Сторона равностороннего треугольника $= a = 6$ дюймов

Периметр равностороннего треугольника $= 3a$

$=3 \times 6$

$= 1 8$ дюймов

2. Чему равен периметр равнобедренного треугольника, равные стороны которого равны 4 футам каждая, а неравная сторона равна 6 футам?

Решение:

Пусть равные стороны равны $a = 4$ футам, а неравные стороны равны $b = 6$ футам

Периметр заданного равнобедренного треугольника $= 2a+b$ $=(2 \ раз 4)+ 6$

$= 14$ футов

3. Если периметр данного треугольника равен 34 футам, какова длина недостающей стороны?

Решение:

В $\Delta XYZ$ имеем

$XY = 9$ футов

$XZ = 12$ футов

Периметр $= 34$ футов … задано

Периметр треугольника $= XY + YZ + XZ$

$34 = 9 + 12 + YZ$

$34 = YZ + 21$

$YZ = 13$ футов

4. Каково значение x, если периметр треугольника PQR равен 40 единицам? Также найдите длину трех сторон.

Решение:

Периметр треугольника $PQR = PQ + QR + PR$

$40 = x + x + 4 + x + 6$ 92} = \sqrt{36+36} = \sqrt{72} = 6\sqrt{2}$ дюймов

Периметр прямоугольного треугольника$ = b + p + h = 6 + 6 + 6\sqrt{2} = (12 + 6\sqrt{2})$ дюймов

Практические задачи на периметр треугольника

1
Каков периметр $\Delta ABC$?
12 единиц
10 единиц
8 единиц
7 единиц
Правильный ответ: 10 единиц
Периметр равнобедренного треугольника $= 3 + 3 + 4 = 6 + 4 = 10$ дюймов 9 0007 2
Периметр равностороннего треугольника равен 45 дюймам. Чему равна сторона треугольника?
22,5 дюйма
25 дюймов
15 дюймов
9 дюймов
Правильный ответ: 15 дюймов
Пусть сторона равностороннего треугольника равна а дюймам
Периметр равностороннего треугольника = 3a = 45 дюймов
$3a = 45$
$a = \frac{45}{3} = 15$ дюймов
3
Если периметр разностороннего треугольника равен 32 футам.
Если две стороны равны 12 футам и 7 футам, то чему равна третья сторона?
13 футов
10 футов
27 футов
20 футов
Правильный ответ: 13 футов
Пусть $a = 12$ футов, $b = 7$ футов и $c = ?$ футов
Peri метр треугольник $= a + b + c$
$32 = 12 + 7 + c$
$c = 32\;-\;12\;-\;7 = 32\;-\;19 = 13$ футов
4
Найдите периметр прямоугольного равнобедренного треугольника, две стороны которого равны 4 дюймам каждая.
$(4 + 4\sqrt{2})$ дюймов
$32\sqrt{2}$ дюймов
$12\sqrt{2}$ дюймов 92} = \sqrt{16 + 16} = \sqrt{32} = 4\sqrt{2}$ дюймов
Периметр прямоугольного треугольника $= b + p + h = 4 + 4 + 4\sqrt{2} = (8 + 4\sqrt{2})$ дюймов
Часто задаваемые вопросы о периметре треугольника
В чем разница между площадью и периметром?
Площадь — это область, ограниченная сторонами 2D-фигуры, тогда как периметр — это общая длина границы фигуры.
По какой формуле находится площадь треугольника?
Площадь треугольника $= \frac{1}{2} \× основание \× высота$
Чему равен полупериметр треугольника?
Полупериметр — это половина периметра треугольника. Если стороны треугольника равны a, b и c, то полупериметр $= \frac{a + b + c}{2}$
Периметр треугольника ⭐ Формула, определение, примеры, факты
Дом
>
База знаний
>
Периметр треугольника – формула с примерами
Добро пожаловать в Brighterly, где наша миссия состоит в том, чтобы сделать математику увлекательной и увлекательной для детей всех возрастов! Сегодня мы исследуем увлекательный мир геометрии, сосредоточившись на периметре треугольника. Эта фундаментальная концепция важна для понимания учащимися, поскольку она закладывает основу для более сложных математических тем. Итак, без лишних слов, давайте отправимся в приключение в царство периметров треугольников и откроем секреты этого геометрического чуда!
Каков периметр треугольника?
Периметр любой формы относится к общей длине ее внешних краев. В случае треугольника периметр равен сумме длин трех его сторон. Треугольники бывают разных типов, включая разносторонние, равнобедренные, равносторонние и прямоугольные треугольники. В зависимости от типа треугольника способ вычисления его периметра может незначительно отличаться. Продолжайте читать, чтобы узнать, как найти периметр треугольника и формулы для каждого типа треугольника!

Как найти периметр треугольника?
Найти периметр треугольника очень просто! Все, что вам нужно сделать, это сложить длины его трех сторон. Однако, если вам не хватает некоторых длин сторон, вам может понадобиться использовать другую информацию о треугольнике, чтобы найти недостающие значения. Например, вы можете использовать теорему Пифагора для прямоугольных треугольников или применить свойства равнобедренных и равносторонних треугольников. Ниже мы обсудим формулы для нахождения периметра различных типов треугольников.
Формула периметра треугольника
Общая формула для нахождения периметра треугольника:
Периметр = a + b + c
где ‘a’, ‘b’ и ‘c’ представляют длины из сторон треугольника.
Эта формула применима ко всем типам треугольников, но некоторые определенные типы треугольников обладают уникальными свойствами, которые могут упростить вычисления. Давайте изучим формулы для каждого типа треугольника!
Периметр разностороннего треугольника
Разносторонний треугольник имеет три стороны разной длины. Чтобы найти периметр разностороннего треугольника, просто используйте общую формулу:
Периметр = a + b + c
Периметр равнобедренного треугольника
У равнобедренного треугольника две стороны одинаковой длины. Поскольку две стороны равны, формула для его периметра:
Периметр = 2a + b
, где «a» — длина равных сторон, а «b» — длина оставшейся стороны.
Периметр равностороннего треугольника
У равностороннего треугольника три стороны одинаковой длины. Следовательно, формула для его периметра:
Периметр = 3а
, где «а» — длина каждой стороны.
Периметр прямоугольного треугольника
В прямоугольном треугольнике один угол равен 90 градусов. Чтобы найти его периметр, вы можете использовать общую формулу:
Периметр = a + b + c
Однако, если у вас есть только длины двух катетов (сторон, прилегающих к прямому углу), вы можете использовать по теореме Пифагора найти длину гипотенузы (стороны, противоположной прямому углу):
c² = a² + b²
Затем можно рассчитать периметр по общей формуле.
Периметр равнобедренного прямоугольного треугольника
Равнобедренный прямоугольный треугольник имеет один угол в 90 градусов и две равные стороны. Поскольку к прямому углу примыкают равные стороны, можно воспользоваться теоремой Пифагора, чтобы найти гипотенузу:
c² = a² + a²
Затем вычислить периметр по общей формуле.
Периметр равнобедренного, равностороннего и разностороннего треугольника
В качестве резюме, вот формулы для нахождения периметра равнобедренного, равностороннего и разностороннего треугольника:
Равнобедренный: Периметр = 2a + b
Равносторонний: Периметр = 3a
Scalene: Периметр = a + b + c
Помните об этих формулах, когда мы рассмотрим несколько примеров ниже!
Примеры периметра треугольника
Давайте рассмотрим несколько примеров, которые помогут вам понять, как найти периметр треугольника:
Разносторонний треугольник: Если разносторонний треугольник имеет стороны с длинами 5, 7 и 8, периметр равен: Периметр = 5 + 7 + 8 = 20
Равнобедренный треугольник: Если у равнобедренного треугольника две равные стороны с длинами 6 и оставшаяся сторона с длиной 4, периметр равен: Периметр = 2(6) + 4 = 12 + 4 = 16
Равносторонний треугольник: если длина сторон равностороннего треугольника равна 9, периметр равен: Периметр = 3(9) = 27
Практические вопросы по периметру треугольника
Разносторонний треугольник имеет длины сторон 6, 10 и 8. Каков его периметр?
Равнобедренный треугольник имеет две равные стороны длиной 5 и оставшуюся сторону длиной 2. Каков его периметр?
Стороны равностороннего треугольника равны 7. Чему равен его периметр?
Заключение
Мы надеемся, что это подробное руководство по периметру треугольника не только помогло вам понять концепцию, но и вдохновило на новое понимание геометрии. В Brighterly мы считаем, что практика — это ключ к раскрытию вашего полного потенциала. Поэтому не стесняйтесь решать другие задачи и применять формулы для каждого типа треугольника. Продолжая оттачивать свои навыки, вы скоро станете мастером вычисления периметров треугольников и будете готовы решать еще более сложные математические задачи!
Помните, обучение должно быть радостным путешествием, и мы в Brighterly стремимся сделать это путешествие как можно более приятным и увлекательным. Продолжайте исследовать, оставайтесь любопытными и, самое главное, получайте удовольствие!
Часто задаваемые вопросы о периметре треугольника
Что такое периметр треугольника?
Периметр треугольника представляет собой общую длину его внешних сторон или сумму длин трех его сторон. Периметр является важным понятием в геометрии и используется для измерения границ любой формы. В случае треугольников периметр помогает нам понять размер и масштаб треугольника на основе длин его сторон.
Как найти периметр треугольника?
Чтобы найти периметр треугольника, нужно сложить длины трех его сторон. Способ вычисления периметра может незначительно различаться в зависимости от типа треугольника (разносторонний, равнобедренный, равносторонний или прямоугольный). Для каждого типа треугольника существует определенная формула, по которой можно вычислить периметр:
Неравномерность: Периметр = a + b + c
Равнобедренный: Периметр = 2a + b
Равносторонний: Периметр = 3a
Прямоугольный треугольник: Периметр = a + b + c (при необходимости используйте теорему Пифагора)
Какова формула периметра треугольника?
Общая формула для периметра треугольника: Периметр = a + b + c , где «a», «b» и «c» представляют длины сторон треугольника.
No related posts.