Перпендикулярні вектори: Умова перпендикулярності векторів a•b=0

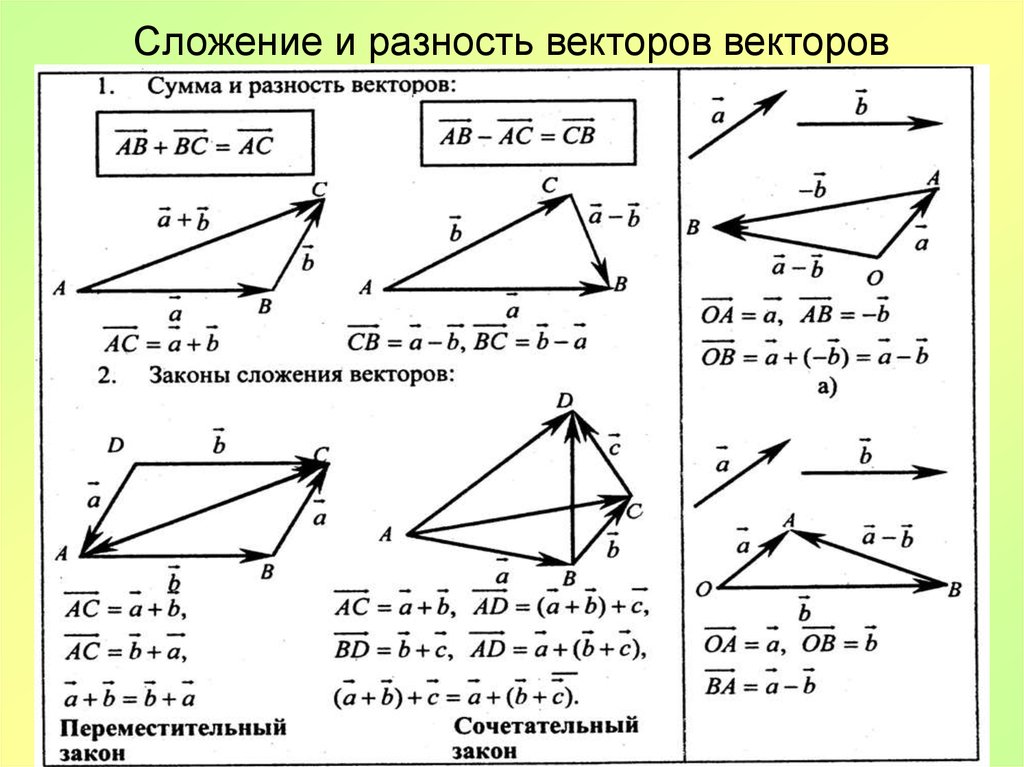
Необхідна і достатня умова перпендикулярності двох векторів

Нагадаємо визначення перпендикулярних векторів на площині і в тривимірному просторі.

Два ненульових вектора називаються перпендикулярними. якщо кут між ними дорівнює дев’яноста градусам (радіан).

Для перпендикулярності двох ненульових векторів і необхідно і достатньо, щоб їх скалярний твір дорівнювало нулю, тобто, щоб виконувалося рівність.

Нехай вектори і перпендикулярні. Доведемо виконання рівності.

За визначенням скалярний добуток векторів дорівнює добутку їх довжин на косинус кута між ними. Так як вектори і перпендикулярні, то кут між ними дорівнює дев’яноста градусів, отже,. що й потрібно було довести.

Переходимо до другої частини докази.

Тепер вважаємо, що. Доведемо, що вектори і перпендикулярні.

Так як вектори і ненульові, то з рівності випливає, що. Таким чином, косинус кута між векторами і дорівнює нулю, отже, кут дорівнює. що вказує на перпендикулярність векторів і.

Отже, необхідна і достатня умова перпендикулярності двох векторів повністю доведено.

Як же виглядає умова перпендикулярності двох векторів в координатної формі?

У розділі скалярний твір в координатах ми показали, що для двох векторів з заданими координатами і на площині справедливо рівність. а для двох векторів і в просторі. Таким чином, необхідна і достатня умова перпендикулярності двох векторів в координатах має вигляд на площині, а в тривимірному просторі.

Розглянемо застосування отриманих умов на практиці, для цього розберемо рішення кількох прикладів.

Перпендикулярні вектори.

Обчислимо їх скалярний добуток за координатами. Отже, умова перпендикулярності двох векторів на площині виконано, тобто, вони перпендикулярні.

да, вектори перпендикулярні.

Перпендикулярні вектори і. де — координатні вектори прямокутної системи координат в тривимірному просторі.

Вектори і мають відповідно координати і (при необхідності дивіться статтю координати вектора в прямокутній системі координат). Перевіримо виконання необхідного і достатнього умови перпендикулярності двох векторів:

Так як . то вектори і не перпендикулярні.

ні, не перпендикулярні.

Знайдіть значення. при якому вектори і перпендикулярні.

Скористаємося умовою перпендикулярності двох векторів в просторі в координатної формі

вектори перпендикулярні при.

У деяких випадках можливе відповісти на питання про перпендикулярність двох векторів без використання необхідного і достатнього умови перпендикулярності. Наприклад, коли відомі довжини всіх сторін трикутника, побудованого на двох векторах, то можна знайти кут між векторами і подивитися, чи рівний він дев’яноста градусів.

Сторони АВ, АС і ВС трикутника АВС дорівнюють відповідно 8, 6 і 10 см. Переконайтеся, що вектори і перпендикулярні.

Якщо вектори і перпендикулярні, то трикутник АВС — прямокутний і його гіпотенузою є сторона ВС. Тоді по теоремі Піфагора має виконуватися рівність. Перевіримо його справедливість:.

Отже, АВ і АС — катети прямокутного трикутника АВС. тому, вектори і перпендикулярні.

Схожі статті

• Умови ефективності організації дозвільної діяльності — студопедія

• Розрахунок необхідного приросту оборотного капіталу — студопедія

• Дисконтування — студопедія

Iнтерактивне навчання

• Час: 00:00/03:00:00
• Питання: 0/9

1. Знайдіть координати вектора , якщо ; .

    

   (Кількість балів 1.00)

   • А

      

   • Б

      

   • В

      

   • Г

      

2. Знайдіть довжину вектора , якщо  .

   (Кількість балів 1.00)

   • А

     2 

   • Б

     50 

   • В

     —50 

   • Г

     —2 

3. Серед векторів ,  , , виберіть колінеарні вектори.

    

   (Кількість балів 1.00)

   • А

      і 

   • Б

      і 

   • В

     і 

      

   • Г
     і  

4. Дано вектори  і . Знайдіть координати вектора .

   (Кількість балів 1.00)

   • А

      

   • Б

      

   • В

      

   • Г

      

5. Довжина сторони рівностороннього трикутника ABC дорівнює 8. Знайдіть скалярний добуток векторів  і .

   (Кількість балів 1.00)

   • А

     16 

   • Б

     32 

   • В

     64 

   • Г

     —32 

6. Знайдіть кут між векторами  і .

   (Кількість балів 1.00)

   • А

     60°  

   • Б

     45° 

   • В

     30°  

   • Г

     90°  

7. Діагоналі паралелограма

   ABCD перетинаються в точці О,  , . Виразіть через вектори і  вектор .

   (Кількість балів 2.00)

   • А

      

   • Б

      

   • В

      

   • Г

      

8. Знайдіть значення x, якщо  , .

   (Кількість балів 2.00)

9. Дано взаємно перпендикулярні векториі  , причому,  . Знайдіть  .

   (Кількість балів 3.00)

Час вичерпано

Перекрестное произведение перпендикулярных векторов

Вектор — это двумерный объект, имеющий как величину, так и направление. Геометрию вектора можно проиллюстрировать как направленный отрезок линии со стрелкой, указывающей в правильном направлении, и длиной, равной величине вектора. Направление векторов от хвоста к голове. Под прямым углом перпендикулярные линии пересекаются друг с другом.

В трехмерном ориентированном евклидовом векторном пространстве перекрестное произведение или векторное произведение представляет собой бинарную операцию над двумя векторами.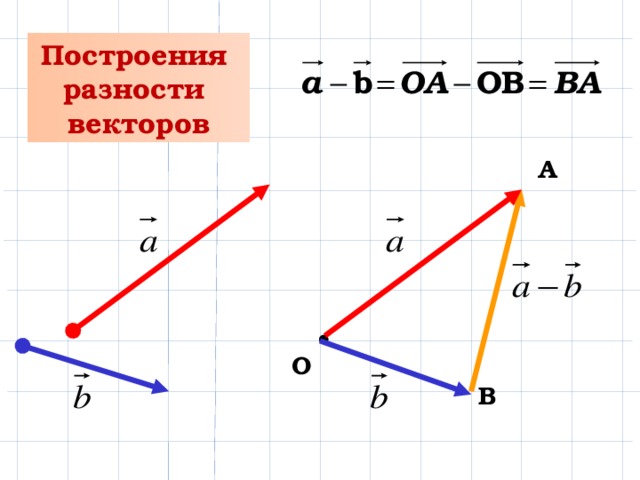 Третий вектор, перпендикулярный двум исходным векторам, представляет собой векторное произведение двух векторов. Площадь параллелограмма между ними определяет его величину, а правило большого пальца правой руки определяет его направление.

Перекрестное произведение перпендикулярных векторов

Он перпендикулярен обоим векторам v и w, если векторное произведение v,w двух ненулевых векторов v и w также является ненулевым вектором. Когда два вектора перпендикулярны друг другу, угол, образованный между ними, равен 90 градусов.

Перекрестное произведение двух векторов равно произведению их модулей и синуса угла между ними, как мы все знаем. Перекрестное произведение дает вектор, перпендикулярный обоим векторам, потому что вектор площади любой поверхности определяется в направлении, перпендикулярном этой поверхности. и величина которого равна площади параллелограмма, смежные стороны которого являются этими двумя векторами.

                                                                           Рис. 0017  

Если A и B — два независимых вектора, результат их перекрестного произведения (A×B) перпендикулярен обоим векторам и нормален к плоскости, в которой они оба расположены.

А ×В= |А| |Б| sin θ n

 

|A| = длина вектора A

B= длина вектора B

θ= угол между A и B

n = единичный вектор, перпендикулярный плоскости, содержащей a и b

 

Например, если два вектора лежат в плоскости X-Y, их векторное произведение даст результирующий вектор в направлении оси Z, который перпендикулярна плоскости XY. Между исходными векторами используется символ . Перекрестное произведение двух векторов, также известное как векторное произведение, обозначается как:

ab=c

 

Величина перекрестного произведения перпендикулярных векторов

Мы получаем еще один вектор, выровненный перпендикулярно плоскости, содержащей два вектора, когда находим векторное произведение двух векторов. Величина результирующего вектора равна произведению синуса угла между векторами и величины двух векторов. а × б = | а | |б| грех θ.

Величина векторного произведения максимальна, когда a и b перпендикулярны, как показывает эта формула. С другой стороны, перекрестное произведение является нулевым вектором, если a и b параллельны или если любой из векторов является нулевым вектором. Не существует уникальной прямой, перпендикулярной как к a, так и к b, если векторы параллельны или один вектор является нулевым вектором. Более того, поскольку существует только один вектор нулевой длины, векторное произведение однозначно определяется определением.

 

 

Угол, образованный углами a и c, всегда равен 90 градусов.

Угол между точками b и c всегда равен 90 градусам.

Мы можем выровнять a и b параллельно друг другу или под углом 0°, что приведет к нулевому вектору.

Исходные векторы должны быть перпендикулярны (угол 90°), чтобы векторное произведение двух векторов было наибольшим.

Перекрестное произведение перпендикулярных векторов пример

Пример: найти векторное произведение. Затем используйте скалярное произведение, чтобы проверить перпендикулярность.

Решение: 

Теперь проверьте перпендикулярность.

Заключение

В этой статье мы заключаем, что когда два вектора перпендикулярны друг другу, угол между ними составляет 90 градусов. Как мы все знаем, перекрестное произведение двух векторов равно произведению их модулей плюс синус угла между ними. Вектор, перпендикулярный основанию плоскости, также перпендикулярен всей плоскости. В результате перекрестное произведение двух (линейно независимых) векторов ортогонально плоскости, которую они охватывают, потому что оно ортогонально каждому из них.

 

Объяснение урока: Параллельные и перпендикулярные векторы в пространстве

В этом объяснении мы научимся распознавать параллельные и перпендикулярные векторы в пространстве.

Вектор в пространстве определяется двумя величинами: величиной и направлением. Особые отношения формируются между двумя или более векторами когда они указывают в одном направлении или в противоположных направлениях. В этом случае говорят, что векторы параллельны. Это может быть представлен математически.

Определение: параллельные векторы в пространстве

Векторы ⃑𝐴 и ⃑𝐵 параллельны тогда и только тогда, когда они скалярны. кратны друг другу: ⃑𝐴=𝑘⃑𝐵, где 𝑘 — ненулевое действительное число.

Другой способ думать об этом состоит в том, что если два вектора параллельны, то отношения каждого из их соответствующих компоненты одинаковые. Итак, если у нас есть два вектора ⃑𝐴=𝑎,𝑎,𝑎 и ⃑𝐵=𝑏,𝑏,𝑏, то 𝑎𝑏=𝑎𝑏=𝑎𝑏.

Второе особое отношение, которое может возникнуть между двумя векторами, возникает, когда направления двух векторов образуют 9угол 0∘. Когда это происходит, мы говорим, что два вектора перпендикулярны друг другу. Чтобы определить, когда два вектора перпендикулярны, мы можем использовать скалярное произведение.

Определение: скалярное произведение

Скалярные произведения двух векторов, ⃑𝐴 и ⃑𝐵, можно определить как ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖‖‖⃑𝐵‖‖𝜃, потому что где 𝜃 — угол, образованный между ⃑𝐴 и ⃑𝐵.

В случае, когда векторы ⃑𝐴 и ⃑𝐵 перпендикулярны, 𝜃=90∘. Следовательно, cos𝜃=0, а значит, ⃑𝐴⋅⃑𝐵=0.

Примечание:

Когда два вектора параллельны, угол между ними равен 0∘ или 180∘.

Другой способ определения скалярного произведения двух векторов ⃑𝐴=𝑎,𝑎,𝑎 и ⃑𝐵=𝑏,𝑏,𝑏 находится по формуле ⃑𝐴⋅⃑𝐵=𝑎𝑏+𝑎𝑏+𝑎𝑏.

Конечно, если векторы перпендикулярны, то эта сумма произведений соответствующих компонент будет равна нулю: 𝑎𝑏+𝑎𝑏+𝑎𝑏=0.

Определение: перпендикулярные векторы в пространстве

Векторы ⃑𝐴 и ⃑𝐵 перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю: ⃑𝐴⋅⃑𝐵=0.

Давайте теперь рассмотрим несколько примеров с параллельными и перпендикулярными векторами.

Пример 1. Использование свойств параллельных и перпендикулярных векторов для решения задачи

Верно или неверно: если составляющая вектора в направлении другого вектора равна нулю, то они параллельны.

Ответ

Чтобы наглядно представить, что здесь происходит, начнем с рассмотрения двух векторов, ⃑𝐴 и ⃑𝐵. Это могут быть любые два произвольных вектора. Предположим, что эти векторы начинаются в одной и той же точке. Вот как они могут выглядеть.

Теперь добавим компонент ⃑𝐴 в направлении ⃑𝐵.

Используя эту диаграмму вместе с некоторой правой тригонометрией, мы можем видеть, что величина компонента ⃑𝐴 в направлении ⃑𝐵 можно рассчитать, используя ‖‖⃑𝐴‖‖𝜃cos.

В вопросе указано, что эта величина должна быть равна нулю. С ‖‖⃑𝐴‖‖≠0, cos𝜃 должен быть равен нулю. Решение это для 𝜃 дает нам 𝜃=90. ∘

Это говорит нам о том, что когда компонент ⃑𝐴 в направлении ⃑𝐵 равен 0, угол между векторами должен быть прямым. Следовательно, ⃑𝐴 и ⃑𝐵 перпендикулярны друг другу.

Наше решение вопроса — «Ложь»: если составляющая вектора в направлении другого вектора равна нулю, то они не параллельны.

Еще один способ решить эту задачу — изобразить два параллельных вектора, как показано на рисунке.

Так как векторы ⃑𝐴 и ⃑𝐵 параллельны, угол между двумя векторами 𝜃=0∘. Следовательно, составляющая ⃑𝐴 в направлении ⃑𝐵 есть ‖‖⃑𝐴‖‖(0)cos∘. С cos(0)=1∘, эта компонента есть просто вектор ⃑𝐴. ⃑𝐴 отличен от нуля; следовательно, ответ на вопрос должен быть «Неверно».

В следующем примере мы найдем отсутствующие параметры, чтобы два заданных вектора были параллельны.

Пример 2. Поиск пропущенного значения с помощью пары параллельных векторов

Найдите значения 𝑚 и 𝑛 так, чтобы вектор 2⃑𝑖+7⃑𝑗+𝑚⃑𝑘 параллелен вектору 6⃑𝑖+𝑛⃑𝑗−21⃑𝑘.

Ответ

Чтобы решить эту задачу, мы можем использовать тот факт, что когда два вектора параллельны друг другу, они скалярно кратны друг другу. Поэтому, 2⃑𝑖+7⃑𝑗+𝑚⃑𝑘=𝑐6⃑𝑖+𝑛⃑𝑗+21⃑𝑘, где 𝑐 — это просто константа, которую можно найти.

Приравнивая коэффициенты каждой из компонент вектора, мы получаем три уравнения: 2=6𝑐,7=𝑐𝑛,𝑚=−21𝑐.

Мы можем решить первое из этих уравнений, чтобы найти 𝑐. При этом получаем 𝑐=13.

Теперь нам просто нужно подставить это значение в два других уравнения и найти недостающие значения. Чтобы найти 𝑛, мы имеем 7=𝑛3𝑛=21.

Чтобы найти 𝑚, у нас есть 𝑚=−213𝑚=−7.

Теперь мы пришли к нашему решению, которое состоит в том, что значения 𝑚 и 𝑛, которые делают векторы параллельными, равны 𝑚=−7 и 𝑛=21.

Мы можем проверить наше решение, убедившись, что отношения соответствующих компонентов двух векторов равны.

Для двух параллельных векторов должно быть верно, что 26=7𝑛=𝑚−21.

Если мы подставим полученные значения, то получим 26=721=-7-21, которые все упрощаются до 13. Это подтверждает правильность нашего решения.

В следующем примере мы рассмотрим, как мы можем идентифицировать перпендикулярные векторы.

Пример 3. Определение вектора, не перпендикулярного заданной прямой

Какой из следующих векторов не перпендикулярен прямой, вектор направления которой ⃑𝑟 равен (2,−3,5)?

1. (10,10,2)
2. (-10,-5,1)
3. (2,-2,-2)
4. (1,-2,3)
5. (2,3,1) )

Ответ

Чтобы два вектора были перпендикулярны друг другу, должно быть верно, что их скалярное произведение равно нулю. Чтобы найти решение, нам просто нужно найти, какой из векторов не дает нуля при расставлении точек (2,−3,5).

Начнем с вектора в A. Мы находим, что скалярное произведение дает нам (10,10,2)⋅(2,−3,5)=10×2+10×(−3)+2×5=20−30+10=0.

Следовательно, (10,10,2) перпендикулярно (2,−3,5).

Далее мы можем проверить вектор в B. Получаем (−10,−5,1)⋅(2,−3,5)=(−10)×2+(−5)×(−3)+1×5=−20+15+5=0.

Поскольку это ноль, ответ также не B.

Расставляя точки над вектором в C с помощью (2,−3,5), мы получаем (2,−2,−2)⋅(2,−3,5)=2×2+(−2)×(−3)+(−2)×5=4+6−10=0.

Значит, решение тоже не может быть C.

Далее нам нужно проверить вектор D: (1,−2,3)⋅(2,−3,5)=1×2+(−2)×(−3)+3×5=2+6+15=23.

Поскольку это скалярное произведение не равно нулю, (1,−2,3) и (2,−3,5) не перпендикулярны. Итак, наше решение вопроса состоит в том, что вектор, не перпендикулярный прямой, равен D, (1,−2,3).

Мы можем быстро проверить вектор E, просто чтобы убедиться, что этот вектор перпендикулярен прямой: (2,3,1)⋅(2,−3,5)=2×2+3×(−3)+1×5=4−9+5=0.

Поскольку этот результат равен нулю, это помогает подтвердить наше решение: D.

В следующем примере мы будем определять, являются ли два вектора параллельными, перпендикулярными или ни тем, ни другим.

Пример 4. Определение того, являются ли два вектора параллельными, перпендикулярными или нет

Даны два вектора ⃑𝐵=(64⃑𝑖−56⃑𝑗+8⃑𝑘), определите, являются ли эти два вектора параллельны, перпендикулярны или иным образом.

Ответ

Начнем с того, что вспомним условия, при которых эти векторы параллельны или перпендикулярны. Векторы параллельны, если ⃑𝐴=𝑘⃑𝐵, где 𝑘 — ненулевая действительная константа. Векторы перпендикулярно, если ⃑𝐴⋅⃑𝐵=0. Если ни одно из этих условий не выполняется, то векторы не параллельны и не перпендикулярны друг другу.

Начнем с проверки, параллельны ли они. Если они параллельны, то верно, что (8⃑𝑖−7⃑𝑗+⃑𝑘)=𝑘(64⃑𝑖−56⃑𝑗+8⃑𝑘).

Мы можем проверить, так ли это, попытавшись найти значение 𝑘. Мы можем составить три уравнения, приравнивая компоненты этих векторов. Мы получаем 8 = 64 𝑘, −7 = −56 𝑘, 1 = 8 𝑘.

Решив любое из этих уравнений, мы получим одно и то же значение 𝑘=18. Это говорит нам о том, что наши векторы на самом деле параллельны.

Мы уже нашли решение, но для иллюстрации метода завершим доказательство того, что они не перпендикулярны. Находим скалярное произведение ⃑𝐴 и ⃑𝐵 быть (8⃑𝑖−7⃑𝑗+⃑𝑘)⋅(64⃑𝑖−56⃑𝑗+8⃑𝑘)=8×64+(−7)×(−56)+1×8=512+392+8=912.

Так как это не равно нулю, векторы не перпендикулярны, что не противоречит нашему решению, что векторы параллельны.

Теперь мы знаем, как определить, параллельны два вектора или перпендикулярны. Мы можем использовать это, чтобы выяснить, параллельны или перпендикулярны две прямые линии. В следующем примере мы увидим, как мы можем найти недостающую константу в уравнении прямой линии по другой линии, перпендикулярной ей.

Пример 5. Решение задачи с парой перпендикулярных прямых

Если прямая 𝑥+8−10=𝑦+8𝑚=𝑧+10−8 перпендикулярна 𝑥+5−4=𝑦+810 и 𝑧=8, найдите 𝑚.

Ответ

Итак, нам дали уравнения двух прямых в трехмерном пространстве и сказали, что они перпендикулярны друг другу. Мы можем использовать эту информацию, чтобы найти недостающую константу.

Во-первых, нам нужно найти вектор направления каждой линии. Мы знаем, что строка вида 𝑥−𝑥𝑎=𝑦−𝑦𝑏=𝑧−𝑧𝑐 проходит через точку (𝑥,𝑦,𝑧) и имеет вектор направления (𝑎,𝑏,𝑐).

Используя это, мы можем видеть, что линия 𝑥+8−10=𝑦+8𝑚=𝑧+10−8 имеет вектор направления (−10,𝑚,−8).

Другая строка не совсем такого вида, потому что у нас 𝑧=8. Однако это всего лишь означает, что 𝑧-координата этой прямой постоянна, так как наша прямая существует в плоскости 𝑧=8. Итак, в векторе направления 𝑧-компонента будет быть нулем. Следовательно, вектор направления линии 𝑥+5−14=𝑦+810 при 𝑧=8 равен (−4,10,0).

Теперь, когда у нас есть векторы направления двух прямых, нам нужно взять скалярное произведение этих векторов и установите его равным нулю, так как две линии перпендикулярны друг другу. Это дает нам (−10,𝑚,−8)⋅(−4,10,0)=0.

Все, что нам нужно сделать, это решить это, чтобы найти 𝑚. Мы получаем (-10)×(-4)+𝑚×10+(-8)×0=040+10𝑚=010𝑚=-40𝑚=-4.

Здесь мы пришли к решению: чтобы эти две прямые были перпендикулярны, 𝑚=−4.

Мы рассмотрели множество примеров того, как мы можем находить и использовать параллельные и перпендикулярные векторы. Напомним некоторые ключевые моменты эксплейнера.

Ключевые точки

• Когда два вектора параллельны, угол между ними равен 0∘ или 180∘. Когда два вектора перпендикулярны, угол между ними равен 90∘.
• Два вектора, ⃑𝐴=𝑎,𝑎,𝑎 и ⃑𝐵=𝑏,𝑏,𝑏 параллельны, если ⃑𝐴=𝑘⃑𝐵. Это эквивалентно тому, что отношения соответствующих компонентов каждого из векторов равны: 𝑎𝑏=𝑎𝑏=𝑎𝑏.
• Два вектора, ⃑𝐴=𝑎,𝑎,𝑎 и ⃑𝐵=𝑏,𝑏,𝑏, перпендикулярны, если их скалярное произведение равно нулю, ⃑𝐴⋅⃑𝐵=0, или если 𝑎𝑏+𝑎𝑏+𝑎𝑏=0.
• Мы можем использовать приведенные выше отношения между параллельными и перпендикулярными векторами, чтобы определить, параллельны или перпендикулярны две прямые.

  No related posts.