Свойства графиков чётных и нечётных функций. Примеры. Свойства функции. Алгебра 7-11 класс
12+
4 месяца назад
Математика от Баканчиковой233 подписчика
Алгебра 7-11 класс. Как по графику функции понять является ли она чётной, нечётной или не чётной и не нечётной? Сегодня, продолжая говорить о свойствах функции, мы ответим на этот вопрос. Если Вы не видели наши предыдущие уроки по теме «Чётные и нечётные функции», то обязательно посмотрите их, тогда это урок будет Вам очень понятен. Мы расскажем Вам, какое свойство есть у графиков чётной и нечётной функций. Это поможет Вам видеть чётность и нечётность функции по её графику. А чтобы Вы запомнили эту тему, мы подробно разберём семь графиков функций. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:39 Свойство графика чётной функции.
03:16 Свойство графика нечётной функции.
05:59 Упражнение 1.
07:32 Упражнение 2.
08:50 Упражнение 3.
09:22 Упражнение 4.
09:44 Упражнение 5.
10:16 Упражнение 6.
11:20 Упражнение 7.
Все наши видео уроки по математике для 5-11 классов Вы можете найти на нашем канале на закладке «Плейлисты» https://www.youtube.com/c/МатематикаотБаканчиковой/playlists.
Если Вы впервые на нашем канале и у Вас остались вопросы или Вы хотите освежить в памяти некоторые термины и определения, рекомендуем Вам посмотреть следующие видео:
Чётность функции. Определение чётной функции. Является ли чётной функция. Свойства функции. Алгебра 7-11 класс. https://rutube.ru/video/00526d89c84dd14af604458fc65bca66/
Нечётность функции. Определение нечётной функции. Является ли нечётной функция. Свойства функции. Алгебра 7-11 класс. https://rutube.ru/video/77cdba840f3e6bc8a19371c6d65da264/
Что такое определение. Отличие определения от рассказа. https://rutube.ru/video/f187c6071dfe512aaa2204e3229097e1/
Что такое компоненты. Рассказ о Пете и Диме или зачем нужны компоненты. https://rutube.ru/video/2a05adba43e67d1ea1b5cab6d8e6d18a/
Функция.
Функция квадратного корня — что это, определение и ответ
Функция корня – это функция вида \(y = a\sqrt{\text{kx}},\) где\(\ a \neq 0;x \geq 0\ при\ k > 0;\ x \leq 0\ при\ k < 0\).
Графиком этой функции является перевернутая ветвь параболы.
В этом виде функции \(a = 1,\ k = 1.\)
С изменением коэффициента a меняется внешний вид функции.
ХАРАКТЕРИСТИКИ ФУНКЦИИ КОРНЯ:
В ЗАВИСИМОСТИ ОТ КОЭФФИЦИЕНТА
\(\mathbf{a}\mathbf{\ }\)(при \(\mathbf{k}\mathbf{\ }\mathbf{> 0}\))
| 1. Область определения: | \(D(y) \in \lbrack 0;\ + \infty)\) |
|---|---|
| 2. Область значения: | При \(a\ > \ 0\ \) \(E(y) = \lbrack 0;\ + \infty)\) При \(a\ < \ 0\) |
| 3. Ограниченность и непрерывность: | Непрерывна |
При \(a > 0\) ограничена снизу и слева При \(a < 0\) ограничена сверху и слева | |
| 4. Наибольшее и наименьшее значение функции: | \(\ y_{наиб}\) : \(Если\ a > 0,\ \)отсутствует \(Если\ a < 0,\ при\ x = 0\) \(\ y_{наим}:\) \(Если\ a > 0,\ при\ x = 0\) \(Если\ a < 0,\ \) отсутствует |
5. Промежутки знакопостоянства: | \(y > 0:\ \)При \(a > 0\) \(y\ < \ 0\): При \(a\ < \ 0\) |
| 6. Монотонность: | При \(a > 0\) возрастает При \(a < 0\) убывает |
| 7. Экстремумы: | нет |
| 8. Четность: | Ни четная, ни нечетная |
| 9. Периодичность: | не периодичная |
| 10. Пересекает ось Ох | В точке (\(0;0)\) |
| 11. Пересекает ось Оу | В точке (\(0;0)\) |
В ЗАВИСИМОСТИ ОТ КОЭФФИЦИЕНТА
\(\mathbf{\ }\mathbf{k}\) (при \(\mathbf{a}\mathbf{> 0}\))
| 1. Область определения: | \(При\ k > 0\ D(y) \in \lbrack 0;\ + \infty)\ \) \(При\ k < 0\ D(y) \in (–\infty;0\rbrack\) |
|---|---|
2. Область значения: | \(E(y) = \lbrack 0;\ + \infty)\) |
| 3. Ограниченность и непрерывность: | Непрерывна |
При \(k > 0\) ограничена снизу и слева При \(k < 0\) ограничена снизу и справа | |
| 4. Наибольшее и наименьшее значение функции: | \(y_{наиб}:\ \)отсутствует \(y_{наим}\ при:\ x = 0\) |
| 5. Промежутки знакопостоянства: | \(y > 0\) при: \(x\mathbb{\in R}\) |
| 6. Монотонность: | При \(k > 0\) возрастает При \(k < 0\) убывает |
| 7. Экстремумы: | нет |
| 8. Четность: | Ни четная, ни нечетная |
| 9. Периодичность: | не периодичная |
| 10. Пересекает ось Ох | В точке \((0;0)\) |
| 11. Пересекает ось Оу | В точке \((0;0)\) |
ВЛИЯНИЕ КОЭФФИЦИЕНТОВ НА ВИД ФУНКЦИИ КОРНЯ:
Коэффициент a:
– При увеличении коэффициента a по модулю функция приближается к оси Оу.
– При уменьшении коэффициента a по модулю функция приближается к оси Ох.
– При \(a > 0\) график находится в I четверти
(\(y\ \geq \ 0\)).
– При \(a < 0\) график находится в IV четверти
(\(y\ \leq \ 0\)).
Коэффициент k:
– При \(k > 0\) график находится в l четверти
(\(x\ \geq \ 0\)).
– При \(k < 0\) график находится во ll четверти
(\(x\ \leq \ 0\)).
Нечетные функции — онлайн-обучение и обучение с StudySmarter
Если бы кто-то указал пальцем и закричал: «Эй, смотрите, это странная функция!» вы, вероятно, подумали бы, что они видели график странной формы. На самом деле нечетные функции имеют симметричные графики, и слово «нечетный» используется в его математическом контексте, а не для обозначения «чего-то странного».
Можно было бы также предположить, что нечетные функции являются полной противоположностью четных функций, и положить этому конец.
Это предположение было бы ужасно неверным. Разницу между нечетными и четными функциями нельзя просто классифицировать, думая, что если нечетная, то она должна быть нечетной. 9{\circ}\) вокруг начала координат, \((0,0)\), на наборе осей результирующий график выглядит идентично исходному.
Формальное определение нечетной функции следующее:
нечетная функция — это функция, для которой \(f(-x)=-f(x)\) для всех значений домен \(f\).
Это означает, что для каждого значения \(x\) в области определения нечетной функции \(f(x)\) значение функции \(f(-x)\) совпадает со значением \( -f(x)\).
Это также может быть показано графически и обсуждается более подробно в следующих разделах. 9{\circ}\) относительно начала координат, результат будет выглядеть так же, как исходный график. Таким образом, мы можем видеть, что эта функция симметрична относительно начала координат.
Разница между четными и нечетными функциями
Прежде чем приступить к изучению этого раздела, рекомендуется сначала изучить тему «Четные функции»!
Основное различие между четными и нечетными функциями заключается в их осях симметрии.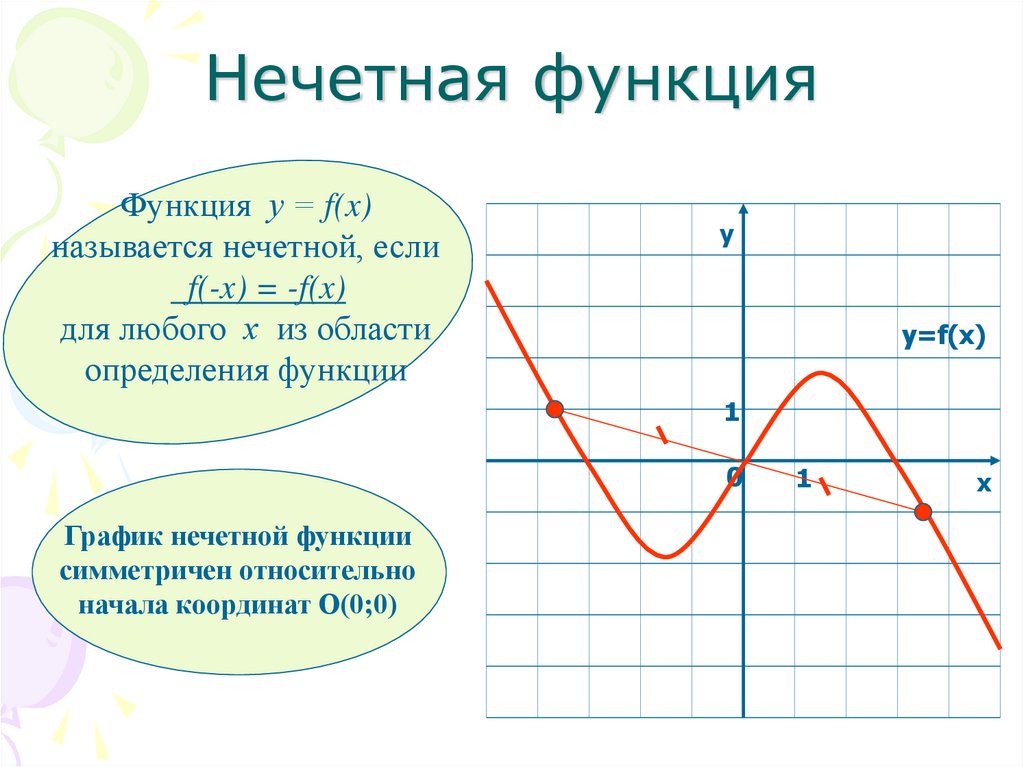
Нечетные функции, как известно, симметричны относительно начала координат . Четные функции, с другой стороны, 9{2}\) — StudySmarter Originals
В следующей таблице приведены два основных различия между нечетными и четными функциями. = -f(x)\) для всех значений \(x\) в области определения \(f(x)\)
Как определить, является ли функция нечетной
Мы можем использовать различия, упомянутые в предыдущем разделе, чтобы определить графически или алгебраически, является ли функция нечетной .
Алгебраическое определение четности или нечетности функции
Чтобы определить четность функции с помощью алгебраических методов, достаточно применить формулу \(f(-x) = -f(x)\) и проверить, является ли она Справедливо.
9{3} — 12x\end{split}\end{equation}\]
\(f(-x) = -f(x)\) для всех значений \(x\) в области определения \(f (x)\), поэтому мы можем заключить, что \(f(x)\) — нечетная функция.
Графическое определение нечетности функции
Самый простой способ определить нечетность функции — использовать ее график. Графики предоставляют нам лучший способ визуализации функций, а также полезны для их интерпретации.
В следующем примере показано, как графически определить, является ли функция нечетной: 9{-3},\) и т. д. — все нечетные функции. Для этих функций \(f(-x) = -f(x)\) для всех значений \(x\). То есть, если вы подставите \(-x\) в каждую из этих функций и упростите, то результирующий ответ будет таким же, как умножение каждой из этих функций на \(-1\).
Другая группа функций, которые часто дают нечетные функции, — это тригонометрические функции. Например, рассмотрим \(y = sin(x)\).
Имеем \(f(-x) = sin(-x)\) и \(-f(x) = -sin(x)\). Мы знаем из тригонометрии, что \(sin(-x)\) то же самое, что сказать \(-sin(x)\) и поэтому \(f(-x)\) равно \(-f(x)\) для всех значений \(х\) в области определения функции.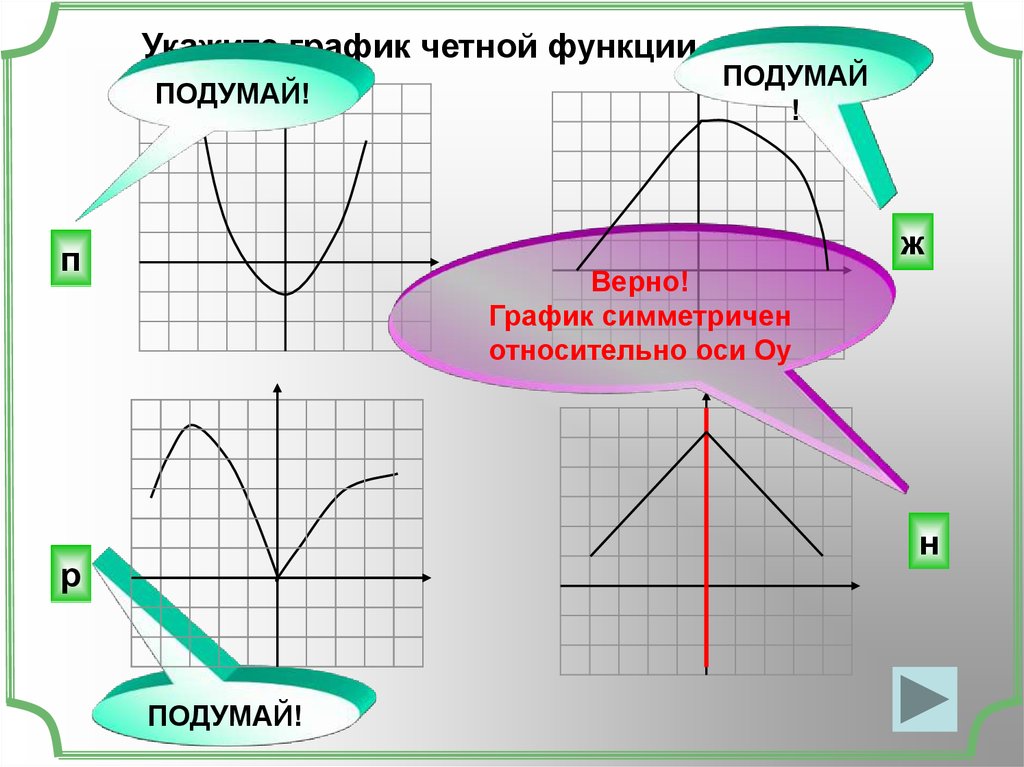
Таким образом, \(y = sin(x)\) — нечетная функция.
Если мы посмотрим на график для \(y=sin(x)\), мы также увидим, насколько он симметричен относительно начала координат:
График \(y = sin(x)\) — StudySmarter Originals
К другим нечетным тригонометрическим функциям относятся \(tan(x), cot(x)\) и \(cosec(x)\). Все они удовлетворяют определению нечетной функции.
Нечетные функции также могут быть дробями. Рассмотрим следующий пример:
Вам задана функция \(g(x) = \frac{cos(x)}{x}\). Определите, является ли функция нечетной функцией, используя алгебраические методы.
Решение
Шаг 1: Определить \(g(-x)\).
\[\begin{equation}\begin{split}g(-x) & = \frac{cos(-x)}{-x} \\& = \frac{cos(x)}{-x} \\& = — \frac{cos(x)}{x}\end{split}\end{equation}\]
Шаг 2: Определить \(-g(x)\).
\[-g(x) = — \frac{cos(x)}{x}\]
Шаг 3: Является ли \(g(x)\) нечетной функцией?
Да.
\(g(-x) = -g(x)\) для всех значений \(x\) в области определения функции, поэтому \(g(x)\) является нечетной функцией. 9{\circ}\) вокруг исходной точки, результирующий график будет выглядеть так же, как и исходный.
Even Functions — онлайн-обучение и обучение с StudySmarter
Сидя и ожидая поезда на станции North Camp, направляющегося в Милфорд для прогулки, я задумался над несколькими тревожными вопросами. Почему произведение двух или более нечетных чисел дает нечетное число? Например, произведение 3 и 7, которые являются нечетными числами, даст 21, еще одно нечетное число. Точно так же, когда четные числа перемножаются между собой, всегда получается четное число; все еще погруженный в мысли, я опоздал на поезд. Тем не менее, мы не упустим цель этого обсуждения, далее мы узнаем о работает даже с .
Что такое четные функции?
Четные функции — это такие функции, как f(x), которые имеют те же значения при замене отрицательных независимых переменных, таких как f(-x). Следовательно, их лучше всего выражать как:
f(x)→f(-x)=f(x)
В соответствии с этой концепцией функции обычно классифицируются как четные, нечетные или никакие.
Подтвердите, что f(x) четно, когда
f(x)=x4-8
Решение:
Поскольку
f(x)=x4-8
Чтобы определить природу этой функции, мы находим f(-x), подставляя -x. Следовательно,
f(-x)=(-x)4-8f(-x)=x4-8
Следовательно,
f(x)=f(-x)
Это доказывает, что f(x) является четной функцией для выражения x4-8.
Нечетные функции
Нечетные функции — это такие функции, как f(x), которые имеют отрицательный эквивалент при замене отрицательных независимых переменных, таких как f(-x). Следовательно, они лучше всего выражены как:
f(x)→f(-x)=-f(x)
Подтвердить, что f(x) нечетно, когда
f(x)=x3+x
Решение:
Начиная с
f(x)=x3+x
Чтобы определить природу этой функции, найдем f(-x), подставив -x.
Отсюда
f(-x)=(-x)3+(-x)f(-x)=-x3-x
При факторизации по -1 получаем
f(-x)=-1(x3 +x)
Звенит ли сейчас звонок?😁
Следовательно,
f(x)→f(-x)=-f(x)
выражение х3+х.
Ни одна из функций
Ни одна из функций не является функцией, подобной f(x), которая не имеет эквивалентных значений при замене отрицательных независимых переменных, таких как f(-x). Это говорит о том, что они не являются ни четными, ни нечетными функциями. Следовательно, их лучше всего выразить как:
f(x)→f(-x)≠f(x)
и
f(x)→f(-x)≠-f(x)
Подтвердите, что f (x) четно, когда
f(x)=x4+x-1
Решение:
Так как
f(x)=x4+x-1
Чтобы определить природу этой функции, мы находим f(-x), подставляя -x. Следовательно,
f(-x)=(-x)4+(-x)-1f(-x)=x4-x-1
Выражение x4-x-1 не эквивалентно x4+x-1 , следовательно, это не четная функция. 1), следовательно, это не нечетная функция
Следовательно,
f(x)→f(-x)≠f(x)
и
f(x)→f(-x)≠-f (х)
Это доказывает, что f(x) не является функцией выражения x4+x-1.
Четные функции в тригонометрических тождествах
Можно определить характер функции (т.е. четная, нечетная или ни одна) среди тригонометрических тождеств. Мы будем использовать диаграммы ниже, чтобы объяснить это.
Рисунок 1, изображение, используемое для доказательства природы функций среди тригонометрических тождеств, когда θ положительное, StudySmarter Originals
Рисунок 2, изображение, используемое для доказательства природы функций среди тригонометрических тождеств, когда θ отрицательное, StudySmarter Originals
Из первой диаграммы мы можем использовать SOHCATOA для определения cosθ. Если мы это сделаем, то обнаружим, что
cosθ=ba2+b2
Но что происходит, когда θ отрицательно? Из второй диаграммы мы замечаем, что хотя противолежащая сторона (а) изменилась (на -а) из-за поворота угла в противоположном направлении, примыкающая сторона (б) остается неизменной. В этом случае
cos(-θ)=b(-a)2+b2cos(-θ)=ba2+b2
Следовательно,
cosθ=cos(-θ)
Насколько это относится к четным функциям ? Теперь, если мы выразим косинус как функцию x, так что у нас будет cos(x) вместо cos(θ).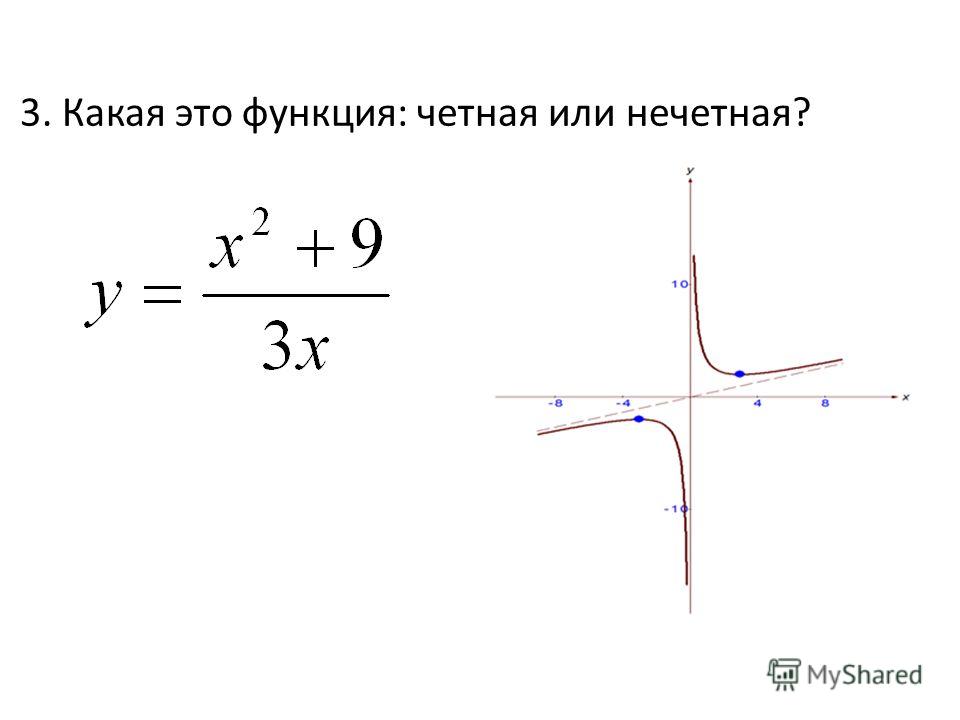
Тогда, если
f(x)=cosx
и
f(-x)=cos-xf-x=cosx
Следовательно,
f(x)=f(-x)
В данном случае это предполагает что cos(x) — четная функция.
Функции косинуса без добавления к другим функциям равны функциям .
Как насчет функций синуса?
Если обратиться к рис. 1, то можно сделать вывод, что
sinθ=aa2+b2
Однако, когда вращение на декартовой плоскости идет в противоположном направлении на угол -θ (как показано на рис. 2), мы обратите внимание, что противоположная сторона «а» на рисунке 1 меняется на «-а» на рисунке 2, потому что а расположена на отрицательной оси y. Это означает, что
sin-θ=-aa2+b2
Если разложить на -1, получится
sin-θ=-1(aa2+b2)
Напомним, что
sinθ=aa2+b2
Следовательно ,
sin-θ=-sinθ
Но насколько полезна эта деталь? Если мы выразим синус как функцию x, а не θ, чтобы мы знали, как sin(x) так же, как и sin(-x), тогда, когда
f(x)=sinx
и
f(- x)=sin(-x)f(-x)=-sin(x)
с факторизацией на -1 в правой части уравнения, мы получили бы
f(-x)=-1(sin(x))
Напомним, что
f(x)=sin(x)
Это, безусловно, означает
f(-x)=-f(x)
Это приводит к представлению, что для функции синуса
f(x)≠f(-x)
но
f(-x)=-f(x)
и, как следствие, мы можем ergo заключить, что синусоидальные функции не являются четными функциями , а нечетными функциями .
Синусоидальные функции без добавления каких-либо других функций — нечетные функции .
Почему бы не поиграть с этими двумя диаграммами, чтобы определить, являются ли касательные функции четными, нечетными или ни одной из них?
Если бы вы попытались определить, какие функции являются касательными, вы бы заметили, что, поскольку
tanθ=ab
Из диаграмм мы также знаем, что
tan(-θ)=-ab
Отсюда следует, что
tan(-θ)=-tan(θ)
Следовательно, касательные функции являются нечетными функциями.
Вы были правы?
Какова формула четных функций?
Чтобы мы могли определить формулу четных функций, показатель степени независимой переменной x всегда четен с константой или без нее. Таким образом, для x n n является четным числом, таким как 2, 4, 6…n. Если a, b и c — константы, такие как 1, 2, 3… и n — четное число, то четная функция выражается как
f(x)=axn+bxn±2+c
или
f(x)=axn+bxn±2
Для нечетных функций показатель степени независимой переменной x всегда нечетен, и константа не должна присутствовать.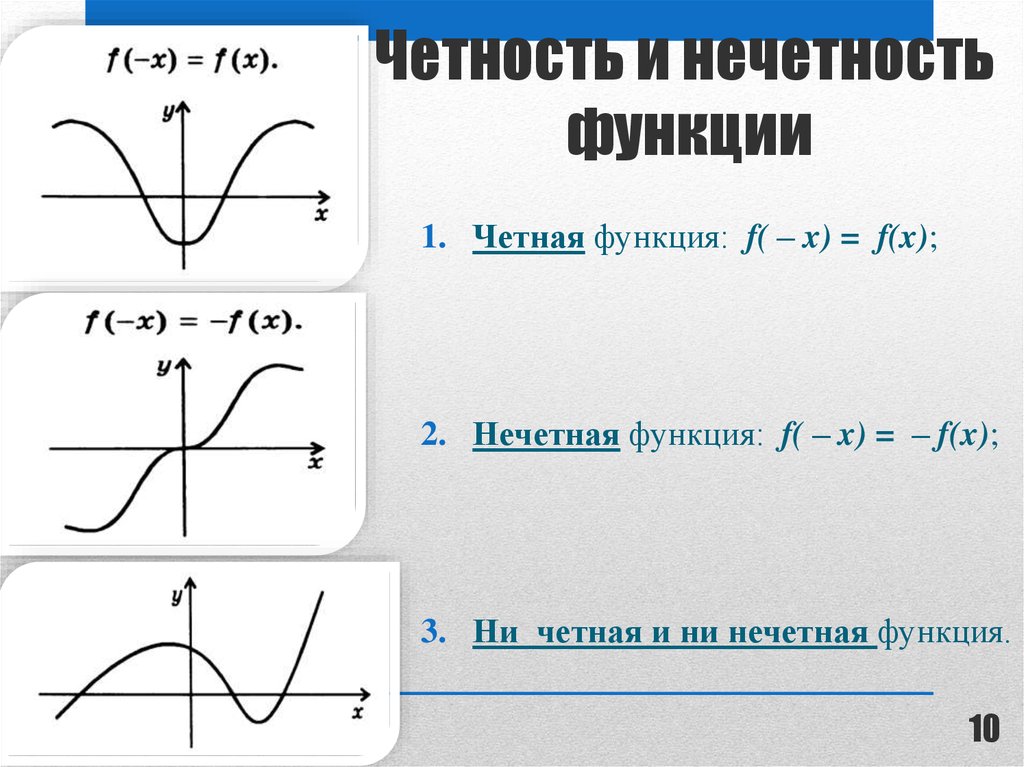
Таким образом, для x n , n — нечетное число, например 1, 3, 5…n. Если a и b — константы, такие как 1, 2, 3… и n — нечетное число, то нечетная функция выражается как
f(x)=axn+bxn±2
Ни для одной из функций показатель степени независимой переменной x может быть как четным, так и нечетным с наличием константы или без нее. Таким образом, для x n n является нечетным и/или четным числом, таким как 1, 2, 3, 4, 5…n. Если a, b и c являются константами, такими как 1, 2, 3… и n, как четными, так и нечетными числами, то ни одна из функций не выражается как
f(x)=axn+bxn±1+c
или
f(x)=axn+bxn±1
или в случае, если все показатели степени значения независимой переменной x нечетны с константой . Ни одна из функций не выражается как
f(x)=axn+bxn±2+c
, где n — нечетное число.
Графики четной функции
График четной функции симметричен относительно вертикальной оси (оси Y).
Когда график симметричен оси, при вращении вокруг точки или при отражении от линии график остается прежним, хотя точка на этой оси остается той же, а точка на другой оси будет иметь противоположный знак потому что они являются отражением, как зеркальное отражение.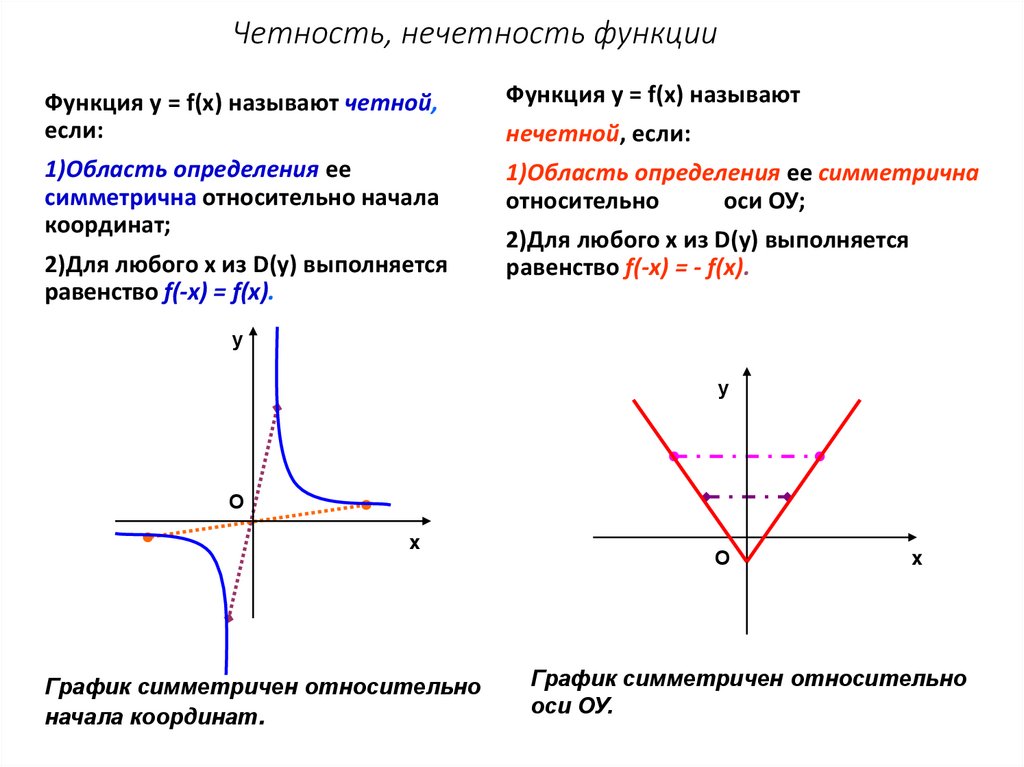
Таким образом, когда график симметричен вертикальной оси, заданные точки (p, q) на этом графике будут иметь точки (-p, q) на этом графике. Обратите внимание, что значение y (точка q на вертикальной оси) не изменилось, в то время как значение x в первой точке (p) имеет противоположное значение для второй точки (-p).
Например, четная функция
f(x)=x4-2
показана ниже мы видим, что две точки (-1, -1) и (1, -1) графика доказывают симметрию к оси y для четной функции x4-2.
В чем разница между четными и нечетными функциями?
Четные и нечетные функции различаются двумя основными способами; в их графиках и общем выражении.
Разница в графике
Мы только что обсуждали, что график четных функций симметричен относительно вертикальной оси (оси Y).
Ты только что забыл об этом?
Но для нечетной функции ее график симметричен относительно начала координат. Это означает, что если кривую повернуть на 180° в начале координат (0, 0), график останется прежним.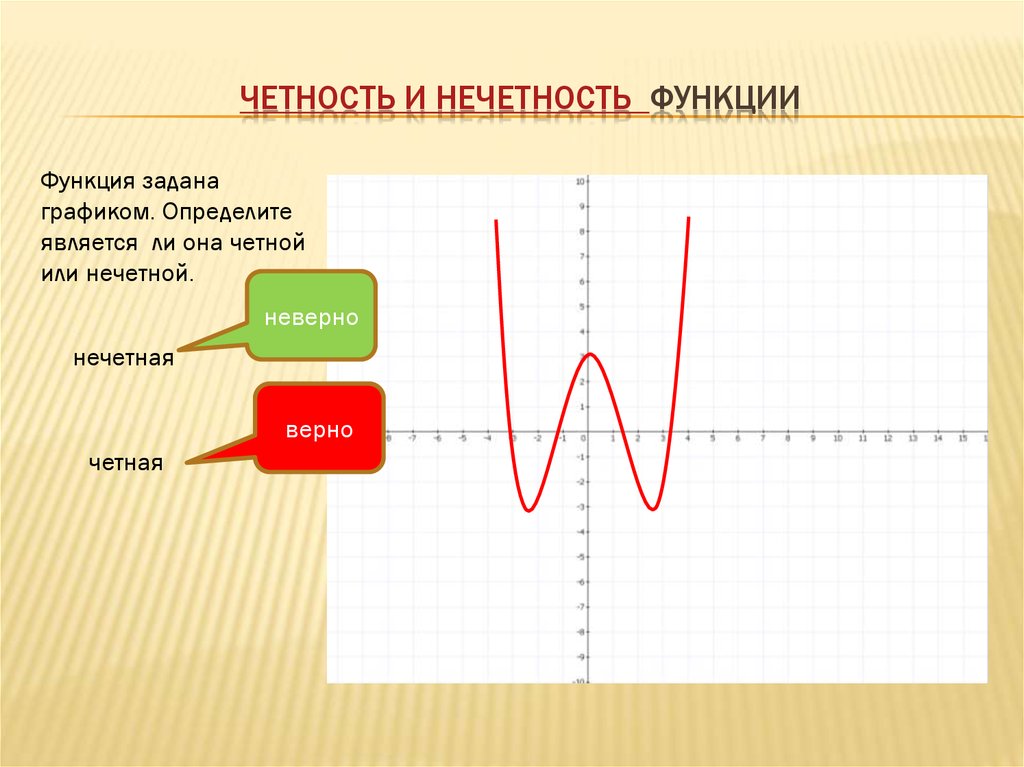
Этого поворота можно добиться, выбрав точки (b, 0) и (0, b) на графике, если вы перетащите точку (b, 0) горизонтально в точку (-b, 0) и перетащите точку (0, b ) по вертикали до точки (0, -b) вы подтвердите, что график точно такой же. Разве это не удивительно?
Обратите внимание, как упоминалось ранее, на графиках четной функции, если вы выберете данную точку (p, q) на графике, у вас обязательно будет другая точка на противоположной горизонтальной стороне кривой, которая будет (-p, q ).
Пожалуйста, обратитесь к графику x 4 -2 в качестве примера.
Между тем, в нечетных функциях, если вы выберете точку (p, q), у вас будет точка (-p, -q) на противоположных вертикальной и горизонтальной осях. Например, график нечетной функции
f(x)=x3
отмечает точки (2, 8) вверх справа, а также другую точку (-2, -8), которая находится внизу слева.
График нечетной функции, f(x)=x 3 , StudySmarter Originals
Общее выражение
Четные функции также отличаются от нечетных по своему общему выражению.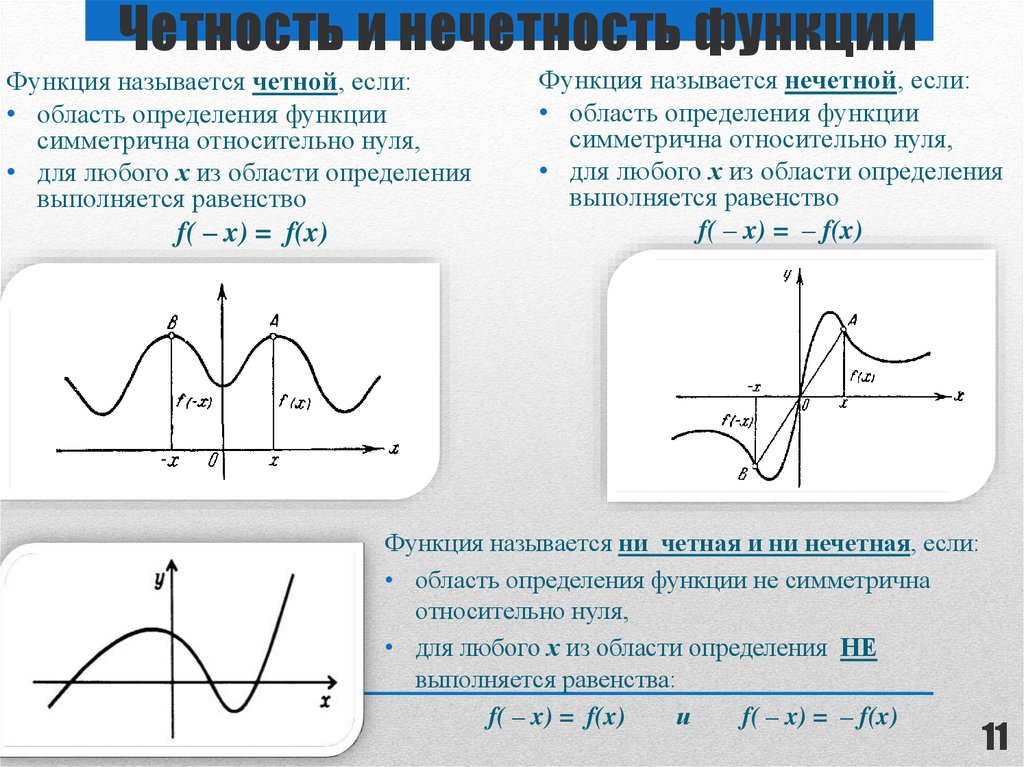
Даже функции выражаются в соответствии с правилом.
f(x)=f(-x)
Однако нечетные функции не подчиняются этому правилу, поскольку в их случае
f(x)≠f(-x)
к правилу
f(-x)=-f(x)
Примеры четных функций
Чтобы лучше понять четные функции, рекомендуется попрактиковаться в некоторых задачах.
Для функции
h(x)=6×6-4×4+2×2-1
Определить, является ли функция четной. Постройте график и выберите любые две точки, чтобы доказать, что это четная функция.
Решение:
Первая задача — определить, является ли функция четной. Если вы примените формулу четной функции, описанную ранее, посмотрев на выражение 6×6-4×4+2×2-1, мы можем сделать вывод, что это четная функция, поскольку все показатели степени x, т.е. 6, 4 и 2, являются четными числами. Тем не менее, для дальнейшего подтверждения мы просто применим правило:
f(x)=f(-x)
Подставляя -x в выражение, получаем
f(-x)=6(-x)6-4(-x)4+2(x2) -1f(-x)=6×6-4×4+2×2-1
Таким образом,
f(x)=f(-x)
Следовательно, мы можем сказать, что приведенное выше выражение действительно является четной функцией.
Следующая задача — построить график и, используя две точки, дополнительно доказать, что это выражение действительно является четной функцией.
Использование точек на графике для доказательства четных функций, StudySmarter Originals
Из приведенного выше графика выражения мы выбрали две точки (-1, 3) и (1, 3). Это еще раз доказывает, что выражение 6×6-4×4+2×2-1 является четной функцией, поскольку пара (-1, 3) и (1, 3) соответствует (p, q) и (-p, q).
Если
f(x)=3×2
и
g(x)=x4
Определите класс суммы обеих функций.
Решение:
f(x)+g(x)=3×2+x4
Теперь определим вид суммы. Пусть h(x) будет суммой, так что
h(x)=3×2+x4h(-x)=3(-x)2+(-x)4h(-x)=3×2+x4h(x) =h(-x)
Следовательно, сумма f(x) и g(x), которые являются четными функциями, дает нам h(x), еще одну четную функцию.
Even Functions — ключевые выводы
- Четные функции — это такие функции, как f(x), которые имеют те же значения при замене отрицательных независимых переменных, таких как f(-x).
