Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
11.17
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
на какой высоте над поверхностью Земли ускорение свободного падения в 4 раза меньше, чем на поверхности Земли? Радиус Земли примите 6400 км.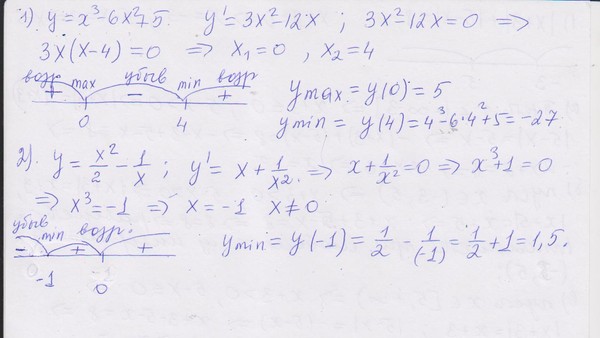
Помогите решить задачу! За пенсией по инвалидности 29 марта 2002 года обратился Мостиков А.Д. 1946 Г. Р. Бюро МСЭК 20 марта 2002 года установило ему 2 группу инвалидности. Его страховой стаж составил
Пользуйтесь нашим приложением
Цепное правило — Подход к исчислению
Подход
к
C A L C U L U S
Содержание | Дом
7
Производная функции от функции
Цепное правило
Доказательство цепного правила
Производная функции от функции
Пусть
f ( x ) = x 5 и г ( x ) = x 2 0 + 03.
Если теперь мы допустим, что g ( x ) будет аргументом f , то f будет функцией g .
f ( г ( x )) = ( x 2 + 1) 5 .
(Тема 3 предварительного расчета.)
Какая производная от f ( г ( x ))?
Во-первых, обратите внимание, что
| d f ( x ) dx | = 5 x 4 . |
То есть: Производная от f по аргументу (который в данном случае равен x ) равна 5-кратной четвертой степени аргумента.
Это означает, что если g — или любая переменная — является аргументом f , применяется та же форма :
| d f ( г ) dg | = 5 г 4 . |
| д ж ( ч ) дх | = 5 ч 4 . |
| д ф ( в ) дв | = 5 v 4 . |
Другими словами, мы действительно можем взять производную функции от аргумента только по этому аргументу.
Следовательно, поскольку г = x 2 + 1,
| d f ( г ) dg | = 5 г 4 | = 5( x 2 + 1) 4 . |
Далее, производная от г равна 2 x . То, что называется цепным правилом, утверждает следующее:
| df ( г ( x )) dx | = | дф ( г ) дг | · | dg ( x ) dx |
«Если f является функцией г и г являются функцией x ,
, то производная от f по отношению к x
равна производной от f ( г ) по отношению к г
, умноженная на производную от г () по отношению к () до x .
»
Следовательно, по цепному правилу производная от
( х 2 + 1) 5
это
5( x 2 + 1) 4
Примечание: In ( x 2 + 1) 5 , x 2 + 1 является «внутри» пятой степени, то есть «снаружи». Возьмем производную снаружи внутрь. Когда мы берем внешнюю производную, мы не меняем того, что внутри. Затем мы умножаем на производную того, что внутри.
Чтобы решить, какая функция является внешней, решите, какую из них вам придется оценивать последней .
Для оценки
( х 2 + 1) 5 ,
, вам сначала нужно будет оценить x 2 + 1. Затем вы возьмете его 5-ю степень. Следовательно, 5-я сила находится снаружи. Вот почему мы сначала возьмем эту производную.
Когда мы пишем f ( г ( x )), f вне г .
Сначала возьмем производную от f по отношению к g .
| Пример 1. f ( x ) = | . Какова его производная? |
Решение . Это имеет вид f ( g ( x )). Какая функция f , то есть что снаружи, а что г , что внутри?
г равно x 4 − 2, потому что это находится внутри функции квадратного корня, которая равна f . Производная квадратного корня приведена в примере к уроку 6. Для любой аргумент г функции извлечения квадратного корня,
Здесь г равно x 4 − 2. Следовательно, поскольку производная от x 4 − 2 равно 4 x 3 ,
| д дх | = ½ ( x 4 — 2) −½ · 4 x 3  |
Пример 2. Какова производная от y = sin 3 х ?
Решение . Это третья степень греха x . Чтобы решить, какая функция находится снаружи, как бы вы ее оценили?
Сначала вы должны вычислить sin x , а затем взять его третью степень. sin x находится внутри третьей степени, то есть снаружи.
Теперь производная третьей степени — от г 3 — равна 3 г 2 . Таким образом, принимая на данный момент, что производная sin x – это cos x (Урок 12), производная от sin 3 x — снаружи внутрь — это
3 sin 2 x · cos x .
| Пример 3. Что является производным от | 1 x 3 + 1 | ? |
Решение . x 3 + 1 находится внутри функции | 1 х | = x −1 , |
, производная которого равна − x −2 ; (Задача 4, Урок 4). Итак, у нас есть
| 1 x 3 + 1 | = | ( х 3 + 1) −1 | . |
Следовательно, его производная
−( x 3 + 1) −2 · 3 x 2
Пример 4. Предположим, что y является функцией x . х = х ( х ). Примените цепное правило к
| д дх | г 2 | . |
| Решение . | dy 2 dx | = | 2 | · | дх дх | = | 2 у | дх дх | . |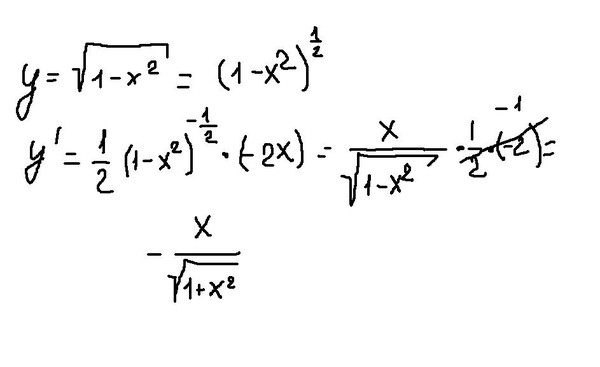
y , которую мы предполагаем как функцию x , находится внутри функции y 2 . Производная y 2 по отношению к y равна 2 y . Что касается производной от
| y по отношению к x , указываем как | дх дх | . (См. Урок 5.) |
Задача 1. Вычислить производную от ( x 2 −3 x + 5) 9 .
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай проблему сам!
9( х 2 −3 х + 5) 8 (2 х − 3)
Задача 2. Вычислить производную от ( x 4 − 3 x 2 + 4) 2/3 .
2/3( x 4 − 3 x 2 + 4) −1/3 (4 x 3 − 6 x )
Задача 3.
Вычислить производную sin 5 x .
5 sin 4 x cos x
Задача 4. Вычислить производную от sin x 5 .
Внутренняя функция равна x 5 — вы должны оценить это в последнюю очередь. Внешняя функция — sin x . (это синус x 5 .) Следовательно, производная равна
cos x 5 · 5 x 4 .
Задача 5. Вычислить производную от sin(1 + 2).
cos (1 + 2) x -1/2 .
Задача 6. Вычислить производную от
¼(sin x ) −3/4 , потому что x .
Пример 5. Более двух функций. Цепное правило может быть расширено до более чем двух функций. Например, пусть
| f ( x ) | = | . |
Внешней функцией является квадратный корень. Внутри это (1 + 2 степень). А внутри это sin x .
Следовательно, производная равна
.| ½(1 + sin 2 x ) −1/2 · 2 sin x · cos x x | = | sin x cos x | . |
| Задача 7. Вычислить производную от |
(Сравните пример 3)
| — [SIN ( x 2 + 5)] −2 · COS ( x 2 + 5) · 2 x 9999494 4. · 4 2 x 9 | · 4 2 x 99994 · 2 + 5)= | — | 2 x cos ( x 2 + 5) sin 2 ( x 2 + 5) |
Задача 8. Вычислить производную от |
Задача 9. Предположим, что y является функцией x , и примените цепное правило, чтобы выразить каждую производную относительно x .
| а) | д дх | г 3 = | 3 г 2 | дх дх |
| б) | д дх | грех у = | потому что у | дх дх |
| в) | д дх | = | ½ г −½ | дх дх |
Доказательство цепного правила
Чтобы доказать цепное правило, вернемся к основам.
Пусть f будет функцией g , что, в свою очередь, является функцией x , так что у нас есть f ( g ( x )). Тогда, когда значение г изменится на величину Δ г , значение f изменится на величину Δ f . У нас будет отношение
| Δ f Δ г | . |
Опять же, поскольку г является функцией x , то при изменении x на величину Δ x , г изменится на величину Δ г . У нас будет отношение
| Δ г Δ x | . |
Но изменение x влияет на f , потому что оно зависит от g . У нас будет
| Δ f Δ x | . Это будет произведение этих отношений: |
| Δ f Δ x | = | Δ f Δ г | · | Δ г Δ x | . |