Первообразная корня из x: Mathway | Популярные задачи

2

найти первообразную f функции f(x)=2 корень из x , график которой проходит через точку a(0;7/8) — вопрос №1846630 — Учеба и наука

Лучший ответ по мнению автора

16. 02.16 Лучший ответ по мнению автора

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его . .. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.

Стоимость автомобиля с гаражом составляет…

как решить задачу за 4 класс часть 2 автор муравьёва и урбан на странице129 №2

Прямоугольник разрезали на 8 равных…

шмель и оса полетели с…

Пользуйтесь нашим приложением

Мэтуэй | Популярные задачи

92) 9(3x) по отношению к x 92+1

1	Найти производную — d/dx	бревно натуральное х
2	Оценить интеграл	интеграл натурального логарифма x относительно x
3	Найти производную — d/dx
21	Оценить интеграл	интеграл от 0 до 1 кубического корня из 1+7x относительно x
22	Найти производную — d/dx	грех(2x)
23	Найти производную — d/dx
41	Оценить интеграл	интеграл от cos(2x) относительно x
42	Найти производную — d/dx	1/(корень квадратный из х)
43	Оценка интеграла 9бесконечность
45	Найти производную — d/dx	х/2
46	Найти производную — d/dx	-cos(x)
47	Найти производную — d/dx	грех(3x)
68	Оценить интеграл	интеграл от sin(x) по x
69	Найти производную — d/dx	угловой синус(х)
70	Оценить предел	ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х
85	Найти производную — d/dx	лог х
86	Найти производную — d/dx	арктан(х)
87	Найти производную — d/dx	бревно натуральное 5х92

Интегрирование корня x — Формула, примеры

Интегрирование корня x определяется по формуле интегрирования, заданной ∫x ⁿ dx = x ⁿ⁺¹ /(n + 1) + C , Поскольку корень x является радикалом, поэтому мы подставляем n = 1/2 в формулу, чтобы получить интегрирование корня x.

Интеграл от квадратного корня x равен двум третям x, возведенным в степень три на два плюс постоянная интегрирования. Математически интегрирование корня x записывается как ∫√x dx = (2/3) x ^3/2 + C.

Далее в этой статье мы выведем интеграл от квадратного корня x, используя формулу интегрирования, а также интегрирование корня x в квадрате плюс квадрат и интеграл корня x в квадрате минус квадрат. Мы также решим несколько примеров для лучшего понимания.

1.	Что такое интеграция Root x?
2.	Интеграл квадратного корня x доказательство
3.	Определенная интеграция корня x
4.	Интеграция Root x Square Plus a Square
5.	Часто задаваемые вопросы по интеграции Root x

Что такое интеграция Root x?

Интегрирование корня x есть не что иное, как интеграл квадратного корня x относительно x, который определяется выражением ∫√x dx = (2/3) x ^3/2 + C, где C — постоянная интегрирования, ∫ — символ интегрирования, а dx — интеграл квадратного корня x по отношению к x.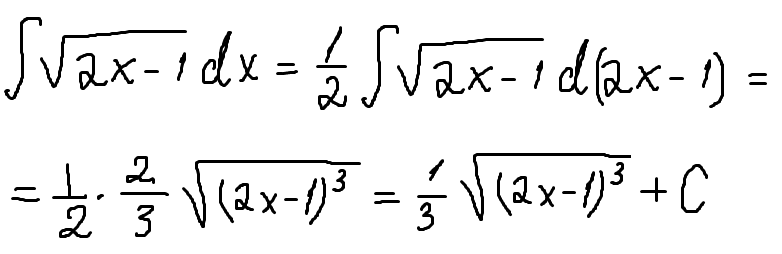 Мы можем вычислить интегрирование корня х, используя формулу интегрирования . Следовательно, формула интегрирования корня x имеет вид ∫√x dx = (2/3) x ^3/2 + C, где C — постоянная интегрирования.

Интеграл квадратного корня x доказательство

Теперь, когда мы знаем, что интегрирование корня x равно (2/3) x ^3/2 + C, докажем это, используя формулу интегрирования. Мы будем использовать формулу ∫x ⁿ dx = x ⁿ⁺¹ /(n + 1) + C, подставив в нее n = 1/2, поскольку √x есть не что иное, как x, возведенное в степень один на два. , то есть √x = x

1/2 . Следовательно, имеем

∫√x dx = ∫x ^1/2 dx

= х ^{1/2 + 1} /(1/2 + 1) + С

= х ^3/2 /(3/2) + С

= (2/3) х ^3/2 + C

Следовательно, интеграл от квадратного корня x равен (2/3) x ^3/2 + C, где C — постоянная интегрирования.

Определенная интеграция корня x

Далее мы найдем определенное интегрирование корня x с пределами от 1 до 10. Мы знаем, что интеграл формулы квадратного корня x равен ∫√x dx = (2/3) x 909{\ гидроразрыва {3} {2}}-1] \ конец {выравнивание} \)

Интеграция Root x Square Plus a Square

В этом разделе мы найдем интеграл квадратного корня из квадрата x плюс квадрат, то есть √(x ² + a ² ). Для нахождения этого интеграла воспользуемся методом интегрирования по частям и формулой ∫1/√(x ² + a ² ) dx = log |x + √(x ² + a ² ) | + C. Формула интегрирования по частям: ∫f(x) g(x) dx = f(x) ∫g(x) dx — ∫[d(f(x))/dx ∫ g(x) dx] дх. Здесь f(x) = √(x ² + a ² ) и g(x) = 1, так как мы можем записать √(x ² + a ² ) как √(x ² + a ² ).1. Отсюда имеем

∫√(x ² + a ² ) dx = ∫√(x ² + a ² ).1 dx

90

⇒ ∫9 0 + а ² ) dx = √(x ² + a ² ) ∫dx — ∫[d(√(x ² + a ² ))/dx ∫dx] dx

∫ 9090 ² + a ² ) dx = x√(x ² + а ² ) — ∫x ² /√(x ² + a ² ) dx

⇒ ∫√(x ^{2 х 9 х 9 х 9 0 9 0 9 0 9 0 9 0 9 ) √(х 2 + а 2 ) — ∫(а 2 — а 2 + х 2 )/√(х 2 + а 2 ) 6 ∫ 5 dx 9091 √(х 2 + A 2 ) DX = X√ (x 2 + A 2 ) + A 2 ∫1/√ (x 2 + A 2 ) DX -∫ (x 2 + +. а 2 )/√(х 2 + a 2 ) dx}

⇒ ∫√(x ² + a ² ) dx = x√(x ² + a 909 909 + 1 9) 909 10909 2 ^{∫1/√( x 2 + a 2 ) dx — ∫√(x 2 + a 2 ) dx}

⇒ ∫√(x ² + a 9090d ∫√(х ² + а ² ) dx = х√(х ² + а ² ) + а ² ∫1/√(х ² + а ^{2 09} ) 9 2 ∫√( х ² + а ² ) dx = x√(x ² + a ² ) + a ² [log |x + √(x ² + a ² )| + C]

⇒ ∫√(x ² + a ² ) dx = (x/2)√(x ² + a ² ) + (a ² /2) [log х + √(х ² + a ² )| + C]

⇒ ∫√(x ² + a ² ) dx = (x/2)√(x ² + a ² ) + (a ² /2) log |x + √(x ² + a ² )| + K, где K = C(a ² /2)

Таким образом, интеграл корня x квадрат плюс квадрат определяется как a ² ) + (a ² /2) log |x + √(x ² + a ² )| + K, где K — постоянная интегрирования. Точно так же мы можем определить внутреннюю часть корня x квадрат минус квадрат.

Интегрирование корня x квадрат минус квадрат

Поскольку мы получили интегрирование корня x квадрат плюс квадрат, теперь мы определим интегрирование корня x квадрат минус квадрат, то есть √(x ² — ² ). Воспользуемся формулой интегрирования ∫1/√(x ² + a ² ) dx = log |x + √(x ² + a ² )| + C и интегрирование по частям. Следовательно, имеем

∫√(x ² — a ² ) dx = ∫√(x ² — a ² ).1 dx

90

⇒ ∫9 0 — а ² ) dx = √(x ² — a ² ) ∫dx — ∫[d(√(x ² — a ² ))/dx ∫dx] dx

∫ 9090 ² — а ² ) dx = х√(х ² — а ² ) — ∫х ² /√(х ² — а 9

9 2 9009 06 ⇒ ∫√( x ² — a ² ) dx = x√(x ² — a ² ) — ∫(a ² — a ² + x ²⁾⁹⁰⁹¹ — a ² ) dx

⇒ ∫√(x ² — a ² ) dx = x√(x ² — a ² ) — a 209090 √(х ² — а ² ) dx — ∫(x ² — а ² )/√(х ² — а ² ) дх

⇒ ∫√(х ² — а ^{2 )} 9 2 — а ² ) — а ² ∫1/√(х ² — а ² ) дх — ∫√(х ² — а ^{2 ∫ 6} ) 1 дх 909 √(х ² — a ² ) dx + ∫√(x ² — a ² ) dx = x√(x ² — a ² ) — a ^{2 0909×2 ∫1/ 10 — а 2 ) дх}

⇒ 2 ∫√(x ² — a ² ) dx = x√(x ² — a ² ) — a ² [log |x + 90 — 9 a √ ^{09 1 2} )| + C]

⇒ ∫√(x ² — a ² ) dx = (x/2)√(x ² — a ² ) — (a ² /2) [log х + √(х ² — а ² )| + C]

⇒ ∫√(x ² — a ² ) dx = (x/2)√(x ² — a ² ) — (a ² /2) log |x + √(х ² — а ² )| + K, где K = C(a ² /2)

Следовательно, интеграл от квадрата корня x минус квадрат равен ∫√(x ² — a ² ) dx = (x/ 2)√(x ² — a ² ) — (a ² /2) log |x + √(x ² — a ² )| + K, где K — постоянная интегрирования.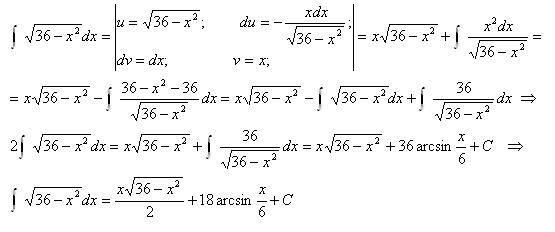

Важные замечания по интегрированию корня x

• Интегрирование корня x равно ∫√x dx = (2/3) x ^3/2 + C, где C — постоянная интегрирования.
• ∫√(x ² — a ² ) dx = (x/2)√(x ² — a ² ) — (a ² /2) log |x + √(x 9090 2 — а ² )| + К
• ∫√(x ² + a ² ) dx = (x/2)√(x ² + a ² ) + (a ² /2) log |x + √(x 9090 2 + a ² )| + К

☛ Похожие темы:

• Интеграция Sin 4x
• Интеграция Sec 3x
• Интеграция Tan Square x

Часто задаваемые вопросы по интеграции Root x

Что такое интеграция Root x?

Интеграция корня x равна (2/3) x ^3/2 + C, где C — постоянная интегрирования. Его можно определить по формуле ∫x ⁿ dx = x ⁿ⁺¹ /(n + 1) + C.