Модуль x 1 график: График функции y = (|x-1|)/(x-1)

Функции у=|x| и ей график

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Функции у=|x| и ей график.
По определению
x, если x 0,
x, если x 0,
y
| x |
x, если x 0;
x
,
если
x
0
;
y
y
y
1
1
1
0
1
x
-1 0
x
0
1
x
Функция y=|x| и ее график
y
y=|x|
1
-1 0 1
x
Основные свойства функции y=|x|
1) определена для все x, т.

е. D(y) = R;
2) принимает
только
неотрицательные значения, т.е.
E(y) = R+;
3) при x≥0 возрастает;
при x≤0 убывает;
4) четная функция |-x|=|x|, график
симметричен относительно оси Oy
Построить график функции y=|x|-2
y
1) Строим график
функции y=|x|
1
-1 0
1
x
2) Сдвигаем все
точки графика
функции y=|x|
на 2 единицы
вниз.
Построить график функции y=|x|+2
y
1) Строим график
функции y=|x|
1
-1 0
1
x
2) Сдвигаем все
точки графика
функции y=|x|
на 2 единицы
вверх.
Построить график функции y=|x-3|
y
1) Строим график
функции y=|x|
1
-1 0
1
x
2) Сдвигаем все
точки графика
функции y=|x|
на 3 единицы
вправо.
Построить график функции y=|x+3|
y
1) Строим график
функции y=|x|
1
-1 0
1
x
2) Сдвигаем все
точки графика
функции y=|x|
на 3 единицы
влево.
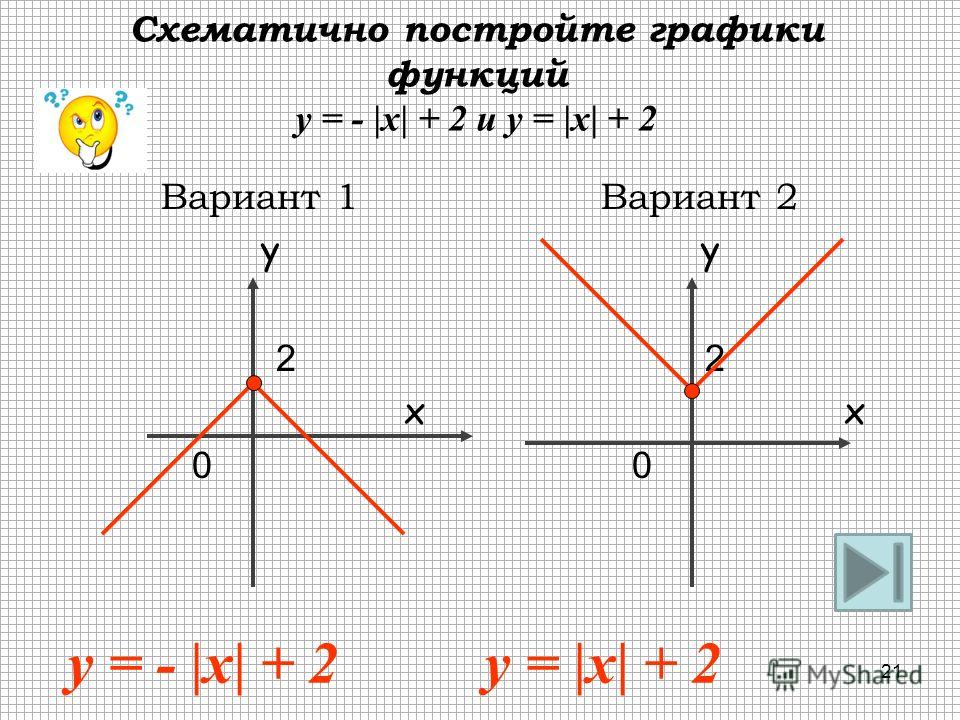
Построить график функции y=|x+1|-3
1) Строим график
функции y=|x|
y
2) Сдвигаем все
точки графика
функции y=|x|
на 1 единицу
влево.
1
-1 0
1
x
3) Сдвигаем все
точки графика
функции y=|x+1|
на 3 единицы
вниз.
На рисунке изображены графики трех функций
вида у=|x-b|+c. Определите числа b и
c для
каждого из этих функций.
у
1
2
3
1
-4
0
-2
1
5
х
Построить график функции y=||x+2|-3|
y
1
-1 0
1
x
1) Строим график
функции y=|x|
2) Сдвигаем все
точки графика
функции
y=|x|
3)
Сдвигаем
все
4) Неотрицательна
2 графика
единицу
точки
ную часть гравлево.
функции
y=|x+2|
фика y=|x+2|-3
на
3 единицы
сохраним,
а
Получили
вниз.
отрицательную
график
(y<0) отразим
функции
симметрично
y=||x+2|-3|
относительно
оси OX.
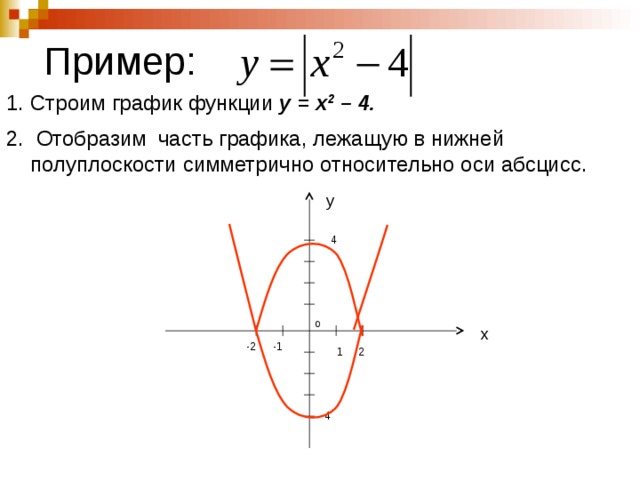
Построить график функции y=|||x|-3|-2|
y
y=|||x|-3|-2|
1
-1 0
1
x
1) Строим график
функции y=|x|
2) Сдвигаем все
точки графика
функции
y=|x|
5)Неотрицательную
3) Неотрицательную
на
единицы
часть3 (y≥0)
часть
графика
вниз.
графика функций
функции
y=|x|-3
y=||x|-3|-2 график
4) Сдвигаем
сохраним,
а отрисохраним,y=||x|-3|
а (y<0)
функций
цательную
отрицательную
на
2 единицы
отразим
симме6)Получен
график
(y<0) отразим
вниз.
трично
функций относисимметрично
тельно
оси OX.
относительно
y=|||x|-3|-2| оси
Ox.
Построить график функции
у=2|x+1|+|x-1|
1.Область определения функции: х — любое число
2.Нули подмодульных выражений:
I
II
x+1=0 x-1=0
x=1
x=-1
I
-2
II
-1
-1
0
III
1
x
III
1
2
х
Построить график функции
у=2|x+1|+|x-1|
3.Снятие модуля
— -I
-2
I: y= -2(x+1) -(x-1)
y=-3x-1
II: y= 2(x+1) -(x-1)
y=x+3
III: y= 2(x+1)+(x-1)
y=3x+1
+ — II
-1
0
+ +III
1
2
х
3x 1, x 1;
y x 3, 1 x 1;
3x 1, x 1.
4. Построение графика функции
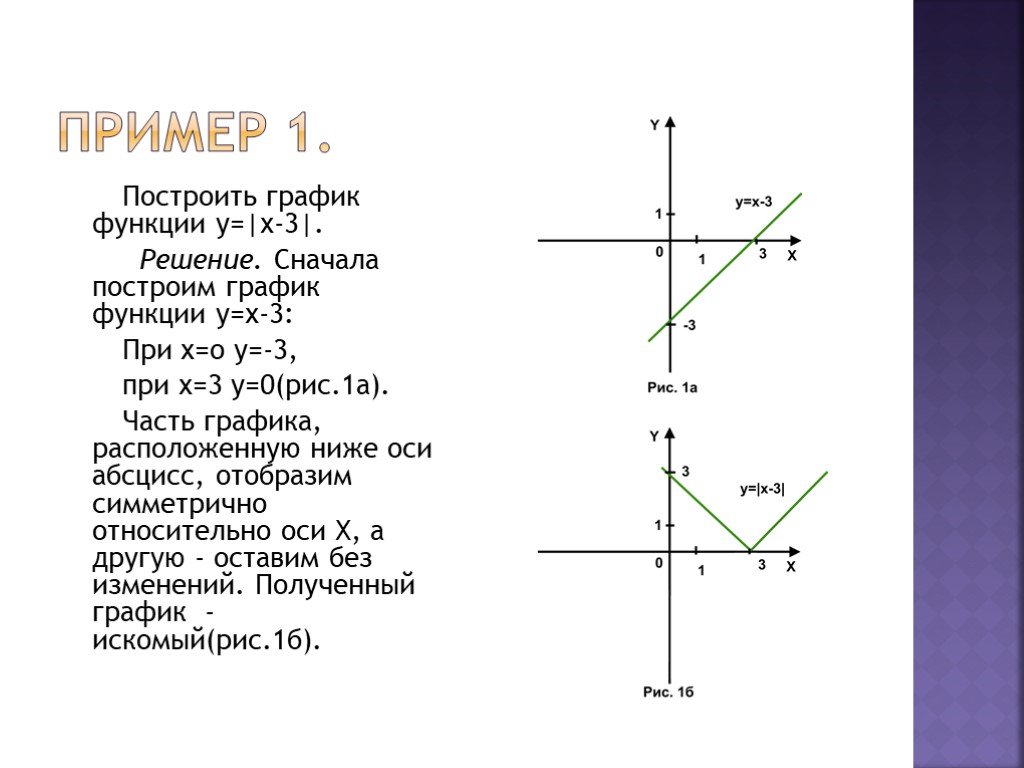
у=2|х+1|+|х-1|
3x 1, x 1;
y x 3, 1 x 1;
3x 1, x 1.
у
7
5
3
1
-2 -1
1
2
х
Графическое решение уравнения
x 3 x 1
Алгоритм графического решения уравнений:
1.Рассмотрим функции
y x 1, y x 3
2.Построим их графики в одной системе координат.
3.Определим существуют ли точки пересечения этих
графиков.
4.Абсциссы точек пересечения –корни данного
уравнения.
Графическое решение уравнения
Построим графики
функций
y
x 3 x 1
|
y x 1
y x 1
y x 3
1
-1 0
1
3
x=1
x
y x 3
Графическое решение уравнения
x 1 4
Построим графики
функций
y
|
y 4
y 4
y x 1
1
-5
-1 0
y x 1
1
3
х=-5, х=3
x
Графическое решение уравнения
x 1 4
Построим графики
функций
y
|
y 4
y x 1
y x 1
1
-1 0
x
1
y 4
Нет решений
Домашнее задание.
П.6.5;Самостоятельно
составить 2 функции вида
y=|||x-a|+b|+c|, составить и
решить графически 2
уравнения. При оценке будут
учитываться сложность
задания и аккуратность
выполнения.
Список использованной литературы
1.Учебник «Алгебра» 8 класс, авторы: С.М. Никольский,
М.К.Потапов, Н.Н. Решетников, А.В. Шевкин.
2. Дидактический материал к учебнику «Алгебра» 8 класс.
М.К.Потапов, А.В. Шевкин.
3. 1С: Репетитор. Математика часть1.
4. Живая геометрия.
5.super-videouroki http://um-razum.ru.

English     Русский Правила

«Построение графика квадратной функции, содержащей модуль»

Тема: “Построение графика квадратной функции, содержащей модуль”.
(На примере графика функции у = х²— 6x + 3.)

Цель.

• Исследовать расположение графика функции на координатной плоскости в зависимости от модуля.
• Развить навыки построения графика функции, содержащей модуль.

Ход урока.

1. Этап актуализации знаний.

а) Проверка домашнего задания.

Пример 1. Построить график функции у = х² — 6х + 3. Найти нули функции.

Решение.

1. Направление “ветвей” параболы: если а = 1, а > 0, то “ветви” параболы направлены вверх.

2. Координаты вершины параболы: х= — b/2а = — (-6)/2=3, у(3) = 9 – 18 + 3 = — 6, А(3; -6).

3. Уравнение оси симметрии: х = 3.

4. Нули функции: у(х) = 0, х² — 6х + 3 = 0, D = 36 — 4·3 = 36 – 12 = 24, D>0,

x _1,2 = (6 ± )/2 = 3 ± ; В(3 — ;0), С(3 + ;0).

График на рис.1.

Рис.1.

Алгоритм построения графика квадратной функции.

1. Определить направление “ветвей” параболы.

2. Вычислить координаты вершины параболы.

3. Записать уравнение оси симметрии.

4. Вычислить несколько точек.

б) Рассмотрим построение графиков линейных функций, содержащих модуль:

1. у = |х|. График функции на рисунке 2.

Рис. 2.

2.у = |х| + 1. График функции на рисунке 3.

Рис.3.

3. у = |х + 1|. График функции рисунке 4.

Рис.4.

Вывод.

1. График функции у = |х| + 1 получается из графика функции у = |х| параллельным переносом на вектор {0;1}.

2. График функции у = |х + 1| получается из графика функции у = |х| параллельным переносом на вектор {-1;0}.

2.Опирационно-исполнительная часть.

Этап исследовательской работы. Работа в группах.

Группа 1. Построить графики функций:

а) у = х² — 6|x| + 3,

б) у = |х² — 6х + 3|.

Решение.

а)

1.Построить график функции у = х²-6х+3.

2. Отобразить его симметрично относительно оси Оу.

График на рисунке 5.

Рис.5.

б) 1. Построить график функции у = х² — 6х + 3.

2. Отобразить его симметрично относительно оси Ох.

График функции на рисунке 6.

Рис. 6.

Вывод.

1. График функции у = f(|x|) получается из графика функции у = f(x), отображением относительно оси Оу.

2. График функции у = |f(x)| получается из графика функции у = f(x), отображением относительно оси Ох.

Группа 2.Построить графики функций:

а) у = |x² — 6|x| + 3|;

б) y = |x² — 6x + 3| — 3.

Решение.

а)

1. График функции у = х² + 6x + 3 отображаем относительно оси Оу, получается график функции у = х² — 6|x| + 3.

2. Полученный график отображаем симметрично относительно оси Ох.

График функции на рисунке 7.

Рис.7.

Вывод.

График функции y = |f (|x|)| получается из графика функции у = f(х), последовательным отображением относительно осей координат.

б)

1. График функции у = х² — 6х + 3 отображаем относительно оси Ох.

2. Полученный график переносим на вектор {0;-3}.

График функции на рисунке 8.

Рис.8.

Вывод. График функции у = |f(x)| + a получается из графика функции у = |f(x)| параллельным переносом на вектор {0,a}.

Группа 3.Построить график функции:

а) у = |x|(х — 6) + 3; б) у = х|x — 6| + 3.

Решение.

а) у = |x| (x — 6) + 3, имеем совокупность систем:

Строим график функции у = -х² + 6x + 3 при х < 0 для точек у(0) = 3, у( — 1) = — 4.

График функции на рисунке 9.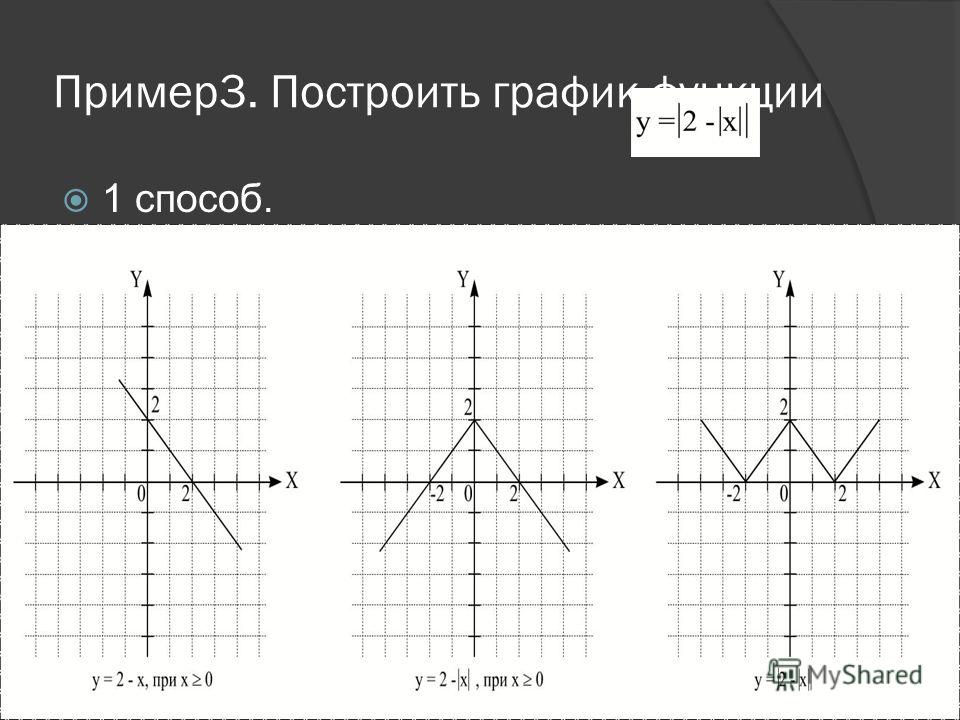

Рис.9.

б) у = х |х — 6| + 3, имеем совокупность систем:

Строим график функции у = — х² + 6х + 3 при х 6.

1. Направление “ветвей” параболы: а = — 1, а < 0, “ветви” параболы направлены вниз.

2. Координаты вершины параболы: х = — b/2a = 3, у(3) =1 2, А(3;12).

3. Уравнение оси симметрии: х = 3.

4. Несколько точек: у(2) = 11, у(1) = 3; у(-1) = — 4.

Строим график функции у = х² — 6х + 3 при х = 7 у(7) = 10.

График на рис.10.

Рис.10.

Вывод. При решении данной группы уравнений необходимо рассматривать нули модулей, содержащихся в каждом из уравнений. Затем строить график функции на каждом из полученных промежутков.

(При построении графиков данных функций каждая группа исследовала влияние модуля на вид графика функции и сделала соответствующие заключения. )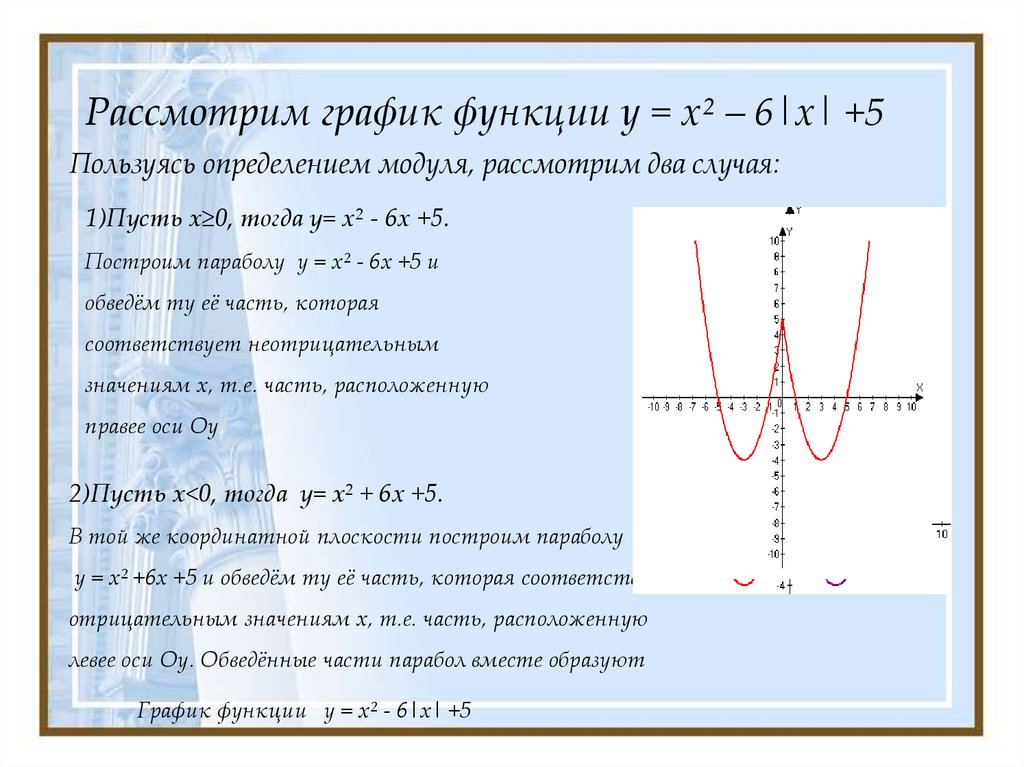

Получили сводную таблицу для графиков функций, содержащих модуль.

Таблица построения графиков функций, содержащих модуль.

Вид функции	Способ построения графика функции
1. у = f(|x|) 2. у = |f(x)| 3. у = |f(|x|)| 4. у = |f(x)| + a	1. Отобразить график функции у = f(x) симметрично относительно оси Оу. 2. Отобразить график функции у = f(x) симметрично относительно оси Ох. 3. Последовательно отобразить график функции у = f(x) симметрично относительно осей координат. 4. Параллельный перенос перенос графика функции у = |f(x)|на вектор {0;а}.

Группа 4.

Построить график функции:

а) у = х² — 5x + |x — 3|;

б) у = |x² — 5x| + x — 3.

Решение.

а) у = х² — 5х + |х — 3|, переходим к совокупности систем:

Строим график функции у = х² -6х + 3 при х 3,
затем график функции у = х² — 4х — 3 при х > 3 по точкам у(4) = -3, у(5) = 2, у(6) = 9.

График функции на рисунке 11.

Рис.11.

б) у = |х² — 5х| + х — 3, переходим к совокупности систем:

Строим каждый график на соответствующем интервале.

График функции на рисунке 12.

Рис.12.

Вывод.

Выяснили влияние модуля в каждом слагаемом на вид графика.

Самостоятельная работа.

Построить график функции:

а) у = |х² — 5х + |x — 3||,

б) у= ||x² — 5x| + х — 3|.

Решение.

Предыдущие графики отображаем относительно оси Ох.

 

Рис.13.

Рис. 14.

Группа.5

Построить график функции: у =| х — 2| (|x| — 3) — 3.

Решение.

Рассмотрим нули двух модулей: x = 0, х – 2 = 0. Получим интервалы постоянного знака.

Имеем совокупность систем уравнений:

Строим график на каждом из интервалов.

График на рисунке 15.

Рис.15.

Вывод. Два модуля в предложенных уравнениях существенно усложнили построение общего графика, состоящего из трех отдельных графиков.

Учащиеся записывали выступления каждой из групп, записывали выводы, участвовали в самостоятельной работе.

3. Задание на дом.

Построить графики функций с различным расположением модуля:

1. у = х² + 4х + 2;

2. у = — х² + 6х — 4.

4. Рефлексивно – оценочный этап.

1.Оценки за урок складываются из отметок:

а) за работу в группе;

б) за самостоятельную работу.

2. Какой момент был наиболее интересен на уроке?

3. Трудное ли домашнее задание?

Урок окончен.

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Графики функций абсолютного значения | Purplemath

Curvy Lines

Purplemath

Получение абсолютного значения отрицательного числа делает его положительным.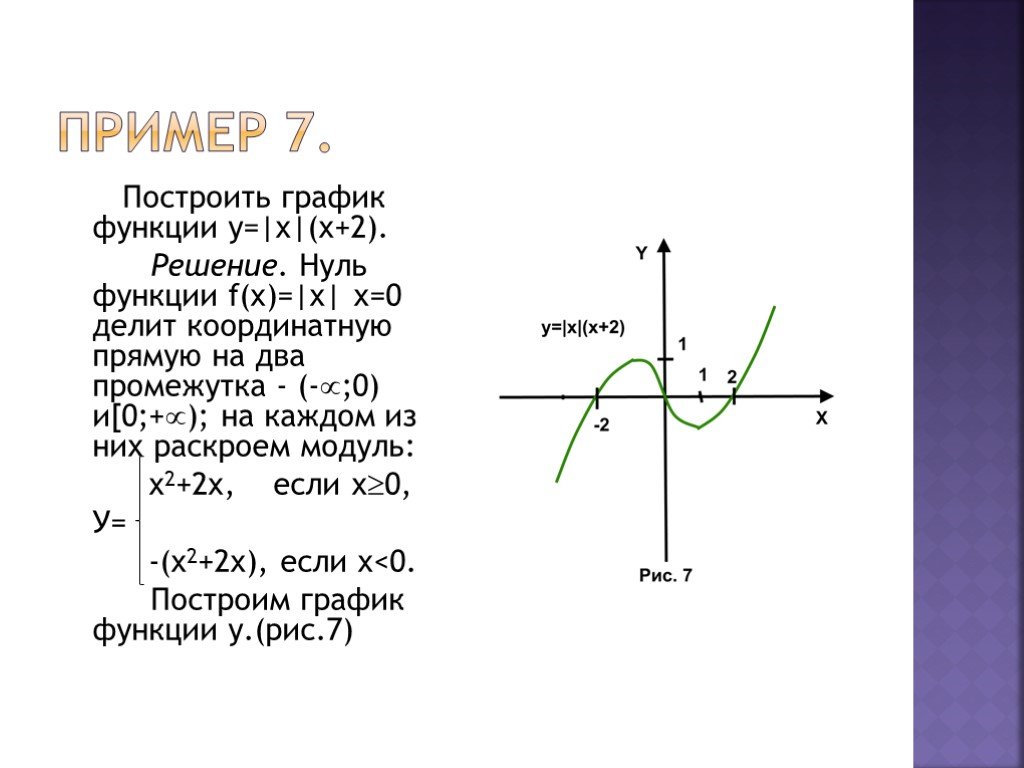 По этой причине графики функций абсолютного значения, как правило, не совсем похожи на графики линейных функций, которые вы уже изучали. Однако из-за того, как ведут себя абсолютные значения, важно включать отрицательные входные данные в вашу T-диаграмму при графическом отображении функций абсолютных значений. Если вы не выберете x -значения, которые помещают отрицательные значения в абсолютное значение, вы обычно вводите себя в заблуждение относительно того, как выглядит график.

Например, предположим, что ваш класс проходит следующий тест:

Содержание продолжается ниже

MathHelp.com

• График

  y = | x  + 2 |

Один из других студентов делает то, что обычно делают: он выбирает только положительные x -значения для его Т-диаграммы:

Затем он наносит свои точки:

Эти точки хороши, насколько они идут, но их недостаточно; они не дают точного представления о том, как должен выглядеть график.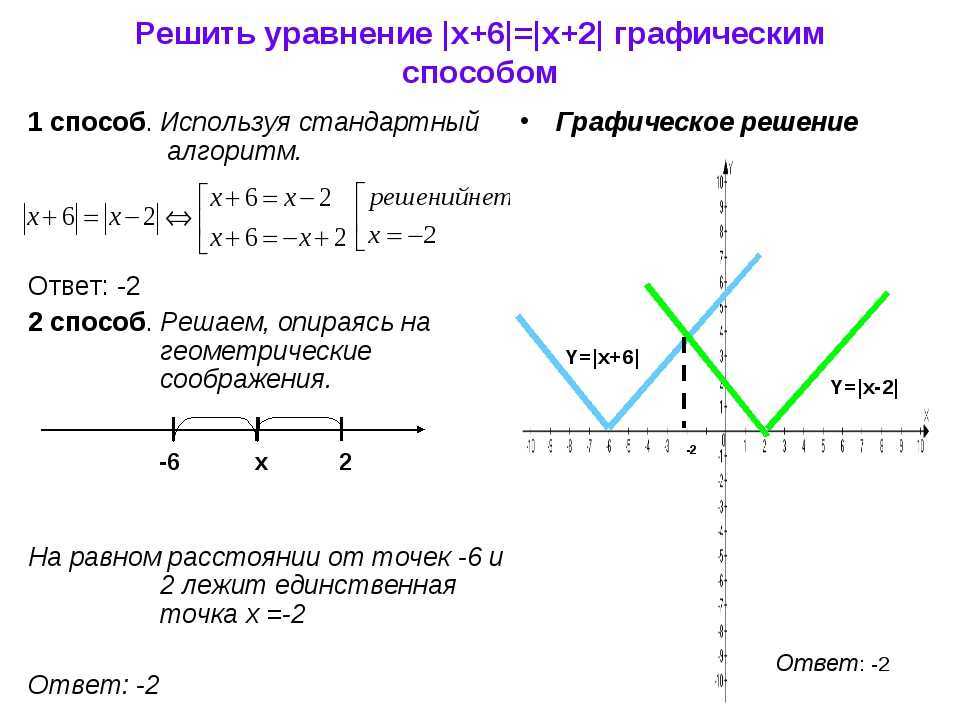 В частности, они не включают никаких «минусовых» входных данных, поэтому легко забыть, что эти столбцы абсолютного значения означают что-то. В результате учащийся забывает учитывать эти столбцы и рисует ошибочный график:

НЕПРАВИЛЬНЫЙ ОТВЕТ!

Аааааа… он только что завалил тест.

Но ты осторожнее. Вы помните, что графики абсолютных значений включают абсолютные значения, и что абсолютные значения влияют на «минусовые» входные данные. Таким образом, вы выбираете x значений, которые помещают «минус» в абсолютное значение, и вы выбираете еще несколько точек. Ваша Т-диаграмма выглядит примерно так:

Затем вы наносите точки:

…и, наконец, соединяете точки:

У вас есть правильный график:

Правильный ответ!

Ааааа… ты только что прошел тест. Хорошая работа!

---

Хотя графики абсолютных значений обычно выглядят так, как показано выше, с «локтем» посередине, это не всегда так. Однако, если вы видите график с таким изгибом, вы должны ожидать, что уравнение графика, вероятно, включает абсолютное значение. Во всех случаях вы должны позаботиться о том, чтобы выбрать хороший диапазон значений x , потому что три значения x рядом друг с другом почти наверняка не дадут вам достаточно информации, чтобы нарисовать правильное изображение.

Примечание. Полосы абсолютных значений делают введенные значения всегда неотрицательными (то есть положительными или нулевыми). В результате буква «V» на приведенном выше графике возникла там, где знак внутри был равен нулю. Когда x было меньше -2, выражение x  + 2 было меньше нуля, а столбцы абсолютных значений переворачивали эти «минусовые» значения снизу оси x вверх. Когда x равняется -2, тогда аргумент (то есть выражение внутри столбцов) равняется нулю. Для всех x -значения справа от -2, аргумент был положительным, поэтому столбцы абсолютных значений ничего не изменили.

Другими словами, графически столбцы абсолютных значений взяли этот график:

…и перевернули «минусовую» часть (зеленую на графике) из-под оси x вверх. Заметив, где аргумент столбцов абсолютного значения будет равен нулю, можно убедиться, что вы правильно строите график.

---

• График

  y = | x  | + 2

Эта функция почти аналогична предыдущей.

Однако аргумент предыдущего выражения абсолютного значения был x  + 2. В этом случае только x находится внутри столбцов абсолютного значения. Этот аргумент будет равен нулю, если 90 911 x  = 0, поэтому я должен ожидать увидеть изгиб в этой области. Кроме того, поскольку «плюс два» находится за пределами столбцов абсолютного значения, я ожидаю, что мой график будет выглядеть как обычный график абсолютного значения (будучи буквой «V» с изгибом в начале координат), но сдвинутым вверх на две единицы.