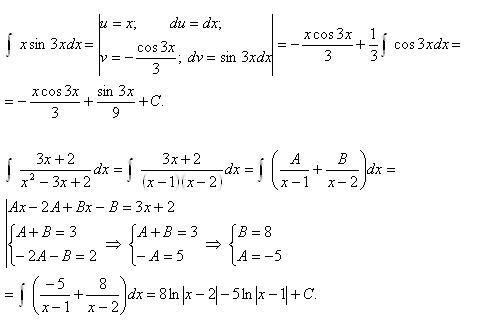Первообразная sin3x: Mathway | Популярные задачи

2

Первообразная и интеграл

Не пропустите весеннюю распродажу инструментов учителя! Доступ ко всем комплектам со скидкой до 90%

 

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Тест ограничен по времени.

Вопрос 1

Выберите первообразную для функции f(x)=4x-1

Варианты ответов

• F(x) = 16x² — x

• F(x) = 2x²

• F(x) = 2x² -x+1

• F(x)=16x²

Вопрос 2

Какая из данных функций не является первообразной для функции f(x)=sin(2x)?

Варианты ответов

• F(x)=-1\2cos2x

• F(x)=2-1\2cos2x

• F(x)=-2-cos2x

• F(x)=4-1\2cos2x

Вопрос 3

Найдите общий вид первообразных для функций f(x)=-5

Варианты ответов

• -5x+C

• -5x

• -5+C

• 5x+C

Вопрос 4

Вычислите интеграл \(\int_0^п\ \cos x\ dx\)

Варианты ответов

• п
• 0
• 1
• 2

Вопрос 5

Вычислите интеграл \(\int_{-1}^1x^6\ dx\)

Варианты ответов

• 2\7

• 0

• 1\7

• 1

Вопрос 6

Вычислите интеграл \(\int_1^2\frac{24\ dx}{^{x^2}}\)

Варианты ответов

• 9
• -7
• 8
• 7

Вопрос 7

Выберите первообразную для функции f(x)=2-x

Варианты ответов

• F(x)=2x-2x²

• F(x)=-0,5x² +2x+1

• F(x)=-2-x²

• F(x)=-0,5x²

Вопрос 8

Какая из данных функций не является первообразной для функции f(x)=cos 3x?

Варианты ответов

• F(x)=2+\(\frac{1}{3}\)sin3x

• F(x)=\(\frac{1}{3}\)sin3x

• F(x)=2-\(\frac{1}{3}\)sin3x

• F(x)=4+\(\frac{1}{3}\)sin3x

Вопрос 9

Найдите общий вид первообазной для функции f(x) =-5

Варианты ответов

• -5x+C
• -5x
• -5+C
• 5x+C

Вопрос 10

Вычислите интеграл \(\int_{-1}^0x^5\ dx\)

Варианты ответов

• \(-\frac{1}{6}\)

• \(\frac{5}{6}\)

• \(\frac{1}{6}\)

• -1

Вопрос 11

Вычислите нтеграл \(\int_1^2\frac{16dx}{x^3}\)

Варианты ответов

• \(\frac{11}{4}\)

• \(\frac{15}{4}\)

• \(\frac{13}{4}\)

• \(\frac{17}{4}\)

Пройти тест

Сохранить у себя:

© 2021, Екимченко Елизавета Борисовна  703

4+1}\,dx $ без сложного интегрирования

@Nanayajitzuki дал вам очень хорошее решение этой проблемы, используя интегральное правило Лейбница (или трюк Фейнмана, если вы физик!) Действительно, этот интеграл невероятно сложен без сложного Анализ.

Это выполнимо… но любой реальный метод будет весьма нетривиальным.

Для другого решения мы могли бы снова параметризовать интеграл и использовать преобразование Лапласа. Технически формальное обращение преобразования Лапласа в конце потребовало бы сложной интеграции, однако мы можем очень легко вычислить инверсию многих стандартных функций, используя свойства преобразования Лапласа вместе со знанием преобразования Лапласа стандартных функций. 92 + 3\sqrt{2}s + 9\right)}=\mathcal{L}\{I(t)\}}$$

(Записывать полный способ решения этого интеграла было бы огромным, но по существу вам нужно делать частичные дроби и подстановки кучу.Можно оценить это, используя реальные методы, просто потому, что это чудовищный интеграл, я не буду описывать шаги для него здесь.Но вы можете попробовать, если вы чувствую себя смелым 😛 Это не должно быть сложно — просто утомительно).

Теперь осталось инвертировать преобразование Лапласа! Для этого обратите внимание на 9{-\frac{3}{\sqrt{2}}}\sin\left(\frac{3}{\sqrt{2}}\right)}$$

Интеграл от Sin(3x): формула, доказательство , Примеры, Решение

Интеграл от sin3x вместе с его формулой и доказательством с примерами.

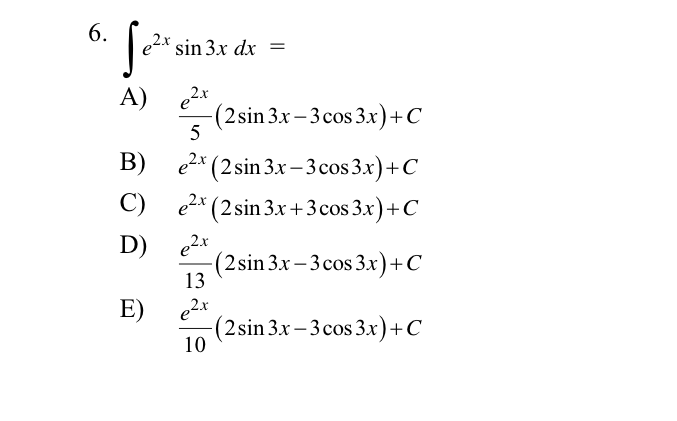Также узнайте, как вычислить интегрирование sin(3x) с пошаговыми примерами.

от Алана Уокера — Опубликовано на 28 февраля 2023 г.

Введение в интеграл от sin(3x)

В исчислении интеграл — это фундаментальное понятие, которое присваивает числа функциям для определения смещения, площади, объема и всех тех функций, которые содержат комбинацию крошечных элементов. Он подразделяется на две части: определенный интеграл и неопределенный интеграл. Процесс интегрирования вычисляет интегралы. Этот процесс определяется как нахождение первообразной функции.

Интегралы могут обрабатывать почти все функции, такие как тригонометрические, алгебраические, экспоненциальные, логарифмические и т. д. В этой статье вы узнаете, что является интегралом тригонометрической функции синуса. Вы также поймете, как вычислить интеграл греха, используя различные методы интегрирования.

Чему равен интеграл sin(3x)?

Интеграл sin(3x) является первообразной функции синуса, которая равна –cos x.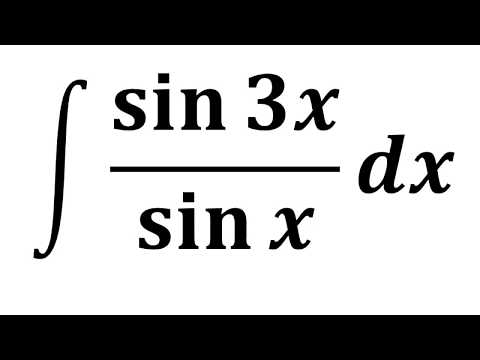 Это также известно как обратная производная функции синуса, которая является тригонометрической идентичностью.

Функция синуса представляет собой отношение противолежащего катета к гипотенузе треугольника, которое записывается как:

Sin = противолежащий катет / гипотенуза

Интеграл от формулы sin(3x)

Формула интеграла от sin содержит знак интеграла , коэффициент интегрирования и функция как синус. Он обозначается ∫sin(3x)dx. В математической форме интеграл от sin(3x):

$$∫\sin(3x)dx = -\frac{\cos 3x}{3} + c$$

Где c — любая вовлеченная константа, dx — коэффициент интегрирования, ∫ — символ интеграла.

Как вычислить интеграл от sin(3x)?

Интеграл от sin(3x) является его первообразной, которую можно вычислить с помощью различных методов интегрирования. В этой статье мы обсудим, как вычислить интеграл синуса, используя:

1. Производные
2. Метод замены
3. Определенный интеграл

Интеграл от sin(3x) с использованием производных

Производная функции вычисляет скорость изменения, а интегрирование — это процесс нахождения первообразной функции.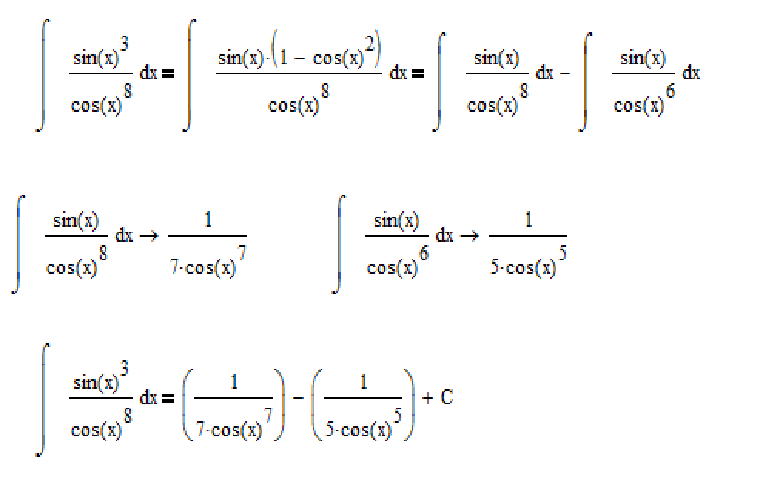 Следовательно, мы можем использовать производную для вычисления интеграла функции. Давайте обсудим вычисление интеграла от sin(3x) с использованием производных.

Доказательство интеграла от sin(3x) с использованием производных

Поскольку мы знаем, что интегрирование является обратной производной. Следовательно, мы можем вычислить интеграл от sin(3x), используя его производную. Для этого нам нужно найти какие-то формулы производных или формулу, которая дает sin 3x как производную любой функции.

В производной мы знаем, что

$$\frac{d}{dx}(\cos 3x) = -3\sin(3x)$$

Это означает, что производная от cos 3x дает нам sin 3x . Но он имеет отрицательный знак. Следовательно, чтобы получить интеграл от синуса, мы должны умножить приведенное выше уравнение на знак минус, то есть:

$$-\frac{d}{dx}(\cos 3x) = 3\sin(3x)$$

Следовательно, интеграл от sin(3x) равен минусу 3cos 3x. Записывается как:

$$∫\sin(3x)dx = -\frac{\cos (3x)}{3} + c$$

Интеграл от sin(3x) методом подстановки

Подстановка Метод включает множество тригонометрических формул. Мы можем использовать эти формулы для проверки интегралов различных тригонометрических функций, таких как синус, косинус, тангенс и т. д. Давайте разберемся, как доказать интеграл от греха с помощью метода подстановки.

Доказательство интеграла от sin(3x) с использованием метода подстановки

В методе подстановки мы можем использовать тригонометрические тождества, а также параметры, чтобы мы могли записать уравнение в простой форме. Этот метод помогает легко вычислять интегралы. Чтобы доказать интеграл от sin(3x) методом подстановки, предположим, что:

$$y = \sin (3x)$$

Используя интеграл, предположим, что u = 3x и du = 3dx, поэтому интеграл от sin (3x) можно записать как:

$$∫\sin (3x)dx = \frac{1}{3}∫\sin u du$$

Интегрируя по соответствующей переменной, получаем

$$∫\sin (3x) dx = -\frac{\cos u}{3} + c$$

Теперь подставим u = 3x, чтобы получить решение.

$$∫\sin (3x)dx=-\frac{\cos 3x}{3} + c$$

Следовательно, мы проверили интеграл от sin (3x) методом подстановки.