Первообразная таблица первообразных: Таблица первообразной — Интегралы,первообразные

Математика: Справ. материалы

Математика: Справ. материалы

Гусев В. А., Мордкович А. Г. Математика: Справ. материалы: Кн. для учащихся.— М.: Просвещение, 1988.— 416 с. В книге дано краткое изложение основных разделов школьных курсов алгебры и начал анализа, геометрии. Книга окажет помощь в систематизации и обобщении знаний по математике. Оглавление СЛОВО К УЧАЩИМСЯ ГЛАВА I. ЧИСЛА § 1. Натуральные числа 2. Арифметические действия над натуральными числами. 3. Деление с остатком. 4. Признаки делимости. 5. Разложение натурального числа на простые множители. 6. Наибольший общий делитель нескольких натуральных чисел. 7. Наименьшее общее кратное нескольких натуральных чисел. 8. Употребление букв в алгебре. Переменные. § 2. Рациональные числа 10. Равенство дробей. Основное свойство дроби. Сокращение дробей. 11. Приведение дробей к общему знаменателю. 12. Арифметические действия над обыкновенными дробями. 13. Десятичные дроби. 14. Арифметические действия над десятичными дробями. 15. Проценты. 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь. 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь. 18. Координатная прямая. 19. Множество рациональных чисел. § 3. Действительные числа 21. Действительные числа. Числовая прямая. 22 Обозначения некоторых числовых множеств. 23. Сравнение действительных чисел. 25. Числовые промежутки. 26. Модуль действительного числа. 27. Формула расстояния между двумя точками координатной прямой. 28. Правила действий над действительными числами. 29. Свойства арифметических действий над действительными числами. 30. Пропорции. 31. Целая часть числа. Дробная часть числа. 32. Степень с натуральным показателем. 33. Степень с нулевым показателем. Степень с отрицательным целым показателем. 34. Стандартный вид положительного действительного числа. 35. Определение арифметического корня. 36. Корень нечетной степени из отрицательного числа. 37. Степень с дробным показателем. 38. Свойства степеней с рациональными показателями. 39. Приближенные значения чисел. Абсолютная и относительная погрешности. 40. Десятичные приближения действительного числа по недостатку и по избытку. 41. Правило извлечения квадратного корня из натурального числа. 42. Понятие о степени с иррациональным показателем. 43. Свойства степеней с действительными показателями. § 4. Комплексные числа 45. Арифметические операции над комплексными числами. 46. Алгебраическая форма комплексного числа. 47. Отыскание комплексных корней уравнений. ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 49. 3. 112. Построение графика функции y = f(x-m)+n 113. График квадратичной функции. 114. Способы построения графика квадратичной функции 115. Построение графика функции y = f(kx). 116. Сжатие и растяжение графиков тригонометрических функций. 117. График гармонического колебания ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ § 12. Преобразование выражений, содержащих переменную под знаком логарифма 119. Определение логарифма положительного числа по данному основанию. 120. Свойства логарифмов. 121. Переход к новому основанию логарифма. 122. Логарифмирование и потенцирование. 123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма. § 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений 125. Формулы сложения и вычитания аргументов. 126. Формулы приведения. 127. Соотношения между тригонометрическими функциями одного и того же аргумента. 128. Формулы двойного угла. 129. Формулы понижения степени. 130. Преобразование суммы тригонометрических функций в произведение. 131. Преобразование произведения тригонометрических функций в сумму. 132. Преобразование выражения a cos t + b sin t к виду A sin (t + a). 133. Примеры преобразований выражений, содержащих обратные тригонометрические функции. ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ § 14. Уравнения с одной переменной 135. Равносильность уравнений. 136. Линейные уравнения. 137. Квадратные уравнения. 138. Неполные квадратные уравнения. 139. Теорема Виета. 140. Системы и совокупности уравнений. 141. Уравнения, содержащие переменную под знаком модуля. 142. Понятие следствия уравнения. Посторонние корни. 143. Уравнения с переменной в знаменателе. 144. Область определения уравнения. 145. Рациональные уравнения. 146. Решение уравнения p(x) = 0 методом разложения его левой части на множители. 147. Решение уравнений методом введения новой переменной. 148. Биквадратные уравнения. 149. Решение задач с помощью составления уравнений. 150. Иррациональные уравнения. 151. Показательные уравнения. 152. Логарифмические уравнения. 153. Примеры решения показательно-логарифмических уравнений. 154. Простейшие тригонометрические уравнения. 155. Методы решения тригонометрических уравнений. 156. Универсальная подстановка (для тригонометрических уравнений). 157. Метод введения вспомогательного аргумента (для тригонометрических уравнений). 158. Графическое решение уравнений. 159. Уравнения с параметром. § 15. Уравнения с двумя переменными 161. График уравнения с двумя переменными. 162. Линейное уравнение с двумя переменными и его график. § 16. Системы уравнений 164. Решение систем двух уравнений с двумя переменными методом подстановки. 165. Решение систем двух уравнений с двумя переменными методом сложения. 167. Графическое решение систем двух уравнений с двумя переменными. 168. Исследование системы двух линейных уравнений с двумя переменными. 169. Решение систем двух уравнений с двумя переменными методами умножения и деления. 170. Системы показательных и логарифмических уравнений. 171. Системы тригонометрических уравнений с двумя переменными. 172. Системы трех уравнений с тремя переменными. 173. Решение задач с помощью составления систем уравнений. Глава VI. НЕРАВЕНСТВА § 17. Решение неравенств с переменной 175. Графическое решение неравенств с одной переменной. 176. Линейные неравенства с одной переменной. 177. Системы неравенств с одной переменной. 178. Совокупность неравенств с одной переменной. 179. Дробно-линейные неравенства. 180. Неравенства второй степени. 181. Графическое решение неравенств второй степени. 182. Неравенства с модулями. 183. Решение рациональных неравенств методом промежутков. 184. Показательные неравенства. 185. Логарифмические неравенства. 186. Иррациональные неравенства. 187. Решение тригонометрических неравенств. 188. Неравенства и системы неравенств с двумя переменными. § 18. Доказательство неравенств 190. Синтетический метод доказательства неравенств. 191. Доказательство неравенств методом от противного. 192. Использование неравенств при решении уравнений. ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 19. Числовые последовательности 194. Способы задания последовательности. 195. Возрастание и убывание последовательности. 196. Определение арифметической прогрессии. 197. Свойства арифметической прогрессии 198. Определение геометрической прогрессии. 199. Свойства геометрической прогрессии. 200. Понятие о пределе последовательности. 201. Вычисление пределов последовательностей. 202. Сумма бесконечной геометрической прогрессии при |q| § 20. Предел функции 204. Вычисление пределов функции при х->оо. 205. Предел функции в точке. Непрерывные функции. 206. Вертикальная асимптота. 207. Вычисление пределов функций в точке. § 21. Производная и ее применения 209. Определение производной. 210. Формулы дифференцирования. Таблица производных. 211. Дифференцирование суммы, произведения, частного. 212. Сложная функция и ее дифференцирование. 213. Физический смысл производной. 214. Вторая производная и ее физический смысл. 215. Касательная к графику функции. 216. Применение производной к исследованию функций на монотонность. 217. Применение производной к исследованию функций на экстремум. 218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке. 219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке. 220. Задачи на отыскание наибольших или наименьших значений величин. 221. Применение производной для доказательства тождеств. 222. Применение производной для доказательства неравенств. 223. Общая схема построения графика функции. § 22. Первообразная и интеграл 225. Таблица первообразных. 226. Правила вычисления первообразных. 227. Интеграл. 228. Связь между интегралов и первообразной (формула Ньютона—Лейбница). 229. Правила вычисления интегралов. 230. Использование интеграла для вычисления площадей плоских фигур. ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ 2. Точка. Прямая. 3. Определения. Аксиомы. Теоремы. § 2. Основные свойства простейших геометрических фигур 5. Луч. 6. Окружность. Круг. 7. Полуплоскость. 8. Угол. Градусная мера угла. 9. Смежные и вертикальные углы. 10. Центральные и вписанные углы. 11. Параллельные прямые. 12. Признаки параллельности прямых. 13. Перпендикулярные прямые. 14. Касательная к окружности. 15. Треугольники. 16. Равенство треугольников. 17. Равнобедренный треугольник. 18. Сумма углов треугольника. 19. Прямоугольный треугольник. Теорема Пифагора. 20. Окружности, вписанные в треугольник и описанные около треугольника. § 3. Геометрические построения на плоскости 22. Простейшие задачи на построение. 23. Геометрическое место точек на плоскости. § 4. Четырехугольники 25. Параллелограмм. 26. Прямоугольник. Ромб. Квадрат. 27. Трапеция. § 5. Многоугольники 29. Выпуклые многоугольники. 30. Правильные многоугольники. 31. Длина окружности. § 6. Решение треугольников 33. Соотношения между сторонами и углами в прямоугольном треугольнике. 34. Теорема косинусов. Теорема синусов. 35. Решение треугольников. § 7. Площади плоских фигур 37. Площади многоугольников. 38. Площади подобных фигур. 39. Площадь круга. ГЛАВА II. Прямые и плоскости в пространстве § 9. Параллельность прямых и плоскостей 42. Параллельность прямой и плоскости. 43. Параллельные плоскости. § 10. Перпендикулярность прямых и плоскостей 45. Перпендикуляр и наклонная к плоскости. 46. Перпендикулярность плоскостей. ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ § 11. Многогранники 48. Многогранные углы. Многогранники. 49. Призма. Параллелепипед. Куб. 50. Пираприда. 51. Правильные многогранники. § 12. Тела вращения 53. Конус. 54. Шар. § 13. Изображение пространственных фигур на плоскости 56. Ортогональное проектирование. 57. Геометрическое место точек в пространстве. § 14. Объемы тел 59. Объем параллелепипеда, призмы и пирамиды. 60. Объем цилиндра и конуса. 61. Общая формула объемов тел вращения. § 15. Площади поверхностей тел 63. Понятие площади поверхности. 64. Площади поверхностей тел вращения. ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ § 16. Координаты на плоскости и в пространстве 66. Координаты середины отрезка. § 17. Уравнения фигур на плоскости 68. Пересечение двух окружностей. 69. Уравнение прямой. 70. Пересечение прямой и окружности. § 18. Уравнения фигур в пространстве 72. Уравнение сферы. 73. Взаимное расположение сферы и плоскости. 74. Пересечение двух сфер. ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР 76. Понятие движения. § 20. Подобие фигур 78. Подобные фигуры. ГЛАВА VI. ВЕКТОРЫ 80. Понятие вектора. 81. Координаты вектора. § 22. Операции над векторами 83. Умножение вектора на число. Коллинеарные векторы. 84. Скалярное произведение векторов. ПРИЛОЖЕНИЯ ГЕОМЕТРИЯ

11 класс. Алгебра. Интеграл. Первообразная. Неопределенный и определенный интеграл. — Первообразная. Правила отыскания первообразных.

Комментарии преподавателя

При­мер на­хож­де­ния пер­во­об­раз­ной

Ма­те­ма­ти­че­ские за­да­чи, опе­ра­ции часто раз­ли­ча­ют­ся как пря­мые и об­рат­ные. На­при­мер: сло­же­ние и вы­чи­та­ние, умно­же­ние и де­ле­ние. Мы в по­след­нее время за­ни­ма­лись диф­фе­рен­ци­ро­ва­ни­ем, то есть на­хож­де­ни­ем про­из­вод­ных. На этом уроке мы зай­мем­ся об­рат­ной опе­ра­ци­ей – ин­те­гри­ро­ва­ни­ем, или на­хож­де­ни­ем пер­во­об­раз­ных.

Пря­мая за­да­ча:

Дано: .

Найти:.

При­мер:

Об­рат­ная за­да­ча:

Дано: .

Найти: .

При­мер:

  

 – пер­во­об­раз­ная для .

Стро­гое опре­де­ле­ние пер­во­об­раз­ной функ­ции

Опре­де­ле­ние:

Функ­цию  на­зы­ва­ют пер­во­об­раз­ной для функ­ции  на за­дан­ном про­ме­жут­ке , если для всех  вы­пол­ня­ет­ся ра­вен­ство:

За­кре­пим опре­де­ле­ние кон­крет­ны­ми при­ме­ра­ми.

При­ме­ры:

 – пер­во­об­раз­ная для , так как

 – пер­во­об­раз­ная для , так как

, то есть 

 – пер­во­об­раз­ная для , так как

 

Вспом­ним, что для на­хож­де­ния про­из­вод­ных су­ще­ство­ва­ла таб­ли­ца про­из­вод­ных. Точно так же, для на­хож­де­ния пер­во­об­раз­ных, име­ет­ся таб­ли­ца пер­во­об­раз­ных, часть ко­то­рой пред­став­ле­на далее (Табл. 1):

	Функ­ция	Пер­во­об­раз­ная
1	0	1
2	1
3
4
5

Табл. 1. Таб­ли­ца пер­во­об­раз­ных

Про­ве­рим рас­смот­рен­ную часть таб­ли­цы, то есть про­ве­рим опре­де­ле­ние:

1.   

2. 

3. 

4. 

5.  

Таким об­ра­зом, эта часть таб­ли­цы про­ве­ре­на.

Про­дол­жим изу­че­ние и обос­но­ва­ние таб­ли­цы. Сле­ду­ю­щая часть таб­ли­цы пер­во­об­раз­ных пред­став­ле­на ниже (Табл. 2):

	Функ­ция	Пер­во­об­раз­ная
6
7
8
9
10

Табл. 2. Таб­ли­ца пер­во­об­раз­ных (про­дол­же­ние)

По­лез­но про­ве­рить, обос­но­вать и до­ка­зать дан­ную часть таб­ли­цы.

6.  

7. 

8. 

9.  

10.  

Таб­ли­ца обос­но­ва­на.

Те­перь мы имеем опре­де­ле­ние пер­во­об­раз­ной и таб­ли­цу пер­во­об­раз­ных, обос­но­ван­ную этим опре­де­ле­ни­ем. Про­дол­жим ре­ше­ние задач на опре­де­ле­ние пер­во­об­раз­ной.

До­ка­жи­те: 

 

а) 

До­ка­за­тель­ство:

б) 

До­ка­за­тель­ство:

Рас­смот­рим еще одну за­да­чу.

До­ка­жи­те: 

 

До­ка­за­тель­ство:

На­по­ми­на­ние:

1. 

2. 

Рас­смот­рим за­да­чу с тан­ген­сом.

До­ка­жи­те: 

До­ка­за­тель­ство:

Рас­смот­рим за­да­чу с ко­си­ну­сом.

До­ка­жи­те: 

 

До­ка­за­тель­ство:

Рас­смот­рим ана­ло­гич­ную за­да­чу с ир­ра­ци­о­наль­ным вы­ра­же­ни­ем.

До­ка­жи­те: 

До­ка­за­тель­ство:

Опре­де­ле­ние. Функ­цию на­зы­ва­ют пер­во­об­раз­ной для функ­ции  на за­дан­ном про­ме­жут­ке , если для всех  из  вы­пол­ня­ет­ся ра­вен­ство .

Несколь­ко разъ­яс­ня­ю­щих при­ме­ров:

 – пер­во­об­раз­ная для 

Чтобы это под­твер­дить, возь­мем про­из­вод­ную

 пер­во­об­раз­ная для 

Итак, мы при­ве­ли 2 при­ме­ра, ко­то­рые под­твер­жда­ют опре­де­ле­ние и ис­поль­зу­ют его.

На­пом­ним две за­да­чи:

Пря­мая за­да­ча: Дана функ­ция . Найти . Про­цесс на­зы­ва­ет­ся диф­фе­рен­ци­ро­ва­ни­ем.

Об­рат­ная за­да­ча: Дана функ­ция  – про­из­вод­ная неиз­вест­ной функ­ции Найти Про­цесс на­зы­ва­ет­ся ин­те­гри­ро­ва­ни­ем.

Какие ос­нов­ные ин­стру­мен­ты для на­хож­де­ния пер­во­об­раз­ных?

На­хож­де­ние 

— таб­ли­це пер­во­об­раз­ных, ко­то­рую мы по­вто­рим;

— пра­ви­лам отыс­ка­ния пер­во­об­раз­ных, ко­то­рые мы изу­чим.

Таб­ли­ца

Функ­ция	Пер­во­об­раз­ная
0	1
1

Про­ве­рим:

Таким об­ра­зом про­ве­ря­ют­ся все строч­ки таб­ли­цы. То есть, вы­пол­ня­ет­ся со­от­но­ше­ние: .

Пе­ре­хо­дим к пра­ви­лам отыс­ка­ния пер­во­об­раз­ных.

Пра­ви­ло 1.

Пер­во­об­раз­ная суммы равна сумме пер­во­об­раз­ных.

Дано:

До­ка­зать:

До­ка­за­тель­ство: что и тре­бо­ва­лось до­ка­зать.

Функ­ция со­сто­ит из двух функ­ций. Найти пер­во­об­раз­ную функ­ции:

При­мер под­твер­жда­ет пра­ви­ло 1.

Пра­ви­ло 2. (о по­сто­ян­ном мно­жи­те­ле)

Дано:, то есть  – пер­во­об­раз­ная для f, k – const.

До­ка­зать: kF – пер­во­об­раз­ная для kf.

До­ка­за­тель­ство:

До­ка­за­тель­ство ос­но­вы­ва­ет­ся на опре­де­ле­нии пер­во­об­раз­ной и на пра­ви­ле диф­фе­рен­ци­ро­ва­ния: . Что и тре­бо­ва­лось до­ка­зать.

Смысл пра­ви­ла: если мы знаем пер­во­об­раз­ную для f, то чтобы по­лу­чить пер­во­об­раз­ную для kf, нужно пер­во­об­раз­ную Fумно­жить на k.

Под­твер­жда­ю­щий при­мер:

Пра­ви­ло 3. Если  – пер­во­об­раз­ная для функ­ции, то  пер­во­об­раз­ная для .

Дано:.

До­ка­зать:

, что и тре­бо­ва­лось до­ка­зать.

6. При­мер 2

Если  ,то 

Про­вер­ка: ( ..

Необ­хо­ди­мые по­яс­не­ния: вме­сто мы имеем скоб­ку (). Как это от­ра­жа­ет­ся на на­хож­де­нии пер­во­об­раз­ной? Сле­ду­ю­щим об­ра­зом: пер­во­об­раз­ная от но надо раз­де­лить на ко­эф­фи­ци­ент при х.

При­мер 1.

Найти одну из пер­во­об­раз­ных для функ­ции

a)      

Ре­ше­ние:

a) 

Ответ:

Про­вер­ка:..

При­мер 2.

Найти одну из пер­во­об­раз­ных для функ­ции

б)

Ре­ше­ние:

б)

Ответ:

Про­вер­ка: =

.

ИСТОЧНИК

http://interneturok. ru/ru/school/algebra/11-klass/integralb/pervoobraznaya

http://interneturok.ru/ru/school/algebra/11-klass/integralb/pravila-otyskaniya-pervoobraznyh

http://www.youtube.com/watch?v=Drm_qFaEpks

http://fs1.ppt4web.ru/uploads/ppt/5418/2f87298026d3cf2e17ad4aa4c42304bc.pptx

http://test-training.ru/tag/tri-pravila-nahozhdeniya-pervoobraznoy-test

http://test-training.ru/news/otvet-k-testam-po-algebre-dlya-11-klassa.html

https://downloader.disk.yandex.ru/disk/197fa925c280a3c019e8f0b97c7065779aec80a75626f3c3c7877370509af9a4/56a1139b/gl1wdmatkHwr1IvHwfPzjlCbLxx51K2AXTrKx-khOfQ1WIGwVJDIxTfxWZJp9W23tYCJlb2c61QroEWHqjfeTQ%3D%3D?uid=0&filename=%D0%9C%D0%BE%D1%80%D0%B4%D0%BA%D0%BE%D0%B2%D0%B8%D1%87-%D0%90.%D0%93.-%D0%90%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0-%D0%B8-%D0%BD%D0%B0%D1%87%D0%B0%D0%BB%D0%B0-%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7%D0%B0.11-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-%D0%A7%D0%B0%D1%81%D1%82%D1%8C-1.pdf&disposition=attachment&hash=Ev/JAxs9FONy74%2BMIKGz214ILPNlyMZo/xnQbixz5Z8%3D%3A/%D0%9C%D0%BE%D1%80%D0%B4%D0%BA%D0%BE%D0%B2%D0%B8%D1%87-%D0%90. %D0%93.-%D0%90%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0-%D0%B8-%D0%BD%D0%B0%D1%87%D0%B0%D0%BB%D0%B0-%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7%D0%B0.11-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-%D0%A7%D0%B0%D1%81%D1%82%D1%8C-1.pdf&limit=0&content_type=application%2Fpdf&fsize=18366111&hid=c9e0cd334be9f7c6de02c1f2d04edf87&media_type=document&tknv=v2

 

Правила первообразных — список, формулы, примеры

Правила первообразных в исчислении являются основными правилами, которые используются для нахождения первообразных различных комбинаций функций. Как следует из названия, антидифференцировка — это процесс, обратный дифференцировке. Эти первообразные правила помогают нам найти первообразную суммы или разности функций, произведение и частное функций, скалярное кратное функции и постоянной функции, а также композицию функций. Правила первообразных помогают нам сделать процесс нахождения первообразных проще и проще.

Далее в этой статье мы приступим к подробному изучению первообразных правил. Мы также рассмотрим первообразные правила некоторых важных и конкретных функций вместе с некоторыми решенными примерами для лучшего понимания концепции.

1.	Что такое первообразные правила?
2.	Список антипроизводных правил
3.	Основные антипроизводные правила
4.	Первообразные правила для конкретных функций
5.	Часто задаваемые вопросы об антипроизводных правилах

Что такое первообразные правила?

Правила первообразных являются одними из важных правил для нахождения первообразных различных форм комбинаций функций. Мы можем использовать эти правила первообразных, чтобы найти первообразные произведения, частного, суммы, разности, скалярного кратного и композиции функций. Эти правила можно использовать для антидифференцирования алгебраических функций, экспоненциальной функции, тригонометрических функций, гиперболических функций, логарифмической функции и постоянной функции. Давайте рассмотрим важные правила первообразных в разделах ниже.

Список первообразных правил

Список наиболее часто используемых первообразных правил для произведения, частного, суммы, разности и композиции функций выглядит следующим образом:

• Степенное первообразное правило
• Антипроизводное цепное правило
• Антипроизводное правило произведения
• Правило первообразных частных
• Правило первообразной для скалярного кратного функции
• Правило первообразной суммы и разности функций

Основные антипроизводные правила

В этом разделе мы подробно рассмотрим формулы для различных правил первообразных, рассмотренных выше. Мы обсудим правила антидифференцирования алгебраических функций со степенью и различные комбинации функций. Правила первообразных являются общими для типов функций, таких как тригонометрические, экспоненциальные, логарифмические и алгебраические функции.

Правило первообразной степени

Теперь правило первообразной степени x определяется как ∫x ⁿ dx = x ⁿ⁺¹ /(n + 1) + C, где n ≠ -1. Это правило широко известно как правило первообразной мощности. Давайте рассмотрим некоторые примеры этого первообразного правила, чтобы лучше понять это правило.

• ∫x ² dx = x ²⁺¹ /(2+1) + C = x ³ /3 + C
• ∫x ^-4 dx = x ^-4+1 /(-4+1) + C = x ^-3 /(-3) + С = -х ^-3 /3 + С

Используя правило степени первообразной, мы можем заключить, что для n = 0 имеем ∫x ⁰ dx = ∫1 dx = ∫dx = x ⁰⁺¹ /(0+1) + C = x + C. Пожалуйста, не путайте это правило степенной первообразной ∫x ⁿ dx = x ⁿ⁺¹ /(n + 1) + C, где n ≠ -1, со степенным правилом производной d(x ⁿ )/dx = nx ^n-1 .

Правило первообразной цепи

Мы знаем, что антидифференцировка — это процесс, обратный дифференцированию, поэтому правила производных приводят к некоторым первообразным правилам.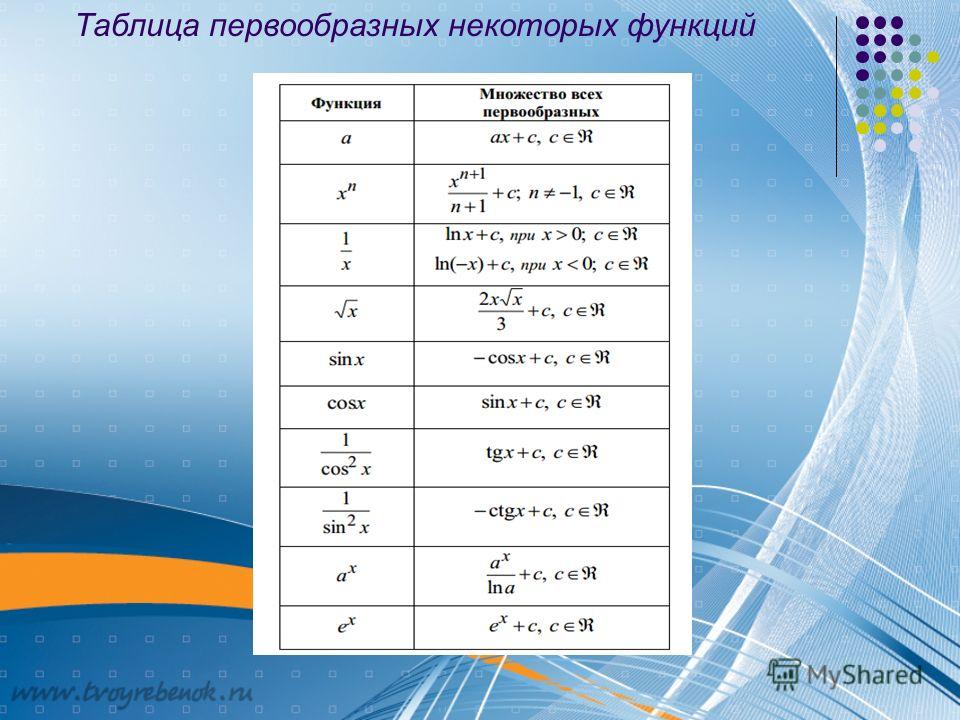 Цепное правило производных дает нам цепное правило первообразных, также известное как метод антидифференцирования u-подстановки. Цепное правило первообразных используется, если интеграл имеет вид ∫u'(x) f(u(x)) dx. Давайте посмотрим на пример и решим интеграл, используя это правило первообразной.

Пример: Решить ∫2x cos (x ² ) dx

Решение: Предположим, что x ² = u ⇒ 2x dx = du. Подставим это в интеграл, получим

∫2x cos (x ² ) dx = ∫cos u du

= sin u + C

= sin (x ² ) + C 9077 Правило 9 Антипроизводная

Правило первообразного произведения также обычно называют методом интегрирования по частям. Это одно из важных правил антипроизводных, которое используется, когда необходимо определить антидифференцирование произведения функций. Формула правила первообразного произведения: ∫f(x).g(x) dx = f(x) ∫g(x) dx − ∫(f′(x) [ ∫g(x) dx)]dx + C , Выбор первой функции осуществляется на основе приведенной ниже последовательности. Этот метод также широко известен как метод интегрирования ILATE или LIATE, сокращенно:

• I — Обратная тригонометрическая функция
• L — Логарифмическая функция
• А — Алгебраическая функция
• T — Тригонометрическая функция
• E — Экспоненциальная функция

Например, нам нужно найти первообразную x ln x. Тогда, в соответствии с приведенной выше последовательностью, первая функция — это ln x, а вторая функция — это x. Следовательно, имеем

∫x ln x dx = ln x ∫x dx — ∫[(ln x)’ ∫x dx] dx

= (x ² /2) ln x — ∫(1/x)(x ² /2) dx

= (x ² /2) ln x — ∫(x/2) dx

= (x ² /2) ln x — x ² /4 + C

Правило первообразных частных

Правило первообразных частных используется, когда функция представлена ​​в виде числителя и знаменателя. Если в состав функции входят алгебраические функции, то можно использовать интегрирование дробями методом антидифференцирования. Другой способ определить первообразную отношения функций — рассмотреть функцию вида f(x)/g(x). Теперь, дифференцируя это, мы имеем,

d(f(x)/g(x))/dx = [f'(x)g(x) — g'(x)f(x)]/[g(x)] ²

Теперь, интегрируя обе части приведенного выше уравнения, мы имеем

f(x)/g(x) = ∫{[f'(x)g(x) — g'(x)f(x)]/[g (x)] ² } dx

= ∫[f'(x)/g(x)] dx — ∫[f(x)g'(x)/[g(x)] ² ] dx

⇒ ∫[f'(x)/g(x)] dx = f(x)/g(x) + ∫[f(x)g'(x)/[g(x)] ² ] dx

Если f(x) = u и g(x) = v, то мы имеем правило антидеривативных частных как:

∫du/v = u/v + ∫[u/v ² ] dv

Правило первообразной для скалярного кратного функции

Чтобы найти первообразную скалярного кратного функции f(x), мы можем найти ее, используя формулу, заданную ∫kf(x) dx = k ∫ f(x)dx. Это означает, что антидифференциация kf(x) равна k, умноженной на антидифференциацию f(x), где k — скаляр. Пример использования этого правила первообразной:

∫4x dx = 4 ∫xdx

= 4 × x ² /2 + C

= 2x ² + C

Правило первообразной суммы и разности

Это правило является одним из самых простых первообразных правил. Когда необходимо определить антидифференцирование суммы и разности функций, то это можно сделать, используя следующие формулы:

• ∫[f(x) + g(x)] dx = ∫f(x) dx + ∫g(x)dx
• ∫[f(x) — g(x)] dx = ∫f(x) dx — ∫g(x) dx

Вот некоторые примеры правила первообразной суммы и разности функций:

• ∫[4 + x ² ] dx = ∫4 dx + ∫x ² dx = 4x + x ³ /3 + C
• ∫(sin x — log x) dx = ∫sin x dx — ∫ log x dx = -cos x — x log x + x + C

Первообразные правила для конкретных функций

Чтобы использовать правила первообразных, мы должны знать первообразные некоторых определенных функций, таких как экспоненциальная функция, тригонометрические функции, логарифмические функции, гиперболические функции и обратные тригонометрические функции. Пройдемся по правилам первообразных для этих функций:

Правила первообразных для тригонометрических функций

У нас есть шесть основных тригонометрических функций, а именно синус, косинус, тангенс, котангенс, секанс и косеканс. Теперь мы исследуем их первообразные правила этих тригонометрических функций следующим образом:

• ∫sin x dx = -cos x + C
• ∫cos x dx = sin x + C
• ∫tan x dx = ln |sec x| + С
• ∫cot x dx = ln |sin x| + С
• ∫sec x dx = ln |sec x + tan x| + С
• ∫csc x dx = ln |cosec x — кроватка x| + С

Правила первообразных для обратных тригонометрических функций

У нас есть шесть основных обратных тригонометрических функций, а именно арксинус, арккосинус, арктангенс, арккотангенс, арксеканс и арккосеканс. Теперь мы исследуем их первообразные правила этих тригонометрических функций следующим образом:

• ∫sin ^-1 x dx = x sin ^-1 x + √(1 — x ² ) + C
• ∫cos ^-1 x dx = x cos ^-1 x — √(1 — x ² ) + C
• ∫tan ^-1 x dx = x tan ^-1 x — (1/2) ln(1 + x ² ) + C
• ∫cot ^-1 x dx = x cot ^-1 x + (1/2) ln(1 + x ² ) + C
• ∫сек ^-1 x dx = x сек ^-1 x — ln |x + √(x ² — 1)| + С
• ∫csc ^-1 x dx = x csc ^-1 x + ln |x + √(x ² — 1)| + С

Правила первообразных для показательных функций

Показательная функция имеет вид f(x) = a ^x , где a — основание (действительное число), а x — переменная. Когда a равно числу Эйлера e, тогда мы имеем f(x) = e ^x , где e — константа, значение которой приблизительно равно 2,718. Теперь первообразные правила для этих двух форм показательных функций таковы:

• ∫a ^x dx = a ^х /лн а + С
• ∫e ^x dx = e ^x + C [Поскольку ln e = 1]

Правила первообразных для логарифмических функций

Логарифмическая функция обычно имеет вид f(x) = log _a x, где a — основание, а x — переменная. Если основание a равно числу Эйлера e, то она называется функцией натурального логарифма и записывается как f(x) = ln x. Правила первообразной для логарифмической функции:

• ∫log _a x dx = x log _a x — x/ln a + C
• ∫ln x dx = x ln x — x + C

Правила первообразия для гиперболических функций

Теперь гиперболические функции аналогичны тригонометрическим функциям, но они выводятся с использованием гиперболы, а не единичного круга, как в случае тригонометрических функций. Шесть основных гиперболических функций — это sinh x, ch x, tanh x, coth x, sech x и csch x. Правила первообразных гиперболических функций:

• ∫sin x dx = ch x + C
• ∫кош х дх = ш х + С
• ∫tanh x dx = ln (ch x) + C
• ∫coth x dx = ln (sinx x) + C
• ∫sech x dx = arctan(sinx) + C
• ∫csch x dx = ln(tanh (x/2)) + C

Важные замечания по правилам первообразных

• Правила первообразных используются для нахождения первообразных различных комбинаций алгебраических, тригонометрических, логарифмических, экспоненциальных, обратных тригонометрических и гиперболических функций.
• Большинство правил дифференцирования имеют соответствующие первообразные правила для антидифференцирования.
• Правило первообразной для постоянной функции f(x) = k имеет вид ∫k dx = kx + C.

☛ Статьи по теме:

• Первообразная формула
• Первообразная Ln x
• Интегральное исчисление

Часто задаваемые вопросы об антипроизводных правилах

Что такое первообразные правила в исчислении?

Правила первообразных — это некоторые из важных правил исчисления, которые используются для нахождения первообразных различных форм комбинаций функций.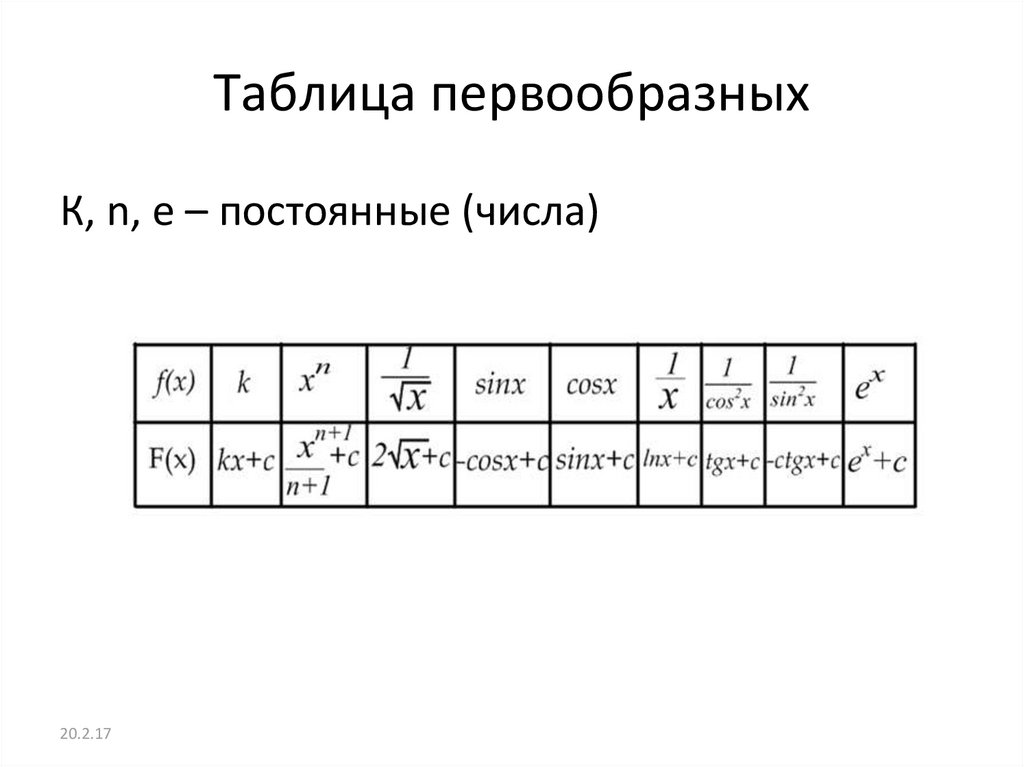 Эти первообразные правила помогают нам найти первообразную суммы или разности функций, произведение и частное функций, скалярное кратное функции и постоянной функции, а также композицию функций.

Как использовать цепное правило первообразной производной?

Цепное правило первообразных используется, если интеграл имеет вид ∫u'(x) f(u(x)) dx. Он широко известен как метод антидифференцировки с u-замещением. Обычно мы заменяем функцию u(x), предполагая, что это другая переменная.

Каковы обычно используемые первообразные правила?

Наиболее часто используемые первообразные правила для произведения, частного, суммы, разности и композиции функций следующие:

• Правило первообразной степени
• Антипроизводное цепное правило
• Антипроизводное правило произведения
• Правило первообразных частных
• Правило первообразной для скалярного кратного функции
• Правило первообразной суммы и разности функций

Каковы первообразные правила для триггерных функций?

Правила первообразия шести тригонометрических функций следующие:

• ∫sin x dx = -cos x + C
• ∫cos x dx = sin x + C
• ∫tan x dx = ln |sec x| + С
• ∫cot x dx = ln |sin x| + С
• ∫sec x dx = ln |sec x + tan x| + С
• ∫csc x dx = ln |cosec x — кроватка x| + С

Как использовать первообразные правила для экспоненциальных функций?

Правила первообразия для двух форм показательных функций:

• ∫a ^x dx = a ^x /ln a + C
• ∫e ^x dx = e ^x + C

Что такое правило первообразного произведения?

Формула правила первообразного произведения: ∫f(x). g(x) dx = f(x) ∫g(x) dx − ∫(f′(x) [ ∫g(x) dx)]dx + C где нам нужно найти первообразную произведения двух или более функций.

9x f(t) \, dt\) определяют новую функцию \(A\text{?}\)

Повторяющейся темой в нашем обсуждении дифференциального исчисления был вопрос: «Если у нас есть информация о производной неизвестной функции \(f\text{,}\), сколько информации мы можем получить о самой \(f\)?» В упражнении 1.8.3 график \(y = f'(x)\) был известен (вместе со значением \(f\) в одной точке), и мы попытались набросать возможный график \(f \) вблизи известной точки. В примере 3.1.7 мы исследовали, как тест первой производной позволяет нам использовать информацию о \(f’\), чтобы определить, где исходная функция \(f\) возрастает и убывает, а также где \(f\) имеет относительные экстремальные значения. Если мы знаем формулу или график \(f’\text{,}\) путем вычисления \(f»\), мы можем найти, где исходная функция \(f\) вогнута вверх и вогнута вниз. Таким образом, знание \(f’\) и \(f»\) позволяет нам понять форму графика \(f\text{. }\)

Мы еще более подробно вернулись к этому вопросу в Разделе 4.1. В этих условиях мы знали мгновенную скорость движущегося объекта и старались как можно больше узнать о функции положения объекта. Мы обнаружили связи между чистой площадью со знаком под функцией скорости и соответствующим изменением положения функции, а Теорема о полном изменении дополнительно пролила свет на эти связи между \(f’\) и \(f\text{,}\), показывая что общее изменение значения \(f\) на интервале \([a,b]\) определяется чистой площадью со знаком, ограниченной \(f’\) и осью \(x\) на тот же интервал.

Далее мы исследуем ситуацию, когда у нас есть точный график производной функции вместе с единственным значением функции \(f\text{.}\). Из этой информации мы хотели бы определить график \(f\), который показывает, где \(f\) увеличивается, уменьшается, вогнут вверх и вогнут вниз, а также обеспечивает точное значение функции в любой точке.

Предварительный просмотр 5.1.1.

Предположим, что о функции \(f\text{:}\) известна следующая информация: график ее производной, \(y = f'(x)\text{,}\) приведен на рис. 1 f'(x) \, dx\text{.} \end{уравнение*}

Каково точное значение \(f(1)\text{?}\)

Используйте данную информацию и рассуждения, аналогичные приведенным в (d), чтобы определить точное значение \(f(2)\text{,}\) \(f(3)\text{,}\) \(f (4)\text{,}\) \(f(5)\text{,}\) и \(f(6)\text{.}\)

Основываясь на ваших ответах на все предыдущие вопросы, нарисуйте полный и точный график \(y = f(x)\) на предоставленных осях, обязательно указав поведение \(f\) для \( х \lt 0\) и \(х \gt 6\текст{.}\)

Подраздел 5.1.1 Построение графика первообразной

Предварительное задание 5.1.1 демонстрирует, что, когда мы можем найти точную площадь под графиком функции на любом заданном интервале, можно построить график первообразной функции. То есть мы можем найти функцию, производная которой задана. Теперь мы можем определить не только общую форму графа первообразных, но и фактическую высоту графика в любой интересующей точке. 9б f(x) \, dx\text{. }\)

Мероприятие 5.1.2.

Предположим, что функция \(y = f(x)\) задана графиком, показанным на рис. 5.1.2, и что части \(f\) являются либо частями линий, либо частями окружностей. Кроме того, пусть \(F\) является первообразной \(f\) и пусть \(F(0) = -1\text{.}\) Наконец, предположим, что для \(x \le 0\) и \(x \ge 7\text{,}\) \(f(x) = 0\text{.}\)

Рисунок 5.1.2. Слева график \(y = f(x)\text{.}\)

1. На каком интервале(ах) \(F\) является возрастающей функцией? На каких промежутках \(F\) убывает?

2. На каком интервале(ах) \(F\) вогнута вверх? вогнутый вниз? ни один?

3. В какой точке (точках) \(F\) имеет относительный минимум? относительный максимум?

4. Используйте данную информацию, чтобы определить точное значение \(F(x)\) для \(x = 1, 2, \ldots, 7\text{.}\) Кроме того, каковы значения \( F(-1)\) и \(F(8)\text{?}\)

5. Основываясь на ваших ответах на все предыдущие вопросы, нарисуйте полный и точный график \(y = F(x)\) на предоставленных осях, обязательно указав поведение \(F\) для \( x \lt 0\) и \(x \gt 7\text{. }\) Четко укажите масштаб по вертикальной и горизонтальной осям вашего графика.

6. Что произойдет, если мы изменим одну ключевую часть информации: в частности, скажем, что \(G\) является первообразной \(f\) и \(G(0) = 0\text{.}\) Как ( если вообще) изменятся ли ваши ответы на предыдущие вопросы? Начертите график \(G\) на тех же осях, что и график \(F\), который вы построили в (e).

Подраздел 5.1.2 Множественные первообразные одной функции

В последнем вопросе задания 5.1.2 мы столкнулись с очень важной идеей: функция \(f\) имеет более одной первообразной. Каждая первообразная \(f\) однозначно определяется своим значением в одной точке. Например, предположим, что \(f\) — это функция, указанная слева на рис. 5.1.3, и предположим, далее, что \(F\) — первообразная функции \(f\), удовлетворяющая условию \(F(0) = 1 \текст{.}\) 91 f(x) \, dx\\ &= 1 + 0,5\\ &= 1,5\текст{.} \конец{выравнивание*}

Аналогично \(F(2) = 1.5\text{,}\) \(F(3) = -0. 1 f(x) \, dx = 0,5\text{,}\) так же, как \(F(1) — F(0) = 0,5\ text{,}\), но поскольку \(G(0) = 3\text{,}\) \(G(1) = G(0) + 0,5 = 3,5\text{,}\), тогда как \(F( 1) = 1.5\text{.}\) Таким же образом, если бы мы присвоили другое начальное значение первообразной, скажем, \(H(0) = -1\text{,}\) мы получили бы еще одну первообразную , как показано пурпурным цветом на рисунке 5.1.3.

Этот пример демонстрирует важный факт, который имеет более широкое значение:

Если \(G\) и \(H\) являются первообразными функции \(f\text{,}\), то функция \(G — H\) должна быть постоянной.

Чтобы понять, почему этот результат верен, заметим, что если \(G\) и \(H\) являются первообразными \(f\text{,}\), то \(G’ = f\) и \(H ‘ = f\text{.}\) Следовательно,

\begin{уравнение*} \frac{d}{dx}[ G(x) — H(x) ] = G'(x) — H'(x) = f(x) — f(x) = 0\text{.} \end{уравнение*}

Поскольку функция может иметь нулевую производную только в том случае, если она является постоянной функцией, отсюда следует, что функция \(G — H\) должна быть постоянной.

Теперь мы видим, что если у функции есть хотя бы одна первообразная, то их должно быть бесконечно много: мы можем добавить любую константу по нашему выбору к первообразной и получить другую первообразную. По этой причине мы иногда ссылаемся на общую первообразную функции \(f\text{.}\)

Чтобы идентифицировать конкретную первообразную \(f\text{,}\), мы должны знать единственное значение первообразной \(F\) (это значение часто называют 93 + \frac{1}{3}\text{.}\)

Мероприятие 5.1.3.

Для каждой из следующих функций нарисуйте точный график первообразной, удовлетворяющей заданному начальному условию. Кроме того, нарисуйте график двух дополнительных первообразных данной функции и укажите соответствующие начальные условия, которым каждая из них удовлетворяет. Если возможно, найдите алгебраическую формулу первообразной, удовлетворяющую начальному условию.

1. исходная функция: \(g(x) = \left| x \right| — 1\text{;}\) начальное условие: \(G(-1) = 0\text{;}\) интервал для эскиз: \([-2,2]\) 92, \amp \text{ если } 1 \lt x \lt 2 \\ 0 \amp \text{ иначе } \end{cases}\text{;}\) начальное условие: \(P(0) = 1\ text{;}\) интервал для скетча: \([-1,3]\)

Подраздел 5.

b f(x) \, dx\text{.} \end{уравнение*}

В нескольких ситуациях мы использовали эту формулу для вычисления \(F(b)\) для нескольких различных значений \(b\text{,}\), а затем наносили на график точки \((b,F(b)) \), чтобы помочь нам нарисовать точный график \(F\text{.}\) Это говорит о том, что мы можем думать о \(b\text{,}\) верхнем пределе интегрирования как о самой переменной. С этой целью введем понятие целочисленной функции , функции, в формулу которой входит определенный интеграл.

Определение 5.1.4.

9x f(t) \, dt\text{.}\tag{5.1.2} \end{equation}

Обратите внимание, что поскольку \(x\) является независимой переменной в функции \(A\text{,}\) и определяет конечную точку интервала интегрирования, нам нужно использовать другую переменную в качестве переменная интегрирования. Стандартным выбором является \(t\text{,}\), но допустима любая переменная, кроме \(x\).

Один из способов представить функцию \(A\) — это «чистая область со знаком от \(a\) до \(x\)», где мы рассматриваем область, ограниченную \(y = f(t )\text{. x f(t) \, dt\) показано справа. 9x f(t) \ dt\text{.}\)

Функция \(A\) измеряет чистую площадь со знаком от \(t = 0\) до \(t = x\), ограниченную кривой \(y = f(t)\text{;}\) это значение затем сообщается как соответствующая высота на графике \(y = A(x)\text{.}\) Рисунок 5.1.5 к жизни. Там пользователь может переместить красную точку на функции \(f\) и посмотреть, как изменяется соответствующая высота в голубой точке на графике \(A\text{.}\)

Выбор \(a\) несколько произволен. В следующем упражнении мы исследуем, как значение \(a\) влияет на график интегральной функции. 9x g(t) \ dt\text{.}\)

1. На каком интервале(ах) \(A\) является возрастающей функцией? На каких промежутках \(А\) убывает? Почему?

2. Как вы думаете, на каком интервале \(A\) является вогнутым вверх? вогнутый вниз? Почему?

3. В какой точке (точках) \(A\) имеет относительный минимум? относительный максимум?

4. Используйте данную информацию для определения точных значений \(A(0)\text{,}\) \(A(1)\text{,}\) \(A(2)\text{,}\ ) \(A(3)\text{,}\) \(A(4)\text{,}\) \(A(5)\text{,}\) и \(A(6)\text{ . }\) 93 f(x) \, dx\text{.}\) Когда мы объединяем эту информацию о значениях функции \(F\) вместе с нашим пониманием того, как поведение \(F’ = f\) влияет на общий формы \(F\text{,}\) мы можем построить полностью точный график первообразной \(F\text{.}\)

5. Поскольку производная константы равна нулю, если \(F\) является первообразной \(f\text{,}\), то \(G(x) = F(x) + C\) будет также быть первообразной функции \(f\text{.}\). Более того, любые две первообразные функции \(f\) отличаются ровно на константу. Таким образом, у любой функции хотя бы с одной первообразной на самом деле их бесконечно много, и графики любых двух первообразных будут отличаться только вертикальным переносом. 9x f(t) \, dt\) определяет новую функцию \(A\), которая измеряет площадь со знаком сети, ограниченную \(f\) на интервале \([a,x]\text{.}\). назовите функцию \(A\) интегральной функцией, соответствующей \(f\text{.}\)

Упражнения 5.1.5 Упражнения

1. Определенный интеграл кусочно-линейной функции.



Используйте график \(f(x)\), показанный ниже, чтобы найти следующие интегралы.

(Нажмите на график, чтобы увеличить его)

97{f(x)dx} \приблизительно\)

B. Если \(F\) является первообразной той же функции \(f\) и \(F(0) = 30\text{,} \) оценка \(F(7)\text{:}\)

\(F(7) \приблизительно\)

3. Кусочно-постоянная функция.

Предположим, что \(f’\) задается графиком ниже. Предположим, что \(f\) является непрерывным и что \(f(3)=0\text{.}\)

(Щелкните на графике, чтобы увеличить его.)

Эскиз на листе бумаги , точный график \(f\text{,}\) и использовать его, чтобы найти каждый из 97 f'(x)\,dx =\)

(Обратите внимание, что это можно сделать двумя разными способами!)

4. Еще одна кусочно-линейная функция.

На рисунке ниже показано \(f\text{.}\)

(Щелкните график, чтобы увеличить его.)

Если \(F’=f\) и \(F(0)=0 \text{,}\) найдите \(F(b)\) для \(b=\)1, 2, 3, 4, 5, 6 и заполните эти значения в следующей таблице.

\(б\)	1	2	3	4	5	6
\(Ф(б)\)

5.

Скорость движущейся частицы определяется квадратичной функцией \(v\), изображенной на рисунке 5.1.7. Кроме того, дано, что \(A_1 = \frac{7}{6}\) и \(A_2 = \frac{8}{3}\text{,}\), а также для соответствующей функции положения \(s\текст{,}\) \(s(0) = 0,5\текст{.}\)

1. Используйте данную информацию для определения \(s(1)\text{,}\) \(s(3)\text{,}\) \(s(5)\text{,}\) и \ (s(6)\text{.}\) Что означают эти значения в контексте движущейся частицы?

2. На каком интервале(ах) \(s\) возрастает? То есть когда частица движется вперед? На каком интервале(ах) \(s\) убывает? То есть когда частица движется назад?

3. На каком интервале(ах) \(s\) вогнуты вверх? То есть, когда частица ускоряется? На каком интервале(ах) \(s\) вогнута вниз? То есть, когда частица замедляется?

4. Нарисуйте точный помеченный график \(s\) по осям справа на рисунке 5. 1.7. 92\text{.}\) Найдите формулу для \(s\text{.}\)

Рисунок 5.1.7. Слева заданный график \(v\text{.}\) Справа оси для построения \(s\text{.}\)

6.

Человек, занимающийся на беговой дорожке, испытывает разные уровни сопротивления и, следовательно, сжигает калории с разной скоростью, в зависимости от настроек беговой дорожки. На конкретной тренировке скорость, с которой человек сжигает калории, определяется кусочно-постоянной функцией \(c\), изображенной на рисунке 5.1.8. Обратите внимание, что единицами измерения \(c\) являются «калории в минуту».

Рисунок 5.1.8. Слева — заданный график \(c\text{.}\) Справа — оси для построения \(C\text{.}\)

1. Пусть \(C\) — первообразная \(c\ text{.}\) Что измеряет функция \(C\)? Каковы его единицы?

2. Предположим, что \(C(0) = 0\text{.}\) Определите точное значение \(C(t)\) при значениях \(t = 5, 10, 15, 20, 25, 30 \текст{.}\)

3. Нарисуйте точный график \(C\) по осям, указанным справа на рисунке 5.

   No related posts.