Первый и второй признаки равенства треугольников: 3 признака равенства треугольников

3 признака равенства треугольников

Поможем понять и полюбить математику

Начать учиться

530.8K

Чего только не приходится делать на уроках геометрии! Но нет ничего приятнее, чем сесть и доказать равенство треугольников, используя три признака равенства.

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать. 

Давайте рассмотрим три признака равенства треугольников. 

Теорема 1. Равенство треугольников по двум сторонам и углу между ними. 

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.  

Даны два треугольника △ABC  и  △A₁B₁C₁,  у которых AC = A₁C₁,  AB = A₁B₁, ∠A = ∠A₁.

Докажите, что △ABC  =  △A₁B₁C₁.

Доказательство:

При наложении △A

1B₁C₁ на △ABC вершина  A₁  совмещается с вершиной  A,  и сторона  A₁B₁ накладывается на сторону AB,  AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

B₁C₁ = BC, следовательно, △ABC совмещается с △A₁B₁C_{, значит, △ABC = △A1B1C1.}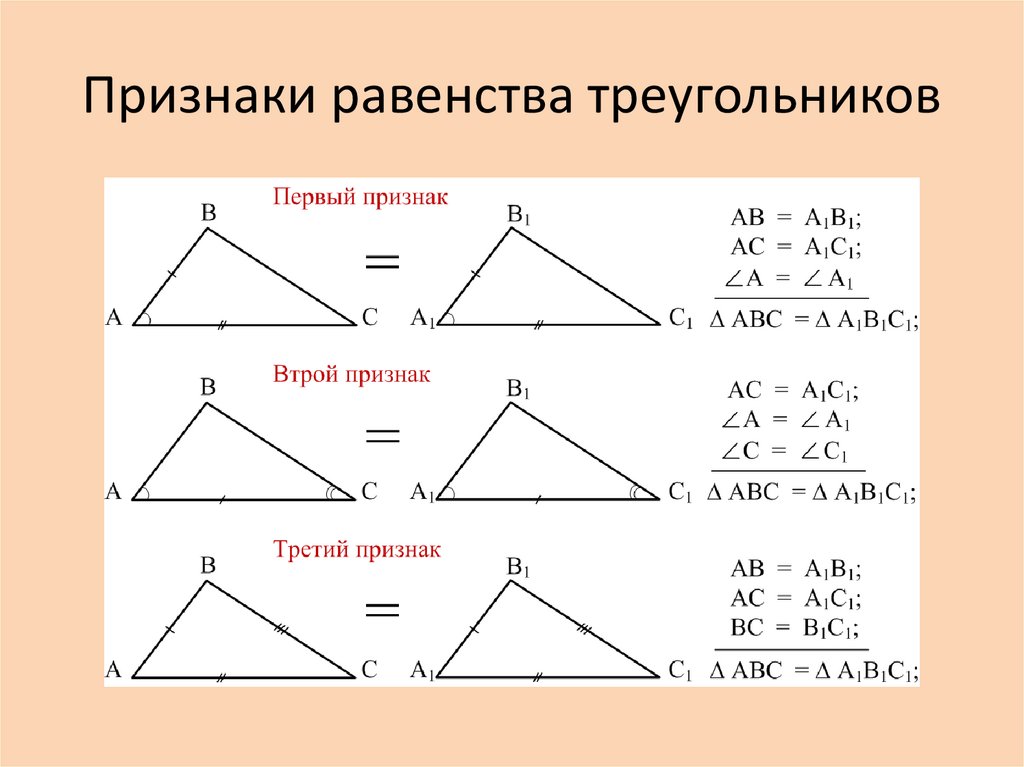

Теорема доказана.

Важно!

Первый признак используют при доказательстве второго и третьего признаков равенства треугольников.

Познавайте математику вместе с нашими лучшими преподавателями на курсах по математике для учеников с 1 до 11 класса!

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Второй признак равенства треугольников

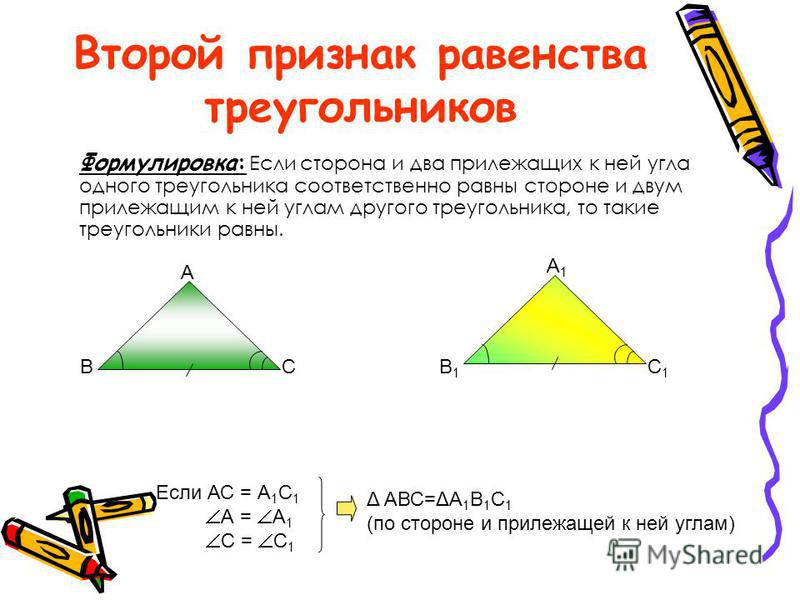
Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам. 

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. 

Даны два треугольника △ABC  и  △A₁B₁C₁,  у которых:
AC = A₁C₁,  ∠A = ∠A₁,  ∠C = ∠C₁.

Докажите, что △ABC  =  △A₁B₁C₁.

Доказательство:

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной  A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с  A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Если АВ совмещается с А₁В₁, ВС совмещается с В₁С₁, то △ABC совмещается с △A₁B₁C₁, значит, △ABC = △A₁

B₁C₁ .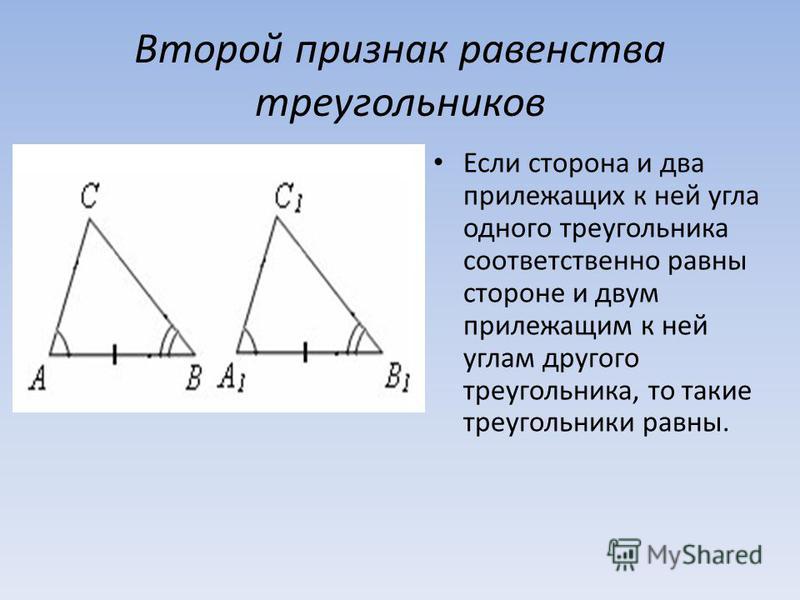

Теорема доказана.

Пройдите тест и узнайте, какие темы отделяют от пятёрки по математике

Добро пожаловать в школу магии.

О нет! Мальчик-молния случайно попал в школьные часы. Теперь они отстают. Мы все можем задержаться в школе

Жми на стрелки сверху, чтобы путешествовать в истории→

‌

Одна ученица когда-то была в школьной кладовке и видела там схему часов

Но в кладовку просто так не попадёшь→

‌

Реши два примера от волшебной статуи на входе в кладовку

\frac{1}{7} + \frac{3}{7} =\frac{4}{7}\frac{5}{7}\frac{4}{14}\frac{2}{7}

\frac{4}{15} — \frac{1}{15} =\frac{1}{3}\frac{1}{5}\frac{3}{30}\frac{1}{10}

‌

Деталь можно сделать из проволоки и формы для заливки металла. Найди их на картинке

‌

Теперь осталось взять инструменты у садовника! Он обменяет их на волшебные бобы для его сада

‌

Для починки часов нужны: молоток, отвертка и плоскогубцы.

2

‌

Мальчик-молния выплавил деталь, часы должны работать! Но они почему-то не идут… Кажется, одной шестерёнки не хватает — она куда-то упала

‌

В коробке, шкатулке, ящике и банке находятся пыльца, волчий корень, золото и шестерёнка. Шестерёнка и пыльца не в коробке, ёмкость с волчьим корнем стоит между ящиком и ёмкостью с золотом, в банке не волчий корень и не шестерёнка. Шкатулка стоит около банки и ёмкостью с пыльцой. В какой ёмкости что находится?

Соедини ёмкости с содержимым на картинках ниже

ШестерёнкаЗолотоВолчий кореньПыльца

‌

Дальше узнаешь свои результаты →

‌

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Даны два треугольника △ABC  и  △A₁B₁C₁,  у которых:
AC = A₁C₁,
AB = A₁B₁,
CB = C₁B₁.   

Докажите, что △ABC  = △A₁B₁C₁.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

AC = A₁C

1, BC = B₁C₁, то △A₁C₁С и △B₁C₁С — равнобедренные.
∠1=∠2, ∠3=∠4 (по свойству равнобедренного треугольника), значит,
∠A₁СB₁ = ∠A₁C₁B₁.
AC = A₁C₁, BC = B₁C₁. 
∠C = ∠C₁, тогда △ABC  = △A₁B₁C₁ (по первому признаку равенства треугольников).

Теорема доказана. 

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

 

1. Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
   


2. Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
   


3. Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
   


4. Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
   


5. Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.
   

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Анастасия Белова

К предыдущей статье

Как умножать отрицательные числа

К следующей статье

102.9K

Сумма разрядных слагаемых

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Первый и второй признаки равенства треугольников.

Равнобедренный треугольник

Цель: Формирование знаний и умений учащихся по указанной теме на репродуктивном уровне, то есть добиться понимания и воспроизведения конкретного программного материала в ходе решения задач по темам “Первый и второй признаки равенства треугольников. Равнобедренный треугольник”.

Задачи: Формирование логического, системного мышления; овладение интеллектуальными умениями и мыслительными операциями – анализом и синтезом, доказательством, сравнением, обобщением.

Оборудование:

— ноутбук;

— мультимедиа проектор;

— плакат с таблицей для разгадывания слова;

— раздаточный материал: бланки для написания математического диктанта, файлы с геометрическими фигурами, бланки таблиц для разгадывания слова, распечатки домашних заданий;

— маркер для оформления плаката.

Структура урока:

1. Организационный момент.
2. Постановка цели урока.
3. Проверка знания базовых понятий и определений по теме в ходе решения кроссворда.
4. Решение задач на готовых чертежах с целью повторения первых двух признаков равенства треугольников (устно).
5. Математический диктант.
6. Решение задач.
7. Разгадывание фамилии великого ученого древности в ходе решения задач на повторение (устно).
8. Постановка домашнего задания.
9. Подведение итогов урока.

Ход урока

1. Организационный момент

Проверяется подготовленность классного помещения и готовность учащихся к уроку.

2. Постановка целей урока

Отмечается, что данный урок является уроком обобщения и систематизации знаний по темам “Первый и второй признаки равенства треугольников.

Равнобедренный треугольник”.

В ходе его будут проверены знания базовых понятий и определений в ходе решения кроссворда, практические навыки применения знаний по теме в стандартных условиях в ходе решения задач на готовых чертежах, навыки самостоятельного применения знаний по темам в ходе написания математического диктанта. А также будут предложены задания, для решения которых понадобится привлечение всего комплекса знаний и умений в том числе алгебраических методов решения геометрических задач.

3. Проверка знания базовых понятий и определений

Учащиеся разгадывают кроссворд, представленный на экране проектора

Вопросы к кроссворду:

1. Луч, который выходит из вершины угла, проходит между его сторонами и делит угол пополам. “А что называется биссектрисой треугольника?” Ответ учащихся.
2. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
3. Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону треугольника.
4. Фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
5. Треугольник, у которого две стороны равны.
6. Треугольник, у которого все стороны равны.
7. Сумма длин всех сторон треугольника.
8. Как называются равные стороны равнобедренного треугольника?
9. Как называется третья сторона равнобедренного треугольника, неравная двум другим?

(Ответы на вопросы кроссворда см. приложение)

4. Решение задач на готовых чертежах с целью повторения первых двух признаков равенства треугольников

Учащиеся решают устно задачи на готовых чертежах, представленные на экране проектора.

Задание: Найдите пары равных треугольников и докажите их равенство.

Наводящие вопросы:

— Обратите внимание: на чертежах одним цветом отмечены равные элементы.

— а – какой является сторона АС для этих двух треугольников?

— б – обратите внимание на углы ВСD и ЕСА. Они какие? Какое свойство вертикалых углов вы знаете?

— в – какой является сторона ВD для рассматриваемых треугольников? Каким является треугольник АВС? Чем в треугольнике АВС является высота ВD? Каким образом биссектриса ВD делит угол АВС?

5. Математический диктант

Учащимся раздаются бланки для решения заданий математического диктанта. Чертежи к заданиям математического диктанта проецируются на экран, а сами задания диктуются учителем.

Учащиеся подписывают листочки.

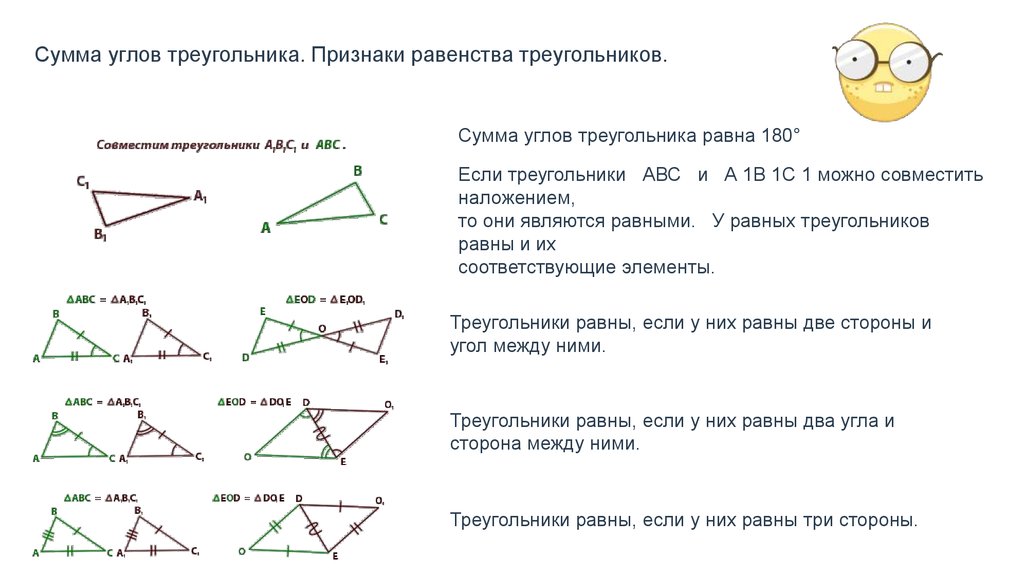
1. Какой признак равенства треугольников нужно использовать для доказательства равенства представленных треугольников

 

2. Сколько пар равных треугольников изображено на чертеже?

 

3.

5.

Вариант 1	Вариант 2
В каком треугольнике любая его высота делит треугольник на два равных треугольника?	В каком треугольнике только одна его высота делит треугольник на два равных треугольника?

По окончании его написания обучающиеся меняются тетрадями с соседями по парте и проверяют правильность выполнения им работы под диктовку учителя.

Далее листочки сдаются на проверку учителю.

(Решения математического диктанта см. в приложении)

6. Решение задач

На экране проектора включается условие задачи. Один из обучающихся вызывается к доске, а остальные записывают решение этой задачи у себя в тетрадях.

Задача

В треугольнике АВС с периметром 31,2 см. АВ=ВС, АС - АВ = 6 см. найдите АВ, ВС и АС.

Решение: Пусть АВ = х см, тогда ВС = х см. Получаем АС = АВ + 6 = х + 6 (см). Составим уравнение и решим его

х + х + х + 6 = 31,2

3х = 25,2

х = 8,4

Ответ: АВ = ВС = 8,4 см; АС = 14,4 см.

7. Разгадывание фамилии великого ученого древности в ходе решения задач на повторение

Общее задание для всех задач: Найти угол DВА.

м	р	и	д	х	е	а
1	2	3	4	5	6	7

“Расположите буквы в клетках таким образом, чтобы градусные меры углов, соответствующих этим буквам находились в порядке убывания и заполните таблицу, находящуюся у вас на столе”.

К доске вызывается ученик для заполнения таблицы на плакате.

(Ответы к таблице см. в приложении)

Нет, не всегда смешон и узок
Мудрец, глухой к делам земли,
Уже на рейде в Сиракузах
Стояли римлян корабли.
Над математиком курчавым
Солдат занес короткий нож,
А он на отмели песчаной
Окружность вписывал в чертеж.
Ах, если б смерть – лихую гостью –
Мне так же встретить повезло,
Как Архимед, чертивший тростью
В минуту гибели, — число!

8. Постановка домашнего задания

Домашнее задание находится на столах учащихся на листах с напечатанными на них готовыми чертежами (см. Приложение).

9. Подведение итогов урока

Учитель: “Итак, отработкой какой темы мы с вами занимались на сегодняшнем уроке?

А чем конкретно мы занимались, и что нам дал этот урок?”

Сообщаются оценки учащимся, отвечавшим на уроке.

Приложение 1

Приложение 2

Первый признак равенства треугольников. Второй и третий признаки равенства треугольников

Среди огромного количества многоугольников, которые по сути представляют собой замкнутую непересекающуюся ломаную, треугольник является фигурой с наименьшим числом углов. Другими словами, это самый простой многоугольник. Но, несмотря на всю свою простоту, эта фигура таит в себе множество загадок и интересных открытий, которым посвящен специальный раздел математики — геометрия. Эта дисциплина преподается в школах с седьмого класса, и теме «Треугольник» здесь уделяется особое внимание. Дети не только узнают правила о самой фигуре, но и сравнивают их, изучая 1, 2 и 3 признаки равенства треугольников.

Первая встреча

Одно из первых правил, с которым знакомятся студенты, звучит так: сумма величин всех углов треугольника равна 180 градусам. Чтобы убедиться в этом, достаточно измерить каждую вершину с помощью транспортира и сложить все полученные значения. Исходя из этого, по двум известным величинам легко определить третью. Например : В треугольнике один из углов равен 70°, а другой — 85°, чему равен третий угол?

180 — 85 — 70 = 25.

Ответ: 25°.

Проблемы могут быть более сложными, если указано только одно значение угла, а второе значение говорит только во сколько или во сколько раз он больше или меньше.

В треугольнике для определения каких-либо его признаков могут быть проведены специальные линии, каждая из которых имеет свое название:

• Высота — перпендикулярная линия, проведенная от вершины к противоположной стороне;
• Все три высоты, проведенные одновременно в центре фигуры, пересекаются, образуя ортоцентр, который в зависимости от типа треугольника может быть как внутри, так и снаружи;
• Медиана — линия, соединяющая вершину с серединой противоположной стороны;
• Пересечение медиан является точкой притяжения, находится внутри фигуры;
• Биссектриса — прямая, проходящая от вершины до точки пересечения с противоположной стороной, точка пересечения трех биссектрис — центр вписанной окружности.

Простые истины о треугольниках

Треугольники, как, впрочем, и все фигуры, имеют свои особенности и свойства. Как уже было сказано, эта фигура представляет собой простейший многоугольник, но со своими характерными особенностями:

• Против большей стороны всегда находится угол с большей величиной, и наоборот;
• Равные углы лежат на равных сторонах, например, равнобедренный треугольник;
• Сумма внутренних углов всегда равна 180°, что уже было продемонстрировано на примере;
• При продолжении одной стороны треугольника за его пределы образуется внешний угол, который всегда будет равен сумме углов, не смежных с ним;
• Любая из сторон всегда меньше суммы двух других сторон, но больше их разности.

Типы треугольников

Следующий этап знакомства — определение группы, к которой относится изображенный треугольник. Принадлежность к той или иной форме зависит от углов треугольника.

• Равный — с двумя равными сторонами, которые называются боковыми, третья в данном случае выступает в качестве основания фигуры. Углы при основании такого треугольника равны, а медиана, проведенная из вершины, есть биссектриса и высота.
• Правильный или равносторонний треугольник — это треугольник, у которого все стороны равны.
• Прямоугольный: один из его углов равен 90°. При этом сторона, противоположная этому углу, называется гипотенузой, а две другие – катетами.
• Остроугольный треугольник — все углы меньше 90°.
• Тупоугольный — один из углов больше 90°.

Равенство и подобие треугольников

В процессе обучения не только рассматривать одну фигуру, но и сравнивать два треугольника. И в этой, казалось бы, простой теме есть масса правил и теорем, по которым можно доказать, что рассматриваемые фигуры являются равными треугольниками. Признаки равенства треугольников имеют следующее определение: треугольники равны, если их соответствующие стороны и углы равны. При этом равенстве, если наложить эти две фигуры друг на друга, все их прямые сойдутся. Также фигуры могут быть похожими, в частности, это касается практически одинаковых фигур, отличающихся только размером.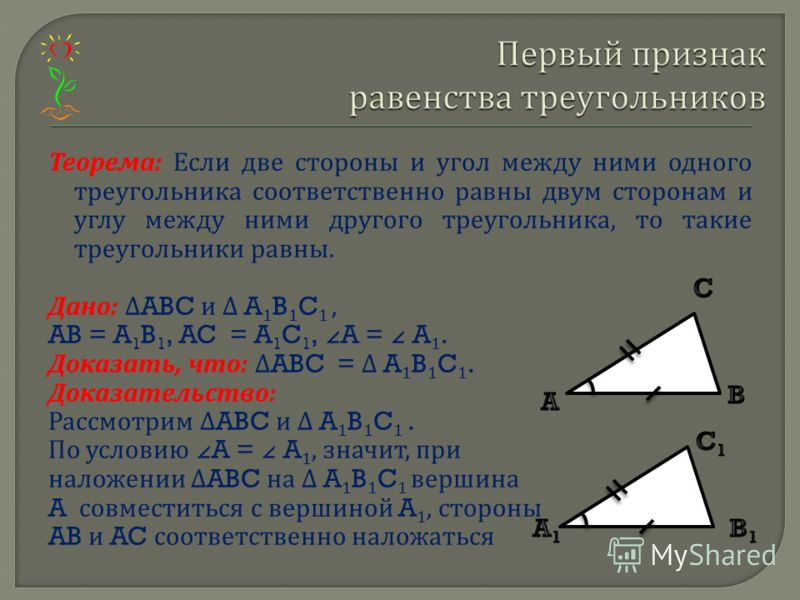 Для того, чтобы сделать такой вывод о изображенных треугольниках, необходимо соблюсти одно из следующих условий:

• Два угла одной фигуры равны двум углам другой;
• Две стороны одного пропорциональны двум сторонам второго треугольника, а углы, образованные сторонами, равны;
• Три стороны второй фигуры такие же, как у первой.

Конечно, для бесспорного равенства, которое не вызовет ни малейшего сомнения, необходимо, чтобы все элементы обеих фигур имели одинаковые значения, но с помощью теорем задача сильно упрощается, и допускаются лишь некоторые условия доказать равенство треугольников.

Первый признак равенства треугольников

Задачи по данной теме решаются на основании доказательства теоремы, которая гласит: «Если две стороны треугольника и образуемый ими угол равны двум сторонам и угол другого треугольника, то и фигуры равны».

Как звучит доказательство теоремы о первом признаке равенства треугольников? Всем известно, что два отрезка равны, если они имеют одинаковую длину, или равны окружности, если они имеют одинаковый радиус.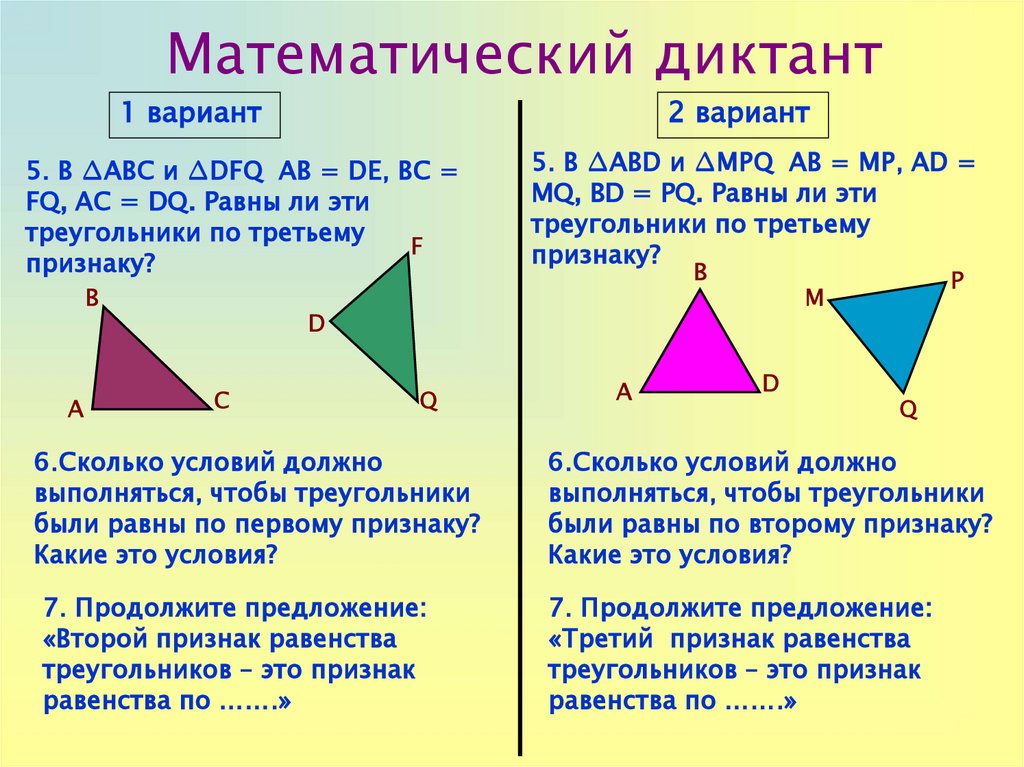 А в случае с треугольниками имеется несколько признаков, имея которые, можно предположить, что фигуры идентичны, что очень удобно для решения различных геометрических задач.

Как звучит теорема «Первый признак равенства треугольников», описана выше, но ее доказательство:

• Предположим, треугольники ABC и A ₁ B ₁ C ₁ имеют одинаковые стороны AB и А ₁ В ₁ и, соответственно, ВС и В ₁ С ₁ , причем углы, которые образованы этими сторонами, имеют одинаковую величину, то есть равны. Затем, применяя △ ABC к △ A ₁ B ₁ C _1, получаем совпадение всех прямых и вершин. Отсюда следует, что эти треугольники абсолютно тождественны, а значит, равны друг другу.

Теорему «Первый признак равенства треугольников» еще называют «О двух сторонах и углу». Собственно, в этом его суть.

Вторая характеризационная теорема

Второй признак равенства доказывается аналогично, доказательство основано на том, что при наложении фигур друг на друга они полностью совпадают по всем вершинам и сторонам. А теорема звучит так: «Если сторона и два угла, в образовании которых она участвует, соответствуют стороне и двум углам второго треугольника, то эти фигуры тождественны, то есть равны».

Третий знак и доказательство

Если и двойки, и единицы равенства треугольников касаются сторон и углов фигуры, то третья относится только к сторонам. Итак, теорема имеет следующую формулировку: «Если все стороны одного треугольника равны трем сторонам второго треугольника, то фигуры равны».

Чтобы доказать эту теорему, нам нужно более подробно остановиться на самом определении равенства. В самом деле, что означает выражение «треугольники равны»? Тождество означает, что если наложить одну фигуру на другую, то все их элементы совпадут, это может быть только в том случае, если их стороны и углы равны. При этом угол, противолежащий одной из сторон, такой же, как и у другого треугольника, будет равен соответствующей вершине второй фигуры. Следует отметить, что на этом этапе доказательство легко можно перевести в 1 признак равенства треугольников. При несоблюдении такой последовательности равенство треугольников просто невозможно, за исключением случаев, когда фигура является зеркальным отражением первого.

Прямоугольные треугольники

В структуре таких треугольников всегда есть вершины с углом 90°. Следовательно, верны следующие утверждения:

• Треугольники с прямым углом равны, если катет одного равен катету второго;
• Фигуры равны, если равны их гипотенуза и один из катетов;
• Такие треугольники равны, если их стороны и острый угол равны.

Этот атрибут относится к прямоугольным треугольникам. Для доказательства теоремы применим приложение фигур друг к другу, в результате чего треугольники складываются катетами так, что из двух прямых получается развернутый угол со сторонами СА и СА ₁ .

Практическое применение

В большинстве случаев на практике применяется первый признак равенства треугольников. На самом деле такая, казалось бы, простая тема 7-го класса по геометрии и планиметрии используется и для расчета длины, например, телефонного кабеля без измерения местности, над которой он пройдет.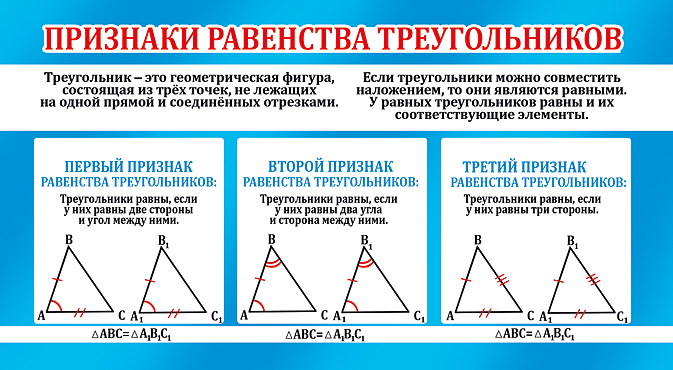 С помощью этой теоремы легко произвести необходимые расчеты для определения длины острова посредине реки, не пересекая ее. Либо армировать забор, поместив брусок в пролет так, чтобы он делил его на два равных треугольника, либо рассчитать сложные элементы столярных работ, либо при расчете стропильной системы крыши при строительстве.

Первый признак равенства треугольников имеет широкое применение в реальной «взрослой» жизни. Хотя в школьные годы именно эта тема многим кажется скучной и совершенно ненужной.

Конгруэнтные треугольники

Треугольники, имеющие одинаковые размеры и форму, называются конгруэнтными треугольниками. Символ конгруэнтности ≅. Два треугольника равны, если три стороны и три угла одного треугольника имеют те же размеры, что и три стороны и три угла другого треугольника. Треугольники на рисунке 1 являются конгруэнтными треугольниками.

Рисунок 1  Конгруэнтные треугольники.

Соответствующие детали

Части двух треугольников, имеющие одинаковые размеры (конгруэнтные), называются соответствующими частями. Это означает, что соответствующих частей конгруэнтных треугольников конгруэнтны (CPCTC). Конгруэнтные треугольники называются путем перечисления их вершин в соответствующем порядке. На рисунке Δ BAT ≅ Δ ICE .

Пример 1: Если Δ PQR ≅ Δ STU , какие детали должны иметь одинаковые размеры?

Эти части равны, потому что соответствующие части конгруэнтных треугольников конгруэнтны.

Тесты на конгруэнтность

Чтобы показать, что два треугольника конгруэнтны, нет необходимости доказывать, что все шесть пар соответствующих частей равны. Следующие постулаты и теоремы являются наиболее распространенными методами доказательства конгруэнтности (или равенства) треугольников.

Постулат 13 (Постулат SSS): Если каждая сторона одного треугольника конгруэнтна соответствующей стороне другого треугольника, то треугольники конгруэнтны (рис. 2).

                                             

Рисунок 2  Соответствующие стороны (SSS)  двух треугольников конгруэнтны.

Постулат 14 (постулат SAS): Если две стороны и угол между ними в одном треугольнике конгруэнтны соответствующим частям другого треугольника, то эти треугольники конгруэнтны (рис. 3).

Рисунок 3  Две стороны и прилежащий к ним угол (SAS) одного треугольника равны

соответствующих частей другого треугольника.

Постулат 15 (Постулат АСА): Если два угла и сторона между ними в одном треугольнике конгруэнтны соответствующим частям в другом треугольнике, то такие треугольники конгруэнтны (рис. 4).

Рисунок 4  Два угла и их общая сторона  (ASA)  в одном треугольнике конгруэнтны

соответствующих частей другого треугольника.

Теорема 28 (Теорема ААС): Если два угла и сторона, не заключенная между ними в одном треугольнике, конгруэнтны соответствующим частям в другом треугольнике, то такие треугольники конгруэнтны (рис. 5).

Рисунок 5  Два угла и сторона, противолежащая одному из этих углов  (ААС)  в одном треугольнике

равны соответствующим частям другого треугольника.

Постулат 16 (постулат HL): Если гипотенуза и катет одного прямоугольного треугольника конгруэнтны соответствующим частям другого прямоугольного треугольника, то эти треугольники конгруэнтны (рис. 6).

Рис. 6  Гипотенуза и катет (HL) первого прямоугольного треугольника равны

соответствующих частей второго прямоугольного треугольника.

Теорема 29 (Теорема HA): Если гипотенуза и острый угол одного прямоугольного треугольника конгруэнтны соответствующим частям другого прямоугольного треугольника, то эти треугольники конгруэнтны (рис. 7).

Рисунок 7  Гипотенуза и острый угол  (HA)  первого прямоугольного треугольника равны

к соответствующим частям второго прямоугольного треугольника.

Теорема 30 (Теорема LL): Если катеты одного прямоугольного треугольника конгруэнтны соответствующим частям другого прямоугольного треугольника, то треугольники конгруэнтны (рис. 8).

Рисунок 8 Катеты (LL) первого прямоугольного треугольника конгруэнтны соответствующим частям

второго прямоугольного треугольника.

Теорема 31 (теорема LA): Если один катет и острый угол одного прямоугольного треугольника равны соответствующим частям другого прямоугольного треугольника, то эти треугольники равны (рис. 9).

Рисунок 9  Одна сторона и острый угол  (LA)  первого прямоугольного треугольника конгруэнтны

соответствующих частей второго прямоугольного треугольника.

Пример 2: Основываясь на маркировке на рисунке 10, завершите заявление о сравнении Δ ABC ≅Δ .

Рисунок 10  Конгруэнтные треугольники.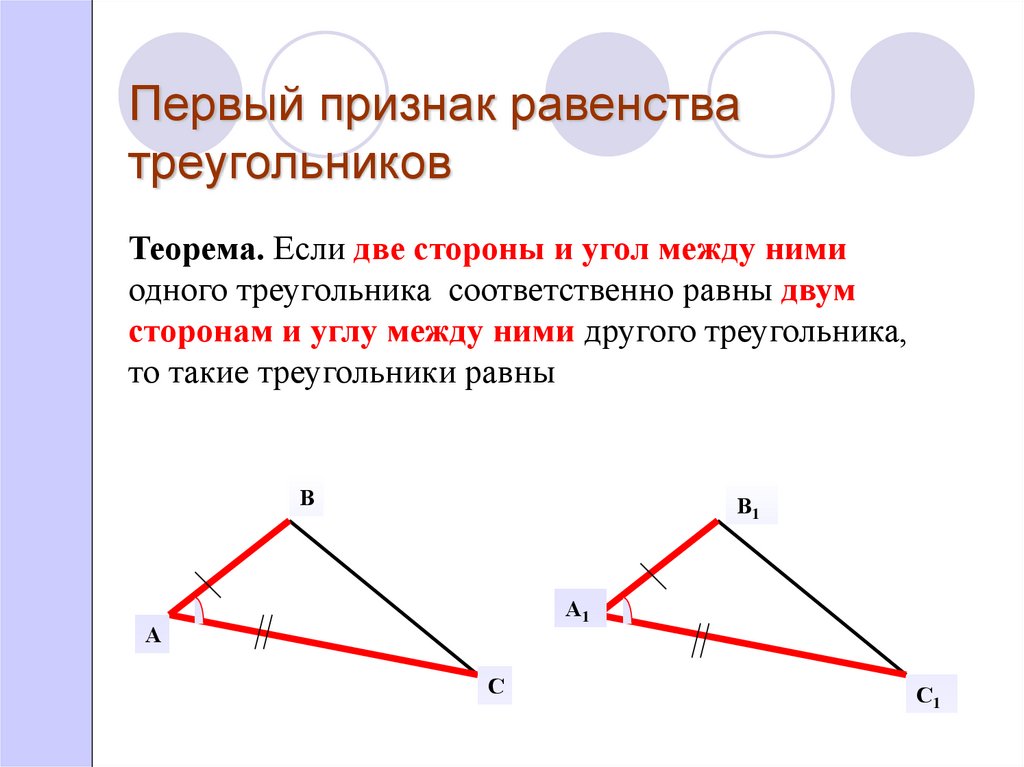

Δ YXZ , потому что A соответствует Y, B соответствует X и C соответствует З .

Пример 3: Каким методом будет доказана конгруэнтность каждого из треугольников на рисунках с 11 (а) по 11 (i)?

Рисунок 11  Методы доказательства конгруэнтности пар треугольников.

• (а) САС.

• (б) Нет. Метода AAA не существует.

• (с) HL.

• (г) ААС.

• (e) ССС. Третья пара конгруэнтных сторон — это сторона, общая для двух треугольников.

• (f) SAS или LL.

• (г) LL или SAS .

• (h) HA или AAS.

• (i) Нет. Метода SSA не существует.

Пример 4: Назовите дополнительные равные соответствующие части, необходимые для доказательства конгруэнтности треугольников на рисунках с 12 (a) по 12 (f) согласно указанному постулату или теореме.