Первый признак равенства треугольников задачи: Задачи на первый признак равенства треугольников

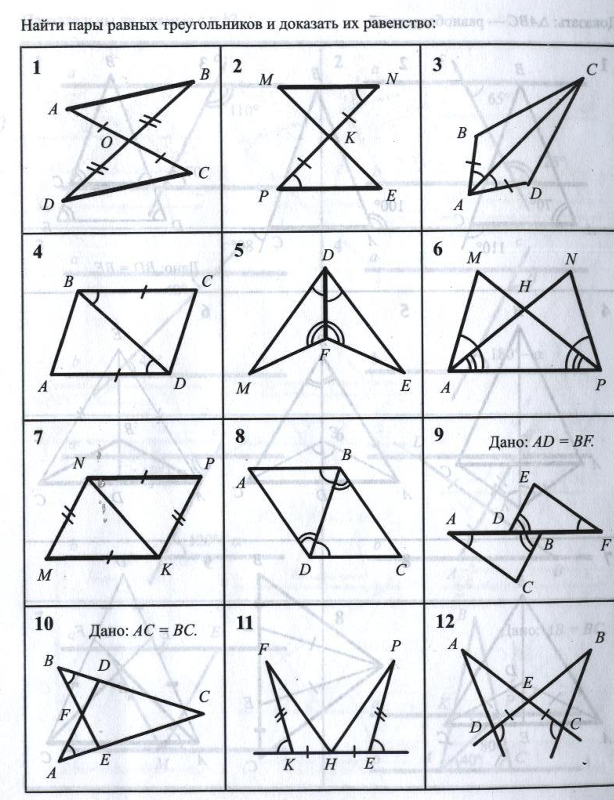
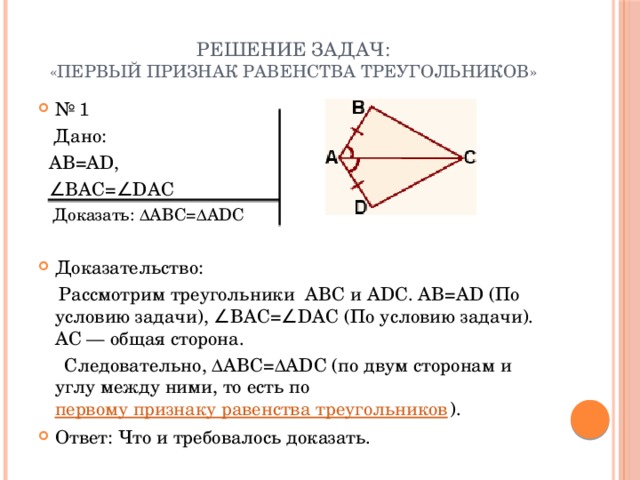
Решение задач на применение признаков равенства треугольников

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Геометрия является самым могущественным средством для изощрения наших умственных способностей. Г. Галилей

Если вы хотите научиться плавать, то смело входите в воду, а если
хотите научиться решать задачи, то решайте их.
Лучший способ изучить что-либо — это открыть самому.
Дьёрдь Пойа

2.

Тема урока : « Решение задач на применение признаков равенства треугольников».Цель: совершенствование навыков решения задач на применение признаков
равенства треугольников, показать практическое применение признаков
равенства треугольников.
Учебная задача: научить использовать признаки равенства треугольников при
решении задач.
Развивающая : использовать проблемные задачи и исследовательскую
деятельность для развития интеллекта, познавательного интереса и
индивидуальных компетенций.
Воспитательная задача : формирование навыков поиска рациональных путей
решения задач , воспитать уважение к значимости полученных знаний.

3. План урока.

1. Орг.момент. Мотивация к учебной деятельности.
2.Актуализация знаний.
2.Проверка домашнего задания
3.Решение проблемных задач
А) Коллективная работа
Б) Групповая работа
4)Практическое применение признаков равенства
треугольников ( исследовательский проект)
5) Тестовая самостоятельная работа.
6) Рефлексия
7) Домашнее задание.

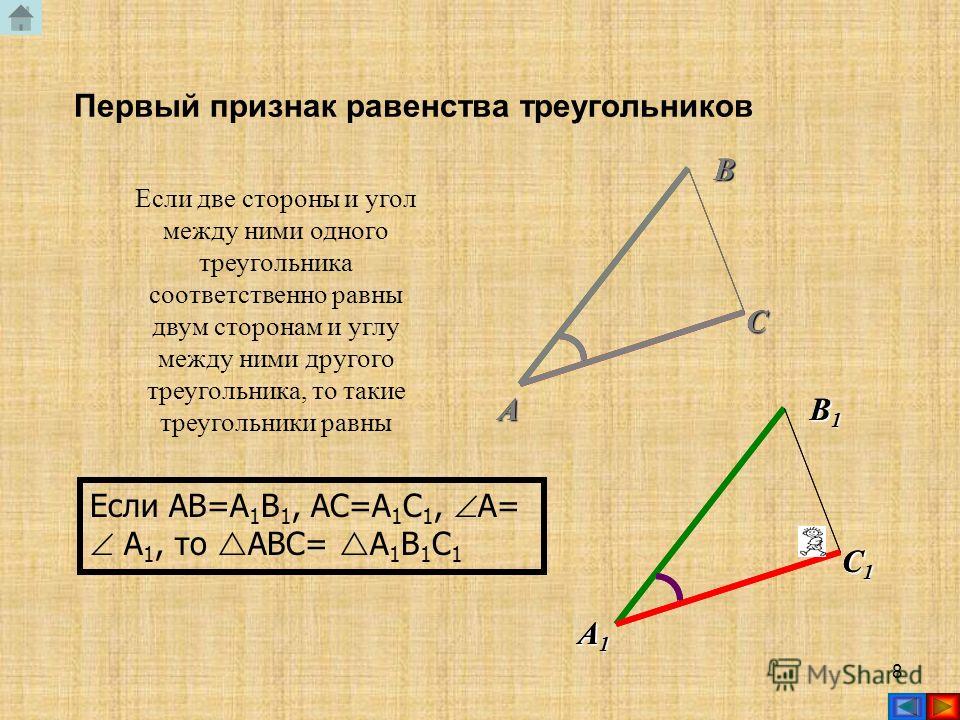
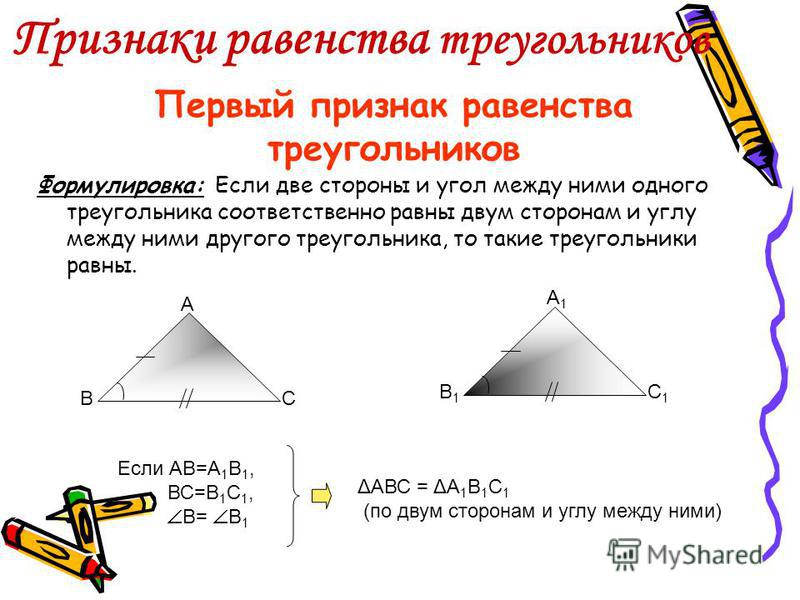
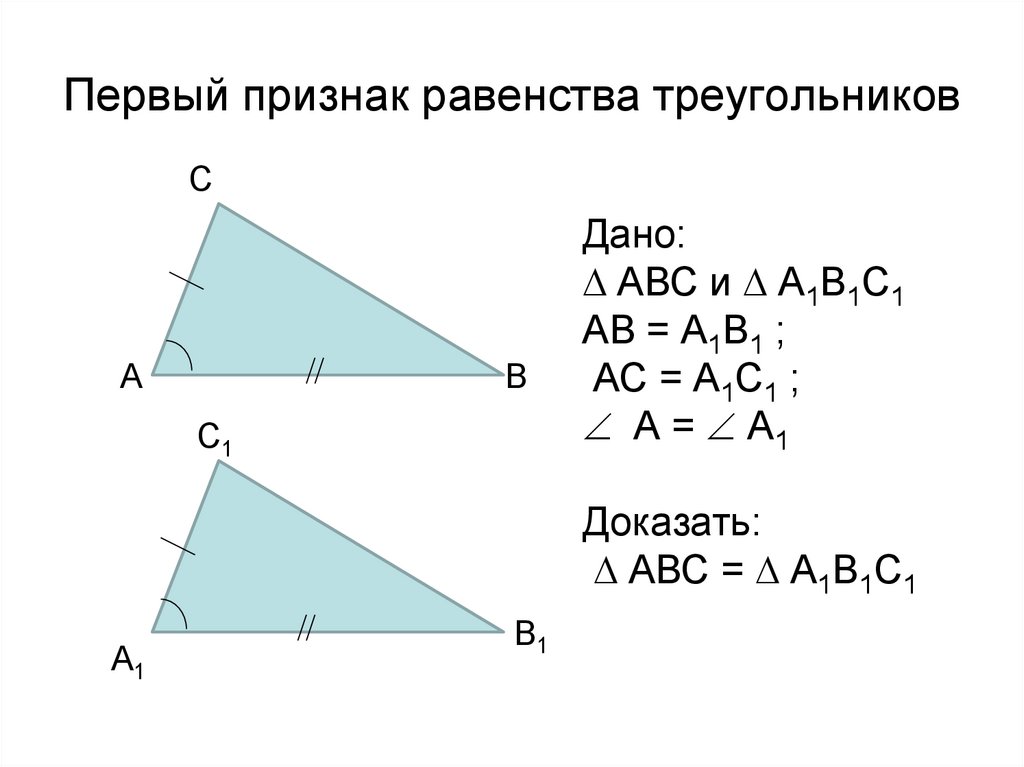
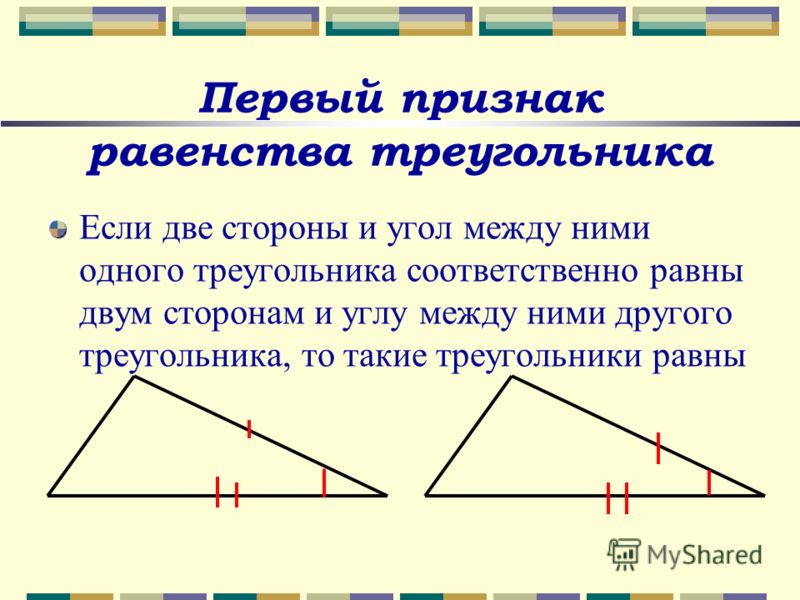
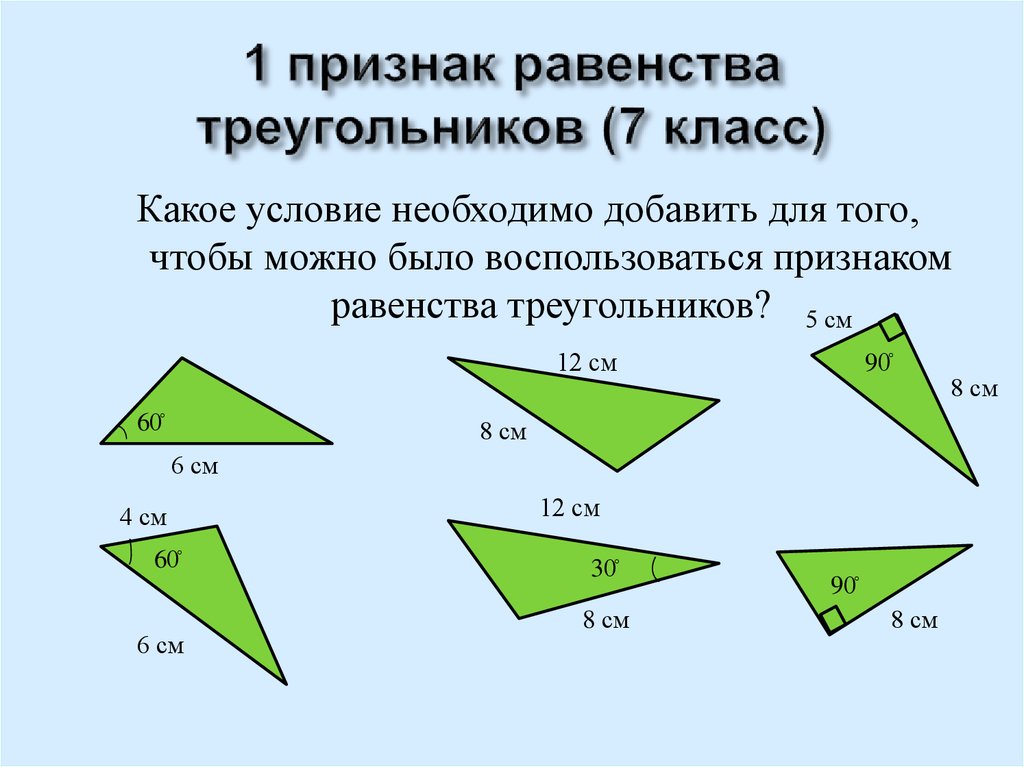
4. Первый признак равенства треугольников

Если две стороны и угол между ними одного
треугольника соответственно равны двум сторонам и
углу между ними другого треугольника, то такие
треугольники равны.
В
Т
R
О
А
S
Р
∆ POS = ∆TOR
С
D
∆ АСВ = ∆ADB

5. Второй признак равенства треугольников

Если сторона и два прилежащих к ней угла
одного треугольника, соответственно равны
стороне и двум прилежащим углам другого
треугольника, то такие треугольники равны.
M
S
O
R
∆ROS = ∆MOS

6. Третий признак равенства треугольников

угла
Если три стороны
одного треугольника
соответственно равны трем сторонам
углам другого
треугольника, то такие треугольники равны.
=
А
С
=
В
∆АВС = ∆ADC
D

7. №1.На рисунке показаны равные отрезки. Какие точки достаточно соединить , чтобы получить равные треугольники ?

8.

№2. Сколько отрезков можно провести, чтобы получились равные треугольники ?

9. №3. На рисунке даны две окружности с общим центром О и равными отрезками АВ и СD. Какие пары точек достаточно соединить , чтобы

получились равные
треугольники ?

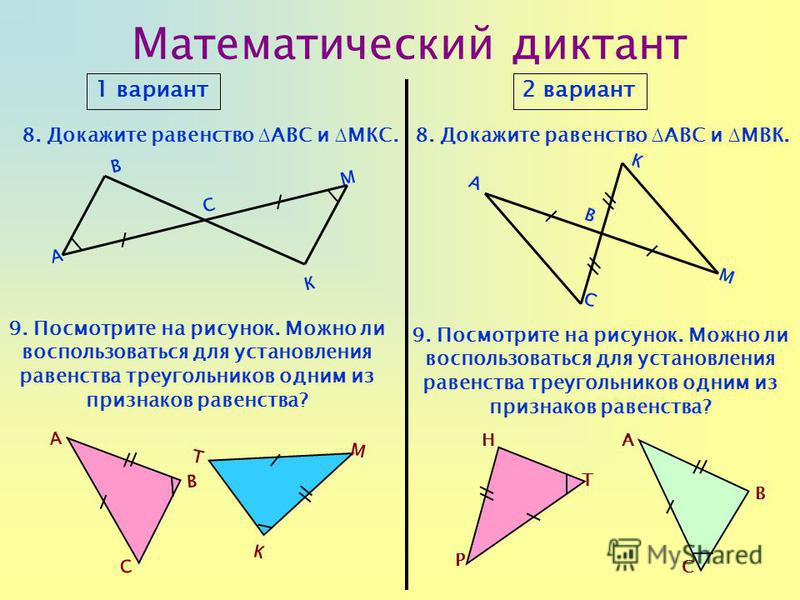
10. Проверка домашнего задания. №128 Докажите, что в равных треугольниках биссектрисы , проведённые к соответственно равным

сторонам, равны.
Дано:∆

English     Русский Правила

3. Примеры задач — Проект по геометрии «Треугольники. Признаки равенства треугольников»

Примеры задач на первый признак равенства треугольников.  Отрезки AE и DC пересекаются в точки B, являющейся серединой каждого из них. а) Докажите, что треугольники ABC и EBD равны; б) найдите углы A и C треугольника ABC, если в треугольнике BDE ∠D = 470, ∠E = 420.    Решение. Дано: Отрезки AE   CD; B – середина AE и CD; ∠D = 470; ∠E = 420. а) Докажите: треугольник ABC = треугольнику BDE б) ∠A — ? ; ∠C — ? Решение: а) Так как AE   CD в точке B, значит ∠ABC = ∠DBE  (так как вертикальные) Так как B – середина EA и CD, значит AB = BE и CB = BD. Если AB = BE  и CB = BD, ∠ABC = ∠DBE, то по первому признаку равенства треугольников Треугольник ABC = треугольнику DBE. б) Так как треугольник ABC = треугольнику DBE, значит по определению равных треугольников ∠D =  ∠C и  ∠E  = ∠A, значит ∠C = 470;  ∠A = 420. Ответ: ∠C = 470;  ∠A = 420. Примеры задач на второй признак равенства треугольников.      2) Дано: AB∥CD, AB=CD Доказать: ∆AOB=∆DOC.      Выделим треугольники AOB и DOC разными цветами. По условии, данные треугольники имеют одну пару равных элементов — стороны AB и CD равны. Видим пару равных вертикальных углов AOB и DOC. Однако, они нам не подходят — раз равные   стороны AB и CD, углы должны быть рядом с ними. Доказательство: 1) AB=CD (по условию). 2) ∠ABO=∠DCO (как внутренние накрест лежащие при AB∥CD и секущей BC). 3) ∠BAO=∠CDO (как внутренние накрест лежащие при AB∥CD и секущей AD). Следовательно, ∆AOB=∆DOC (по стороне и двум прилежащим к ней углам). Примеры задач на третий признак равенства треугольников. 3)  Дано: AF=BK, AK=BF Доказать: ∆AFB=∆BKA   Доказательство: Рассмотрим треугольники AFB и BKA.   1) AF=BK (по условию). 2) AK=BF (по условию). 3) AB — общая сторона.   Следовательно, ∆AFB=∆BKA по третьему признаку равенства треугольников (по трем сторонам).

2.4: Доказательство равенства линий и углов

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

34127

• Генри Африк
• CUNY Нью-Йоркский технологический колледж через Нью-Йоркский городской технологический колледж в CUNY Academic Works

Мы можем доказать равенство прямых и углов, если мы можем показать, что они являются соответствующими частями конгруэнтных треугольников. Мы считаем удобным представить эти доказательства в форме двух столбцов с утверждениями в левом столбце и причиной каждого утверждения в правом.

Пример \(\PageIndex{1}\)

Даны \(AB || CD\) и \(AB = CD\) доказано \(AD = BC\)

Решение

Заявления	Причины
1. \(AB = CD\).	1. Дано.
2. \(\угол ABD = \угол CDB\).	2. Альтернативные внутренние углы параллельных прямых \((AB || CD)\) равны.
3. \(BD = DB\).	3. Личность.
4. \(\треугольник ABD \cong \треугольник CDB\)	4. \(SAS = SAS\): \(AB, \угол B, BD\) из \(\треугольник ABD = CD\), \(\угол D\), \(DB\) из \(\ треугольник CDB\).
5. \(АД = ВС\)	5. Соответствующие стороны равных треугольников равны,

Объяснение: Каждое из первых трех утверждений говорит о том, что сторона или угол \(\треугольника ABD\) равна соответствующей стороне или углу \(\треугольника CDB\).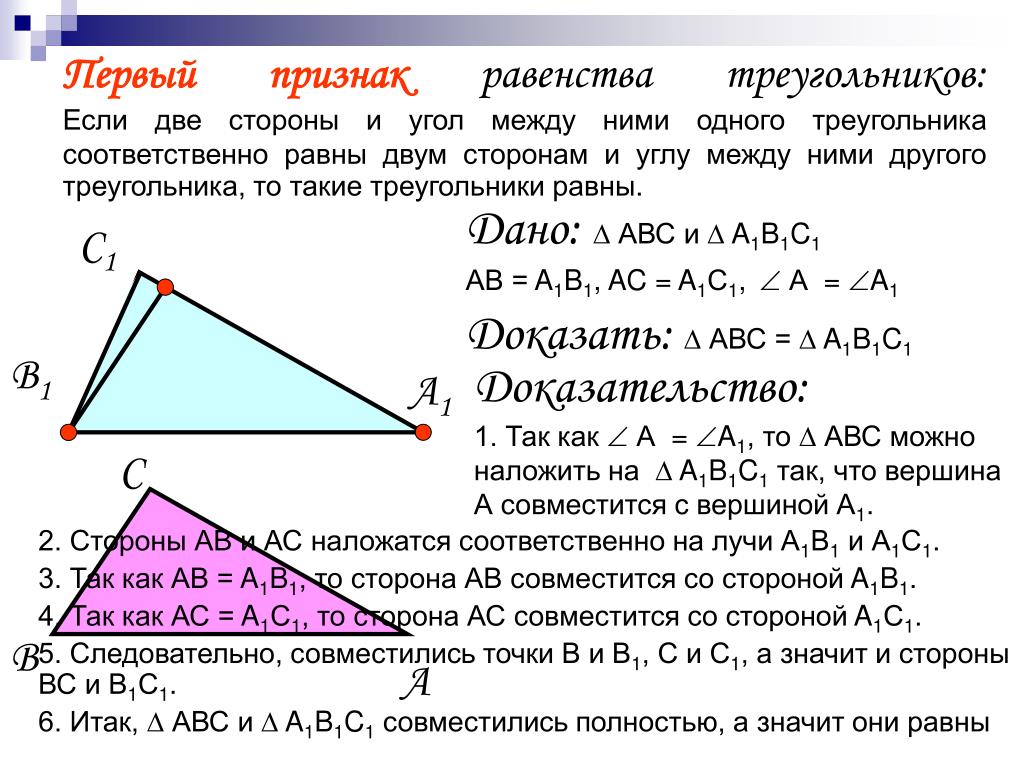

Чтобы получить эти утверждения, мы должны сначала написать конгруэнтность, используя методы предыдущих разделов. Затем мы выбираем три пары соответствующих сторон или углов, которые равны по одной из следующих причин:0034

Причины равенства строк

1. Дано. Это означает, что в начале упражнения нас просят предположить, что линии равны. Например, в задаче будет указано «дано \(AB = CD\)» или \(AB\) и \(CD\) будут отмечены так же на схеме.
2. Личность. Это означает, что в обоих треугольниках появляется один и тот же отрезок прямой. Например, \(BD\) и \(DB\) представляют один и тот же отрезок прямой. Конечно, длина отрезка равна самой себе.

Причины равенства углов

1. Дано.
2. Личность.
3. Альтернативные внутренние углы параллельных прямых равны. Чтобы применить эту причину, мы должны иметь в виду, что прямые параллельны.
4. Соответствующие углы параллельных прямых равны.
5. Вертикальные углы равны.

Это не единственные возможные причины, но это все, что мы будем использовать в первую очередь.

Мы также должны выбрать три пары равных сторон или углов, чтобы одну из причин \(SAS = SAS\), \(ASA = ASA\) или \(AAS = AAS\) можно было использовать для обоснования сравнения утверждение в утверждении 4. В разделах 2.6 и 2.7 мы приведем некоторые дополнительные причины конгруэнтности двух треугольников.

Мы хотим доказать утверждение 5. Причина в том, что соответствующие стороны (или углы) конгруэнтных треугольников равны. Мы можем использовать эту причину здесь, потому что конгруэнтность треугольников уже доказана в утверждении 4,

.

Последнее замечание. Обратите внимание, что решение примера \(\PageIndex{1}\) согласуется с нашим первоначальным определением доказательства. Каждое новое утверждение показывается истинным с использованием предыдущих утверждений и причин, которые уже были установлены.

Приведем другой пример:

Пример \(\PageIndex{2}\)

Учитывая \(QP || ST\) и \(QR = TR\), докажите \(PR = SR\).

Решение

Заявления	Причины
1. \(QR = TR\)	1. Дано.
2. \(\угол Q = \угол T.\)	2. Альтернативные внутренние углы параллельных прямых (\(QP || ST\)) равны.
3. \(\угол PRQ = \угол SRT\).	3. Вертикальные углы равны.
4. \(\треугольник PQR \cong \треугольник STR\).	4. \(ASA = ASA: \угол Q, QR, \угол R\) из \(\треугольник PQR = \угол T\), \(TR, \угол R\) из \(\треугольник STR\) .
5. \(PR = SR\).	5. Соответствующие стороны равных треугольников равны,

1. Даны \(\угол A = \угол D\), \(\угол B = \угол E\), \(AB = DE\). Докажите \(AC = DF\).

2. Даны \(AC=DF\), \(BC = EF\), \(\угол C = \угол F\).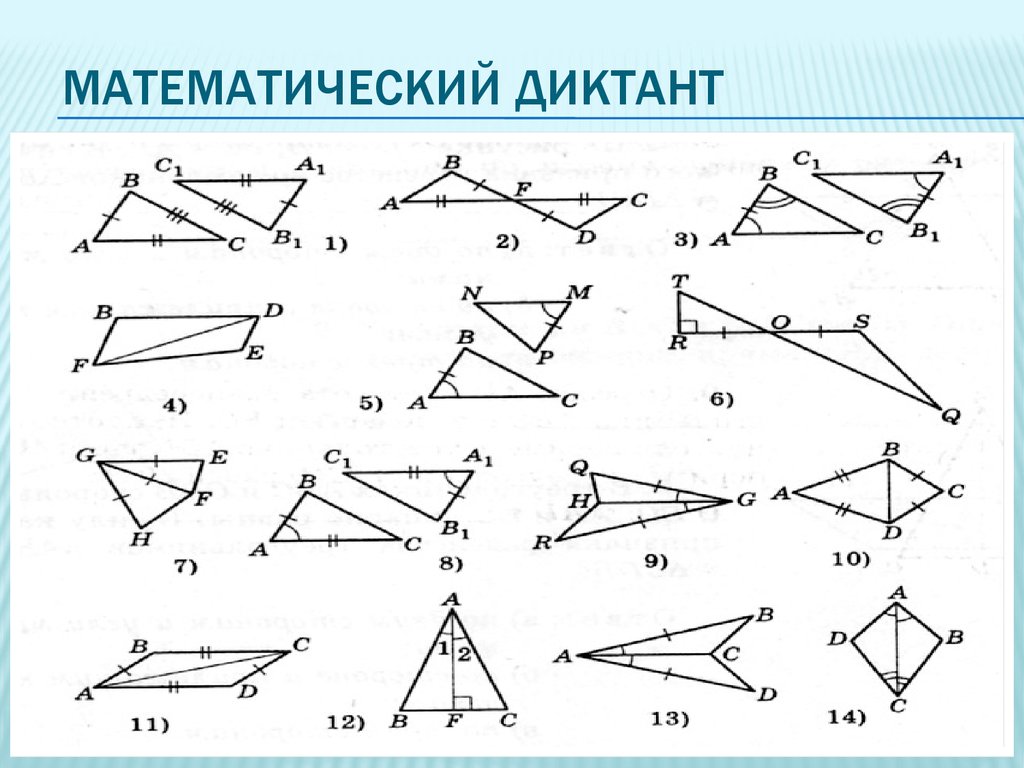 Докажите \(AB = DE\).

3. Даны \(AC = EC\) и \(BC = DC\). Докажите \(AB = ED\).

4. Даны \(AC = DC\), \(\угол A = \угол D\). Докажите \(BC = EC\).

5. Даны \(\угол ABD = \угол CDB\) и \(\угол ADB = \угол CBD\). Докажите \(AB = CD\).

6. Даны \(AB || CD\) и \(AD || CB\). Докажите \(AB = CD\).

7. Даны \(AC = BC\) и \(\угол ACD = \угол BCD\). Докажите \(\угол А = \угол В\).

8. Даны \(\угол A = \угол B\), \(\угол ACD = \угол BCD\). Докажите \(AC = BC\).

9. Даны \(AB || CD\) и \(AB = CD\). Докажите \(AE = CE\). (Подсказка: покажите \(\треугольник ABE \cong \треугольник CDE\))

10. Даны \(AE = CE\) и \(BE = DE\). Докажите \(\угол BAC = \угол CDB\).

11. Даны \(\угол A = \угол D\), \(AC = DE\), \(AB || DC\). Докажите \(BC = CE\).

12. Даны \(AB || DE\), \(AC || FE\) и \(DC = FE\). Докажите \(BE = EC\).

13. Даны \(AD = BC\) и \(\угол BAD = \угол ABC\). Докажите \(AC = BD\). (Подсказка: покажите \(\треугольник ABD \cong \треугольник BAC\))

14. Даны \(AD = BE\), \(\угол BAC = \угол ABC\). Докажите \(AE = BD\).

---

Эта страница под названием 2.4: Proving Lines and Angles Equal распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Генри Африком (Нью-Йоркский технологический колледж в CUNY Academic Works) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Генри Африк

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать страницу TOC

   нет

2. Теги

   1. двухколоночная форма (корректура)
   2. источник@https://academicworks. cuny.edu/ny_oers/44

Использование свойств треугольников для решения задач

Результаты обучения

• Зная величины двух углов треугольника, найдите третий
• Используйте свойства подобных треугольников, чтобы найти неизвестные длины треугольников

Что вы уже знаете о треугольниках? Треугольник имеет три стороны и три угла. Треугольники называются по их вершинам. Треугольник ниже называется [латекс]\Delta ABC[/латекс], читайте «треугольник [латекс]\текст{ABC}[/латекс]». Мы помечаем каждую сторону строчной буквой, чтобы она соответствовала прописной букве противоположной вершины. 9\circ [/латекс]. Найдите величину третьего угла.

Решение

Шаг 1. Прочтите проблему. Нарисуйте рисунок и подпишите его с помощью данной информации.
Шаг 2. Определите , что вы ищете.	Мера третьего угла треугольника.
Шаг 3. Имя. Выберите переменную для ее представления.	Пусть [latex]x=[/latex]мера угла.
Шаг 4. Перевести. Напишите соответствующую формулу и подставьте.	[латекс]м\угол А+м\угол В+м\угол С=180[/латекс]
Шаг 5. Решите уравнение.	[латекс]55+82+x=180[/латекс] [латекс]137+x=180[/латекс] [латекс]x=43[/латекс]
Шаг 6. Проверка: [латекс] 55+82+43\stackrel{?}{=}180[/латекс] [латекс]180=180\галочка[/латекс]
Шаг 7. Ответьте на вопрос.	Третий угол равен [латекс]43°[/латекс]

 

попробуйте

В следующем видео мы покажем пример того, как найти величину неизвестного угла в треугольнике. В этом примере у нас есть два треугольника с общей стороной и два неизвестных внутренних угла.

Прямоугольные треугольники

Некоторые треугольники имеют специальные названия. Сначала рассмотрим прямоугольный треугольник. Прямоугольный треугольник имеет один [латекс]9\circ [/latex] больше, чем мера наименьшего угла. Найдите меры всех трех углов.

Показать раствор

 

попробуй

Подобные треугольники

Когда мы используем карту для планирования поездки, эскиз для сборки книжного шкафа или выкройку для пошива платья, мы работаем с похожими фигурами. В геометрии, если две фигуры имеют одинаковую форму, но разные размеры, мы говорим, что они похожи. Один является масштабной моделью другого. Соответствующие стороны двух фигур имеют одинаковое отношение, и все их соответствующие углы имеют одинаковые размеры.

Два треугольника ниже похожи. Каждая сторона [латекс]\Delta ABC[/латекс] в четыре раза длиннее соответствующей стороны [латекс]\Дельта XYZ[/латекс], а их соответствующие углы имеют равные размеры.

[латекс]\Delta ABC[/латекс] и [латекс]\Delta XYZ[/латекс] — подобные треугольники. Их соответствующие стороны имеют одинаковое отношение и соответствующие углы имеют одинаковую меру.

Свойства подобных треугольников

Если два треугольника подобны, то их соответствующие меры углов равны, и их соответствующие длины сторон находятся в одном и том же отношении.

Длину стороны треугольника можно определить по ее концам, двум вершинам треугольника. Например, в [latex]\Delta ABC\text{:}[/latex]

[latex]\begin{array}{c}\text{длина }a\text{также может быть записана}BC\hfill \\ \text{длина}b\text{ также может быть записана }AC\hfill \\ \text{длина }c\text{ также может быть записана }AB\hfill \end{массив}[/latex]

Мы будем часто использовать это обозначение при решении подобных треугольников, потому что это поможет нам сопоставить соответствующие длины сторон.