Первый замечательный предел и второй замечательный предел: определение, следствия и примеры решения

alexxlab / / Разное

Содержание

Второй замечательный предел

Примеры решенийПроизводная онлайн Интегралы онлайнПределы онлайн Точки разрыва функцииПравило Лопиталя Первый замечательный предел Второй замечательный предел

Предел последовательности обозначается буквой e: (1)
Число e является иррациональным и приблизительно равно 2.718. Это число принято за основание логарифмов, которые называют натуральными логарифмами и обозначают ln(x) (ln(x)=logex).
Формула (1) выполняется и для функций
(2)
Предел (2) называется вторым замечательным пределом. Критерий для его распознавания включает в себя три требования:
1) должна быть неопределенность вида 1∞,
2) 1+бесконечно малая, или короче: 1+б.м.,
3) , причем в показателе степени стоит не произвольная бесконечно большая, а величина, обратная той бесконечно малой, которая прибавляется к числу 1.

Так, среди пределов , , , только второй и третий равны e.
lim
x →

Примечание: число «пи» (π) записывается как pi, знак ∞ как infinity

Типовые замены в пределах

  1. cos(π x) ≈ (-1)x, x → ∞
  2. sin(π x) ≈ (-1)x, x → ∞
  3. cos(x) ≈ [-1;1], x → ∞
  4. sin(x) ≈ [-1;1], x → ∞
  5. cos2(x) ≈ [0;1], x → ∞
  6. sin2(x) ≈ [0;1], x → ∞

Примеры решений

Пример 1. Используя свойства бесконечно малых и бесконечно больших функций, найти следующие пределы:
.

Пример 2.
.

Пример 3.
.

Пример 4.
.

Пример 5.
.

Пример 6.

.
Единицу можно было бы получить делением многочлена на многочлен: , тогда
.

Следствиями второго замечательного предела являются следующие пределы (эквивалентные функции):
, в частности .
, если a=e, то .
.
С их помощью легко решаются многие задачи на раскрытие неопределенностей.

Пример 7.
. (Здесь ).

Пример 8. .

Пример 9.
.

Пример 10.

.

Пример 11. .

Пример 12.


.

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.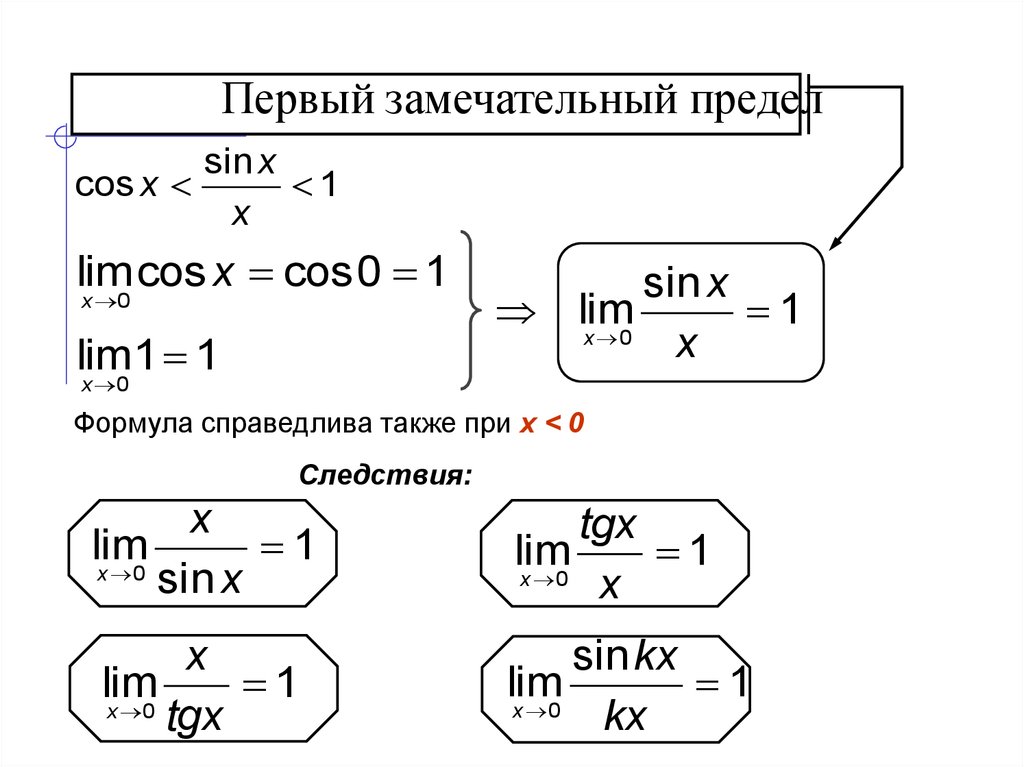
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

8. Первый замечательный предел. Следствия.

Первым замечательным пределом называется предел Пользуемся теоремой. ( Если функция  имеет оба односторонних предела при  и эти пределы равны одному и тому же числу  , то существует двусторонний предел  , который также равен  ; ноаборот, если существует двусторонний предел  , то существуют оба односторонних предела и оба они равны числу  ).

Следствия:

Следствия

9.Второй замечательный предел. Следствия.

 или  

 Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что  . Рассмотрим два случая:

1. Пусть  . Каждое значение x заключено между двумя положительными целыми числами:  , где   — это целая часть x.

Отсюда следует:  , поэтому

.

Если  , то  . Поэтому, согласно пределу  , имеем:

.

По признаку (о пределе промежуточной функции) существования пределов  .

2. Пусть  . Сделаем подстановку − x = t, тогда

.

Из двух этих случаев вытекает, что   для вещественного x.    

Следствия

  5.  для  , 

10.Непрерывность функции. Односторонние пределы.

Непрерывная функция — функция без «скачков», то есть такая у которой малые изменения аргумента приводят к малым изменениям значения отображения. График непрерывной функции можно начертить «не отрывая карандаш от бумаги».

Непрерывная функция вообще говоря, — синоним понятия непрерывное отображение, тем не менее, чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающих вещественные значения.

Пусть на некотором числовом множестве   задана числовая функция   и число   — предельная точка

 области определения  . Существуют различные определения для односторонних пределов функции   в точке  , но все они эквивалентны.

Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (или преде́лом спра́ва).

Основные свойства односторонних пределов идентичны свойствам обычных пределов и являются частными случаями свойств пределов вдоль фильтра.

Для существования (двустороннего) предела функции необходимо и достаточно, чтобы оба односторонних предела существовали и равнялись между собой.

11. Классификация точек разрыва.

Если функция f (x) не является непрерывной в точке x = a, то говорят, что 

f (x) имеет разрыв в этой точке.

Классификация точек разрыва функции

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.  Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке

При этом возможно следующие два случая:

Такая точка называется точкой устранимого разрыва.

Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов  называется скачком функции.

Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности. 

1.1: Введение в понятие лимита

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    11015

    • Эта страница является черновиком и находится в активной разработке.

    Цели обучения

    • Используя правильные обозначения, опишите предел функции.
    • Используйте таблицу значений, чтобы оценить предел функции или определить, когда предел не существует.
    • Используйте график, чтобы оценить предел функции или определить, когда предел не существует.
    • Дайте определение односторонним ограничениям и приведите примеры.
    • Объясните взаимосвязь между односторонними и двусторонними пределами.
    • Используя правильные обозначения, опишите бесконечный предел.
    • Задайте вертикальную асимптоту.

    Пределы

    Две ключевые проблемы привели к первоначальной формулировке исчисления:

    (1) проблема касательной, или как определить наклон линии, касательной к кривой в точке;

    и (2) задача площади, или как определить площадь под кривой.

    Концепция предела или ограничивающего процесса, необходимая для понимания исчисления, существует уже тысячи лет. На самом деле ранние математики использовали ограничивающий процесс для получения все более и более точных приближений площадей кругов. Однако формальное определение предела — в том виде, в каком мы его знаем и понимаем сегодня — появилось только в конце XIX в.2}\),

    , которые показаны на рисунке \(\PageIndex{1}\). В частности, давайте сосредоточим наше внимание на поведении каждого графа при \(x=2\) и около него.

    Рисунок \(\PageIndex{1}\): Эти графики показывают поведение трех различных функций вокруг \(x=2\).

    Каждая из трех функций не определена в точке \(x=2\), но если мы делаем это утверждение и никакое другое, мы даем очень неполную картину того, как каждая функция ведет себя вблизи точки \(x=2\). Чтобы более полно выразить поведение каждого графа в окрестности \(2\), нам нужно ввести понятие предела. 92−4)/(x−2)\) ведет себя примерно так, как \(x=2\) на рисунке \(\PageIndex{1}\). Поскольку значения \(x\) приближаются к \(2\) по обе стороны от \(2\), значения \(y=f(x)\) приближаются к \(4\). Математически мы говорим, что предел \(f(x)\) при приближении \(x\) к \(2\) равен \(4\). Символически мы выражаем этот предел как

    \(\displaystyle \lim_{x \to 2} f(x)=4\).

    Из этого очень краткого неформального взгляда на один предел давайте начнем разрабатывать интуитивное

    определение предела . Мы можем думать о пределе функции при числе а как об одном действительном числе \(L\), к которому функциональные значения приближаются по мере того, как \(х\)-значения приближаются к а, при условии, что такое действительное число \(L\ ) существуют. Сформулировав более тщательно, мы имеем следующее определение:

    Определение (интуитивное): Предел

    Пусть \(f(x)\) — функция, определенная для всех значений в открытом интервале, содержащем \(a\), за возможным исключением самого a, и пусть \(L \) быть действительным числом. Если все значения функции \(f(x)\) приближаются к действительному числу \(L\), а значения \(x(≠a)\) приближаются к числу a, то мы говорим, что предел \( f(x)\) при приближении \(x\) к \(a\) есть \(L\). (Более кратко, поскольку \(x\) приближается к \(a\), \(f(x)\) приближается и остается близким к \(L\).) Символически мы выражаем эту идею как

    \[\lim_{x \to a} f(x)=L.\]

    Мы можем оценить пределы, составив таблицы функциональных значений и просмотрев их графики. Этот процесс описан в следующей стратегии решения проблем.

    Стратегия решения проблем: оценка предела с использованием таблицы функциональных значений

    1. Чтобы оценить \(\displaystyle \lim_{x \to a} f(x)\), мы начнем с заполнения таблицы функциональных значений . Мы должны выбрать два набора \(x\)-значений: один набор значений приближается к \(a\) и меньше \(a\), а другой набор значений приближается к \(a\) и больше \(a\) \). В таблице \(\PageIndex{1}\) показано, как могут выглядеть ваши таблицы.

    Таблица \(\PageIndex{1}\)
    \(х\) \(f(x)\) \(х\) \(f(x)\)
    \(а-0,1\) \(ф(а-0,1)\) \(а+0,1\) \(f(а+0,1)\)
    \(а-0,01\) \(f(a-0,01)\) \(а+0,001\) \(f(а+0,001)\)
    \(а-0,001\) \(f(a-0,001)\) \(а+0,0001\) \(f(а+0,001)\)
    \(а-0,0001\) \(ф(а-0,0001)\) \(а+0,00001\) \(ф(а+0,0001)\)
    При необходимости используйте дополнительные значения. При необходимости используйте дополнительные значения.

    2. Далее давайте посмотрим на значения в каждом из столбцов \(f(x)\) и определим, приближаются ли значения к одному значению по мере продвижения вниз по каждому столбцу. В наших столбцах мы смотрим на последовательность \(f(a-0,1)\), \(f(a-0,01)\), \(f(a-0,001)\), \(f(a-0,0001) \) и так далее, и \(f(a+0,1), \;f(a+0,01), \;f(a+0,001), \;f(a+0,0001)\) и так далее. (Примечание. Хотя мы выбрали \(x)-значения \(a±0,1, \;a±0,01, \;a±0,001, \;a±0,0001\) и т. д., и эти значения, вероятно, работают почти каждый раз, в очень редких случаях нам может потребоваться изменить наш выбор.)

    3. Если оба столбца приближаются к общему \(y\)-значению \(L\), мы указываем \(\displaystyle \lim_{x \to a}f(x)=L\). Мы можем использовать следующую стратегию для подтверждения результата, полученного из таблицы, или в качестве альтернативного метода оценки предела.

    4. С помощью графического калькулятора или компьютерной программы, которая позволяет нам графически отображать функции, мы можем построить график функции \(f(x)\), убедившись, что функциональные значения \(f(x)\) для \(x\ )-значения рядом с a находятся в нашем окне. Мы можем использовать функцию трассировки, чтобы перемещаться по графику функции и наблюдать за показаниями \(y\)-значения по мере того, как \(x\)-значения приближаются к a. Если \(y\)-значения приближаются к \(L\), когда наши \(x\)-значения приближаются к \(a\) с обоих направлений, то \(\displaystyle \lim_{x \to a}f(x )=L\). Возможно, нам придется увеличить наш график и повторить этот процесс несколько раз.

    Мы применяем эту стратегию решения проблем для вычисления лимита в примерах \(\PageIndex{1A}\) и \(\PageIndex{1B}\).

    Пример \(\PageIndex{1A}\): оценка предела с помощью таблицы функциональных значений

    Оценка \(\displaystyle \lim_{x \to 0}\frac{\sin x}{x}\) с таблица функциональных значений.

    Решение

    Мы рассчитали значения \(f(x)=\dfrac{\sin x}{x}\) для значений \(x\), перечисленных в таблице \(\PageIndex{2 }\).

    Таблица \(\PageIndex{2}\)
    \(х\) \(\frac{\sin x}{x}\) \(х\) \(\frac{\sin x}{x}\)
    -0,1 0,998334166468 0,1 0,998334166468
    -0,01 0,999983333417 0,01 0,999983333417
    -0,001 0,999999833333 0,001 0,999999833333
    -0,0001 0,999999998333 0,0001 0,999999998333

    Примечание. Значения в этой таблице были получены с помощью калькулятора и с использованием всех мест, указанных в выходных данных калькулятора.

    Читая каждый столбец \(\dfrac{\sin x}{x}\), мы видим, что значения в каждом столбце приближаются к единице. Таким образом, вполне разумно заключить, что \(\displaystyle \lim_{x\to0}\frac{\sin x}{x}=1\). График \(f(x)=\dfrac{\sin x}{x}\), построенный калькулятором или компьютером, будет аналогичен графику, показанному на рисунке \(\PageIndex{2}\), и подтверждает наши оценивать.

    Рисунок \(\PageIndex{2}\): График \(f(x)=(\sin x)/x\) подтверждает оценку из табл.

    Пример \(\PageIndex{1B}\): оценка предела с помощью таблицы функциональных значений

    Оценить \(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x−4}\) с помощью таблицы функциональных значений.

    Решение

    Как и прежде, мы используем таблицу — в данном случае Table \(\PageIndex{3}\) — для перечисления значений функции для заданных значений \(x\).

    Таблица \(\PageIndex{3}\)
    \(х\) \(\frac{\sqrt{x}−2}{x−4}\) \(х\) \(\frac{\sqrt{x}−2}{x−4}\)
    3,9 0,251582341869 4. 1 0,248456731317
    3,99 0,25015644562 4.01 0,24984394501
    3,999 0,250015627 4.001 0,249984377
    3,9999 0,250001563 4.0001 0,249998438
    3,99999 0,25000016 4. 00001 0,24999984

    Изучив эту таблицу, мы видим, что функциональные значения меньше 4 уменьшаются до 0,25, тогда как функциональные значения больше 4 увеличиваются до 0,25. Мы заключаем, что \(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x−4}=0,25\). Мы подтверждаем эту оценку, используя график \(f(x)=\dfrac{\sqrt{x}−2}{x−4}\), показанный на рисунке \(\PageIndex{3}\).

    Рисунок \(\PageIndex{3}\): График \(\frac{\sqrt{x}−2}{x−4}\) подтверждает оценку из таблицы

    . Упражнение \(\PageIndex{1}\ )

    Оцените \(\displaystyle \lim_{x \to 1} \frac{\frac{1}{x}−1}{x−1}\), используя таблицу функциональных значений. Используйте график, чтобы подтвердить свою оценку.

    Подсказка

    Используйте 0,9, 0,99, 0,999, 0,9999, 0,99999 и 1,1, 1,01, 1,001, 1,0001, 1,00001 в качестве табличных значений.

    Ответ

    \[\lim_{x\to1}\frac{\frac{1}{x}−1}{x−1}=−1\nonumber\]

    На данный момент из примеров \(\PageIndex{1A}\) и \(\PageIndex{1b}\) мы видим, что может быть так же просто, если не проще, оценить предел функции, исследуя его график, как он есть, для оценки предела с помощью таблицы функциональных значений. В примере \(\PageIndex{2}\) мы оцениваем ограничение исключительно по графику, а не по таблице функциональных значений.

    Пример \(\PageIndex{2}\): оценка предела с помощью графика

    Для \(g(x)\), показанного на рис. {х\к-1}г(х)\).

    Рисунок \(\PageIndex{4}\): График \(g(x)\) включает одно значение не на гладкой кривой.

    Решение :

    Несмотря на то, что \(g(-1)=4\), при приближении \(x\)-значений к \(-1\) с любой стороны, \(g(x) \) значения приближаются к \(3\). Следовательно, \(\displaystyle \lim_{x\to-1}g(x)=3\). Заметим, что мы можем определить этот предел, даже не зная алгебраического выражения функции.

    На основе примера \(\PageIndex{2}\) мы делаем следующее наблюдение: возможно, что предел функции существует в точке, и функция может быть определена в этой точке, но предел функции и значение функции в точке могут быть разными.

    Упражнение \(\PageIndex{2}\)

    Используйте график \(h(x)\) на рисунке \(\PageIndex{5}\) для оценки \(\displaystyle \lim_{x \to 2 }h(x)\), если это возможно.

    Рисунок \(\PageIndex{5}\):
    Подсказка

    К какому \(y\)-значению приближается функция, когда \(x\)-значение приближается к \(2\)?

    Решение

    \(\displaystyle \lim_{x \to 2}h(x)=−1.\)

    Глядя на таблицу функциональных значений или глядя на график функции, мы получаем полезную информацию о значении предела функции в данной точке. Однако эти методы слишком полагаются на догадки. Со временем нам потребуется разработать альтернативные методы оценки пределов. Эти новые методы носят более алгебраический характер, и мы рассмотрим их в следующем разделе; однако на этом этапе мы вводим два специальных ограничения, которые лежат в основе будущих методов.

    Два важных ограничения

    Пусть \(a\) — действительное число, а \(c\) — константа.

    1. \(\displaystyle \lim_{x \to a}x=a\)
    2. \(\displaystyle \lim_{x \to a}c=c\)

    Мы можем сделать следующие замечания относительно этих двух пределов.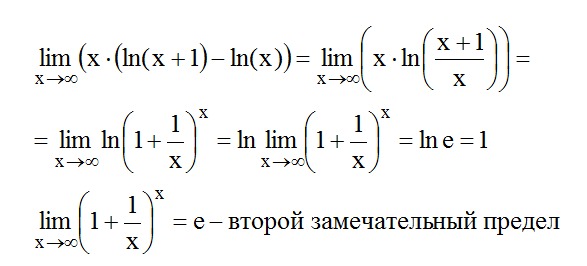

    1. Для первого предела заметим, что по мере того, как \(x\) приближается к \(a\), приближается и \(f(x)\), потому что \(f(x)=x\). Следовательно, \(\displaystyle \lim_{x \to a}x=a\).
    2. Для второго ограничения рассмотрим таблицу \(\PageIndex{4}\).
    Таблица \(\PageIndex{4}\)
    \(х\) \(f(x)=c\) \(х\) \(f(x)=c\)
    \(а-0,1\) \(с\) \(а+0,1\) \(с\)
    \(а-0,01\) \(с\) \(а+0,01\) \(с\)
    \(а-0,001\) \(с\) \(а+0,001\) \(с\)
    \(а-0,0001\) \(с\) \(а+0,0001\) \(с\)

    Обратите внимание, что для всех значений \(x\) (независимо от того, приближаются ли они к \(a\)), значения \(f(x)\) остаются постоянными при \(c\).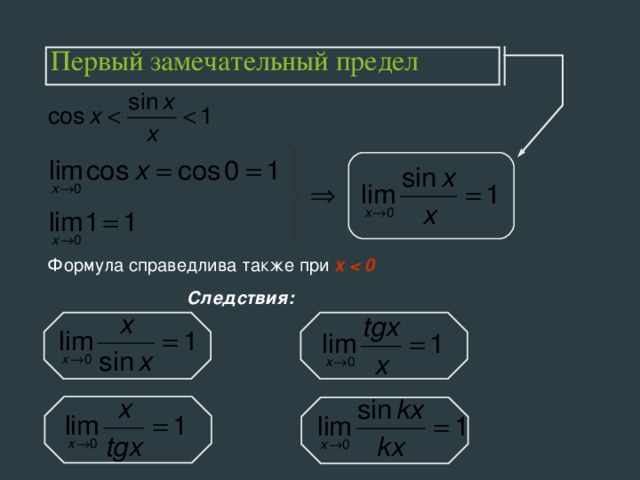 У нас нет другого выбора, кроме как заключить \(\displaystyle \lim_{x \to a}c=c\).

    Существование предела

    Когда мы рассматриваем предел в следующем примере, имейте в виду, что для того, чтобы предел функции существовал в точке, функциональные значения должны приближаться к единственному вещественному значению в этой точке. Если функциональные значения не приближаются к единому значению, то предела не существует.

    Пример \(\PageIndex{3}\): оценка несуществующего предела

    Вычислить \(\displaystyle\lim_{x \to 0}\sin(1/x)\) с помощью таблицы значений.

    Решение

    В таблице \(\PageIndex{5}\) перечислены значения функции \(\sin(1/x)\) для заданных значений \(x\).

    Таблица \(\PageIndex{5}\)
    \(х\) \(\sin(1/x)\) \(х\) \(\sin(1/x)\)
    -0,1 0,544021110889 0,1 −0,544021110889
    -0,01 0,50636564111 0,01 −0,50636564111
    -0,001 −0,8268795405312 0,001 0,8268795405312
    -0,0001 0,305614388888 0,0001 −0,305614388888
    -0,00001 −0,035748797987 0,00001 0,035748797987
    -0,000001 0,349993504187 0,000001 −0,349993504187

    Изучив таблицу функциональных значений, мы видим, что \(y\)-значения не приближаются ни к одному единственному значению.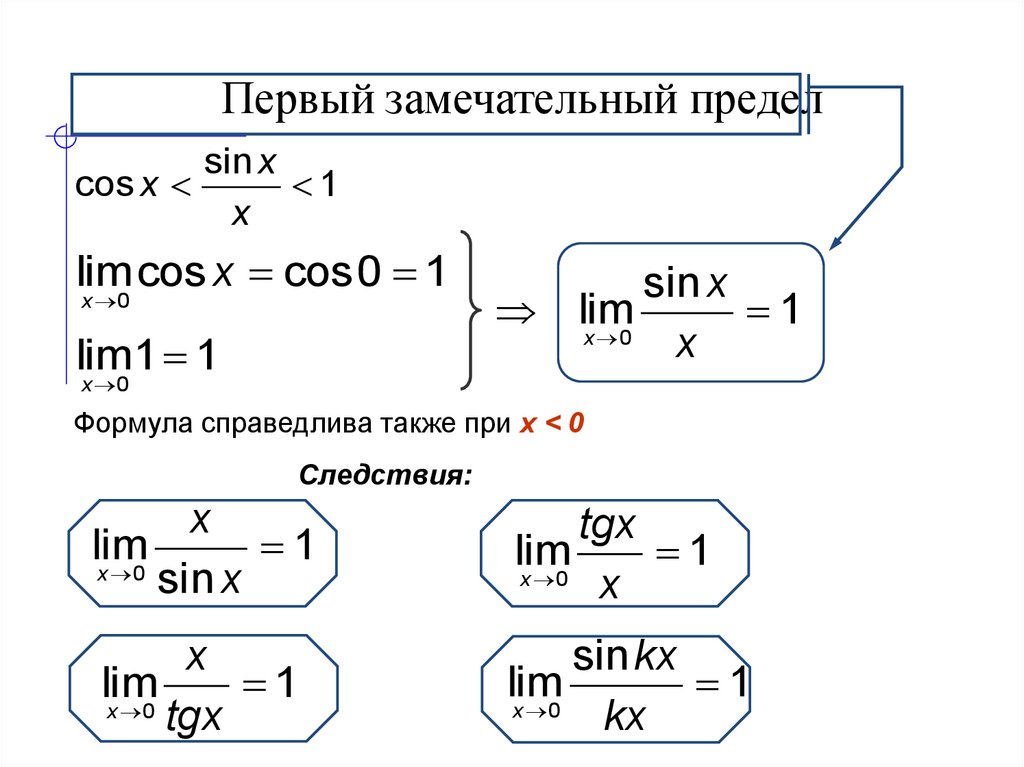 Получается, что предела не существует. Прежде чем сделать такой вывод, давайте подойдем более системно. Возьмем следующую последовательность \(x\)-значений, приближающихся к \(0\):

    \[\frac{2}{π},\;\frac{2}{3π},\;\frac{2}{5π},\;\frac{2}{7π},\;\frac {2}{9π},\;\frac{2}{11π},\;….\nonumber\]

    Соответствующие \(y\)-значения равны

    \[1,\;-1,\ ;1,\;-1,\;1,\;-1,\;….\nonumber\]

    На данный момент мы действительно можем заключить, что \(\displaystyle \lim_{x \to 0} \ sin(1/x)\) не существует. (Математики часто сокращают «не существует» до DNE. Таким образом, мы будем писать \(\displaystyle \lim_{x \to 0} \sin(1/x)\) DNE.) График \(f(x) =\sin(1/x)\) показан на рисунке \(\PageIndex{6}\) и дает более четкое представление о поведении \(\sin(1/x)\) при \(x\) приближается к \(0\). Вы можете видеть, что \(\sin(1/x)\) все более сильно колеблется между \(-1\) и \(1\) по мере того, как \(x\) приближается к \(0\). 92−4∣}{x−2}\) не существует.

    Авторы и ссылки

    • Гилберт Стрэнг (MIT) и Эдвин «Джед» Херман (Харви Мадд) со многими сотрудничающими авторами. Этот контент от OpenStax лицензирован по лицензии CC-BY-SA-NC 4.0. Скачать бесплатно на http://cnx.org.

    • Памини Тангараджа (Университет Маунт-Рояль, Калгари, Альберта, Канада)

    1. Наверх
      • Была ли эта статья полезной?
      1. Тип изделия
        Раздел или Страница
        Лицензия
        CC BY-NC-SA
        Показать страницу TOC
        да
        Стадия
        Проект
      2. Теги
        1. расчет: да
        2. юпитер: питон

      Добро пожаловать в Great Western Bank | Первый межгосударственный банк

      Добро пожаловать Great Western Bank | Первый межгосударственный банк
      • Перейти к основному содержанию
      • Включить высокую контрастность
      • Перейти к поиску

      В понедельник, 23 мая 2022 г. , Great Western Bank стал первым межгосударственным банком, предоставив вам доступ к более чем 300 отделениям в 14 штатах. Тем временем вы по-прежнему будете пользоваться персонализированным обслуживанием от банкиров, которых вы знаете и которым доверяете. Мы с нетерпением ждем возможности познакомиться с вами и стать вашим надежным финансовым партнером.

      В рамках слияния Great Western Bank с First Interstate Bank учетные записи Great Western Wealth Management теперь являются учетными записями First Interstate Wealth Management (FIWM) с 31 июля 2022 года. С 1 августа вы можете получить доступ к своим учетным записям FIWM в Интернете, посетив Firstinterstate. ком. Нажмите кнопку «Войти» в правом верхнем углу, затем выберите «Управление капиталом» в раскрывающемся списке. Для получения дополнительной информации о доступе к вашей учетной записи в первый раз ознакомьтесь с брошюрой «Руководство по вашей учетной записи», в которой содержится информация об онлайн-платформе FIWM, предоставленная SEI.

      Путеводитель по буклету вашей учетной записи Последнее обновление руководства
      : 26 июля 2022 г.

      Сообщение от Кевина Райли, президента и генерального директора

      Наше Руководство по переходу клиентов содержит важную информацию о том, как ваши счета будут переведены из Great Western Bank, а также другие важные сведения о First Interstate и переходе. Вы также должны были получить копию руководства по почте.

      Руководство по конвертации Great Western Bank 9Последнее обновление руководства 0698: 20.04.2022

      Кредитные карты Great Western Bank

      Если у вас была карта Great Western Rewards Visa® или Great Western Bank Business Visa®, вы должны были получить новую кредитную карту First Interstate FirstRewards® Mastercard®, а также отдельный почтовый ящик с PIN-кодом для Наличные в банкомате. Если вы не получили новую карту, позвоните по номеру 1-888-833-3454.

      Пожалуйста, активируйте вашу новую кредитную карту Mastercard® Первого межгосударственного банка, так как ваша GWB Visa больше не будет работать. Доступ к Visa Intellilink для карт Great Western Bank будет открыт до 18 июля 2022 года. Для получения более подробной информации см. руководство по конвертации клиентов.

      Visa Intellilink

      Войти

      Руководство по переходу клиентов казначейства

      В Руководстве по переходу клиентов казначейства подробно описывается, как ваши услуги Treasury Solutions будут преобразованы в First Interstate, а также рассказывается о различных сетевых и мобильных платформах.

      Руководство по переходу на программу Treasury Client

      Сеансы обучения клиентов