Площа прямокутника формула: Периметр и площадь прямоугольника

Одиниці вимірювання площі Обчислення площі квадрата, прямокутника, фігури за допомогою палетки » Допомога учням

Інші завдання дивись тут…

Площа.

Визначити площу фігури — означає з’ясувати, скільки одиничних квадратів у ній уміщується.

Площу можна вимірювати, обчислювати і виконувати з цими числами різні дії. 

Для цього визначили такі одиниці — квадратний метр (м²), квадратний міліметр (мм²), квадратний дециметр (дм²), квадратний сантиметр (см²), квадратний міліметр (мм²), квадратний кілометр (км²), сотка (ар), гектар (га).

1 мм² — це площа квадрата зі стороною 1 мм. Тобто 1 мм • 1 мм = 1 мм²

1 см² — це площа квадрата зі стороною 1 см. Тобто 1 см • 1 см = 1 см²

1 дм² — це площа квадрата зі стороною 1 дм. Тобто 1 дм • 1 дм = 1 дм²

1 м² — це площа квадрата зі стороною 1 м. Тобто 1 м • 1 м = 1 м²

1 км² — це площа квадрата зі стороною 1 км. Тобто 1 км • 1 км = 1 км

2

1 сотка — це площа квадрата зі стороною 10 м. Тобто 10 м • 10 м = 100 м² = 1 сотка = 1 ар

1 гектар — це площа квадрата зі стороною 100 м. Тобто 100 м • 100 м = 10000 м² = 1 га

 

Одиниці вимірювання площі.

1 см² = 1 см • 1 см = 10 мм • 10 мм = 100 мм²

1 дм² = 1 дм • 1 дм = 10 см • 10 см = 100 см²

1 дм² = 1 дм • 1 дм = 100 мм • 100 мм = 10000 мм²

1 м² = 1 м • 1 м = 10 дм • 10 дм = 100 дм² 

1 м² = 1 м • 1 м = 100 см • 100 см = 10000 см²

1 км² = 1 км • 1 км = 1000 м • 1000 м = 1 000 000 м²

1 сотка = 1 ар = 10 м • 10 м = 100 м² (площа квадрата зі стороною 10 м)

1 га = 100 ар = 100 м • 100 м = 10000 м² (площа квадрата зі стороною 100 м)

1 га = 100 а.

У квадратних сантиметрах вимірюють площу зошита, стола; у квадратних метрах вимірюють площу кімнати; у квадратних кілометрах вимірюють площі країн, областей, водоймищ тощо; площі невеликих ділянок землі вимірюють в арах (сотках), а великих — у гектарах. Наприклад, площа України становить шістсот три тисячі шістсот двадцять вісім квадратних кілометрів (площа України — 603 628 км²). 

 

Зведена таблиця

Квадратний міліметр	1 мм • 1 мм = 1 мм2	Площа квадрата зі стороною 1 мм
Квадратний сантиметр	1 см • 1 см = 1 см2 1 см2 = 100 мм 2	Площа квадрата зі стороною 1 см
Квадратний дециметр	1 дм • 1 дм = 1 дм2 1 дм2 = 100 см2 = 10 000 мм2	Площа квадрата зі стороною 1 дм
Квадратний метр	1 м • 1 м = 1 м2 1 м2 = 100 дм2 = 10 000 см2	Площа квадрата зі стороною 1 м
Ар	10 м • 10 м = 1 а 1 а = 100 м2	Площа квадрата зі стороною 10 м
Гектар	100 м • 100 м = 1 га 1 га = 10 000 м2 = 100 а	Площа квадрата зі стороною 100 м
Квадратний кілометр	1 км • 1 км = 1 км2 1 км2 = 1 000 000 м2 = 100 га	Площа квадрата зі стороною 1 км

 

Площа квадрата.

Квадрат — це прямокутник із рівними сторонами. Щоб знайти площу квадрата, треба довжину сторони помножити саму на себе.

S = а • а, де а — довжина сторони квадрата, S — площа квадрата.

Задача на знаходження площі квадрата. 

Сторона квадрата дорівнює 3 м. Знайти його площу.

Розв’язання.

S = З м • 3 м = 9 м² — площа квадрата зі стороною 9 см.

Відповідь: площа квадрата дорівнює 9 м².

Якщо сторону квадрата виміряли в сантиметрах, то площу дістаємо в квадратних сантиметрах; якщо сторону квадрата виміряли в дециметрах, то й площу дістаємо в квадратних дециметрах; якщо вимірювання в метрах, то площа — в квадратних метрах і т.п.

 

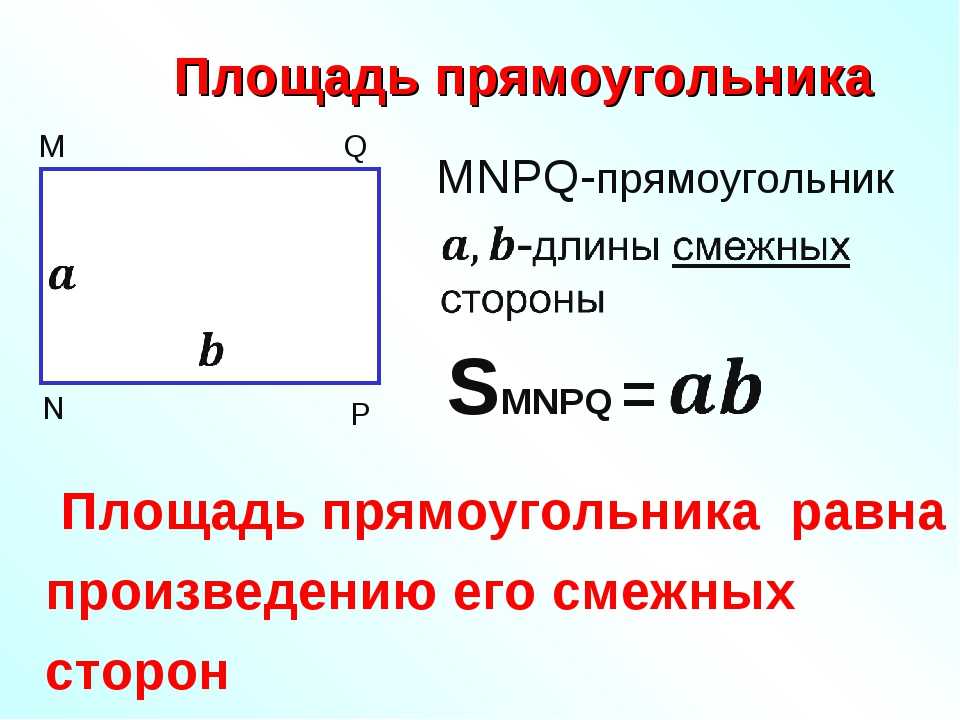
Площа прямокутника.

Щоб знайти площу прямокутника, треба його довжину помножити на ширину.

Формула площі прямокутника S = а • Ь, де а — довжина прямокутника, Ь — ширина прямокутника, S — площа прямокутника.

Щоб знайти довжину невідомої сторони прямокутника, треба його площу поділити на довжину відомої сторони.

 

Задача на знаходження площі прямокутника. 

Довжина прямокутника дорівнює 3 м, а ширина — 2 м. Знайди його площу.

Розв’язання.

S = З м • 2 м = 6 м² — площа прямокутника довжиною 3 м і шириною 2 м.

Відповідь: площа прямокутника 6 м².

Обернена задача на знаходження довжини прямокутника.

Площа прямокутника 6 м². Знайти довжину прямокутника, якщо його ширина дорівнює 2 м.

Розв’язання.

6 : 2 = 3 (м) 

Відповідь: довжина прямокутника дорівнює 3 м.

Обернена задача на знаходження ширини прямокутника.

Площа прямокутника 6 м². Знайти ширину прямокутника, якщо його довжина  дорівнює 3 м.

Розв’язання.

6 : 3 = 2 (м) 

Відповідь: ширина прямокутника дорівнює 2 м.

Якщо довжину і ширину прямокутника виміряли в сантиметрах, то площу дістаємо в квадратних сантиметрах; якщо довжину і ширину виміряли в дециметрах, то й площу дістаємо в квадратних дециметрах; якщо вимірювання в метрах, то площа — в квадратних метрах і т.

п.

 

Площа фігури (знаходження за допомогою палетки).

Для фігур, які не є прямокутниками, площу можна визначити за допомогою палетки. 

Палетка — прозора плівка, розділена на однакові квадрати: це можуть бути квадратні міліметри, квадратні сантиметри, квадратні дециметри.

На фігуру накладають плівку, розділену на квадратні сантиметри. 

Спочатку підраховують, скільки цілих квадратних сантиметрів (квадратів) містить фігура.  

Потім лічать кількість неповних квадратів, причому домовились два неповні квадрати рахувати за один. 

Площа фігури, визначена за допомогою палетки, є орієнтовною (неточною).

 

Приклад. Накладемо палетку з одиничними квадратами площею 1 см². Нехай фігура має 5 повних одиничних квадратів і 8 — неповних одиничних квадратів. Знайти площу фігури.

Розв’язання.

S = 5 + 8 : 2 = 9 (см²) — приблизна площа фігури.

Відповідь: приблизна площа фігури 9 см²

 

Порівняння площі фігур.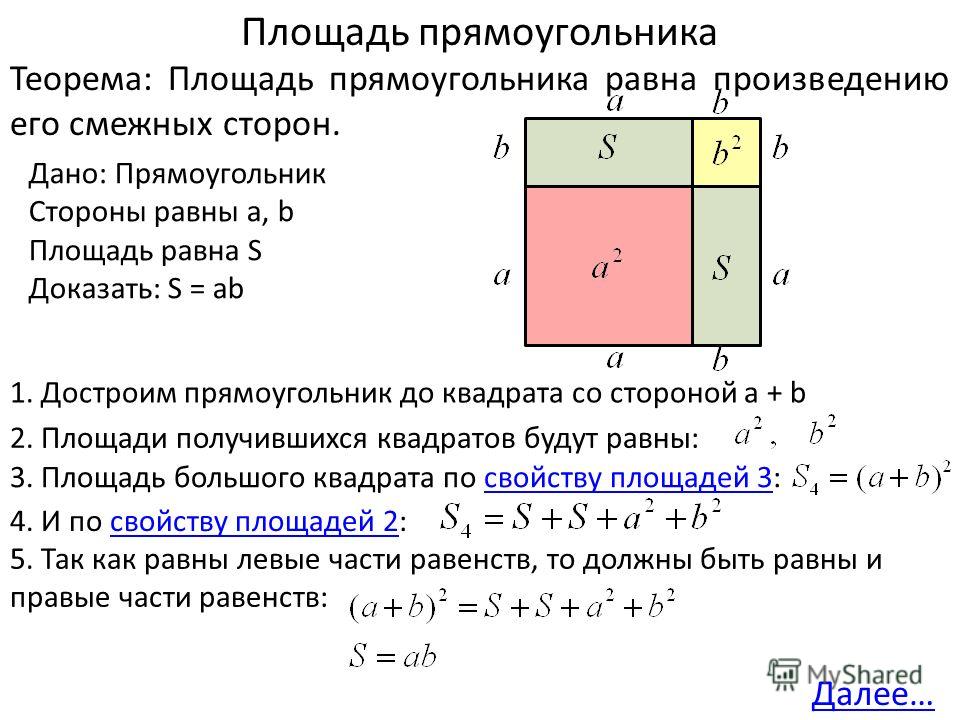

Щоб порівняти фігури за величиною, ділять кожну з них на однакові квадрати. Порівнюють кількість квадратів за методом палетки, причому фігура з більшою кількістю квадратів буде більшою. 

Інші завдання дивись тут…

 

Як ми знаходимо площа. Як знайти площу прямокутника

Прямокутник — це окремий випадок чотирикутника. Це означає, що у прямокутника чотири сторони. Його супротивники рівні: так наприклад, якщо одна з його сторін дорівнює 10 см, то протилежна їй буде так само рівні 10 см. Окремим випадком прямокутника є квадрат. Квадрат — це прямокутник, у якого всі сторони рівні. Для обчислення площі квадрата можна користуватися тим же алгоритмом, що і для обчислення площі прямокутника.

  Як дізнатися площа прямокутника по двом сторонам

Для того щоб знайти площу прямокутника, треба помножити його довжину на ширину: Площа \u003d Довжина × Ширина. У випадку, зазначеному нижче: Площа \u003d AB × BC.

  Як дізнатися площа прямокутника по боці і довжині діагоналі

У деяких завданнях необхідно знайти площу прямокутника, використовуючи довжину діагоналі і одну зі сторін. 2 × sin (гострого кута між діагоналями) / 2.

Одна з перших формул, яка вивчається в математиці, пов’язана з тим, прямокутника. Вона ж є і самої часто респонденти користуються послугами. Прямокутні поверхні оточують нас всюди, тому часто потрібно знати їх площі. Хоча б для того, щоб дізнатися, чи вистачить наявної фарби для фарбування підлог.

Які одиниці вимірювання площі існують?

Якщо говорити про ту, яка прийнята за міжнародну, то це буде квадратний метр. Його зручно використовувати при розрахунку площ стін, стелі або підлоги. У них вказується площа житла.

Коли мова йде про менших предметах, то вводять квадратні дециметр, сантиметри або міліметри. Останні потрібні, якщо фігура не більше нігтя.

При вимірюванні площі міста або країни найбільш підходящими виявляються квадратні кілометри. Але є ще і одиниці, які використовують для того, щоб вказати розмір площі: ар і гектар. Перша з них ще називається сотнею.

Як бути, якщо задані боку прямокутника?

Подібним чином розраховується який є окремим випадком прямокутника. Так як у нього всі сторони рівні, то твір стає квадратом літери а.

Як бути, якщо фігура зображена на картатій папері?

У цій ситуації потрібно покладатися на кількість клітинок усередині фігури. За їх кількістю буває просто порахувати площу прямокутника. Але це можна зробити тоді, коли сторони прямокутника збігаються з лініями клітин.

Часто має місце такий стан прямокутника, при якому його боку нахилені по відношенню до разлиновке паперу. Тоді кількість клітин визначити складно, тому розрахунок площі прямокутника ускладнюється.

Буде потрібно спочатку дізнатися площа прямокутника, який можна прокреслити по клітинках точно навколо даного. Це просто: перемножити висоту і ширину. Потім відняти від отриманого значення площі всіх А їх чотири. До слова, їх розраховують як половину твору катетів.

Підсумковий результат дасть значення площі даного прямокутника.

Як вчинити, якщо сторони невідомі, зате дані його діагональ і кут між діагоналями?

До того в цій ситуації потрібно обчислити його боку, щоб скористатися вже знайомої формулою. Спочатку потрібно згадати властивість його діагоналей. Вони рівні і діляться точкою перетину навпіл. Можна побачити на кресленні, що діагоналі ділять прямокутник на чотири рівнобедрених трикутника, які попарно рівні один одному.

Рівні сторони цих трикутників визначаються як половини діагоналі, яка відома. Тобто в кожному трикутнику є дві сторони і кут між ними, які дані в завданні. можна скористатися

Одна сторона прямокутника буде обчислена за формулою, в якій фігурують рівні сторони трикутника і косинус заданого кута. Для обчислення другий значення косинуса доведеться брати від кута, рівного різниці 180 і відомого кута.

Що робити, якщо в задачі дано периметр?

Зазвичай в умови вказується ще й співвідношення довжини і ширини. Питання про те, як порахувати площу прямокутника, в цьому випадку простіше на конкретному прикладі.

Припустимо, що в завданні периметр деякого прямокутника дорівнює 40 см. Відомо також, що його довжина в півтора рази більше ширини.

Необхідно дізнатися його площу.

Рішення завдання починається з запису формули периметра. Його зручніше розписати як суму довжини і ширини, кожну з яких помножити на два окремо. Це буде першим рівнянням в системі, яку потрібно вирішити.

Друге пов’язане з відомим за умовою співвідношенням сторін. Перша сторона, тобто довжина, дорівнює добутку другий (ширини) і числа 1,5. Це рівність потрібно підставити в формулу для периметра.

Вийде, що він дорівнює сумі двох одночленним. Перший — твір 2 і невідомої ширини, другий — твір чисел 2 і 1,5 і тієї ж ширини. У цьому рівнянні всього одна невідома — це ширина. Потрібно її порахувати, а потім скористатися другим рівністю, щоб порахувати довжину. Залишиться тільки перемножити ці два числа, щоб дізнатися площа прямокутника.

Розрахунки дають такі величини: ширина — 8 см, довжина — 12 см, а площа — 96 см 2. Останнє число — відповідь розглянутої задачі.

З таким поняттям, як площа, нам доводиться стикатися в своєму житті повсякденно. Так, наприклад, при будівництві будинку її потрібно знати для того, щоб розрахувати кількість необхідного матеріалу. Розмір садової ділянки також буде характеризуватися площею. Навіть ремонт в квартирі неможливо зробити без цього визначення. Тому питання, як знайти площу прямокутника, на нашому встає дуже часто і є важливим не тільки для школярів.

Для тих, хто не знає, прямокутник — це плоска фігура, у якої протилежні сторони рівні, а кути складають 90о. Для позначення площі в математиці використовують англійську букву S. Її вимірюють у квадратних одиницях: метрах, сантиметрах і так далі.

Тепер спробуємо дати докладну відповідь на питання, як знайти площу прямокутника. Існує кілька способів визначення цієї величини. Найбільш часто ми стикаємося з способом визначення площі за допомогою ширини і довжини.

Візьмемо прямокутник із шириною b і довжиною k. Для обчислення площі даного прямокутника необхідно ширину помножити на довжину. Це все можна представити у вигляді формули, яка буде виглядати так: S \u003d b * k.

А тепер розглянемо цей спосіб на конкретному прикладі. Необхідно визначити площу садової ділянки з шириною 2 метри і довжиною 7 метрів.

S \u003d 2 * 7 \u003d 14 м2

В математиці, особливо в доводиться визначати площу іншими способами, так як у багатьох випадках ні довжина, ні ширина прямокутника нам не відома. Разом з тим мають місце інші відомі величини. Як знайти площу прямокутника в цьому випадку?

• Якщо нам відома довжина діагоналі і один з кутів, що становить діагональ з будь-якою стороною прямокутника, то в цьому випадку буде потрібно згадати про площі Адже якщо розібратися, то прямокутник складається з двох рівних прямокутних трикутників. Отже, повернемося до обумовленої величиною. Для початку необхідно визначити косинус кута. Отриману величину помножити на довжину діагоналі. В результаті отримаємо довжину однієї зі сторін прямокутника. Аналогічно, але вже за допомогою визначення синуса, можна визначити довжину другої сторони. А як знайти площу прямокутника тепер? Та дуже просто, перемножити отримані величини.

У вигляді формули це буде виглядати так:

S \u003d cos (a) * sin (a) * d2, де d- довжина діагоналі

• Ще один спосіб визначення площі прямокутника — через вписану в нього коло. Він застосовується в тому випадку, якщо прямокутник є квадратом. Для використання даного способу необхідно знати Як обчислити площу прямокутника таким способом? Звичайно ж, за формулою. Доводити ми її не будемо. А виглядає вона так: S \u003d 4 * r2, де r-радіус.

Трапляється так, що замість радіуса нам відомий діаметр вписаного кола. Тоді формула буде виглядати так:

S \u003d d2, де d — діаметр.

• Якщо відома одна зі сторін і периметр, то як дізнатися площа прямокутника в цьому випадку? Для цього необхідно провести ряд простих обчислень. Як ми знаємо, протилежні сторони прямокутника рівні, тому від значення периметра необхідно відняти відому довжину, помножену на два. Отриманий результат розділити на два і отримаємо довжину другої сторони. Ну, а далі стандартний прийом, перемножуємо обидві сторони і отримуємо площа прямокутника. У вигляді формули це буде виглядати так:

S \u003d b * (P — 2 * b), де b — довжина сторони, P — периметр.

Як бачимо площа прямокутника можна визначати різними способами. Все залежить від того, які величини нам відомі перед розглядом цього питання. Звичайно ж, останні методи обчислення в життя практично не зустрічаються, але можуть стати в нагоді для рішень багатьох завдань в школі. Можливо, і для вирішення ваших завдань ця стаття виявиться корисною.

Площа геометричної фігури — чисельна характеристика геометричної фігури показує розмір цієї фігури (частини поверхні, обмеженої замкнутим контуром даної фігури). Величина площі виражається числом полягають в неї квадратних одиниць.

Формули площі трикутника

1. Формула площі трикутника по стороні і висоті
   Площа трикутника   дорівнює половині твори довжини сторони трикутника на довжину проведеної до цієї сторони висоти
   
2. Формула площі трикутника за трьома сторонами і радіусу описаного кола
   
3. Формула площі трикутника за трьома сторонами і радіусу вписаного кола
   Площа трикутника   дорівнює добутку напівпериметр трикутника на радіус вписаного кола.
   
  де S — площа трикутника,
  — довжини сторін трикутника,
  — висота трикутника,
  — кут між сторонами і,
  — радіус вписаного кола,
  R — радіус описаного кола,

Формули площі квадрата

1. Формула площі квадрата по довжині боку
   Площа квадрата   дорівнює квадрату довжини його сторони.
2. Формула площі квадрата по довжині діагоналі
   Площа квадрата   дорівнює половині квадрата довжини його діагоналі.
   

   S \u003d	1	2
   	2

  де S — Площа квадрата,
  — довжина сторони квадрата,
  — довжина діагоналі квадрата.

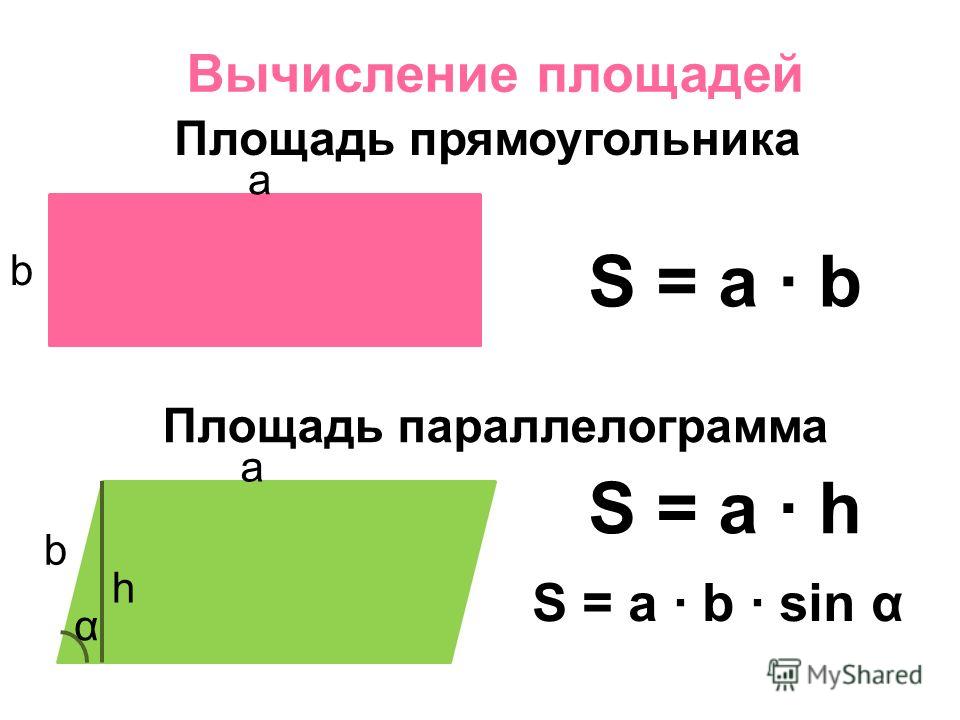
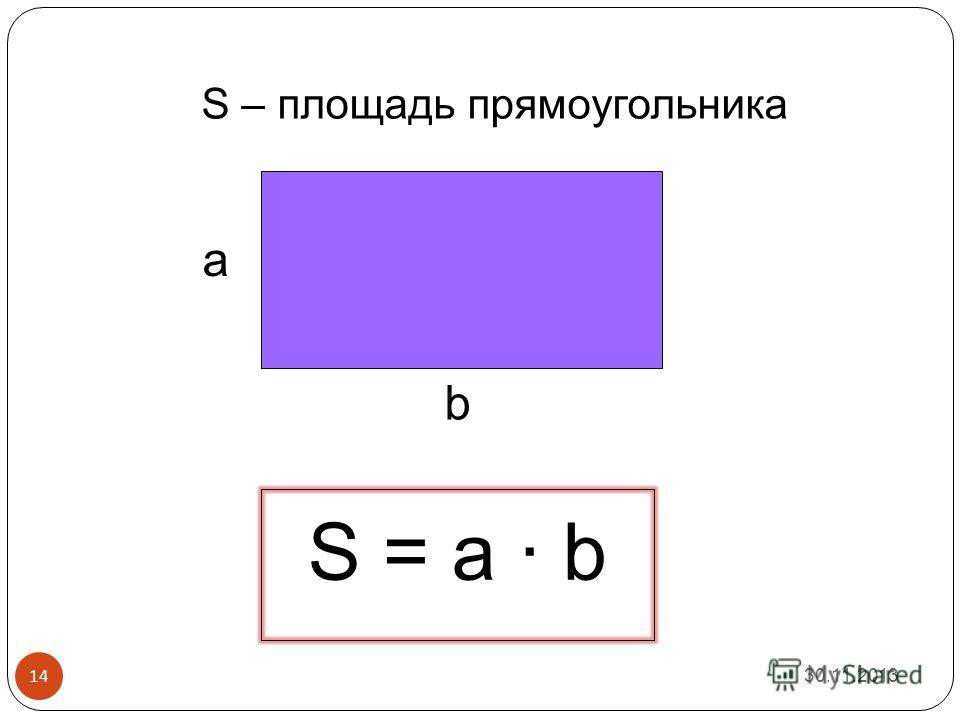
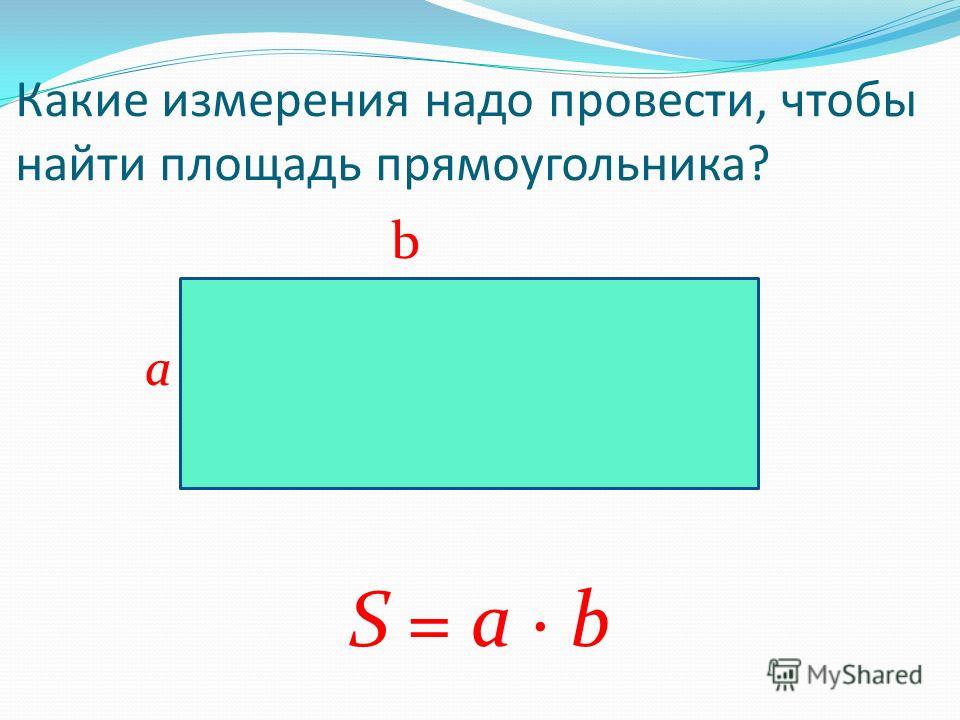
Формула площі прямокутника

Площа прямокутника   дорівнює добутку довжин двох його суміжних сторін

  де S — Площа прямокутника,
  — довжини сторін прямокутника.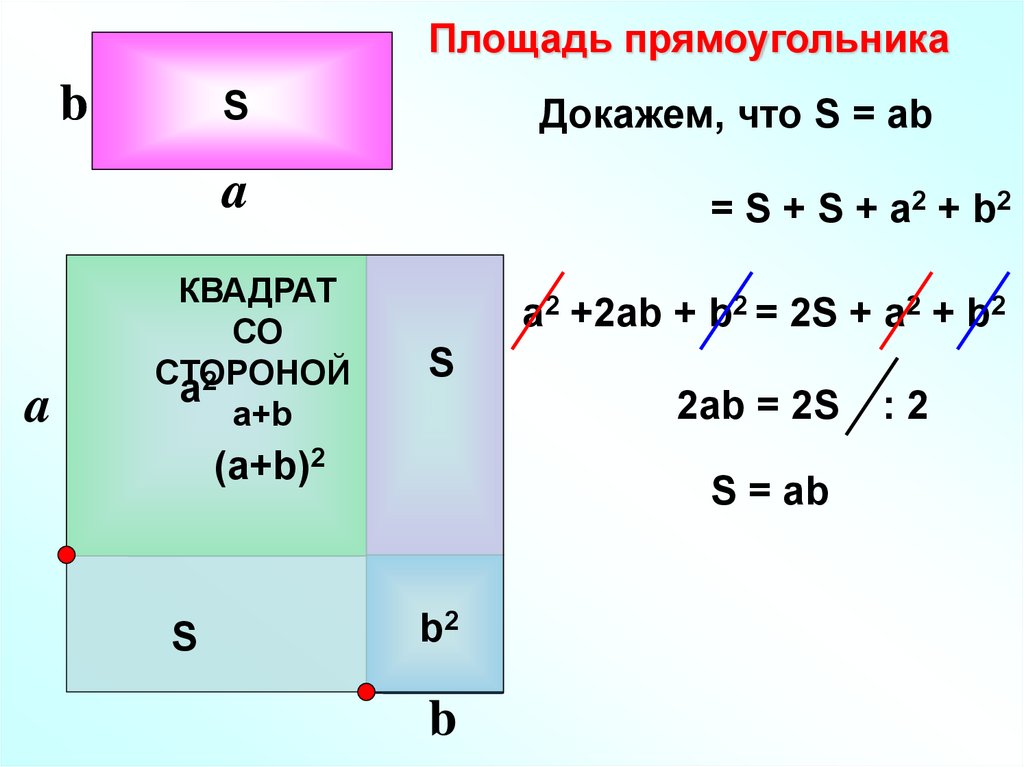

Формули площі паралелограма

1. Формула площі паралелограма по довжині боку і висоті
   Площа паралелограма
2. Формула площі паралелограма за двома сторонами і кутом між ними
   Площа паралелограма   дорівнює добутку довжин його сторін помноженому на синус кута між ними.

   a · b · sin α

  де S — Площа паралелограма,
  — довжини сторін паралелограма,
  — довжина висоти паралелограма,
  — кут між сторонами паралелограма.

Формули площі ромба

1. Формула площі ромба по довжині боку і висоті
   Площа ромба   дорівнює добутку довжини його сторони і довжини опущеною на цю сторону висоти.
2. Формула площі ромба по довжині боку і розі
   Площа ромба   дорівнює добутку квадрата довжини його сторони і синуса кута між сторонами ромба.
3. Формула площі ромба по довжинах його діагоналей
   Площа ромба   дорівнює половині добутку довжин його діагоналей.
  де S — Площа ромба,
  — довжина сторони ромба,
  — довжина висоти ромба,
  — кут між сторонами ромба,
  1, 2 — довжини діагоналей.

Формули площі трапеції

1. Формула Герона для трапеції

   Де S — Площа трапеції,
     — довжини основ трапеції,
     — довжини бічних сторін трапеції,
   

Інструкція

Наприклад, вам, що довжина однієї із сторін (а) дорівнює 7 см, а периметр прямокутника (P) дорівнює 20 см. Так як периметр   будь-якої фігури дорівнює сумі довжин її сторін, а у прямокутника   протилежні сторони рівні, то його периметра буде виглядати наступним чином: P \u003d 2 x (a + b), або P \u003d 2a + 2b. З цієї формули випливає, що знайти довжину другої сторони (b) можна за допомогою нескладної операції: b \u003d (P — 2a): 2. Так, в нашому випадку сторона b буде дорівнює (20 — 2 х 7): 2 \u003d 3 см .

Тепер, знаючи довжини обох суміжних сторін (a і b), ви зможете підставити їх в формулу площі S \u003d ab. В даному випадку прямокутника   дорівнюватиме 7х3 \u003d 21. Зверніть на те, що одиницями вимірювання будуть вже не, а сантиметри квадратні, так як довжин двох сторін одиниці їх вимірювання (сантиметри) ви теж множили один на одного.

джерела:

• як знаходиться периметр прямокутника

Плоска фігура, що складається з чотирьох сторін і чотирьох прямих кутів. З усіх фігур площа прямокутника   доводиться обчислювати частіше за інших. це і площа   квартири, і площа   садової ділянки, і площа   поверхні столу або полиці. Наприклад, щоб просто обклеїти кімнату шпалерами, обчислюють площа   її прямокутних стін.

Інструкція

До речі, з прямокутника   можна легко обчислити площа   . Досить добудувати прямокутний до прямокутника   так, щоб гіпотенуза стала діагоналлю прямокутника. Тоді буде зрозуміло, що площа   такого прямокутника   дорівнює добутку катетів трикутника, а площа   самого трикутника, відповідно, дорівнює половині твори катетів.

Відео по темі

Окремий випадок паралелограма — прямокутник — відомий тільки в геометрії Евкліда. У прямокутника   рівні всі кути, і кожен з них окремо становить 90 градусів. Виходячи з приватних властивостей прямокутника, А також з властивостей паралелограма про паралельність протилежних сторін можна знайти боку   фігури за заданими діагоналях і куті від їх перетину. обчислення сторін прямокутника   грунтується на додаткових побудовах і застосуванні властивостей одержуваних фігур.

Інструкція

Буквою А відзначте точку перетину діагоналей. Розгляньте утворений побудовами EFА. Відповідно до властивості прямокутника   його діагоналі рівні і навпіл точкою перетину А. Обчисліть значення FА і EА. Так як трикутник EFА рівнобедреним і його боку   EА і FА рівні між собою і відповідно рівні половині діагоналі EG.

Далі обчисліть першу EF прямокутника. Дана сторона є третьою невідомою стороною розглянутого трикутника EFА. Згідно з теоремою косинусів за відповідною формулою знайдіть сторону EF. Для цього підставте в формулу косинусів отримані раніше значення сторін FА EА і косинус відомого кута між ними α. Обчисліть і запишіть отримане значення EF.

Знайдіть другу сторону прямокутника FG. Для цього розгляньте інший трикутник EFG. Він є прямокутним, де відомі гіпотенуза EG і катет EF. Згідно з теоремою Піфагора знайдіть другий катет FG за відповідною формулою.

Відноситься до найпростіших плоским геометричним фігурам і є одним з окремих випадків паралелограма. Відмітна риса такого паралелограма — прямі кути у всіх чотирьох вершинах. обмежену сторонами прямокутника площа   можна обчислити декількома способами, використовуючи розміри його сторін, діагоналі і кути між ними, радіус вписаного кола і т.д.

Інструкція

Якщо відома величина кута (α), який становить діагональ прямокутника   з однією з його сторін, а також довжина (С) цієї діагоналі, то для обчислення площі можна задіяти визначення тригонометричних в прямокутному. Прямокутний трикутник тут утворюють дві сторони чотирикутника і його діагональ. З визначення косинуса випливає, що довжина однієї із сторін буде дорівнює добутку довжини діагоналі на кута, величина відома. З визначення синуса можна вивести формулу довжини іншого боку — вона дорівнює добутку довжини діагоналі на синус все того ж кута. Підставте ці тотожності в формулу з попереднього кроку, і вийде, що для знаходження площі треба перемножити синус і косинус відомого кута, а також довжини діагоналі прямокутника: S \u003d sin (α) * cos (α) * ².

Якщо крім довжини діагоналі (С) прямокутника   відома величина кута (β), який утворюють діагоналі, то для обчислення площі фігури можна теж задіяти одну з тригонометричних функцій — синус. Зведіть в квадрат довжину діагоналі і помножте отриманий результат на половину синуса відомого кута: S \u003d с? * Sin (β) / 2.

Якщо відомий (r) вписаною в прямокутник кола, то для обчислення площі зведіть цю величину до другого степеня і збільште результат в чотири рази: S \u003d 4 * r². Чотирикутник, у який можна, буде квадратом, а довжина його боку дорівнює діаметру вписаного кола, тобто подвоєному радіусу. Формула отримана підстановкою довжин сторін, виражених через радіус в тотожність з першого кроку.

Якщо відомі довжини (P) і однієї зі сторін (A) прямокутника, То для знаходження площі всередині цього периметру обчисліть половину твору довжини сторони на різницю між довжиною периметра і двома довжинами цього боку: S \u003d A * (P-2 * A) / 2.

Відео по темі

Із завданням знайти периметр або площа багатокутника стикаються не тільки учні на уроках геометрії. Часом її трапляється вирішувати і дорослій людині. Чи доводилося вам розраховувати необхідну кількість шпалер для кімнати? Або, може бути, ви вимірювали довжину дачної ділянки, щоб обгородити його парканом? Так знання основ геометрії іноді незамінні для здійснення важливих проектів.

Формули площі плоских фігур – Відпочинок та цікаві факти

В цій статті ми вирішили допомогти українським школярам та студентам з геометрією: ми розглянули формули площі плоских фігур.

Отже, тут ви знайдете формулу площі прямокутника, формулу площі квадрата, формула площі трапеції, формулу площі паралелограма, формулу площі правильного багатокутника, формулу площі ромба, формулу площі сектора кола та окружності, формулу площі круга, формулу площі сегмента кола, окружності. Також тут описана формула площі кільця через радіуси, формула площі кільця через діаметри, формула площі сектора кільця.

Першою в нашому списку буде розглянута формула площі прямокутника. Спочатку коротка теорія, а далі формула і пояснення до неї.

Площа прямокутника, формула

Прямокутником називається чотирикутник, у якого всі кути рівні. Всі кути в прямокутнику прямі, тобто складають 90°. Площа прямокутника дорівнює добутку його сторін (a, b):

S = a*b

 де (a, b – сторони прямокутника)

 Формула площі квадрата

Квадратом називається паралелограм з прямими кутами і рівними сторонами.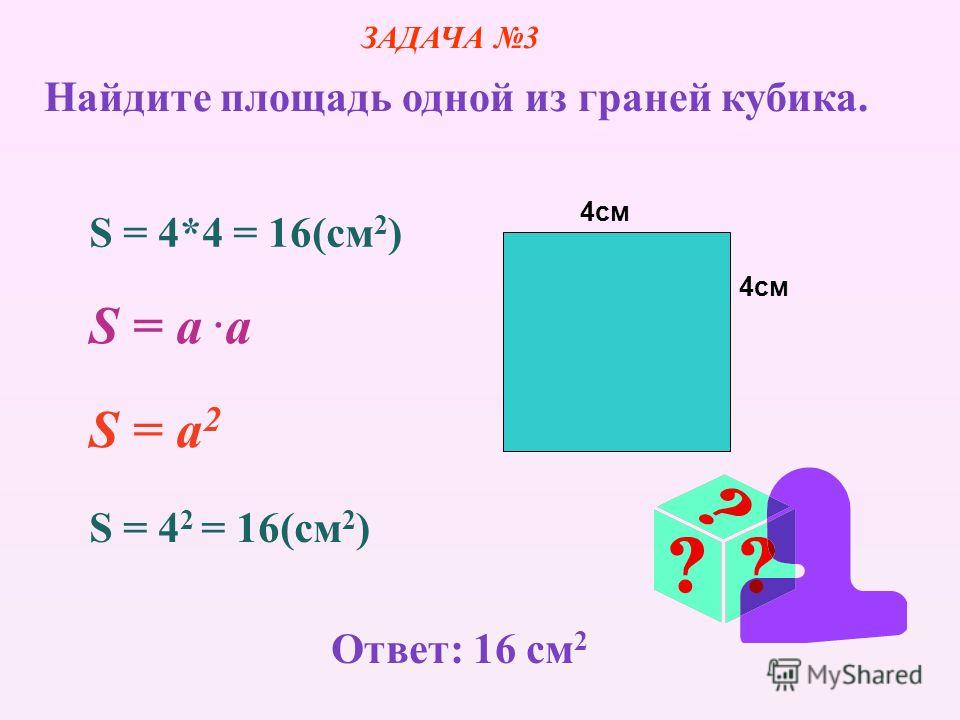 Квадрат є окремим випадком прямокутника, а також окремим випадком ромба. Площа квадрата дорівнює квадрату довжини його сторони, або половині квадрата діагоналі.

S = H 2

де H – довжина сторони квадрата

(d – діагональ квадрата)

Формула площі трапеції

Трапецією називається чотирикутник, у якого дві сторони паралельні, а дві інші не паралельні. Площа трапеції дорівнює добутку півсуми її основ (a, b) на висоту (h):

(a, b – основи трапеції; h – висота трапеції)

Формула площі паралелограмма

Параллелограммом називається чотирикутник, у якого протилежні сторони попарно паралельні. Площа паралелограма дорівнює добутку його заснування (a) на висоту (h). Площа паралелограма, формула:

S = a*h

(a – основа паралелограма; h – висота паралелограма)

Площа правильного багатокутника, формула

Для того щоб обчислити площу правильного багатокутника, його розбивають на рівні трикутники із загальною вершиною в центрі вписаного кола. А площа правильного багатокутника дорівнює добутку його півпериметру на радіус вписаного кола правильного багатокутника. Площа правильного багатокутника обчислюється за формулою:

де n – кількість сторін правильного багатокутника
p – півпериметр правильного багатокутника
a – сторона правильного багатокутника
r – радіус вписаного кола правильного багатокутника

Також є ще така формула:

Площа ромба, формула

Ромбом називається паралелограм з рівними сторонами. Квадрат є окремим випадком ромба. У квадрата діагоналі рівні. Площа ромба дорівнює половині добутку його діагоналей. Площа ромба знаходиться за формулою:

де (d _1,2 – довжини діагоналей ромба)

Площа сектора кола, формула

Сектор кола – це частина кола, обмежена дугою і двома радіусами, проведеними до кінців дуги. Площа сектора кола визначається за формулами:

• Площа сектора кола через довжину дуги сектора

Площа сектора кола дорівнює добутку половини довжини дуги сектора p на радіус кола:

• Площа сектора кола через кут сектора в градусах

Площа сектора кола з дугою n ° дорівнює добутку площі окружності з радіусом r на відношення кута сектора n ° до кута повної окружності, тобто 360 °:

• Площа сектора кола через кут сектора в радіанах

Площа сектора кола з дугою α радіан дорівнює добутку квадрата радіуса на половину кута:

Площа круга, формула

Коло – це геометричне місце точок площини, рівновіддалених від однієї точки – центра. Рівні відрізки, що з’єднують центр з точками кола, називаються радіусами. Коло є частиною площини, що лежить всередині кола. Площа круга дорівнює добутку півкола на радіус:

(r – радіус кола круга)

Площа сегмента круга, кола – формула

Сегмент кола, окружності – це частина круга, кола, обмежена дугою і хордою, що її стягує.

Площа сегмента круга, кола знаходиться, як різниця площі сектора AOB і площі рівнобедреного трикутника AOB, вираженої через кут:

• Площа сегмента круга, кола, якщо кут в градусах

• Площа сегмента круга, кола, якщо кут в радіанах

Площа кільця, формула

Площа кільця через радіуси знаходиться як добуток числа π на різницю квадратів зовнішнього і внутрішнього радіусів кільця.

• Площа кільця через діаметри, формула

Площа кільця через діаметри знаходиться як добуток однієї четвертої числа π на різницю квадратів зовнішнього і внутрішнього діаметрів кільця:

Площа сектора кільця, формула

Сектор кільця – це частина кола, обмежена дугами різних радіусів і двома лініями радіусами, проведеними до кінців дуги більшого радіусу.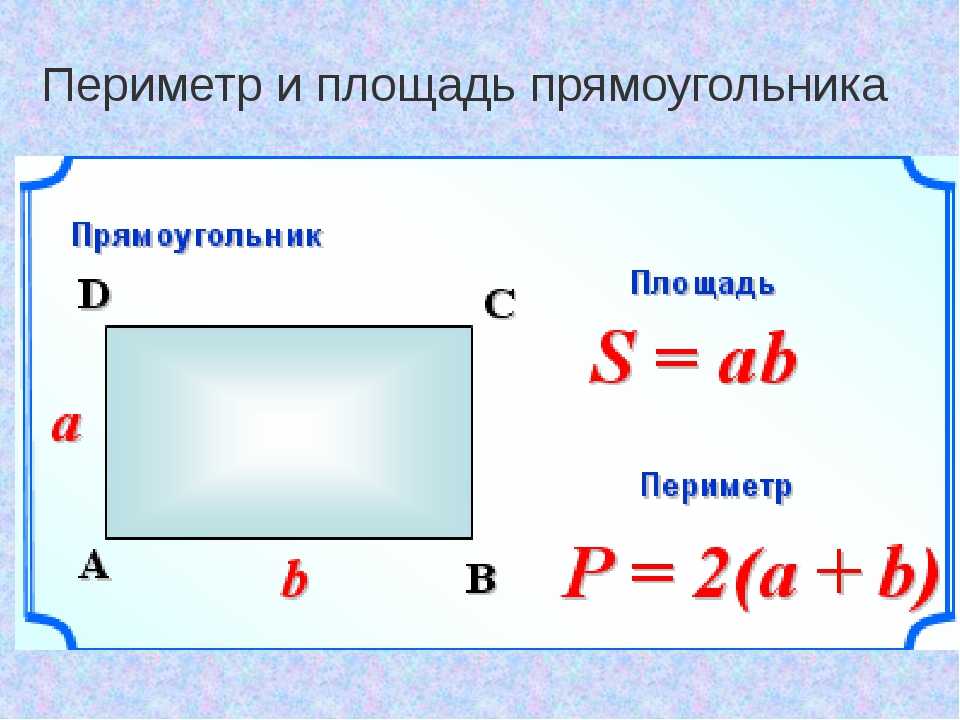

Площа сектора кільця обчислюється як різниця площ більшого і меншого секторів кола.

• Площа сектора кільця якщо кут в градусах

Площа сектора кільця, якщо кут в градусах, обчислюється як добуток числа π на відношення кута сектора до кута повної окружності 360 ° і на різницю квадратів більшого і меншого радіусів. Формула:

• Площа сектора кільця якщо кут в радіанах

Площа сектора кільця якщо кут в радіанах, обчислюється як добуток половини кута сектора на різницю квадратів більшого і меншого радіусів. Формула:

 Ось і всі формули визначення площі плоских фігур. Слідкуйте за оновленнями на нашому сайті.

Площадь прямоугольника — определение, формула, примеры

Количество единичных квадратов, которые могут вписаться в любую форму, является ее площадью. Термин «единица» относится к одному ( 1) , поэтому единичный квадрат — это квадрат, имеющий одну (1) единицу стороны.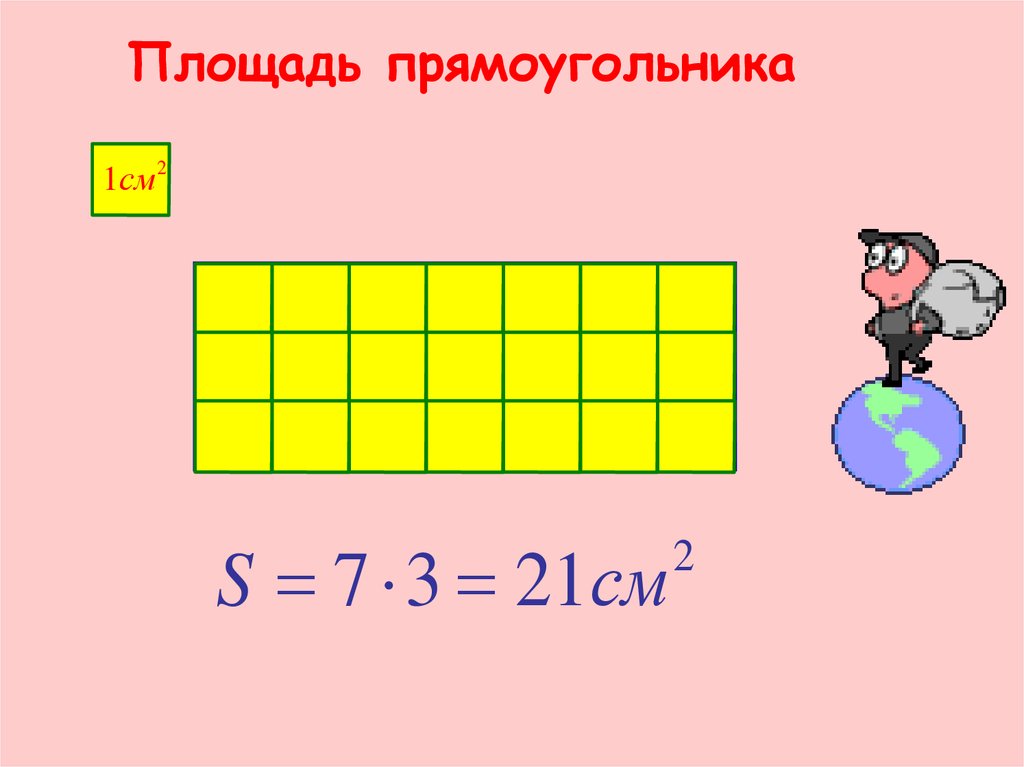 В результате площадь прямоугольника равна количеству единичных квадратов внутри края прямоугольника. Площадь прямоугольника, с другой стороны, это пространство, занимаемое внутри периметра прямоугольника. Плитка единичной длины в вашем доме — фантастическая иллюстрация прямоугольной формы. Подсчитав количество плитки на полу, можно быстро определить, сколько площади она занимает. Это также поможет вам определить площадь прямоугольного пола. Вы также можете прочитать Определение, формулы, вопросы и ответы скорости, времени и расстояния!

 

Содержание-
1.

Бесплатные демонстрационные занятия

Зарегистрируйтесь здесь, чтобы получить бесплатные демонстрационные занятия

Выберите курсExcel (10 часов)Цифровой маркетингГрафический дизайнПрограмма предпринимательстваОбработка данныхОблачные вычисленияCUET 2023UPSSSC PETОборонаSSCUP PoliceSchoolSchool Skill Courses Interview SBI CLERKCTETIBPS PO

Пожалуйста, введите имя

Пожалуйста, введите только 10-значный номер мобильного телефона

Пожалуйста, выберите курс

Пожалуйста, заполните адрес электронной почты

Какова площадь прямоугольника?
2. Формула площади прямоугольника
3. Как вычислить площадь прямоугольника?
4. Площадь прямоугольника по диагонали
5. Важные факты
6. Почему площадь прямоугольника равна длине в ширину?

Определение:  Площадь прямоугольника – это площадь, занимаемая прямоугольником внутри его границ.

Площадь плоской поверхности определенной формы может быть описана как количество пространства, которое она покрывает. Он рассчитывается как «количество» квадратных единиц (квадратных сантиметров, квадратных дюймов, квадратных футов и т. д.). Количество единичных квадратов, которые могут поместиться в прямоугольник, называется его площадью. Примерами могут служить плоские поверхности дисплеев ноутбуков, классных досок, холстов для рисования и других прямоугольных форм. Формула площади прямоугольника может быть использована для расчета площади, занимаемой этими предметами. Рассмотрим прямоугольник длиной 4 дюйма и шириной 3 дюйма.

Площадь прямоугольника = длина x ширина   А = фунт

 

Формула для нахождения площади прямоугольника зависит от его длины и ширины. Площадь прямоугольника рассчитывается в единицах путем умножения ширины (или ширины) на длину прямоугольника. Площади боковой и полной поверхности можно вычислить только для трехмерных фигур. Мы не можем вычислить прямоугольник, так как это двумерная фигура. Таким образом, периметр и площадь прямоугольника равны:

Формула площади прямоугольника
Площадь прямоугольника	А = l × b

 

Площадь любого прямоугольника вычисляется, если известны его длина и ширина. Перемножив длину и ширину, площадь прямоугольника будет равна квадратной единице измерения. В случае квадрата площадь станет стороной квадрата. Основное различие между квадратом и прямоугольником заключается в том, что длина и ширина квадрата равны.

Связанные ссылки-

• Объем сферы
• Конвертер см в дюймы (см в дюймы)
• Преобразование римских цифр

 

Выполните следующие шаги, чтобы найти площадь:

Шаг 1 : Обратите внимание на размеры длины и ширины из заданных данных

Шаг 2 : Умножьте значения длины и ширины

Шаг 3:  Запишите ответ в квадратных единицах
 

Мы знаем, что диагональ прямоугольника рассчитывается по формуле:

(Диагональ)2 = (Длина)2 + (Ширина)2

Отсюда

(Длина)2 = (Диагональ)2 – (Ширина)2

Длина = √Диагональ2–Ширина3Диагональ2–Ширина3

Или

(Ширина)2 = (Диагональ)2 – (Длина)2

Ширина = Диагональ2 –Length3Diagonal2–Length3

Теперь площадь прямоугольника = Длина × Ширина

Area = Length × √Diagonal2–Length3Diagonal2–Length3

Or

Area = √Diagonal2–Width3Diagonal2–Width3 × Width

You may also read-

• Perimeter of a rectangle
• Площадь квадрата

 

Важные факты

Ниже приведены некоторые специальные формулы, относящиеся к площади прямоугольника:

1. Как найти площадь диагонали прямоугольника и ширины

Формула: область = ширина √ (диагональ2 — ширина3) Ширина (диагональ2 — ширина3)

2. Найдите недостающую сторону длины. Диагонали прямоугольника делят его на два равновеликих прямоугольных треугольника. Следовательно, площадь прямоугольника будет равна сумме площадей этих двух треугольников.

 

Пусть теперь диагональ AC делит прямоугольник на два прямоугольных треугольника, т.е. ∆ABC и ∆ADC.

Мы знаем, что треугольники ∆ABC и ∆ADC равны.

Площадь ∆ABC = ½ x основание x высота =  ½ x AB x BC =  ½ x b x l

Площадь ∆ADC = ½ x основание x высота = ½ x CD x AD =  ½ x b x l

Площадь прямоугольника ABCD = площадь ∆ABC + площадь ∆ADC

Площадь (ABCD) = 2(½ x b x l)

Площадь (ABCD) = l x b 

Таким образом, площадь прямоугольника = длина x ширина

Вы также можете прочитать-

Подробнее

Источник: Safalta.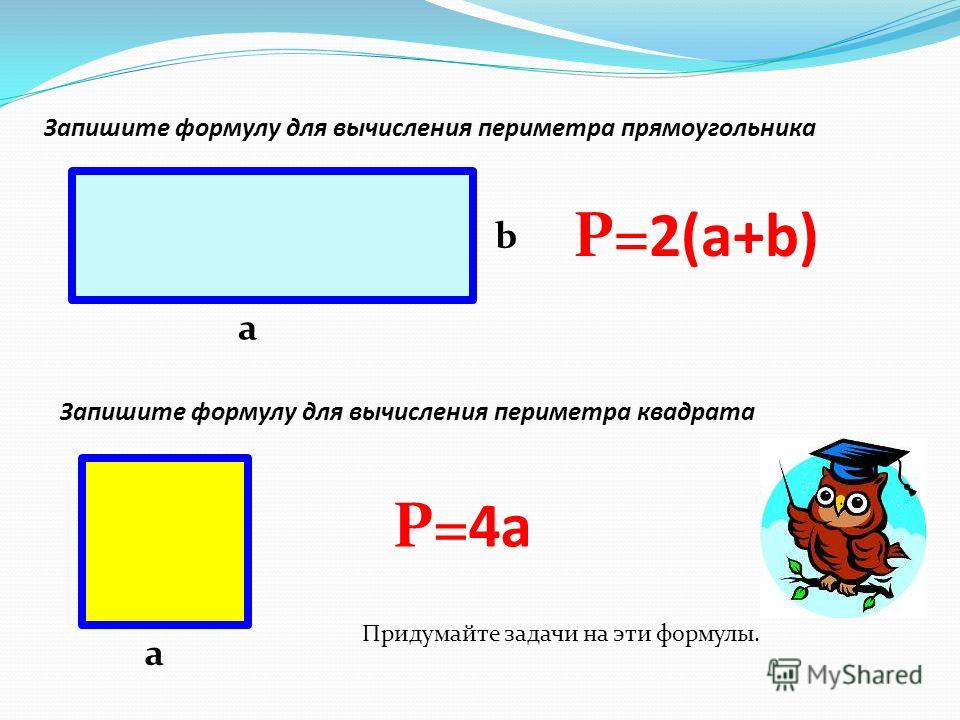 com

Источник: Safalta.com

Площадь a прямоугольника — это область, покрываемая прямоугольником в двумерной плоскости в геометрии. Прямоугольник — это тип четырехугольника, двумерная фигура, имеющая четыре стороны и четыре вершины. Все четыре угла прямоугольника прямые или равны 90 градусам. Противоположные стороны прямоугольника равны и параллельны друг другу. Следует отметить, что противоположные стороны параллелограмма также равны и параллельны друг другу, но углы не равны 90 градусов.  Присоединяйтесь к онлайн-школе Safalta и готовьтесь к экзаменам на доску под руководством наших опытных преподавателей. Наша онлайн-школа призвана помочь учащимся подготовиться к экзаменам на совет директоров, обеспечив учащимся концептуальную ясность по всем предметам и возможность набрать максимальные баллы на экзаменах. Вы также можете прочитать Определение, формулы, вопросы и ответы о скорости, времени и расстоянии!

Содержание-
1. Какова площадь прямоугольника?
2. Площадь прямоугольника формула
3. Как вычислить площадь прямоугольника?
4. Площадь прямоугольника по диагонали
5. Важные факты
6. Почему площадь прямоугольника равна длине в ширину?

 

Определение:  Площадь прямоугольника — это область, занимаемая прямоугольником в пределах его четырех сторон или границ.

Площадь прямоугольника зависит от его сторон. По сути, формула площади равна произведению длины и ширины прямоугольника. С другой стороны, периметр прямоугольника равен сумме его четырех сторон. В результате область, содержащаяся в периметре прямоугольника, равна его площади. Однако в случае квадрата, поскольку все стороны равны, площадь квадрата будет равна квадрату длины стороны.

Площадь прямоугольника = длина x ширина   А = фунт

 

Формула для нахождения площади прямоугольника зависит от его длины и ширины.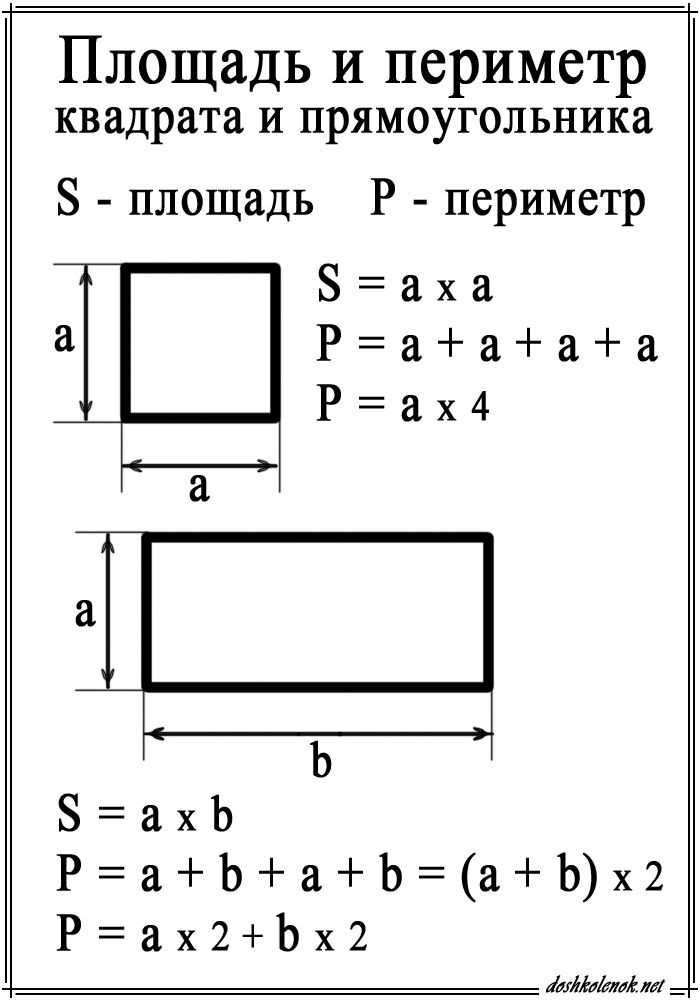 Площадь прямоугольника рассчитывается в единицах путем умножения ширины (или ширины) на длину прямоугольника. Площади боковой и полной поверхности можно вычислить только для трехмерных фигур. Мы не можем вычислить прямоугольник, так как это двумерная фигура. Таким образом, периметр и площадь прямоугольника равны:

Формула площади прямоугольника
Площадь прямоугольника	А = l × b

 

Площадь любого прямоугольника вычисляется, если известны его длина и ширина. Перемножив длину и ширину, площадь прямоугольника будет равна квадратной единице измерения. В случае квадрата площадь станет стороной квадрата. Основное различие между квадратом и прямоугольником заключается в том, что длина и ширина квадрата равны.

Связанные ссылки-

• Объем сферы
• Конвертер см в дюймы (см в дюймы)
• Преобразование римских цифр

 

Выполните следующие шаги, чтобы найти площадь:

Шаг 1 : Обратите внимание на размеры длины и ширины из заданных данных

Шаг 2 : Умножьте значения длины и ширины

Шаг 3:  Запишите ответ в квадратных единицах

 

Мы знаем, что диагональ прямоугольника рассчитывается по формуле:

(Диагональ)2 = (Длина)2 + (Ширина)2

Отсюда

(Длина)2 = (Диагональ)2 – (Ширина)2

Длина = √Диагональ2–Ширина3Диагональ2–Ширина3

Или

(Ширина)2 = (Диагональ)2 – (Длина)2

3 900 Diagonal2–Length3Diagonal2–Length3

Теперь площадь прямоугольника = длина × ширина

Area = Length × √Diagonal2–Length3Diagonal2–Length3

Or

Area = √Diagonal2–Width3Diagonal2–Width3 × Width

You may also read-

• Perimeter of a rectangle
• Площадь квадрата

 

Важные факты

Ниже приведены некоторые специальные формулы, относящиеся к площади прямоугольника:

1. Как найти площадь с диагональю прямоугольника и шириной

Формула: область = ширина √ (диагональ2 — ширина3) Ширина (диагональ2 — ширина3)

2. Найдите недостающую сторону длины. Диагонали прямоугольника делят его на два равновеликих прямоугольных треугольника. Следовательно, площадь прямоугольника будет равна сумме площадей этих двух треугольников.

 

Теперь пусть диагональ AC делит прямоугольник на два прямоугольных треугольника, то есть ∆ABC и ∆ADC.

Мы знаем, что треугольники ∆ABC и ∆ADC равны.

Площадь ∆ABC = ½ x основание x высота =  ½ x AB x BC =  ½ x b x l

Площадь ∆ADC = ½ x основание x высота = ½ x CD x AD =  ½ x b x l

Площадь прямоугольника ABCD = площадь ∆ABC + площадь ∆ADC

Площадь (ABCD) = 2(½ x b x l)

Площадь (ABCD) = l x b

Таким образом, площадь прямоугольника = длина x ширина

 

4   5 9 0 : Найдите площадь прямоугольника, длина которого 15 см, а ширина 4   см.

Решение:

, дано,

Длина = 15 см

Ширина = 4 см

Площадь прямоугольника = длина × ширина

15 × 4 = 6013

SO

 

Пример 2. Найдите площадь прямоугольной доски, длина и ширина которой равны 120 см и 100 см соответственно.

Решение:

Длина доски = 120 см = 1,2 м

Ширина доски = 100 см = 1 м

Площадь доски = площадь прямоугольника = длина x ширина = 1,2 м x 1 м = 1,2 квадратных метра

Формула площади прямоугольника:
Площадь = Длина x Ширина

Периметр прямоугольника – это сумма всех его четырех сторон. Следовательно,
Периметр (прямоугольник) = 2 (Длина + Ширина)

Площадь прямоугольника – это область, занимаемая сторонами прямоугольника.

Площадь прямоугольника равна LB, потому что здесь мы вычисляем квадратные единицы прямоугольника. После умножения общего количества квадратов на длину и общего количества квадратов на ширину прямоугольника мы получим общее количество квадратов в прямоугольнике. 92.

блог площадь прямоугольника формула площади прямоугольника площадь прямоугольника примеры

Площадь прямоугольника — определение, формула, примеры решений

Математические формулы

Площадь любой фигуры – это количество единичных квадратов, которые помещаются внутри нее. Здесь «единица» означает единицу, а единичный квадрат — это квадрат со стороной в 1 единицу. В качестве альтернативы пространство, занимаемое периметром этой фигуры, называется площадью прямоугольника. Отличным примером прямоугольной формы являются плитки единичной длины в вашем доме. Подсчитав плитку, можно быстро определить, сколько места занимает пол. Это также поможет вам выбрать площадь прямоугольного пола.

Содержание

Определение Формула площади прямоугольника Как вычислить площадь прямоугольника Площадь прямоугольника по диагонали Почему площадь прямоугольника равна длине x ширине? Часто задаваемые вопросы (FAQ)

Определение

Площадь прямоугольника зависит от его сторон. Следовательно, формула площади прямоугольника равна произведению длины и ширины прямоугольника. Тогда как, когда мы говорим о периметре прямоугольника, он равен сумме всех его четырех сторон. Таким образом, мы можем сказать, что площадь, ограниченная периметром прямоугольника, является его площадью. Но в случае квадрата, так как все стороны равны, площадь квадрата будет равна квадрату длины стороны.

Формула площади прямоугольника

Формула нахождения площади прямоугольника зависит от его длины и ширины. Площадь прямоугольника можно вычислить в единицах, умножив длину прямоугольника на ширину (или ширину). Боковая и общая площади поверхности могут быть рассчитаны только для трехмерных фигур. Мы не можем вычислить прямоугольник, потому что это двумерная фигура. Таким образом, периметр и содержимое прямоугольника определяются как:

Площадь реактивного угла = L x B

Зная его длину и ширину, можно вычислить площадь любого прямоугольника. Перемножая длину и ширину, площадь прямоугольника получает размер квадратных единиц. В случае квадрата площадь становится стороной2. Основное отличие квадрата от прямоугольника в том, что длина и ширина у квадрата одинаковы.

Как вычислить площадь прямоугольника

Площадь прямоугольника равна произведению его длины на ширину (или ширину). Выполните следующие шаги, чтобы найти площадь прямоугольника

• Шаг 1: Запишите измерения длины и ширины по заданным данным.
• Шаг 2: Найдите произведение значений длины и ширины.
• Шаг 3: Дайте ответ в квадратных единицах.

Площадь прямоугольника по диагонали

Диагональ прямоугольника — это прямая линия внутри прямоугольника, соединяющая его противоположные вершины. В прямоугольнике одинаковой длины две диагонали. Теперь мы можем найти диагональ прямоугольника, используя теорему Пифагора.

(Диагональ) ² = (Длина) ² + (Ширина) ²

(Длина) ² = (Диагональ) ² — (Ширина) ²

Длина = ⎷(Диагональ) ² — (Ширина) ²

Мы знаем, что формула для вычисления площади прямоугольника — длина × ширина. Поэтому мы можем записать эту формулу как ⎷((Диагональ) ² — (Ширина) ² ) × Ширина.

Итак, площадь прямоугольника = ширина (⎷(диагональ) ² — (Ширина) ² ).

Почему площадь прямоугольника равна длине x ширине?

Диагональ данного прямоугольника разбита на два равновеликих прямоугольных треугольника. Следовательно, площадь прямоугольника будет равна сумме площадей этих двух треугольников.

Пусть диагональ AC делит прямоугольник на два прямоугольных треугольника, т. е. ∆ABC и ∆ADC.

Мы знаем, что треугольники ∆ABC и ∆ADC равны.

Площадь ∆ABC = 1/2 x основание x высота = 1/2 x AB x BC = 1/2 x b x l

Площадь ∆ADC = 1/2x основание x высота = 1/2 x CD x AD = 1/2 x b x l

Площадь прямоугольника ABCD = площадь ∆ABC + площадь ∆ADC

Площадь (ABCD) = 2(1/2 x b x l)

Площадь (ABCD) = l x b

Таким образом, площадь прямоугольника = длина х ширина.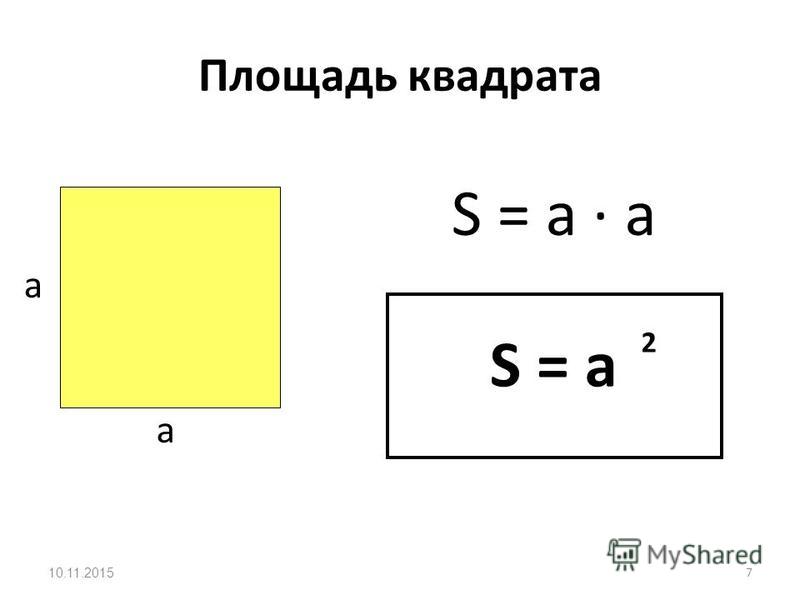

Решенные примеры

Q1. Найдите площадь прямоугольника, длина которого 14 см, а ширина 3 см.

Ответ. Дано,

Длина = 14 см

Ширина = 3 см

Площадь прямоугольника = длина × ширина (или ширина)

14 × 3 = 42

Значит площадь прямоугольника = 42 см2

Q2. Вычислите площадь прямоугольной доски, длина и ширина которой равны 140 см и 90 см соответственно.

Ответ. Длина доски = 140 см = 1,4 м

Ширина доски = 90 см = 0,9 м

Площадь доски = длина x ширина = 1,4 м x 0,9 м = 1,26 м2

Q3. Длина прямоугольного экрана 14 см. Его площадь составляет 160 кв.см. Найдите его ширину.

Ответ. Площадь экрана = 160 кв.см.

Длина экрана = 14 см

Площадь прямоугольника = длина х ширина

Итак, ширина = площадь/длина

Таким образом, ширина экрана = 160/14 = 11,42 см

Часто задаваемые вопросы (FAQ)

Q1. Какая формула площади прямоугольника?

Ответ. Площадь прямоугольника = L x B

Q2. Как вычислить площадь прямоугольника?

Ответ. Чтобы вычислить площадь прямоугольника, необходимо найти площадь, занимаемую прямоугольником внутри его периметра.

Q3. Как проверить правильность площади прямоугольника?

Ответ. Чтобы найти площадь прямоугольника, умножьте его ширину на длину.

Q4. Как вычислить площадь, если все стороны разные?

Ответ. Данную площадь любого неправильного четырехугольника можно вычислить, разделив его на треугольники.

В5. Чему равен периметр прямоугольника?

Ответ. Периметр данного прямоугольника равен сумме всех его четырех сторон. Следовательно,

Периметр = 2 (длина + ширина)

Найдите p​df решаемого примера и формулы площади прямоугольника

Расчет площади прямоугольника — Расчет площади прямоугольника онлайн

Площадь прямоугольника, расчет онлайн

Резюме :

онлайн калькулятор площади, который может рассчитать площадь прямоугольника по его длине и ширине.

area_rectangle онлайн

---

Описание :

Калькулятор имеет несколько функций , позволяющих выполнять вычисления площади . Таким образом, можно вычислить поверхность прямоугольника, также известную площадь прямоугольника с функцией area_rectangle, но и поверхность квадрата , или поверхность круга .

Вычисление площади прямоугольника

площадь прямоугольника это площадь, ограниченная его стороной. Площадь прямоугольника может быть вычислена по формуле `(L*l)` где L представляет длину, а l ширину стороны.

Таким образом, вычисление площади прямоугольника , длина которого равна 3, а ширина 2, выполняется путем ввода следующей формулы area_rectangle(3;2), после вычисления возвращается результат 6.

Символьное вычисление площади прямоугольника

Также возможно произвести символьное вычисление и вычислить площадь прямоугольника длина которого и ширину 1+y, введя следующую формулу area_rectangle(1+x;1+y), после вычисления возвращается результат.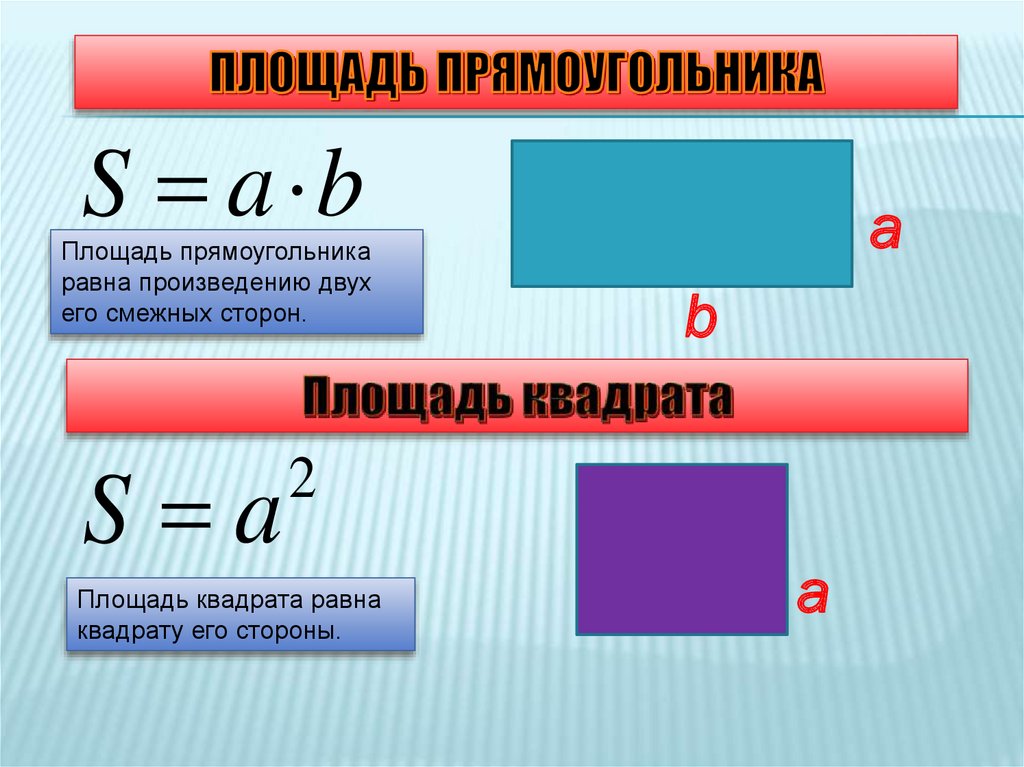

Игры и викторины по вычислению площадей обычных геометрических фигур

Чтобы применить различные формулы расчета, несколько викторины по вычислению площади квадрата, прямоугольника и круга предлагаются.

Синтаксис:

area_rectangle(длина;ширина)

---

Примеры:

area_rectangle(`3;2`) возвращает `6`

Расчет онлайн с area_rectangle (площадь прямоугольника)

См. также

Список связанных калькуляторов:

• Площадь квадрата : area_square. Онлайн-калькулятор площади, который может рассчитать площадь квадрата по длине стороны.
• Площадь круга : area_circle. Онлайн-калькулятор площади, который может рассчитать площадь круга по его радиусу или по диаметру.
• Площадь прямоугольника : area_rectangle. Онлайн-калькулятор площади, который может рассчитать площадь прямоугольника по его длине и ширине.
• Найти уравнение прямой из двух точек: уравнение_прямой_линии. Калькулятор уравнения прямой позволяет рассчитать уравнение прямой по координатам двух точек с пошаговым расчетом.
• Калькулятор периметра: периметр. Онлайн-калькулятор периметра, который вычисляет периметр прямоугольника, периметр квадрата, периметр треугольника или периметр круга.
• Периметр квадрата: perimeter_square. Онлайн-калькулятор позволяет рассчитать периметр квадрата по длине стороны.
• Периметр круга: perimeter_circle. Онлайн-калькулятор, вычисляющий периметр круга по его радиусу.
• Периметр прямоугольника : perimeter_rectangle. Онлайн-калькулятор позволяет вычислить периметр прямоугольника по его длине и ширине.
• Калькулятор теоремы Пифагора: пифагорейский. Калькулятор использует теорему Пифагора, чтобы проверить прямоугольность треугольника или найти длину одной стороны прямоугольного треугольника.
• Вычисление площади геометрической фигуры. : область. Онлайн-калькулятор площади, позволяющий вычислить площадь прямоугольника, квадрата, треугольника или круга.
• Объем куба : volume_cube. Онлайн-калькулятор позволяет рассчитать объем куба по длине стороны.
• Объем прямоугольного параллелепипеда : volume_rectangle. Онлайн-калькулятор позволяет рассчитать объем прямоугольника по его длине, ширине и высоте.
• Объем сферы : volume_sphere. Онлайн-калькулятор позволяет рассчитать объем сферы по ее радиусу.

---

Список связанных упражнений:

• Вычисление площади прямоугольника.

  No related posts.