Как из десятичной дроби сделать обыкновенную дробь. Перевод обыкновенной дроби в десятичную дробь и обратно, правила, примеры
Десятичная дробь состоит из двух частей, которые разделены запятыми. Первая часть — это целая единица, вторая часть — это десятки (если число после запятой одно), сотни (два числа после запятой, как два нуля в ста), тысячные итд. Посмотрим на примеры десятичной дроби: 0, 2; 7, 54; 235,448; 5,1; 6,32; 0,5. Всё это — десятичные дроби. Как же перевести десятичную дробь в обыкновенную?
Пример первый
У нас есть дробь, к примеру, 0,5. Как уже выше писалось, она состоит из двух частей. Первое число 0, показывает, сколько целых единиц у дроби. В нашем случае их нет. Второе число показывает десятки. Дробь даже читается ноль целых пять десятых. Десятичное число перевести в дробь теперь не составит труда, пишем 5/10. Если видите, что у цифр есть общий делитель, можете сократить дробь.
У нас это число 5, поделив обе части дроби на 5, получаем — 1/2.
Пример второй
Возьмем более сложную дробь — 2,25. Читается она так — две целых и двадцать пять сотых. Обратите внимание — сотых, так как чисел после запятой две. Теперь можно перевести в обыкновенную дробь. Записываем — 2 25/100. Целая часть — 2, дробная 25/100. Как и в первом примере, эту часть можно сократить. Общим делителем для цифр 25 и 100 является число 25. Заметьте, что мы всегда подбираем наибольший общий делитель. Разделив обе части дроби на НОД, получили 1/4. Итак, 2, 25 это 2 1/4.
Пример третий
И для закрепления материала возьмем десятичную дробь 4,112 — четыре целых и сто двенадцать тысячных. Почему тысячных, думаю, ясно. Записываем теперь 4 112/1000. По алгоритму находим НОД чисел 112 и 1000. В нашем случае — это число 6. Получаем 4 14/125.
Вывод
- Разбиваем дробь на целую и дробную части.
- Смотрим, сколько цифр после запятой. Если одна — это десятки, две — сотни, три -тысячные итд.
- Записываем дробь в обыкновенном виде.
- Сокращаем числитель и знаменатель дроби.
- Записываем полученную дробь.
- Выполняем проверку, делим верхнюю часть дроби на нижнюю. Если есть целая часть, прибавляем к полученной десятичной дроби. Получился исходный вариант — замечательно, значит, вы все сделали правильно.
На примерах я показала, как можно перевести десятичную дробь в обыкновенную. Как видите, сделать это очень легко и просто.
Очень часто в школьной программе математики дети сталкиваются с проблемой, как перевести обычную дробь в десятичную. Для того чтобы перевести обычную дробь в десятичную, вспомним для начала, что такое обычная дробь и десятичная дробь. Обычная дробь – это дробь вида m/n , где m – числитель, а n – знаменатель. Пример: 8/13; 6/7 и т.д. Дроби делятся на правильные, неправильные и смешанные числа. Правильная дробь – это когда числитель меньше знаменателя: m/n, где m 3. Неправильную дробь всегда можно представить в виде смешанного числа, а именно: 4/3 = 1 и 1/3;
Перевод обычной дроби в десятичную
Теперь рассмотрим, как перевести смешанную дробь в десятичную.
Любую обыкновенную дробь, будь она правильной или не правильной, можно перевести в десятичную. Для этого нужно числитель разделить на знаменатель. Пример: простая дробь (правильная) 1/2. Делим числитель 1 на знаменатель 2, получаем 0,5. Возьмем пример 45/12, сразу видно, что это дробь неправильная. Здесь знаменатель меньше числителя. Превращаем неправильную дробь в десятичную: 45: 12 = 3,75.
Перевод смешанных чисел в десятичную дробь
Пример: 25/8. Сначала мы превращаем смешанное число в неправильную дробь: 25/8 = 3х8+1/8 =3 и 1/8; затем делим числитель равный 1 на знаменатель равный 8, столбиком или на калькуляторе и получим десятичную дробь равную 0,125. В статье приведены самые легкие примеры перевода в десятичные дроби. Поняв методику перевода на простых примерах, вы легко сможете решать самые сложные из них.
В самом начале нужно все-таки узнать, что такое дробь и каких видов она бывает. А бывает она трех видов. И первый из них это обыкновенная дробь, например ½, 3/7,3/432 и т.
д. Эти числа также можно записывать при помощи горизонтальной черточки. И первое, и второе будет одинаково верно. Цифра сверху называется числительным, а снизу знаменателем. Есть даже поговорка, для тех людей, кто постоянно путает эти два названия. Она звучит так: «Зззззапомни! Зззззнаменатель — внизззззу! ». Это поможет не запутаться. Обыкновенная дробь это всего лишь два числа, которые делятся друг на друга. Черточка в них и обозначает знак деления. Ее можно заменить знаком двоеточие. Если стоит вопрос «как дробь перевести в число», то это очень просто. Следует всего лишь числитель поделить на знаменатель. И все. Дробь переведена.
Второй вид дробей называется десятичным. Это ряд цифр с запятой. К примеру, 0,5, 3,5 и т. д. Назвали их десятичными, только потому, что после запетой первая цифра обозначает «десятки», вторая в десять раз больше «сотни» и так далее. А первые цифра до запятой, называются целыми. Например, число 2,4 звучит так, двенадцать целых и двести тридцать четыре тысячных.
Такие дроби появляются в основном из-за того, что поделив два числа без остатка не получается. И большинство обыкновенных дробей, во время того как их будут переводить в числа, в конечном итоге имеют вид десятичной дроби. Например, одна вторая ровняется ноль целым пяти десятым.
И заключительный третий вид. Это смешанные числа. Пример этого можно привести такой, как 2½. Звучит так, две целых и одна вторая. В старших классов такой вид дробей уже не используются. Их наверняка необходимо будет приводить или в обыкновенный вид дроби, или в десятичный. Сделать это так же легко. Просто целое число нужно умножить на знаменатель и, полученное обозначение, сложить с числительным. Возьмем наш пример 2½. Два умножается на два, получается четыре. Четыре плюс один, равно пяти. И дробь формой 2½ образуется в 5/2. А пять, поделив на два можно получить десятичную дробь. 2½=5/2=2,5. Уже стало понятно, как переводить дроби в числа. Следует всего лишь разделить числитель на знаменатель. Если числа большие можно воспользоваться калькулятором.
Если на нем получается не целые числа и после запятой идет очень много цифр, то тогда данное значение можно округлить. Округляется все очень просто. Сначала следует определиться, к какой цифре нужно округлить. Следует рассмотреть пример. Человеку нужно округлить число ноль целых, девять тысяч семьсот пятьдесят шесть десятитысячных или в цифровом значении 0,6. Округление необходимо сделать до сотых. Это означает, что в данный момент до семи сотых. После цифры семь в дроби идет пять. Теперь нужно использовать правила для округления. Цифры больше пяти округляются в большую сторону, а меньшие – в меньшую. В примере у человека — пять, она стоит на пограничье, но считается, что округление происходит в большую сторону. Значит, все цифры после семерки убираем и к ней прибавляем единицу. Получается 0,8.
Также возникают ситуации, когда человеку необходимо быстро перевести обыкновенную дробь в число, а калькулятора рядом нет. Для этого стоит применить деление столбиком. Первым делом следует на листке написать рядом друг с другом числитель и знаменатель.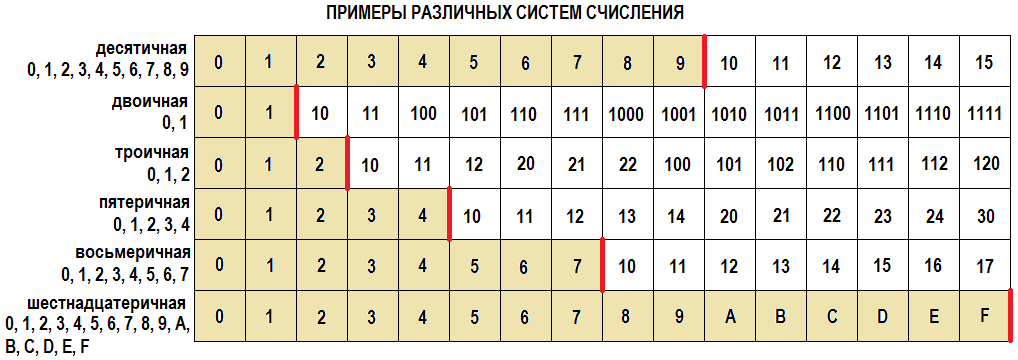
Между ними ставится уголок деления, он похож на букву «Т», только лежащую на боку. Для примера можно взять дробь десять шестых. И так, десять следует поделить на шесть. Сколько шестерок может вместиться в десятке, только одна. Единица записывается под уголком. Десять отнять шесть получится четыре. Сколько шестерок будет в четверке, несколько. Значит, в ответе после единицы ставится запятая, а четверка умножается на десять. В сорока шесть шестерок. В ответе дописывается шестерка, а от сорока отнимается тридцать шесть. Получается опять четыре.
В данном примере произошло зацикливание, если продолжить делать все точно также получится ответ 1,6(6) Цифру шесть продолжается для бесконечности, но применив правило округления, можно привести получение число к 1,7. Что намного удобней. Из этого можно сделать вывод, что не все обыкновенные дроби можно перевести в десятичные. В некоторых происходит зацикливание. Но зато любую десятичную дробь можно перевести в простую. Здесь поможет элементарное правило, как слышится, так и пишется.
Вот и было разобраны самые основные правила и преобразования, которые связанны с дробями. Все они несложные, но знать их следует. В повседневную жизнь уже давно вошли дроби, особенно десятичные. Это хорошо видно на ценниках в магазинах. Круглые цены уже давно не кто не пишет, а с дробями цена кажется визуально на много дешевле. Также одна из теорий гласит, что человечество отвернулось от римских цифр и приняла в оборот арабские, только потому, что в римских не было дробей. И многие ученые соглашаются с этим предположением. Ведь с дробями можно вести подсчеты более точней. А в наш век космических технологий, точность в расчетах нужна как никогда. Так что изучать дроби в школе по математики жизненно необходимо для понимания многих наук и технических достижений.
Преобразование обыкновенной дроби в десятичную
Допустим, мы хотим преобразовать обыкновенную дробь 11/4 в десятичную. Проще всего сделать это так:
2∙2∙5∙5 |
Это удалось нам потому, что в данном случае разложение знаменателя на простые множители состоит только из двоек. Мы дополнили это разложение еще двумя пятерками, воспользовались тем, что 10 = 2∙5, и получили десятичную дробь. Подобная процедура возможна, очевидно, тогда и только тогда, когда разложение знаменателя на простые множители не содержит ничего, кроме двоек и пятерок. Если в разложении знаменателя присутствует любое другое простое число, то такую дробь в десятичную преобразовать нельзя.
В строке ответа мы получили целую часть ( 2 ), и еще у нас есть остаток ( 3 ). Раньше мы деление на этом заканчивали, но теперь мы знаем, что к делимому ( 11 ) можно приписать справа запятую и несколько нулей, что мы теперь мысленно и сделаем. Следом после запятой идет разряд десятых. Ноль, который стоит у делимого в этом разряде, припишем к полученному остатку ( 3 ):
Теперь деление можно продолжать как ни в чем не бывало. Надо только не забыть поставить в строке ответа запятую после целой части:
Теперь приписываем к остатку ( 2 ) ноль, который стоит у делимого в разряде сотых и доводим деление до конца:
В результате получаем, как и раньше,
Попробуем теперь точно таким же способом вычислить, чему равна дробь 27/11:
Мы получили в строке ответа число 2,45, а в строке остатка — число 5
. Но такой остаток нам уже раньше встречался.
Поэтому мы уже сразу можем сказать, что, если мы продолжим наше деление «уголком», то следующей цифрой в строке ответа будет 4, затем пойдет цифра 5, потом — снова 4 и снова 5, и так далее, до бесконечности:
27 / 11 = 2,454545454545…
Мы получили так называемую периодическую десятичную дробь с периодом 45. Для таких дробей применяется более компактная запись, в которой период выписывается только один раз, но при этом он заключается в круглые скобки:
2,454545454545… = 2,(45).
Вообще говоря, если делить «уголком» одно натуральное число на другое, записывая ответ в виде десятичной дроби, то возможно только два исхода: (1) либо рано или поздно в строке остатка мы получим ноль, (2) либо там окажется такой остаток, который уже нам раньше встречался (набор возможных остатков ограничен, поскольку все они заведомо меньше делителя). В первом случае результатом деления является конечная десятичная дробь, во втором случае — периодическая.
Преобразование периодической десятичной дроби в обыкновенную
Пусть нам дана положительная периодическая десятичная дробь с нулевой целой частью, например:
a = 0,2(45).
Как преобразовать эту дробь обратно в обыкновенную?
Умножим ее на число 10 k , где k — это число цифр, стоящих между запятой и открывающей круглой скобкой, обозначающей начало периода. В данном случае k = 1 и 10 k = 10:
a ∙ 10 k = 2,(45).
Полученный результат умножим на 10 n , где n — «длина» периода, то есть число цифр, заключенных между круглыми скобками. В данном случае n = 2 и 10 n = 100:
a ∙ 10 k ∙ 10 n = 245,(45).
Теперь вычислим разность
a ∙ 10 k ∙ 10 n − a ∙ 10 k = 245,(45) − 2,(45).
Поскольку дробные части у уменьшаемого и вычитаемого одинаковы, то у разности дробная часть равна нулю, и мы приходим к простому уравнению относительно a :
a ∙ 10 k ∙ (10 n − 1) = 245 − 2.
Решается это уравнение с помощью следующих преобразований:
a ∙ 10 ∙ (100 − 1) = 245 − 2.
a ∙ 10 ∙ 99 = 245 − 2.
245 − 2 | ||
10 ∙ 99 |
Мы специально пока не доводим вычисления до конца, чтобы было наглядно видно, как можно сразу выписать этот результат, опуская промежуточные рассуждения. Уменьшаемое в числителе ( 245 ) — это дробная часть числа
a = 0,2(45)
если в ее записи стереть скобки. Вычитаемое в числителе ( 2 ) — это непериодическая часть числа а , располагающаяся между запятой и открывающей скобкой. Первый сомножитель в знаменателе ( 10 ) — это единица, к которой приписано столько нулей, сколько цифр в непериодической части (k ). Второй сомножитель в знаменателе ( 99 ) — это столько девяток, сколько цифр содержит период (n ).
Теперь наши вычисления можно довести до конца:
Здесь в числителе стоит период, а в знаменателе — столько девяток, сколько цифр в периоде.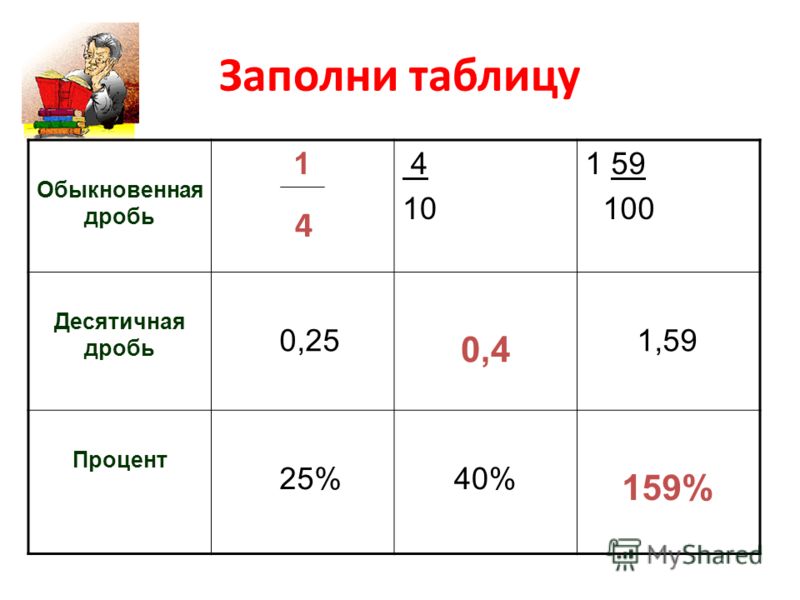
После сокращения на 9 полученная дробь оказывается равной
Подобным же образом,
Большое количество учащихся, и не только, задаются вопросом, как перевести дробь в число. Чтобы это сделать, имеется несколько достаточно простых и понятных способов. Выбор конкретного способа зависит от предпочтений решающего.
В первую очередь нужно знать, как дроби записываются. А записываются они следующим образом:
- Обыкновенная. Пишется с числителем и знаменателем через наклонную или столбиком (1/2).
- Десятичная. Пишется через запятую (1,0, 2,5 и так далее).
Перед тем как приступить к решению, нужно знать, что такое неправильная дробь, ведь она встречается достаточно часто. Она имеет числитель больше знаменателя, например, 15/6. Неправильную дробь также можно решать такими способами, без каких-либо усилий и затрат времени.
Смешанное число — это когда в результате выходит целое число и дробная часть, к примеру 52/3.
Любое натуральное число можно записать дробью с совершенно разными натуральными знаменателями, например:1= 2/2=3/3 = и т.
д.
Перевести можно еще и с помощью калькулятора, но не все они имеют такую функцию. Существует специальный инженерный калькулятор, где есть такая функция, но не всегда есть возможность его использовать, особенно в школе. Поэтому лучше разобраться в данной теме.
Первым делом стоит обратить внимание на то, какая дробь. Если ее можно с легкостью множить до 10 на одинаковые с числителем значения, то можно воспользоваться первым способом. Например: обыкновенная ½ умножаете в числителе и знаменателе на 5 и получаете 5/10, которое можно записать как 0,5.
Данное правило основано на том, что десятичная всегда имеет в знаменателе круглое значение, такое как 10,100,1000 и так далее.
Из этого выходит, что если множить числитель и знаменатель, то нужно добиваться получения в знаменателе именно такого значения в результате умножения, независимо от того, что выходит в числителе.
Стоит помнить, что некоторые дроби нельзя перевести, для этого необходимо перед началом решения проверить ее.
Например: 1,3333, где цифра 3 повторяется до бесконечности, причем калькулятор тоже не избавит от нее. Решением такой проблемы может быть только округление таким образом, чтобы получилось целое число, если это возможно. Если такой возможности не имеется, то следует вернуться в начало примера и проверить правильность решения задачи, возможно, была допущена ошибка.
Рисунок 1-3. Перевод дробей путем умножения.
Рассмотрим для закрепления описанной информации следующий пример перевода:
- Например, необходимо перевести 6/20 в десятичную. Первым делом ее следует проверить, как показано на рисунке 1.
- Только после того как убедились, что можно разложить, как в данном случае на 2 и 5, нужно приступать к самому переводу.
- Наиболее простым вариантом будет умножить знаменатель, получив результат 100, является 5, так как 20х5=100.
- Следуя примеру на рисунке 2, в итоге получится 0,3.
Можно закрепить результат и еще раз все просмотреть по рисунку 3.
Для того чтобы полностью разобраться в теме и больше не прибегать к изучению этого материала. Эти знания помогут не только ребенку, но и взрослому человеку.
Перевод путем деления
Второй вариант перевода дробей является немного сложней, но более популярным. Таким методом в основном пользуются в школах учителя для объяснения. В целом, он намного проще объясняется и быстрее понимается.
Стоит помнить, что для правильного преобразования простой дроби необходимо ее числитель поделить на знаменатель. Ведь если задуматься, то решение это и есть процесс деления.
Для того чтобы понять это простое правило, нужно рассмотреть следующий пример решения:
- Возьмем 78/200, которую нужно перевести в десятичную. Для этого следует 78 разделить на 200, то есть числитель на знаменатель.
- Но перед тем как начать, стоит провести проверку, как показано на рисунке 4.
- После того как убедились, что ее можно решить, следует приступать к процессу. Для этого стоит разделить числитель на знаменатель в столбик или уголком, как показано на рисунке 5. В начальных классах школ учат такому делению, и трудностей с этим не должно возникнуть.
В начальных классах школ учат такому делению, и трудностей с этим не должно возникнуть.На рисунке 6 показаны примеры наиболее распространенных примеров, их просто можно запомнить, чтобы при необходимости не тратить время для решения. Ведь в школе на каждую контрольную или самостоятельную работы дается мало времени для решения, поэтому не стоит тратить его на то, что можно выучить и просто помнить.
Перевод процентов
Переводить проценты в десятичное число тоже достаточно легко. Этому начинают учить в 5 классе, а в некоторых школах еще раньше. Но если ваш ребенок на уроке математики не понял эту тему, можно наглядно ему еще раз объяснить. Для начала следует выучить определения понятия, что такое процент.
Процент — это одна сотая часть от какого-либо числа, другими словами, абсолютная произвольная. Например, от 100 это будет 1 и так далее.
На рисунке 7 показан наглядный пример перевода процентов.
Чтобы перевести процент, надо всего лишь убрать значок %, а затем разделить его на 100.
Еще 1 пример показан на рисунке 8.
Если надо провести обратную «конвертацию», необходимо все сделать с точностью до наоборот. Другими словами, число необходимо умножить на сто и после приписать значок процентов.
А для того чтобы обычную перевести в проценты, также можно использовать этот пример. Только изначально следует перевести дробь в число и только потом в проценты.
Исходя из описанного выше, можно легко понять принцип перевода. С помощью этих способов можно ребенку объяснять тему, если он ее не понял или не присутствовал на уроке в момент ее прохождения.
И никогда не будет необходимости нанимать репетитора, чтобы он объяснил ребенку, как перевести дробь в число или процент.
Сравнение десятичных дробей
Тема: Сравнение десятичных дробей
Дробь — это число в математике, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число.
Есть два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
Например, в дроби 1/2: 1 — делимое и числитель, а 2 — делитель и знаменатель.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Можно сказать, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Ее записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,1
- 2,53
- 9,932
Возьмем последнюю дробь из примера и разложим ее: 9,932; где 9 — целая часть, 9 после запятой — десятые, 3 — сотые, 2 — тысячные.
Конечная десятичная дробь — это когда количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
Основные свойства десятичных дробей:
- Дробь не имеет значения, при условии, если делитель равен нулю.
- Дробь равна нулю, если числитель равен нулю, а знаменатель — нет.
- Две дроби a/b и c/d называются равными, если a * d = b * c.
- Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
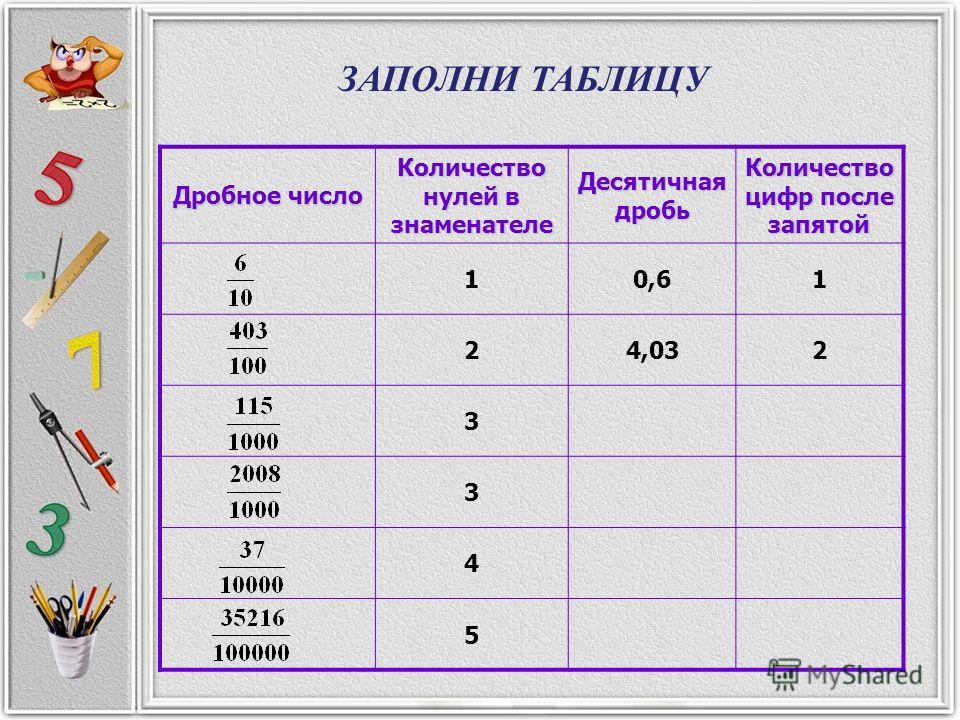
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Если числитель меньше знаменателя, то целая часть равна нулю.Правила сравнения десятичных дробей:
Чтобы сравнить две десятичные дроби, сначала нужно сравнить их целые части. Если целые части равны, продолжаем искать первый несовпадающий разряд. Большей будет та дробь, у которой соответствующий разряд больше.
Вот так с первой строчки раскрыли тему сравнения десятичных дробей. Но это еще не все — едем дальше.
Алгоритм сравнения десятичных дробей:
- Убедиться, что у обеих десятичных дробей одинаковое количество знаков (цифр) справа от запятой. Если нет, то дописать (убрать) нужное количество нулей в одной из десятичных дробей.
- Сравнить десятичные дроби слева направо. Целую часть с целой, десятые с десятыми, сотые с сотыми и т. д.
- Когда одна из частей десятичной дроби окажется больше, чем другая, эту дробь можно назвать большей.
Целую часть с целой, десятые с десятыми, сотые с сотыми и т. д.Применим правило на практике.
Сравним десятичные дроби: 15,7 и 15,719.
Как решаем:
- Допишем в 1-й десятичной дроби нужное количество нулей, чтобы уравнять количество знаков справа от запятой: 15,700 и 15,719.
- Сравним десятичные дроби слева направо.
Целую часть с целой частью: 15 = 15. Целые части равны.
Десятые с десятыми: 7 = 7. Десятые также равны.
Сотые с сотыми: 0 < 1. Так как сотые второй десятичной дроби больше, значит и сама дробь больше: 15,700 < 15,719.
Ответ: 15,7 < 15,719.
Еще один способ сравнения десятичных дробей: Чтобы сравнить две десятичные дроби, нужно уравнять количество знаков после запятой (приписать к одной из них справа нули), затем отбросить запятую, и сравнить два натуральных числа.
Сравним десятичные дроби: 3,656 и 3,48.
Как решаем:
- Уравниваем количество знаков справа после запятой: 3,656 и 3,480.
- Отбросим запятые: 3656 и 3480.
- Сравним полученные числа: 3656 > 3480.
Ответ: 3,656 > 3,48.
Запоминаем!
Меньшая десятичная дробь лежит на координатном луче левее большей, а большая — правее меньшей.
Например, 0,3 < 0,4 < 0,5, поэтому точка A (0,3) лежит левее точки B (0,4), а точка C (0,5) лежит правее точки B (0,4).
Задания для самостоятельного решения:
1. Перевести в десятичный вид, а затем сравнить дроби —
а) 36/100 и 56/1000; б) 15/10 и 98/100;
в) 21/100 и 37/100; г) 101/100 и 1001/1000
2. Расставьте в порядке возрастания числа:
5,101; 5,001; 3,752; 3,275, 3,725; 4,989; 5,099
3. Сравните числа, заменив звездочку знаком < или > :
а) 1,601 * 1,599; б) 3,02 * 3,019; в) 8,698 * 9,001
г)10,6 * 10,599; д) 4,62 * 4,588; е) 0,099 * 0,810
4.
Запишите в виде десятичных дробей:
3/10; 2 53/100; 4 673/1000; 23/1000; 5 84/100
Что такое 0,5 как целое число?
Числительные — это математические числа, используемые в финансовой, профессиональной, а также в социальной сфере в социальном мире. Цифры и разрядное значение в числе и основание системы счисления определяют значение числа. Числа используются в различных математических операциях, таких как суммирование, вычитание, умножение, деление, процент и т. д., которые используются в нашей повседневной деятельности и торговой деятельности.
Что такое числа?
Числа используются в различных арифметических значениях, применимых для выполнения различных арифметических операций, таких как сложение, вычитание, умножение и т. д., которые применяются в повседневной жизни для целей вычислений. Значение числа определяется цифрой, ее разрядностью в числе и основанием системы счисления.
Числа , также известные как цифры, представляют собой математические значения, используемые для подсчета, измерения, маркировки и измерения основных величин.
Числа — это математические значения или цифры, используемые для измерения или вычисления величин. Он представлен цифрами 2, 4, 7 и т. д. Примерами чисел являются целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д.
Типы чисел
Существуют различные типы чисел, разделенные на наборы по системе счисления. Типы описаны ниже:
- Натуральные числа: Натуральные числа — это положительные числа, которые считаются от 1 до бесконечности. Подмножество не включает дробные или десятичные значения. Множество натуральных чисел представлено ‘ Н ’. Это числа, которые мы обычно используем для счета. Набор натуральных чисел может быть представлен как N=1,2,3,4,5,6,7,……………
- Целые числа: Целые числа — это положительные натуральные числа, включая ноль, который отсчитывается от 0 до бесконечности. Целые числа не включают дроби или десятичные дроби. Набор целых чисел представлен как « W ». Набор может быть представлен как W=0,1,2,3,4,5,………………
- Целые числа: Целые числа представляют собой набор чисел, включающий все положительные счетные числа, ноль, а также все отрицательные числа, которые считают от отрицательной бесконечности до положительной бесконечности. В наборе нет дробей и десятичных знаков. Набор целых чисел обозначается ‘ З . Набор целых чисел можно представить в виде Z=………..,-5.-4,-3,-2,-1,0,1,2,3,4,5,………….
- Десятичные числа: Любое числовое значение, состоящее из десятичной точки, является десятичным числом. В некоторых случаях он также может быть выражен в дробной форме. Его можно выразить как 2,5, 0,567 и т. д.
- Действительное число: Действительные числа — это заданные числа, не содержащие мнимых значений. Он включает в себя все положительные целые числа, отрицательные целые числа, дроби и десятичные значения. Обычно обозначается ‘ Р ».
- Комплексный номер: Комплексные числа — это набор чисел, включающий мнимые числа. Его можно выразить как a+bi, где «a» и «b» — действительные числа. Обозначается ‘ C ’.
- Рациональные числа: Рациональные числа — это числа, которые можно представить как отношение двух целых чисел. Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается ‘ Q ’.
- Иррациональные числа: Иррациональные числа — это числа, которые не могут быть выражены в дробях или отношениях целых чисел. Он может быть записан десятичными знаками и иметь бесконечные неповторяющиеся цифры после запятой. Обозначается ‘ P ’.
Набор может быть представлен как W=0,1,2,3,4,5,………………
Его можно выразить как a+bi, где «a» и «b» — действительные числа. Обозначается ‘ C ’.Что такое целые числа?
Целые числа — это числа без дробей, представляющие собой набор положительных целых чисел от 0 до бесконечности. Все целые числа существуют в числовых рядах. Все целые числа являются действительными числами, но мы не можем сказать, что все действительные числа являются целыми числами. Целые числа не могут быть отрицательными.
Целые числа представлены символом «9».0005 Вт ”.
Примеры целых чисел
Натуральные числа также известны как счетные числа, в том числе ноль является частью целых чисел, таких как 0,1,2,3,4,5 и т. д., кроме отрицательных целых чисел, дробей и десятичных дробей. .
0, 10, 12, 56, 100 и т. д. — все это примеры целых чисел.
Что такое 0,5 как целое число?
Ответ:
Целые числа представляют собой набор действительных чисел, включающий ноль и все положительные счетные числа. Принимая во внимание, что исключаются дроби, отрицательные целые числа, дроби и десятичные числа.
Поскольку 0,5 является десятичным числом, оно не считается целым числом. Однако его можно преобразовать в целое число, округлив до ближайшего целого числа.
0,5 при округлении до ближайшего целого числа равно 1. Так как значение после запятой равно 5, то число округляется до следующего целого числа в большую сторону.
Следовательно, все число 0,5 будет равно 1.Подобные вопросы
Вопрос 1. Чему равно 2,8 как целое число?
Ответ:
Дано: Число равно 2,8
Объяснение:
Целые числа — это числа, начинающиеся с нуля.
Рассмотрим число 2.8 как Y.
Округлив его до ближайшего целого числа, получим 3. Поскольку значение после запятой больше 5.
Следовательно, целое число 2.8 равно 3
Вопрос 2. Что такое 49/4 как целое число?
Ответ:
Дано:- Число 49/4
Объяснение:
Целые числа — это числа, начинающиеся с нуля.
Рассмотрим число 49/4 как Y.
Y = 49/4
Разделив 49/4, мы получим целое число,
, так что получим
Y = 49/4
Y = 12,23
2 Округляя до ближайшего целого числа, получаем 12.
Следовательно, целое число 49/4 равно 12.
Вопрос 3. Что такое 2,4 как целое число?
Ответ:
Дано: Число равно 2,4
Объяснение:
Целые числа — это числа, начинающиеся с нуля.
Рассмотрим число 2.4 как Y.
Y = 2,4
Округлив 2,4 до ближайшего целого числа, мы получим 2, так как значение после запятой меньше 5, следовательно, оно округляется до предыдущего целого числа.
Следовательно, целое число 2.4 равно 2.
Десятичные дроби: введение в десятичные дроби
Урок 1: Знакомство с десятичными дробями
Что такое десятичные дроби?
Десятичное число — это еще один способ записи дроби . Вы можете думать о десятичной дроби как о части целого числа . Это меньше , чем 1 целое, но больше 0 .
Вы можете этого не осознавать, но вы часто видите десятичные дроби в реальной жизни. Одним из самых распространенных примеров являются деньги.
Узнаете эти монеты? У нас есть квартал , копеек и два пенни . Вы можете записать каждое из них в виде десятичной дроби. Это потому, что каждая монета стоит на меньше, чем целый доллар на .
Щелкните слайд-шоу, чтобы узнать, как работают десятичные дроби.
Это доллар. Доллар представляет собой целых чисел. Это равно 1.
Мы могли бы также записать это как 1,00. Другими словами, 1 = 1,00.
1.00 — десятичная цифра .0006 . Здесь это означает, что у нас есть 1 доллар и 0 центов.
Как вы, возможно, уже знаете, в одном долларе 100 пенни. Это означает, что 100 пенни равны 1,00.
Один пенни составляет часть доллара.
Точнее, это 1 цент. Мы могли бы также записать это в виде десятичной дроби: 0,01.Давайте посмотрим еще на несколько десятичных знаков. 9 центов — это 0,09 доллара.
Квартал, или 25 центов, равен 0,25 доллара. Каждый раз, когда у вас есть часть целого, вы можете записать ее в виде десятичной дроби.
Давайте рассмотрим другой пример. Этот кувшин вмещает 1 литр воды. Сейчас он полный.
Мы могли бы записать это в виде десятичной дроби: 1,00 литра.
Кувшин разделен на 10 частей . Это означает, что каждая часть равна 0,10 литра.
С течением дня кувшин становится все пустее. Сейчас у него 0,70 л. Это потому, что мы израсходовали 0,30 литра.
Теперь 0,50 литра или половина литр.
Теперь 0,20 л. Несмотря на то, что у нас меньше, чем на один литр, у нас есть больше нуля литров, поэтому мы можем записать это как десятичное число .
Точнее, это 1 цент. Мы могли бы также записать это в виде десятичной дроби: 0,01.
Чтение десятичных знаков
Как вы видели на предыдущей странице, десятичных знаков очень похожи на обычные числа, но с некоторыми важными отличиями. Во-первых, все десятичные числа имеют десятичной точки ( . ). Десятичная точка выглядит как точка. Любое число до слева десятичной точки — это целое число. Числа после справа от подобны дробям — они меньше 1 целого, но больше 0.
Например, давайте посмотрим на эту десятичную дробь.
9,6
9 стоит слева от десятичной точки, поэтому у нас есть 9 целых чисел. 6 находится справа, поэтому у нас также есть 6 частей целого.
В реальной жизни мы постоянно видим записанные десятичные дроби. Например, вы можете знать, что средняя температура тела составляет 98,6 градусов. Или вы можете настроиться на радиостанцию, например 97,5. Но знаете ли вы, как читать эти десятичные дроби вслух?
Щелкните слайд-шоу, чтобы научиться читать десятичные дроби.
Давайте попробуем прочитать эту десятичную дробь: 9.6.
Сначала мы прочитаем число слева от десятичной точки. Это девять.
Далее мы прочитаем десятичную точку. Обычно вы просто говорите «точка » .
Наконец, мы прочитаем любое число справа от десятичной точки. Это шесть.
Итак, мы читаем 9.6 так: девять целых шесть десятых.
Но можно было бы прочитать и так: девять и шесть десятых.
Когда вы читаете десятичные числа, каждое место справа от десятичной точки имеет особое имя.
Сразу справа от запятой стоит десятых долей место .
Здесь десятичная дробь означает, что у нас есть 0,6 или шесть десятых целого.
Возможно, вы помните из «Введения в дроби», что шесть десятых — это просто другой способ сказать 6/10.
Таким образом, 9,6 означает, что у нас есть 9 целых вещей и 6/10, или шесть десятых , другой вещи.
Так как у нас девять и шесть десятых, слово «и» заменяет десятичную точку.
Попробуем другой пример. Как бы вы прочитали эту десятичную дробь? 0,25.
Мы можем прочитать 0,25 как ноль целых два десятых пять…
Мы можем прочитать 0,25 как ноль целых два десятых пять… или пропустить ноль и просто сказать, что точка два пять.
Но мы могли бы прочитать и так: двадцать пять сотых.
Давайте еще раз посмотрим на наши десятичные разряды. 2 находится в десятых месте , поэтому у нас есть две десятых.
Далее идет сотых место . В этом примере 5 находится в сотых месте , поэтому у нас есть пятисотые.
Когда мы читаем это число вслух, мы произносим 2 и 5 вместе как «двадцать пять » .
Мы также назовем самый дальний десятичный разряд от справа . В нашем примере это сотых место .
Итак, мы будем читать 0,25 как двадцать пять сотых.
Это просто другой способ записи 25/100.
Чтобы вычислить, сколько всего сотых у нас было, мы могли бы сложить эти числа: две десятых и пять сотых.
2 десятых равны 0,20 , или двадцать сотых.
0,20 плюс 0,05 равно 0,25, или двадцать пятисотых.
Попробуйте!
Попробуйте прочитать вслух десятичные дроби ниже.
Десятичные дроби и деньги
Что, если бы вам пришлось читать эту десятичную дробь вслух?
Несмотря на то, что мы используем десятичные дроби, когда говорим о деньгах, мы читаем их немного по-другому.
Вместо трех целых две десятых три или три и двадцать три сотых мы скажем три доллара и двадцать три цента .
Вы также можете прочитать это так: «три двадцать три » . Чтобы сэкономить время, большинство людей опускают десятичную точку, говоря о деньгах. Как насчет 5,9 долларов?9? Это будет пять долларов и девяносто девять центов или пять девяносто девять .
Помните, что эти правила работают только с деньгами. Их нельзя использовать для чтения других десятичных знаков.
Попробуйте это!
Попробуйте прочитать эти суммы в долларах.
Сравнение десятичных дробей
Предположим, вы покупаете новый кувшин для воды. Вы найдете два, которые вам нравятся: один вмещает 0,7 галлона, а другой — 0,5 галлона. Вы знаете, какой кувшин больше? Нажмите на стрелки, чтобы узнать.
Чтобы узнать, какой кувшин вмещает больше, вы можете просто сравнить десятичные дроби, чтобы увидеть, какой из них больше.
7 больше 5, поэтому 0,7 больше 0,5. Чем больше число справа от запятой, тем больше десятичный знак.
Как насчет этих двух десятичных знаков:
Опять же, вы просто сравните числа с справа от десятичной точки.
74 больше 72, поэтому 0,74 больше 0,72.
Теперь давайте сравним эти десятичные дроби:
Поскольку целое число 1 одинаково для обеих десятичных дробей, мы сравним числа справа от десятичной точки.
Если вы думали, что 0,2 больше, чем 0,19, вы были правы!
Помните, что 1.2 можно также записать как 1.20.
20 больше, чем 19, поэтому 1,20 больше, чем 1,19.
Вернуться к плейлисту: десятичные дроби
Далее:Сложение и вычитание десятичных дробей
/en/decimals/adding-and-subtracting-decimals/content/
Калькулятор дробей
Этот калькулятор дробей выполняет основные и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.
е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример |
|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 |
| — | minus sign | subtraction | 1 1/2 — 2/3 |
| * | asterisk | multiplication | 2/3 * 3/4 |
| × | times sign | multiplication | 2/3 × 5/6 |
| : | division sign | division 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
|
Наиболее распространенные мнемоники для запоминания этого порядка операций: 