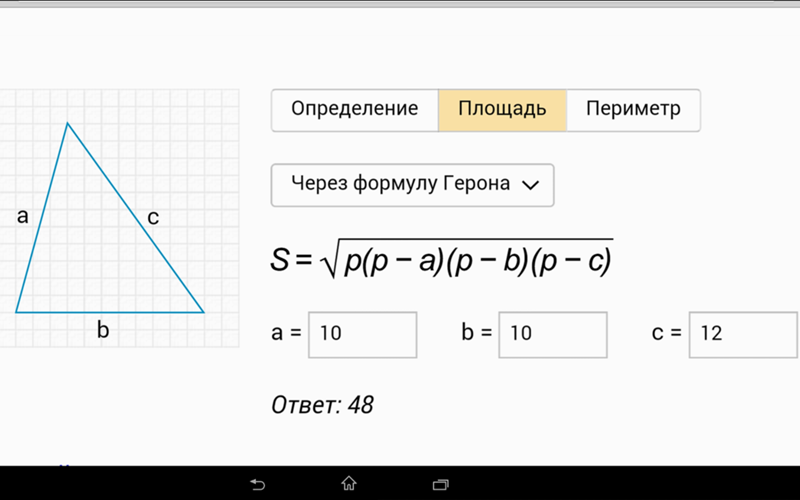
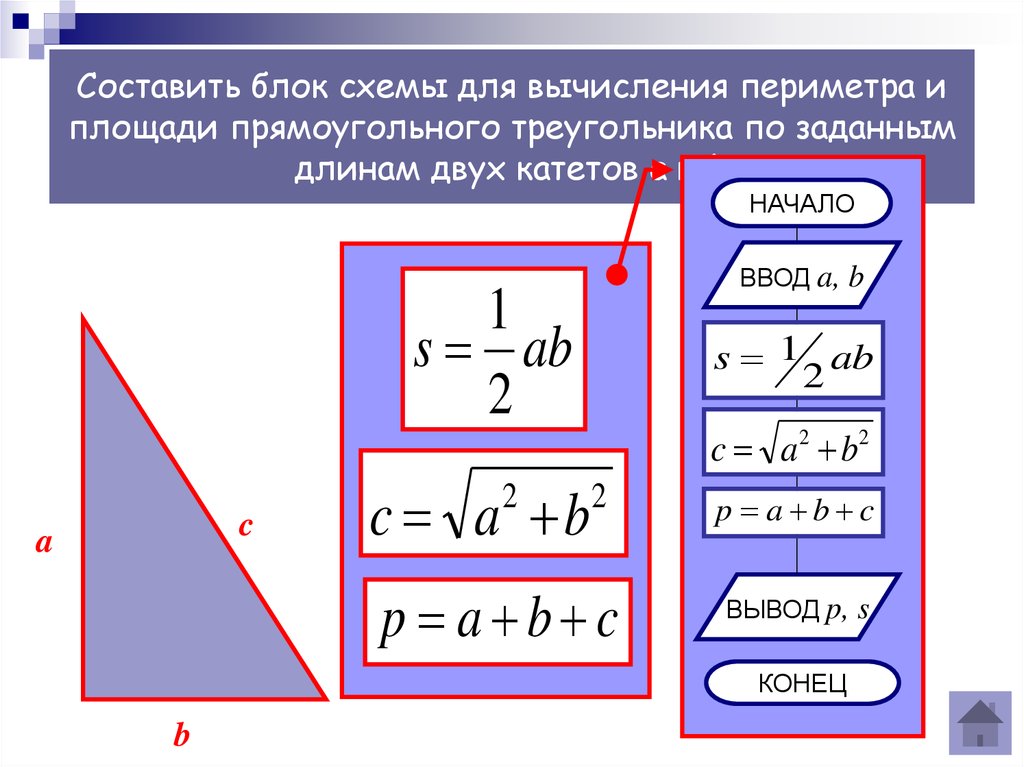
Как найти площадь и периметр прямоугольного треугольника
Прямоугольный треугольник формулы
Прямоугольный треугольник – это треугольник, у которого один из углов прямой (90°).
Другие виды треугольников:
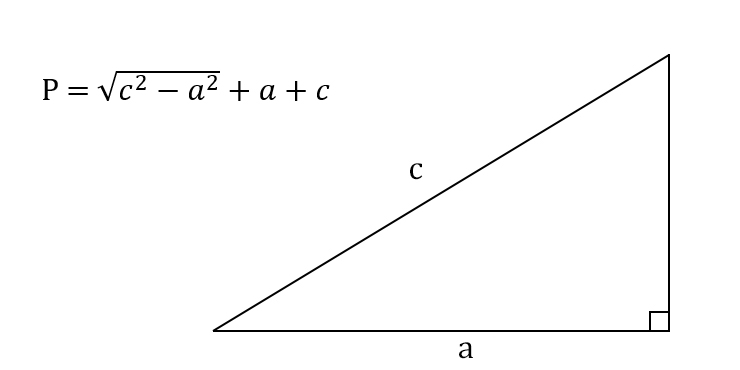
Любой прямоугольный треугольник характеризуется катетами a и b и гипотенузой c (см. рисунок).
Катет – это сторона прямоугольного треугольника, образующая прямой угол с другой стороной (также катетом).
Гипотенуза – это сторона прямоугольного треугольника, лежащая напротив прямого угла.
Именно эти характеристики используются в формулах прямоугольного треугольника при вычислении площади, периметра, а также радиусов вписанной и описанной окружностей.
Формула радиуса вписанной окружности для прямоугольного треугольника
Радиус вписанной окружности r можно вычислить, зная стороны прямоугольного треугольника:
Формула радиуса описанной окружности для прямоугольного треугольника
Радиус описанной окружности R можно вычислить, зная гипотенузу прямоугольного треугольника:
Формула периметра прямоугольного треугольника
Периметр P прямоугольного треугольника можно получить, зная его стороны:
При вычислении площади прямоугольного треугольника часто требуется знать его полупериметр:
p = P/2 = (a + b + c)/2
Формулы площади прямоугольного треугольника
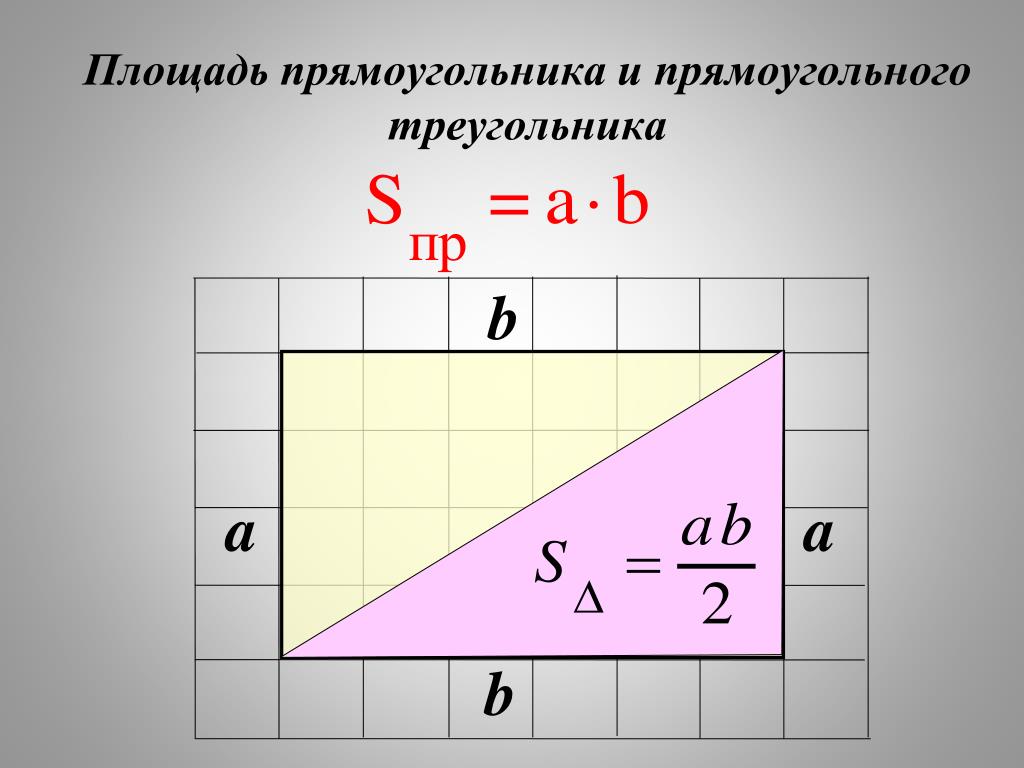
При вычислении площади прямоугольного треугольника можно пользоваться формулами, которые применяются для вычисления площади произвольного треугольника, так как прямоугольный треугольник является частным случаем для треугольников.
Площадь прямоугольного треугольника S можно вычислить, зная его катеты a и b:
Еще одна формула позволяет вычислить площадь прямоугольного треугольника по его катетам a и b и полупериметру p (формула Герона):
Поделитесь статьей с одноклассниками «ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК формулы площади, периметра, радиуса».
Формулы треугольника: площадь, периметр и примеры задач + обсуждение
В математике нас учат различным формам. Один из них — треугольник. Форма треугольника — это самая простая форма среди различных типов фигур.
Треугольник образован тремя сторонами с тремя углами, ограниченными отрезком. Также общий угол треугольника составляет 180 градусов.
Есть несколько типов треугольников. В зависимости от длины сторон бывают равносторонние треугольники с равной длиной сторон, равнобедренные треугольники с двумя равными сторонами ног и любой треугольник с разной длиной трех сторон.
Между тем, исходя из угла, существует острый треугольник с углом менее 90 градусов, тупой треугольник с одним углом более 90 градусов и прямоугольный треугольник с одним углом 90 градусов.
Что касается треугольников, необходимо знать несколько компонентов, включая площадь и периметр треугольника. Ниже приводится объяснение площади и периметра треугольника вместе с примером проблемы.
Площадь Треугольника
Площадь, площадь или площадь — это величина, которая выражает двумерный размер, а именно часть поверхности, четко обозначенную замкнутой кривой или линией.
Площадь треугольника равна размеру самого треугольника. Ниже приводится формула площади треугольника:
где L — площадь треугольника (см 2 ), a — основание треугольника (см), а h — высота треугольника (см).
Пример площади треугольника.
Пример проблемы 1
Есть острый треугольник с длиной основания a = 10 см и высотой h = 8 см. Вычислите площадь треугольника.
Также прочтите: Животные: характеристики, типы, примеры [ПОЛНОЕ объяснение]
Решение:
Если: a = 10 см, h = 8 см
Разыскивается: Площадь треугольника?
Ответ:
= 40 см2
Итак, площадь острого треугольника 40 см2.
Пример проблемы 2
Прямоугольный треугольник имеет основание 15 см и высоту 20 см. Найдите и вычислите площадь прямоугольного треугольника.
Решение:
Если: a = 15 см, h = 20 см
Разыскивается: Площадь треугольника?
Ответ:
= 150 см2
Итак, площадь прямоугольного треугольника составляет 150 см2.
Пример проблемы 3
Тупой треугольник с основанием 8 см и высотой 3 см, тогда какова площадь треугольника?
Решение:
Если: a = 8 см, h = 3 см
Разыскивается: Площадь треугольника?
Ответ:
= 12 см2
Итак, площадь тупого треугольника составляет 12 см2.
Пример задачи 4
Равнобедренный треугольник с такой же длиной стороны составляет 13 см, а основание треугольника — 10 см. Какова площадь равнобедренного треугольника?
Решение:
Вы знаете: s = 13 см, a = 10 см
Разыскивается: Площадь треугольника?
Ответ:
Высота треугольника неизвестна, поэтому мы используем формулу Пифагора, чтобы найти высоту треугольника:
Так как высота треугольника известна, то:
= 60 см2
Итак, площадь равнобедренного треугольника составляет 60 см2.
Периметр треугольника
Периметр — это количество сторон двумерной формы. Итак, периметр треугольника — это сумма сторон самого треугольника.
Вот формула периметра треугольника:
где K — периметр треугольника (см), а a, b, c — длины сторон треугольника (см).
Пример периметра треугольника
Пример проблемы 1
У равностороннего треугольника длина сторон 15 см. Каков периметр треугольника?
Решение:
Вы знаете: длина стороны = 15 см.
Ответ:
K = сторона a + сторона b + сторона c
поскольку это равносторонний треугольник, длины трех сторон равны.
= 45 см
Итак , периметр равностороннего треугольника 45 см.
Также прочтите: Социальное взаимодействие — полное определение и объяснение
Пример проблемы 2
У произвольного треугольника стороны 3 см, 5 см и 8 см. Вычислите периметр треугольника.
Решение:
Вы знаете: a = 3 см, b = 5 см и c = 8 см.
Ответ:
K = сторона a + сторона b + сторона c
= 16 см
Итак, периметр треугольника равен 16 см.
Пример проблемы 3
Равнобедренный треугольник имеет стороны 10 см и основание 6 см. Вычислите периметр равнобедренного треугольника.
Решение:
Вы знаете: стороны 10 см в длину, а 6 см в длину.
Ответ:
K = сторона a + сторона b + сторона c
поскольку треугольник равнобедренный, то есть две стороны одинаковой длины, а именно 10 см, тогда K = 10 + 10 + 6 = 26 см.
Итак, периметр равнобедренного треугольника равен 26 см.
Пример задачи 4
Равнобедренный треугольник имеет высоту 8 см и основание 12 см. Вычислите периметр треугольника.
Решение:
Вы знаете: высота треугольника h = 8 см.
сторона основания a = 12 см
Спросил : окружность =…. ?
?
Ответ:
K = сторона a + сторона b + сторона c
Две стороны треугольника неизвестны, поэтому мы используем формулу Пифагора, чтобы найти длину этой стороны.
К = 32 см
Итак, периметр равнобедренного треугольника равен 32 см.
Это объяснение площади треугольника и периметра треугольника, а также примеры и обсуждение. Может быть полезно.
Формулы прямоугольного треугольника
Если один из углов треугольника прямой (то есть равен ), то треугольник называется прямоугольным.
В прямоугольном треугольнике с , гипотенузой и катетами и
Площадь прямоугольного треугольника:
Радиус окружности, вписанной в прямоугольный треугольник
Радиус окружности, описанной около прямоугольного треугольника
Примеры решения задач
| Задание | В прямоугольном треугольнике с катетом 6 см и прилежащим к нему острым углом найти периметр и площадь.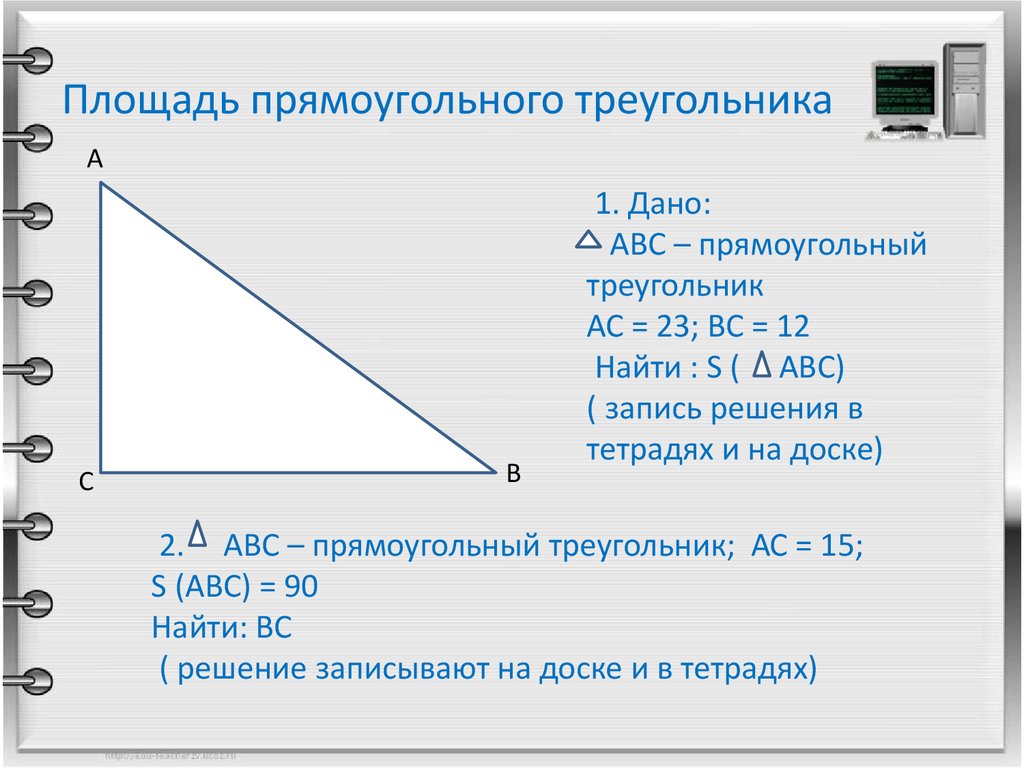 |
| Решение | Рассмотрим прямоугольный треугольник . Пусть катет см и . Найдем длину гипотенузы : |
Тогда по теореме Пифагора второй катет
Найдем периметр и площадь треугольника
| Задание | В прямоугольном треугольнике известно, что радиус описанной окружности см, а радиус вписанной окружности см. Найти стороны треугольника. |
| Решение | Рассмотрим прямоугольный треугольник с катетами и гипотенузой . Поскольку радиус описанной окружности равен половине гипотенузы, то |
Подставим в формулу для радиуса вписанной окружности известные данные:
откуда , а тогда . Воспользуемся теоремой Пифагора:
Решая квадратное уравнение , получим и . Тогда .
Как найти периметр треугольника с прямым углом. Как найти периметр треугольника если известны не все стороны
Периметром треугольника , как в прочем и любой фигуры, называется сумма длин всех сторон. Довольно часто это значение помогает найти площадь или используется для расчета других параметров фигуры.
Довольно часто это значение помогает найти площадь или используется для расчета других параметров фигуры.
Формула периметра треугольника выглядит так:
Пример расчета периметра треугольника. Пусть дан треугольник со сторонами a = 4см, b = 6 см, c = 7 см. подставим данные в формулу: см
Формула расчета периметра равнобедренного треугольника будет выглядеть так:
Формула расчета периметра равностороннего треугольника :
Пример расчета периметра равностороннего треугольника. Когда все стороны фигуры равны, то их можно просто умножить на три. Допустим, дан правильный треугольник со стороной 5 см в таком случае: см
В общем, когда все стороны даны, найти периметр довольно просто. В остальных же ситуациях требуется найти размер недостающей стороны. В прямоугольном треугольнике можно найти третью сторону по
Рассмотрим пример расчета периметра равнобедренного треугольника при условии, что мы знаем длину катетов в прямоугольном равнобедренном треугольнике.
Дан треугольник с катетами a
=b
=5 см. Найти периметр. Для начала найдем недостающую сторону с
. см
Теперь посчитаем периметр: см
Периметр прямоугольного равнобедренного треугольника будет равен 17 см.
В случае, когда известна гипотенуза и длина одного катета, можно найти недостающий по формуле:
Если в прямом треугольнике известна гипотенуза и один из острых углов, то недостающая сторона находится по формуле.
Прямоугольный треугольник — это частный вид произвольного треугольника. Как и любой другой треугольник он имеет три стороны, но один из его углов обязательно должен составлять 90 градусов. Ка только вы определили, что заданный треугольник является прямоугольным, можно приступить к нахождению его основных величин. Одной из характеристик прямоугольного треугольника является его периметр. Нахождению периметра прямоугольного треугольника посвящено много задач по геометрии. Перед тем как мы рассмотрим основные способы нахождения периметра прямоугольного треугольника, хотелось бы напомнить, что периметр любой геометрической фигуры на плоскости равен сумме длин все ее сторон.
где P — периметр треугольника;
a, b, c — стороны треугольника.
В прямоугольном треугольнике, как уже было сказано выше присутствует отличительная особенность в виде одного из углов, составляющего 90 градусов. Две стороны треугольника, прилегающие к данному углу называют катетами. Противоположную прямому углу сторону принято называть гипотенузой.
Необычные свойства прямоугольного треугольника было открыто Пифагором, который обнаружил, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов, что может быть записано в виде выражения:
Прямоугольный треугольник — это частный вид произвольного треугольника. Как и любой другой треугольник он имеет три стороны, но один из его углов обязательно должен составлять 90 градусов. Ка только вы определили, что заданный треугольник является прямоугольным, можно приступить к нахождению его основных величин. Одной из характеристик прямоугольного треугольника является его периметр.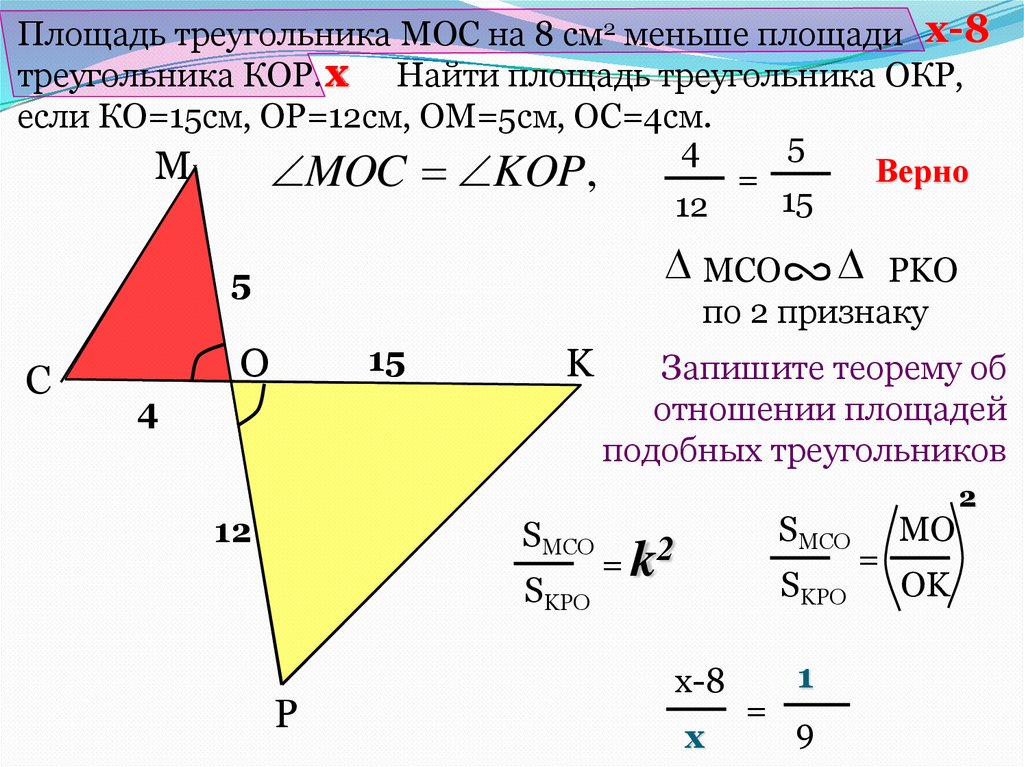 Нахождению периметра прямоугольного треугольника посвящено много задач по геометрии.
Нахождению периметра прямоугольного треугольника посвящено много задач по геометрии.
Где P — периметр треугольника;
A, b, c — стороны треугольника.
Исходя из теоремы Пифагора появилась возможность определять периметр прямоугольного треугольника по его двум любым сторонам известной длины. Если известны длины катетов, то периметр треугольника определяется через нахождение величины гипотенузы по формуле:
Если известен только один из катетов и длина гипотенузы, то периметр треугольника определяется через нахождение величины недостающего катета по формуле:
Если в прямоугольном треугольнике известна только длина гипотенузы с и один из прилегающих к ней острых углов α, то периметр треугольника в данном случае может быть определен по формуле:
В том случае, когда условиями задачи задана длина катета a и величина противолежащего ему острого угла α, то периметр прямоугольного треугольника в данном случае вычисляется по формуле:
Если же задан катет a с прилежащим к нему углом β, то периметр треугольника может быть рассчитан на основе выражения:
P = a + b + c, где, допустим,
P = v(a2 + b2) + a + b, или
P = v(c2 – b2) + b + с.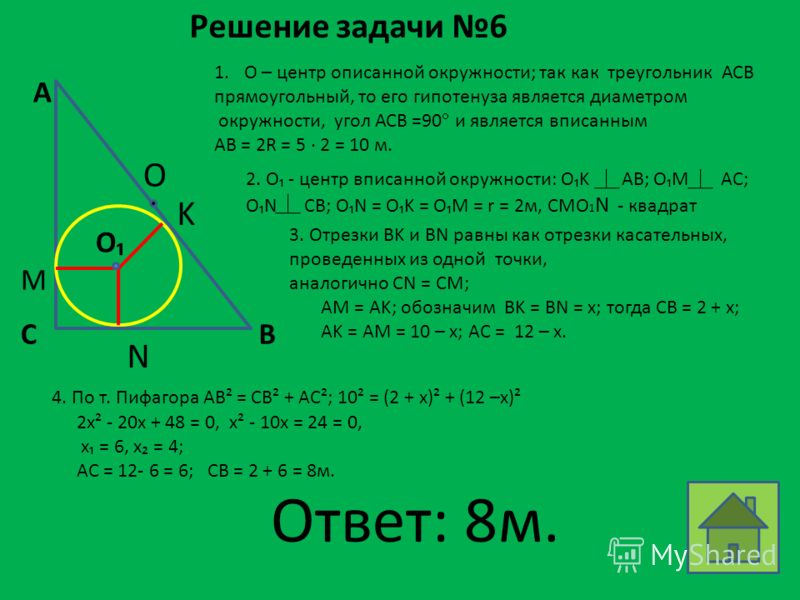
P = (1 + sin? + cos?)*с.
P = a*(1/tg? + 1/sin? + 1)
P = a*(1/сtg? + 1/cos? + 1)
Другие новости по теме:
Как найти периметр прямоугольного треугольника
Прямоугольным треугольником считается такой треугольник, один из углов которого равен 90 градусам, а два других являются острыми углами. Расчет периметра такого треугольника будет зависим от количества известных о нем данных.
В зависимости от случая, знание двух из трех сторон треугольника, а также одного из его острых углов.
Спонсор размещения P&G Статьи по теме «Как найти периметр прямоугольного треугольника» Как найти площадь поверхности пирамиды Как найти периметр если известна площадь Как найти периметр равностороннего треугольника
Способ 1.Если известны все три стороны треугольника, то, независимо от того, прямоугольный ли треугольник или нет, его периметр будет рассчитан так:
P = a + b + c, где, допустим,
Способ 2. Если в прямоугольнике известны только 2 стороны, то, используя теорему Пифагора, периметр этого треугольника можно рассчитать по формуле:
P = v(a2 + b2) + a + b, или
P = v(c2 – b2) + b + с.
Способ 3. Пусть в прямоугольном треугольнике даны гипотенуза c и острый угол?, то найти периметр можно будет таким образом:
P = (1 + sin? + cos?)*с.
Способ 4. Дано, что в прямоугольном треугольнике длина одного из катета равна a, а напротив него лежит острый угол?. Тогда расчет периметра этого треугольника будет вестись по формуле:
P = a*(1/tg? + 1/sin? + 1)
Способ 5. Пускай нам известен катет a и прилежащий к нему угол?, тогда периметр будет рассчитан так:
P = a*(1/сtg? + 1/cos? + 1)
Другие новости по теме:
Площадь и периметр — основные числовые характеристики любых геометрических фигур. Нахождение этих величин упрощается благодаря общепринятым формулам, согласно которым можно также вычислить одно через другое с минимумом или полным отсутствием дополнительных начальных данных. Спонсор размещения P&G
Равносторонний треугольник наряду с квадратом является, пожалуй, самой простой и симметричной фигурой в планиметрии. Разумеется, все соотношения, справедливые для обычного треугольника, верны также и для равностороннего. Однако для правильного треугольника все формулы становятся намного проще. Вам
Однако для правильного треугольника все формулы становятся намного проще. Вам
Периметр треугольника, как и любой другой плоской геометрической фигуры, составляет сумма длин ограничивающих его отрезков. Поэтому, чтобы вычислить длину периметра, надо знать длины его сторон. Но в силу того, что длины сторон в геометрических фигурах связаны определенными соотношениями с
Прямоугольным считается такой треугольник, у которого один из углов прямой. Сторона треугольника, расположенная напротив прямого угла, называется гипотенузой, а две другие стороны — катетами. Чтобы найти длины сторон прямоугольного треугольника, можно воспользоваться несколькими способами. Спонсор
Периметр любой геометрической фигуры, в том числе треугольника, равен совокупной длине границ этой фигуры. Он обозначается заглавной латинской буквой P и легко находится методом сложения длин всех сторон данной фигуры. Спонсор размещения P&G Статьи по теме «Как вычислить периметр треугольника»
Треугольник — это многоугольник, имеющий три стороны и три угла.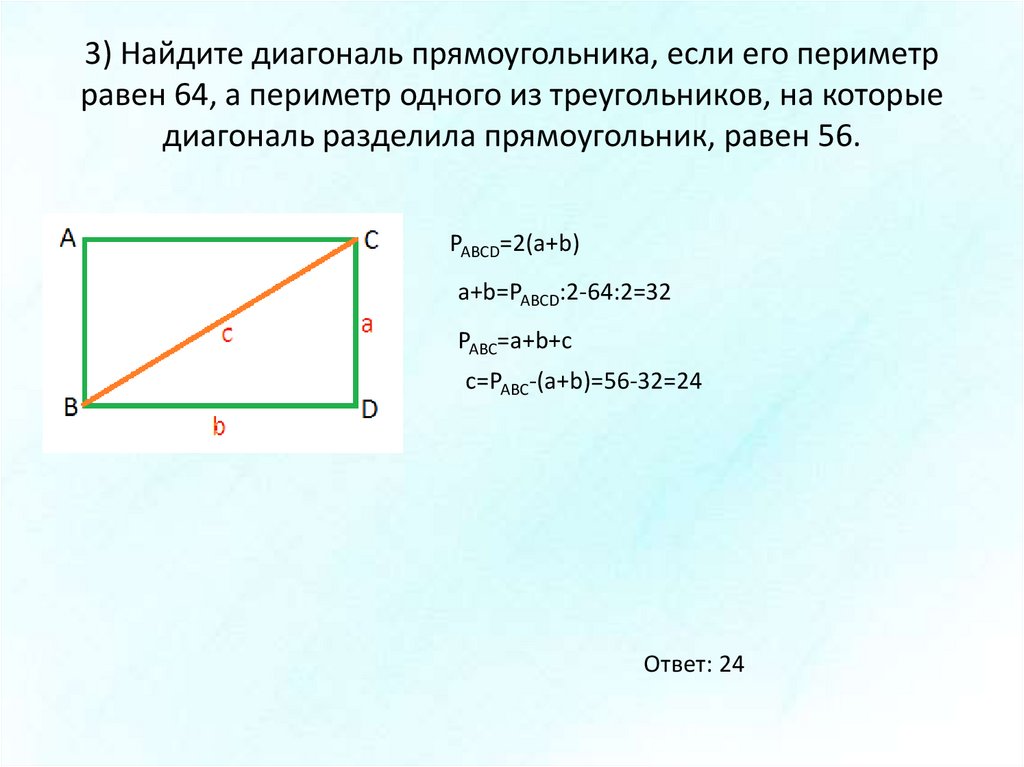 Как же вычислить его периметр? Спонсор размещения P&G Статьи по теме «Как находить периметр треугольника» Как найти периметр треугольника, заданного координатами своих вершин Как найти площадь треугольника Как найти длину и ширину
Как же вычислить его периметр? Спонсор размещения P&G Статьи по теме «Как находить периметр треугольника» Как найти периметр треугольника, заданного координатами своих вершин Как найти площадь треугольника Как найти длину и ширину
Гипотенуза – самая длинная сторона прямоугольного треугольника. Она расположена противоположно прямому углу. Способ нахождения гипотенузы прямоугольного треугольника зависит от того, какими исходными данными вы обладаете. Спонсор размещения P&G Статьи по теме «Как найти гипотенузу треугольника» Как
Прямоугольный треугольник характеризуется определенными соотношениями между углами и сторонами. Зная значения одних из них, можно вычислять другие. Для этого используются формулы, основанные, в свою очередь, на аксиомах и теоремах геометрии. Спонсор размещения P&G Статьи по теме «Как определить
Казалось бы, что может быть проще, чем вычисление площади и периметра треугольника – измерил стороны, поставил цифры в формулу – и все. Если вы так считаете, значит, забыли, что для этих целей существует не две простенькие формулы, а гораздо больше – для каждого вида треугольника – своя.
Периметр треугольника – сумма длин его сторон. Найти периметр треугольника часто требуется как в задачах начальной геометрии, так и в более трудных заданиях. При их решении недостающие величины находят из других данных. Основные зависимости периметра треугольника от его других измерений отражены в
Прямоугольным треугольником считается такой треугольник, один из углов которого равен 90 градусам, а два других являются острыми углами. Расчет периметра такого треугольника будет зависим от числа знаменитых о нем данных.
Вам понадобится
- В зависимости от случая, умение 2-х из 3 сторон треугольника, а также одного из его острых углов.
Инструкция
1. Метод 1.Если знамениты все три стороны треугольника , то, самостоятельно от того, прямоугольный ли треугольник либо нет, его периметр будет рассчитан так:P = a + b + c, где, возможен,c – гипотенуза;a и b – катеты.
2. Метод 2. Если в прямоугольнике вестимы только 2 стороны, то, применяя теорему Пифагора, периметр этого треугольника дозволено рассчитать по формуле:P = v(a2 + b2) + a + b, илиP = v(c2 – b2) + b + с.
3. Метод 3. Пускай в прямоугольном треугольнике даны гипотенуза c и острый угол?, то обнаружить периметр дозволено будет таким образом:P = (1 + sin ? + cos ?)*с.
4. Метод 4. Дано, что в прямоугольном треугольнике длина одного из катета равна a, а наоборот него лежит острый угол?. Тогда расчет периметра этого треугольника будет вестись по формуле:P = a*(1/tg ? + 1/sin ? + 1)
5. Метод 5. Пускай нам вестим катет a и прилежащий к нему угол?, тогда периметр будет рассчитан так:P = a*(1/сtg ? + 1/cos ? + 1)
Видео по теме
Прямоугольный треугольник — простая, но крайне важная для математики фигура. Знание о его свойствах и умение оперировать основными параметрами прямоугольного треугольника позволит вам справиться как со школьными, так и с реальными задачами.
Геометрия прямоугольного треугольника
Геометрически треугольник — это три точки, не лежащие на одной прямой, которые соединены между собой отрезками. Прямоугольный треугольник — фигура, две стороны которой образуют прямой угол. Эти стороны называются катетами треугольника, а третья, самая длинная сторона, носит название гипотенузы. Соотношение квадратов катетов и гипотенузы устанавливает теорема Пифагора — одна из фундаментальных теорем евклидовой геометрии.
Прямоугольный треугольник — фигура, две стороны которой образуют прямой угол. Эти стороны называются катетами треугольника, а третья, самая длинная сторона, носит название гипотенузы. Соотношение квадратов катетов и гипотенузы устанавливает теорема Пифагора — одна из фундаментальных теорем евклидовой геометрии.
Соотношения гипотенузы и катетов также положили основу для целого раздела математики — тригонометрии. Изначально синусы и косинусы определялись как функции углов прямоугольного треугольника, но в современном значении тригонометрические функции расширены на всю числовую ось. Сегодня тригонометрия используется во многих областях человеческой деятельности: от астрономии и океанографии до анализа финансовых рынков и разработки компьютерных игр.
Прямоугольный треугольник в реальности
Непосредственно прямоугольный треугольник встречается в реальности на каждом углу, как в прямом, так и в переносном смысле. Форму прямоугольного треугольника имеют грани тетраэдров и призм, которые в реальности превращаются в детали машин, керамическую плитку или скаты крыш. Угольник — чертежный инструмент, с которым человек впервые встречается на уроке геометрии, имеет форму именно прямоугольного треугольника и используется в проектировании, строительстве и столярном деле.
Угольник — чертежный инструмент, с которым человек впервые встречается на уроке геометрии, имеет форму именно прямоугольного треугольника и используется в проектировании, строительстве и столярном деле.
Периметр треугольника
Периметр — это численная оценка длин всех сторон плоской геометрической фигуры. Периметр n-угольника находится как сумма длин n сторон. Для определения периметра прямоугольного треугольника используется простая формула:
a и b – катеты, c – гипотенуза.
Вычисляя периметр треугольника вручную, вам пришлось бы измерять все три стороны, проводить дополнительные тригонометрические операции или вычисления по теореме Пифагора. Используя онлайн-калькулятор вам достаточно узнать следующие пары переменных:
- два катета;
- катет и угол;
- гипотенуза и угол.
В школьных задачах или на практике вам будут заданы исходные данные, поэтому калькулятор позволяет найти периметр, зная разные пары параметров. Кроме того, инструмент автоматически рассчитывает все остальные атрибуты прямоугольного треугольника, то есть длины всех сторон и величины всех углов. Рассмотрим пару примеров.
Рассмотрим пару примеров.
Примеры из жизни
Школьная задача
Пусть в школьной задаче вам задан прямоугольный треугольник с длиной катета равным 5 см и прилежащим углом, величина которого составляет 60 градусов. Требуется найти периметр геометрической фигуры. Онлайн-калькулятор сопровождается рисунком, на котором изображены стороны и углы прямоугольного треугольника. Мы видим, что если катет a = 5 см, то его прилежащий угол — это угол бета. Это важный момент, так как если вы используете для расчетов угол альфа, то результат будет неверным. Вбиваем эти данные в форму и получаем ответ в виде:
Помимо непосредственно периметра, наша программа также определила величину противолежащего угла, а также длину второго катета и гипотенузы.
Обустройство клумбы
Допустим, вы хотите сделать ограду для клумбы, которая имеет форму прямоугольного треугольника. Для этого вам необходимо узнать периметр фигуры. Конечно, в реальности вы можете просто замерить все три стороны, но легко упростить себе задачу и измерить только два катета. Пусть они имеют длину 8 и 15 метров. Вбиваем эти данные в форму калькулятора и получаем ответ:
Пусть они имеют длину 8 и 15 метров. Вбиваем эти данные в форму калькулятора и получаем ответ:
Итак, вам понадобится закупить материалы для обустройства 40 метров ограды. Наш калькулятор также подсчитал длину гипотенузы — 17 метров. Числа 8, 15 и 17 составляют пифагорову тройку — натуральные числа, которые удовлетворяют условиям теоремы Пифагора.
Заключение
Прямоугольные треугольники получили широкое распространение в повседневности, поэтому определение площади или периметра геометрической фигуры наверняка пригодится вам при решении школьных задач или бытовых вопросов.
Прямоугольным треугольником считается такой треугольник, один из углов которого равен 90 градусам, а два других являются острыми углами. Расчет периметра такого треугольника будет зависим от количества известных о нем данных.
Вам понадобится
- В зависимости от случая, знание двух из трех сторон треугольника, а также одного из его острых углов.
Инструкция
- Способ 1.
 Если известны все три стороны треугольника , то, независимо от того, прямоугольный ли треугольник или нет, его периметр будет рассчитан так:
Если известны все три стороны треугольника , то, независимо от того, прямоугольный ли треугольник или нет, его периметр будет рассчитан так:
P = a + b + c, где, допустим,
c — гипотенуза;
a и b — катеты. - Способ 2. Если в прямоугольнике известны только 2 стороны, то, используя теорему Пифагора, периметр этого треугольника можно рассчитать по формуле:
P = v(a2 + b2) + a + b, или
P = v(c2 – b2) + b + с. - Способ 3. Пусть в прямоугольном треугольнике даны гипотенуза c и острый угол?, то найти периметр можно будет таким образом:
P = (1 + sin ? + cos ?)*с. - Способ 4. Дано, что в прямоугольном треугольнике длина одного из катета равна a, а напротив него лежит острый угол?. Тогда расчет периметра этого треугольника будет вестись по формуле:
P = a*(1/tg ? + 1/sin ? + 1) - Способ 5. Пускай нам известен катет a и прилежащий к нему угол?, тогда периметр будет рассчитан так:
P = a*(1/сtg ? + 1/cos ? + 1)
Чему равен периметр прямоугольника треугольника.
 Находим периметр треугольника различными способами
Находим периметр треугольника различными способамиПрямоугольный треугольник — простая, но крайне важная для математики фигура. Знание о его свойствах и умение оперировать основными параметрами прямоугольного треугольника позволит вам справиться как со школьными, так и с реальными задачами.
Геометрия прямоугольного треугольника
Геометрически треугольник — это три точки, не лежащие на одной прямой, которые соединены между собой отрезками. Прямоугольный треугольник — фигура, две стороны которой образуют прямой угол. Эти стороны называются катетами треугольника, а третья, самая длинная сторона, носит название гипотенузы. Соотношение квадратов катетов и гипотенузы устанавливает теорема Пифагора — одна из фундаментальных теорем евклидовой геометрии.
Соотношения гипотенузы и катетов также положили основу для целого раздела математики — тригонометрии. Изначально синусы и косинусы определялись как функции углов прямоугольного треугольника, но в современном значении тригонометрические функции расширены на всю числовую ось.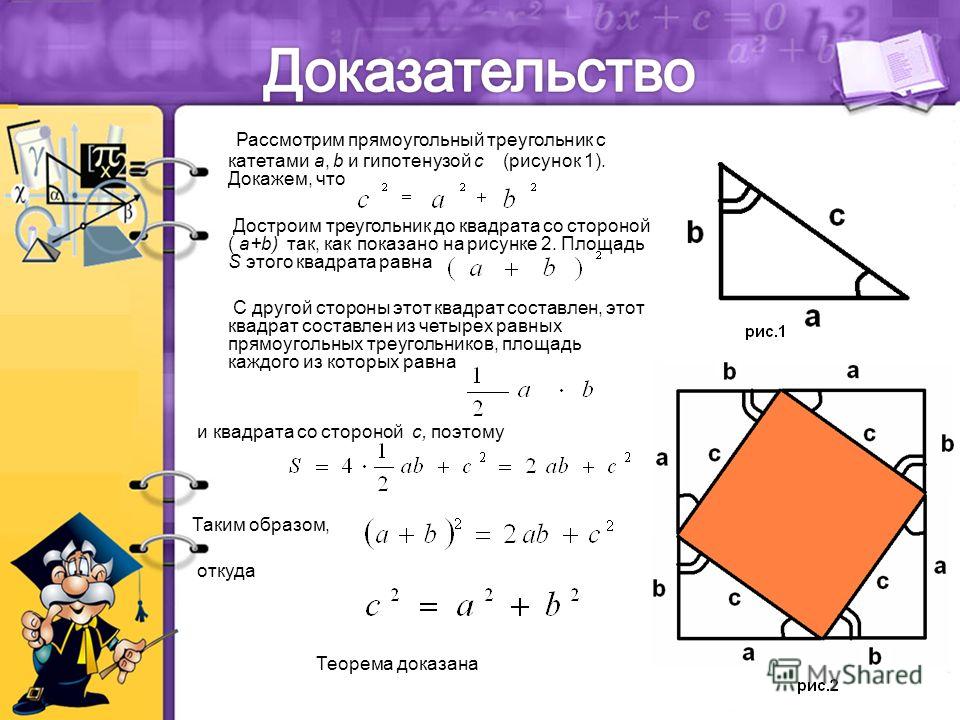 Сегодня тригонометрия используется во многих областях человеческой деятельности: от астрономии и океанографии до анализа финансовых рынков и разработки компьютерных игр.
Сегодня тригонометрия используется во многих областях человеческой деятельности: от астрономии и океанографии до анализа финансовых рынков и разработки компьютерных игр.
Прямоугольный треугольник в реальности
Непосредственно прямоугольный треугольник встречается в реальности на каждом углу, как в прямом, так и в переносном смысле. Форму прямоугольного треугольника имеют грани тетраэдров и призм, которые в реальности превращаются в детали машин, керамическую плитку или скаты крыш. Угольник — чертежный инструмент, с которым человек впервые встречается на уроке геометрии, имеет форму именно прямоугольного треугольника и используется в проектировании, строительстве и столярном деле.
Периметр треугольника
Периметр — это численная оценка длин всех сторон плоской геометрической фигуры. Периметр n-угольника находится как сумма длин n сторон. Для определения периметра прямоугольного треугольника используется простая формула:
a и b – катеты, c – гипотенуза.
Вычисляя периметр треугольника вручную, вам пришлось бы измерять все три стороны, проводить дополнительные тригонометрические операции или вычисления по теореме Пифагора.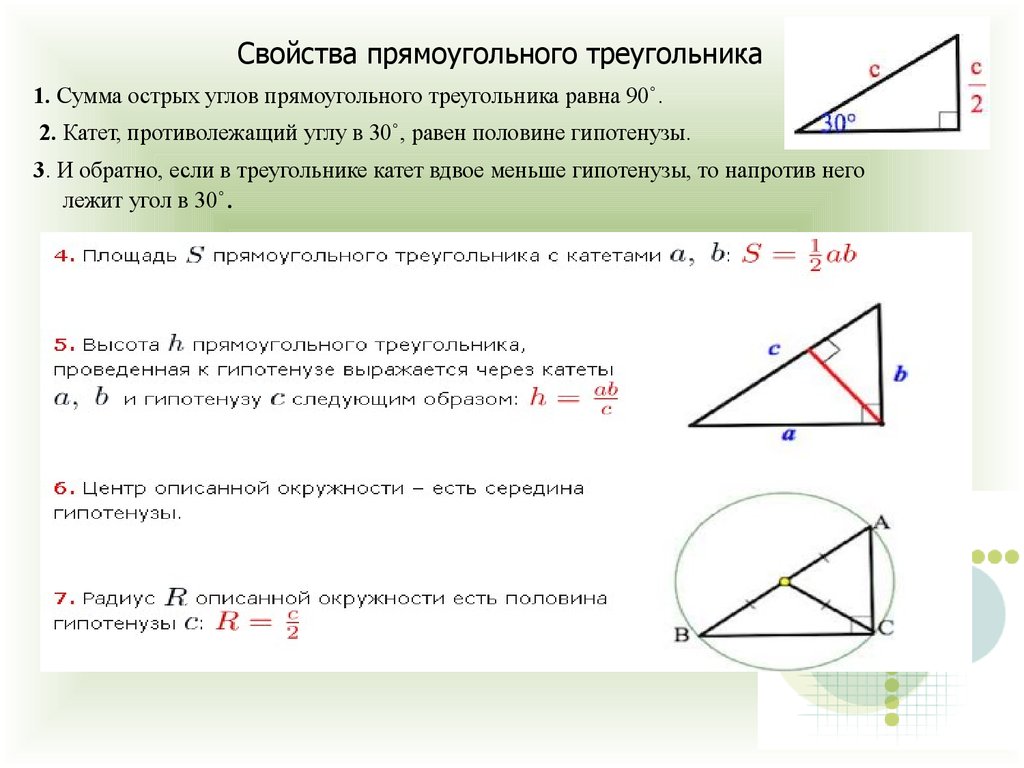 Используя онлайн-калькулятор вам достаточно узнать следующие пары переменных:
Используя онлайн-калькулятор вам достаточно узнать следующие пары переменных:
- два катета;
- катет и угол;
- гипотенуза и угол.
В школьных задачах или на практике вам будут заданы исходные данные, поэтому калькулятор позволяет найти периметр, зная разные пары параметров. Кроме того, инструмент автоматически рассчитывает все остальные атрибуты прямоугольного треугольника, то есть длины всех сторон и величины всех углов. Рассмотрим пару примеров.
Примеры из жизни
Школьная задача
Пусть в школьной задаче вам задан прямоугольный треугольник с длиной катета равным 5 см и прилежащим углом, величина которого составляет 60 градусов. Требуется найти периметр геометрической фигуры. Онлайн-калькулятор сопровождается рисунком, на котором изображены стороны и углы прямоугольного треугольника. Мы видим, что если катет a = 5 см, то его прилежащий угол — это угол бета. Это важный момент, так как если вы используете для расчетов угол альфа, то результат будет неверным.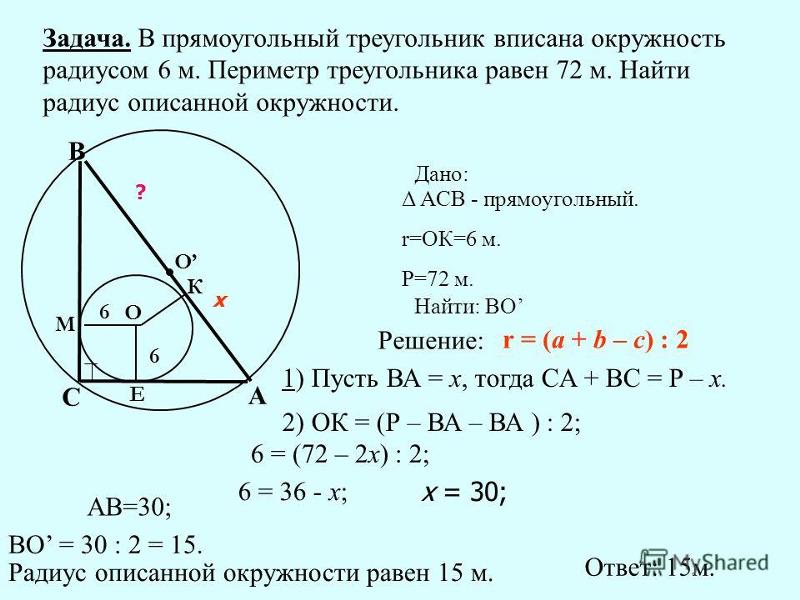 Вбиваем эти данные в форму и получаем ответ в виде:
Вбиваем эти данные в форму и получаем ответ в виде:
Помимо непосредственно периметра, наша программа также определила величину противолежащего угла, а также длину второго катета и гипотенузы.
Обустройство клумбы
Допустим, вы хотите сделать ограду для клумбы, которая имеет форму прямоугольного треугольника. Для этого вам необходимо узнать периметр фигуры. Конечно, в реальности вы можете просто замерить все три стороны, но легко упростить себе задачу и измерить только два катета. Пусть они имеют длину 8 и 15 метров. Вбиваем эти данные в форму калькулятора и получаем ответ:
Итак, вам понадобится закупить материалы для обустройства 40 метров ограды. Наш калькулятор также подсчитал длину гипотенузы — 17 метров. Числа 8, 15 и 17 составляют пифагорову тройку — натуральные числа, которые удовлетворяют условиям теоремы Пифагора.
Заключение
Прямоугольные треугольники получили широкое распространение в повседневности, поэтому определение площади или периметра геометрической фигуры наверняка пригодится вам при решении школьных задач или бытовых вопросов.
Одной из базовых геометрических фигур является треугольник. Он образуется при пересечении трех отрезков прямых. Данные отрезки прямых формируют стороны фигуры, а точки их пересечения называются вершинами. Каждый школьник, изучающий курс геометрии, обязан уметь находить периметр этой фигуры. Полученное умение будет полезным для многих и во взрослой жизни, к примеру, пригодится студенту, инженеру, строителю,
Существуют разные способы найти периметр треугольника. Выбор необходимой для вас формулы зависит от имеющихся исходных данных. Чтобы записать данную величину в математической терминологии используют специальное обозначение – Р. Рассмотрим, что такое периметр, основные способы его расчета для треугольных фигур разных видов.
Самым простым способом найти периметр фигуры, если есть данные всех сторон. В этом случае используется следующая формула:
Буквой «P» обозначается сама величина периметра. В свою очередь «a», «b» и «c» – это длины сторон.
Зная размер трех величин, достаточно будет получить их сумму, которая и является периметром.
Альтернативный вариант
В математических задачах все данные длины редко бывают известны. В таких случаях рекомендуется воспользоваться альтернативным способом поиска нужной величины. Когда в условиях указана длина двух прямых, а также угол, находящийся между ними, расчет производится через поиск третьей. Для поиска этого числа необходимо добыть квадратный корень по формуле:
.
Периметр по двум сторонам
Для расчета периметра не обязательно знать все данные геометрической фигуры. Рассмотрим способы расчета по двум сторонам.
Равнобедренный треугольник
Равнобедренным называется такой треугольник, не меньше двух сторон которого имеют одинаковую длину. Они называются боковыми, а третья сторона – основанием. Равные прямые образовывают вершинный угол. Особенностью в равнобедренном треугольникеявляется наличие одной оси симметрии. Ось – вертикальная линия, выходящая из вершинного угла и заканчивающаяся посредине основания. По своей сути ось симметрии включает в себя такие понятия:
- биссектриса вершинного угла;
- медиана к основанию;
- высота треугольника;
- срединный перпендикуляр.

Чтобы определить периметр равнобедренного вида треугольной фигуры, воспользуйтесь формулой.
В данном случае вам необходимо знать только две величины: основание и длину одной стороны. Обозначение «2а» подразумевает умножение длины боковой стороны на 2. К полученной цифре нужно добавить величину основания – «b».
В исключительном случае, когда длина основания равнобедренного треугольника равна его боковой прямой, можно воспользоваться более простым способом. Он выражается в следующей формуле:
Для получения результата достаточно умножить это число на три. Эта формула используется для того, чтобы найти периметр правильного треугольника.
Полезное видео: задачи на периметр труегольника
Треугольник прямоугольный
Главным отличием прямоугольного треугольника от других геометрических фигур этой категории является наличие угла 90°. По этому признаку и определяется вид фигуры. Прежде, чем определить, как найти периметр прямоугольного треугольника, стоит заметить, что данная величина для любой плоской геометрической фигуры составляет сумму всех сторон.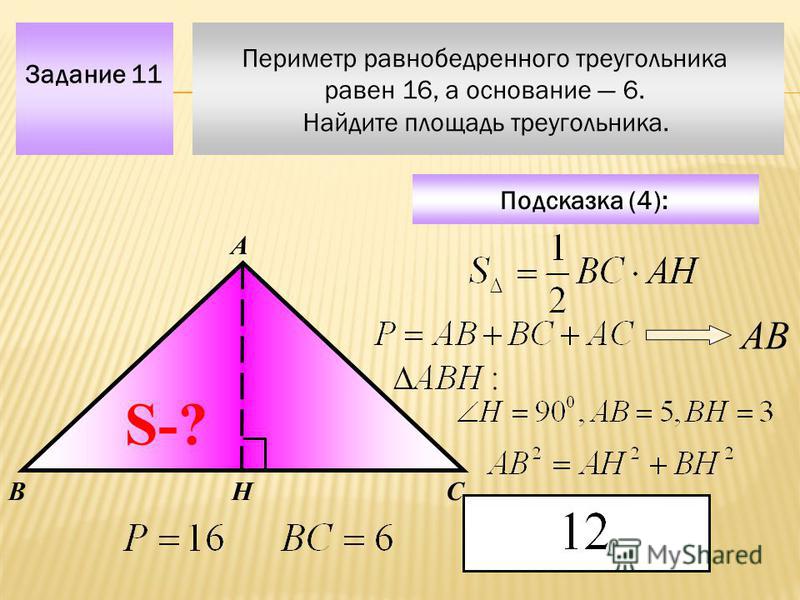 Так и в этом случае самый простой способ узнать результат – суммировать три величины.
Так и в этом случае самый простой способ узнать результат – суммировать три величины.
В научной терминологии те стороны, которые прилегают к прямому углу, имеют название «катеты», а противоположная к углу 90º – гипотенуза. Особенности этой фигуры исследовались еще древнегреческим ученым Пифагором. Согласно с теоремой Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
.
На основании данной теоремы выведена еще одна формула, объясняющая, как найти периметр треугольника по двум известным сторонам. Рассчитать периметр при указанной длине катетов можно, используя следующий способ.
.
Чтобы узнать периметр, имея информацию о размере одного катета и гипотенузы, нужно определить длину второй гипотенузы. С этой целью используют такие формулы:
.
Также периметр описанного вида фигуры определяется и без данных о размерах катетов.
Вам потребуется знать длину гипотенузы, а также угол, прилегающий к ней. Зная длину одного из катетов, если имеется угол, прилегающий к нему, периметр фигуры рассчитывают по формуле:
.
Расчет через высоту
Рассчитать периметр таких категорий, как равнобедренные и прямоугольные треугольники, можно через показатель их средней линии. Как известно, высота треугольника разделяет его основание пополам. Таким образом, она образует две прямоугольных фигуры. Далее, нужный показатель вычисляется при помощи теоремы Пифагора. Формула будет иметь следующий вид:
.
Если известна высота и половина основания, используя этот способ, вы получите нужное число без поиска остальных данных о фигуре.
Полезное видео: нахождение периметра треугольника
Периметром треугольника , как в прочем и любой фигуры, называется сумма длин всех сторон. Довольно часто это значение помогает найти площадь или используется для расчета других параметров фигуры.
Формула периметра треугольника выглядит так:
Пример расчета периметра треугольника. Пусть дан треугольник со сторонами a = 4см, b = 6 см, c = 7 см. подставим данные в формулу: см
Формула расчета периметра равнобедренного треугольника будет выглядеть так:
Формула расчета периметра равностороннего треугольника :
Пример расчета периметра равностороннего треугольника.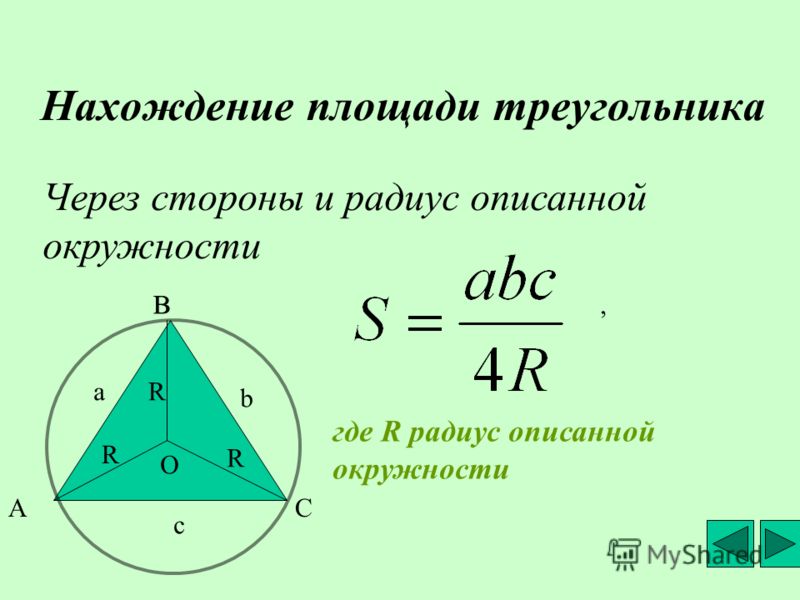 Когда все стороны фигуры равны, то их можно просто умножить на три. Допустим, дан правильный треугольник со стороной 5 см в таком случае: см
Когда все стороны фигуры равны, то их можно просто умножить на три. Допустим, дан правильный треугольник со стороной 5 см в таком случае: см
В общем, когда все стороны даны, найти периметр довольно просто. В остальных же ситуациях требуется найти размер недостающей стороны. В прямоугольном треугольнике можно найти третью сторону по теореме Пифагора . К примеру, если известны длины катетов, то можно найти гипотенузу по формуле:
Рассмотрим пример расчета периметра равнобедренного треугольника при условии, что мы знаем длину катетов в прямоугольном равнобедренном треугольнике.
Дан треугольник с катетами a
=b
=5 см. Найти периметр. Для начала найдем недостающую сторону с
. см
Теперь посчитаем периметр: см
Периметр прямоугольного равнобедренного треугольника будет равен 17 см.
В случае, когда известна гипотенуза и длина одного катета, можно найти недостающий по формуле:
Если в прямом треугольнике известна гипотенуза и один из острых углов, то недостающая сторона находится по формуле.
Периметр – это величина, подразумевающая длину всех сторон плоской (двумерной) геометрической фигуры. Для разных геометрических фигур существуют разные способы нахождения периметра.
В данной статье вы узнаете как находить периметр фигуры разными способами, в зависимости от известных его граней.
Возможные методы:
- известны все три стороны равнобедренного или любого другого треугольника;
- как найти периметр прямоугольного треугольника при двух известных его гранях;
- известны две грани и угол, который расположен между ними (формула косинусов) без средней линии и высоты.
Первый метод: известны все стороны фигуры
Как находить периметра треугольника, когда известны все три грани , необходимо использовать следующую формулу: P = a + b + c, где a,b,c – известные длины всех сторон треугольника, P – периметр фигуры.
Например, известны три стороны фигуры: a = 24 см, b = 24 см, c = 24 см. Это правильная равнобедренная фигура, чтобы вычислить периметр пользуемся формулой: P = 24 + 24 + 24 = 72 см.
Данная формула подходит к любому треугольнику , необходимо просто знать длины всех его сторон. Если хотя бы одна из них неизвестна, необходимо воспользоваться другими способами, о которых мы поговорим ниже.
Еще один пример: a = 15 см, б = 13 см, c = 17 см. Вычисляем периметр: P = 15 + 13 + 17 = 45 см.
Очень важно помечать единицу измерения в полученном ответе. В наших примерах длины сторон указаны в сантиметрах (см), однако, существуют разные задачи, в условиях которых присутствуют другие единицы измерения.
Второй метод: прямоугольный треугольник и две известные его стороны
В том случае, когда в задании, которое нужно решить, дана прямоугольная фигура, длины двух граней которой известны, а третья нет, необходимо воспользоваться теоремой Пифагора.
Описывает соотношение между гранями прямоугольного треугольника. Формула, описываемая этой теоремой, является одной из самых известных и наиболее часто применяемых теорем в геометрии. Итак, сама теорема:
Стороны любого прямоугольного треугольника описываются таким уравнением: a^2 + b^2 = c^2, где а и b – катеты фигуры, а c – гипотенуза.
2 – (2 * a * b * cos(C)), где a,b,c – стандартно длины граней, а A,B и С – это углы, которые лежат напротив соответствующих граней треугольника. То есть, A – угол, противолежащий стороне a и так далее.
Представим, что описан треугольник, стороны а и б которого составляют 100 см и 120 см соответственно, а угол, лежащий между ними, составляет 97 градусов. То есть а = 100 см, б = 120 см, C = 97 градусов.
Все, что нужно сделать в данном случае – это подставить все известные значения в теорему косинусов. Длины известных граней возводятся в квадрат, после чего известные стороны перемножаются между друг другом и на два и умножаются на косинус угла между ними. Далее, необходимо сложить квадраты граней и отнять от них второе полученное значение. Из итоговой величины извлекается квадратный корень – это будет третья, неизвестная до этого сторона.
После того как все три грани фигуры известны, осталось воспользоваться уже полюбившейся нам стандартной формулой поиска периметра описываемой фигуры из первого метода.
1) у = 2х + 5 2) у = 4 – 3х 3) у = 8х – 2 4) у = 5х 5) у = 0,1х + 8 6) Х = 2 7) У = х – 3, у = 2х + 3 у = -3х + 1 у = 4х – 2 у = 5х + 2 у = 3 у = -х у = -3 + х, 1) 0 2) 0 3) 1 4) 0 5) 1 6) 1 7) Бесконечное множество. с тестами по карточкам. Карточка № 1. А10. Соотнесите функции, заданные формулами с их графиками (рис. 1).
?
Прямоугольный треугольник — это частный вид произвольного треугольника. Как и любой другой треугольник он имеет три стороны, но один из его углов обязательно должен составлять 90 градусов. Ка только вы определили, что заданный треугольник является прямоугольным, можно приступить к нахождению его основных величин. Одной из характеристик прямоугольного треугольника является его периметр. Нахождению периметра прямоугольного треугольника посвящено много задач по геометрии.
Где P — периметр треугольника;
A, b, c — стороны треугольника.
Исходя из теоремы Пифагора появилась возможность определять периметр прямоугольного треугольника по его двум любым сторонам известной длины.
Если известны длины катетов, то периметр треугольника определяется через нахождение величины гипотенузы по формуле:
Если известен только один из катетов и длина гипотенузы, то периметр треугольника определяется через нахождение величины недостающего катета по формуле:
Если в прямоугольном треугольнике известна только длина гипотенузы с и один из прилегающих к ней острых углов α, то периметр треугольника в данном случае может быть определен по формуле:
В том случае, когда условиями задачи задана длина катета a и величина противолежащего ему острого угла α, то периметр прямоугольного треугольника в данном случае вычисляется по формуле:
Если же задан катет a с прилежащим к нему углом β, то периметр треугольника может быть рассчитан на основе выражения:
Как найти периметр прямоугольного треугольника
P = a + b + c, где, допустим,
P = v(a2 + b2) + a + b, или
P = v(c2 – b2) + b + с.
P = (1 + sin? + cos?)*с.
P = a*(1/tg? + 1/sin? + 1)
P = a*(1/сtg? + 1/cos? + 1)
Другие новости по теме:
Площадь и периметр — основные числовые характеристики любых геометрических фигур.
Нахождение этих величин упрощается благодаря общепринятым формулам, согласно которым можно также вычислить одно через другое с минимумом или полным отсутствием дополнительных начальных данных. Спонсор размещения P&G
Равносторонний треугольник наряду с квадратом является, пожалуй, самой простой и симметричной фигурой в планиметрии. Разумеется, все соотношения, справедливые для обычного треугольника, верны также и для равностороннего. Однако для правильного треугольника все формулы становятся намного проще. Вам
Периметр треугольника, как и любой другой плоской геометрической фигуры, составляет сумма длин ограничивающих его отрезков. Поэтому, чтобы вычислить длину периметра, надо знать длины его сторон. Но в силу того, что длины сторон в геометрических фигурах связаны определенными соотношениями с
Прямоугольным считается такой треугольник, у которого один из углов прямой. Сторона треугольника, расположенная напротив прямого угла, называется гипотенузой, а две другие стороны — катетами.
Чтобы найти длины сторон прямоугольного треугольника, можно воспользоваться несколькими способами. Спонсор
Периметр любой геометрической фигуры, в том числе треугольника, равен совокупной длине границ этой фигуры. Он обозначается заглавной латинской буквой P и легко находится методом сложения длин всех сторон данной фигуры. Спонсор размещения P&G Статьи по теме «Как вычислить периметр треугольника»
Треугольник — это многоугольник, имеющий три стороны и три угла. Как же вычислить его периметр? Спонсор размещения P&G Статьи по теме «Как находить периметр треугольника» Как найти периметр треугольника, заданного координатами своих вершин Как найти площадь треугольника Как найти длину и ширину
Гипотенуза – самая длинная сторона прямоугольного треугольника. Она расположена противоположно прямому углу. Способ нахождения гипотенузы прямоугольного треугольника зависит от того, какими исходными данными вы обладаете. Спонсор размещения P&G Статьи по теме «Как найти гипотенузу треугольника» Как
Прямоугольный треугольник характеризуется определенными соотношениями между углами и сторонами.
Зная значения одних из них, можно вычислять другие. Для этого используются формулы, основанные, в свою очередь, на аксиомах и теоремах геометрии. Спонсор размещения P&G Статьи по теме «Как определить
Казалось бы, что может быть проще, чем вычисление площади и периметра треугольника – измерил стороны, поставил цифры в формулу – и все. Если вы так считаете, значит, забыли, что для этих целей существует не две простенькие формулы, а гораздо больше – для каждого вида треугольника – своя. Вам
Периметр треугольника – сумма длин его сторон. Найти периметр треугольника часто требуется как в задачах начальной геометрии, так и в более трудных заданиях. При их решении недостающие величины находят из других данных. Основные зависимости периметра треугольника от его других измерений отражены в
Периметр прямоугольного треугольника формула
Как найти периметр прямоугольного треугольника
Прямоугольным треугольником считается такой треугольник, один из углов которого равен 90 градусам, а два других являются острыми углами.
Расчет периметра такого треугольника будет зависим от количества известных о нем данных.
В зависимости от случая, знание двух из трех сторон треугольника, а также одного из его острых углов.
Спонсор размещения P&G Статьи по теме «Как найти периметр прямоугольного треугольника» Как найти площадь поверхности пирамиды Как найти периметр если известна площадь Как найти периметр равностороннего треугольника
Способ 1.Если известны все три стороны треугольника, то, независимо от того, прямоугольный ли треугольник или нет, его периметр будет рассчитан так:
P = a + b + c, где, допустим,
Способ 2. Если в прямоугольнике известны только 2 стороны, то, используя теорему Пифагора, периметр этого треугольника можно рассчитать по формуле:
P = v(a2 + b2) + a + b, или
P = v(c2 – b2) + b + с.
Способ 3. Пусть в прямоугольном треугольнике даны гипотенуза c и острый угол?, то найти периметр можно будет таким образом:
P = (1 + sin? + cos?)*с.
Способ 4.
Дано, что в прямоугольном треугольнике длина одного из катета равна a, а напротив него лежит острый угол?. Тогда расчет периметра этого треугольника будет вестись по формуле:
P = a*(1/tg? + 1/sin? + 1)
Способ 5. Пускай нам известен катет a и прилежащий к нему угол?, тогда периметр будет рассчитан так:
P = a*(1/сtg? + 1/cos? + 1)
Периметр прямоугольного треугольника
Периметр геометрической фигуры – это общая длина ее границы. Следовательно, периметр прямоугольного треугольника означает сумму всех его сторон. Давайте рассмотрим различные формулы и методы, связанные с периметром прямоугольного треугольника.
1. Каков периметр прямоугольного треугольника? 2. Как найти периметр прямоугольного треугольника? 3. Часто задаваемые вопросы о периметре прямоугольного треугольника Каков периметр прямоугольного треугольника?
Периметр прямоугольного треугольника равен сумме всех его сторон.
Например, если a, b и c — стороны прямоугольного треугольника, то его периметр будет равен: (a + b + c). Теперь, поскольку это прямоугольный треугольник, можно сказать, что его периметр равен сумме длин двух сторон и гипотенузы. Обратите внимание на следующий рисунок, на котором показан прямоугольный треугольник со сторонами a, b и c, где c — гипотенуза, а a, b — стороны, которые вместе образуют треугольник.угол 0°. Три стороны можно назвать следующим образом: a = высота, b = основание и c = гипотенуза.
Как найти периметр прямоугольного треугольника?
Существуют различные методы нахождения периметра прямоугольного треугольника. Для этого нам нужно проверить параметры по заданному условию. Давайте посмотрим на различные методы в соответствии с заданными параметрами.
Методы нахождения периметра прямоугольного треугольника
Метод 1. Когда известны все стороны прямоугольного треугольника.
Если мы знаем длины всех сторон прямоугольного треугольника, то нам нужно просто просуммировать их длины.Например, если заданы стороны p, q и r, то периметр = p + q + r. Этот метод возможен только тогда, когда известны измерения всех сторон.
Способ 2: Когда длины сторон не указаны, но прямоугольный треугольник нарисован в масштабе.
В этом случае мы используем линейку для измерения сторон и складываем измерения каждой стороны. Периметр прямоугольного треугольника = сумма всех сторон, измеренных линейкой.Метод 3: Когда даны любые две стороны прямоугольного треугольника.
В этом случае мы сначала находим недостающую сторону по теореме Пифагора, а затем вычисляем периметр прямоугольного треугольника. Теорема Пифагора утверждает, что квадрат длины гипотенузы равен сумме квадратов двух других сторон прямоугольного треугольника. (Гипотенуза) 2 = (Основание) 2 + (Высота) 2
Обратите внимание на приведенный ниже треугольник, где «а» и «b» — стороны, которые вместе образуют 92}\) (если b не указано)Статьи по теме о периметре прямоугольного треугольника
Прочтите следующие статьи, чтобы узнать больше о периметре прямоугольного треугольника.
- Периметр
- Прямоугольный треугольник
- Треугольники
- Типы треугольников
- Площадь треугольника
- Высота треугольника Формула
- Формула подобных треугольников
Примеры по периметру прямоугольного треугольника
Пример 1: Найдите периметр прямоугольного треугольника, если его основание равно 4 единицам, высота (высота) равна 12 единицам, а гипотенуза равна 20 единицам.
Решение: Дано: основание = 4 единицы, высота = 12 единиц, гипотенуза = 20 единиц.
Периметр прямоугольного треугольника = основание + высота + гипотенуза = 4 + 12 + 20 = 36 единицПример 2: В прямоугольном треугольнике, если основание равно 6 единицам, а высота равна 8 единицам, найдите его периметр.
Решение: Дано: основание = 6 единиц, высота = 8 единиц
Сторона гипотенузы отсутствует, поэтому для вычисления гипотенузы воспользуемся теоремой Пифагора.
(Гипотенуза) 2 = (Основание) 2 + (Высота) 2
(Гипотенуза) 2 = (6) 2 + (8) 2(Гипотенуза) 2 = (36 + 64)
Гипотенуза = √102 периметра √100 = 10 единиц прямоугольный треугольник = 8 + 6 + 10 = 24 единицы.
Пример 3: Найдите периметр прямоугольного треугольника, если основание равно 5 единицам, а гипотенуза 13 единицам.
Решение: Дано: основание = 5 единиц, гипотенуза = 13 единиц
Используя теорему Пифагора, найдем высоту.
(Гипотенуза) 2 = (Основание) 2 + (Высота) 2
(13) 2 = (5) 2 + (а) 2
(13) 2 — (5) 2 = (а) 2
169 — 25 = √144
Высота = 12 шт.
Следовательно, периметр данного прямоугольного треугольника = 5 + 13 + 12 = 30 единиц.перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.
Забронировать бесплатный пробный урок
Практические вопросы по периметру прямоугольного треугольника
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о периметре прямоугольного треугольника
Что такое периметр прямоугольного треугольника в математике?
Периметр прямоугольного треугольника равен сумме длин всех трех сторон, включая гипотенузу, высоту (высоту) и основание. Если x, y и z — стороны прямоугольного треугольника, то его периметр = (x + y + z).
Что такое теорема Пифагора для прямоугольного треугольника?
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов двух других сторон. Например, если «a» и «b» — стороны, образующие угол 90°, а «c» — гипотенуза, то теорема Пифагора записывается как c 2 = a 2 + b 2 .
В чем разница между площадью и периметром прямоугольного треугольника?
Площадь прямоугольного треугольника равна площади, которую он занимает. Он рассчитывается по формуле: Площадь = ½ × основание × высота. Периметр прямоугольного треугольника — это общая длина его границы или сумма длин всех трех сторон, включая гипотенузу, высоту и основание. Это вычисляется по формуле: P = основание + высота + гипотенуза.
Какая формула периметра прямоугольного треугольника?
Формула периметра прямоугольного треугольника равна сумме всех сторон. Предположим, что p, q, r — стороны треугольника, тогда периметр = p + q + r.
Как найти площадь и периметр треугольника?
Чтобы найти площадь треугольника, мы используем формулу: Площадь = ½ × основание × высота, и ответ выражается в квадратных единицах. Периметр треугольника со сторонами x, y и z можно рассчитать по формуле: Периметр = x + y + z и ответ выражается в единицах.
Каков максимально возможный периметр прямоугольного треугольника, если одна из сторон имеет длину 12?
Максимально возможный периметр прямоугольного треугольника равен 84 (12 + 35 + 37), а стороны треугольника равны 12, 35, 37.
Предположим, что b — ширина, а — гипотенуза, а длина равна 12 (дана). Используя теорему Пифагора, b 2 + (12) 2 = а 2
(a 2 — b 2 ) = 144 ⇒ (a + b)(a -b) = 144. Составляем список всех возможных способов выражения числа 144 в виде произведения двух чисел, каждое из которых четно. Ответ исходит из того факта, что 144 = 2 × 72. Теперь путем разложения мы получаем a = 35 и b = 37.Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы площади и периметра
Диофантовы уравнения — Прямоугольный треугольник, где периметр = площадь*k
Спросил
Изменено 1 год, 4 месяца назад
Просмотрено 4k раз
$\begingroup$
Я рисовал на листе бумаги проблему, которая пришла мне в голову.
После нескольких минут безрезультатных попыток я попытался решить проблему с помощью компьютерных средств.
Заявленная проблема
Создает ли прямоугольный треугольник с целыми сторонами такой, что $$P = A\cdot k \quad \quad \text{or} \quad \quad k\cdot P = A$$, где существуют $(P , \ A , \ k )\in \mathbb{N}$?
(Здесь P — периметр треугольника. Сумма сторон. А — площадь треугольника. a*b/2 в треугольнике с a b c и c — гипотенуза)
Очевидно, для простых случаев таких треугольники существуют. Для примера когда
$ A=2P \qquad $ работает треугольник $12,16,20$
$ A=P \qquad \; \; $ треугольник $6,8,10$ работает
$2A=P \qquad $ треугольник $3,4,5$ работает
Я попытался решить это вручную, сначала для особого случая, когда $2P=A$. Это закончилось тем, что дало мне 92 $$
Теперь у нас есть два уравнения и три неизвестных, которые также должны быть целыми числами! К сожалению, я не смог продолжить отсюда.
Я только научился решать линейные диофантовы уравнения. Не система нелинейных диофантовых уравнений.
Просто чтобы переформулировать мой вопрос ниже =)
Существует ли прямоугольный треугольник с целыми сторонами такой, что $$P = A\cdot k \quad \quad \text{or} \quad \quad k\cdot P = A$$ где $(P , \ A , \ k )\in \mathbb{N}$ ?
92=2n(m-n)$, поэтому $A/P=k=n(m-n)/2$. Варианты теперь таковы: либо $2$ делит $n$, либо $2$ делит $m-n$, так что у нас либо $n=2d$ и $m=k/d+2d$, либо $n=d$ и $m=2. (k/d)+d$ для делителей $d$ числа $k$.(чтобы получить $P/A=k$, нам нужно $2n(m-n)$, чтобы разделить $4$, поэтому $n(m-n)$ должно разделить $2$, таким образом, $n=1$, $m=2$, $n=1$, $m=3$ и $n=2$, $m=3$ — единственные решения, дающие нам $(3,4,5)$, $(8,6,10)$ , $(5,12,13)$ с $k=2,1,2$ единственными возможными вариантами).
$\endgroup$
1 92)$.
Уравнение (i) быстро перестает работать.
Отмена дает $k\lambda n(m-n)=2$, и список решений невелик. Есть две возможности: $k=2$ и $k=1$. Если $k=2$, то $\lambda=1$ и $m=2$, $n=1$, что дает ваш пример $(3,4,5)$. Если $k=1$, то $\lambda=2$, $m=2$, $n=1$ или $\lambda=1$, $m=3$, $n=1$ или $\lambda =1$, $m=3$, $n=2$. Получаем примеры $(6,8,10)$ и $(5,12, 13)$. Это все.
Уравнение (ii) более интересно. Отмена дает $$\лямбда n(m-n)=2k. \qquad(\аст\аст)$$ Для любого $k$ мы можем найти решение, например, положив $\lambda=1$, $n=2k$ и $m=2k+1$. Или, что менее интересно, мы можем положить $\lambda=k$, $m=2$, $n=1$, что дает масштабированную версию знакомого треугольника $3$-$4$-$5$.
Для данного $k$ мы можем найти явный способ сгенерировать все решения $(\ast\ast)$ и получить их количество. Для любого фиксированного $k$ существует только конечное число решений. Грубо говоря, если $k$ имеет много делителей, то и решений много, так как мы генерируем решения, рассматривая множители $2k$.
$\endgroup$
5
$\begingroup$
Если вы выберете положительные целые числа $a$ и $b$, вы можете составить прямоугольный треугольник со сторонами 92)\раз k = 2a(a+b).
$$ Мы можем записать это как $$ab(a-b)(a+b) = 2a(a+b)$$ а затем отмените $a$ и $(a+b)$ с каждой стороны (они не равны нулю, так что все в порядке) и получите $$b(a-b)k = 2\quad\text{, и наконец}$$ $$k = \frac{2}{b(a-b)}.$$
Мы хотим, чтобы $k$ было целым числом, поэтому оно может быть только 1 или 2.
Если $k=1$ , $b( a-b)$ должно равняться $2$, и это может произойти двумя способами: когда $a=3\text{ и }b=2$, что дает треугольник 5-12-13, и когда $a=3$ и $b =1$, что дает треугольник 6-8-10.
Если $k=2$ , $b(a-b)$ должно равняться $1$, и это может произойти только тогда, когда $a=2\text{ и }b=1$. Эти значения $a$ и $b$ образуют треугольник 3-4-5. 92) = 2a(a+b)\times k.$$ Мы можем уменьшить это, как и раньше, и прийти к $$k = \frac{b(a-b)}{2}.$$ Существует множество различных значений $a$ и $b$, которые делают $k$ целым числом.$\endgroup$
1
$\begingroup$
Мы можем найти пифагоровы тройки для любого отношения $R$ площади к периметру, найдя целое число $m,n$, представляющее их, используя следующую формулу, которая включает определенный конечный поиск значений $m$.
Обратите внимание, все известные коэффициенты кратны $0,5$. 92-8*0,5}}{2}=1\qquad f(2,1)=(3,4,5)$$ Эти тройки обычно встречаются парами, а иногда и более одной пары.
$$R=1\стрелка вправо 3\le m \le 3\quad f(3,2)=(5,12,13)\quad f(3,1)=(8,6,10)$$
$$R=2\стрелка вправо 4\le m \le 5\quad f(4,2)=(12,16,20)\quad f(5,4)=(9,40,41)\quad f(5,1)=(24,10,26)$$
$$R=3\стрелка вправо 4\le m \le 7\quad f(5,3)=(16,30,34)\quad f(5,2)=(21,20,29)\quad f(7,6)=(13,84,85)\quad f(7,1)=(48,14,50)$$
Кроме того, мы всегда можем найти одну примитивную тройку для данного $R$, если мы допустим $(m,n)=(2R+1,2R)$.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.Периметр прямоугольного треугольника — DewWool
Периметр треугольника можно определить как сумму всех трех сторон. В большинстве случаев формула для периметра выглядит просто как a+b+c. Но в некоторых случаях одна или две стороны могут быть неизвестны. Таким образом, мы должны применить некоторые теоремы или использовать некоторые формулы, чтобы найти периметр. В этой статье мы рассмотрим способы, как узнать периметр прямоугольного треугольника
Формула периметра прямоугольного треугольника1) Простой 3 3 метод: сложить все стороны
- Простой метод: Сложите все стороны
- Теорема: Используйте теорему Пифагора для вычисления гипотенузы.
- Используйте закон косинусов, чтобы найти неизвестную сторону
- Используйте закон синуса [a sin A = b sin B = c sin C]
- Используйте формулу площади
Это основной метод нахождения периметра прямоугольного треугольника.
Добавьте все стороны треугольника.
Формула периметра прямоугольного треугольника = a + b+ c
Например, в следующем случае:
Метод 1: Сложите все стороны треугольникаa = 4 см; b = 3 см и c = 5 см
Периметр этого прямоугольного треугольника будет = a + b + c = 4 + 3 + 5 = 12 см. Единицей периметра всегда будет см, м, км и т. д.
2) Использование теоремы ПифагораИногда бывает, что мы не знаем всех сторон прямоугольного треугольника. Предположим, если мы не знаем сторону, противоположную прямому углу (90 o ), то мы можем использовать теорему Пифагора, чтобы найти его.
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон.
c 2 = a 2 + b 2
Периметр треугольника, когда гипотенуза неизвестнаНа изображении выше a = 4; б= 3; с неизвестно.
Мы можем найти это по теореме Пифагора.
с 2 = 4 2 + 3 2
c = sqrt(25)
c = 5
противоположный угол. Этот закон применим к любому треугольнику вообще. уравнение закона косинусовВ приведенном выше уравнении неизвестная сторона равна c, a и b известны, а y — угол, противоположный неизвестной стороне. Если с — гипотенуза, то у будет 90 о . Поскольку cos(90) равен нулю, уравнение сводится к sqrt(a 2 + b 2 ). Это доказывает, что этот закон согласуется с теоремой Пифагора.
периметр прямоугольного треугольника, когда заданы две стороны и хотя бы один уголНапример, на изображении выше две стороны известны как 3 см и 4,24 см (гипотенуза), длина стороны x неизвестна. Применяя закон косинуса, получаем:
x = sqrt {(3) 2 + (4,24) 2 – 2*3*4,24 } = ~3 см
Проверим наш ответ с помощью теоремы Пифагора:
Левая сторона : квадрат гипотенузы = (4.
24) 2 = ~18
Правая сторона : сумма квадрата двух других сторон = (3) 2 + (3) 2 = 18
левый = правый. Следовательно, наш ответ подтвержден.
Теперь мы можем вычислить периметр прямоугольного треугольника, который представляет собой сумму трех сторон: 3 + 3 + 4,24 = 13,24 см.
Этот инструмент можно использовать для вычисления значений косинуса.
4) Использование закона синусовЭтот закон можно использовать, когда известны по крайней мере два угла вместе с двумя сторонами. Этот закон также можно использовать в сочетании с другими законами и формулами для нахождения периметра любого треугольника. В прямоугольном треугольнике мы уже знаем один угол как 90 o , поэтому этот закон можно предпочесть для вычисления периметра прямоугольных треугольников.
Закон синусовПериметр прямоугольного треугольника, когда заданы два угла и хотя бы одна сторонаВ приведенном выше примере известны две стороны и два угла.
Вычислим неизвестную сторону x по закону синусов.
sin(45)/x = sin(45)/3
x = 3
Проверим наш ответ, также используя другую сторону.
sin(45)/x = sin(90)/4,24
0,707/x = 1/4,24
x = 0,707 * 4,240 = 3 см
Следовательно, наш ответ подтвержден. Этот метод очень полезен, когда известны два угла и хотя бы одна сторона. Периметр этого прямоугольного треугольника теперь можно рассчитать как 3 + 3 + 4,24 = 10,24 см.
Этот инструмент можно использовать для вычисления значений синуса.
5) Используя формулу площади для прямоугольного треугольникаМы видели случаи, когда известны все три стороны или хотя бы две стороны. Бывают случаи, когда известна только одна сторона. Затем нам нужно использовать 2 или более формул, чтобы получить периметр прямоугольного треугольника.
Мы знаем, что формула площади прямоугольного треугольника равна ab/2. Это уравнение можно использовать с другими законами, когда известны две стороны.
Периметр прямоугольного треугольника при заданной площадиЗатем мы можем решить два уравнения с двумя переменными, чтобы получить две другие стороны, а затем, соответственно, вычислить периметр прямоугольного треугольника.
В приведенном выше примере площадь = 4 см 2 , а одна сторона равна 3 см.
Формула площади прямоугольного треугольника = a*b/2
6 = 1/2 * 3 * (x)
x = 4 см
Теперь вычислим гипотенузу по теореме Пифагора:
H 2 = 3 2 + 4 2
H = 5 см
Отсюда периметр этого треугольника будет: 3 + 4 + 5 = 12 см.
Численные задачи на периметр прямоугольного треугольникаНайдите периметр прямоугольного треугольника, показанного ниже:
Найдите периметр этого прямоугольного треугольникаЗдесь мы знаем два угла (A = 60 и B = 30) и одна сторона (с=12). Мы можем использовать закон синусов в этом сценарии:
a/sin(60) = 12/sin(90)
a/0,866 = 12/1
a = 10,4 см
Найдите периметр этого прямоугольного треугольника.

 Если известны все три стороны треугольника , то, независимо от того, прямоугольный ли треугольник или нет, его периметр будет рассчитан так:
Если известны все три стороны треугольника , то, независимо от того, прямоугольный ли треугольник или нет, его периметр будет рассчитан так:
 2 – (2 * a * b * cos(C)), где a,b,c – стандартно длины граней, а A,B и С – это углы, которые лежат напротив соответствующих граней треугольника. То есть, A – угол, противолежащий стороне a и так далее.
2 – (2 * a * b * cos(C)), где a,b,c – стандартно длины граней, а A,B и С – это углы, которые лежат напротив соответствующих граней треугольника. То есть, A – угол, противолежащий стороне a и так далее.
 Если известны длины катетов, то периметр треугольника определяется через нахождение величины гипотенузы по формуле:
Если известны длины катетов, то периметр треугольника определяется через нахождение величины гипотенузы по формуле: Нахождение этих величин упрощается благодаря общепринятым формулам, согласно которым можно также вычислить одно через другое с минимумом или полным отсутствием дополнительных начальных данных. Спонсор размещения P&G
Нахождение этих величин упрощается благодаря общепринятым формулам, согласно которым можно также вычислить одно через другое с минимумом или полным отсутствием дополнительных начальных данных. Спонсор размещения P&G Чтобы найти длины сторон прямоугольного треугольника, можно воспользоваться несколькими способами. Спонсор
Чтобы найти длины сторон прямоугольного треугольника, можно воспользоваться несколькими способами. Спонсор Зная значения одних из них, можно вычислять другие. Для этого используются формулы, основанные, в свою очередь, на аксиомах и теоремах геометрии. Спонсор размещения P&G Статьи по теме «Как определить
Зная значения одних из них, можно вычислять другие. Для этого используются формулы, основанные, в свою очередь, на аксиомах и теоремах геометрии. Спонсор размещения P&G Статьи по теме «Как определить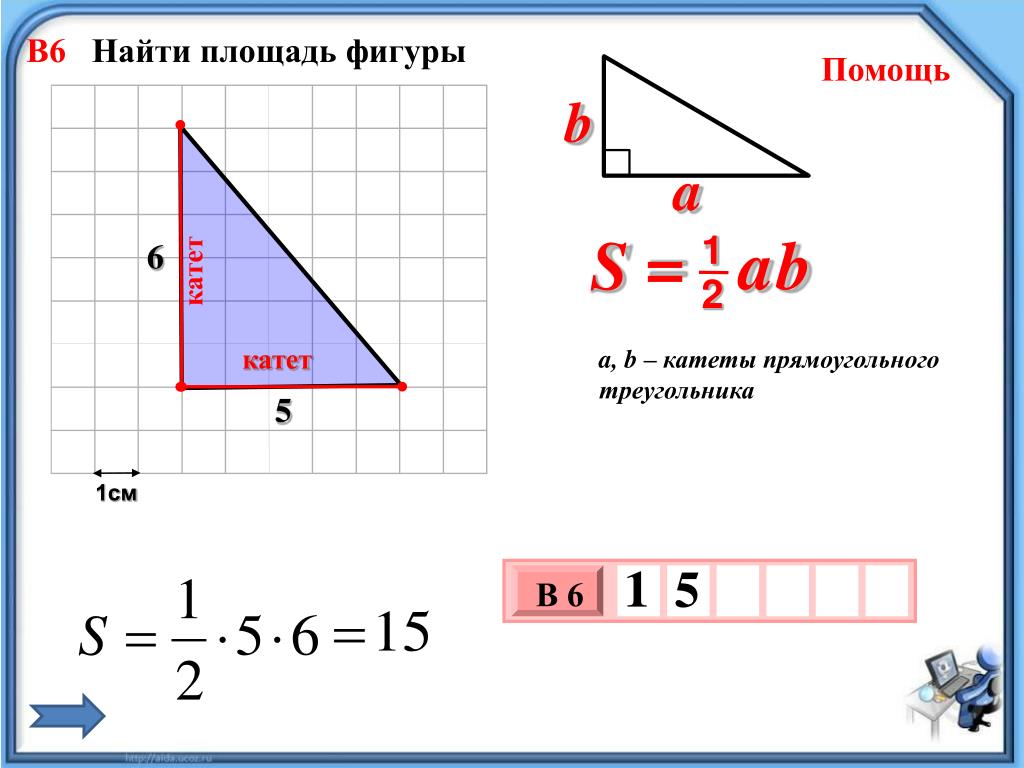 Расчет периметра такого треугольника будет зависим от количества известных о нем данных.
Расчет периметра такого треугольника будет зависим от количества известных о нем данных. Дано, что в прямоугольном треугольнике длина одного из катета равна a, а напротив него лежит острый угол?. Тогда расчет периметра этого треугольника будет вестись по формуле:
Дано, что в прямоугольном треугольнике длина одного из катета равна a, а напротив него лежит острый угол?. Тогда расчет периметра этого треугольника будет вестись по формуле: Например, если a, b и c — стороны прямоугольного треугольника, то его периметр будет равен: (a + b + c). Теперь, поскольку это прямоугольный треугольник, можно сказать, что его периметр равен сумме длин двух сторон и гипотенузы. Обратите внимание на следующий рисунок, на котором показан прямоугольный треугольник со сторонами a, b и c, где c — гипотенуза, а a, b — стороны, которые вместе образуют треугольник.угол 0°. Три стороны можно назвать следующим образом: a = высота, b = основание и c = гипотенуза.
Например, если a, b и c — стороны прямоугольного треугольника, то его периметр будет равен: (a + b + c). Теперь, поскольку это прямоугольный треугольник, можно сказать, что его периметр равен сумме длин двух сторон и гипотенузы. Обратите внимание на следующий рисунок, на котором показан прямоугольный треугольник со сторонами a, b и c, где c — гипотенуза, а a, b — стороны, которые вместе образуют треугольник.угол 0°. Три стороны можно назвать следующим образом: a = высота, b = основание и c = гипотенуза.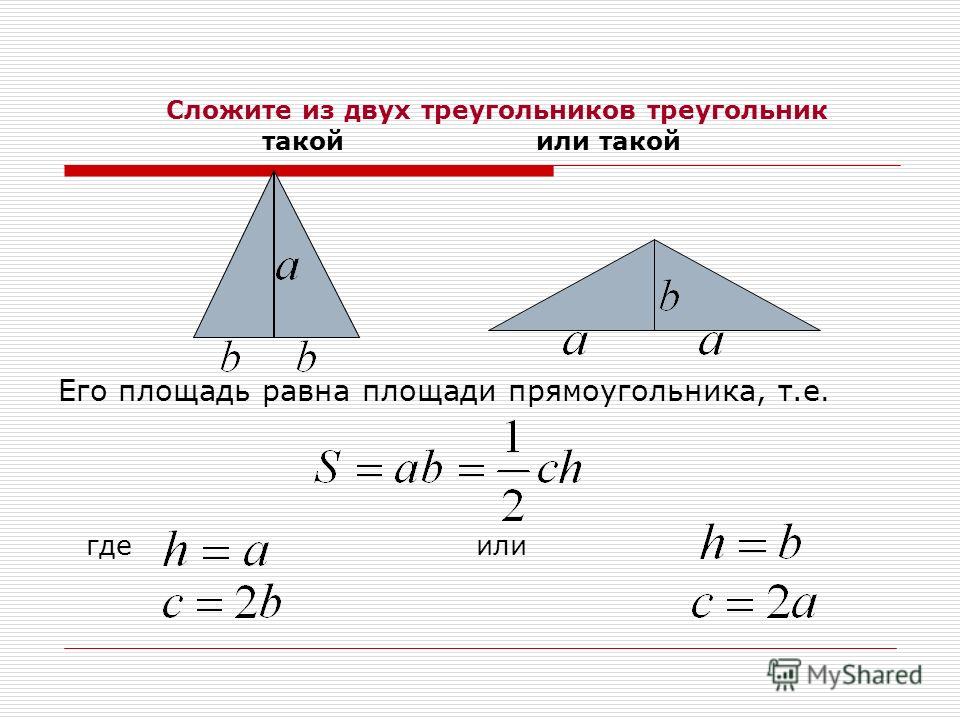 Например, если заданы стороны p, q и r, то периметр = p + q + r. Этот метод возможен только тогда, когда известны измерения всех сторон.
Например, если заданы стороны p, q и r, то периметр = p + q + r. Этот метод возможен только тогда, когда известны измерения всех сторон.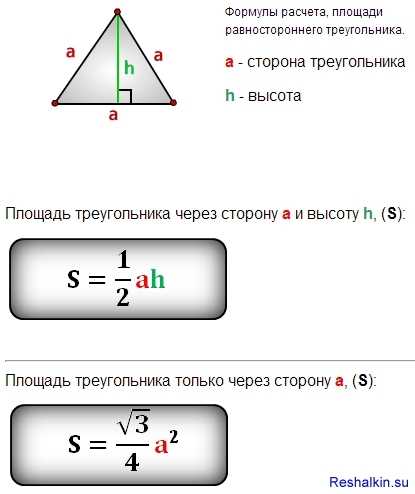

 Предположим, что b — ширина, а — гипотенуза, а длина равна 12 (дана). Используя теорему Пифагора, b 2 + (12) 2 = а 2
Предположим, что b — ширина, а — гипотенуза, а длина равна 12 (дана). Используя теорему Пифагора, b 2 + (12) 2 = а 2 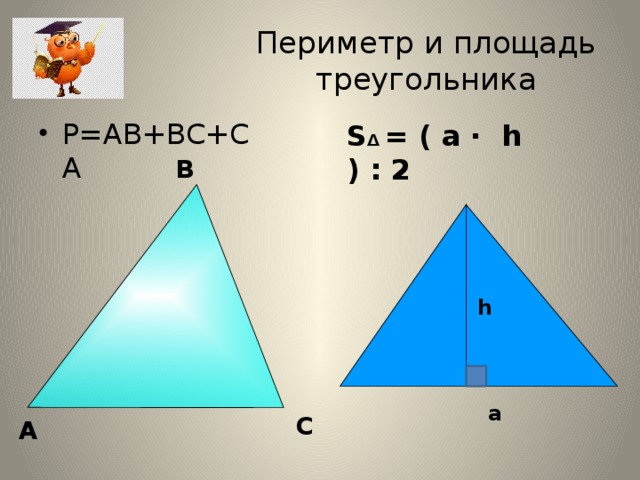 После нескольких минут безрезультатных попыток я попытался решить проблему с помощью компьютерных средств.
После нескольких минут безрезультатных попыток я попытался решить проблему с помощью компьютерных средств. Я только научился решать линейные диофантовы уравнения. Не система нелинейных диофантовых уравнений.
Я только научился решать линейные диофантовы уравнения. Не система нелинейных диофантовых уравнений. Отмена дает $k\lambda n(m-n)=2$, и список решений невелик. Есть две возможности: $k=2$ и $k=1$. Если $k=2$, то $\lambda=1$ и $m=2$, $n=1$, что дает ваш пример $(3,4,5)$. Если $k=1$, то $\lambda=2$, $m=2$, $n=1$ или $\lambda=1$, $m=3$, $n=1$ или $\lambda =1$, $m=3$, $n=2$. Получаем примеры $(6,8,10)$ и $(5,12, 13)$. Это все.
Отмена дает $k\lambda n(m-n)=2$, и список решений невелик. Есть две возможности: $k=2$ и $k=1$. Если $k=2$, то $\lambda=1$ и $m=2$, $n=1$, что дает ваш пример $(3,4,5)$. Если $k=1$, то $\lambda=2$, $m=2$, $n=1$ или $\lambda=1$, $m=3$, $n=1$ или $\lambda =1$, $m=3$, $n=2$. Получаем примеры $(6,8,10)$ и $(5,12, 13)$. Это все.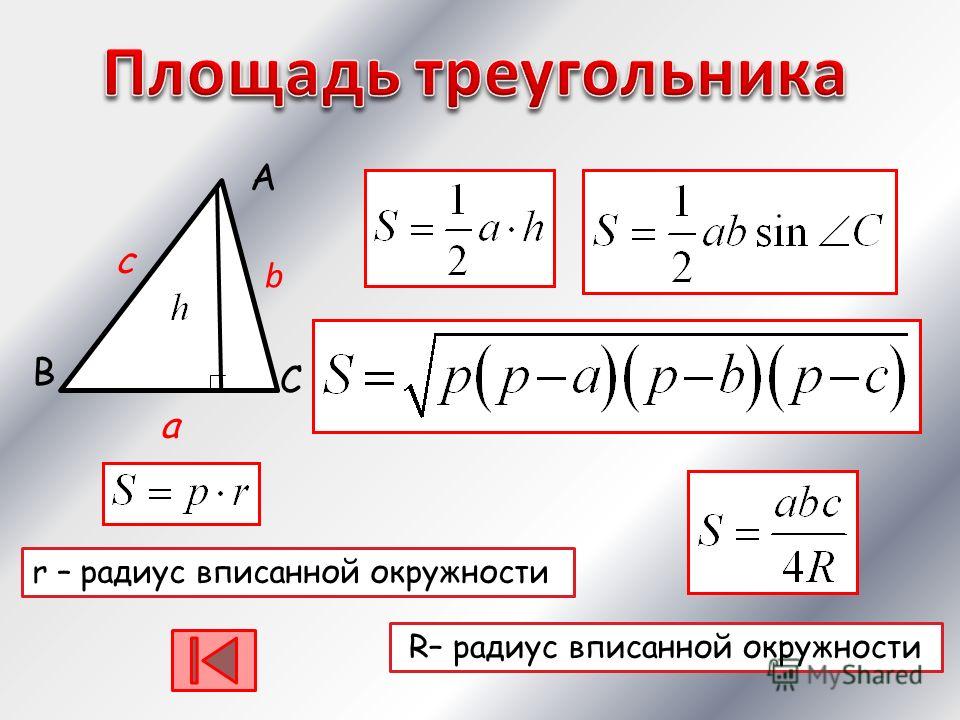 $$
Мы можем записать это как
$$ab(a-b)(a+b) = 2a(a+b)$$
а затем отмените $a$ и $(a+b)$ с каждой стороны (они не равны нулю, так что все в порядке) и получите
$$b(a-b)k = 2\quad\text{, и наконец}$$
$$k = \frac{2}{b(a-b)}.$$
$$
Мы можем записать это как
$$ab(a-b)(a+b) = 2a(a+b)$$
а затем отмените $a$ и $(a+b)$ с каждой стороны (они не равны нулю, так что все в порядке) и получите
$$b(a-b)k = 2\quad\text{, и наконец}$$
$$k = \frac{2}{b(a-b)}.$$ Обратите внимание, все известные коэффициенты кратны $0,5$. 92-8*0,5}}{2}=1\qquad f(2,1)=(3,4,5)$$
Эти тройки обычно встречаются парами, а иногда и более одной пары.
Обратите внимание, все известные коэффициенты кратны $0,5$. 92-8*0,5}}{2}=1\qquad f(2,1)=(3,4,5)$$
Эти тройки обычно встречаются парами, а иногда и более одной пары.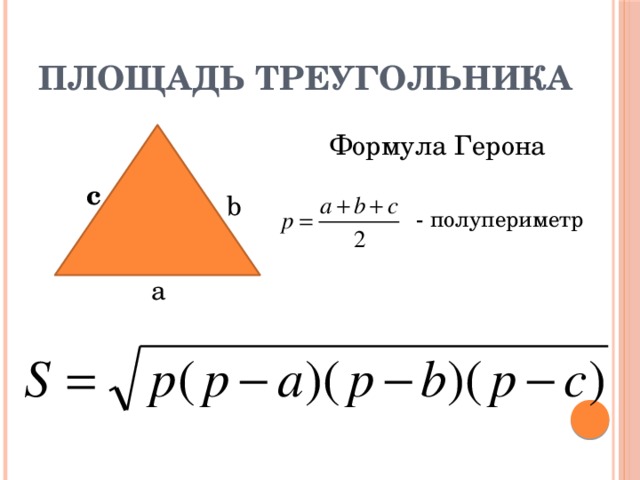
 Добавьте все стороны треугольника.
Добавьте все стороны треугольника.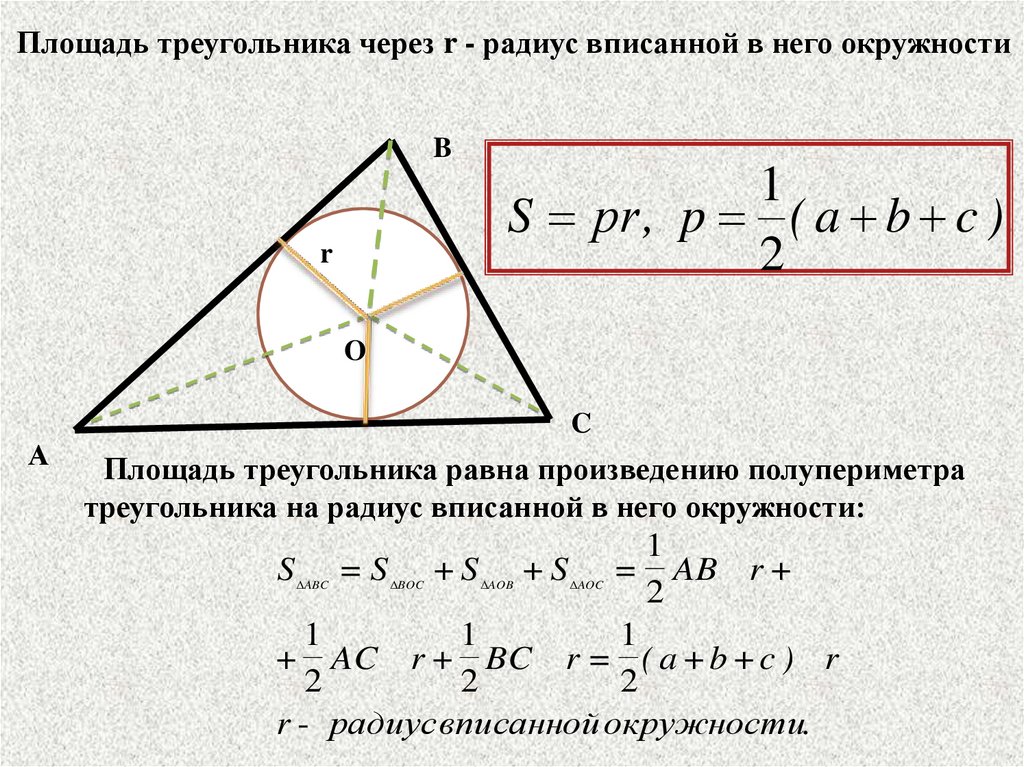 Мы можем найти это по теореме Пифагора.
Мы можем найти это по теореме Пифагора. 24) 2 = ~18
24) 2 = ~18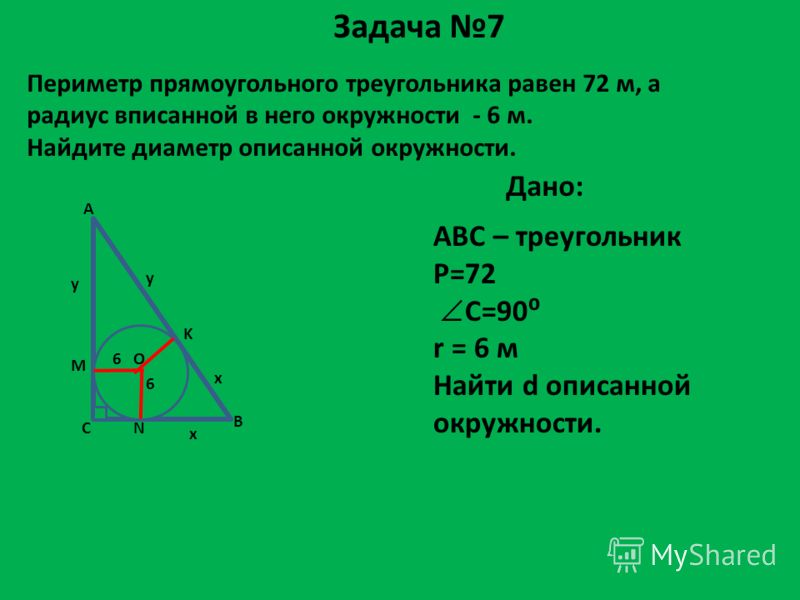 Вычислим неизвестную сторону x по закону синусов.
Вычислим неизвестную сторону x по закону синусов.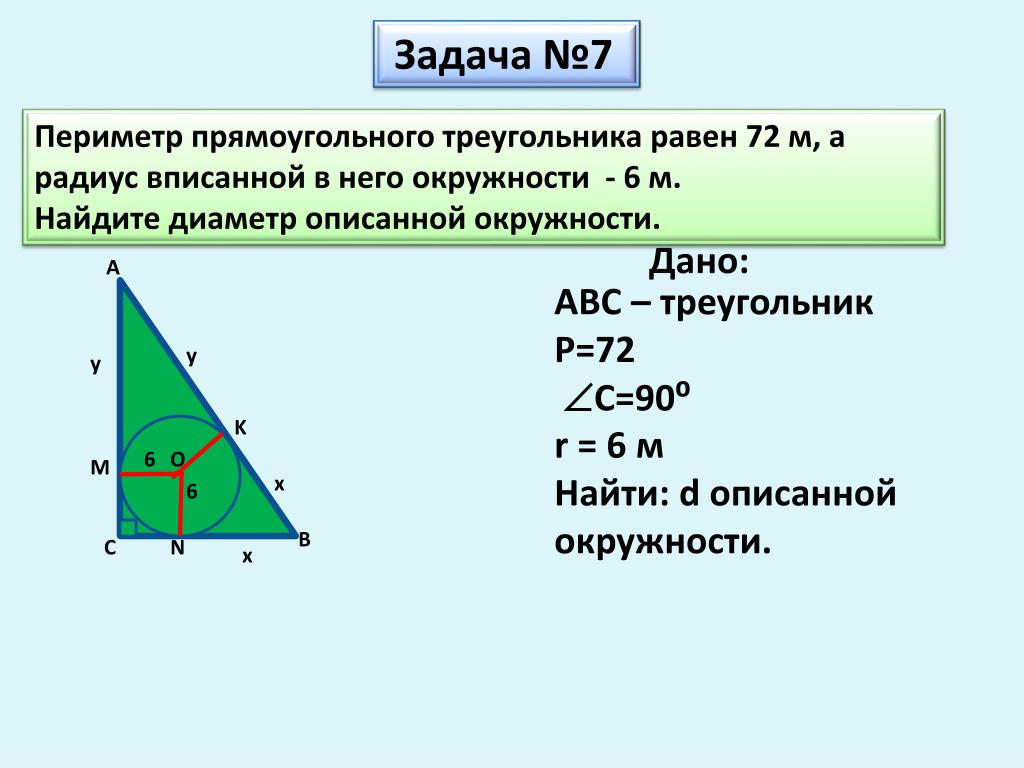 Затем мы можем решить два уравнения с двумя переменными, чтобы получить две другие стороны, а затем, соответственно, вычислить периметр прямоугольного треугольника.
Затем мы можем решить два уравнения с двумя переменными, чтобы получить две другие стороны, а затем, соответственно, вычислить периметр прямоугольного треугольника.