Добавление математических уравнений в Pages на Mac
В документ можно включать математические выражения и уравнения. Чтобы добавить уравнение, его необходимо создать в диалоговом окне уравнения Pages с помощью команд LaTeX или элементов MathML, а затем вставить в документ.
Добавляя уравнение в текстовый документ, можно сделать его встроенным в текст, чтобы оно оставалось на той же строке и перемещалось вместе с текстом по мере ввода, либо сделать его плавающим объектом и разместить в любой части страницы. В документах с макетом страницы новые уравнения всегда добавляются на страницу как плавающие объекты.
В текстовых документах и документах с макетом страницы можно добавлять уравнения, встроенные в текст внутри текстовых блоков и фигур.
Примечание. После установки приложения для ввода математических выражений MathType версии 6.7d или новее Вы можете создавать в нем математические записи, нажимая символы и вводя текст в окне MathType.
Добавление уравнения с помощью LaTeX или MathML
Выполните одно из описанных ниже действий.
Добавление уравнения, встроенного в текст. Поместите точку вставки внутри текста, текстового блока, фигуры или ячейки таблицы либо выберите текст, вместо которого нужно вставить уравнение.
Добавление уравнения, которое может перемещаться свободно. Нажмите в углу страницы, чтобы отменить выбор любых объектов. Также можно выбрать миниатюру страницы в панели «Миниатюры страниц».
Нажмите в панели инструментов, затем выберите «Уравнение».
Можно также выбрать «Вставка» > «Уравнение» (меню «Вставка» расположено у верхнего края экрана).
Если установлено приложение MathType, отобразится диалоговое окно с вопросом о создании уравнения в Pages. Нажмите «Использовать Pages».
С помощью команд LaTeX или элементов MathML введите уравнение в поле.
Подробнее об использовании поддерживаемых команд LaTeX и элементов и атрибутов MathML см. в статье службы поддержки Apple Поддержка LaTeX и MathML.
Нажмите «Вставить».
Если Вы добавили встроенное уравнение, оно появится в точке вставки в документе, а размер и цвет уравнения будут такими же, как у окружающего текста. При изменении размера или цвета окружающего текста размер и цвет уравнения также меняются.
Если Вы добавили уравнение на страницу, оно появится в центре экрана, а его размер и цвет будут заданы по умолчанию. Эти параметры можно изменить в боковой панели «Формат» . Перетяните уравнение, чтобы изменить его положение на странице.
Добавление уравнения с помощью MathType
Если у Вас есть приложение MathType 6.7d или более поздней версии, его можно использовать для добавления уравнений в документ.
Совет. Чтобы задать приложение MathType в качестве редактора формул по умолчанию, выберите «Pages» > «Настройки» (меню «Pages» расположено у верхнего края экрана), нажмите «Основные», затем установите флажок «Вставлять уравнения MathType».
Выполните одно из описанных ниже действий.
Добавление уравнения, встроенного в текст. Поместите точку вставки внутри текста, текстового блока, фигуры или ячейки таблицы либо выберите текст, вместо которого нужно вставить уравнение.
Добавление уравнения, которое может перемещаться свободно. Нажмите в углу страницы, чтобы отменить выбор любых объектов. Также можно нажать миниатюру страницы в панели «Миниатюры страниц».
Нажмите в панели инструментов, затем выберите «Уравнение».
Если в качестве редактора уравнений по умолчанию задано приложение MathType, оно откроется автоматически (после первого ввода уравнения). В ином случае нажмите «Исп. MathType» в появившемся диалоговом окне.
Для ввода уравнения нажимайте символы и вводите числа и обозначения в окне MathType.
Инструкции по работе с инструментами MathType см. в Справке MathType.
Чтобы сохранить уравнение, выберите «Файл» > «Закрыть и вернуться к Pages» (меню «Файл» расположено у верхнего края экрана), затем в появившемся диалоговом окне нажмите «Да».
Если Вы добавили встроенное уравнение, оно появится в точке вставки, а размер и цвет уравнения будут такими же, как у окружающего текста. Для редактирования уравнения дважды нажмите его, чтобы открыть окно MathType.
Если Вы добавили уравнение на страницу, оно появится в центре экрана. Его можно перетянуть в другое место страницы. Для изменения внешнего вида или редактирования уравнения дважды нажмите его, чтобы открыть в приложении MathType. Затем дважды нажмите элементы управления в нижней части окна.
Перетяните уравнение, чтобы изменить его положение на странице.
Редактирование, удаление или перемещение встроенного уравнения с помощью LaTeX или MathML
Добавив встроенное уравнение в текст, Вы можете его изменить.
Редактирование уравнения. Дважды нажмите уравнение, внесите изменения и нажмите «Обновить».
Перемещение уравнения внутри текста.
Выберите уравнение и перетяните его на новое место в основном тексте, сноске или колонтитуле. Также можно перетянуть его в другой текстовый блок или фигуру.Изменение размера, цвета или выравнивания уравнения. Нажмите уравнение и используйте элементы управления на вкладке «Текст» в боковой панели «Формат» , чтобы изменить размер шрифта, цвет и выравнивание уравнения.
Копирование уравнения. Нажмите уравнение, выберите «Правка» > «Скопировать» (меню «Правка» расположено у верхнего края экрана), поместите точку вставки в место вставки уравнения, — в текст, ячейку таблицы или колонтитул на странице — затем выберите «Правка» > «Вставить». Также можно выбрать объект на странице (например, фигуру), затем выбрать «Правка» > «Вставить», чтобы вставить уравнение на страницу как плавающий объект.
Удаление уравнения. Нажмите уравнение, затем нажмите клавишу Delete на клавиатуре.
Перемещение встроенного уравнения на страницу (за пределы текста).
В текстовом документе выберите уравнение, затем в боковой панели «Расстановка» нажмите всплывающее меню «Обтекание текстом» и выберите вариант, отличающийся от варианта «Встроено в текст». См. раздел Обтекание объекта текстом.В документе с макетом страницы выберите уравнение, выберите «Правка» > «Вырезать» (или «Скопировать», затем выберите «Правка» > «Вставить». Перетяните уравнение в нужное место на странице.
Выберите уравнение и перетяните его на новое место в основном тексте, сноске или колонтитуле. Также можно перетянуть его в другой текстовый блок или фигуру.
В текстовом документе выберите уравнение, затем в боковой панели «Расстановка» нажмите всплывающее меню «Обтекание текстом» и выберите вариант, отличающийся от варианта «Встроено в текст». См. раздел Обтекание объекта текстом.Редактирование, удаление или перемещение плавающего уравнения с помощью LaTeX или MathML
Добавив плавающее уравнение на страницу, Вы можете его изменить.
Редактирование уравнения. Дважды нажмите уравнение, внесите изменения и нажмите «Обновить».
Перемещение уравнения. Перетяните уравнение в другое место на странице.
Изменение размера, цвета или выравнивания уравнения. Нажмите уравнение, затем воспользуйтесь элементами управления в боковой панели, чтобы изменить размер шрифта и цвет уравнения.
Также можно изменить размер шрифта для уравнения, перетягивая манипулятор.Копирование уравнения. Нажмите уравнение, выберите «Правка» > «Скопировать», прокрутите до той страницы, на которую нужно поместить уравнение, и выберите «Правка» > «Вставить». Также можно поместить точку вставки в ячейку таблицы или колонтитул страницы. Выберите «Правка» > «Вставить», чтобы вставить уравнение как встроенный объект.
Удаление уравнения. Нажмите уравнение, затем нажмите клавишу Delete на клавиатуре.
Перемещение плавающего уравнения вместе с текстом. В текстовом документе выберите уравнение, затем в боковой панели «Расстановка» нажмите кнопку «Двигать с текстом». Нажмите всплывающее меню «Обтекание текстом» и выберите вариант «Встроенный в текст». Перетяните уравнение на нужное место.
В документе с макетом страницы выберите плавающее уравнение и вставьте его в текстовый блок или фигуру. См. раздел Встраивание объектов в текстовый блок или фигуру.
Также можно изменить размер шрифта для уравнения, перетягивая манипулятор.
См. такжеАвтоматическое форматирование дробей в Pages на MacПоднятие и опускание символов и текста в Pages на MacДиакритические знаки и специальные символы в Pages на MacРазмещение и выравнивание объектов в Pages на Mac
1.2.3 Запись уравнений состояния сети по законам Кирхгофа
Запишем уравнения состояния электрической сети по законам Кирхгофа:
(19)
или, введя составные или блочные матрицы, получим:
(20)
Матрицы соединений [M], [N] и диагональную матрицу сопротивления ветвей [Zв] также можно представить в виде блоков для дерева и хорд схемы:
(21)
или
. (22)
Здесь [J] ‑ задающие токи узлов, [Eв] ‑ ЭДС ветвей — независимые характеристики режима.
[I] – искомая характеристика режима – токи ветвей схемы
[А] – составная
матрица, описывающая конфигурацию и
параметры сети, порядка m.
Заметим, что эта
матрица содержит информацию об узловой
и контурной моделях конфигурации сети
– матрицах [M] и [N]
и о параметрах сети [Z
Уравнение (22) решается относительно токов ветвей [I].
!!!!!!!! (23)
По найденному токораспределению и известному напряжению в балансирующем узле могут быть найдены падения напряжения на ветвях ΔUв и напряжения остальных узлов сети UΔy. Таким образом, задача расчета режима в линейной постановке решается по уравнениям Кирхгофа, однако для промышленных программ этот подход не применяется, так как порядок системы уравнений и обращаемой матрицы [A] велик – равен числу ветвей схемы m. Для разработки промышленных программ применяются методы, приводящие к системам уравнений состояния c матрицами меньшей размерности – узловые методы или контурные методы расчета установившихся режимов электрических систем.
1.3 Метод уравнений узловых напряжений
1.
3.1 Вывод узловых уравненийЭти уравнения выводятся из выражения 1-го закона Кирхгофа.
I закон Кирхгофа для электрической сети в матричной форме записи:
[M]∙[Iв] = [-Jу], (24)где Jу – вектор‑столбец задающих токов узлов;
Iв – вектор‑столбец искомых токов ветвей.
В общем случае из этого уравнения нельзя найти токораспределение Iв, так как число уравнений равно числу узлов n, а число неизвестных равно числу ветвей m. Выразим токи ветвей через падения напряжения на ветвях [Uв], принимая Ев = 0 (что достаточно типично)
. (25)
Падения напряжения на ветвях [Uв], с использованием I‑ой матрицы соединений [M], [M]Т можно выразить через напряжения узлов электрической сети [Uу] или [Uy], т.е. вектор‑столбец меньшей размерности, чем число ветвей:
(26) или
(27)
Здесь [м]т – транспонированная 1-я матрица инциденций,
[UУ] – вектор-столбец падений напряжений в узлах сети относительно базисного узла,
[Uу] – вектор-столбец напряжений узлов электрической сети n-ого порядка,
(27)
—
составной вектор (n+1)-ого
порядка, содержащий [Uу]
n-ого порядка и напряжение
в балансирующем узле Uб.
Подставив в уравнение (24) токи ветвей из (25) и падения напряжения на ветвях сети из (26), получим:
(28)
Обозначим произведения трех матриц через [Yу]
[Yу]= (29)
[Yy] — матрица собственных и взаимных проводимостей узлов электрической сети – важнейшая матрица параметров в анализе электрических сетей.
С учетом подстановки формула (28) примет следующий вид:
(30)
Выражение (30) представляет систему линейных узловых уравнений установившегося режима электрической сети.
Здесь [Jу] – вектор‑столбец независимых переменных – задающих токов в узлах сети;
[Uу] – искомый вектор падений напряжений в узлах сети n‑го порядка;
[n]‑ число независимых узлов в схеме.
Если выразить Uв по (27) через абсолютные значения напряжений узлов Uу и подставить в (25), (24), то получим:
(31)
Произведение представляет собой матрицу [Yу], дополненную столбцом проводимостей между i-м и балансирующим узлами [yiб]:
=[Yу]+[yiб] , (32)
С учетом (32) левая часть системы узловых уравнений (30) получит вид:
(33)
Перенеся известное произведение в правую часть, получим систему узловых уравнений, составленную для напряжений узлов электрической сети [Uy]:
(34)
Замечаем, что обе
системы узловых уравнений (30) и (34) имеют
матрицы коэффициентов [Yy]
– матрицы узловых собственных и взаимных
проводимостей.
Поскольку матрица узловых проводимостей [Yу] для совокупности независимых узлов схемы невырожденная, то системы уравнений (30) и (34) могут быть решены (путем обращения этой матрицы) относительно векторов зависимых переменных или [Uy]
(35)
(36)
Нагрузки в узлах сети часто представляют через узловые задающие мощности:
, i = 1,2…n; (37)
или
.
Тогда
,
или через UΔy в знаменателе:
(38)
или через Uу:
(39)
Из уравнений (38) –
(39) очевидно, что задача расчета
установившегося режима электрической
сети по природе своей нелинейна, так
как токи нагрузок в правой части зависят
от искомых узловых напряжений и в
знаменателе также используются
неизвестные Uyi
или Uyi.
Системы нелинейных уравнений (38) – (39) могут разрешаться относительно искомых напряжений узлов аналогично (35), (36) с организацией внешнего итерационного процесса коррекции задающих токов по узловым мощностям Syi и рассчитанным напряжениям Uyi или Uyi.
, (40)
или через Uу:
(41)
Если напряжения узлов рассчитаны с желаемой точностью (по выражениям (35), (36) или (40), (41) или какими-либо другими методами), то остальные параметры режима – токи ветвей [Iв], потоки и потери мощности на ветвях – определятся однозначно и точно.
Ниже выражения (40), (41), использующие обратную матрицу узловых проводимостей [Yy]-1, будут названы обращенной формой уравнений узловых напряжений, в отличие от исходных узловых уравнений (линейных — (30), (34), и нелинейных – (38), (39)) в форме баланса токов узлов.
Математика.
Алгоритм решения уравнений | Материал по математике (3 класс) по теме:Алгоритм решения уравнений на нахождение уменьшаемого.
| х – 4 = 6 |
| уменьшаемое, вычитаемое, разность |
| вычитаемое 4, разность 6. |
| уменьшаемое |
| чтобы найти неизвестное уменьшаемое надо к разности 6 прибавить вычитаемое 4 |
| х = 6 + 4 |
| х = 10 |
| в первую запись вместо х запиши полученное число 10 – 4 = 6 |
| Сосчитай, чему равна левая часть, посмотри, равна ли она правой части 6=6 |
| уравнение решено верно |
У вас получилась запись: 4 6
вычитаемое разность
Х – 4 = 6
Х = 6 + 4
Х = 10
10 – 4 = 6 ? (уменьшаемое)
6 = 6 Сумма
Алгоритм решения уравнений на нахождение вычитаемого.
| 8 – у = 3 |
| уменьшаемое, вычитаемое, разность |
| уменьшаемое 8, разность 3 |
| вычитаемое |
| чтобы найти неизвестное вычитаемое надо из уменьшаемого 8 вычесть разность 3. |
| у = 8 — 3 |
| у = 5 |
| в первую запись вместо у запиши полученное число 8 – 5 = 3 |
| сосчитай, чему равна левая часть, посмотри, равна ли она правой части 3= 3 |
| уравнение решено верно |
У вас получилась запись: вычитаемое 3
? разность
8 – у = 3
у = 8 – 3
у = 5 8
8 – 5 = 3 уменьшаемое
3 = 3
Алгоритм решения уравнений на нахождение слагаемого.
| 6 + у = 9 |
| 1 слагаемое, 2 слагаемое, сумма |
| 1 слагаемое – 6, сумма — 9 |
| 2 слагаемое |
| Чтобы найти неизвестное 2 слагаемое надо из суммы 9 вычесть 1 слагаемое 6 |
| у = 9 — 6 |
| у = 3 |
| в первую запись вместо у запиши полученное число 6 + 3 = 9 |
| сосчитай, чему равна левая часть, посмотри, равна ли она правой части
|
| уравнение решено верно |
У вас получилась запись:
6 + у = 9 1 слагаемое 2 слагаемое
у = 9 – 6 6 ?
у = 3
6 + 3 = 9
9 = 9 9 сумма (целое)
Уравнение
Уравнение — математическое равенство с одной или несколькими неизвестными величинами (числами), верное только для определённых наборов этих величин.
Неизвестные числа обозначаются латинскими буквами Х (икс) и У (игрек)
равенство
Х + 5 = 9
левая часть правая часть
Решить уравнение – это значит найти неизвестное число (неизвестную величину). Если подставить его в уравнение вместо буквы, то должно получиться верное равенство.
Запись: 6 + у = 9
у = 9 – 6
у=3
6 + 3 = 9
9 = 9
Алгоритм решения уравнений
| |||||
| |||||
Суммы | Разности | Произведения | Частного | ||
| |||||
Х+5=12 7+У=12 Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. | Х-5=7 Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое. | 12-У=7 Чтобы найти вычитаемое, надо из уменьшаемого вычесть разность. | Х×4=12 3×У=12 Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель. | Х:3=4 Чтобы найти делимое, надо делитель умножить на частное.
| 12:У=4 Чтобы найти делитель, надо делимое разделить на частное. |
| |||||
Х=12-5 Х=7 У=12-7 У=5 | Х=5+7 Х=12 | У=12-7 У=5 | Х=12:4 Х=3 У=12:3 У=4 |
Х=3×4 Х=12 | У=12:4 У=3 |
| |||||
7+5=12 12=12 | 12-5=7 7=7 | 12-5=7 7=7 | 3×4=12 12=12 | 12:3=4 4=4 | 12:3=4 4=4 |
7. Если получилось неравенство, проверь вычисления! |
Алгоритм решения уравнений
| |||||
| |||||
Суммы | Разности | Произведения | Частного | ||
| |||||
Х+5=12 7+У=12 Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. | Х-5=7 Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое. | 12-У=7 Чтобы найти вычитаемое, надо из уменьшаемого вычесть разность. | Х×4=12 3×У=12 Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель. | Х:3=4 Чтобы найти делимое, надо делитель умножить на частное.
| 12:У=4 Чтобы найти делитель, надо делимое разделить на частное. |
| |||||
Х=12-5 Х=7 У=12-7 У=5 | Х=5+7 Х=12 | У=12-7 У=5 | Х=12:4 Х=3 У=12:3 У=4 |
Х=3×4 Х=12 | У=12:4 У=3 |
| |||||
7+5=12 12=12 | 12-5=7 7=7 | 12-5=7 7=7 | 3×4=12 12=12 | 12:3=4 4=4 | 12:3=4 4=4 |
7. Если получилось неравенство, проверь вычисления! |
Что такое бухгалтерское уравнение и как его рассчитать?
Что такое бухгалтерское уравнение?
Уравнение бухгалтерского учета гласит, что общие активы компании равны сумме ее обязательств и акционерного капитала.
Эта прямая связь между активами, обязательствами и собственным капиталом считается основой системы бухгалтерского учета с двойной записью. Уравнение бухгалтерского учета гарантирует, что баланс остается сбалансированным. То есть каждая запись, сделанная на стороне дебета, имеет соответствующую запись (или покрытие) на стороне кредита.
Уравнение бухгалтерского учета также называют основным уравнением бухгалтерского учета или уравнением баланса.
Основные выводы
- Уравнение бухгалтерского учета считается основой системы бухгалтерского учета с двойной записью.
- Бухгалтерское уравнение показывает на балансе компании, что общие активы компании равны сумме обязательств компании и акционерного капитала.
- Активы представляют собой ценные ресурсы, контролируемые компанией. Обязательства представляют собой их обязательства.
- Как обязательства, так и собственный капитал представляют собой то, как финансируются активы компании.
- Финансирование за счет заемных средств отражается как обязательство, а финансирование за счет выпуска акций отражается в составе акционерного капитала.
Уравнение бухгалтерского учета
Понимание уравнения бухгалтерского учета
Финансовое положение любого предприятия, большого или малого, основано на двух ключевых компонентах баланса: активах и пассивах. Собственный капитал, или акционерный капитал, является третьим разделом баланса.
Уравнение бухгалтерского учета представляет собой представление того, как эти три важных компонента связаны друг с другом.
Активы представляют собой ценные ресурсы, контролируемые компанией, а пассивы — ее обязательства. И обязательства, и собственный капитал представляют собой то, как финансируются активы компании. Если он финансируется за счет долга, он будет отображаться как обязательство, но если он финансируется за счет выпуска акций для инвесторов, он будет отображаться в акционерном капитале.
Уравнение бухгалтерского учета помогает оценить, точно ли бизнес-операции, осуществляемые компанией, отражаются в ее бухгалтерских книгах и счетах. Ниже приведены примеры статей, перечисленных в балансе.
Активы
Активы включают денежные средства и их эквиваленты или ликвидные активы, которые могут включать казначейские векселя и депозитные сертификаты.
Дебиторская задолженность перечисляет суммы денег, которые клиенты должны компании за продажу ее продукции. Инвентарь также считается активом.
Основным и часто наиболее ценным активом большинства компаний являются машины, здания и собственность этой компании.
Это основные средства, которые обычно хранятся в течение многих лет.
Обязательства
Обязательства — это долги, которые компания должна, и расходы, которые она должна платить, чтобы поддерживать работу компании.
Долг — это обязательство, будь то долгосрочный кредит или счет, который должен быть оплачен.
Расходы включают арендную плату, налоги, коммунальные услуги, заработную плату, заработную плату и выплачиваемые дивиденды.
Акционерный капитал
Акционерный капитал представляет собой общую сумму активов компании за вычетом ее общей суммы обязательств.
Его можно определить как общее количество долларов, которое осталось бы у компании, если бы она ликвидировала все свои активы и выплатила все свои обязательства. Затем это будет распределено среди акционеров.
Нераспределенная прибыль является частью акционерного капитала. Это число представляет собой сумму общей прибыли, которая не была выплачена акционерам в качестве дивидендов.
Думайте о нераспределенной прибыли как о сбережениях, поскольку она представляет собой общую прибыль, которая была сохранена и отложена (или «удержана») для будущего использования.
Формула уравнения бухгалтерского учета и расчет
Ресурсы знак равно ( Обязательства + Собственный капитал ) \text{Активы}=(\text{Обязательства}+\text{Собственный капитал}) Активы = (Обязательства + Собственный капитал)
Бухгалтерский баланс содержит элементы, которые вносят вклад в уравнение бухгалтерского учета:
- Найдите общие активы компании в балансе за период.
- Итого все обязательства, которые должны быть отдельной строкой в балансе.
- Найдите общую сумму акционерного капитала и добавьте число к общей сумме обязательств.
- Общие активы будут равны сумме обязательств и общего капитала.
Например, скажем, ведущая розничная компания XYZ Corporation сообщила в своем балансе за последний полный финансовый год следующее:
- Общие активы: 170 миллиардов долларов
- Общие обязательства: 120 миллиардов долларов
- Общий акционерный капитал: 50 миллиардов долларов
Если мы посчитаем правую часть уравнения бухгалтерского учета (капитал + обязательства), мы получим (50 миллиардов долларов + 120 миллиардов долларов) = 170 миллиардов долларов, что соответствует стоимости активов, заявленных компанией.
О системе двойной записи
Бухгалтерское уравнение представляет собой краткое выражение сложного, расширенного и многоэлементного отображения баланса.
По сути, репрезентация приравнивает все виды использования капитала (активов) ко всем источникам капитала, где заемный капитал ведет к обязательствам, а собственный капитал ведет к акционерному капиталу.
Для компании, ведущей точные счета, каждая бизнес-транзакция будет отражена как минимум в двух ее счетах. Например, если бизнес берет кредит в банке, заемные деньги будут отражены в его балансе как увеличение активов компании, так и увеличение ее кредитных обязательств.
Если бизнес покупает сырье и платит наличными, это приведет к увеличению запасов компании (актив) при уменьшении денежного капитала (другой актив). Поскольку каждая транзакция, осуществляемая компанией, затрагивает два или более счетов, система бухгалтерского учета называется бухгалтерским учетом с двойной записью.
Практика двойной записи гарантирует, что уравнение бухгалтерского учета всегда остается сбалансированным, а это означает, что значение левой части уравнения всегда будет соответствовать значению правой части.
Другими словами, общая сумма всех активов всегда будет равна сумме обязательств и собственного капитала.
Глобальное соблюдение системы бухгалтерского учета с двойной записью делает процессы ведения учета и подсчета более стандартизированными и более надежными.
Уравнение бухгалтерского учета гарантирует, что все записи в бухгалтерских книгах и отчетах проверены, и существует поддающаяся проверке связь между каждым обязательством (или расходом) и его соответствующим источником; или между каждой статьей дохода (или актива) и его источником.
Пределы уравнения бухгалтерского учета
Хотя бухгалтерский баланс всегда уравновешен, бухгалтерское уравнение не может сказать инвесторам, насколько хорошо работает компания. Инвесторы должны интерпретировать цифры и решить для себя, имеет ли компания слишком много или слишком мало обязательств, недостаточно активов или, возможно, слишком много активов, достаточно ли ее финансирования для обеспечения ее долгосрочного роста.
Реальный пример
Ниже представлена часть баланса Exxon Mobil Corporation (XOM) в миллионах по состоянию на 31 декабря 2019 года.:
- Общая сумма активов составила 362 597 долларов США
- Общая сумма обязательств составила 163 659 долларов США
- Общая сумма капитала составила 198 938 долларов США
Уравнение бухгалтерского учета рассчитывается следующим образом:
- Уравнение бухгалтерского учета = 163 659 долларов США (общая сумма обязательств) + 198 938 долларов США (собственный капитал) равно 362 597 долларов США (что равняется общей сумме активов за период)
Почему бухгалтерское уравнение важно?
Уравнение бухгалтерского учета отражает взаимосвязь между тремя компонентами баланса: активами, обязательствами и собственным капиталом. При прочих равных условиях собственный капитал компании будет увеличиваться при увеличении ее активов, и наоборот. Добавление обязательств уменьшит собственный капитал, в то время как уменьшение обязательств — например, путем погашения долга — увеличит собственный капитал. Эти основные понятия необходимы для современных методов бухгалтерского учета.
Каковы 3 элемента бухгалтерского уравнения?
Тремя элементами уравнения бухгалтерского учета являются активы, обязательства и акционерный капитал. Формула проста: совокупные активы компании равны ее обязательствам плюс акционерный капитал. Система двойной записи, принятая во всем мире, предназначена для точного отражения совокупных активов компании.
Что такое актив в бухгалтерском уравнении?
Актив – это что-либо, имеющее экономическую ценность, находящееся под контролем компании, которое может быть использовано на благо бизнеса сейчас или в будущем. Они включают в себя основные средства, такие как машины и здания. Они могут включать финансовые активы, такие как инвестиции в акции и облигации. Они также могут быть нематериальными активами, такими как патенты, товарные знаки и деловая репутация.
Что такое пассив в бухгалтерском уравнении?
Обязательства компании включают все взятые ею долги. К ним могут относиться кредиты, кредиторская задолженность, ипотечные кредиты, доходы будущих периодов, выпуски облигаций, гарантии и начисленные расходы.
Что такое акционерный капитал в бухгалтерском уравнении?
Акционерный капитал представляет собой общую стоимость компании, выраженную в долларах. Иными словами, это сумма, которая осталась бы, если бы компания ликвидировала все свои активы и выплатила все свои долги. Остаток — это собственный капитал акционеров, который будет им возвращен.
Уравнение бухгалтерского учета: определение, формула и примеры
Содержание- Что такое уравнение бухгалтерского учета?
- Каковы конкретные названия капитала в балансе?
- Что такое двойная бухгалтерия (бухгалтерия)?
- Пример основного уравнения бухгалтерского учета. Как рассчитать
- Что такое расширенное уравнение бухгалтерского учета?
- Пример расширенного уравнения бухгалтерского учета – как рассчитать
- Чем уравнение бухгалтерского учета отличается от формулы оборотного капитала?
- Выводы
Компании рассчитывают уравнение бухгалтерского учета на основе своего баланса.
Они доказывают, что финансовая отчетность сбалансирована и система двойной записи работает. Активы компании равны сумме ее обязательств и собственного капитала.
В этой статье дается определение бухгалтерского уравнения и объясняется двойная бухгалтерия. Мы показываем формулы для расчета в виде основного уравнения бухгалтерского учета и расширенного уравнения бухгалтерского учета.
Что такое бухгалтерское уравнение?Уравнение бухгалтерского учета представляет собой формулу, которая показывает, что сумма обязательств компании и акционерного капитала равна ее совокупным активам (Активы = Обязательства + Капитал). Четкая взаимосвязь между обязательствами, активами и собственным капиталом компании является основой двойной бухгалтерии. Источником бухгалтерских уравнений компании является ее бухгалтерский баланс. Собственный капитал может быть акционерным капиталом, акционерным капиталом или собственным капиталом.
Как и в других уравнениях, если известны два члена основного бухгалтерского уравнения, вы можете найти третий член.
Например, общие активы — общие обязательства = общий капитал или общие активы — общий капитал = общие обязательства. Вы перемещаете термин из правой части бухгалтерского уравнения в левую, используя знак минус.
Названия, означающие то же, что и «Балансовый отчет», — это «Отчет о финансовом положении» или «Отчет о финансовом состоянии».
Каковы конкретные названия капитала в балансе?Собственный капитал в балансе именуется Собственным капиталом, Акционерным капиталом или Акционерным капиталом. Владельцы бизнеса с индивидуальным владением и малые предприятия, не являющиеся корпорациями, используют собственный капитал. Корпорации с акционерами могут называть Капитал либо Акционерным капиталом, либо Акционерным капиталом.
Что такое двойная бухгалтерия (бухгалтерия)? При двойной записи в бухгалтерском учете общая сумма дебетов в левой части должна равняться общей сумме кредитов в правой части. Это касается каждой бизнес-операции и записи в журнале.
В результате финансовая отчетность сбалансирована.
Ежемесячный пробный баланс представляет собой список имен счетов из плана счетов с общими остатками или суммами счетов. Общие суммы дебета и кредита должны быть равны перед проводкой транзакций в главную книгу для цикла учета.
Двойная бухгалтерия начала использоваться купцами в Италии как ручная система в 14 веке.
Бухгалтерское программное обеспечение представляет собой систему бухгалтерского учета с двойной записью, автоматически формирующую пробный баланс. Пробный баланс включает столбцы с общими дебетовыми и кредитовыми транзакциями в нижней части отчета.
Пример основного уравнения бухгалтерского учета — как рассчитать Ниже следует скриншот консолидированных балансов Alphabet Inc из годового отчета 10-K, поданного в SEC за год, закончившийся 31 декабря 2021 года. Alphabet Inc — материнская компания Google. В качестве нашего примера мы вычисляем уравнение бухгалтерского учета на основе баланса компании по состоянию на 31 декабря 2021 года.
Обратите внимание, что суммы указаны в миллионах долларов.
Решение основной формулы бухгалтерского уравнения Alphabet Inc.:
Общие активы = общая сумма обязательств + общий капитал акционеров
359 268 долл. США = 107 633 долл. США + 251 635 долл. США
долл. США 359, 268 = 359 268 долл. США
, потому что расчет Alphabet, Inc. показывает, что базовый уравнение в балансе. И система двойной записи работает.
Что такое расширенное уравнение учета?Расширенное уравнение бухгалтерского учета удлиняет базовое уравнение бухгалтерского учета (Активы = Обязательства + Акционерный капитал). Он показывает элементы в разделе акционерного капитала баланса в формуле.
Расширенное уравнение учета:
Общие активы = Общие обязательства + CC +/- AOCIL + BRE + R – E – D – SR
Где термины из раздела Акционерный капитал баланса включают:
CC Внесенный капитал
AOCIL – накопленный прочий совокупный доход (убыток)
BRE – начальная нераспределенная прибыль
R – доход
E – расходы
D – дивиденды (выплаченные)
выкуп акций0005
В этом расширенном уравнении бухгалтерского учета CC, внесенный капитал или оплаченный капитал, представляет собой акционерный капитал.
AOCIL добавляется к доходу или вычитается из-за убытка. Нераспределенная прибыль начинается Нераспределенная прибыль + Доход – Расходы – Дивиденды – Выкуп акций.
Накопленный прочий совокупный доход (убыток), AOCIL, является компонентом акционерного капитала помимо внесенного капитала и нераспределенной прибыли. AOCIL включает нереализованные прибыли или убытки по ценным бумагам, имеющимся в наличии для продажи, прибыли или убытки от пересчета иностранной валюты, а также статьи, связанные с пенсионным планом, включая прибыли или убытки, расходы на предыдущие пенсионные услуги и кредиты.
Выкуп акций называется казначейскими акциями, если акции не погашены. Операции с казначейскими акциями и их аннулирование отражаются в составе нераспределенной прибыли и оплаченного капитала. Запись в журнале зависит от специфики транзакции.
Акционерный капитал состоит из привилегированных акций, если таковые имеются, и обыкновенных акций. Нераспределенная прибыль рассчитывается как первоначальная нераспределенная прибыль плюс годовые прибавления к нераспределенной прибыли (от выручки минус расходы = чистая прибыль) минус выплаченные дивиденды минус выкуп акций.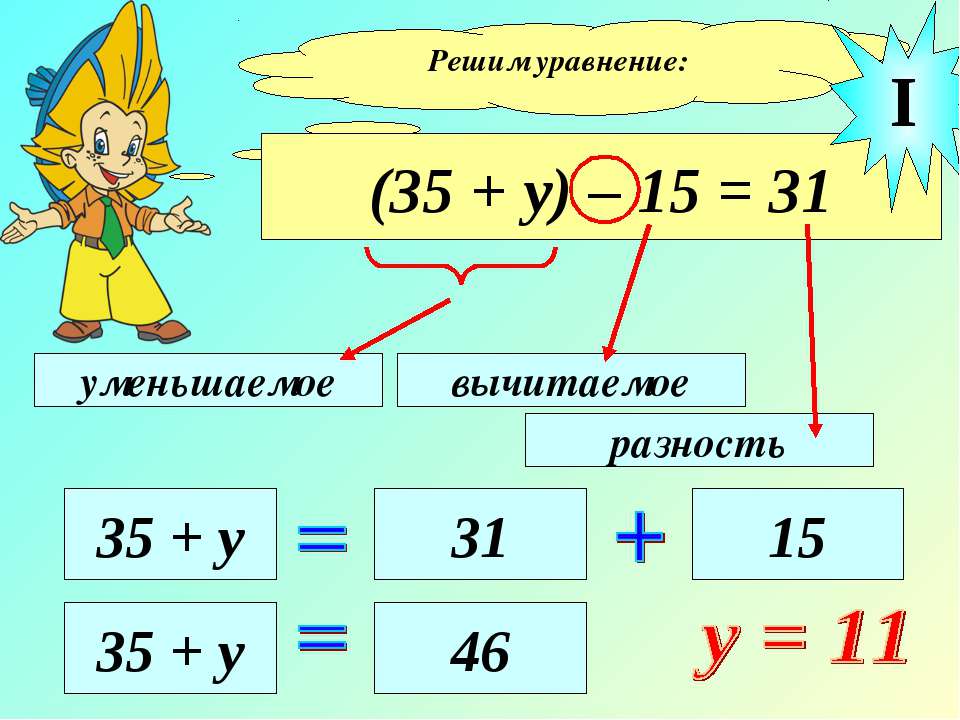
Для EAE вам все равно понадобится бухгалтерский баланс. Обратите внимание, что вам также понадобится отчет о прибылях и убытках и, возможно, подробный отчет об акционерном капитале.
Не все компании будут выплачивать дивиденды, выкупать акции или накапливать другой совокупный доход или убыток.
Пример расширенного уравнения бухгалтерского учета – Как рассчитатьДля этого примера мы рассчитываем расширенное уравнение бухгалтерского учета, используя финансовую отчетность за 2021 год. Чтобы проследить цифры, обратитесь к тем же балансовым отчетам Alphabet Inc., показанным выше, а также к отчету о прибылях и убытках и подробному отчету об акционерном капитале в этом разделе.
Alphabet — технологическая компания, которая не выплачивает дивиденды. Из Отчета об акционерном капитале можно увидеть выкуп акций Alphabet. Выкуп их акций влияет как на капитал, так и на баланс нераспределенной прибыли.
Общие активы = Общие обязательства + CC +/- AOCIL + BRE + R – E – D – SR
359 268 = 107 633 долл.
0 – 47 950 долл. США)
359 268 долл. = 107 633 долл. США + (61 774 долл. США – 1 623 долл. США + 163 401 долл. США + 257 637 долл. США – 181 604 долл. США – 0 – 47,9 долл. США)50)
359 268 долл. США = 107 633 долл. США + 251 635 долл. США
359 268 долл. США = 359 268 долл. США
Преобразуйте способ работы
вашей финансовой команды.
Обеспечьте масштабирование и эффективность своего бизнеса с помощью полностью автоматизированного сквозного расчета кредиторской задолженности.
Подробнее
Чем уравнение бухгалтерского учета отличается от формулы оборотного капитала?В уравнении бухгалтерского учета для расчета используются общие активы, общие обязательства и общий капитал. Эта формула отличается от оборотного капитала, основанного на текущих активах и текущих обязательствах.
Оборотный капитал измеряет ликвидность. Формула оборотного капитала: Текущие активы – Текущие обязательства.
Текущие активы включают денежные средства и их эквиваленты, дебиторскую задолженность, запасы и предварительно оплаченные активы. Краткосрочные обязательства представляют собой краткосрочные финансовые обязательства, подлежащие оплате денежными средствами в течение года. Текущие обязательства включают кредиторскую задолженность, начисленные расходы и краткосрочную часть долга.
Оборотный капитал показывает, будет ли у компании сумма денег, необходимая для своевременной оплаты счетов и других обязательств.
Выводы- Уравнение бухгалтерского учета — это математическая формула в финансовом учете. Это доказывает, что общие активы равны общим обязательствам плюс общий капитал из баланса компании.
- Точное название Total Equity зависит от юридического лица компании.
- Уравнение бухгалтерского учета также называют уравнением баланса и фундаментальным уравнением бухгалтерского учета.
- Формула уравнения бухгалтерского учета основана на системе бухгалтерского и бухгалтерского учета с двойной записью. Дебет и кредит равны при регистрации хозяйственных операций и подготовке финансовой отчетности.
- Основное уравнение бухгалтерского учета менее подробно, чем расширенное уравнение бухгалтерского учета. Расширенное уравнение бухгалтерского учета показывает больше компонентов акционерного капитала в расчетах. Результаты эквивалентны.
- Денежный поток не учитывается в уравнении бухгалтерского учета. Вам не нужно использовать отчет о движении денежных средств компании для расчета уравнения бухгалтерского учета.
Дебет и кредит равны при регистрации хозяйственных операций и подготовке финансовой отчетности.Уравнение бухгалтерского учета (определение, базовый пример)
Уравнение бухгалтерского учета является основным принципом бухгалтерского учета, утверждающим, что общие активы предприятия эквивалентны сумме его обязательств и собственного капитала. Оно также известно как уравнение баланса и составляет основу системы бухгалтерского учета с двойной записью.
Ниже приведено уравнение бухгалтерского учета
Активы = обязательства + акционерный капитал
Уравнение бухгалтерского учета основано на системе двойной записи, что означает, что все активы должны быть равны всем обязательствам в бухгалтерской книге.
Все записи, сделанные в дебетовой части баланса, должны иметь соответствующую кредитовую запись в балансовом отчете. Таким образом, оно также известно как уравнение балансового отчета. более.
Соглашение о таблице
- Определение уравнения бухгалтерского учета
- Основное уравнение бухгалтерского учета
- Разрушение уравнения
- Пример № 1
- Пример № 2
- Аккумуляция. Актуальная операция. Видео
- Рекомендуемые статьи
- Основное уравнение бухгалтерского учета
Вы можете свободно использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство? Ссылка на статью должна быть гиперссылкой
для EG:
Источник: уравнение бухгалтерского учета (WallStreetMojo.com)
Основное уравнение бухгалтерского учета
Активы = обязательства + акционеры капитал
. Разрушение уравнения
- Assets: Ascome Ascome Ascome Ascome Ascome Ascome As The Views. ; они могут быть материальными или нематериальными, но принадлежать компании.
- Обязательство: Это термин для общей стоимости, которую компания должна выплатить в краткосрочной или долгосрочной перспективе.
- Акционерный капитал: Акционерный капитал Акционерный капитал Акционерный капитал представляет собой остаточную долю акционеров в компании и рассчитывается как разница между Активами и Обязательствами. Отчет об акционерном капитале в балансовом отчете подробно описывает изменение стоимости акционерного капитала с начала до конца отчетного периода.Подробнее — это сумма денег, которую компания привлекла посредством выпуска акций. В качестве альтернативы, это также сумма нераспределенной прибыли. Он отображается как часть собственного капитала в пассиве баланса компании. Читать далее компании. В качестве акционеровАкционерыАкционером является физическое лицо или организация, владеющая одной или несколькими акциями государственной или частной корпорации и, следовательно, являющаяся законными владельцами компании. Процент владения зависит от количества акций, которыми они владеют, по отношению к общему количеству акций компании. Более того, инвестируйте свои деньги в компанию, они должны быть оплачены определенной суммой прибыли, поэтому это является обязательством в бухгалтерских книгах компании.
; они могут быть материальными или нематериальными, но принадлежать компании.
Процент владения зависит от количества акций, которыми они владеют, по отношению к общему количеству акций компании. Более того, инвестируйте свои деньги в компанию, они должны быть оплачены определенной суммой прибыли, поэтому это является обязательством в бухгалтерских книгах компании.Следовательно, общие активыОбщие активыОбщие активы представляют собой сумму оборотных и внеоборотных активов компании. Общие активы также равны сумме общих обязательств и общих фондов акционеров. Общие активы = обязательства + акционерный капитал и далее всегда должны быть равны общим обязательствам в балансе, который по существу составляет основу всей системы бухгалтерского учета любой компании, когда она следует системе двойной бухгалтерии.
Пример #1
1 декабря 2007 года Картик начал свой бизнес FastTrack Movers and Packers. Первая транзакция, которую Картик запишет для своей компании, — это его инвестиция в размере 20 000 долларов в обмен на 5 000 обыкновенных акций FastTrack Movers & Packers.
Дохода нет, потому что 1 декабря компания не получила комиссию за доставку, и не было никаких расходов. Как эта сделка будет отражена в балансе?
Денежные средства и обыкновенные акции
- Обыкновенные акции будут увеличены, когда корпорация выпустит акции. Они отражаются как собственный капитал в балансе Компании. Подробнее акций в обмен на денежные средства (или другие активы)
- Нераспределенная прибыль будет увеличиваться, когда корпорация получает прибыль, и будет уменьшаться, когда корпорация имеет чистый убыток Чистый убыток Чистый убыток или чистый операционный убыток означает превышение понесенных расходов над доходом, полученным в данном отчетном периоде. Он оценивается как разница между доходами и расходами и отражается как обязательство в балансе.читать далее
- Основная ссылка между балансовым отчетом компании и отчетом о прибылях и убытках
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т.
д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство? Ссылка на статью будет гиперссылкой
Например, :
Источник: Accounting Equation (wallstreetmojo.com)
Пример #2
Система бухгалтерского учета с двойной записью помогает нам понять поток любой конкретной транзакции от источника до конца. Давайте возьмем еще одно базовое, расширенное уравнение бухгалтерского учета. Расширенное уравнение бухгалтерского учета. Расширенное уравнение бухгалтерского учета относится к расширенной версии базового уравнения бухгалтерского учета для конкретной корпорации или индивидуального предпринимателя, предоставляя информацию о финансовых операциях корпорации, таких как активы, обязательства, акционерный капитал, доходы, расходы, и вывод средств.читать дальше пример.
При покупке актива в компании сумма покупки также должна быть снята с какого-либо счета в компании (как правило, с кассового счета). Следовательно, счет, с которого снимается сумма, кредитуется, и должен быть дебетован счет для приобретенного актива (дебетуется счет, связанный с приобретенным активом).
Рассмотрим следующие записи:
- 27 декабря Джо основал новую компанию, вложив 15 000 долларов в качестве капитала.
- 3 января Джо купил офисный стол для своей компании, который обошелся ему в 5000 долларов.
- Он заплатил за свой труд 5 января на общую сумму 15 000 долларов.
- 10 января он получил контракт от своих клиентов, и они заплатили ему 2000 долларов.
- 13 января Джо получил еще один контракт, за который клиент заплатил 4000 долларов вперед.
- 15 января он выполнил контракт на обслуживание, полученный 13 января, и клиент оплатил оставшуюся сумму в размере 8000 долларов США.
The Journal entries for the above transactions are as below:
| Date | Account Description | Debit | Credit | |
|---|---|---|---|---|
| 27-Dec | Cash | $15,000 | ||
| Акционеры капитал | $ 15 000 | |||
| 3-январь | Офис таблица | $ 5 000 | ||
КЕРСА. 0457 | ||||
| 5-Jan | Wages Expense | $15,000 | ||
| Cash | $15,000 | |||
| 10-Jan | Cash | $2,000 | ||
| Service Revenue | $2,000 | |||
| 13-января | Денежные средства | $ 4000 | ||
| ДИТАЛА | .0457 | $12,000 | ||
| 15-Jan | Cash | $8,000 | ||
| Account Receivables | $8,000 | |||
| Total | $57,000 | $57,000 |
The corresponding entries in баланс на 15 января должен быть следующим:
| Активы | Сумма | Обязательства | Сумма |
|---|---|---|---|
| Cash | $9,000 | Service Revenue | $14,000 |
| Furniture A/C | $5,000 | ||
| Total | $14,000 | Total | $14,000 |
Видно, что общая сумма кредита равна общей сумме долга.
Это фундаментальная система бухгалтерского учета с двойной записью, которая помогает нам понять из иллюстрации выше, что общая сумма активов должна быть равна общей сумме обязательств.
На этом рисунке активы — это денежные средства, мебель, кондиционер и дебиторская задолженность. Дебиторская задолженность. Дебиторская задолженность — это деньги, причитающиеся бизнесу от клиентов, которым бизнес предоставил услуги или поставил продукт, но еще не получил оплату. Они классифицируются как оборотные активы в балансе как платежи, ожидаемые в течение года. читать далее; Обязательства – это расходы на заработную плату и доходы от услуг.
Если мы обратимся к любому балансовому отчету, то поймем, что активы и обязательства, а также собственный капитал представлены на определенную дату и время. Таким образом, по состоянию на 15 января существует только три счета с остатком — «Денежные средства», «Мебель А/С» и «Доходы от услуг» (остальные списываются в течение всего периода транзакции до 15 января).
В балансе отражаются только те счета, которые существуют с остатком (положительным или отрицательным) на определенную дату.
В качестве альтернативы мы также можем понять, что общая сумма обязательств может быть получена, если упомянута только стоимость активов. Собственный капитал также можно определить, если доступны общие активы и общие обязательства. Формула основного бухгалтерского уравнения также может быть использована, как показано ниже:
Общие обязательства = Общие активы – Акционерный капитал
Акционерный капитал = Общие активы – Общие обязательства
Следовательно, это составляет основу многих анализов для рыночных инвесторов. , финансовые аналитики, аналитики-исследователиАналитики-исследователиАналитики-исследователи — это профессия, основная задача которой включает исследования в конкретных областях, анализ фактов и цифр, интерпретацию анализа и, наконец, представление их структурированной аудитории, которая может относиться к маркетингу, финансам, операциям.
читать далее и другие финансовые учреждения.
Уравнение бухгалтерского учета в отчете о прибылях и убытках
Бухгалтерский баланс отражает не только основное бухгалтерское уравнение в том виде, в каком оно реализовано, но и отчет о прибылях и убытках. Отчет о прибылях и убытках. чтобы определить прибыль или убыток компании и измерить ее деловую активность с течением времени на основе требований пользователей. подробнее.
- Отчет о прибылях и убытках составляется для отражения общих расходов и общих доходов компании для расчета чистой прибыли для различных целей. Этот отчет также составляется вместе с бухгалтерским балансом. Однако немного по-другому применяется.
- Здесь у нас нет общей суммы активов и пассивов. Тем не менее, выписка подготовлена таким образом, что, если расход зачисляется, он будет иметь равную и противоположную запись в долге в связанной бухгалтерской книге AccountLedger AccountLedger в бухгалтерских записях и обрабатывает финансовые данные фирмы, взятые из журнальных записей. Это становится важной финансовой записью для дальнейшего использования. Он используется для создания финансовой отчетности. Она также известна как вторая книга записи.Подробнее.
- Отчет о прибылях и убытках включает в себя счета, которые непосредственно относятся к доходам или расходам компании, таким как себестоимость проданных товаров, налоговые расходы и проценты к уплате — это сумма расходов, которые были понесены, но еще не выплачены. Это обязательство, которое появляется на балансе компании. читать больше Проценты к уплатеПроценты к уплатеПроценты к уплате — это сумма расходов, которые были понесены, но еще не оплачены. Это обязательство, которое появляется на балансе компании. Подробнее расходы.
Это становится важной финансовой записью для дальнейшего использования. Он используется для создания финансовой отчетности. Она также известна как вторая книга записи.Подробнее.Заключительные мысли
Понятно, что система бухгалтерского учета с двойной записью используется во всем мире и придерживается правил дебета. Правила дебетованияДебет представляет собой либо увеличение расходов компании, либо снижение ее доходов. читать больше и кредитные записи.
Эти записи должны совпадать друг с другом на конец определенного периода, и если есть разрыв в общем остатке, его необходимо исследовать. Эта система значительно упрощает учет, создавая взаимосвязь между расходом/обязательством и причиной расхода/обязательства (или доходом/активом и источником дохода/актива). Нам необходимо понять основную концепцию и эмпирическое правило бухгалтерского учета. Здесь каждая транзакция должна иметь как минимум 2 счета (одинаковая сумма), один из которых дебетуется, а другой кредитуется. читать далее, что относится к дебетовым и кредитовым записям на корневом уровне. Таким образом, хотя формула уравнения бухгалтерского учета кажется однострочной, она содержит много смысла и может быть изучена глубже с помощью сложных проводок расходов.
Видео по уравнению бухгалтерского учета
Рекомендуемые статьи
Эта статья представляет собой руководство по уравнению бухгалтерского учета и его определению. Здесь мы подробно обсудим уравнение бухгалтерского учета, разбив его на практические примеры.