Урок математики в 4 -м классе «Площадь треугольника»
Цель:
- Сформировать понятие площади треугольника.
- Вывести формулу S треугольника.
- Повторить основные математические понятия (катеты, гипотенуза, высота…)
- Тренировать навыки быстрого счета
- Развитие мыслительных операций: (анализ, синтез, сравнение, обобщение)
Ход урока
I этап: Самоопределение к деятельности.
— У нас сегодня большое количество гостей, поздороваемся с ними. (Дети здороваются и садятся).
— Как думаете, какое количество гостей присутствует на нашем уроке? (Дети не считая отвечают и дают примерный результат).
— 1/6 часть всего кол-ва, это учителя нашей школы. Сколько их?
— Что мы сейчас делали? (Считали гостей).
— Всегда ли ваши ответы были точными? (Нет).
— По какой причине? (Не было времени считать, сделали прикидку, на глаз оценили).
— Используем ли мы данный прием на уроках? (Да).
— В каких ситуациях? (Нехватка времени, нет иного способа действия).
— Но математика наука точная, еще древний философ Платон говорил: «Математика приближает разум к истине». А значит ответы все же должны быть верными.
— А вот современное высказывание гласит: «Математику изучить нельзя…».
— Вы согласны с этим утверждением? (Нет, тогда что мы на уроках делаем?)
— Дело в том, что у этой фразы есть продолжение, которое вносит иной смысл , но вот какой и какое же у фразы продолжение мы узнаем в конце урока.
II этап: Актуализация знаний и фиксация затруднения в деятельности.
- Быстрый счет. (Конечный ответ цепочки примеров дети фиксируют на планшете).
- Внимание на экран. Какое из слов может быть лишним и почему?
(демонстрация № 1)
(Погода ,т.
к не имеет к математике отношения).
— Но и не все оставшиеся слова будут иметь отношение к сегодняшнему уроку математики. Определить круг ключевых слов урока нам поможет арифметический диктант.
Арифметический диктант: (1 за доской, остальные работают в тетради)
— третья часть 18 6, 15, 7, 70, 24
— 3/4 от 20
— 1% числа 700
— 7 % от 1000
— 1/6 часть числа это 4, найди все число
(Проверка числового ряда, на экране исчезают лишние слова и числа).
— Что объединяет оставшиеся числа? (Целые, натуральные).
— На какие две группы можно разбить? (Дети предлагают варианты).
— А вот оставшиеся слова объединены темой сегодняшнего урока. Чтобы нам ее сформулировать как можно точнее, давайте вспомним основные математические понятия и поиграем
(Детям предлагаются карточки двух цветов, вопросы и ответы).
Основанием треугольника называется |
Сторона, на которую опущен перпендикуляр |
Сторона треугольника, лежащая против прямого угла называется… |
гипотенузой |
Площадь… |
Это место, которое фигура занимает на плоскости |
формула |
Это равенство, устанавливающее взаимосвязь между величинами |
Тупоугольным называется треугольник, у которого |
Один из углов тупой |
Стороны треугольника, образующие прямой угол, называются |
катетами |
Перпендикулярные линии это |
Линии, которые при пересечении образуют прямой угол |
Высота треугольника |
Перпендикуляр, опущенный из любой вершины на противоположную сторону |
Остроугольным называют треугольник |
У которого все углы острые |
В зависимости от длины сторон треугольники бывают |
Равносторонние, разносторонние, равнобедренные |
Прямоугольным называют треугольник, у которого |
Один из углов прямой |
Чтобы найти площадь прямоугольника, надо |
Длину умножить на ширину |
Предлагаю поиграть еще в одну игру, которую придумали китайцы, всегда слывшие хорошими математиками.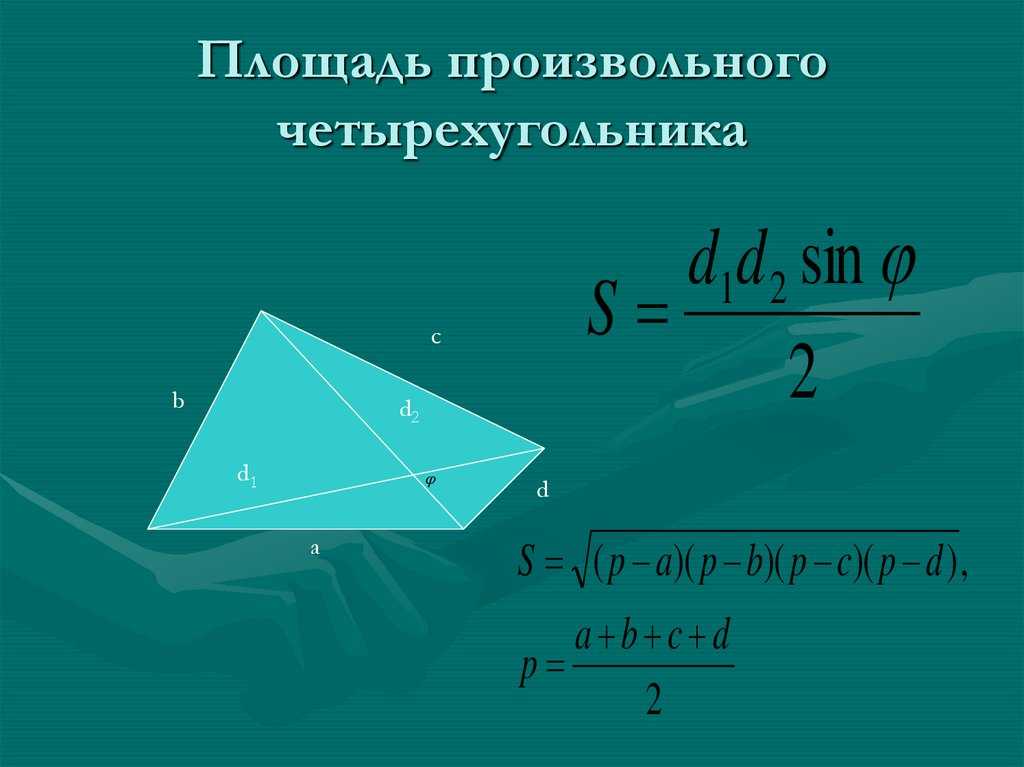
Она называется «Танграм».
Суть ее состоит в собирании фигур из более мелких геометрических фигур. Работать будем в парах. Откройте конверт №1 и выложите все фигуры перед собой. Перечислите все, что перед вами. (4 маленьких и 2 больших прямоугольных треугольника разного цвета).
— Соберите из всех фигур:
1 ряд – квадрат
2 ряд – прямоугольник
3 ряд – треугольник
(Практическая работа в парах, проверка построений с помощью компьютера).
(демонстрация № 2)
— Что объединяет все получившиеся фигуры? (Многоугольники, состоят из равного кол-ва фигур).
— Сравните их по площади. (Равные, т.к. состоят из одинаковых частей).
— Как называются такие фигуры? (Равновеликие).
— Взгляните на фигуры. (демонстрация № 3)
— Можете ли вы утверждать, что данные фигуры также равновеликие? (нет, другая ситуация, иной значит способ действия).
— Используете знания свои и сравните фигуры по площади).
(Дети без труда по формуле находят S квадрата и прямоугольника, но возникает проблема при работе с треугольником).
III этап: Постановка проблемы, формулирование темы урока.
— Почему возникло затруднение? (Не знаем как найти S треугольника, можем только найти неточный результат).
— Значит какова цель сегодняшнего урока? ( научиться находить S треугольника).
— На основе поставленной цели и ключевых слов урока, попробуйте как можно точнее сформулировать тему сегодняшнего урока.
IV этап: Проектирование и фиксация нового знания.
(демонстрация № 4)
Расскажите все о треугольнике, который перед вами. (Прямоугольный, разносторонний).
— В группах попробуйте найти способ нахождения S прямоугольного треугольника, создать формулу и прокомментировать свои действия.
(Результаты вывешиваются на доску, в громкой речи проговаривается способ действия).
— Что такое стороны а и в? (Катеты).
— Сформулируйте свои выводы в знаковой и словесной форме.
— S = ( а в ) : 2 , Площадь прямоугольного треугольника равна половине произведения его катетов).
— Сверим свою формулировку с предложенной в учебнике (стр. 95).
— Площадь какого треугольника мы находили? (Прямоугольного).
— А для других треугольников эта формула будет верна? (Нет, т.к. нет катетов).
— Тогда давайте составим алгоритм наших действий.
Алгоритм.
- Выдели прямой угол
- Измерь длину катетов
- Найди S по формуле.
V этап: Первичное закрепление во внешней речи.
Выполняется в парах задание из учебника (стр. 95 № 5).
(демонстрация № 5)
VI этап: Самостоятельная работа с самопроверкой.
— Сравните фигуры по площади.
(Появляются в тетрадях записи:
S = ( 4 * 3 ): 2 = 6 кв.см
S = ( 2 * 6 ): 2 = 6 кв.см
S = S
VII этап: Включение в систему знаний и повторение.
— Вернемся к заданию, вызвавшему затруднение. Выполните расчеты в тетради и сравните площади данных фигур.
S = 2 * 2 = 4 кв.см
S = 1 * 3 = 3 кв.см
S = (3 * 2 ) : 2 = 3 кв.см
— Что можете сказать о S прямоугольника и треугольника? (Она одинаковая, значит фигуры равновеликие).
(демонстрация № 6)
Что вы можете сказать о данном треугольнике?
(Разносторонний, тупоугольный).
— Можем ли мы воспользоваться нашим алгоритмом для нахождения его площади?
(Нет, т.
к. должен быть треугольник прямоугольным).
— А нельзя ли с помощью построений сделать из данного треугольника два прямоугольных?
(Можно, надо провести высоту).
Чему будет равна площадь всего треугольника?
(Сумме S двух прямоугольных треугольников, их S мы умеем находить).
S = ( а* h ) : 2
S = ( а * h ) : 2
S = ( ( а + а ) * h ) : 2
( а + а ) -основание , значит
S = ( а * в ) : 2, где а – катет основание; в – катет высота
— Давайте дополним алгоритм.
Алгоритм.
VII этап: Рефлексия деятельности.
— Какова была цель урока?
— Удалось ли нам ее выполнить?
— А теперь узнаем окончание фразы «Математику нельзя изучить, наблюдая как это делает сосед».
— Вы согласны с этим утверждением. (да, на уроке мы делали все сами, а не только наблюдали)
— Что на уроке было главным, а что интересным?
Д/З : (На выбор). – Найди S фигур и сравни фигуры по S.
(Задание в конвертах, на основе демонстрации дети выбирают нужное для себя, определив уровень понимания темы на данном этапе и берут задание из конверта)
как найти площадь прямоугольника, треугольника? 4 класс — Спрашивалка
как найти площадь прямоугольника, треугольника? 4 класс — СпрашивалкаАО
Алексей Обутов
4 класс
- площадь
- треугольник
- класс
- прямоугольник
АГ
Анна Галкина
длину умножить на ширину=)))
АГ
Антон Гомелько
ответ:
S =a x d прямоугольник
s = (a x h)/2 треугольник
Дархан
A*C:2
Иван Ветров
площадь прямоугольника = ширина*длина
треугольника = 1/2 ah
ЛЕ
Лена-Алена Еленова
площадь прямоугольника равна ширина на высоту, а треугольники разные бывают.
ПБ
Пашка Борисов
основание * на высоту и всё это разделить на 2
ИП
Иван Платаный
Такое и не знать? ? О_о позор!! !
площадь прямоугольника: длину умножить на ширину.
площадь треугольника : 1/2 a*h
Вспомни теорему Пифагора.
НМ
Наталья Макеева
площадь прямоугольника: длина*ширина
площадь треугольника : 1/2 a*h
но для прямоугольного треугольника другая формула!
Регина
площадь квадрата — а * а
площадь прямоугольника — а*в
площадь треугольника — а*в: с
периметр прямоугольника — (а+в) *2
периметр квадрата — а*4
СМ
Сергей Маркин
Чтобы найти площадь прямоугольника нужно длину умножить на ширину.
МК
Мария Карпенко
ПРосто способом палетки
ПС
Полина Стародубова
Длину умножаем на ширину
площадь прямоугольника
АК
Алексей Карташов
нужно длину умножить длину на ширин
Людмила Богданова
ответ Тогу какая теорема пефагора пишут же 4 класс а не 6 или 7
а чтобы посчитать площадь треугольника надо его 2 стороны умножить на 2 а затем поделить на 2 я решаю так
ОИ
Олеся Ильина
апчи
АК
Андрей Калинин
S=a*b — прямоугольник
Похожие вопросы
как найти площадь прямоугольника
как узнать площадь не равностороннего треугольника для 4 класса?
как найти площадь треугольника в 3 классе
очень нужна помощь задача на 4 класс нужно найти площадь треугольника.
Как найти площадь объемного прямоугольника?
площадь прямоугольника. Как найти площадь прямоугольника, зная 1 сторону и периметр?
Как найти площадь прямоугольника математика 4 класс
прямоугольник разделен на 4 треугольника своими диагоналями, найти площадь если площадь одного тре-ка 27
как найти площадь треугольника 4 класс с 46
Как найти площадь треугольника? 2-4 класс.
Формулы площади четырехугольника — Что такое формулы площади четырехугольника? Примеры
Формулы площади четырехугольника используются для вычисления площади замкнутой фигуры, имеющей четыре стороны, называемой четырехугольником. Существуют различные типы четырехугольников в зависимости от свойств различных параметров. Мы изучим формулы площади квадрата в следующих разделах.
Что такое формулы площади четырехугольника?
Различные формулы площади четырехугольника используются для различных четырехугольников в зависимости от их типов.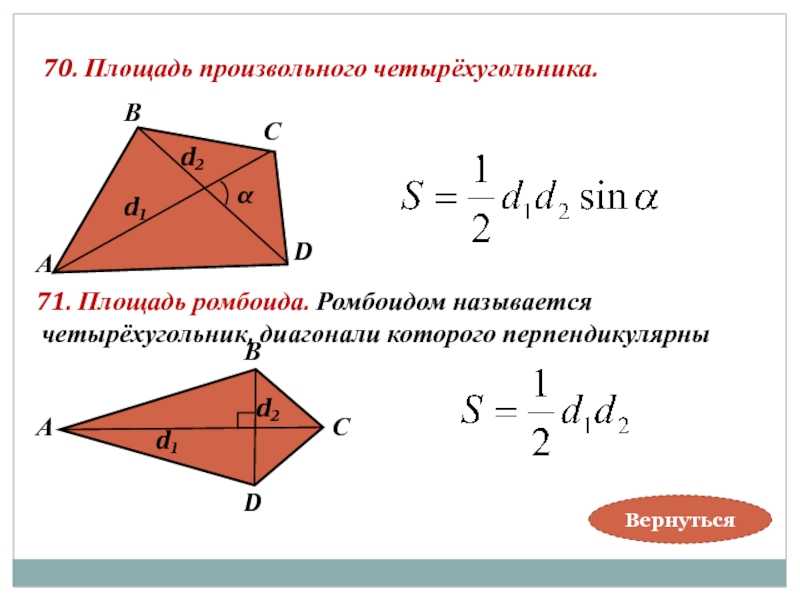
К этим различным типам четырехугольников относятся квадрат, прямоугольник, параллелограмм, ромб, воздушный змей, трапеция и многие другие. Здесь мы увидим формулы для площадей параллелограмма, квадрата, трапеции, прямоугольника и воздушного змея.
Площадь четырехугольника, разделенного на отдельные треугольники, как показано на рисунке ниже:
На приведенном выше рисунке у нас есть два треугольника BCD и ABD
При расчете площадей треугольников по отдельности,
Площадь треугольника BCD = (1/2) × d × \(h_1\)
Площадь треугольника ABD = (1/2) × d × \(h_2\)
Площадь четырехугольника ABCD = Сумма площадей ΔBCD и ΔABD.
Таким образом, площадь четырехугольника ABCD = (1/2) × d × \(h_1\) + (1/2) × d × \(h_2\) = (1/2) × d × (\( h_2\) + \(h_2\)).
Таким образом, площадь формулы четырехугольника, если известны одна из его диагоналей и высоты треугольников (образованных данной диагональю), равна, Площадь = (1/2) × Диагональ × (Сумма высот)
Список формул площади четырехугольника
Давайте посмотрим, что таблица состоит из списка формул площади для различных типов четырехугольников.
Примечание: обратите внимание, что все ромбы можно считать воздушными змеями, но не все воздушные змеи ромбами .
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Закажите бесплатный пробный урок
Примеры формул площади четырехугольника
Давайте рассмотрим несколько иллюстраций, основанных на формулах площади четырехугольника, в этом разделе решенных примеров.
Пример 1: Ной измерил стороны квадрата как 9 м, какова будет площадь квадрата?
Решение:
Найти: Площадь квадрата.
Дано:
Сторона квадрата = 9 м
Используя формулы площади четырехугольника,
Формула площади квадрата = (сторона) 2
Площадь квадрата = (9) 2
Площадь = 81 м 2
Следовательно, площадь квадрата равна 81 м 2 .
Пример 2: Если вы гуляете по трапециевидному парку, у которого одно основание имеет длину 200 м, а длина другого основания составляет 100 м, а высота трапеции составляет 50 м, какова площадь этого трапециевидного парка?
Решение: Найти: Площадь трапециевидного парка.
Одно основание парка = 200 м
Вторая база парка = 100 м
Высота парка = 50 м
Используя формулы площади четырехугольника,
Площадь трапеции = 1/2 × (сумма длин параллельных сторон) × высота
= 1/2 × 300 × 50
= 150 × 50
= 7500 м 2
Следовательно, площадь трапециевидного парка равна 7500 м 2 .
Пример 3: Длина основания параллелограмма 7 единиц, а высота 9 единиц. Используя формулу площади четырехугольника параллелограмма, найдите его площадь.
Решение:
Чтобы найти площадь четырехугольника
Дано:
Основание = 7 шт.
, высота = 9 шт.
Используя формулу площади четырехугольника параллелограмма
Формула площади параллелограмма = основание × высота
Площадь = 7 × 9
Площадь = 63 единицы 2
Следовательно, площадь четырехугольника равна 63 квадратных единиц.
Часто задаваемые вопросы о формулах площади четырехугольника
Что такое формула площади четырехугольника для параллелограмма?
Площадь параллелограмма определяется как пространство, занимаемое параллелограммом в двумерной плоскости. Параллелограмм – это особый вид четырехугольника. Это четырехсторонний четырехугольник, формула площади которого выражается как произведение его основания и высоты, т. Е. A = основание × квадратные единицы высоты.
Какая формула площади четырехугольника для прямоугольника?
Площадь прямоугольника — это количество единичных квадратов, покрываемых границами прямоугольника. Прямоугольник представляет собой четырехугольник с четырьмя сторонами, у которого противоположные стороны равны.
Формула его площади выражается как произведение его длины и ширины, т. Е. A = длина × ширина в квадратных единицах.
Что такое формула площади четырехугольника для квадрата?
Площадь квадрата – это мера занимаемой им площади или поверхности. Это четырехугольник со всеми равными сторонами, формула площади которого равна произведению длины двух его сторон, т. е. A = (сторона) 2 кв.
Какая формула площади четырехугольника для ромба?
Ромб – это четырехугольник с четырьмя сторонами, формула площади которого равна половине произведения длин диагоналей. Формула для вычисления площади ромба, когда даны диагонали, выражается как
.
Площадь ромба = (1 ⁄ 2) × произведение диагоналей на квадратные единицы.
Площадь четырехугольника – Введение, формулы, расчеты
Площадь четырехугольника – это область, ограниченная четырьмя сторонами этого многоугольника. Общая формула площади четырехугольника — основание * высота, также записывается как b * h, а единица измерения — м2.
Четырехугольники бывают двух видов — правильные и неправильные. На этой странице вы узнаете, как найти площадь любого четырехугольника, будь то квадрат или трапеция. Давайте сначала разберемся, что такое площадь, чтобы вы могли понять концепцию площади четырехугольника.
Темы, затронутые в этой статье
На этой странице вы изучите следующие темы.
1. Определение площади четырехугольника
2. Виды четырехугольника
3. Как вычислить площадь четырехугольника?
4. Свойства четырехугольника
5. Формулы площади четырехугольников разных типов
6. Решенные примеры площади четырехугольника
7. Практические вопросы
Определение площади четырехугольника
Область определяется как любая область, включенная в определенную границу или фигуру. Если эта фигура имеет четыре стороны, область внутри этих четырех сторон будет называться площадью четырехугольника.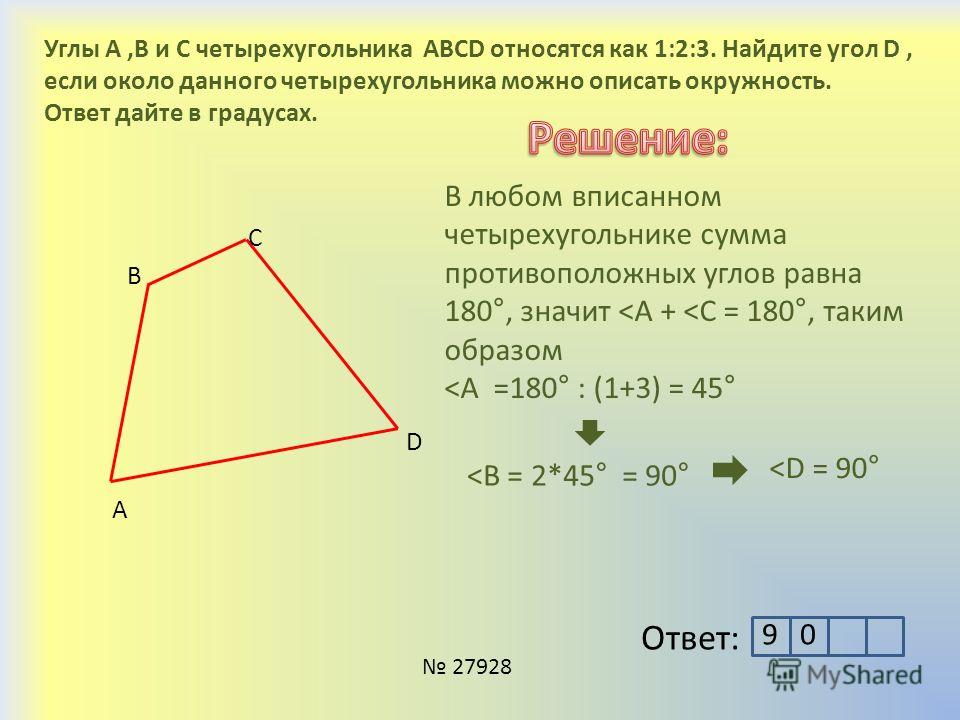
Площадь четырехугольника измеряется в квадратных единицах. Стандартной единицей измерения площади в основном являются квадратные метры, также обозначаемые как м2.
Площадь различных типов четырехугольников
Как объяснялось в предыдущем абзаце, любой многоугольник, имеющий четыре стороны, является четырехугольником, поэтому у нас есть много типов четырехугольников. Некоторые из них:
Square
Rectangle
Parallelogram
Kite
Rhombus
Trapezium
How to Calculate the Area of a Quadrilateral?
Шаг 1: Постройте диагональ PR, которая соединит противоположные вершины четырехугольника PQRS.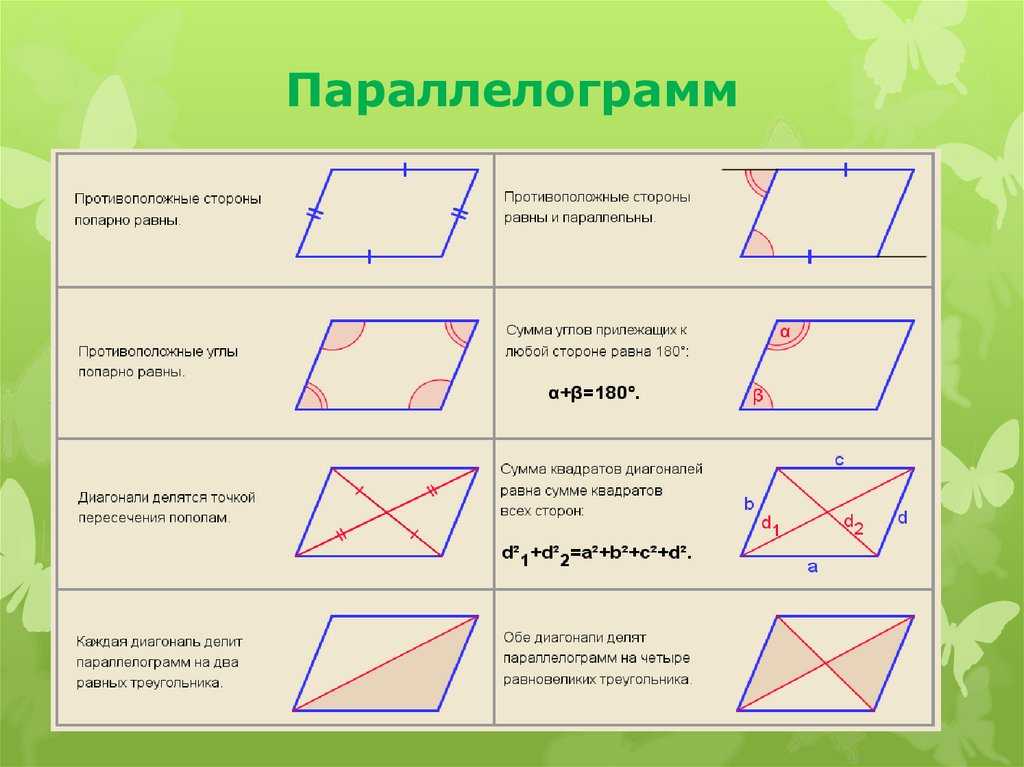
Шаг 2: Из каждой из этих вершин проведите перпендикуляр по диагонали PR.
Шаг 3: Площадь четырехугольника PQRS = Площадь △PQR + Площадь △PRS
Следовательно, площадь четырехугольника PQRS = ( ½ * PR * PT) + (½ * PR * RU), где T и U — перпендикуляры из вершин P и R на диагонали.
Каковы свойства четырехугольника?
Давайте изучим основные свойства четырехугольника.
Каждый четырехугольник имеет четыре вершины, четыре стороны и четыре угла.
Сумма всех внутренних углов четырехугольника всегда равна 360 градусов.
Длины всех четырех сторон четырехугольника могут быть равны или не равны. Например, стороны квадрата равны, а все четыре стороны трапеции не равны.
Формулы площади четырехугольников различных типов
Поскольку длины четырех сторон четырехугольника могут быть равными, а могут и не быть, формулы для определения их площадей также различаются.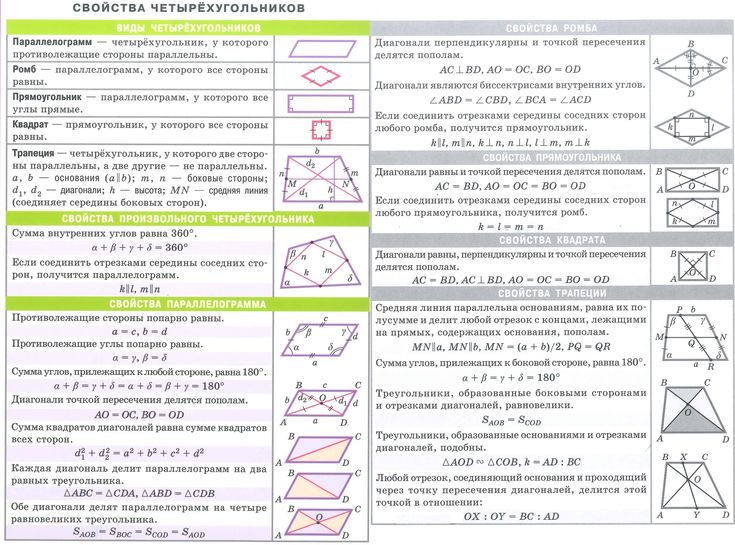
Давайте выучим формулы для нахождения площади всех типов четырехугольников в табличной форме.
.0229 | Квадрат | а * а = а2, где а — длина стороны квадрата. | Пусть a = 4 м, тогда площадь квадрата = 4*4 = 16 м2 , h= 4 м, тогда площадь прямоугольника = 2 * 4 = 8 м20140 Пусть B = 4 м, H = 5 м, затем площадь прямоугольника = 4 * 5 = 20m2 |
Kite | ½ * Диагональный 1 * Диагонал 2 | . = 10 м, площадь воздушного змея = ½*16*10 = 80 м2 | |
Ромб | Основание * Высота или (b * h) | Пусть b = 63 м тогда площадь прямоугольника = 3 * 6 = 18 м2 | |
трапеция | (a+b)/2 * h, где a и b — противоположные основания, а h — высота. | Пусть a = 2 м, b = 4 м и h = 3 м, тогда площадь трапеции = (2+4)/2*3 = 9 м2 1 : Рассчитайте площадь четырехугольника с заданными размерами: Диагональ = 50 м, Высота перпендикуляра = 60 м и 20 м. Решение: площадь четырехугольника = ½ * (a+b) * h Дано : a = 60 м , b = 20 м и h = 50 м Подставляя значения в формулу получаем, A = ½ *(60+20) * 50 = ½ * 80 *50 = 40 * 50 = 2000 м2
Пример 2. Четырехугольник имеет четыре равные стороны по 4 см каждая. Найдите его площадь? Решение: Четырехугольник, у которого все стороны равны, называется квадратом. Площадь квадрата — а 2, где а — сторона квадрата. А = 4м * 4м = 16м2 Пример 3: Длина четырехугольника (прямоугольника) равна 6 м, а ширина 5 м. Какова будет площадь этого прямоугольника? Решение: Площадь прямоугольника = l *b Дано: l = 6 м и b = 5 м Площадь прямоугольника = 6 м * 5 м = 30 м2 диагонали длиной 6 м и 8 м. Решение: Площадь воздушного змея = ½ *1d1 *d2 Дано: d1 = 6 м и d2 = 8 м A = ½ * 6 м * 8 м = 24 м2 Пример 5. Длина сторон прямоугольника 5 м и 10 м. Найдите площадь этого прямоугольника? Решение: площадь прямоугольника = длина * ширина Дано: l = 5 м и b = 10 м A = 5 м * 10 м = 50 м2 Теперь, когда вы знаете, что такое площадь четырехугольника и как ее найти, пришло время попрактиковаться в заданных вопросах, чтобы проверить свои знания.
Практические вопросы по четырехугольникамКак найти площадь четырехугольника? Найдите площадь параллелограмма с основанием 10 м и высотой 12 м? Вычислите площадь воздушного змея, имеющего диагонали длиной 13 м и 10 м? Какой из них не является четырехугольником — треугольником, квадратом, прямоугольником? Знаете ли вы? В слове Четырехугольник Четырехугольник означает Четыре, а Боковой означает стороны. |
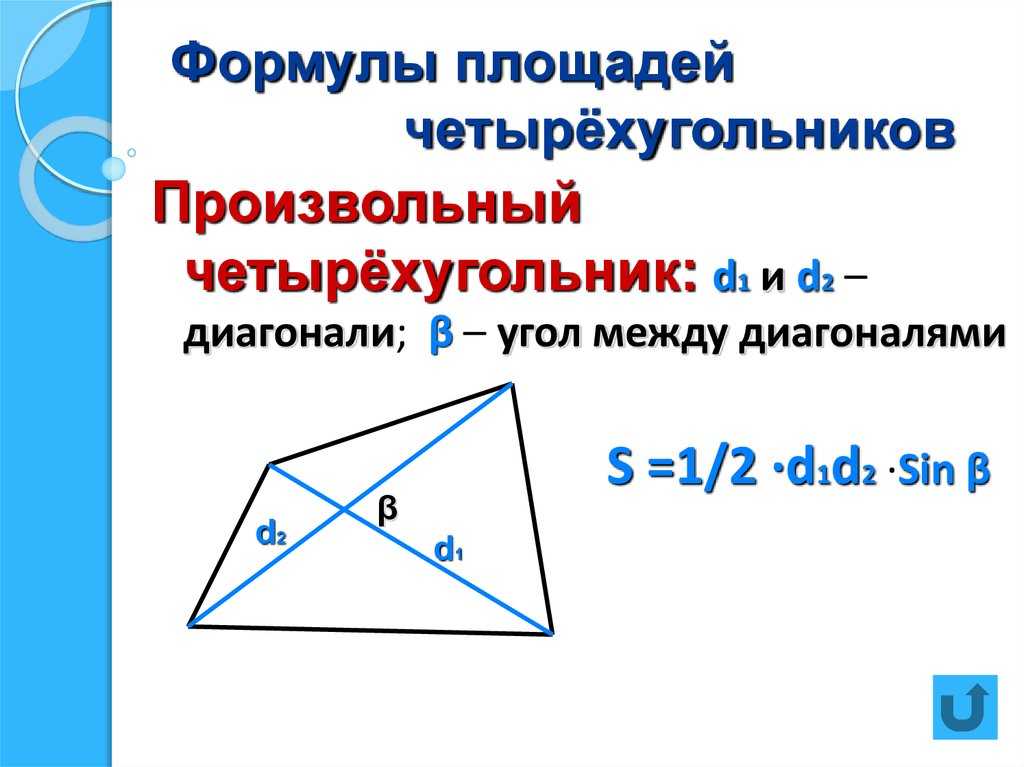
Найдите площадь этого четырехугольника?