Измерение объема. Единицы объема | Физика
С измерением объема приходится сталкиваться постоянно: заправляя бак автомобиля топливом, принимая микстуру, оплачивая расход воды и т. д. Как измеряют объем?
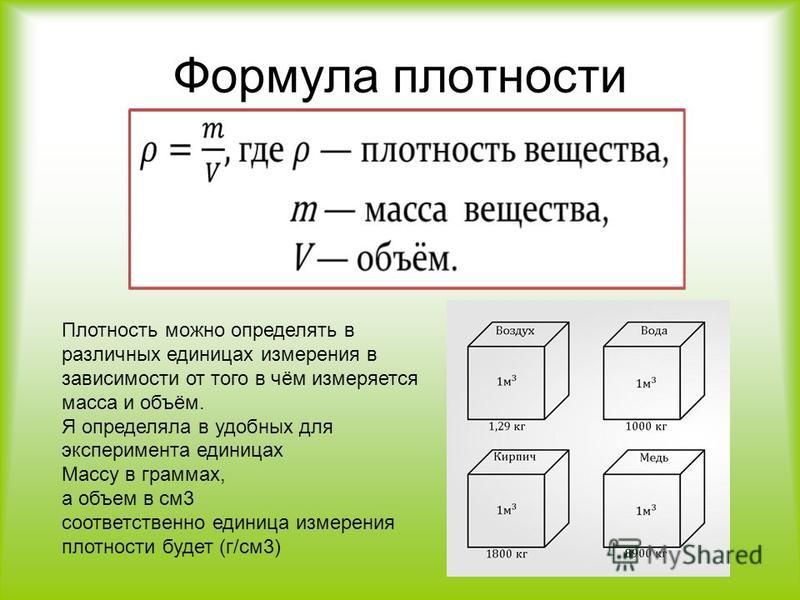
При измерении объема поступают так же, как при измерении площади. В качестве единицы измерения выбирают кубик с ребром, равным какой-нибудь единице длины, например 1 см. Тогда единицей измерения объема будет объем такого кубика.
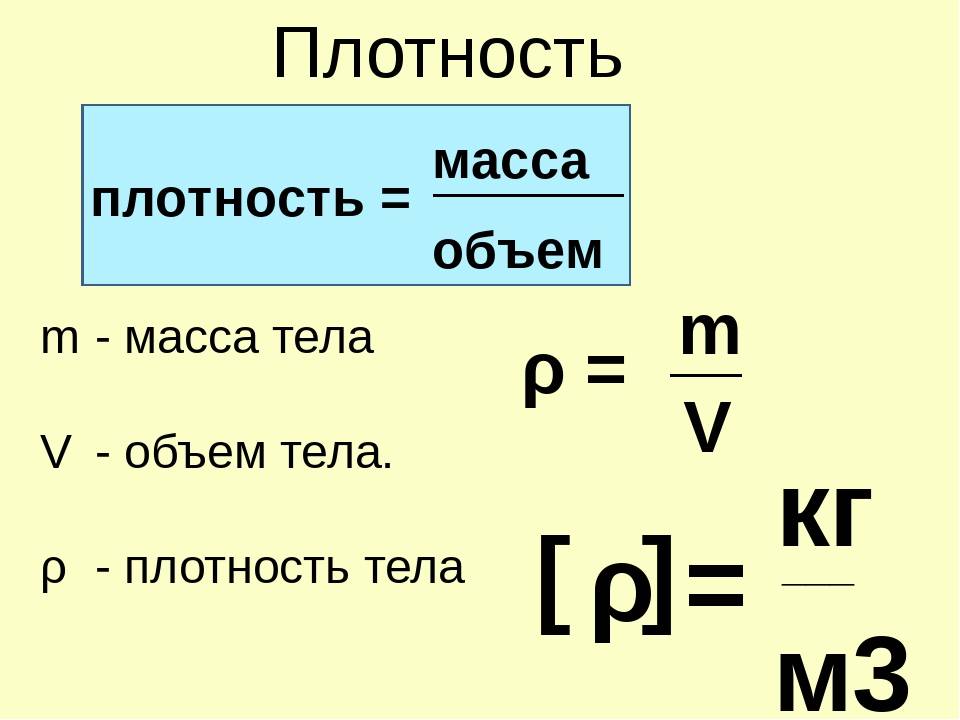
Например, объем прямоугольного параллелепипеда равен 24 см3. Это значит, что его объем содержит 24 кубика объемом по 1 см3. Этот же результат можно получить, если измерить длину a, ширину b и высоту c тела, а затем их значения перемножить. Объем обозначается латинской буквой V:
V = abc;
V = 3 см ⋅ 2 см ⋅ 4 см = 24 см3.
По данной формуле можно находить объемы тел, имеющих форму прямоугольного параллелепипеда, куба.
В СИ единицей объема является 1 м3. Другие единицы: дм3, см3, мм3 — дольные единицы м3.
1 м3 = 1000 дм3 = 1 ⋅ 103 дм3;
1 дм3 = 1000 см3 = 1 ⋅ 103 см3;
1 см3 = 1000 мм3 = 1 ⋅ 103 мм3;
1 дм3 = 0,001 м3 = 1 ⋅ 10-3 м3;
1 см3 = 0,001 дм3 = 0,000 001 м3 = 1 ⋅ 10-6 м3;
1 мм3 = 0,001 см3 = 1 ⋅ 10-3 см3;
1 мм3 = 0,000 001 дм3 = 1 ⋅ 10-6 дм3;
1 мм3 = 0,000 000 001 м3 = 1 ⋅ 10-9 м3.
А как измерить объем тела неправильной формы, например гири? Здесь наиболее удобный способ — опустить тело (гирю) в мензурку с водой и определить объем вытесненной им воды.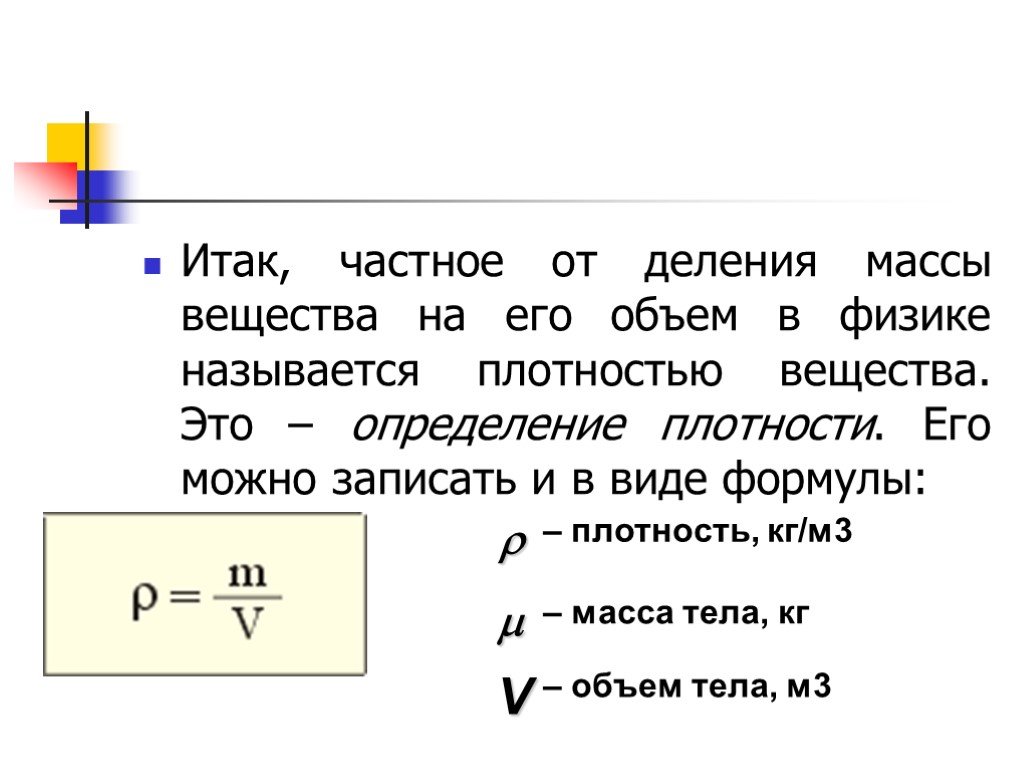
V = 49 мл — 21 мл = 28 мл = 28 см3.
В быту распространена единица объема 1 литр (л). Один литр есть не что иное, как один кубический дециметр:
1 л = 1 дм3;
1 миллилитр (мл) = 0,001 л = 1 см3.
Точность измерения объема зависит от цены деления шкалы измерительного прибора. Чем она меньше, тем точность измерения больше.
В английской системе мер единицей площади является 1 акр:
1 акр = 4046,86 м2;
единицей объема — 1 баррель:
1 баррель = 163,65 дм3 ≈ 0,16 м3.
В США различают сухой баррель:
1 сухой баррель = 115,628 дм3
и нефтяной баррель:
1 нефтяной баррель = 158,988 дм
3 = 0,159 м3. Теперь вам будет понятно, о каком объеме нефти идет речь, когда обсуждается цена за 1 баррель нефти.
Читать далее
| ← Измерение площади. Единицы площади | Тела и вещества. Дискретное строение вещества → |
Объем и масса. Плотность тела. Лабораторная работа №4 «Измерение массы и объема» – методическая разработка для учителей, Иванченко Ольга Сергеевна
|
Цели урока: |
— понимать, что масса является мерой количества вещества в теле; — выполнять лабораторную работу по измерению массы и объема вещества. 
|
|
Критерии успеха: |
Учащийся достиг цели, если… |
|
Языковые цели: |
Я думаю, что… |
|
Привитие ценностей: |
Уважение к любой профессии, открытость, труд и творчество |
|
Межпредметные связи |
Математика |
|
Навыки использования ИКТ |
Объяснение материала с помощью ноутбуков, интерактивной доски |
|
Предварительные знания |
Строение вещества из курса естествознания |
| Этапы урока | Содержание | Ресурсы | ||||||
|---|---|---|---|---|---|---|---|---|
|
Начало 0-10 мин.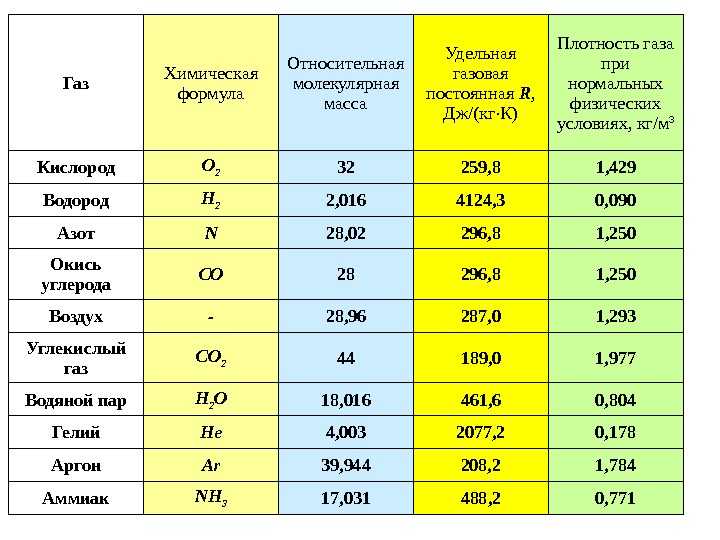 |
Концентрация внимания Постановка вопроса и выход на тему урока Что вы знаете о массе? Заполнение первого столбца таблицы ЗУХ
Ответы учащихся |
|
||||||
|
Середина 10-20 мин.
20-25 мин.
25-30 мин.
30-45 мин.
45-70 мин. 70-75 мин. |
Попробуйте самостоятельно сформулировать определение массы тела (масса-мера количества вещества) Просмотр видео фрагмента «Различные массы» Выполнение задания в парах — Ребята, посмотрите еще раз на тела, которые лежат у вас на столе, что общего у этих тел? Что различно? Прочитайте внимательно определение плотности и назовите формулу, по которой мы можем определить плотность. Закрепление 1. Используя таблицу плотности, сравните плотность воды и нефти, азота и угарного газа, во сколько раз плотность одного вещества, больше плотности второго? 2. Используя таблицу плотности, сравните плотность воды и льда. Почему у одного и того же вещества плотность разная? Выполнение лабораторной работы №4 «Измерение массы и объема тел» Заполнение второго и третьего столбца таблицы ЗУХ |
два бруска: алюминиевый и железный; электронные весы https://bilimland.kz/ru/content/category/search#p=5&pn=6&s=%D0%BC%D0%B0%D1%81%D1%81%D0%B0&lesson=11092
Алюминиевый и железный брусок
https://bilimland. 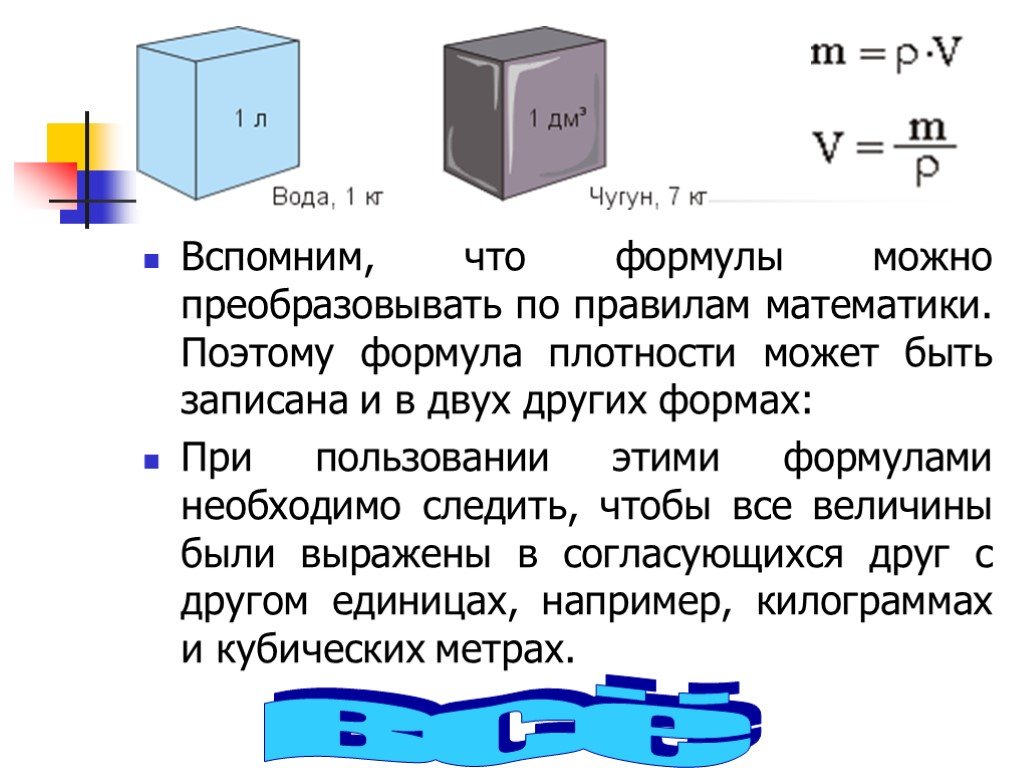 kz/ru/content/category/search#p=1&pn=6&s=%D0%BC%D0%B0%D1%81%D1%81%D0%B0&lesson=11092 kz/ru/content/category/search#p=1&pn=6&s=%D0%BC%D0%B0%D1%81%D1%81%D0%B0&lesson=11092
|
||||||
|
Конец 75-79 мин.79-80 мин. |
Рефлексия Домашнее задание |
|
|
Дифференциация – каким образом вы планируете оказать больше поддержки? Какие задачи вы планируете поставить перед более способными учащимися? |
Оценивание – как вы планируете проверить уровень усвоения материала учащимися? |
Здоровье и соблюдение техники безопасности |
|||
|
Все учащиеся выяснят, что такое масса и плотность тела, будут решать задачи. |
Самооценка на этапе решения задач |
Использование активных методов обучения |
|||
|
Некоторые учащиеся самостоятельно дадут определение массы, назовут формулу и единицы измерения массы и плотности, переведут единицы измерения плотности в СИ. Некоторые учащиеся решат все задачи самостоятельно. Дифференциация по типу мышления. |
Оценивание на этапе работы с порталом |
Инструктаж по ТБ |
|||
|
Рефлексия по уроку: Были ли цели урока/цели обучения реалистичными? Все ли учащиеся достигли ЦО? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Выдержаны ли были временные этапы урока? Какие отступления были от плана урока и почему? |
|
||||
|
Общая оценка: Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1: 2: Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1: 2: Что я выявил(-а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках? |
|||||
Единица объема — Объяснение, преобразование и часто задаваемые вопросы
Мы часто посещаем молокозавод, чтобы купить молоко, и просим продавца дать нам несколько литров молока.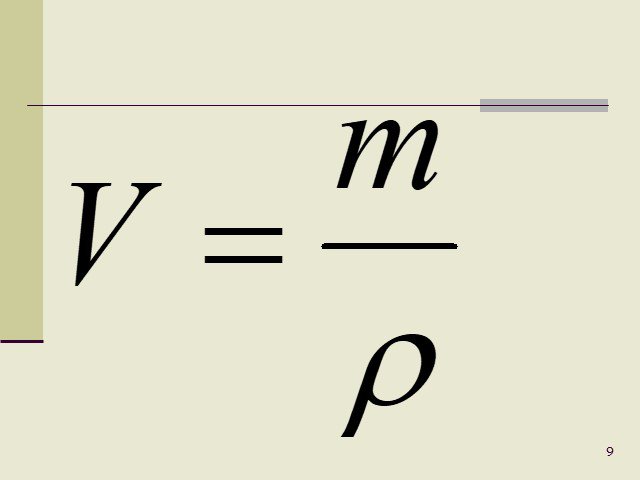 Вы когда-нибудь задумывались, что означает этот «литр»? Это объем, а литр — одна из многих его единиц. Здесь Веданту предоставил вам описание Объема, его различных Единиц и их взаимного Преобразования. Во-первых, давайте начнем с понимания того, что такое объем.
Вы когда-нибудь задумывались, что означает этот «литр»? Это объем, а литр — одна из многих его единиц. Здесь Веданту предоставил вам описание Объема, его различных Единиц и их взаимного Преобразования. Во-первых, давайте начнем с понимания того, что такое объем.
Вы знаете, что Объем — это пространство, занимаемое состоянием материи. Итак, что же такое единица СИ для объема считается для его измерения? Хорошо! Единицей объема в системе СИ является м³. Тем не менее, многие другие единицы используются для тома по физике. На этой странице подробно обсуждается список единиц объема.
Объем — это основная физическая величина, которую мы считаем производной величиной, и она выражает трехмерные пропорции объекта.
Итак, мы понимаем, что единица измерения объема в СИ в физике количественно определяется с использованием производной единицы СИ, кубического метра.
Объем в физике
Объем – это объем трехмерного пространства, заключенного в замкнутую поверхность, выраженный в числовом выражении.
Например, пространство, в котором вещество может быть твердым, жидким, газообразным или плазменным, или иметь любую занимающую пространство форму.
Объем контейнера считается вместимостью, которую он может вместить; т. е. количество жидкости, газа или жидкости, которое может вместить контейнер, а не объем пространства, вытесняемый самим контейнером, как выталкивающая сила в воде.
Обратите внимание
Трехмерным математическим фигурам также присваиваются объемы. Объемы таких фигур, как правильные, прямоугольные и круглые, можно легко рассчитать с помощью арифметических формул.
Объемы сложных форм можно вычислить с помощью интегрального исчисления, только если существует формула для границы формы.
Одномерным линиям и двумерным формам, таким как квадраты, присваивается нулевой объем в трехмерном пространстве.
Объем твердого тела
Объем твердого тела правильной или неправильной формы можно определить по вытеснению жидкости.
Если вытеснение жидкости используется для расчета объема газа. Суммарный объем двух веществ всегда больше, чем объем только одного из веществ (жидкости или газа). Однако иногда бывает так, что одно вещество растворяется в другом, и в этих случаях объединенный объем не является аддитивным.
Список единиц объема
Объем измеряет емкость. Таким образом, единица объема СИ — это единица измерения объема или пропорций объекта или пространства. Единица м³ в основном используется для указания объема веществ или жидкости (жидкостей).
Однако учащиеся должны помнить, что масса и объем — это две разные физические величины. Хотя единица объема — интересная тема, давайте посмотрим, какие единицы измерения используются во всем мире ниже в табличной форме:
Unit of Volume in Physics | SI Unit of Volume is: Cubic Metre | Litre | |||
1 Cubic metre | 1 | 1000 | |||
1 barrel | 0. | 158.987294928 | |||
1 cubic foot | 0.028316846592 | 28.316846592 | |||
1 cubic decimetre | 0.001 | 1 | |||
1 litre | 0.001 | 1 | |||
1 галлон (США) | 0,003785411784 | 3,785411784 | 9 9 t (US штифт)0003 | 0.000473176473 | 0.473176473 |
1 cubic inch | 0.000016387064 | 0.016387064 | |||
1 cubic centimetre | 0. | 0.001 |
Объем в термодинамике
В области термодинамики объем системы является важным параметром для описания термодинамического состояния состояния.
Удельный объем является интенсивным свойством, это объем системы на ее единицу.
Объем является функцией состояния и не зависит от некоторых термодинамических свойств, таких как давление и температура.
Для идеального газа объем связан с давлением и температурой в соответствии с законом идеального газа.
Преобразование единиц объема
Любая единица длины дает производную единицу объема в системе СИ, например, объем куба со сторонами заданной длины в метрах.
Кубический сантиметр или см3 — это объем куба, сторона которого равна одному сантиметру, а длина — 1 см.
В Международной системе единиц или СИ стандартной единицей объема является кубический метр (м3).
(Изображение будет загружено в ближайшее время)
В метрической системе единица объема также включает литр (л), где один литр равен 10-сантиметровому кубу.
Следовательно, 1 литр = (10 см)3 = 1000 кубических сантиметров
= 0,001 кубических метра,
Итак,
1 кубический метр равен 1000 литрам.
Небольшие количества жидкости измеряются в миллилитрах Единицы, где
1 миллилитр = 0,001 литра или 1 кубический сантиметр.
Точно так же большие количества измеряются в мегалитрах, т. е.
1 миллион литров = 1000 кубических метров или 1 мегалитр.
Различные традиционные единицы объема все еще используются, включая следующий список единиц объема:
кубический дюйм,
the cubic foot,
the cubic yard,
the cubic mile,
the teaspoon,
the tablespoon,
the fluid ounce,
Fluid DRAM,
The Gill,
The Pint,
Кварта,
Галлон,
91, минимальная,1,the barrel,
the cord,
the peck,
the bushel,
the hogshead,
Drams grill
Bushels
Pecks
акр-фут и
доск-фут
,
91,,
910003 Vedantu также предоставил подробное введение в тему Volume. Если вам трудно понять эту тему напрямую, рекомендуется обратиться к теме формул объема, прежде чем приступить к ней.
Если вам трудно понять эту тему напрямую, рекомендуется обратиться к теме формул объема, прежде чем приступить к ней.
Заключение
Прочитав эту статью, вы хорошо знакомы с различными единицами объема, их взаимными преобразованиями и традиционно используемыми единицами объема. Изучив эту статью, вы узнали, насколько важны Объем и его Единицы. Эти формулы преобразования пригодятся во многих местах на экзаменах, а также в практической жизни. Таким образом, вы должны приложить все усилия, чтобы понять эту тему и попытаться применить ее в различных местах, чтобы убедиться, что вы освоите ее.
1.4: Объем, толщина и плотность
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 189531
- OpenStax
- OpenStax
Цели обучения
- Расчет площади, объема, плотности и толщины и преобразование в различные единицы измерения.

Производные единицы СИ
Многие единицы можно получить из семи основных единиц СИ. Например, мы можем использовать базовую единицу длины для определения единицы объема, а базовые единицы массы и длины — для определения единицы плотности.
Объем
Объем — это мера объема пространства, занимаемого объектом. Стандартная единица объема в системе СИ определяется базовой единицей длины (рис. \(\PageIndex{3}\)). Стандартный объем – кубический метр (м 3 ), куб с длиной ребра ровно один метр. Чтобы распределить кубический метр воды, мы могли бы построить кубический ящик с длиной ребра ровно один метр. В эту коробку поместится кубический метр воды или любого другого вещества.
Более часто используемая единица объема получается из дециметра (0,1 м или 10 см). Куб с длиной ребра ровно в один дециметр содержит объем в один кубический дециметр (дм 3 ). Литр (л) — более распространенное название кубического дециметра. Один литр равен примерно 1,06 кварт. Кубический сантиметр (см 3 ) — это объем куба с длиной ребра ровно один сантиметр. Аббревиатура cc (от c ubic c entimeter) часто используется медицинскими работниками. Кубический сантиметр также называется миллилитром (мл) и составляет 1/1000 литра.
Кубический сантиметр (см 3 ) — это объем куба с длиной ребра ровно один сантиметр. Аббревиатура cc (от c ubic c entimeter) часто используется медицинскими работниками. Кубический сантиметр также называется миллилитром (мл) и составляет 1/1000 литра.
Плотность
Масса и объем вещества используются для определения его плотности. Таким образом, единицы плотности определяются базовыми единицами массы и длины.
Плотность вещества есть отношение массы навески вещества к его объему. Единицей плотности в системе СИ является килограмм на кубический метр (кг/м 3 ). Однако во многих ситуациях это неудобная единица измерения, и мы часто используем граммы на кубический сантиметр (г/см 3 ) для плотности твердых тел и жидкостей и граммы на литр (г/л) для газов. Хотя есть исключения, большинство жидкостей и твердых тел имеют плотность в диапазоне примерно от 0,7 г/см 3 (плотность бензина) до 19 г/см 3 (плотность золота). Плотность воздуха около 1,2 г/л. В таблице \(\PageIndex{3}\) показаны плотности некоторых распространенных веществ.
Хотя есть исключения, большинство жидкостей и твердых тел имеют плотность в диапазоне примерно от 0,7 г/см 3 (плотность бензина) до 19 г/см 3 (плотность золота). Плотность воздуха около 1,2 г/л. В таблице \(\PageIndex{3}\) показаны плотности некоторых распространенных веществ.
| Твердые вещества | Жидкости | Газы (при 25 °С и 1 атм) |
|---|---|---|
| лед (при 0 °C) 0,92 г/см 3 | вода 1,0 г/см 3 | сухой воздух 1,20 г/л |
| дуб (древесина) 0,60–0,90 г/см 3 | этанол 0,79 г/см 3 | кислород 1,31 г/л |
| железо 7,9 г/см 3 | ацетон 0,79 г/см 3 | азот 1,14 г/л |
| медь 9,0 г/см 3 | глицерин 1,26 г/см 3 | диоксид углерода 1,80 г/л |
| свинец 11,3 г/см 3 | оливковое масло 0,92 г/см 3 | гелий 0,16 г/л |
| серебро 10,5 г/см 3 | бензин 0,70–0,77 г/см 3 | неон 0,83 г/л |
| золото 19,3 г/см 3 | ртуть 13,6 г/см 3 | радон 9,1 г/л |
Хотя существует множество способов определения плотности объекта, возможно, самый простой метод включает отдельное определение массы и объема объекта, а затем деление массы образца на его объем. В следующем примере масса определяется непосредственно путем взвешивания, а объем определяется косвенно путем измерения длины.
В следующем примере масса определяется непосредственно путем взвешивания, а объем определяется косвенно путем измерения длины.
\[\mathrm{density=\dfrac{mass}{volume}}\]
Пример \(\PageIndex{1}\)
Расчет плотности золота в кирпичах, слитках и монетах форма валюты на протяжении веков. Чтобы заставить людей платить за слиток золота, фактически не вкладывая в слиток золота, люди решили заполнить центры полых золотых слитков свинцом, чтобы обмануть покупателей, заставив их думать, что весь слиток состоит из золота. Не получается: свинец — вещество плотное, но плотность его не так велика, как у золота, 193}\]
Упражнение \(\PageIndex{1}\)
- Чему равен с точностью до трех знаков после запятой объем куба (см 3 ) с длиной ребра 0,843 см?
- Если куб в части (а) сделан из меди и имеет массу 5,34 г, какова плотность меди с точностью до двух знаков после запятой?
- Ответить на
0,599 см 3 ;
- Ответ б
8,91 г/см 3
Пример \(\PageIndex{2}\): использование вытеснения воды для определения плотности
Эта симуляция PhET иллюстрирует другой способ определения плотности с использованием вытеснения воды.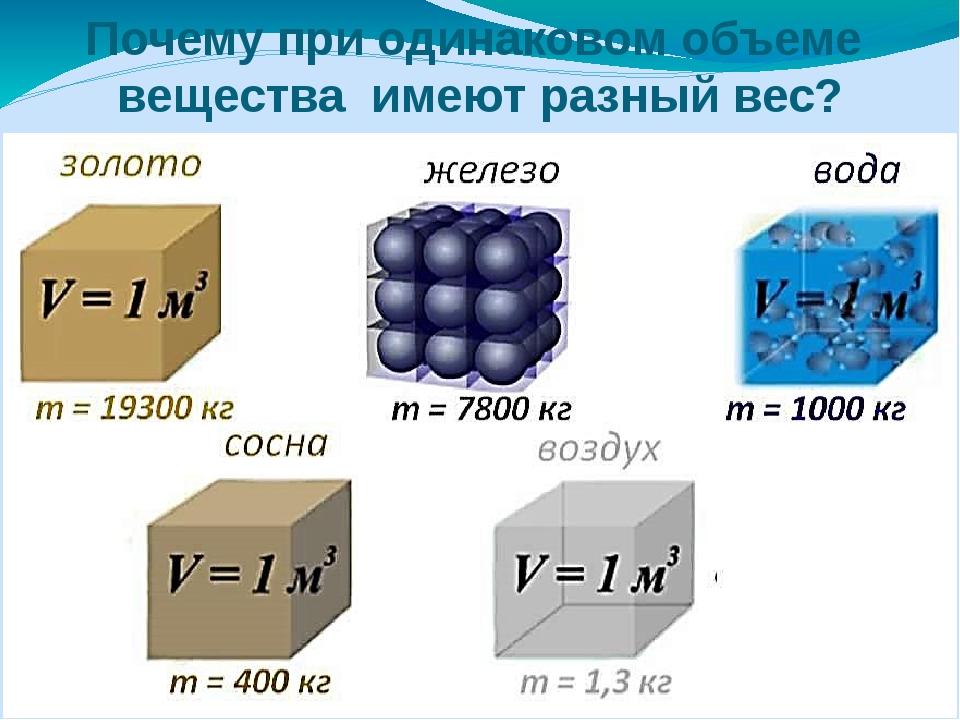 Определите плотность красного и желтого блоков.
Определите плотность красного и желтого блоков.
Решение
Когда вы открываете симуляцию плотности и выбираете ту же массу, вы можете выбрать один из нескольких цветных блоков по 5,00 кг, которые вы можете бросить в резервуар, содержащий 100,00 л воды. Желтый блок всплывает (он менее плотный, чем вода), и уровень воды поднимается до 105,00 л. Во время плавания желтый блок вытесняет 5,00 л воды, количество, равное весу блока. Красный блок тонет (плотнее воды, плотность которой = 1,00 кг/л), а уровень воды поднимается до 101,25 л.
Таким образом, красный блок вытесняет 1,25 л воды, что равно объему блока. Плотность красного блока:
\[\mathrm{плотность=\dfrac{масса}{объем}=\dfrac{5,00\: кг}{1,25\: L}=4,00\: кг/л}\]
Обратите внимание: поскольку желтый блок не полностью погружен в воду, по этой информации нельзя определить его плотность. Но если вы держите желтый блок на дне резервуара, уровень воды поднимается до 110,00 л, что означает, что теперь она вытесняет 10,00 л воды, и ее плотность можно найти:
\[\mathrm{плотность=\dfrac{масса}{объем}=\dfrac{5,00\: кг}{10,00\: L}=0,500\: кг/л}\]
Упражнение \(\PageIndex{1}\)
Удалите все блоки из воды и добавьте зеленый блок в резервуар с водой, поместив его примерно посередине резервуара.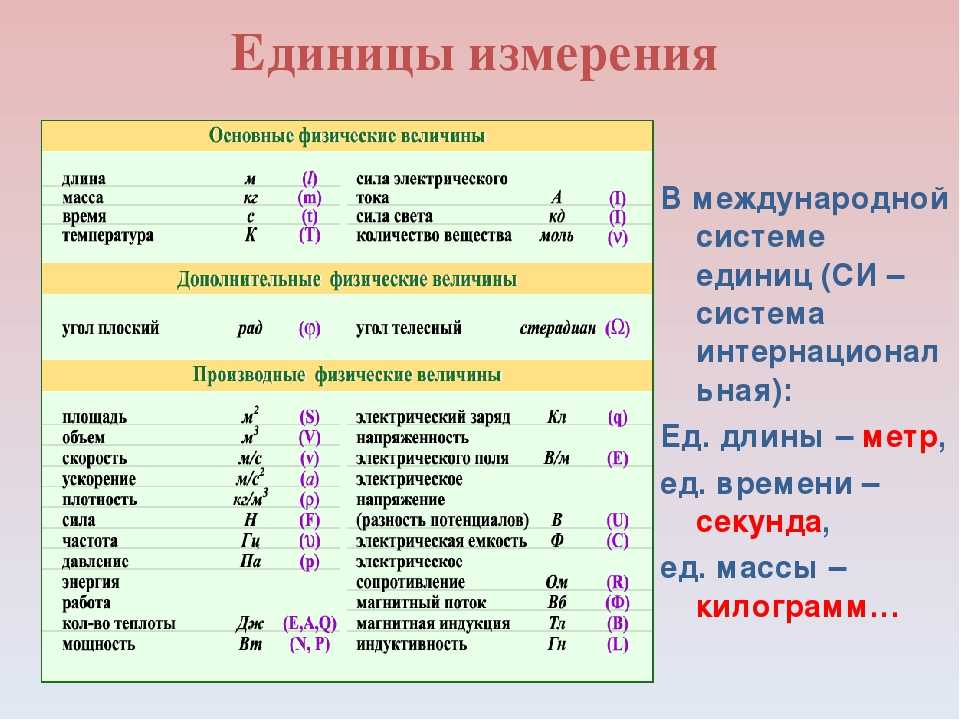 Определите плотность зеленого блока.
Определите плотность зеленого блока.
- Ответить
2,00 кг/л
Толщина
Ширина объекта также иногда определяется как толщина (T). Обычно это происходит, когда ширина объекта значительно меньше других размеров. Для измерения толщины требуется инструмент с высокой точностью, такой как штангенциркуль. Однако, если вы знаете площадь, массу и плотность вещества, вы можете рассчитать толщину.
Используйте эту формулу для расчета толщины: \(\mathrm{толщина=\dfrac{объем}{площадь}}\)
Чтобы найти объем, вы должны изменить формулу плотности. \(\mathrm{volume=\dfrac{mass}{density}}\)
Пример \(\PageIndex{2}\): Расчет толщины
Кусок алюминиевой фольги имеет массу 0,018 г и длину 5,0 см. с каждой стороны. Учитывая плотность алюминия 2,7 г/см3, какова толщина алюминия в см?
Решение
\(\mathrm{толщина=\dfrac{объем}{площадь}}\) 92}=0,00027\: см}\]
Резюме
Ученые используют производные единицы измерения, такие как литры (для объема) и г/см 3 (для плотности).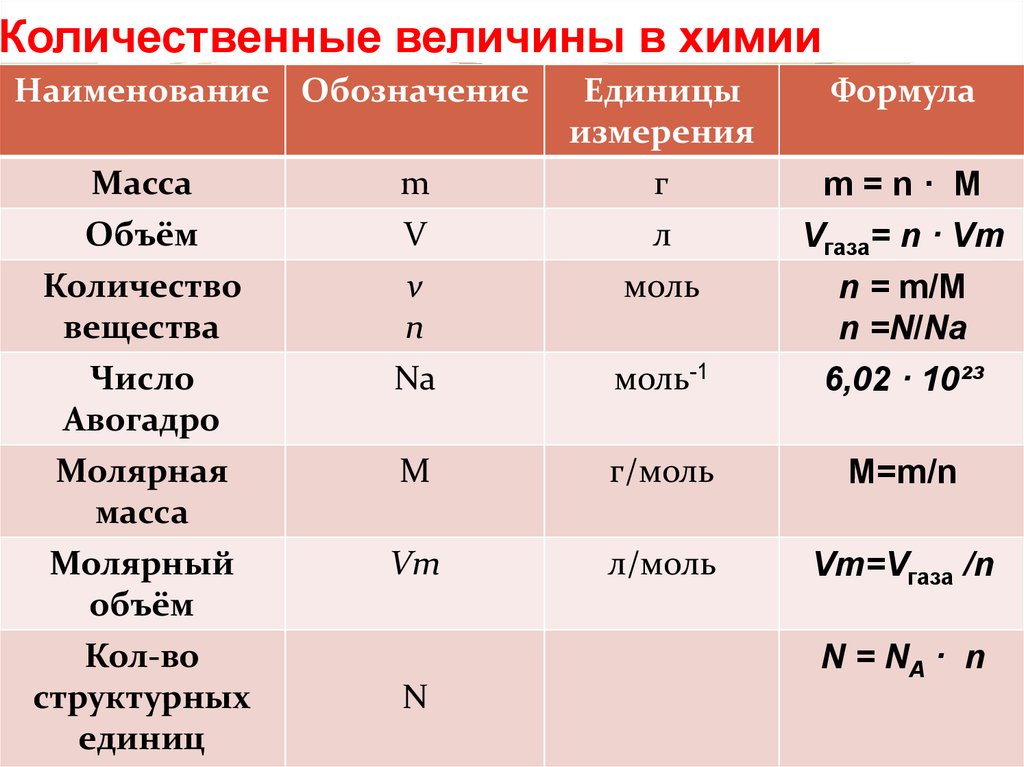 Толщина — это способ выразить ширину объекта, когда этот размер мал.
Толщина — это способ выразить ширину объекта, когда этот размер мал.
Ключевые уравнения
- \(\mathrm{density=\dfrac{mass}{volume}}\)
- \(\mathrm{толщина=\dfrac{объем}{площадь}}\)
Глоссарий
- плотность
- отношение массы к объему вещества или предмета
- литр (л)
- (также кубический дециметр) единица объема; 1 л = 1000 см 3
- миллилитр (мл)
- 1/1000 литра; равен 1 см 3
- секунда (с)
- Единица времени СИ
- Единицы СИ (Международная система единиц)
- стандартов, закрепленных международным соглашением в Международной системе единиц ( Le Système International d’Unités )
- толщина
- другой способ выражения ширины объекта, который можно рассчитать, разделив объем объекта на площадь
- объем
- количество места, занимаемого объектом
Авторы
Пол Флауэрс (Университет Северной Каролины, Пемброк), Клаус Теопольд (Университет Делавэра) и Ричард Лэнгли (Государственный университет Стивена Ф.



 ..
..


 158987294928
158987294928 000001
000001