Площадь четырехугольника формула. Формула площади четырехугольника по диагоналям. Площадь произвольного четырехугольника.
- Альфашкола
- Статьи
- Площадь произвольного четырехугольника
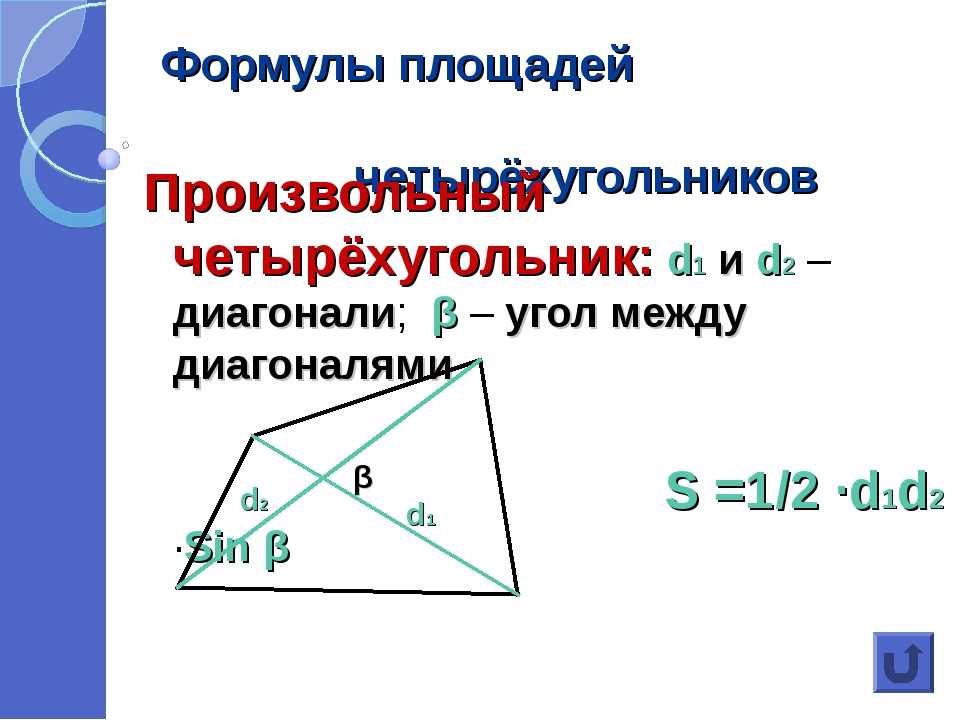
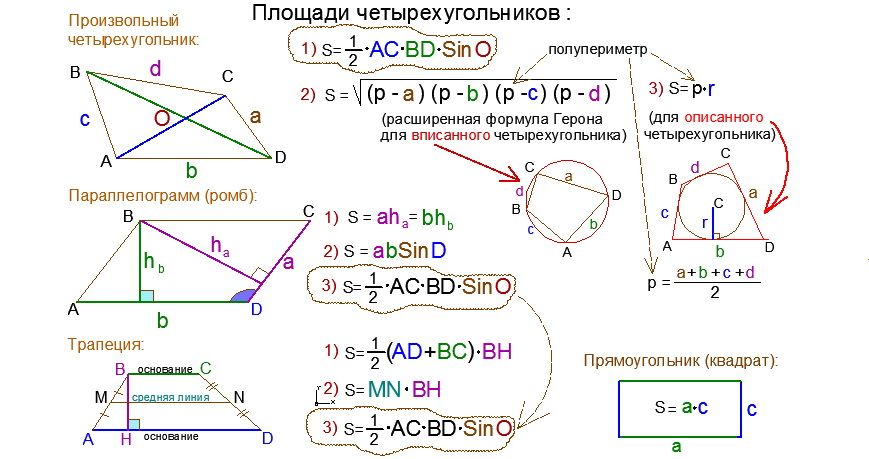
Площадь произвольного четырехугольника можно найти перемножив диагонали данного четырехугольника, полученный результат разделить на \(2\) и умножить результат на синус угла.
\(S=\frac{1}{2} AC⋅BD \ sin\ φ\)
Первая диагональ четырехугольника:
Вторая диагональ четырехугольника:
Угол между диагоналями:
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа».
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Елена Александровна Волынкина
Репетитор по математике
Стаж (лет)
Образование:
ГОУ ВПО Самарский государственный педагогический университет, Куйбышевское педагогическое училище №1
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Я учитель начальных классов с 30-ти летним стажем. Могу помочь ребенку освоить предметы: математику, русский язык, литературное чтение, окружающий мир за курс начальной школы. А также закрепить знания, полученные в школе, наверстать пропущенный материал, подтянуть качество знаний по предметам с 1-4 класс и по математике, по русскому языку 5 класс. Подготовиться к ВПР по предметам за курс начальной школы и за 5 класс по русскому языку и математике..
Мой принцип работы: «Если хочешь, чтобы скорее расцвел цветок, не раскрывай насильно его лепестки, а создай условия, при которых он сам распустится.» Л.Н.Толстой.
Могу помочь ребенку освоить предметы: математику, русский язык, литературное чтение, окружающий мир за курс начальной школы. А также закрепить знания, полученные в школе, наверстать пропущенный материал, подтянуть качество знаний по предметам с 1-4 класс и по математике, по русскому языку 5 класс. Подготовиться к ВПР по предметам за курс начальной школы и за 5 класс по русскому языку и математике..
Мой принцип работы: «Если хочешь, чтобы скорее расцвел цветок, не раскрывай насильно его лепестки, а создай условия, при которых он сам распустится.» Л.Н.Толстой.
Татьяна Дмитриевна Макарова
Репетитор по математике
Образование:
Белорусский государственный педагогический университ имени Максима Танка
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по физике для 7-9 классов и по информатике для 5-9 классов. Помогу понять физику, объясняя сложные понятия простым доступным способом. Люблю общаться с детьми, помогать им постичь мир через такой предмет как физика. Я не только научу, но и смогу расположить ученика к себе, чем создам легкую атмосферу общения и усвоения материала. Так же я учитель информатики и с удовольствием помогу разобраться с компьютерными программами.
Помогу понять физику, объясняя сложные понятия простым доступным способом. Люблю общаться с детьми, помогать им постичь мир через такой предмет как физика. Я не только научу, но и смогу расположить ученика к себе, чем создам легкую атмосферу общения и усвоения материала. Так же я учитель информатики и с удовольствием помогу разобраться с компьютерными программами.
Юлия Геннадьевна Газданова
Репетитор по математике
Стаж (лет)
Образование:
Актюбинский педагогический техникум
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-5 классов.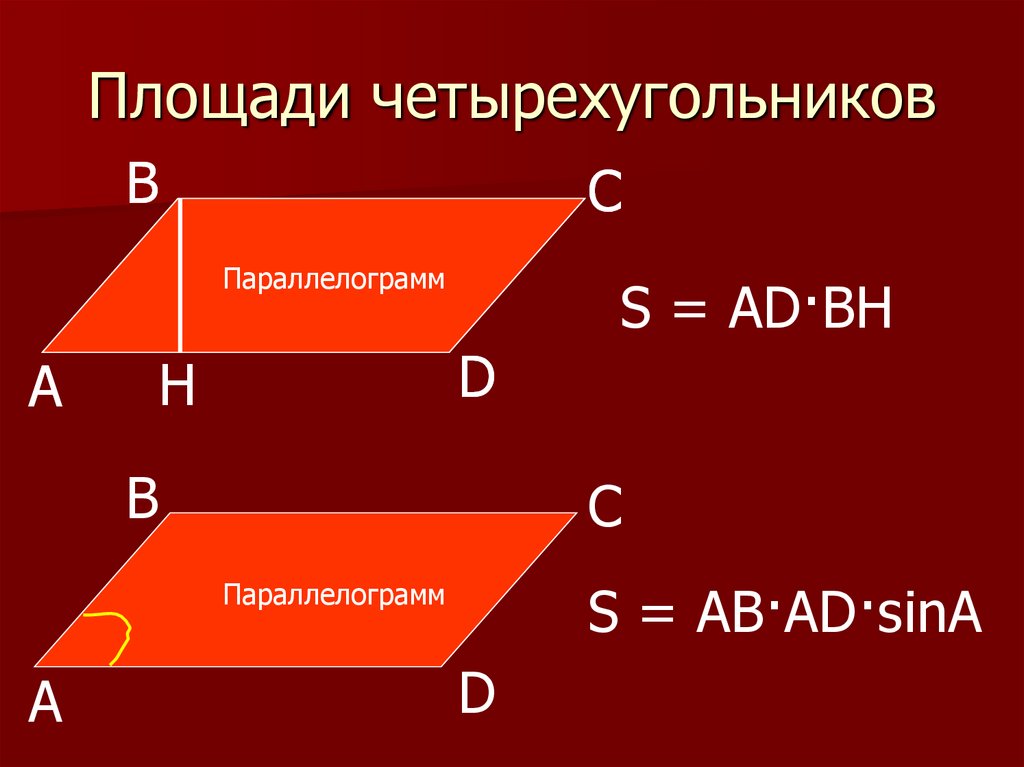
Похожие статьи
- Виды пирамид
- Свойства скалярного произведения
- Задачи на вклад в банк
- Текстовые задачи. Задание №1 из ЕГЭ прошлых лет
- ЕГЭ по математике, базовый уровень. Простейшие уравнения (вариант 1)
- Задачи на прогрессии
- ЕГЭ по математике, базовый уровень.
 Задачи на исследование функций (вариант 5)
Задачи на исследование функций (вариант 5) - Один дома: чем заняться без родителей и как избежать проблем
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Площадь четырёхугольника формула. Как найти площадь четырехугольника
Начальный уровень
Определение площади
Что такое площадь? Странный вопрос — не правда ли? В обычной жизни мы привыкли к тому, что у всяких плоских фигур (таких как поверхность стола, стула, пол наших квартир и т.д.) есть не только длина и ширина, но и какая-то еще характеристика, которую мы, не задумываясь, называем площадью. А теперь вот давай задумаемся: что же все-таки такое площадь?
Давай начнем с самого простого. За основу берется тот факт, что:
Другими словами, площадь квадрата со стороной метр мы считаем одним «метром площади».
Посмотри внимательно на картинку и убедись, что там действительно нарисован — «метр квадратный»! И запомни обозначение.
А вот теперь хитрый вопрос: а что такое? Площадь квадрата со стороной? А вот и нет!
Смотри: квадрат со стороной.
А чтобы получить квадратных метра (то есть,), мы должны нарисовать, например так:
А как получить, скажем, ? Ну например так:
Да и вообще, если мы возьмем прямоугольник, у которого стороны равны метров и метров, то в этом прямоугольнике:
Поместится ровно квадратных метров. Посмотри внимательно: у нас есть «слоев», в каждом из которых ровно квадратных метров.
Значит, всего в прямоугольнике размером x поместилось квадратных метров. Вот это число, сколько квадратных метров поместилось в прямоугольнике, и есть его площадь .
А если фигура — вовсе не прямоугольник, а какая-то абракадабра?
Удивлю тебя — бывают такие ужасные абракадабры, для которых совершенно невозможно установить сколько там квадратных метров. Даже приблизительно! К сожалению нарисовать такие фигуры — невозможно.
Но они есть! Они похожи, например, на такую «расческу» с очень мелкими зубьями.
И вот, для нормальных фигур можно интуитивно (то есть для себя) считать,что площадь фигуры — это такое число, сколько в этой фигуре «поместится» квадратных единиц (метров, сантиметров и т.д.) Более строгое, «настоящее» определение площади смотри в следующих уровнях теории.
И представь себе, математики для многих фигур научились выражать площади через какие-то линейные (те, что можно измерить линейкой) элементы фигур. Эти выражения называются «формулы площади». Формул этих довольно много — математики долго старались. Ты постарайся запомнить сначала самые простые и основные формулы, а потом уже те, что посложнее.
Формулы площади
Квадрат
Прямоугольник
Прямоугольный треугольник
Треугольник (произвольный)
Для треугольника есть сразу несколько формул площади.
Основная формула
Вторая основная формула
Третья формула
Какую же формулу выбрать для твоей задачки? Основными являются формулы 1 и 2.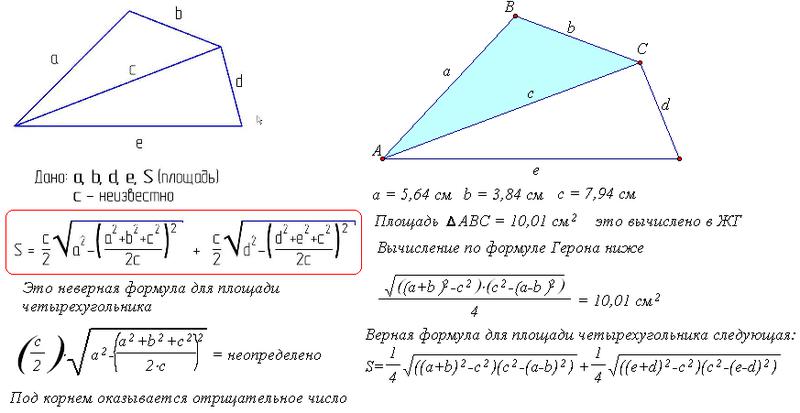 Третью формулу нужно применять, если тебе все дано: и три стороны, и радиус вписанной окружности. Но так ведь не бывает, верно? Поэтому формулу 3 мы используем , скорее наоборот, для нахождения радиуса вписанной окружности . Тогда нужно найти площадь по одной из формул 1, 2 или 4, а потом уже радиус: .
Третью формулу нужно применять, если тебе все дано: и три стороны, и радиус вписанной окружности. Но так ведь не бывает, верно? Поэтому формулу 3 мы используем , скорее наоборот, для нахождения радиуса вписанной окружности . Тогда нужно найти площадь по одной из формул 1, 2 или 4, а потом уже радиус: .
Ну и формула 4 позволяет по -м сторонам с помощью длиннющей арифметики находить площадь. И не ошибайся в арифметике, когда будешь применять формулу Герона!
Произвольный четырехугольник
Для произвольного четырехугольника больше ничего нет, а вот для «хороших» четырехугольников — есть другие формулы.
Параллелограмм
Основная формула
Вторая формула
Ромб
У ромба диагонали перпендикулярны, поэтому основной для него становится формула:
Вторая формула
А дополнительной формулой становится
Трапеция
Основная формула
Вторая формула
«Хитрые вопросы о площади»
Кроме задачек, в которых просят просто найти площадь, встречаются еще всякие вопросики. Ну вот например:
Ну вот например:
Давай ответим на этот вопрос двумя способами. Первый способ — формальный: используем формулу площади квадрата. Итак, было, значит — площадь увеличилась в раз!
В случае с квадратами есть и второй способ «пощупать» и убедится напрямую в этом числе.
Рисуем:
Если же у тебя не квадрат, то остается только подставлять новые значения в формулы — и не удивляйся, если вдруг числа получатся довольно большими.
ПЛОЩАДЬ ТРЕУГОЛЬНИКА И ЧЕТЫРЕХУГОЛЬНИКА. КОРОТКО О ГЛАВНОМ
Прямоугольный треугольник
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны. - Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.S = 1 2 2 где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.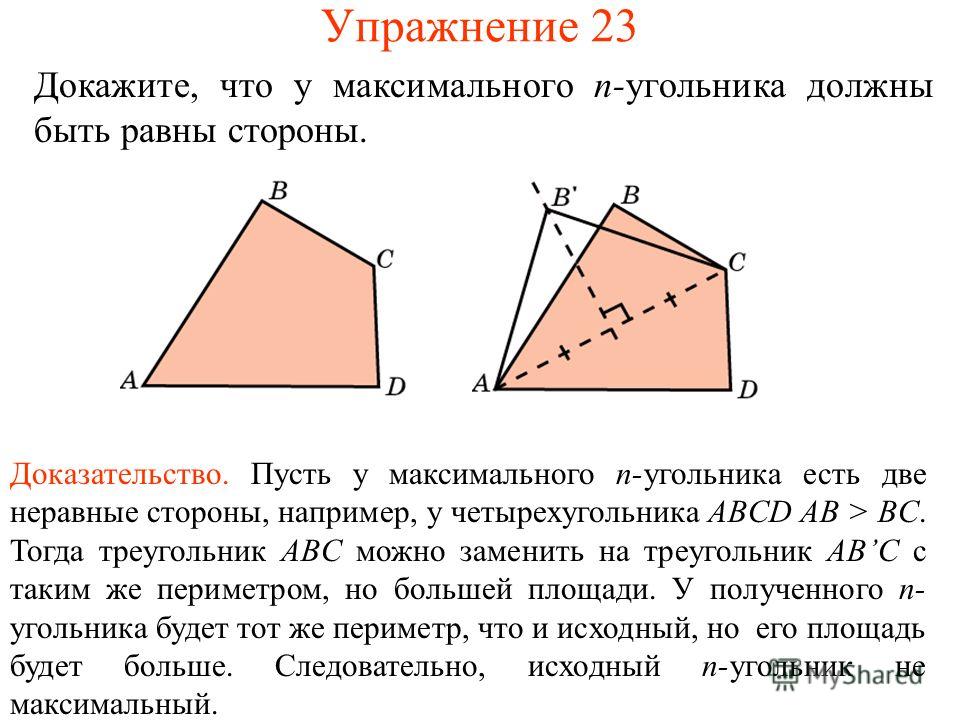
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Данный онлайн калькулятор помогает произвести расчет, определение и вычисление площади земельного участка в онлайн режиме. Представленная программа способна правильно подсказать, как выполнить расчет площади земельных участков неправильной формы.
Важно! Важ участок должен приблизительно вписываться в окружность. Иначе расчеты будут не совсем точными.
Указываем все данные в метрах
A B, D A, C D, B C — Размер каждой стороны делянки.
Согласно введен данным, наша программа в онлайн режиме выполнить расчет и определить, площадь земельных угодий в квадратных метрах, сотках, акрах и гектарах.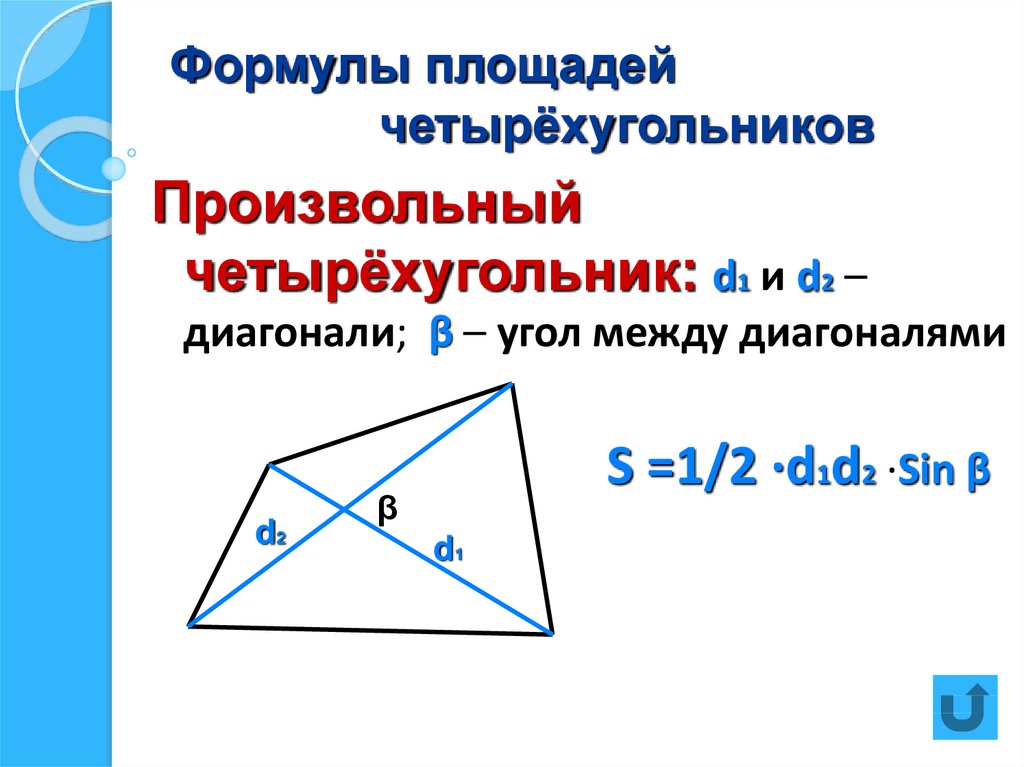
Методика определения размеров участка ручным методом
Чтобы правильно выполнить расчет площади делянок, не нужно использовать сложные инструменты. Мы берем деревянные колышки или металлические прутья и устанавливаем их в углах нашего участка. Далее при помощи измерительной рулетки определяем ширину и длину делянки. Как правило, достаточно выполнить замер одной ширины и одной длины, для прямоугольных или равносторонних участков. Для примера, у нас получились следующие данные: ширина – 20 метров и длина – 40 метров.
Далее переходим к расчету площади делянки. При правильной форме участка, можно использовать геометрическую формулу определения площади (S) прямоугольника. Согласно этой формуле, нужно выполнить умножение ширины (20) на длину (40) , то есть произведение длин двух сторон. В нашем случае S=800 м².
После того, как мы определили нашу площадь, мы можем определить количество соток на земельном участке. Согласно общепринятым данным, в одной сотке – 100 м². Далее при помощи простой арифметики, мы разделим наш параметр S на 100. Готовый результат и станет равен размеру делянки в сотках. Для нашего примера, этот результат – 8. Таким образом, получаем, что площадь участка составляет восемь соток.
Далее при помощи простой арифметики, мы разделим наш параметр S на 100. Готовый результат и станет равен размеру делянки в сотках. Для нашего примера, этот результат – 8. Таким образом, получаем, что площадь участка составляет восемь соток.
В том случае, когда территория угодий очень большая, то лучше всего выполнять все измерения в других единицах – в гектарах. Согласно общепринятым единицам измерения – 1 Га = 100 соток. К примеру, если наша земельная делянка согласно полученным измерениям составляем 10 000 м², то в этом случае его площадь равна 1 гектару или 100 соткам.
Если Ваш участок неправильной формы, то в этом случае количество соток напрямую зависит от площади. Именно по этой причине при помощи онлайн калькулятора Вы сможете правильно рассчитать параметр S делянки, и после этого разделив полученный результат на 100. Таким образом, Вы получите расчеты в сотках. Такой метод предоставляет возможность измерять делянки сложных форм, что весьма удобно.
Общие данные
Расчет площади земельных участков базируется на классических расчетах, которые выполняются согласно общепринятым геодезическим формулам.
Всего доступно несколько методов для расчета площади земельных угодий – механический (рассчитывается по плану при помощи мерных палеток), графический (определяется по проекту) и аналитический (при помощи формулы площади по измеренным линиям границ).
На сегодняшний день самым точным способом заслуженно считается – аналитический. Используя данный метод, ошибки при расчетах, как правило, появляются из-за погрешностей на местности измеренных линий. Данный способ является также и достаточно сложным, если границы криволинейные или количество углом на делянке больше десяти.
Немного проще по расчетам является графическим способ. Его лучше всего использовать в том случае, когда границы участка представлены в виде ломанной линии, с небольшим количеством поворотов.
И самый доступный и простой способ, и наиболее популярный, но и в тоже время самой большой погрешностью – механический способ. Используя данный метод, Вы сможете легко и быстро выполнить расчет площади земельных угодий простой или сложной формы.
Среди серьезных недостатков механического или графического способа, выделяют следующее, кроме погрешностей при измерении участка, при расчетах добавляется погрешность из-за деформации бумаги или погрешность при составлении планов.
I. Предисловие
Вот ведь незадача: проболев две недели, вы пришли в школу и узнали, что пропустили очень важную тему, задачи по которой будут на экзаменах в 9 классе — «Треугольники, четырехугольники и их площадь». Вот тут бы кинуться к учителю геометрии с вопросами: «Как найти площадь четырехугольника?» Но половина учеников боится подходить к учителям, чтобы их не сочли отстающими, а вторая половина встречает от учителей «помощь», похожую на «Посмотри в учебник, там все написано!» или «Не надо было пропускать уроки!» Но в учебнике вообще нет никакой информации по поводу правил нахождения площади треугольников и четырехугольников. А уроки были пропущены по уважительной причине, есть справка от врача. Но многие учителя только махнут на эти доводы рукой. Конечно, их можно понять: им не платят за дополнительное вбивание материала урока в головы ничего не понимающих учеников. Многие ученики бросают это бесполезное дело и через год проваливаются на экзамене, не добрав десяток баллов за задачу по нахождению площади треугольников и четырехугольников. И только некоторые ходят в библиотеки и к знакомым с вопросом: «Как найти площадь четырехугольника?» А разные люди и книги дают разные ответы, и получается большая путаница правил. Ниже я назову основные способы нахождения площадей треугольников и четырехугольников.
Конечно, их можно понять: им не платят за дополнительное вбивание материала урока в головы ничего не понимающих учеников. Многие ученики бросают это бесполезное дело и через год проваливаются на экзамене, не добрав десяток баллов за задачу по нахождению площади треугольников и четырехугольников. И только некоторые ходят в библиотеки и к знакомым с вопросом: «Как найти площадь четырехугольника?» А разные люди и книги дают разные ответы, и получается большая путаница правил. Ниже я назову основные способы нахождения площадей треугольников и четырехугольников.
II. Четырехугольники
Начнем с четырехугольников. В школах и на экзаменах рассматриваются только выпуклые четырехугольники, так что поговорим о них. На среднем уровне образования изучают площади параллелограммов и трапеции. Параллелограммы бывают нескольких видов: прямоугольник, квадрат, ромб и произвольный параллелограмм, в котором соблюдаются только основные его признаки: стороны попарно параллельны и равны, сумма соседних углов 180 о. Но способы нахождения площадей у всех этих фигур разные. Рассмотрим каждую по отдельности.
Но способы нахождения площадей у всех этих фигур разные. Рассмотрим каждую по отдельности.
1. Прямоугольник
S прямоугольника находится по формуле: S = а * b, где а — горизонтальная сторона, b — вертикальная сторона.*
2. Площадь квадратов
S квадрата находится по формуле: S = а * а, где a — сторона квадрата.
3. Площадь ромбов
S ромба находится по формуле: S = 0,5 * (d 1 * d 2), где d 1 — большая дианогональ,** d 2 — меньшая диагональ.
4. Площадь произвольного параллелограмма
S произвольного параллелограмма находится по формуле: S = a * h a , a — сторона параллелограмма, h a
Еще не все?
С параллелограммами мы закончили. «Надо выучить всего лишь это?» — облегченно спросите вы. Отвечаю: из параллелограммов — да, всего лишь это. Но еще остались трапеция и треугольники. Так что продолжаем.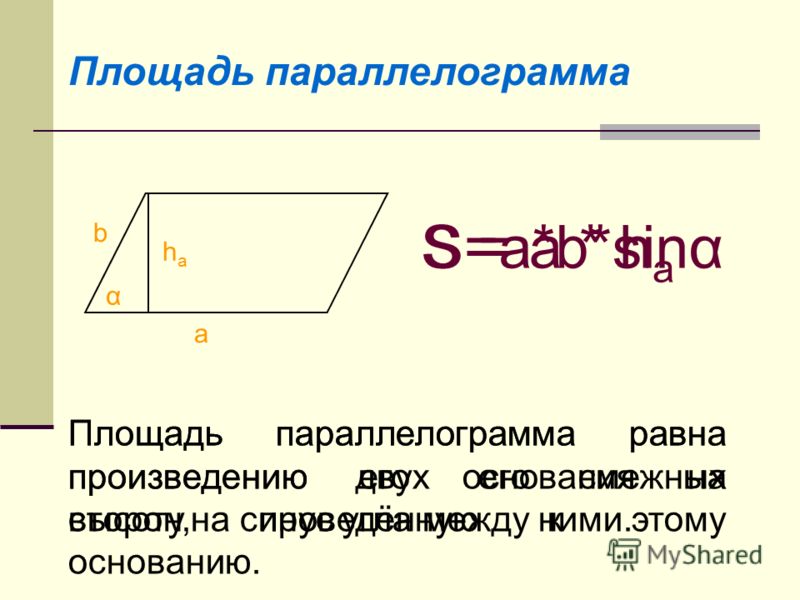
III. Трапец ия
Площадь трапеции
S трапеции можно находить одной формулой, будь она обычной или равнобедренной: S = ((а + b) : 2) * h, где a, b — ee основания, h — ee высота. Это все, что касается трапеции. Теперь на вопрос: «Как найти площадь четырехугольника?» — вы можете не только ответить сами, но и просветить других. А теперь переходим к треугольникам.
IV. Треугольник
В геометрии для нахождения их площади выделили три формулы: для прямоугольного, равностороннего и произвольного треугольников.
1. Площадь треугольника
S произвольного треугольника вычисляется по формуле: S = 0,5а * h a, a — сторона треугольника, h a — высота, проведенная к этой стороне.
2. Площадь равносторонних треугольников
S равностороннего треугольника можно найти по формуле: S = 0,5a * h, где a — основание треугольника, h — высота этого треугольника.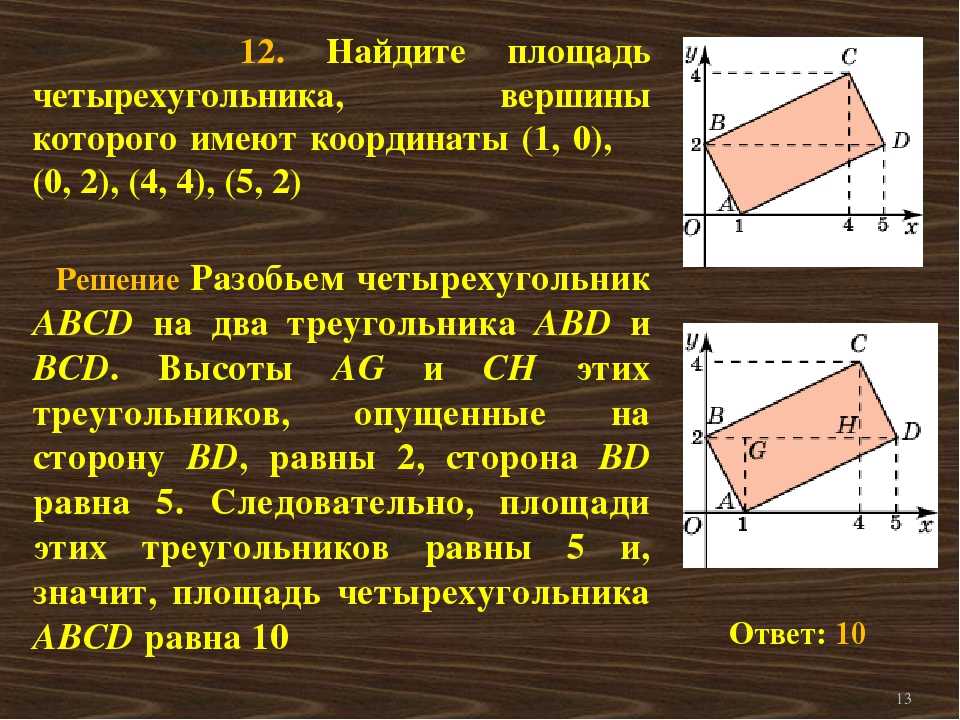
3. Площадь прямоугольных треугольников
Площадь прямоугольных треугольников находится по формуле: S = (а * b) : 2, где а — 1-й катет, b — 2-й катет.
Заключение
Ну вот, это, по-моему, все. Про треугольники тоже немного учить надо, не правда ли? А теперь обозрите все, что я здесь написала. «Елки-палки, чтобы это выучить, месяц понадобится!» — наверное, восклицаете вы. А кто говорил, что всё учится быстро? Но зато, когда вы все это выучите, вам не будут страшны вопросы по теме «Как найти площадь четырехугольника» или «Площадь произвольного треугольника» на аттестации в 9 классе. Так что, если вы хотите вообще хоть куда-нибудь поступить, учите, учитесь и будьте учеными!
___________________________________
Примечание
* — a и b не обязательно должны быть на поставленных мною местах. При решении задач можно вертикальную сторону назвать a , а горизонтальную — b;
** — диагонали можно поменять местами и изменить их названия так же, как и в примечании. *
*
Если на плоскости последовательно начертить несколько отрезков так, чтобы каждый следующий начинался в том месте, где закончился предыдущий, то получится ломаная линия. Эти отрезки называют звеньями, а места их пересечения — вершинами. Когда конец последнего отрезка пересечется с начальной точкой первого, то получится замкнутая ломаная линия, делящая плоскость на две части. Одна из них является конечной, а вторая бесконечной.
Простая замкнутая линия вместе с заключенной в ней частью плоскости (той, которая конечна) называют многоугольником. Отрезки являются сторонами, а образованные ими углы — вершинами. Количество сторон любого многоугольника равно числу его вершин. Фигура, которая имеет три стороны, называется треугольником, а четыре — четырехугольником. Многоугольник численно характеризуется такой величиной, как площадь, которая показывает размер фигуры. Как найти площадь четырехугольника? Этому учит раздел математики — геометрия.
Чтобы найти площадь четырехугольника, нужно знать к какому типу он относится — выпуклому или невыпуклому? весь лежит относительно прямой (а она обязательно содержит какую-либо из его сторон) по одну сторону. Кроме того, есть и такие виды четырехугольников, как параллелограмм с попарно равными и параллельными противоположными сторонами (разновидности его: прямоугольник с прямыми углами, ромб с равными сторонами, квадрат со всеми прямыми углами и четырьмя равными сторонами), трапеция с двумя параллельными противоположными сторонами и дельтоид с двумя парами смежных сторон, которые равны.
Кроме того, есть и такие виды четырехугольников, как параллелограмм с попарно равными и параллельными противоположными сторонами (разновидности его: прямоугольник с прямыми углами, ромб с равными сторонами, квадрат со всеми прямыми углами и четырьмя равными сторонами), трапеция с двумя параллельными противоположными сторонами и дельтоид с двумя парами смежных сторон, которые равны.
Площади любого многоугольника находят, применяя общий метод, который заключается в том, чтобы разбить его на треугольники, для каждого вычислить площадь произвольного треугольника и сложить полученные результаты. Любой выпуклый четырехугольник делится на два треугольника, невыпуклый — на два или три его в этом случае может складываться из суммы и разности результатов. Площадь любого треугольника вычисляют как половину произведения основания (a) на высоту (ħ), проведенную к основанию. Формула, которая применяется в этом случае для вычисления, записывается как: S = ½ . a . ħ.
Как найти площадь четырехугольника, например, параллелограмма? Нужно знать длину основания (a), длину боковой стороны (ƀ) и найти синус угла α, образованного основанием и боковой стороной (sinα), формула для расчета будет выглядеть: S = a . ƀ . sinα. Так как синус угла α есть произведение основания параллелограмма на его высоту (ħ = ƀ) — линию перпендикулярная основанию, то его площадь вычисляют, умножив на высоту его основание: S = a . ħ. Для расчета площади ромба и прямоугольника также подходит эта формула. Так как у прямоугольника боковая сторона ƀ совпадает с высотой ħ, то его площадь вычисляют по формуле S = a . ƀ. потому что a = ƀ, будет равняться квадрату его стороны: S = a . a = a². вычисляется как половина суммы его сторон, умноженная на высоту (она проводится к основанию трапеции перпендикулярно): S = ½ . (a + ƀ) . ħ.
ƀ . sinα. Так как синус угла α есть произведение основания параллелограмма на его высоту (ħ = ƀ) — линию перпендикулярная основанию, то его площадь вычисляют, умножив на высоту его основание: S = a . ħ. Для расчета площади ромба и прямоугольника также подходит эта формула. Так как у прямоугольника боковая сторона ƀ совпадает с высотой ħ, то его площадь вычисляют по формуле S = a . ƀ. потому что a = ƀ, будет равняться квадрату его стороны: S = a . a = a². вычисляется как половина суммы его сторон, умноженная на высоту (она проводится к основанию трапеции перпендикулярно): S = ½ . (a + ƀ) . ħ.
Как найти площадь четырехугольника, если неизвестны длины его сторон, но известны его диагонали (e) и (f), а также синус угла α? В этом случай площадь вычисляют, как половину произведения его диагоналей (линии, которые соединяют вершины многоугольника), умноженное на синус угла α. Формула может быть записана в таком виде: S = ½ . (e . f) . sinα. В частности в этом случае будет равняться половине произведения диагоналей (линии, соединяющие противоположные углы ромба): S = ½ . (e . f).
(e . f).
Как найти площадь четырехугольника, который не является параллелограммом или трапецией, его обычно принято называть произвольный четырехугольник. Площадь такой фигуры выражают через его полупериметр (Ρ — сумма двух сторон с общей вершиной), стороны a, ƀ, c, d и сумму двух противоположных углов (α + β): S = √[(Ρ — a) . (Ρ — ƀ) . (Ρ — c) . (Ρ — d) — a . ƀ . c . d . cos² ½ (α + β)].
Если а φ = 180о, то для расчета его площади используют формулу Брахмагупты (индийский астроном и математик, живший в 6—7 веках нашей эры): S = √[(Ρ — a) . (Ρ — ƀ) . (Ρ — c) . (Ρ — d)]. Если четырехугольник описан окружностью, то (a + c = ƀ + d), а его площадь вычисляют: S = √[ a . ƀ . c . d] . sin ½ (α + β). Если четырехугольник одновременно является описанным одной окружностью и вписанным в другую окружность, то для вычисления площади используют следующую формулу: S = √.
Как узнать площадь четырехугольника с разными сторонами. Формулы вычисления площади произвольного четырёхугольника.
 Как найти площадь четырехугольника – дельтоида
Как найти площадь четырехугольника – дельтоидаКвадрат – это правильный четырехугольник, в котором все углы и стороны равны между собой.
Довольно часто эту фигуру рассматривают, как частный случай или . Диагонали квадрата равны между собой и используются в формуле площади квадрата через диагональ.
Для расчета площади рассмотрим формулу площади квадрата через диагонали:
То есть площадь квадрата равна квадрату длины диагонали поделенному на два. Учитывая, что стороны фигуры равны, можно рассчитать длину диагонали из формулы площади прямоугольного треугольника или по теореме Пифагора.
Рассмотрим пример расчета площади квадрата через диагональ. Пусть дан квадрат с диагональю d
= 3 см. Необходимо вычислить его площадь:
По этому примеру расчета площади квадрата через диагонали мы получили результат 4,5 .
Площадь квадрата через сторону
Найти площадь правильного четырехугольника можно и по его стороне. Формула площади квадрата очень проста:
Так как в предыдущем примере расчета площади квадрата мы рассчитали значение по диаметру, теперь попробуем найти длину стороны:
Подставим значение в выражение:
Длина стороны квадрата будет равна 2,1 cm.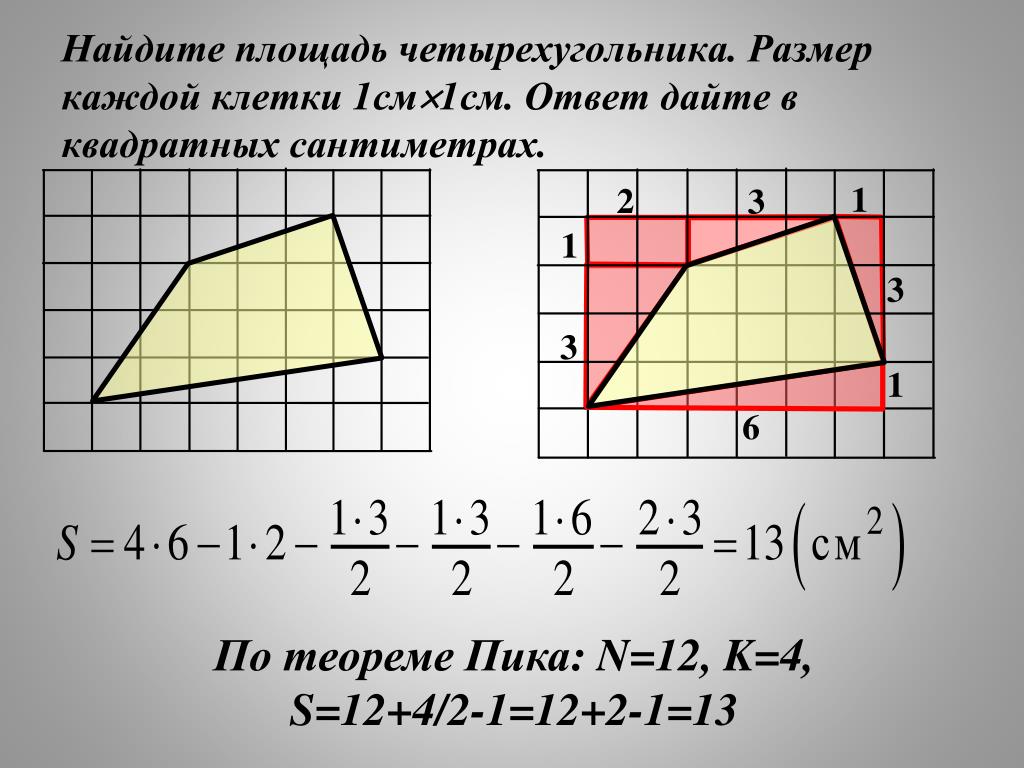
Очень просто можно использовать формулу площади квадрата вписанного в окружность.
Диаметр описанной окружности будет равен диаметру квадрата. Так как квадрат считается правильным ромбом, можно использовать формулу расчета площади ромба. Она равна половине произведения его диагоналей. Диагонали квадрата равны, значит формула будет выглядеть так:
Рассмотрим пример расчета площади квадрата вписанного в окружность.
Дан квадрат, вписанный в окружность. Диагональ окружности равна d
= 6 см. Найдите площадь квадрата.
Мы помним, что диагональ окружности равна диагонали квадрата. Подставляем значение в формулу расчета площади квадрата через его диагонали:
Площадь квадрата равна 18
Площадь квадрата через периметр
В некоторых задачах по условиям дается периметр квадрата и требуется расчет его площади. Формула площади квадрата через периметр выводится из значения периметра. Периметр – это сумма длин всех сторон фигуры. Т.к. в квадрате 4 равных стороны, то он будет равенОтсюда находим сторону фигуры Площадь квадрата по обычной формуле считается так: .
Рассмотрим пример расчета площади квадрата через периметр.
При решении задач по школьной математике часто требуется определить, чему равняется диагональ заданного квадрата. При кажущейся некоторой сложности, эта задача является весьма простой и имеет несколько несложных способов решения. Рассмотрим их, для начала введём некоторые понятия и определения.
- Квадрат — это четырёхугольник с равными сторонами, все углы которого являются прямыми, то есть равны 90 градусов. Данная фигура одновременно и ромб, и прямоугольник, поэтому сохраняет все их свойства.
- Диагональ многоугольника — это отрезок, соединяющий две его противоположные вершины. В статье её будем обозначать буквой d.
- Противоположными называются вершины, не лежащие на одной стороне.
- Корень квадратный из числа , это такое число, которое при умножении само на себя даст исходное. В геометрии используются только положительные значения квадратного корня. В статье его будем обозначать сокращением rad (от латинского radical — корень).
 2. Отсюда найдём сторону: a = radS. Итак, нам удалось выразить сторону через площадь. Подставим полученное выражение в конечную формулу из предыдущей части. Формула примет вид: d = rad2*a = rad2*radS .
2. Отсюда найдём сторону: a = radS. Итак, нам удалось выразить сторону через площадь. Подставим полученное выражение в конечную формулу из предыдущей части. Формула примет вид: d = rad2*a = rad2*radS .Пример: допустим, площадь равна 32 квадратных метра. Подставим это число. Получим rad2*rad32 = rad2*4*rad2 = 4*2 = 8 метров.
Вычисление диагонали по известному периметру
Пусть нам известен периметр . В дальнейшем его будем записывать латинской буквой P, найдём его d. Воспользуемся свойствами прямоугольника и запишем формулу его периметра.
P = два*(a + b). Перепишем для b = a. У нас получится: P = два*(a + a) = 2*2a = 4*a. Выразим из последней формулы сторону. Имеем: a = P/4. Воспользуемся тем, что: d = rad2*a. Выразим сторону через периметр. Наша формула примет видd = rad2*P/4.
Примере: пусть периметр равен 128 метров. Проведём несложный расчёт. Имеем, rad =d2*128/4 = 32*rad2 метров.
Вычисление по радиусу описанной и вписанной окружности
Ещё один способ , который на само деле очень простой.
 Радиус описанной окружности будем обозначать латинской буквой R, радиус вписанной окружности будем обозначать латинской буквой r.
Радиус описанной окружности будем обозначать латинской буквой R, радиус вписанной окружности будем обозначать латинской буквой r.Сначала разберёмся с описанной окружностью. В данной ситуации её радиус составляет ровно половину диагонали (это нетрудно убедиться с использованием построения), таким образом: R = 1/2*d. отсюда имеем: d = два*R . Снова поясним наши рассуждения на примере. Пусть R = 45 километров. Получим, d = два*45 = 90 километров.
И, наконец, рассмотрим метод, связанный с радиусом вписанной окружности. Опять-таки из построения чётко видно, что диаметр вписанной окружности равняется стороне квадрата. Таким образом, её радиус вдвое меньше стороны. Запишем это в виде формулы: r = 1/2*a. Отсюда следует, a = 2*r. Снова воспользуемся формулой из первого метода, подставим вместо стороны её выражение через радиус вписанной окружности. Выражение примет вид: d = rad2*a = rad2*2*r .
Ещё раз воспользуемся помощью примера. Пусть r = 98 метров. Тогда имеем, d = rad2*2*98 = 196*rad2.

Заключение
Таким образом, мы рассмотрели в статье пять принципиально различных методов вычисления диагонали квадрата. Если, на первый взгляд, задача казалась сложной, то после проведённых нами рассуждений стало очевидно, что особых проблем здесь нет. Сведём все полученные нами формулы в одну таблицу.
- d = rad2*a;
- d = rad2*radS;
- d = rad2*P/4;
- d = 2*R;
- d = rad2*2*r.
Хочется ещё отметить , что с помощью первой из наших формул очень легко построить отрезок, равный корню квадратному из двух. Для этого строим квадрат со стороной единица, его диагональ и будет равняться искомому отрезку.
Если на полученной диагонали мы построим прямоугольник, используя её как длину, а ширину возьмём равной единице, то получим отрезок равный ещё одному иррациональному числу корень квадратный из трёх.
Видео
Из видео вы узнаете, как найти диагональ квадрата, если известна его площадь.
Не получили ответ на свой вопрос? Предложите авторам тему.

Читайте статью, чтобы знать, как находить площадь квадрата разными способами.
Квадрат — это равносторонний прямоугольник. У данного правильного и плоского четырехугольника равенство во всех сторонах, углах и диагоналях. Из-за того что существует такое равенство, формула для вычисления площади и других характеристик, немного видоизменяется по сравнению с иными математическими фигурами. Но это не делает задачи слишком сложными. Давайте разберем все формулы и решения задач в этой статье.
Площадь S прямого и квадратного угольников вычисляется по формуле: a умножить на b . Но так как у квадрата полное равенство сторон, то его площадь будет равна: S=(a) во второй степени . Как узнать величину стороны квадрата, зная его площадь?
- Если известна площадь квадратного угольника, то сторону находим путем исчисления площади из-под квадратного корня.
- К примеру, площадь угольника равна 49, то чему равняется сторона?
- 49=(а) во второй степени .
 Решение: а=корень из 49=7. Ответ: 7 .
Решение: а=корень из 49=7. Ответ: 7 .
Если нужно найти сторону квадратного угольника, площадь которого состоит слишком длинного числа, тогда воспользуйтесь калькулятором. Наберите сначала число площади, а потом нажмите знак корня на клавиатуре калькулятора. Получившееся число и будет ответом.
В этом примере будем использовать теорему Пифагора. У квадрата все стороны равны, а диагональ d мы будем рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а . Теперь находим диагональ квадрата, если известна его площадь:
- Чтобы не расписывать всю теорему Пифагора будем решать по второму варианту: d=a√2, где а — это сторона квадрата.
- Итак, нам известна площадь квадрата, например, она равна 64. Значит одна сторона а=√64=8.
- Получается d=8√2 . Корень из 2 не получается целым числом, поэтому в ответе можно написать именно так: d=8√2 . Но, если хочется вычислить значение, тогда воспользуйтесь калькулятором: √2= 1,41421356237 и умножьте на 8, получается 11, 3137084 .

Важно: Обычно в математике не оставляют в ответе цифры с большим количеством чисел после запятой. Нужно округлять или оставить с корнем. Поэтому ответ на нахождение диагонали, если площадь равна 64 будет таким: d=8√2 .
Формула нахождения площади квадрата через диагональ простая:
Теперь напишем решение по нахождению площади квадрата через диагональ:
- Диагональ d=8.
- 8 в квадрате равняется 64.
- 64 разделить на 2 равно 32.
- Площадь квадрата равна 32.
Совет: У этой задачи есть еще одно решение через теорему Пифагора, но оно более сложное. Поэтому используйте решение, которое мы рассмотрели.
Периметр квадратного угольника P — это сумма всех сторон. Чтобы найти его площадь, зная его периметр, нужно сначала вычислить сторону квадратного угольника. Решение:
- Допустим периметр равен 24. Делим 24 на 4 стороны, получается 6 — это одна сторона.

- Теперь используем формулу нахождения площади, зная чему равна сторона квадратного угольника: S=а в квадрате, S=6 в квадрате=36 .
- Ответ: 36
Как видите, зная периметр квадрата, просто найти его площадь.
Радиус R — это половина диагонали квадрата, вписанного в окружность. Теперь можем найти диагональ по формуле: d=2*R . Далее находим площадь квадрата вписанного в окружность с заданным радиусом:
- Диагональ равна 2 умножить на радиус. Например радиус равен 5, тогда диагональ равна 2*5=10 .
- Выше было описано, как находить площадь квадрата, если известна диагональ: S=диагональ в квадрате разделить на 2. S=10*10 и разделить на 2=50.
- Ответ — 50 .
Эта задача немного сложнее, но тоже легко решаемая, если знать все формулы.
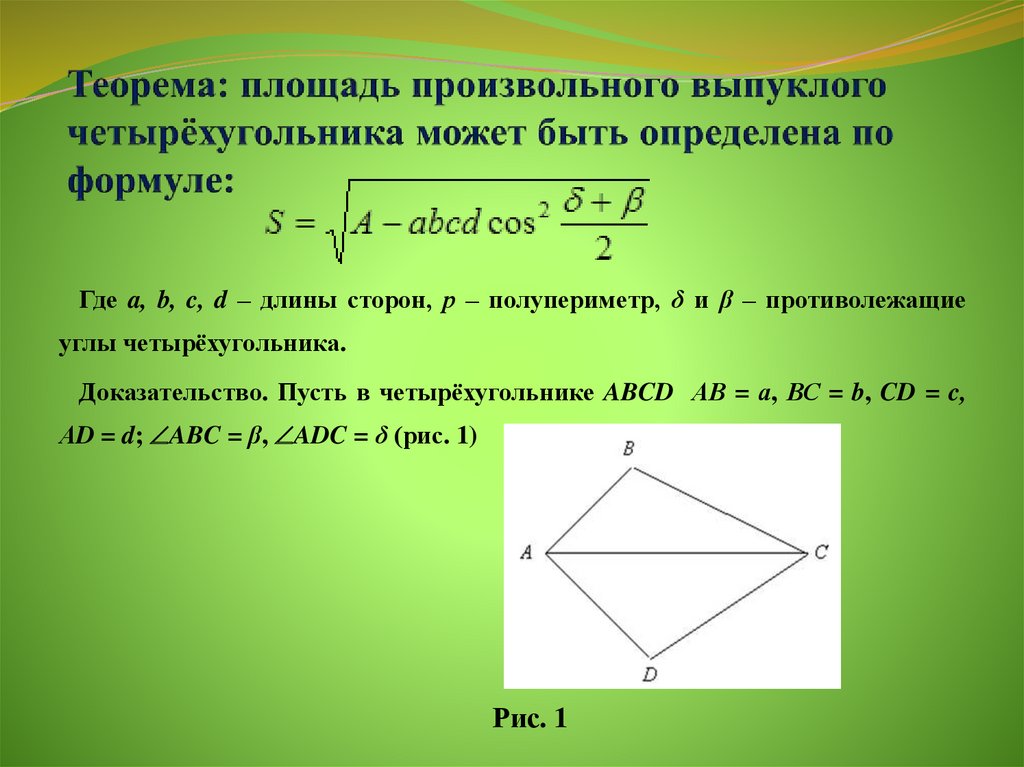
На картинке видно, что радиус вписанной окружности равен половине стороны. Сторона находится по формуле обратной той, которая изображена на картинке: а=2*r .
 Потом уже находим площадь квадрата описанного около окружности с заданным радиусом по формуле S=а в квадрате . Решение:
Потом уже находим площадь квадрата описанного около окружности с заданным радиусом по формуле S=а в квадрате . Решение:- Допустим, радиус равен 7. Сторона квадрата а равна 2*7=14.
- S=14 в квадрате=196 .
Если понять суть решения подобных задач, то можно решать их быстро и просто. Давайте рассмотрим еще несколько примеров.
Примеры решения задач на тему «Площадь квадрата»
Чтобы закрепить пройденный материал и запомнить все формулы, необходимо решить несколько примеров задач на тему «Площадь квадрата». Начинаем с простой задачи и движемся к решению более сложных: Примеры решения сложных задач на тему «Площадь квадрата»
Теперь вы знаете, как пользоваться формулой площади квадрата, а значит, вам любая задача под силу. Успехов в дальнейшем обучении!
Видео: Вычисление площади квадрата
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры).
 Величина площади выражается числом заключающихся в нее квадратных единиц.
Величина площади выражается числом заключающихся в нее квадратных единиц.Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны. - Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.
S = 1 2 2 где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Площадь четырехугольника| Определение, типы и формула для нахождения площади
В геометрии четырехугольник — это замкнутая фигура, полученная путем соединения четырех точек, среди которых любые три точки не лежат на одной прямой.
 2)\).
2)\).Площадь обычного четырехугольника — это сечение, заключенное между 4 сторонами этого многоугольника. Общая формула площади четырехугольника равна произведению основания на его высоту. Для расчета площади существуют заранее определенные формулы для треугольников, прямоугольников, квадратов, кругов, общих четырехугольников и т. д. В этой статье вы узнаете о типах и площади четырехугольника с формулами и примерами решения.
Какова площадь четырехугольника?Четырехугольники бывают двух видов – правильные и неправильные. Из этой статьи о площади четырехугольника вы узнаете, как получить площадь любого типа четырехугольника, будь то квадрат, трапеция или треугольник.
Подход к вычислению площади четырехугольника зависит от типа и имеющихся данных о четырехугольнике. Однако, если четырехугольник не относится ни к одному из многообразий, то его площадь можно получить либо путем деления его на два треугольника, либо с помощью формулы нахождения площади четырехугольника по четырем сторонам, также известной как формула Бретшнейдера.
 .
.Ознакомьтесь с этой статьей о линиях.
Как найти площадь четырехугольника?Теперь, когда мы знаем точное определение четырехугольника, давайте перейдем к различным способам, которыми мы можем получить площадь.
Площадь четырехугольника путем его разделения на два треугольникаПлощадь четырехугольника путем его деления на два треугольника можно получить следующим образом:
Рассмотрим четырехугольник PQRS, как показано выше.
Разделите его на два треугольника, где \(h_{1\ } и\ h_{2\ }\) — высоты треугольников PSR и PQR соответственно, как показано на рисунке ниже:Теперь:
Площадь треугольника PSR + Площадь треугольника PQR =
\( \frac{\left(PR\times h_1\right)}{2}+\frac{\left(PR\times h_2\right)}{2}=PR\frac{\ left(h_1+h_2\right)}{2}\)Следовательно, площадь четырехугольника PQRS=площадь треугольника PSR+площадь треугольника PQR.

\(\frac{1}{2}\times PR\times \left(h_1+h_2\right)\)
\(Площадь=\frac{1}{2}\times d\times\left(h_1+h_{2\ }\right)\)
Здесь d=PR=диагональ
Площадь общего четырехугольника \ (=\frac{1}{2}\times \text{диагональ}\times\text{(Сумма высот двух треугольников)}\)
Рассмотрим приведенный выше четырехугольник PQRS, здесь диагональ = 15 см, а высоты треугольники PSR и PQR равны 5 см и 7 см соответственно. Найдите площадь четырехугольника PQRS.
Площадь общего четырехугольника\(=\frac{1}{2}\times \text{диагональ}\times\text{(Сумма высот двух треугольников)}\). 92\ \frac{θ}{2}}\).
Где = a, b, c, d — стороны четырехугольника и \(\ θ_{1\ } и \ θ_2\) — противоположные углы.
s = полупериметр четырехугольника \ (= \ frac {\ left (a + b + c + d \ right)} {2} \) и \ (\ θ = θ_1 + θ_2 \).
Такой четырехугольник, площадь которого определяется с помощью сторон четырехугольника и 2 его противоположных углов, также известен как формула Бретшнайдера .

Изучите концепции трехмерной геометрии здесь.
Площадь четырехугольника по формуле ГеронаДругой подход к вычислению площади четырехугольника — использование формулы Герона. В общем, мы применяем эту формулу, чтобы получить площадь треугольника, когда три стороны различны. Описанная ниже процедура используется для определения площади четырехугольника.
- Прежде всего, нужно разделить четырехугольник на два треугольника, расположенных по диагонали. Здесь длина диагонали нам известна.
- На следующем шаге примените формулу Герона отдельно для обоих вновь созданных треугольников, чтобы найти площадь четырехугольника по приведенной ниже формуле.
- \(Площадь=\sqrt{s(s−a)(s−b)(s−c)}\)
- Здесь a, b, c — стороны полученного треугольника.
- \(s=\frac{\left(a+b+c\right)}{2}\) = полупериметр треугольника.
- Наконец, сложите площади двух треугольников, чтобы получить площадь полного четырехугольника.
 2\ \frac{θ}{2}}\).
2\ \frac{θ}{2}}\).По формуле Герона Площадь=\(\sqrt{s(s−a)(s−b)(s−c)}\) Четырехугольники обычно имеют стандартную форму с четырьмя сторонами как прямоугольник, квадрат, трапеция и воздушный змей. Различают следующие типы четырехугольников:
Площадь параллелограммаЧетырехугольник называется параллелограммом, противоположные стороны которого параллельны и равны друг другу. Это означает, что параллелограмм имеет две пары параллельных сторон с диагоналями, делящими друг друга пополам. В четырехугольнике сумма любого из двух смежных углов равна 180 градусов.
Рассмотрим рисунок выше:
Площадь параллелограмма =\(b\×h\(основание\×высота)\).
Площадь прямоугольникаПараллелограмм называется прямоугольником, если каждый угол равен 90°.
Рассмотрим приведенный выше рисунок. Здесь AB || CD, Британская Колумбия || AD, AB = CD и BC = AD, а также ∠A = ∠B = ∠C = ∠D = 90° (каждый угол равен 90 градусов) В прямоугольнике противоположные стороны параллельны и равны, а диагонали делят друг друга пополам.

Площадь прямоугольника=\(\text{Длина}\times \text{Ширина}\ (L\times B)\).
Понимание понятий статистики здесь.
Площадь квадратаПараллелограмм считается квадратом, если все стороны равны и каждый угол равен 90°. Диагонали квадрата делятся пополам перпендикулярно друг другу (это означает, что они делятся пополам под углом 90 градусов).
Рассмотрим приведенный выше рисунок. Здесь AB || CD, Британская Колумбия || AD и AB = CD = BC = AD, а также ∠A = ∠B = ∠C = ∠D = 92}{2}\left(\frac{\text{Квадрат диагонали}}{2}\right).\)
Площадь ромбаПараллелограмм считается ромбом, если у него все стороны равны, угол между диагоналями равен 90°. Все стороны ромба равны, противоположные стороны параллельны друг другу, а диагонали пересекаются перпендикулярно.
Если длина двух диагоналей ромба равна\( d_1и\d_2\).
Тогда площадь ромба =\(\frac{1}{2}\times d_1\times d_2\)
Прочтите эту статью о биномиальной теореме.
Площадь трапеции
Четырехугольник называется трапецией, если он имеет только одну пару параллельных противоположных сторон с диагоналями, делящими друг друга пополам в одинаковом отношении.
Учитывая приведенную выше схему;
Если «h» представляет собой высоту трапеции, то; Площадь трапеции определяется как:
\(=\frac{1}{2}\times\text{(Сложение длин параллельных сторон)}\times h\)
\(=\frac{1}{2}\times(AB+CD)\times h.\)
Площадь воздушного змеяЧетырехугольник называется воздушным змеем, если пара смежных сторон равна одинаковой длины с диагоналями, пересекающимися под прямым углом.
Учитывая приведенную выше диаграмму:
Площадь воздушного змея определяется как =\(\frac{1}{2}\times Diagonal_1\times Diagonal_2.\)
\(=\frac{1}{ 2}\раз d_1\раз d_2\).
Кроме того, здесь можно узнать о последовательностях и сериях.
Свойства четырехугольникаНекоторые важные свойства четырехугольника, необходимые для более ясного понимания темы, перечислены ниже:
- Сумма всех внутренних углов четырехугольника составляет 360 градусов.

- Каждый тип четырехугольника содержит четыре вершины и четыре стороны, окружающие четыре угла.
- Как правило, четырехугольник имеет стороны разной длины и углы разной величины. Однако четырехугольники, такие как квадраты, прямоугольники, параллелограммы и т. д., имеют одинаковые стороны и углы.
Существует пять основных типов четырехугольников, а именно:
- Прямоугольник
- Квадрат
- Параллелограмм
- Ромб
- Основные свойства подробно описаны ниже. новые статьи:
Прямоугольник
Свойства прямоугольников следующие:
- Противоположные стороны прямоугольника параллельны и равны друг другу, а диагонали делят друг друга пополам.
- Все углы прямоугольника равны 90 градусов.
Квадрат
- Квадрат похож по форме на прямоугольник, но все его стороны параллельны и идентичны друг другу.
- Все углы квадрата равны 90 градусов, а диагонали делят друг друга пополам перпендикулярно.

Параллелограмм
- В параллелограмме противоположные углы равны. Кроме того, противоположные стороны равны и параллельны.
- Сумма любых двух смежных углов равна 180 градусов.
Ромб
- Подобно параллелограмму в ромбе, противоположные углы равны.
- Здесь все стороны одинаковы плюс противоположные стороны параллельны друг другу.
- Диагонали ромба пересекают друг друга перпендикулярно.
Трапеция
- У трапеции существует только одна пара противоположных сторон, которые параллельны друг другу.
Имея полную информацию о площади, ее формуле, способе расчета, давайте рассмотрим некоторые решенные примеры:
Решенный пример 1: Найдите площадь ромба, диагонали равны 10 см и 8 см соответственно.
Решение:
Площадь ромба =\(\left(\frac{1}{2}\right)\times d_1\times d_2\) квадратных единиц.

Дано: диагональ 1, \(d_1\) =10 см и диагональ 2, \(d_2\) = 8 см. 92\).
Решено Пример 2: Найдите площадь воздушного змея, диагонали которого равны 16 единицам и 13 единицам.
Решение:
Площадь воздушного змея определяется по формуле:
A =\(\left(\frac{1}{2}\right)\times d_1\times d_2\)
From по данным диагонали предоставленного змея \(d_1\) = 16 единиц и \(d_2\) = 13 единиц.
Подставляя значения в формулу:
A =\(\left(\frac{1}{2}\right)\times d_1\times d_2\)
\(A=\left(\frac{1}{2}\right)\times16\times13=104\text{ единиц площади}\)
Решено Пример 3: Получите площадь прямоугольника, имеющего длина равна 20 см, а ширина 10 см.
Решение:
Площадь прямоугольника находится по формуле:
A = l × b
Здесь длина, т.е. l = 20 см, а ширина, т.е. b = 10 см.
Подставляя значения в формулу:
A = l × b = 20 × 10 = 200 \(см^2\).

Мы надеемся, что приведенная выше статья о площади четырехугольника поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Площадь четырехугольника Часто задаваемые вопросыВ.1. Какова формула площади четырехугольника?
Ans.1 Площадь общего четырехугольника можно рассчитать по формуле = 1/2 x длина диагонали x (сумма высот двух треугольников).
Q.2 Что такое четырехугольник?
Ответ 2 Четырехугольник — это многоугольник, который имеет четыре стороны. Это означает, что четырехугольник имеет ровно четыре вершины и ровно четыре угла.
В.3 В чем разница между четырехугольником и треугольником?
Ответ 3 Треугольник – это замкнутая фигура с тремя прямыми сторонами и тремя углами.
 Однако четырехугольник имеет четыре прямые стороны и четыре угла.
Однако четырехугольник имеет четыре прямые стороны и четыре угла.Q.4 Какие существуют типы четырехугольников?
Ответ 4 Четырехугольники бывают квадратного, прямоугольного, ромбического, воздушного змея, параллелограмма и трапеции.
Q.5 Как найти площадь любого четырехугольника?
Ответ 5 Чтобы найти площадь любого четырехугольника, мы можем использовать формулу Бретшнейдера, формулу Герона или разделить четырехугольник на два треугольника, проведя диагональ, а затем вычислить площадь каждого треугольника. Наконец, добавьте площадь, чтобы получить площадь четырехугольника. Также существуют специальные формулы для квадрата, прямоугольника, ромба, воздушного змея, параллелограмма и трапеции для расчета площади.
Скачать публикацию в формате PDFЕще на testbook.com
Таутомерия – определение, различные типы, примеры, механизм, диаграммы Изомерия: определение, типы, позиционные и геометрические изомеры, примеры и диаграммы Конфигурация S-Block, Grouptronic 1 и Группа 2 Различия и использование Элементы F-блока — Электронная конфигурация, типы, лантаноиды и актиноиды Различия и использование Примечания по химическому связыванию: определение, типы, схемы, примеры, теория Косселя и Льюиса Площадь четырехугольника – формула, определение, примеры решений, часто задаваемые вопросы
Площадь четырехугольника – это пространство внутри границы четырехугольника.
 Четырехугольник можно определить как замкнутую двумерную фигуру, имеющую четыре стороны или ребра, а также четыре угла или вершины. При измерении форма объектов классифицируется по количеству сторон четырехугольника. Четырехугольники делятся на две категории: правильные четырехугольники и неправильные четырехугольники. Правильный четырехугольник – это четырехугольник, у которого все стороны одинаковой длины. Неправильный четырехугольник – это четырехугольник, у которого все стороны не равны.
Четырехугольник можно определить как замкнутую двумерную фигуру, имеющую четыре стороны или ребра, а также четыре угла или вершины. При измерении форма объектов классифицируется по количеству сторон четырехугольника. Четырехугольники делятся на две категории: правильные четырехугольники и неправильные четырехугольники. Правильный четырехугольник – это четырехугольник, у которого все стороны одинаковой длины. Неправильный четырехугольник – это четырехугольник, у которого все стороны не равны.Что такое четырехугольник?
Четырехугольник — это многоугольник с четырьмя сторонами. Замкнутая двумерная фигура, образованная соединением четырех точек, среди которых три точки не лежат на одной прямой, называется четырехугольником. Четырехугольник имеет четыре стороны, четыре угла и четыре вершины. Стороны четырехугольника могут быть равными, а могут и не быть.
Как определено выше, любой многоугольник, имеющий четыре стороны, называется четырехугольником.
 Различные типы четырехугольников:
Различные типы четырехугольников:- Прямоугольник
- Квадрат
- Ромб
- Параллелограмм
- Трапеция
- Воздушный змей
3 Четырехсторонняя фигура замкнута.
- Сумма внутренних углов четырехугольника равна 360 градусов.
- Четыре стороны могут быть разной длины или равными, в зависимости от типа четырехугольника.
Какова площадь четырехугольника?
Площадь четырехугольника – это пространство, ограниченное всеми границами четырехугольника. Площадь четырехугольника измеряется в квадратных единицах, таких как м 2 , ин 2 , см 2 и т. д. Площадь правильного четырехугольника рассчитывается по разным формулам. Для вычисления площади неправильного четырехугольника используются различные формулы, которые обсуждаются ниже в этой статье.
Формула площади четырехугольника путем деления его на два треугольника
В четырехугольнике ABCD длина диагонали BD равна «d».
 ABCD можно разделить на два треугольника ΔABD и ΔBCD диагональю BD. Для вычисления площади четырехугольника ABCD мы вычисляем площади отдельных треугольников и соответственно складываем их. Но для вычисления площади треугольника необходимо знать его высоту. Предположим, что высоты треугольников ABD и BCD равны h 1 и ч 2 соответственно.
ABCD можно разделить на два треугольника ΔABD и ΔBCD диагональю BD. Для вычисления площади четырехугольника ABCD мы вычисляем площади отдельных треугольников и соответственно складываем их. Но для вычисления площади треугольника необходимо знать его высоту. Предположим, что высоты треугольников ABD и BCD равны h 1 и ч 2 соответственно.Площадь треугольника ABD = (1/2) × d × h 1 .
Площадь треугольника BCD = (1/2) × d × h 2 .
Из рисунка площадь четырехугольника ABCD = площадь ΔABD + площадь ΔBCD.
Площадь четырехугольника ABCD = (1/2) × d × h 1 + (1/2) × d × h 2 = (1/2) × d ×( h 1 +h 2 ).
Таким образом, формула, используемая для нахождения площади четырехугольника,
Площадь четырехугольника = (1/2) × диагональ × (сумма высот) = (1/2) × d ×( h 1 +h 2 )
Площадь четырехугольника с вершинами
Если известны вершины четырехугольника, то его площадь вычисляется по данной формуле.
 Предположим, что A(x 1 , y 1 ), B(x 2 , y 2 ), C(x 3 , y 3 ) и D(1 5 2 4 9 0, 4 4 ) — вершины четырехугольника ABCD.
Предположим, что A(x 1 , y 1 ), B(x 2 , y 2 ), C(x 3 , y 3 ) и D(1 5 2 4 9 0, 4 4 ) — вершины четырехугольника ABCD.Затем его площадь рассчитывается с использованием двух различных методов, которые обсуждаются ниже:
Площадь четырехугольника с использованием координат (метод 1)
Следуйте направлениям стрелки и сложите диагональные произведения, т. е. x 1 y 2 , x 2 y 3 , x 3 y 4 , и x 4 y 1 90.
(х 1 у 2 + х 2 у 3 + х 3 y 4 + x 4 y 1 )….(i)
Теперь следуйте пунктирным стрелкам и добавьте диагональные произведения, т. е. x 2 y 9 3 1 y 2 , x 4 y 3 , и x 1 y 4 .

(x 2 y 1 + x 3 Y 2 + x 4 Y 3 + x 1 Y 4 ). (ii) из (i) и умножьте результат на 1/2.
(1/2) × [(x 1 y 2 + x 2 Y 3 + x 3 Y 4 + X 4 Y 4 + x 4 Y 1 1 1 1 1 1 1 1 1 1 1 1 1 ) 4 ) 1 1 ) 1 ) 4 + x . 2 y 1 + x 3 y 2 + x 4 y 3 + x 1 y 4 )]
Таким :
Площадь четырехугольника = (1/2) × [(x 1 y 2 + x 2 y 3 + x 3 y 4 + x 4 y 1 ) – (x 2 y 1 + x 3 y 2 + x 4 y 3 + x 1 y 4 )]
Площадь четырехугольника по формуле Герона (метод 2)
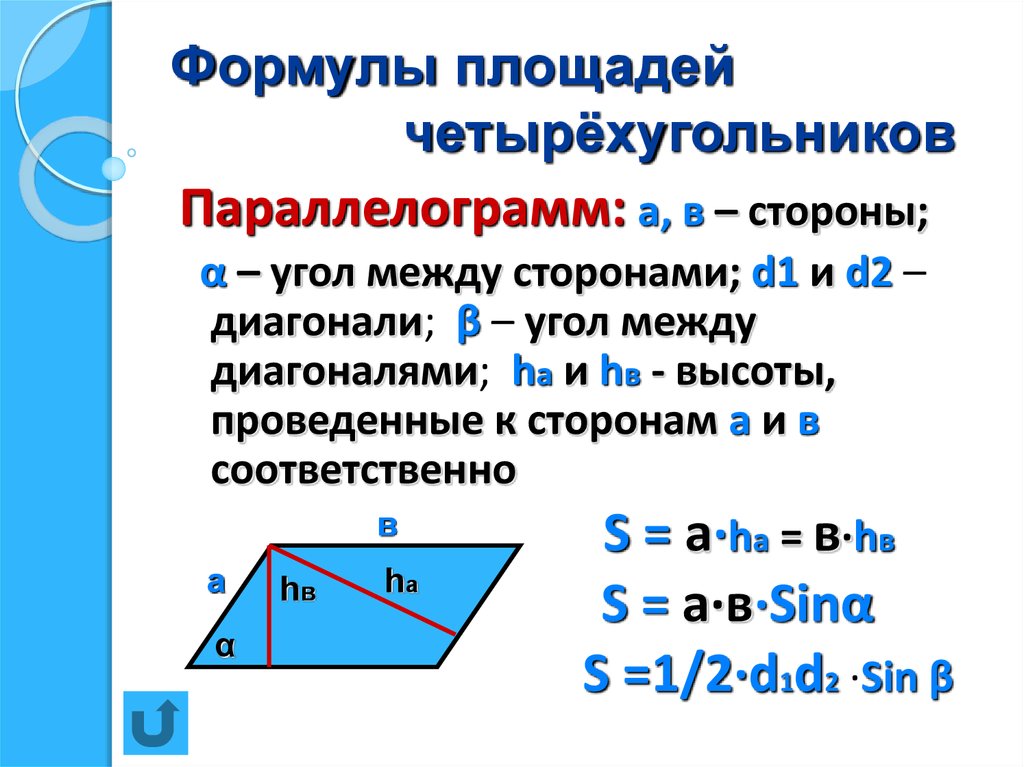
Для этого метода мы делим данный четырехугольник на два треугольника, а затем находим площадь каждого треугольника отдельно по формуле Герона формула.
 Наконец, обе площади треугольников складываются, чтобы найти окончательную площадь четырехугольника.
Наконец, обе площади треугольников складываются, чтобы найти окончательную площадь четырехугольника.Площадь четырехугольника ABCD = площадь треугольника ABD + площадь треугольника BCD
площадь треугольника с вершинами и R(x 3 , y 3 ) определяется выражением
Площадь Δ = (1/2) × {x 1 (y 2 – y 3 – y 3 ) 5 (y 3 – y 1 ) + x 3 (y 1 – y 2 )}
Как найти площадь четырехугольника?
Площадь четырехугольника находится с помощью шагов, описанных ниже:
Шаг 1: Отметьте длину диагонали и длину перпендикуляра к ней из обеих вершин.
Шаг 2: Подставьте эти значения в приведенную формулу Площадь = (1/2) × d ×( h 1 +h 2 ) , где d — длина диагонали и h 1 , h 2 — длины перпендикуляра из диагонали в противоположные вершины.

Шаг 3: Ответ, полученный на предыдущем шаге, представляет собой требуемую площадь и измеряется в единицах 2
Площадь некоторых четырехугольников
Некоторые конкретные четырехугольники очень распространены и используются в нашей повседневной жизни, и их формула для площади объясняются в статье, приведенной ниже:
Площадь прямоугольникаПрямоугольник – это замкнутая фигура, имеющая четыре стороны, в которой противоположные стороны равны и параллельны друг другу, а диагонали прямоугольников делятся пополам в 90 градусов.
Площадь квадратаПлощадь прямоугольника = (длина x ширина) м 2
Квадрат является частным случаем прямоугольника, у которого все четыре стороны равны. стороны параллельны друг другу. В квадрате диагонали делят пополам перпендикулярно друг другу.
Площадь ромбаПлощадь квадрата = (сторона x сторона) м 2
Ромб – это частный случай квадрата, у которого все четыре стороны и противоположные углы равны по размеру, а противоположные стороны параллельны, а сумма смежных углов ромба равна 180 градусам.

Площадь ПараллеграммыПлощадь ромба = (1/2) x D 1 x D 2 M 2
. Оценка, в равной степени, и равной оплот, и равной оплот, и равной оплот, и равной оплот, и равной оплот, и равной оплот, и равной оплот, и равной оплот, и равной оплот
. относительно друг друга называется параллелограммом. При этом диагонали делят друг друга пополам, а противоположные углы равны, в котором сумма двух смежных углов параллелограмма равна 180 градусам.
Площадь трапецииПлощадь параллелограмма = (основание x высота) м 2
Противоположная сторона этого четырехугольника несколько отличается от другой только одной стороной. трапеции параллельны друг другу, а смежные стороны дополняют друг друга, а диагонали делят друг друга пополам в том же отношении.

Площадь воздушного змеяПлощадь трапеции = (1/2) h (AB+CD) м 2
Воздушный змей представляет собой особый четырехугольник, в котором каждая пара последовательных сторон конгруэнтна, но противоположные стороны не конгруэнтны. При этом наибольшая диагональ воздушного змея делит наименьшую диагональ пополам.
Площадь кайта = 1/2 x D 1 x D 2 M 2
, где,
D 1 = WHED,
D 1 = GUNGAL).
D 2 = короткая диагональ воздушного змея (JL)Решенный пример площади четырехугольника
Пример 1. Найдите площадь четырехугольника ABCD, когда его вершины (1, 2), (5) , 6), (4, −6) и (−5, 2).
Решение:
Пусть A(1, 2), B(5, 6), C(4, -6) и D(-5, 2) — вершины четырехугольника ABCD.

А(1, 2) = (х 1 , у 1 ), В(5, 6) = (х 2 , у 2 ), C(4, -6) = (x 3 , y 3 ), D(-5, 2) = (x 4 , y 4 )
Мы знаем, что,
Площадь четырехсторонней = (1/2) × [(x 1 Y 2 + x 2 Y 3 + x 3 Y 4 + x 4 Y 4 + x 4 ). — (x 2 Y 1 + x 3 Y 2 + x 4 Y 3 + x 1 Y 4 )]
. {[1(6) + 5(-6) + 4(2) + (-5)2] – {[5(2) + 4(6) + (-5)(-6) + 1(2) ]}
= (½). [(6-30 + 8-10)-(10 + 24 + 30 + 2)]
= (½) [-26-66]
= 92/2 (область никогда не бывает отрицательный)
= 46 единиц 2
Решение:
Дано, AB = 10 см, CD = 6 см, высота = 5 см
Согласно формулам,
Площадь трапеции = (1/2) h (AB+CD) 6)
Площадь трапеции = 40 см 2
Пример 3: Найдите площадь воздушного змея, самая длинная и самая короткая диагонали которого равны 20 см и 10 см соответственно.

Решение:
Длина наибольшей диагонали, D 1 = 20 см
Длина наименьшей диагонали, D 2 = 10 см
So,
Площадь змея = 1/2 x D 1 x D 2
Площадь змея = 1/2 x 1 x 20 = 100 см 2
Пример 4: Вычислите площадь параллелограмма , если основание и высота равны 10 м и 15 м соответственно.
Решение:
Дано, основание = 10 м, высота = 15 м
Площадь параллелограмма = основание x высота
Площадь параллелограмма = 10 x 15
Площадь параллелограмма = 150 м 2
другая диагональ имеет длину 12 м.
Решение:
Часто задаваемые вопросы о площади четырехугольникаПоскольку мы знаем, что
Площадь ромба = (1/2) x Диагональ 1 x Диагональ 2 ) x Диагональ 1 x Диагональ 2
Диагональ 2 = 20 м
Вопрос 1: Какова площадь четырехугольника?
Ответ:
Площадь четырехугольника – это область внутри границы четырехугольника.
 Это общее пространство, занимаемое четырехугольником в двумерной плоскости. Измеряется в квадратных единицах.
Это общее пространство, занимаемое четырехугольником в двумерной плоскости. Измеряется в квадратных единицах.Вопрос 2: Как найти площадь четырехугольника?
Ответ:
Площадь четырехугольника находится по формуле, приведенной ниже:
Площадь четырехугольника = (1/2) × [(x 1 y 2 + x 2 503 2 y 90 x 3 y 4 + x 4 y 1 ) – (x 2 y 1 + x 3 y 2 + x 4 y 3 + x 1 у 4 )]
где (х 1 , у 1 ), (х 2 , y 2 ), (x 3 , y 3 ) и (x 4 , y 4 ) — вершины четырехугольника.
Вопрос 3: Какие существуют типы четырехугольников?
Answer:
Different types of quadrilateral are:
- Square
- Rectangle
- Rhombus
- Kite
- Parallelogram
- Trapezium
Вопрос 4: Напишите употребление четырехугольников.

Ответ:
Площадь четырехугольника используется в области архитектуры, сельского хозяйства, дизайна и навигации, а также помогает найти расстояние между двумя точками. Требуется найти площадь зданий, парковых и других комплексов.
Вопрос 5: Как вычислить площадь четырехугольника, если даны одна из его диагоналей и оба перпендикуляра из вершин?
Ответ:
Если известны диагональ (d) и длина обоих перпендикуляров (h, H) из вершин, то площадь четырехугольника вычисляется по формуле:
Площадь четырехугольника = (½) × d × (h + H)
Вопрос 6: Какие существуют два основных типа четырехугольников?
Ответ:
Два основных типа четырехугольника:
- Правильный четырехугольник
- Неправильный четырехугольник
Вопрос 7: Как найти площадь четырехугольника по формуле Герона?
Ответ:
Чтобы найти площадь треугольника по формуле Герона, выполните следующие действия:
Шаг 1: Разделите четырехугольник на два треугольника, соединив его диагонали.

Шаг 2: Найдите площади обоих треугольников по формуле Герона.
Шаг 3: Добавьте обе области, чтобы получить окончательный ответ.
Связанные ресурсы
- Площадь прямоугольника
- Площадь квадратной
- Площадь параллелограммы
Расчет площади диагностики
693 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
GMAT Math Help » Проблемные вопросы » Геометрия » Четырехугольники » Другие четырехугольники » Вычисление площади четырехугольника
Какова площадь трапеции с высотой 7, основанием 5 и основанием 13?
Возможные ответы:
Правильный ответ:
Объяснение:
Сообщить об ошибке
Около каждой из следующих фигур можно описать окружность, кроме:
Возможные ответы:
Треугольник со сторонами 30, 40, 50.

- Сумма всех внутренних углов четырехугольника составляет 360 градусов.
- 3 9 Правильный шестиугольник
0002 Правильный пятиугольник
Вокруг каждой из фигур, указанных в других вариантах, может быть описана окружность.
Треугольник
Правильный ответ:
Вокруг каждой из фигур, приведенных в других вариантах, можно описать окружность.
Объяснение:
Вокруг любого треугольника можно описать окружность независимо от длины его сторон или углов, поэтому мы можем исключить два варианта выбора треугольника.
Около любого правильного многоугольника можно описать окружность, поэтому мы можем исключить и эти два варианта.
Правильный выбор состоит в том, что вокруг каждой фигуры можно описать окружность.
Сообщить об ошибке
Какова площадь четырехугольника на координатной плоскости с вершинами ?
Возможные ответы:
Правильный ответ:
Пояснение:
Как видно из этой схемы, это параллелограмм с основанием 8 и высотой 4:
Площадь этого параллелограмма равна произведению его основания на высоту:
Сообщить об ошибке
Какова площадь четырехугольника с вершинами на координатной плоскости?
Возможные ответы:
Правильный ответ:
Объяснение:
Как видно на этой диаграмме, это трапеция с основаниями 10 и 5 и высотой 8.

Задав следующую формулу, мы можем вычислить площадь трапеции:
Сообщить об ошибке
Примечание. Рисунок НЕ выполнен в масштабе
Какова площадь четырехугольника, показанного выше?
Возможные ответы:
Правильный ответ:
Объяснение:
Четырехугольник составляет два прямоугольных треугольника, и , поэтому мы находим площадь каждого и складываем площади. Сначала нам нужно найти и , так как площадь прямоугольного треугольника равна половине произведения длин его катетов.
By the Pythagorean Theorem:
Also by the Pythagorean Theorem:
The area of is .
Площадь .
Добавьте площади, чтобы получить площадь четырехугольника.

Сообщить об ошибке
Какова площадь четырехугольника на координатной плоскости с вершинами ?
Возможные ответы:
Правильный ответ:
Пояснение:
Образованный четырехугольник представляет собой трапецию с двумя горизонтальными основаниями. Одно основание соединяет (0,0) и (9,0) и, следовательно, имеет длину; другой соединяет (4,7) и (7,7) и имеет длину . Высота – это расстояние по вертикали между двумя основаниями, представляющее собой разницу координат: . Следовательно, площадь трапеции равна
Сообщить об ошибке
Какова площадь четырехугольника на координатной плоскости с вершинами .
Возможные ответы:
Правильный ответ:
Пояснение:
Четырехугольник представляет собой трапецию с горизонтальными основаниями; один соединяет и и имеет длину , а другой соединяет и и имеет длину .
 Высота – это расстояние по вертикали между основаниями, представляющее собой разность -координат; Это . Подставьте в формулу площади трапеции:
Высота – это расстояние по вертикали между основаниями, представляющее собой разность -координат; Это . Подставьте в формулу площади трапеции:Сообщить об ошибке
Какова площадь четырехугольника на координатной плоскости с вершинами ?
Возможные ответы:
Правильный ответ:
Объяснение:
Четырехугольник представляет собой параллелограмм с двумя вертикальными основаниями, каждое из которых имеет длину . Его высота — это расстояние между основаниями, представляющее собой разницу —координат: . Площадь параллелограмма равна произведению его основания на высоту:
Сообщить об ошибке
Укажите площадь приведенного выше параллелограмма, если .
Возможные ответы:
Правильный ответ:
Объяснение:
Умножьте высоту на основание, чтобы получить площадь.


 Задачи на исследование функций (вариант 5)
Задачи на исследование функций (вариант 5)
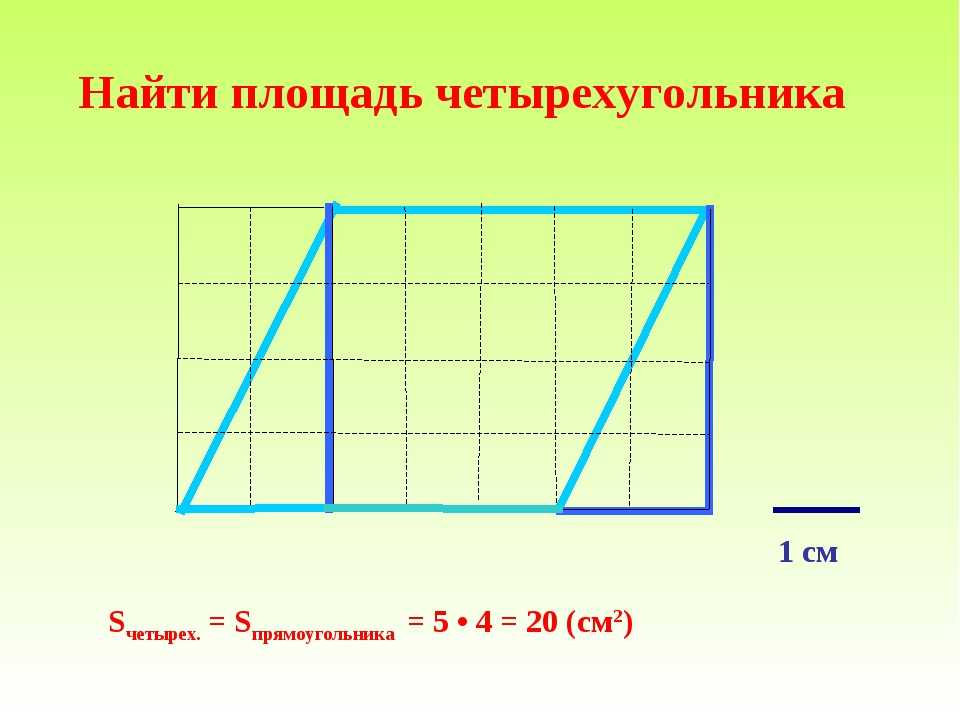 2. Отсюда найдём сторону: a = radS. Итак, нам удалось выразить сторону через площадь. Подставим полученное выражение в конечную формулу из предыдущей части. Формула примет вид: d = rad2*a = rad2*radS .
2. Отсюда найдём сторону: a = radS. Итак, нам удалось выразить сторону через площадь. Подставим полученное выражение в конечную формулу из предыдущей части. Формула примет вид: d = rad2*a = rad2*radS .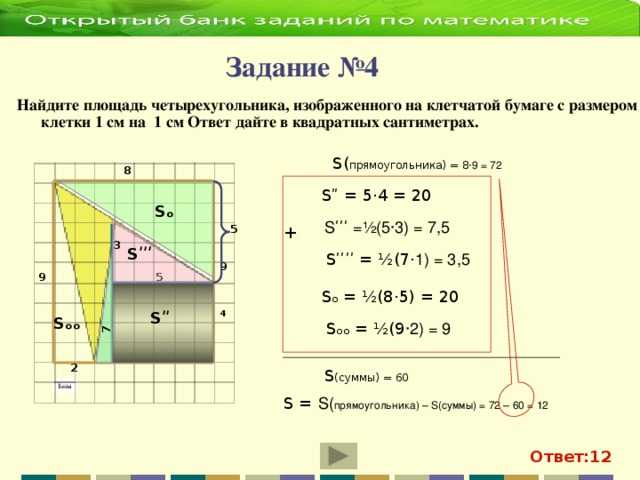 Радиус описанной окружности будем обозначать латинской буквой R, радиус вписанной окружности будем обозначать латинской буквой r.
Радиус описанной окружности будем обозначать латинской буквой R, радиус вписанной окружности будем обозначать латинской буквой r.
 Решение: а=корень из 49=7. Ответ: 7 .
Решение: а=корень из 49=7. Ответ: 7 .

 Потом уже находим площадь квадрата описанного около окружности с заданным радиусом по формуле S=а в квадрате . Решение:
Потом уже находим площадь квадрата описанного около окружности с заданным радиусом по формуле S=а в квадрате . Решение: Величина площади выражается числом заключающихся в нее квадратных единиц.
Величина площади выражается числом заключающихся в нее квадратных единиц.
 2)\).
2)\). .
.

 2\ \frac{θ}{2}}\).
2\ \frac{θ}{2}}\).




 Однако четырехугольник имеет четыре прямые стороны и четыре угла.
Однако четырехугольник имеет четыре прямые стороны и четыре угла. Четырехугольник можно определить как замкнутую двумерную фигуру, имеющую четыре стороны или ребра, а также четыре угла или вершины. При измерении форма объектов классифицируется по количеству сторон четырехугольника. Четырехугольники делятся на две категории: правильные четырехугольники и неправильные четырехугольники. Правильный четырехугольник – это четырехугольник, у которого все стороны одинаковой длины. Неправильный четырехугольник – это четырехугольник, у которого все стороны не равны.
Четырехугольник можно определить как замкнутую двумерную фигуру, имеющую четыре стороны или ребра, а также четыре угла или вершины. При измерении форма объектов классифицируется по количеству сторон четырехугольника. Четырехугольники делятся на две категории: правильные четырехугольники и неправильные четырехугольники. Правильный четырехугольник – это четырехугольник, у которого все стороны одинаковой длины. Неправильный четырехугольник – это четырехугольник, у которого все стороны не равны. Различные типы четырехугольников:
Различные типы четырехугольников: ABCD можно разделить на два треугольника ΔABD и ΔBCD диагональю BD. Для вычисления площади четырехугольника ABCD мы вычисляем площади отдельных треугольников и соответственно складываем их. Но для вычисления площади треугольника необходимо знать его высоту. Предположим, что высоты треугольников ABD и BCD равны h 1 и ч 2 соответственно.
ABCD можно разделить на два треугольника ΔABD и ΔBCD диагональю BD. Для вычисления площади четырехугольника ABCD мы вычисляем площади отдельных треугольников и соответственно складываем их. Но для вычисления площади треугольника необходимо знать его высоту. Предположим, что высоты треугольников ABD и BCD равны h 1 и ч 2 соответственно.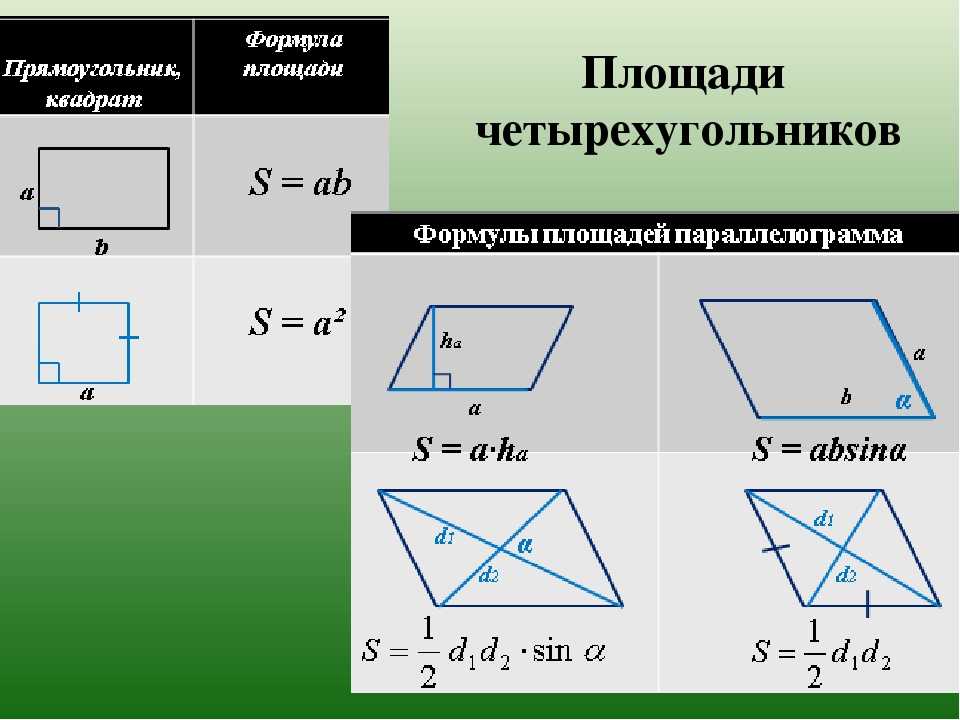 Предположим, что A(x 1 , y 1 ), B(x 2 , y 2 ), C(x 3 , y 3 ) и D(1 5 2 4 9 0, 4 4 ) — вершины четырехугольника ABCD.
Предположим, что A(x 1 , y 1 ), B(x 2 , y 2 ), C(x 3 , y 3 ) и D(1 5 2 4 9 0, 4 4 ) — вершины четырехугольника ABCD.
 Наконец, обе площади треугольников складываются, чтобы найти окончательную площадь четырехугольника.
Наконец, обе площади треугольников складываются, чтобы найти окончательную площадь четырехугольника.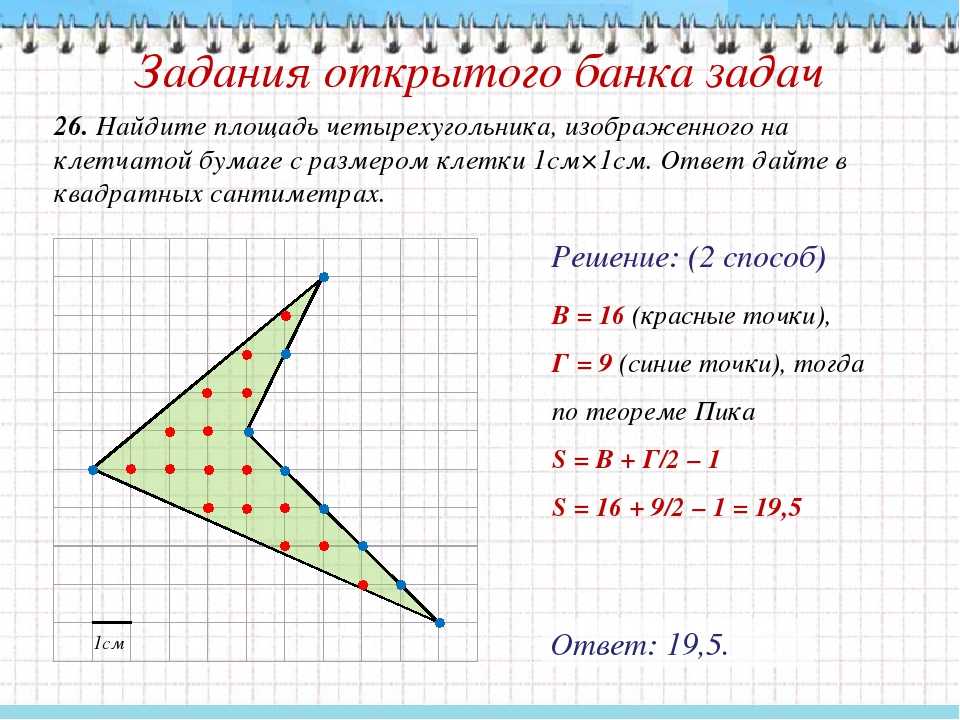
 Это общее пространство, занимаемое четырехугольником в двумерной плоскости. Измеряется в квадратных единицах.
Это общее пространство, занимаемое четырехугольником в двумерной плоскости. Измеряется в квадратных единицах.



 Высота – это расстояние по вертикали между основаниями, представляющее собой разность -координат; Это . Подставьте в формулу площади трапеции:
Высота – это расстояние по вертикали между основаниями, представляющее собой разность -координат; Это . Подставьте в формулу площади трапеции: