Площадь и объем куба: Calculat.org — онлайн калькуляторы, формулы, расчеты

формула через ребро и диагональ грани

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение объема куба: формула и задачи

В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.

• Формула вычисления объема куба
• Примеры задач

Формула вычисления объема куба

1. Через длину ребра

Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.

V = a ⋅ a ⋅ a = a³

2. Через длину диагонали грани

Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√2.

Следовательно, вычислить объем куба можно так:

Примеры задач

Задание 1
Вычислите объем куба, если его ребро равняется 5 см.

Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см³.

Задание 2
Известно, что объем куба равен 512 см³. Найдите длину его ребра.

Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:

Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.

Решение:
Применим формулу, в которой используется диагональ грани:

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

формула через ребро и диагональ грани

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel. ru Математика Геометрия Нахождение площади поверхности куба: формула и задачи

В данной публикации мы рассмотрим, как можно найти площадь поверхности куба и разберем примеры решения задач для закрепления материала.

• Формула вычисления площади куба
  • 1. Через длину ребра
  • 2. Через длину диагонали грани
• Примеры задач

Формула вычисления площади куба

1. Через длину ребра

Площадь (S) поверхности куба равна произведению числа 6 на длину его ребра в квадрате.

S = 6 ⋅ a

2

Данная формула получена следующим образом:

• Куб – это правильная геометрическая фигура, все грани которого являются равными квадратами с длиной стороны a (одновременно является ребром куба).
• Площадь каждой грани считается так: S = a ⋅ a = a².
• Всего у куба 6 граней, а значит, площадь его поверхности равняется шести площадям одной грани: S = 6 ⋅ a².

2. Через длину диагонали грани

Сторона любой грани куба (ребро) может быть рассчитана через длину ее диагонали по формуле: a=d/√2.

Это значит, что вычислить площадь поверхности фигуры можно так:

S = 6 ⋅ (d/√2)²

Примеры задач

Задание 1
Найдите площадь поверхности куба, если длина его ребра составляет 12 см.

Решение:
Используем первую формулу выше и получаем:
S = 6 ⋅ (12 см)² = 864 см².

Задание 2
Площадь поверхности куба равняется 294 см². Вычислите длину его ребра.

Решение:

Примем ребро куба за a. Из формулы расчета площади следует:

Задание 3
Вычислите площадь поверхности куба, если диагональ его грани равняется 5 см.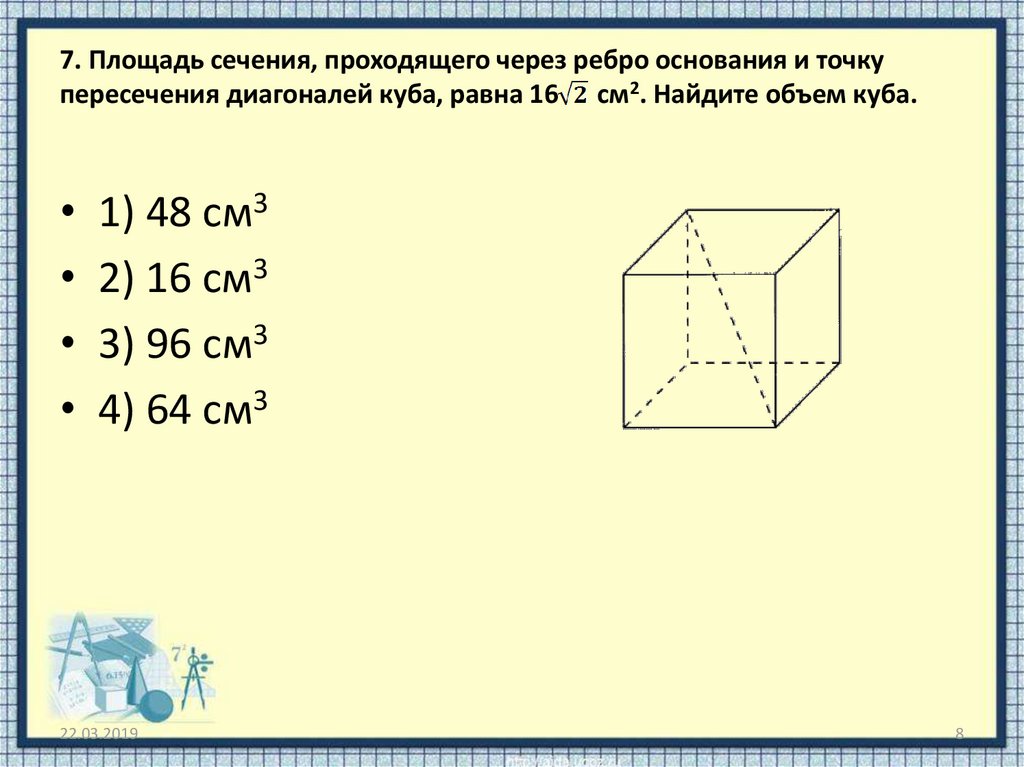

Решение:
Воспользуемся формулой, в которой задействована длина диагонали:
S = 6 ⋅ (5 см : √2)² = 75 см².

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Нахождение объема и площади поверхности куба (видео и практика)

TranscriptPractice

Привет! Добро пожаловать в это видео об объеме и площади поверхности куба!

Мы видим эту форму повсюду, чаще всего с кубиками и кубиками. А еще есть красочная головоломка, известная как кубик Рубика, которая представляет собой куб, который, кажется, состоит из более мелких кубиков.

В математике куб — ​​это особый вид прямоугольной призмы. В большинстве прямоугольных призм длина, ширина и высота формы могут быть разными. Но в кубе они все одинаковые. То есть все ребра имеют одинаковую длину.

Объем куба

Куб имеет два важных измерения. Первый – это объем. Объем куба или любого другого трехмерного объекта является мерой того, сколько места он занимает. Мы измеряем это в кубических единицах, таких как кубические дюймы или кубические сантиметры. Это легко представить с помощью куба. Только представьте, что у нас есть набор маленьких кубиков высотой один сантиметр, шириной один сантиметр и длиной один сантиметр. Каждый из этих кубов равен одному кубическому сантиметру. Это наша единица измерения.

Теперь давайте соберем что-нибудь из этих маленьких кубиков. Давайте построим что-то похожее на кубик Рубика.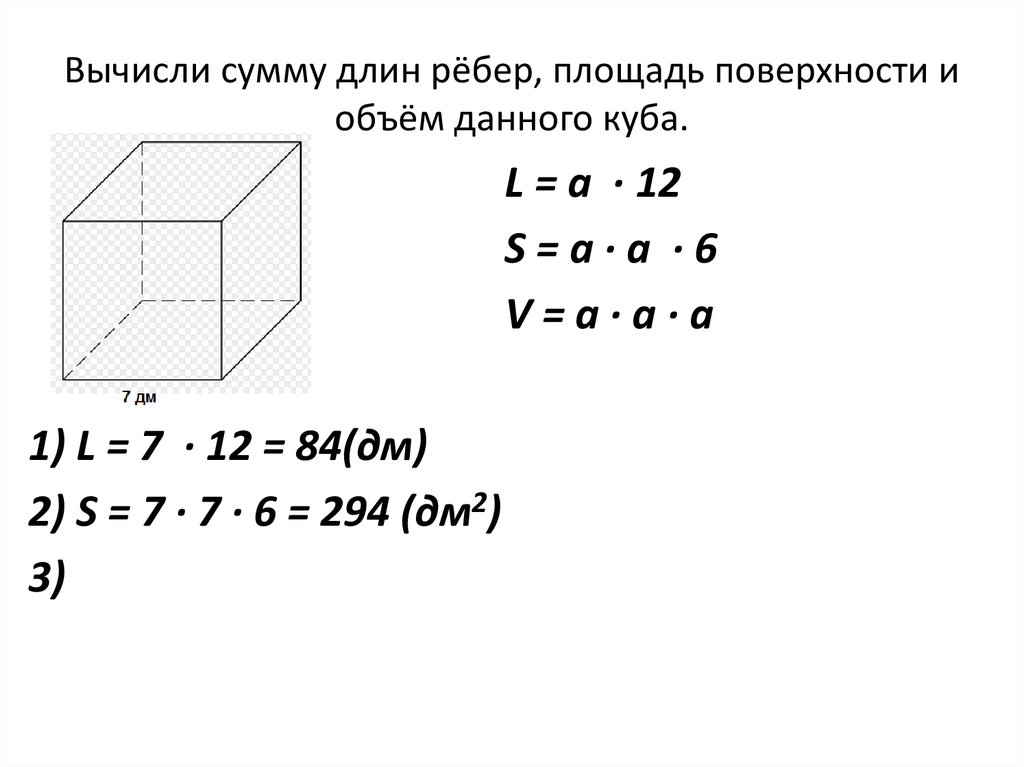 Начнем с верхнего уровня. Нам нужно сделать сетку из кубиков три на три. Каждый куб имеет один сантиметр в высоту и один сантиметр в ширину. Как только мы закончим с этим слоем, мы увидим, что мы использовали девять кубов. Далее строим средний уровень, используя еще девять кубиков. Все вместе 9 и 9 составляют 18 кубических сантиметров. Наконец, мы строим нижний уровень, снова используя еще девять кубиков. Все вместе у нас есть 27 кубических сантиметров. 93\), что имеет смысл, так как нам нужно было использовать 27 маленьких кубиков, чтобы построить наш куб. Помните, что очень важно указать единицы измерения при ответе.

Площадь поверхности куба

Другой основной мерой куба является площадь поверхности. Это измерение площади, так что оно в двух измерениях. Представьте, что мы делаем бумажную оболочку для куба, который построили ранее. Сколько бумаги нам понадобится в квадратных сантиметрах? Если мы посмотрим на куб, который мы построили ранее, и просто посмотрим на одну его сторону, мы увидим кучу этих квадратов размером в один сантиметр. Если мы посчитаем их, то увидим, что на самом деле их девять. Итак, одна сторона состоит из девяти квадратных сантиметров. 93\).

Скрыть Ответ

Вопрос № 5:

 
Если не учитывать единицы измерения, какова разница между объемом и площадью поверхности куба со стороной 7?

49

23

17

64

Показать ответ

Ответ:

Правильный ответ для томов и для s, мы должны решить эту задачу: 49. и площадь поверхности, а затем вычтите два значения. Сначала найдите объем куба. 92=6(49)=294\)

Наконец, вычтем из объема площадь поверхности.
\(343-294=49\)

Скрыть ответ

 

Вернуться к видео о геометрии

Объем куба.

28 января, 2023

Факт проверено

Полом Маццола

Объем куба

объем куба  – это объем пространства, который куб занимает в трех измерениях. Объем куба всегда измеряется в кубических единицах, полученных из линейной единицы, заданной или используемой для измерения длины стороны.

Вы можете найти объем любого куба с одним заданным измерением, используя формулу объема куба :

Что такое куб?

Куб  представляет собой трехмерное тело с шестью конгруэнтными квадратными гранями, встречающимися под прямым углом, восемью вершинами и двенадцатью сторонами одинаковой длины. Куб является одним из пяти Платоновых тел и также называется шестигранником.

Каковы размеры куба?

Куб — это трехмерный объект, поэтому куб имеет три измерения:

• Длина – обычно понимается как большее из «плоских» размеров.

• Ширина – обычно понимается как более короткий из «плоских» размеров.

• Высота или Глубина – Измерение, которое привносит форму в наш трехмерный мир

Обратите внимание, что у нас есть два способа описать третье измерение: возвышается перед вами, как высокое здание.

Глубина — используйте этот термин, если объект падает под вами, как дыра в земле.

Разница между высотой и глубиной

Нам нужна информация хотя бы об одном из этих трех измерений, чтобы измерить объем куба.

Формула объема куба

Формула объема  это объем, равный длине, умноженной на ширину, умноженной на высоту.

Формула объема

Это уравнение объема не работает для каждого твердого тела, но оно работает для кубов, прямоугольных призм и параллелепипедов.

Поскольку все три значения ( l , w и h ) одинаковы в кубе, простейший объем формулы куба:

В этом объеме уравнения куба s  = длина любого ребра .

Объем формулы куба

Объем всегда измеряется в кубических единицах  на основе предоставленных вам линейных единиц. Если вам говорят, что сторона куба имеет размеры 90 226  3 метра 90 227 , объем измеряется в кубических метрах или м3{м}^{3}м3 (метры в кубе).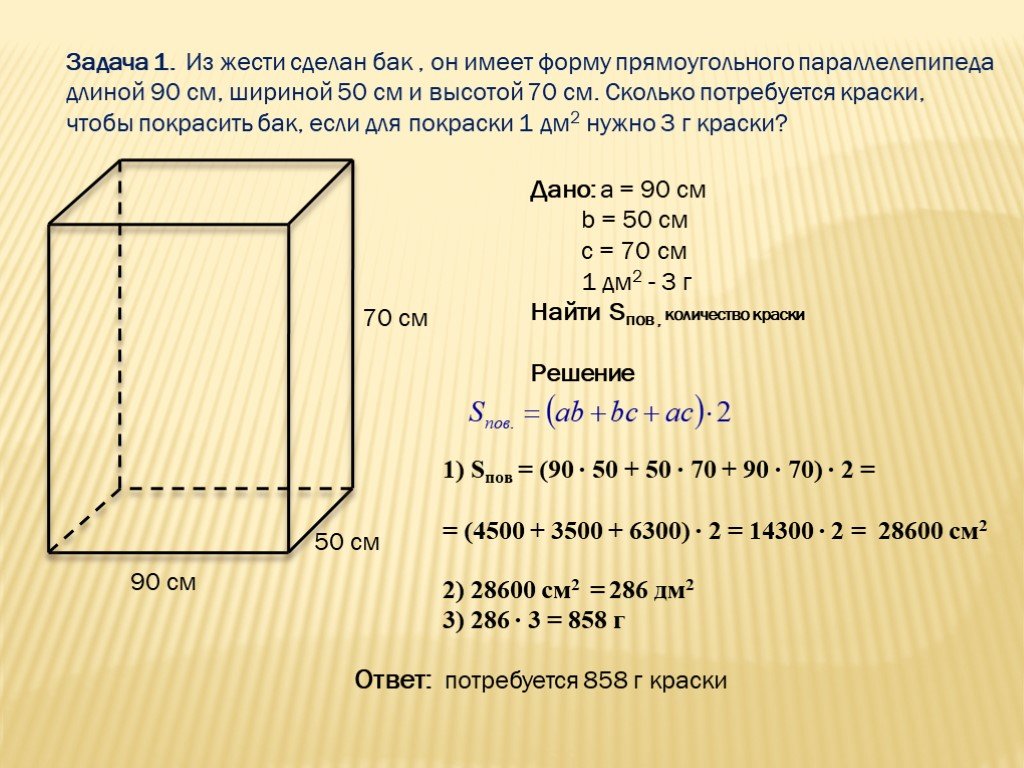

Как найти объем куба

Чтобы найти объем куба, достаточно знать длину любого ребра.

Если вам известна длина одной стороны, вы можете найти объем куба, подставив его в одну из формул объема куба:

Измерение пространства, занимаемого кубом, зависит от знания длины любого одно ребро, потому что все длины сторон куба равны по длине.

Как найти длину, ширину и высоту по объему

Что, если вам дан объем куба и вас попросят найти его размеры?

Если вам дан объем куба и вас попросят найти длину ребра, все, что вам нужно сделать, это извлечь кубический корень из объема:

Ваш ответ больше не будет в кубических единицах; это будет в линейных единицах.

Как найти длину, ширину и высоту по формуле объема

Что если у нас есть куб, и нам говорят, что его объем равен 729 кубических метров . Чтобы найти длину ребра куба:

Как рассчитать объем, используя площадь

Вот еще одна задача. Что если вам скажут площадь одной грани куба? Можете ли вы использовать эту информацию, чтобы найти объем?

Да, площадь одного лица равна произведению длины лица на ширину.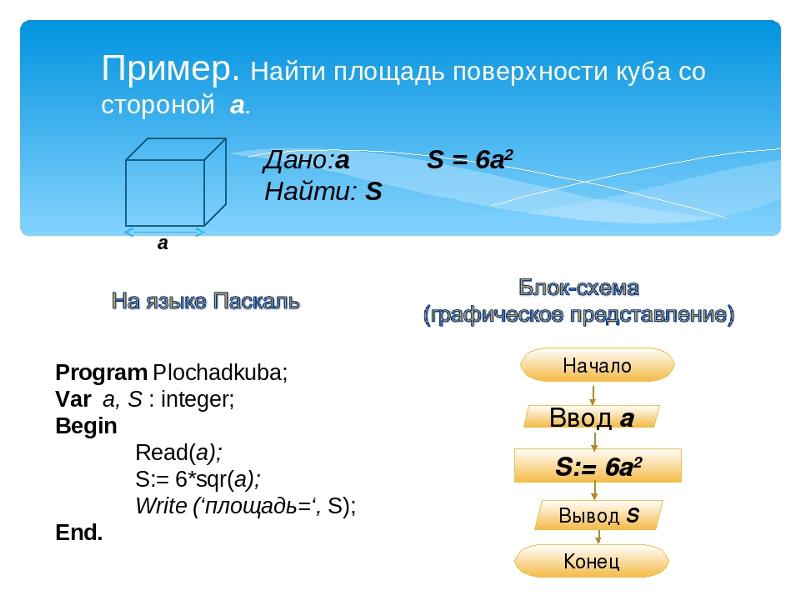 Как только вы найдете ширину или длину, вы можете применить формулу объема:

1. Найдите квадратный корень из заданного измерения площади; это даст вам длину любой стороны, с 9{3}V=s3, чтобы найти площадь.

Как вычислить объем, используя площадь

Как вычислить площадь поверхности куба, используя объем

Если вам известен объем куба, вы можете преобразовать его в длину одной стороны. Затем вы можете использовать длину стороны для расчета общей площади поверхности.

Используйте длину ребра, чтобы вычислить площадь поверхности одной стороны, затем умножьте эту площадь на  6 . Это дает вам общую площадь поверхности куба с использованием объема.

Что если вам сообщат общую площадь поверхности  всего куба? Сможете ли вы найти объем?

Да, общая площадь поверхности включает площади всех шести конгруэнтных граней. Найдите площадь одной грани, а затем выполните действия, описанные выше, чтобы найти объем:

1. Разделите заданную общую площадь поверхности на шесть, чтобы получить площадь одной грани

2. Найдите квадратный корень из площади одной грани, чтобы получить длину любой стороны, 9029{3}V=s3

Как рассчитать объем по общей площади поверхности

Примеры объема куба

Если у вас есть трехмерное тело с шестью гранями, а стороны помечены  4′ ,  6′ и 8′ .

No related posts.