«Какой шанс выиграть в лотерею 4 из 20?» — Яндекс Кью
Популярное
Сообщества
МатематикаЛотереи+2
Саша Голубничий
·
20,6 K
ОтветитьУточнитьДостоверно
Вадим Ольшевский
Математика
74
Профессор математики университета Коннектикута. Член редколлегии ряда математических… · 25 июн 2021
Вначале считается чсило сочетаний, количество всевозможных способов выбрать 4 знака из 20. Вот формула:
Вероятность выигрыша = 1/4845. Одна правильная комбинация знаков из 4845 возможных.
2 эксперта согласны
20,7 K
Комментировать ответ…Комментировать…
Илья Евсеев
27
Любознательный студент, имеющий интерес ко всему) · 28 июн 2021
На самом деле это простая математическая задачка, впрочем Вадим вам уже её пояснил, но, если вы интересуетесь реальной возможностью выигрыша, то математика здесь уже ни к чему.
..
Ведь основная идея организаторов лотерей это заработок для самих себя. Поэтому говорить о реальном выигрыше вряд ли стоит.
Комментировать ответ…Комментировать…
Даша Клиценко
6
бровист · 26 июн 2021
Никакой. У меня есть знакомый и он говорит, что там устроено все как у игровых автоматов. Компьютер не даст никогда выиграть.
Можно и самим глянуть на статистику выигрышей. Всегда ЛОТО в жирном +.
Сергей С.
28 июня 2021
А выигрывают всегда родственники или хорошие знакомые. Короче, разогнать бы их, да некому. Видно отстёгивают… Читать дальше
Комментировать ответ…Комментировать…
Первый
Василий Нарыкин
1
4 июл 2021
Выиграть можно, если Вы организатор лотереи; если Вам выпал Джек- пот по теории вероятности, при этом Вы организатор лотереи; если розыгрыш ведут с помощью ручного барабана и детишек.
которые достают номера в прямом эфире, но последнее уже никто не допустит. Поэтому оставь надежду всяк сюда входящий…
Комментировать ответ…Комментировать…
Первый
александр иванович
2
4 июл 2021
Не каких шансов, это точно!!! На новый год купил 120 билетов в надежде на выигрыш, вернул 4 тысячи из 12 вложенных, так что и не каждый второй билет выигрывает.
Комментировать ответ…Комментировать…
Первый
Илья Куликов
-25
Человек · 26 июн 2021
Шанс есть всегда, это ж лотерея, тут всегда 50 на 50, повезет — выиграете. Мне повезло, я выигрываю частно, как раз в такие лотереи. И в 4 из 20 в том числе выигрывал.
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
Таблицы вероятности или вероятность выигрыша в лотереях
Вероятность или шанс угадать комбинацию, развёрнутую ставку, группу чисел —
в зависимости от количества выбранных номеров, для лотерей 5 из 36, 6 из 45, 7 из 49, 6 из 49, 4 из 20, Рапидо —
смотрим по этой ссылке
5 из 36, 6 из 45, 7 из 49, 6 из 36, 4 из 20, 12 из 24, Рапидо.
В игре одна простая комбинация.
В лотереях 5 из 36 и Рапидо самое малое количество комбинаций — практически не видно на фоне остальных. Если учитывать призовой фонд, то в лотереях Рапидо, 4 из 20, — он самый большой (67% призового фонда), следовательно, выигрыши в низших категория будут чаще, если это можно назвать «выигрышем»… — на дистанции «слив» всё равно обеспечен, если, конечно, не «словится» суперприз! Тем не менее, чем больше возврат при длительной игре, тем больше можно ставить комбинаций, тем вероятней суперприз. По вероятности выиграть суперприз, лотерея 5 из 36 считается лучшей из всех (без дополнительного), — сейчас «приз», который может достигать десятков миллионов. Далее по популярности у игроков следует лотерея 6 из 45, в которой шансы 1 на 8 миллионов комбинаций. Лотерея 6 из 45 отличается ещё от остальных неплохой выплатой за приз второй категории, по такому параметру (вероятность-выплата) При выборе лотереи желательно учитывать потенциальную выплату за приз второй категории, угадать который более реально.
Подробные правила игры, видео, архивы тиражей, стоимость ставок —
на сайте лотерей stoloto.ru
5 из 36
Тиражи проходят ежедневно. Розыгрыши проходят в лотерейном центре «Столото».
Выигрышная комбинация определяется при помощи ГСЧ и состоит из 5 номеров для поля 1 и одного номера для поля 2.
Трансляция розыгрышей проводится на сайте stoloto.ru
6 из 45
Тиражи проводятся ежедневно. Розыгрыши проходят в лотерейном центре «Столото».
Прямая трансляция розыгрышей проводится на сайте stoloto.
ru7 из 49
Тиражи проводятся ежедневно.
Розыгрыши проходят в лотерейном центре «Столото» .
Выигрышная комбинация определяется при помощи лототрона и состоит из 7 номеров.
Прямая трансляция розыгрышей проводится на сайте stoloto.ru
6 из 36
Розыгрыши проводятся еженедельно после подсчета размера призового фонда.
Трансляции розыгрышей проходят по субботам, на канале НТВ в программе «Зарядись удачей»!
Выигрышная комбинация определяется при помощи лототрона.
Рапидо
Тиражи проходят ежедневно. Выигрышная комбинация определяется в течение нескольких секунд.
Если розыгрыш пересекается по времени с «Гослото «4 из 20», то тираж «Рапидо» не проводится.
Трансляция розыгрыша проводится на сайте stoloto.ru
12 из 24
Тиражи проходят ежедневно.
Если розыгрыш пересекается по времени с
«Гослото «5 из 36», то тираж «12/24» не проводится. Комбинация тиража состоит из 12 неповторяющихся чисел.
Для ее определения используется «Генератор случайных чисел».
Трансляция розыгрыша проводится на сайте stoloto.ru
4 из 20 x2
Тиражи проводятся каждый день. Розыгрыши проходят в лотерейном центре «Столото».
Выигрышная комбинация определяется при помощи лототрона и состоит из 4 чисел в диапазоне от 1 до 20 для первого поля
и 4 чисел в диапазоне от 1 до 20 для второго поля. Прямая трансляция розыгрышей проводится на сайте stoloto.ru
калькулятор вероятностей (android версия)
комбинаторика — Распределение и количество уникальных комбинаций
Задавать вопрос
спросил
Изменено 2 года, 5 месяцев назад
Просмотрено 2к раз
$\begingroup$
Я биолог, и мои математические способности немного заржавели, поэтому буду признателен за любую помощь.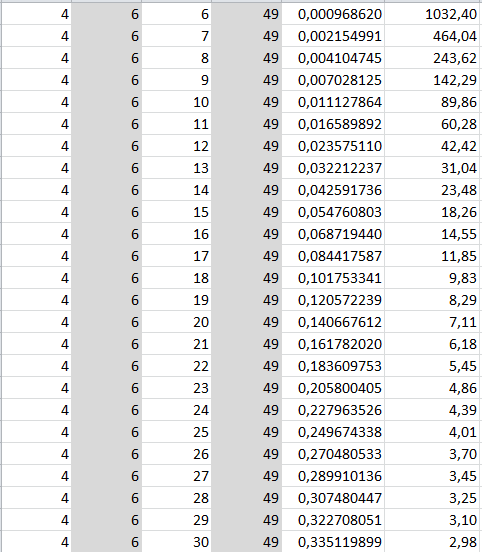
Я хотел бы знать, как рассчитать, сколько комбинаций существует при любом заданном количестве комбинаций и сколько из них уникальны.
Мне очень хотелось бы знать, как вычислить это для любого количества комбинаций (не только 0-9, а например 20 или 30) и чисел в комбинациях (1-1 или 1-1-1 или 1-1-1 ). В этом сценарии 1-2-2 и 2-1-1 и 2-2-1 идентичны (= 1-2), поэтому номер позиции в цифре не важен, и учитываются только неизбыточные числа.
пример данных, сделанных перебором в R для чисел 0-9:
- 1 число в комбинации (0,1,2,3,4,5,6,7,8,9):
- 10 возможностей и 10 уникальных возможностей
2 числа в комбинации (0-1,0-2,0-3,0-4…):
- 100 вариантов (10 комбинаций только по 1 цифре и 90 комбинаций из 2 разных цифр)
- 55 уникальных (10 комбинаций из 1 и 45 из 2 (потому что 1-2 и 2-1 одинаковы)
3 числа в комбинации (0-0-1,0-0-2,0-0-3…):
- 1000 вариантов (10+270+720) и 175 уникальных (10+45+ 120)
4 номера в комбинации (0-0-0-1,0-0-0-2.
..):
- 10000 вариантов (10+630+4320+5040) и 385 уникальных (10+45+120) +210)
Но какой будет общая формула для расчета этих чисел (т.е. для 4-значных комбинаций о том, как рассчитать, что это было 10 630 4320 5040 для комбинаций и 10 45 120 210 для уникальных комбинаций с 10 номерами на цифру, но что такое поисковое пространство для 30 цифр в позиции цифры и 16 цифр в каждой комбинации?
- комбинаторика
$\endgroup$
$\begingroup$
В первом случае сумма проще компонентов; во втором компоненты легче суммы.
Предположим, вы выбираете $m$ раз из $n$ возможных цифр, и вас интересуют случаи, когда вы получаете $k$ различных цифр.
В первом случае упорядоченных цифр, возможно с дубликатами:
- 94=10000$
Есть ${n \выберите k} k! \lbrace\textstyle{m\atop k}\rbrace$ возможных вариантов с $k$ различными цифрами, где ${n \choose k}$ — биномиальный коэффициент, а $\lbrace\textstyle{m\atop k}\rbrace$ является числом Стирлинга второго рода: например, с $n=10$ и $m=4$ и $k=2$ у вас есть $45 \times 2\times 7=630$
Во втором случае неупорядоченных дедуплицированных цифр:
- Существует $\displaystyle {n \choose k}$ возможных вариантов с $k$ различными цифрами (хотя вам нужно $k \le m$: например, с $n =10$ и $m=4$ и $k=2$ у вас есть $45$ 9n-1$
$\endgroup$
2
$\begingroup$
Предположим, что цифр $d$, и мы рассматриваем комбинации длины $n\in\{1,\dots,d\}$.
k$.
Затем вы переходите к комбинации, которая отличается двумя аспектами: во-первых, повторение запрещено, а во-вторых, порядок не имеет значения. Их количество равно ${n \choose k} =\frac{n!}{k!(n-k)!}.$ Интуиция несколько сложнее. Во-первых, предположим, что порядок имеет значение, но повторения не допускаются (это перестановки). Затем вы можете выбрать первое число $n$ способами, следующее $n-1$ способами (без повторения!) и т. д., последний $k$-й элемент $n-k+1$ способами. Итак, у вас есть $n\cdot(n-1)\ldots(n-k+1)=\frac{n!}{(n-k)!} $ способов.
Теперь вы хотите, чтобы порядок не имел значения. Для каждой $k$-длинной перестановки (например, 123) у вас есть $k!$ возможных версий (например, 123 132 231 213 312 321). Поэтому вам нужно разделить последний результат на $k!$, чтобы получить то, что вам нужно. Всего у вас есть $n \выберите k$ возможностей.
То, что вы называете «уникальной комбинацией», на самом деле является суммой всех комбинаций (в математическом смысле) длины $\leq k$.
k{n \выбрать i}$$
В R наверняка есть команда для $n \choose k$, вам просто нужно суммировать ее.
$\endgroup$
Калькулятор комбинаций (nCr, nPr)
Количество элементов (n)
Элементы для выбора (r)
Порядок важен:
Порядок не имеет значения
Комбинации
Без повторений
Идентичные предметы
Все предметы уникальны
|
Combinations Formulas
nCr formula
| Number of combinations without repetitions | = n C r | |||
|
Комбинации с
повторениями формулы
| Количество комбинаций с повторениями |
|
Permutations Formulas
nPr formula
| Number of permutations without repetitions | = n P r | |||
|
Комбинация — это выбор r элементов из набора из n элементов, порядок выбора которых не важен.
Примеры комбинаций
Комбинации без повторений
Допустим, мы хотим выбрать 2 шара из мешка с 3 шарами красного (R), зеленого (G) и фиолетового (P) цветов. 123
Сколько уникальных комбинаций у нас будет, если мы не сможем повторить шары?
3 разных способа. Наши варианты: RG, RP и GP.
121323
Мы можем подсчитать количество комбинаций без повторений, используя формулу nCr, где n равно 3, а r равно 2.
| # комбинаций = | n! | = | 3! | = | 6 | = 3 |
| (n-r)!r! | 2!*1! | 2 |
Примеры такого типа комбинаций мы можем увидеть при подборе команд на спортивную игру или на задание. Мы не можем выбрать члена команды более одного раза (поэтому у нас не может быть команды с Дэнни, Дэнни и мной), и нам все равно, кто будет выбран первым в команду (поэтому, если я в команде с Бобом и Томом для меня это то же самое, что быть в команде с Томом и Бобом).
Комбинации с повторениями
Допустим, нам нужно выбрать 2 шара из мешка с 3 шарами красного (R), зеленого (G) и фиолетового (P) цветов 123
Если каждый раз, когда мы выбираем мяч, мы кладем его обратно в мешок, сколько уникальных комбинаций мы получим?
6 разных способов. Наши варианты: RR, RG, RP, GG, GP и PP.
111213222333
Количество комбинаций с повторениями можно подсчитать математически, используя формулу комбинаций с повторениями, где n = 3 и r = 2.
| # комбинаций = | (n+r-1)! | = | 4! | = | 24 | = 6 |
| (n-1)!r! | (3-1)!2! | 4 |
Примеры такого типа комбинаций можно увидеть при покупке мороженого в магазине мороженого, поскольку мы можем выбирать вкусы более одного раза (я мог бы получить две, три или даже четыре шарика шоколадного мороженого, если бы я хотел), и мне все равно, какая ложка будет сверху (поэтому шоколад сверху и ваниль снизу для меня то же самое, что ваниль сверху с шоколадной основой).
Калькулятор перестановок
Что такое перестановка?
Перестановка — это выбор r элементов из набора из n элементов, где важен порядок, в котором мы выбираем наши элементы.
Примеры перестановок
Перестановки без повторений
Допустим, мы хотим выбрать 2 шара из мешка с 3 шарами красного (R), зеленого (G) и фиолетового (P) цветов 123
Сколько уникальных перестановок получится у нас есть, если мы не можем повторить шары?
6 разных способов. Наши варианты: RG, GR, RP, PR, GP и PG.
122113312332
Мы можем показать это математически, используя формулу перестановок с n = 3 и r = 2
| # перестановок = | n! | = | 3! | = | 3! | = 6 |
| (н-р)! | (3-2)! | 1! |
Мы можем видеть примеры этого типа в реальной жизни в результатах беговых забегов (при условии, что два человека не могут занимать одно и то же место), поскольку нам явно небезразлично, придем ли мы первым, а наш конкурент — вторым или если это наоборот.
Перестановки с повторениями
Допустим, мы хотим выбрать 2 шара из мешка с 3 шарами красного (R), зеленого (G) и фиолетового (P) цветов. 123
Если каждый раз, когда мы выбираем мяч, мы кладем его обратно в мешок, сколько уникальных перестановок мы получим?
9 разных способов. Наши варианты: RR, RG, GR, RP, PR, GG, GP, PG и PP.
111221133122233233
Мы можем показать это математически, используя формулу перестановок с повторениями с n = 3 и r = 2,
# permutations = n r = 3 2 = 9
Мы можем видеть это в реальной жизни по количеству кодов на сейфе — мы можем повторять числа, если хотим (и иметь пароль, например, 1111) и мы заботимся о порядке чисел (поэтому, если 1234 откроет сейф, 4321 не откроет).
Объяснение формул комбинаций и перестановок
Сколько у нас есть способов упорядочить n шаров?
Если у нас есть 3 шара красного (R), зеленого (G) и фиолетового (P) цвета, то есть 6 различных способов.
У нас есть 3 варианта для первого цвета, затем 2 варианта для второго цвета и один вариант для последнего цвета. Поэтому у нас есть 3*2*1 разных вариантов или 3! На 4 мяча у нас 4! доступны различные перестановки. На 5 мячей у нас 5! разные варианты и т.д. Для n шаров имеем n! параметры.
Объяснение формулы перестановок
Сколько существует перестановок для выбора 3 шаров из 5 без повторений? Мы можем выбрать любой из 5 шаров в первом выборе, любой из 4 оставшихся во втором выборе и любой из 3 оставшихся в третьем выборе. Это 5 * 4 * 3, что можно записать как 5!/2! (что равно n! / (n — r)! с n=5, r=3).
Существует также альтернативный способ выбрать набор из 3 шаров. Допустим, мы хотели выбрать 123 шара. Затем мы могли бы также выбрать оставшиеся 2 шара. Это дало бы нам возможные перестановки 12345 и 12354. Мы видим, что их 2! (то есть 2) различные способы выбора 5 шаров, если мы хотим, чтобы 123 были первыми 3 вариантами выбора. Следовательно, мы можем получить количество выборов 3 шаров из 5 шаров, разделив 5! (общее количество выборов) на 2! (перестановки в списке из 5! вариантов, которые начинаются с 123 или любых других 3 шаров, которые вы можете выбрать).
. Сколько 5 перестановок шара он начнет? Ну 2! потому что для этой подборки у вас осталось два шара и их можно разложить по 2! разными способами (как мы видели выше). Следовательно, чтобы получить количество перестановок 3-х шаров, выбранных из 5-ти шаров, нужно разделить 5! на 2!.
Объяснение формулы комбинаций
Каждая комбинация из 3 шаров может представлять 3! разные перестановки. Следовательно, мы можем вывести формулу комбинаций из формулы перестановок, разделив количество перестановок (5!/2!) на 3! чтобы получить 5! / (2! * 3!) = 10 разных способов. Это обобщается и на другие комбинации и дает нам формулу #combinations = n! / ((n — r)! * r!)
Объяснение перестановок с помощью формулы повторений
Если мы снова выбрали 3 из 5 шаров, но с повторениями, то у нас есть 5 вариантов для каждого выбора, что дает нам 5 * 5 * 5 = Всего 125 вариантов. Таким образом, общая формула такова: #permutations = n р .
Объяснение комбинаций с формулой повторений
Посмотрим, сколько существует комбинаций для выбора 3-х шаров из 5 (красный (R), зеленый (G), фиолетовый (P), бирюзовый (T) и желтый (Y)) с повторения.
Вы заметите, что наш трюк с формулой обычных комбинаций не работает. Например, если мы посмотрим на комбинацию двух красных шаров и одного зеленого шара, у нас будет только 3 возможных перестановки (RGG, GRG, GGR) вместо 3! = 6, так как зеленый появляется дважды. Поэтому мы не можем просто разделить количество перестановок на 6! и быть сделано. Вместо этого мы будем использовать красивое представление, чтобы упростить нашу задачу. Мы можем представить выбор в виде таблицы, поэтому, если мы хотим выбрать 2 красных и зеленый шар, мы можем отметить это как: R | г | П | Т | Д
ОО | О | | |
Что можно записать более компактно, опустив заголовок и ненужные пробелы, как OO|O|||
и выбор одного зеленого, одного фиолетового и одного желтого шара можно записать как:
R | г | П | Т | Y
| О | О | | O
, который может быть записан более компактно как |O|O||O
Наконец, выбор 3 бирюзовых шаров может быть записан в виде следующей таблицы:
R | г | П | Т | Y
| | | | ООО
, которое может быть записано как ||||ООО
Каждая строка из 4 | и 3 О соответствует выбору и наоборот.
Следовательно, количество способов выбрать 3 шара из 5 с повторением и там, где порядок имеет значение, такое же, как количество способов написать строки из 4 символов «|» и 3 «О». Чтобы выяснить, сколько их, мы можем начать с 7! а потом видим, что надо делить на 4! потому что мы повторяем строки 4! из-за | повторение (поскольку изначально мы рассматриваем 4 | как отдельные символы) и делим на 3! так как мы повторяем строки 3! раз из-за повторения O. Следовательно, существует 7!/(4!3!) различных комбинаций = (n + r — 1)! / ((n — 1)! * r!), что является формулой, которая нам нужна.
Комбинации и перестановки, в чем разница?
Разница в том, заботимся ли мы о заказе. В комбинациях порядок не имеет значения. Если бы нам нужно было выбрать спортивную команду, то порядок, в котором мы выбираем игроков, не имеет значения. Если мы заботимся о порядке, то мы выбираем перестановку. Если вместо спортивной команды посмотреть на результаты бегового забега, то порядок становится важным.
Нам не все равно, придем ли мы первыми, а наш главный соперник вторым или наоборот, даже если они будут частью одной и той же комбинации.
Как пользоваться калькулятором комбинаций и перестановок?
Порядок важен : определяет, хотите ли вы использовать калькулятор комбинаций (когда он не активен) или калькулятор перестановок (когда он активен).
С повторениями : позволяет выбирать комбинации и перестановки с повторениями (активно) или без (неактивно).
Это относится как к калькулятору комбинаций , так и к калькулятору перестановок .
Идентичные элементы : позволяет указать, есть ли в вашей задаче повторения элементов, но не бесконечная замена (активно) или нет (неактивно). Когда он активен, вы можете указать количество повторений для каждого элемента. Обратите внимание, что в этом случае текстовое поле количества элементов будет представлять количество уникальных элементов.
Переключатель одинаковых предметов актуален как для калькулятора комбинаций , так и для калькулятора комбинаций .