Найти частные производные функции z: Частные производные. Подробное решение

13. Частные производные, частные производные высших порядков

Мы видели, что понятие производной функции оказалось очень полезным для исследования функций одной переменной. Но как применить это понятие для функции двух переменных. Можно считать одну переменную постоянной и взять производную по другой – так мы получим частные производные.

Пусть функция Z=F(X; Y) определена в открытой области D и точка (X0; Y0)ÎD.

Дадим значению Х0 приращение DХ, сохраняя значение второго аргумента неизменным и равным Y0. Тогда функция F получит приращение

, которое, естественно, назвать ее частным приращением по переменной Х или частным приращением в направлении оси ОХ.

Частной производной первого порядка функции F по переменной Х в точке (Х0; Y0) называется предел отношения частного приращения DХZ функции F в точке (Х0; Y0) к приращению DХ, когда DХ®0.

Частная производственная функции Z=F(х; Y) в точке (Х0; Y0) по переменной Х обозначается чаще всего следующим образом:

Итак,

Аналогично определяется частная производная (первого порядка) функции F по переменной Y в точке (Х0; Y0):

Из определения следует, что частная производная функции Z=F(х; Y) по Х есть обыкновенная производная функции Z=F(х; Y0), рассматриваемая как функция одной переменной Х при постоянном значении другой переменной Y. Чтобы найти F’X(X0; Y0), надо взять производную от F(X; Y) по Х, считая Y постоянным, и затем, в полученном результате, заменить х на Х0, а Y – на Y0.

Обратите внимание на отличие в написании производных .

Пример 1. Найти F’x(3;-2), если

Решение. Пользуемся правилами вычисления обычных производных, считая Х переменной, а У постоянным:

Аналогично следует поступать при вычислении частной производной функции Z=F(X;Y) по Y. Только теперь при нахождении F’Y(X0;Y0) надо брать производную от F(X;Y) по Y, считая Х постоянным.

Пример 2. Найти F’Y(-3; -2) функции предыдущего примера.

Решение. Фиксируя Х, получим

Таким образом, приходим к следующему правилу вычисления частных производных.

Чтобы вычислить частную производную от функции Z=Zf(х;Y) по одному из ее аргументов, нужно вычислить производную от функции F по этому аргументу, считая другой аргумент постоянным.

Заметим, что если частные производные функции

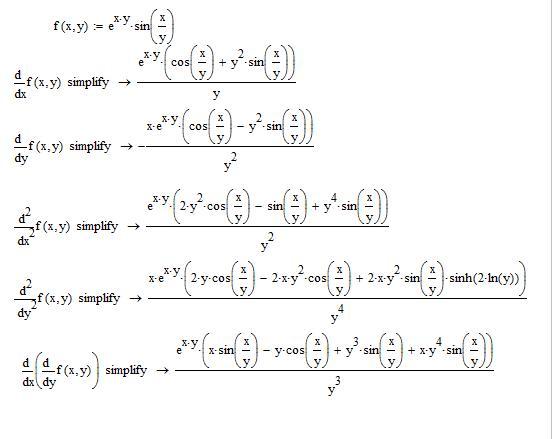Z=F(X;Y) существуют в точке (х0;Y0), то они представляют собой вполне определенные конечные числа, которые мы обозначили F’X(X0;Y0) и F’Y(X0;Y0). Но может оказаться, что функция F, определенная в области D, имеет в каждой точке этой области частные производные. Тогда F’X и F’Y есть функции, определенные в области D. В этом случае функции F’X(X;Y) и F’Y(X;Y), определенные в области D, называют частными производными функциями.

Пример 3. Найти функции Z=Yx.

Решение. Найдем сначала частную производную функцию по Х. При дифференцировании по переменной Х данная функция Z является показательной (здесь основание степени

Y постоянно).

Тогда получим

При дифференцировании по переменной Y функция Z является степенной (здесь показатель степени Х постоянен). Будем иметь:

Пусть в области D функция Z=F(X;Y) имеет частные производные . Естественно поставить вопрос об определении частных производных по X и Y от этих функций в точке (X0; Y0)ÎD. Так мы придем к понятию Частных производных второго порядка от функции Z=F(X; Y) в точке (X0,Y0).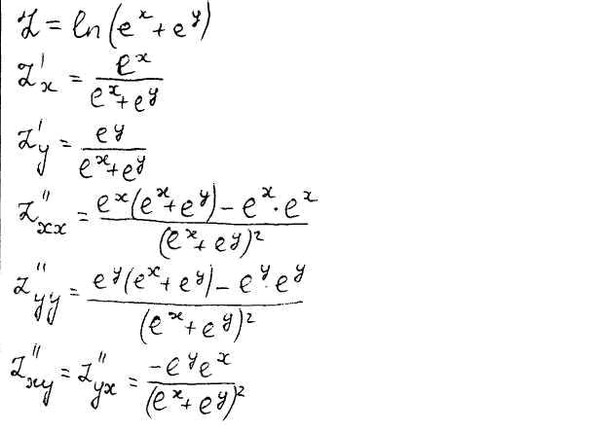 Таким образом, каждая из производных функций порождает две производные второго порядка, которые обозначаются следующим образом:

Возможны и другие обозначения частных производных второго порядка. Например,

Частные производные, взятые по различным переменным, называются

Смешанными.

Пример. Найдем частные производные второго порядка от функции

В точке (-1; 2).

Решение. Найти сначала частные производные функции первого порядка:

Дифференцируя каждую из полученных функций вторично и подставляя после этого вместо X значение –1, а вместо y значение 2, окончательно будем иметь:

Сравните между собой значения смешанных производных . Они совпадают. Это обстоятельство не является случайным. Частные производные, вычисленные по различным переменным и отличающиеся друг от друга лишь последовательностью производных дифференцирований, для широкого класса функций будут равны между собой.

< Предыдущая		Следующая >

Примеры решения частных производных с ответами

Простое объяснение принципов решения частных производных и 10 наглядных примеров.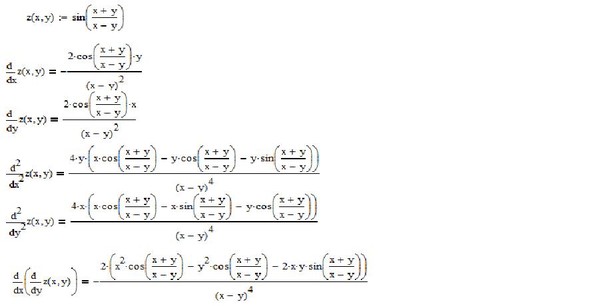 В каждом примере поэтапный ход решения и ответ.

Алгоритм решения частных производных

Вычисление частной производной функции из нескольких переменных осуществляется по тем же правилам, что и функций с одной переменной. Разница лишь той, что другие переменные не участвуют дифференцировании (вычислении производной).

Проще говоря, чтобы найти частную производную функции по переменной ,переменную будем считать константой (производная константы равна нулю), после чего находим производную функции по с помощью таблицы производных элементарных функций – . Готово!

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Примеры решения частных производных

Задача 1

Задача

Найти частные производные функции .

Решение

Частная производная функции по независимой переменной :

Производная суммы равна сумме производных. Производная от вычисляется по правилам вычислений производных функций одного аргумента, производная от слагаемого вычисляется как производная от функции двух аргументов. При этом аргумент считается константой. Производная от слагаемого вычисляется как производная от константы.

.

Частная производная функции по независимой переменной :

Здесь вычисления также происходят по правилам вычисления производной суммы. Производная от вычисляется как производная от константы (независимым аргументом при этом считается ). Производная от слагаемого вычисляется как производная от функции двух аргументов. При этом аргумент считается константой, а – независимым аргументом. Вычисление производной от слагаемого осуществляется по правилам вычисления производных функций с одним аргументом.

.

Ответ

.

Задача 2

Задача

Найти частные производные функции .

Решение

Найдём частную производную функции по независимой переменной :

Функция является сложной. Производной показательной функции с основанием является сама функция. Производная показателя степени вычисляется в при условии, что является константой и равна . Производная функции равна произведению и . В результате получаем:

.

Найдём частную производную функции по независимой переменной :

По аналогии с предыдущим случаем производная функции будет равна произведению производных от функции и показателя её степени :

Считая постоянной величиной, находим производную по независимому аргументу :

.

Ответ

.

Задача 3

Задача

Найти частные производные функции .

Решение

Частная производная функции по независимой переменной будет равна производной от . Производная от слагаемого при этом будет равна нулю как производная от константы.

Частная производная функции по независимой переменной находится аналогичным образом, при этом предполагается, что является константой.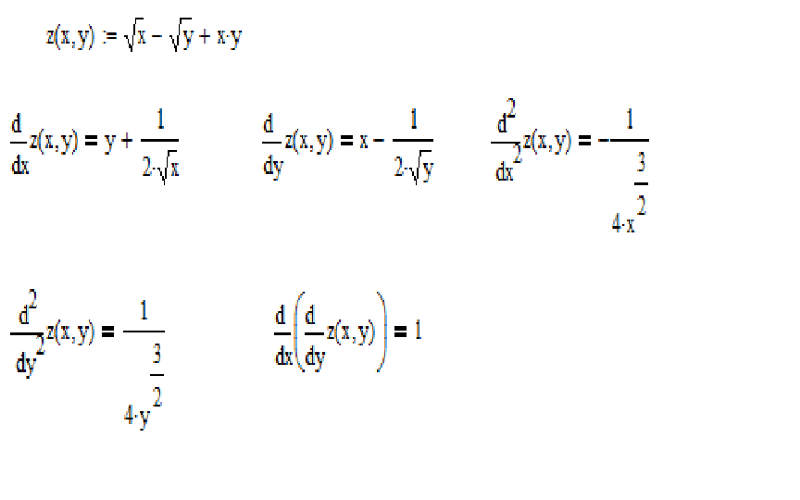

Ответ

Задача 4

Задача

Найти частные производные функции .

Решение

Частная производная функции по независимой переменной определяется слагаемым . Производная второго слагаемого – равна нулю, как производная от константы.

В свою очередь, частная производная функции по независимой переменной будет определяться обоими слагаемым:

Таким образом, окончательно получаем:

Ответ

Задача 5

Задача

Найти частные производные функции .

Решение

При нахождении производной по независимой переменной , функцию следует рассматривать как степенную. По правилу нахождения производной степенной функции получаем:

Производная по независимой переменной находится по правилу вычисления производной показательной функции, которая, в свою очередь, определяется по правилам нахождения производных сложных функций, т. к. переменная входит в показатель степени виде функции .

Производная показательной функции равна:

Производная показателя степени равна:

В результате получаем:

Ответ

Задача 6

Задача

Найти частные производные функции .

Решение

Частная производная по независимой переменной находится как сумма слагаемых:

Частная производная по независимой переменной находится как сумма слагаемых:

Ответ

Задача 7

Задача

Найти частные производные функции .

Решение

По правилу нахождения производной квадратного корня получаем, рассматривая как независимый аргумент:

Т.к. функция является сложной, то результат вычисления производной от квадратного корня – следует домножить на производную подкоренного выражения: .

Рассматривая в качестве независимого аргумента, получаем:

По аналогии с предыдущим случаем, результат вычисления производной от квадратного корня – следует домножить на производную подкоренного выражения: .

Ответ

Задача 8

Задача

Найти частные производные функции .

Решение

Данная функция является сложной, поэтому процесс нахождения производной данной функции целесообразно производить в несколько этапов.

Производная показательной функции с основанием равна самой себе. Далее необходимо найти производную показателя степени: . В свою очередь аргумент функции арктангенс в данном случае также представляет собой сложную функцию: . Результирующая производная будет равна произведению производных трёх функций: и .

Нахождение частной производной функции по аргументу :

Нахождение частной производной функции по аргументу :

Ответ

Задача 9

Задача

Найти частные производные первого и второго порядков функции .

Решение

Найдём частную производную первого порядка по аргументу :

Найдём частную производную второго порядка по аргументу :

Найдём частную производную первого порядка по аргументу :

Найдём частную производную второго порядка по аргументу :

Ответ

Задача 10

Задача

Найти частные производные первого и второго порядков функции .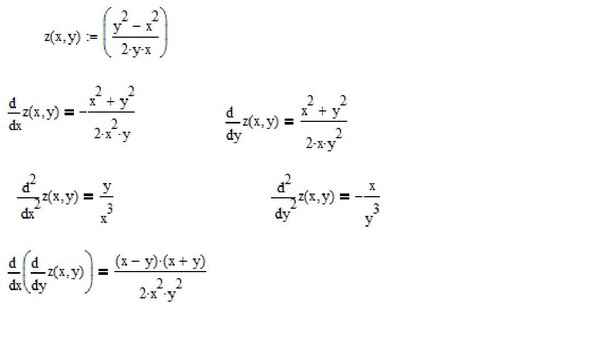

Решение

Найдём частную производную первого порядка по аргументу :

Найдём частную производную второго порядка по аргументу :

Найдём частную производную первого порядка по аргументу :

Найдём частную производную второго порядка по аргументу :

Ответ

Средняя оценка 5 / 5. Количество оценок: 6

Поставьте вашу оценку

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

25127

Закажите помощь с работой

Не отобразилась форма расчета стоимости? Переходи по ссылке

Не отобразилась форма расчета стоимости? Переходи по ссылке

Полезно

Исчисление III — Частные производные

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 13.2: Частные производные

Теперь, когда у нас есть краткое обсуждение пределов, мы можем перейти к получению производных от функций более чем одной переменной. Прежде чем мы действительно начнем брать производные функций более чем одной переменной, давайте вспомним важную интерпретацию производных функций одной переменной.

Напомним, что для функции одной переменной \(f\left( x \right)\), производная \(f’\left( x \right)\) представляет скорость изменения функции как \(х\) меняется. Это важная интерпретация производных, и мы не собираемся терять ее с функциями более чем одной переменной. Проблема с функциями более чем одной переменной заключается в том, что существует более одной переменной. Другими словами, что нам делать, если мы хотим, чтобы изменилась только одна из переменных, или если мы хотим изменить более одной из них? На самом деле, если мы позволим измениться более чем одной переменной, у нас будет бесконечное количество способов их изменения. Например, одна переменная может изменяться быстрее, чем другие переменные в функции. Заметьте также, что вполне возможно, что функция будет изменяться по-разному в зависимости от того, как мы позволяем изменяться одной или нескольким переменным.

Нам нужно разработать способы и обозначения для работы со всеми этими случаями. В этом разделе мы сосредоточимся исключительно на изменении только одной из переменных за раз, в то время как остальные переменные остаются фиксированными. Мы рассмотрим возможность изменения нескольких переменных в следующем разделе.

Поскольку мы позволим изменяться только одной из переменных, получение производной теперь станет довольно простым процессом. Давайте начнем это обсуждение с довольно простой функции. 93}\) и определим скорость изменения функции в точке \(\left( {a,b} \right)\), если зафиксировать \(y\) и разрешить \(x\ ) изменяться, и если мы будем считать \(x\) фиксированным и позволять \(y\) изменяться.

Начнем со случая, когда \(y\) остается фиксированным, а \(x\) изменяется. Поскольку нас интересует скорость изменения функции в точке \(\left({a,b} \right)\) и мы фиксируем \(y\), это означает, что мы всегда будем иметь \(y = б\) (если бы этого не было, то со временем \(y\) пришлось бы изменить, чтобы добраться до сути…). Это даст нам функцию, включающую только \(x\), и мы можем определить новую функцию следующим образом:3}\]

Теперь это функция одной переменной, и на данный момент все, что мы просим, ​​это определить скорость изменения \(g\left( x \right)\) при \(x = a\). Другими словами, мы хотим вычислить \(g’\left( a \right)\), и поскольку это функция одной переменной, мы уже знаем, как это сделать. 3}\] 92}\]

Обратите внимание, что эти две частные производные иногда называют частными производными первого порядка . Как и в случае с функциями одной переменной, мы можем иметь производные всех порядков. Мы рассмотрим производные более высокого порядка в следующем разделе.

Обратите внимание, что обозначения частных производных отличаются от обозначений производных функций одной переменной. С функциями одной переменной мы могли бы обозначать производную одним штрихом. Однако с частными производными нам всегда нужно помнить переменную, по которой мы дифференцируем, и поэтому мы будем индексировать переменную, по которой мы дифференцируем. Вскоре мы увидим некоторые альтернативные обозначения для частных производных. 92}\]

Теперь, как показал этот быстрый пример, получение производных от функций более чем одной переменной выполняется почти так же, как получение производных от одной переменной. Чтобы вычислить \({f_x}\left( {x,y} \right)\), все, что нам нужно сделать, это рассматривать все \(y\) как константы (или числа), а затем дифференцировать \(x\ ) как мы всегда делали. Точно так же, чтобы вычислить \({f_y}\left( {x,y} \right)\), мы будем рассматривать все \(x\) как константы, а затем дифференцировать \(y\), как мы привык делать.

Прежде чем приступить к работе с любыми примерами, давайте отвлечемся от формального определения частной производной, а также от некоторых альтернативных обозначений.

Поскольку мы можем думать о двух приведенных выше частных производных как о производных функций с одной переменной, неудивительно, что определение каждой из них очень похоже на определение производной для функций с одной переменной. Вот формальные определения двух частных производных, которые мы рассмотрели выше.

\[{f_x}\left( {x,y} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left({x + h,y} \right) — f\left( {x,y} \right)}}{h}\hspace{0,5in}{f_y}\left( {x,y} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x,y + h} \right) — f\left( {x,y} \right)}}{h}\]

Если вы помните определение предела в Исчислении I, они должны показаться вам знакомыми, поскольку они очень близки к определению в Исчислении I с (возможно) очевидным изменением.

Теперь давайте кратко рассмотрим некоторые из возможных альтернативных обозначений частных производных. Учитывая функцию \(z = f\left( {x,y} \right)\), следующие все эквивалентные обозначения:

\[\begin{align*}{f_x}\left( {x,y} \right) & = {f_x} = \frac{{\partial f}}{{\partial x}} = \frac{\partial }{{\partial x}}\left( {f\left( {x,y} \right)} \right) = {z_x} = \frac{{\partial z}}{{\partial x}} = {D_x}f\\ {f_y}\left( {x,y} \right) & = {f_y} = \frac{{\partial f}}{{\partial y}} = \frac{\partial}{ {\ partial y}} \ left ( {f \ left ( {x, y} \ right)} \ right) = {z_y} = \ frac {{\ partial z}} {{\ partial y}} = {D_y }f\конец{выравнивание*}\]

При записи дроби для частной производной обратите внимание на разницу между частной производной и обыкновенной производной из исчисления с одной переменной.

\[\begin{align*} & f\left( x \right)\hspace{0.25in} & \Rightarrow & \hspace{0. 25in}& f’\left( x \right) & = \frac{{df }}{{dx}}\\ & f\left( {x,y} \right)\hspace{0.25in} & \Rightarrow & \hspace{0.25in} & {f_x}\left( {x,y} \right) & = \frac{{\partial f}}{{\partial x}}\,\,\,\& \,\,\,{f_y}\left( {x,y} \right) = \frac{{\partial f}}{{\partial y}}\end{align*}\]

Хорошо, теперь давайте поработаем над некоторыми примерами. При работе с этими примерами всегда помните, что нам нужно уделять очень пристальное внимание тому, по какой переменной мы дифференцируем. Это важно, потому что мы будем рассматривать все остальные переменные как константы, а затем будем работать с производной, как если бы она была функцией одной переменной. Если вы помните это, то обнаружите, что вычисление частных производных ненамного сложнее, чем вычисление производных функций одной переменной, как мы это делали в Исчислении I. 93}\]

Обратите внимание, что в этом случае второй и третий члены дифференцируются до нуля. Должно быть ясно, почему третий член продифференцирован до нуля. Это константа, а мы знаем, что константы всегда дифференцируются до нуля. Это также является причиной того, что второй член продифференцирован до нуля. Помните, что, поскольку здесь мы дифференцируем по \(x\), мы будем рассматривать все \(y\) как константы. Это означает, что термины, включающие только \(y\), будут рассматриваться как константы и, следовательно, будут дифференцироваться до нуля. 93} + 43x — 7\tan \left( {4y} \right)\) Показать решение

С помощью этой функции нам нужно вычислить три производные первого порядка. Сначала найдем частную производную по \(x\). Поскольку мы дифференцируем по \(x\), мы будем рассматривать все \(y\) и все \(z\) как константы. Это означает, что второй и четвертый члены будут дифференцированы до нуля, поскольку они включают только \(y\) и \(z\).

Этот первый член содержит как \(x\), так и \(y\), поэтому, когда мы дифференцируем по \(x\), \(y\) будем рассматривать как мультипликативную константу и таким образом, первый член будет дифференцирован так же, как будет дифференцирован третий член.

Здесь частная производная по \(x\).

\[\frac{{\partial w}}{{\partial x}} = 2xy + 43\]

Теперь продифференцируем по \(y\). В этом случае все \(x\) и \(z\) будут рассматриваться как константы. Это означает, что третий член будет дифференцироваться до нуля, поскольку он содержит только \(x\), тогда как \(x\) в первом члене и \(z\) во втором члене будут рассматриваться как мультипликативные константы. Вот производная по \(y\). 93}}}\) Показать решение

Теперь мы не можем забыть правило произведения с производными. Здесь правило произведения будет работать так же, как и с функциями одной переменной. Нам просто нужно быть осторожными, чтобы помнить, по какой переменной мы дифференцируем.

Начнем с дифференцирования по \(x\). В этом случае и косинус, и экспонента содержат \(x\), поэтому у нас действительно есть произведение двух функций, включающих \(x\), и поэтому нам нужно умножить это произведение. {е \ влево ( х \ вправо)}} \] 92}}}\) Показать решение

Теперь нам нужно быть осторожными, чтобы не использовать правило частного, когда в нем нет необходимости. Однако в этом случае у нас есть частное, поскольку \(x\) и \(y\) появляются только в числителе, а \(z\) появляются только в знаменателе, это действительно не так. проблема с частным правилом.

Сначала выполним производные по \(x\) и \(y\). В обоих этих случаях \(z\) являются константами, поэтому знаменатель здесь является константой, и поэтому нам не нужно слишком беспокоиться об этом. Вот производные для этих двух случаев. 9{ — \frac{1}{2}}}\end{align*}\]

Итак, есть несколько примеров частных производных. Надеюсь, вы согласитесь, что до тех пор, пока мы помним, что другие переменные следует рассматривать как константы, они работают точно так же, как и производные функций одной переменной. Итак, если вы умеете вычислять производные в исчислении I, у вас не должно возникнуть особых трудностей при вычислении основных частных производных.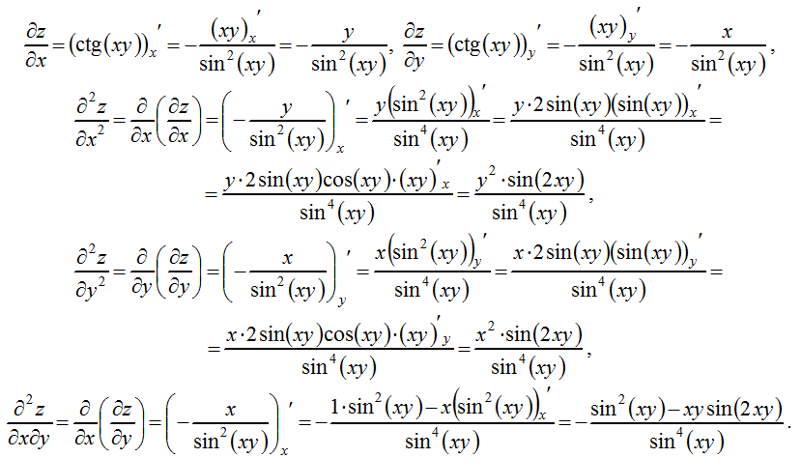 6} = 5\] 93}}}\]

Теперь мы решили эту задачу, потому что неявное дифференцирование работает точно так же с функциями многих переменных. Если у нас есть функция в терминах трех переменных \(x\), \(y\) и \(z\), мы будем считать, что \(z\) на самом деле является функцией \(x\) и \ (у\). Другими словами, \(z = z\left({x,y} \right)\). Затем всякий раз, когда мы дифференцируем \(z\) по \(x\), мы будем использовать цепное правило и добавлять \(\frac{{\partial z}}{{\partial x}}\). Точно так же всякий раз, когда мы дифференцируем \(z\) по \(y\), мы добавляем \(\frac{{\partial z}}{{\partial y}}\). 92}\cos\left( {2y — 5z} \right)\left( { — 5\frac{{\partial z}}{{\partial x}}} \right) = — y\sin \left( { 6zx} \right)\left( {6z + 6x\frac{{\partial z}}{{\partial x}}} \right)\]

Не забудьте использовать цепное правило для каждой триггерной функции, и когда мы дифференцируем внутреннюю функцию по косинусу, нам также нужно будет использовать правило произведения. 2} \cos\left( {2y — 5z} \right) — 6yx\sin \left( {6zx} \right)}}\end{align*}\] 92}\cos\left( {2y — 5z} \right)}}\end{align*}\]

Над ними нужно поработать. В следующем разделе мы увидим более простой способ неявного дифференцирования.

Примеры частных производных — Math Insight

Видео-введение

Примеры частных производных.

Подробнее о видео.

Как только вы поймете концепцию частной производной как скорости изменения чего-либо, вычисление частных производных обычно не составит труда. (К сожалению, есть особые случаи, когда вычисление частных производных затруднено.) Как показывают эти примеры, вычисление частных производных обычно ничем не отличается от вычисления обычной производной в исчислении с одной переменной. Вам просто нужно помнить, с какой переменной вы берете производную. 92$. Вычислите $\displaystyle \pdiff{f}{x}(x,y)$.

Решение . Чтобы вычислить $\displaystyle \pdiff{f}{x}(x,y)$, мы просто просматриваем $y$ как фиксированное число и вычислить обыкновенную производную с помощью относительно $x$. 3x. \конец{выравнивание*} 92)/(x_1x_2x_4)} + 5x_1x_3x_4 \конец{выравнивание*} вычислить $\displaystyle \pdiff{f}{x_3}(a,b,c,d)$.

Решение : хотя сначала это выглядит сложно, на самом деле все просто проблема. Уродливый член не зависит от $x_3$, поэтому при вычислении частная производная по $x_3$, мы рассматриваем ее как константу. Производная константы равна нулю, поэтому этот член выпадает. производная — это просто производная от последнего члена по $x_3$, то есть \начать{выравнивать*} \pdiff{f}{x_3}(x_1,x_2,x_3,x_4) = 5x_1x_4 \конец{выравнивание*} Подставляя значения $(x_1,x_2,x_3,x_4)=(a,b,c,d)$, получаем окончательный ответ \начать{выравнивать*} \pdiff{f}{x_3}(a,b,c,d) = 5ad. \конец{выравнивание*}

Пример 5

Пусть \начать{выравнивать*} p(y_1,y_2,y_3) = 9\frac{y_1y_2y_3}{y_1+y_2+y_3} \конец{выравнивание*} и вычислить $\displaystyle \pdiff{p}{y_3}(y_1,y_2,y_3)$ в точке $(y_1,y_2,y_3)=(1,-2,4)$.

Решение : При вычислении частных производных мы можем использовать все правила для обычных производных.