Система линейных уравнений с двумя переменными. Методы решения систем уравнений.
- Альфашкола
- Статьи
- Методы решения систем уравнений с двумя переменными
Дарим в подарок бесплатный вводный урок!
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ЕГЭ по математике (базовый уровень)
- Репетитор по русскому языку для подготовки к ЕГЭ
- Репетитор по грамматике русского языка
- Репетитор по английскому языку для подготовки к ОГЭ
- Репетитор для подготовки к ВПР по русскому языку
- Репетитор для подготовки к ВПР по обществознанию
- Репетитор по географии для подготовки к ЕГЭ
- Репетитор по информатике для подготовки к ЕГЭ
- Программирование Pascal
- Scratch
Решением системы линейных уравнений двух переменных является любая упорядоченная пара, удовлетворяющая каждому уравнению независимо.
Как можно решить систему уравнений с двумя переменными?
Системы уравнений с двумя переменными можно решить методом подстановки:
Системы уравнений с двумя переменными можно решить методом сложения:
Пример. Решить систему методом сложения: \(\begin{equation*} \begin{cases} x-y-4=0 \\ 3x+y-8=0 \end{cases} \end{equation*}\).
Решение:
Ответ: \((3;-1).\)
Система уравнений состоящее из двух переменных должно удовлетворять всем решениям одновременно. Система линейных уравнений из двух переменных рассматривается одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти численное значение для каждой переменной в системе, которая будет удовлетворять всем уравнениям системы одновременно. Некоторые линейные системы могут не иметь решения, и это будет их решением, другие системы могут иметь бесконечное число решений.
Выводы:
- Система линейных уравнений из двух переменных решается совместно методом подстановки или методом сложения.
- Чтобы найти решение системы линейных уравнений, мы должны найти численное значение для каждой переменной в системе, которая будет удовлетворять всем уравнениям в системе одновременно.
- Для того чтобы линейная система имела единственное решение, должно быть не меньше уравнений, чем переменных.
- Решить систему уравнений это значит найти численное значение для каждой переменной в системе либо доказать что решений нет.
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Григорий Олегович Курто
Репетитор по математике
Стаж (лет)
Образование:
Белорусский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Татьяна Дмитриевна Макарова
Репетитор по математике
Стаж (лет)
Образование:
Белорусский государственный педагогический университ имени Максима Танка
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Ирина Демьяновна Хоухлянцева
Репетитор по математике
Стаж (лет)
Образование:
Могилевский государственный педагогический институт им. А. Кулешова
А. Кулешова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Похожие статьи
- Формулы параболы
- Примеры решения неравенств
- Как перевести центнеры в граммы?
- Решение показательных уравнений
- НИУ ВШЭ: вступительные испытания и проходные баллы
- Решаем ОГЭ по математике. Задание №5. 2
- ОГЭ по математике, базовый уровень. Системы неравенств
- Как организовать режим школьника на каникулах, чтобы потом было легче снова идти в школу
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Внеклассный урок — Система уравнений с двумя переменными.
 Системы уравнений с двумя переменными. Способы решения.Система уравнений с двумя переменными. Уравнения первой степени. Способы решения
Системы уравнений с двумя переменными. Способы решения.Система уравнений с двумя переменными. Уравнения первой степени. Способы решенияУравнение может содержать не одну, а две переменных. Понятно, что такие уравнения называются уравнениями с двумя переменными.
Система уравнений – это два и более уравнений, которыми можно манипулировать для нахождения общих решений. Система из двух уравнений вкючает в себя две переменных, значения которых являются общими для обоих уравнений. С помощью одного уравнения системы решается другое, а в итоге решаются оба уравнения системы.
Способы решения системы уравнений первой степени.
1. Решение методом подстановки.
Суть в том, что в системе уравнений выбираете наиболее простое, в котором одну переменную выражаете через другую. Результат подставляете во второе уравнение, благодаря чему преобразуете его в более простое уравнение с одной переменной. Вычисляете это уравнение и получаете значение одной из переменных. Подставляется его в первое уравнение и получаете значение второй переменной. Так вы решаете всю систему уравнений.
Вычисляете это уравнение и получаете значение одной из переменных. Подставляется его в первое уравнение и получаете значение второй переменной. Так вы решаете всю систему уравнений.
Пример: Решим систему уравнений
│x + y = 1
│2x – y = 2
Решение:
Первое уравнение системы проще второго – его и используем.
Выразим в нем x через у:
x = 1 – y
Подставляем это значение x в наше второе уравнение и находим значение y:
2(1 – y) – y = 2
2 – 2y – y = 2
2 – 3y = 2
3y = 2 – 2
3y = 0
y = 0.
Мы получили значение y. Подставляем его в наше первое уравнение и находим теперь уже значение x:
x + 0 = 1
x = 1
Мы нашли значения обеих переменных.
Ответ:
│x = 1
│y = 0
2. Решение методом сложения.
Этот метод целесообразно применять, если при сложении одно из неизвестных пропадает.
Пример 1: Решим систему уравнений
│x + y = 5
│x – y = 1
Решение.
Сложим (вычтем) почленно оба уравнения системы:
│(x + y) + (x – y) = 5 + 1
│(x + y) – (x – y) = 5 – 1
Раскрываем скобки в обоих уравнениях и сводим подобные члены. В результате в первом уравнении пропадает у, во втором х. Мы получаем уравнения с одной переменной, которые проще решать:
│ x + y + x – y = 6
│ x + y – x + y = 4
↓
│2x = 6
│2y = 4
↓
│x = 6 : 2
│y = 4 : 2
↓
│x = 3
│y = 2
Пример решен.
Необязательно производить взаимное сложение и вычитание двух уравнений системы. Часто достаточно бывает произвести одно из двух действий, чтобы вычислить значение одной из двух переменных. А зная одну переменную, мы уже легко сможем найти и вторую.
Пример 2. Решить систему уравнений
│2х + 4у = 26
│8х + 4у = 44
В обоих уравнениях есть число 4у. Значит, можем применить метод сложения. При этом произвести не взаимное сложение, а совершить лишь одно действие: вычесть из первого уравнения второе, чтобы 4у исчезло и чтобы в результате мы получили уравнение с одной переменной:
2х + 4у – 8х – 4у = 26 – 44.
-6х = -18
х = -18 : (-6)
х = 3
Теперь можем найти и значение у, подставив значение х в любое из двух уравнений системы:
2 · 3 + 4у = 26
6 + 4у = 26
4у = 20
у = 20 : 4
у = 5
Ответ: х = 3, у = 5.
Однако рассмотрим еще один пример.
Пример 3: Решим систему уравнений
│3х + 5у = 21
│8х – 3у = 7
Здесь нет переменных с одинаковыми коэффициентами, чтобы при вычитании они исчезли. Что делать в этом случае? Для таких случаев придумано оригинальное решение: умножим почленно первое уравнение на 3, а второе на 5. От этого истина не пострадает, потому что мы просто получим равносильные уравнения. Зато благодаря этому приему у нас появятся одинаковые переменные 15у:
│(3х + 5у = 21) · 3
│(8х – 3у = 7) · 5
↓
│3 · 3х + 3 · 5у = 3 · 21
│5 · 8х – 5 · 3у = 5 · 7
↓
│9х + 15у = 63
│40х – 15у = 35
Итак, у нас появились одинаковые переменные и мы можем сложить два уравнения, чтобы прийти к уравнению с одной переменной:
9х + 15у + 40х – 15у = 63 + 35
49х = 98
х = 2
Осталось найти значение второй переменной, подставив значение х, например, в первое уравнение системы:
3 · 2 + 5у = 21
6 + 5у = 21
5у = 21 – 6
5у = 15
у = 3.
Ответ: х = 2; у = 3.
Опять же не всегда нужно преобразовывать оба уравнения системы так, как было в предыдущем примере. Бывает и так, что достаточно изменить лишь одно из уравнений.
Пример 4. Решим систему уравнений:
│3х – 4у = 7
│х + 3у = 11
Здесь достаточно второе уравнение умножить на –3. Тогда мы получим число –3х, а при сложении двух уравнений придем к уравнению с одной переменной.
Итак, умножаем второе уравнение на –3:
(х + 3у = 11) · (–3)
–3х – 9у = –33
Теперь складываем два уравнения, приходим к уравнению с одной переменной у и решаем его:
3х – 4у –3х – 9у = 7 – 33
–13у = –26
у = 2.
И находим значение х. Это проще сделать во втором уравнении:
х + 3 · 2 = 11
х + 6 = 11
х = 5.
Ответ: х = 5; у = 2.
3. Решение методом введения новой переменной.
Пример. Решить систему уравнений
│ 2 3
│———— + ———— = 2
│ х – 3у 2х + у
│
│ 8 9
│———— – ———— = 1
│ х – 3у 2х + у
Перед нами система сложных уравнений, осложненных дробными числами. Наша задача – упростить их, чтобы потом решить. Если применить какой-нибудь из первых двух методов, получатся еще более сложные уравнения. Зато хорошо подходит метод введения новой переменной, благодаря которому мы целую дробь можем заменить одной переменной. Как это сделать?
Наша задача – упростить их, чтобы потом решить. Если применить какой-нибудь из первых двух методов, получатся еще более сложные уравнения. Зато хорошо подходит метод введения новой переменной, благодаря которому мы целую дробь можем заменить одной переменной. Как это сделать?
Обратите внимание: у первых чисел обоих уравнений одинаковые знаменатели х – 3у, при этом их числители делятся на 2. У вторых чисел тоже одинаковые знаменатели 2х + у, а их числители делятся на 3. Этим и воспользуемся.
1) Выпишем снова нашу систему уравнений, разложив на множители числители второго уравнения и вынеся их за дробь:
│ 2 3
│———— + ———— = 2
│ х – 3у 2х + у
│
│ 2 3
│4 · ———— – 3 · ———— = 1
│ х – 3у 2х + у
Теперь в обоих уравнениях у нас абсолютно одинаковые первые дроби и абсолютно одинаковые вторые дроби.
2) Заменим эти дроби новыми переменными a и b следующим образом:
2 3
———— = а, ———— = b.
х – 3у 2х + у
Так мы существенно упрощаем уравнения, которые обретают совсем иной вид:
│ а + b = 2
│4а – 3b = 1
3) Применяем уже известный нам метод подстановки.
Первое уравнение проще, поэтому сначала выражаем в нем а через b:
а = 2 – b.
Подставляем полученное значение а во второе уравнение, раскрываем скобки, приводим подобные члены и вычисляем численное значение b:
4 · (2 – b) – 3b = 1
8 – 4b – 3b = 1
8 – 7b = 1
7b = 8 – 1
7b = 7
b = 1
Раз нам известно численное значение b, то мы легко можем найти и численное значение а. Это проще сделать с помощью первого уравнения:
а + b = 2
а + 1 = 2
а = 2 – 1
а = 1.
Итак:
а = 1, b = 1.
Вписываем в дроби эти значения а и b:
│ 2
│———— = 1
│ х – 3у
│
│ 3
│———— = 1
│ 2х + у
4) Преобразуем эти уравнения по известному вам правилу: неизвестные влево, известные вправо:
│ х – 3у = 2 : 1
│2х + у = 3 : 1
↓
│ х – 3у = 2
│2х + у = 3
5) Решаем эту систему уравнений снова с помощью метода подстановки. Для этого в первом уравнении х выражаем через у:
х = 2 + 3у.
Подставляем во второе уравнение и находим у:
2 · (2 + 3у) + у = 3
4 + 6у + у = 3
7у = 3 – 4
7у = –1
у = –1/7
И с помощью первого уравнения находим х:
х – 3у = 2
х – 3 · (–1/7) = 2
х + 3/17 = 2
х = 2 – 3/7
х = 11/7.
Мы нашли значения х и у в нашей исходной системе уравнений – а значит, решили ее.
Ответ: х = 11/7, у = –1/7
ПРИМЕЧАНИЕ.
Как видно из этого примера, нередки случаи, когда при решении системы уравнений надо последовательно применить сразу несколько методов.
Решение систем уравнений (одновременных уравнений)
Если у вас есть два разных уравнения с одними и теми же двумя неизвестными в каждом, вы можете решить для обоих неизвестных. Есть три распространенных метода решения: сложение/вычитание, замена и построение графика.
Метод сложения/вычитания
Этот метод также известен как метод исключения.
Чтобы использовать метод сложения/вычитания, сделайте следующее:
- Умножьте одно или оба уравнения на какое-либо число (числа), чтобы сделать число перед одной из букв (неизвестных) одинаковым или прямо противоположным в каждом уравнение.
- Сложите или вычтите два уравнения, чтобы исключить одну букву.
- Найдите оставшееся неизвестное.
- Найдите другое неизвестное, подставив значение найденного неизвестного в одно из исходных уравнений.
Пример 1
Найдите x и y .
Добавление уравнений устраняет y ‐членов.
Теперь подставив 5 вместо x в первое уравнение, мы получим следующее:
Ответ: x = 5, y = 2
Заменив в исходных уравнениях каждые x на 5 и каждые y на 2, вы увидите, что каждое уравнение станет верным.
В Примере и Примере существовал уникальный ответ для x и y , который делал каждое предложение верным одновременно. В некоторых ситуациях вы не получаете уникальных ответов или не получаете ответов. Вы должны знать об этом, когда используете метод сложения/вычитания.
Пример 2
Решите для x и лет.
Сначала умножьте нижнее уравнение на 3. Теперь y предшествует цифра 3 в каждом уравнении.
Уравнения можно вычесть, исключив члены y .
Вставьте x = 5 в одно из исходных уравнений, чтобы найти y .
Ответ: х = 5, y = 3
Конечно, если число перед буквой в каждом уравнении уже одно и то же, вам не нужно изменять ни одно из уравнений.
Чтобы проверить решение, замените каждое x в каждом уравнении на 5 и замените каждое y в каждом уравнении на 3.
Пример 3
Умножьте верхнее уравнение на 2. Обратите внимание, что получится.
Теперь, если вы должны вычесть одно уравнение из другого, результат будет 0 = 0.
Это утверждение всегда верно .
Когда это происходит, система уравнений не имеет единственного решения. На самом деле, любая замена на и на , которая делает одно из уравнений верным, также делает верным другое уравнение. Например, если a = -6 и b = 5, то оба уравнения выполняются.
[3(– 6) + 4(5) = 2 И 6(– 6) + 8(5) = 4]
На самом деле у нас есть только одно уравнение, записанное двумя разными способами. В этом случае второе уравнение фактически является первым уравнением, умноженным на 2. Решением для этой ситуации является либо исходное уравнение, либо упрощенная форма любого уравнения.
Пример 4
Найдите x и y .
Умножьте верхнее уравнение на 2. Обратите внимание, что получится.
Теперь, если вы вычтете нижнее уравнение из верхнего уравнения, результат будет 0 = 1. Это утверждение равно 9.0023 никогда не верно . В этом случае система уравнений не имеет решения.
В примерах 1–4 только одно уравнение умножалось на число, чтобы числа перед буквой были одинаковыми или противоположными. Иногда каждое уравнение нужно умножать на разные числа, чтобы числа перед буквой были одинаковыми или противоположными.
Найдите x и y .
Обратите внимание, что нет простого числа, на которое можно умножить любое уравнение, чтобы получить числа перед 9.0023 x или y , чтобы стать одинаковыми или противоположными. В этом случае сделайте следующее:
- Выберите букву для исключения.
- Используйте две цифры слева от этой буквы.
 Найдите наименьшее общее кратное этого значения в качестве желаемого числа, которое должно стоять перед каждой буквой.
Найдите наименьшее общее кратное этого значения в качестве желаемого числа, которое должно стоять перед каждой буквой. - Определите, на какое значение нужно умножить каждое уравнение, чтобы получить это значение, и умножьте уравнение на это число.
Предположим, вы хотите исключить x . Наименьшее общее кратное 3 и 5, число перед x , равно 15. Первое уравнение нужно умножить на 5, чтобы получить 15 перед x . Второе уравнение нужно умножить на 3, чтобы получить 15 перед x .
Теперь вычтите второе уравнение из первого уравнения, чтобы получить следующее:
В этот момент вы можете либо заменить y на и найти x (метод 1 ниже), либо начать с исходного два уравнения и исключить y , чтобы вычислить x (способ 2 ниже).
Метод 1
Используя верхнее уравнение: Замените y на и найдите x .
Метод 2
Исключите y и найдите x .
Наименьшее общее кратное 4 и 6 равно 12. Умножьте верхнее уравнение на 3, а нижнее на 2.
Теперь сложите два уравнения, чтобы исключить y .
Решение x = 1 и .
Метод подстановки
Иногда система легче решается методом подстановки . Этот метод включает подстановку одного уравнения в другое.
Пример 6
Решите для x и лет.
Из первого уравнения подставьте ( y + 8) вместо x во второе уравнение.
( у + 8) + 3 г = 48
Теперь найдите г. Упростите, объединив и .
Теперь подставьте y значение 10 в одно из исходных уравнений.
Ответ: y = 10, x = 18
Проверьте решение.
Пример 7
Найдите x и y методом подстановки.
Сначала найдите уравнение, в котором перед буквой стоит либо «1», либо «– 1». Решите для этой буквы через другую букву.
Решите для этой буквы через другую букву.
Затем действуйте, как в примере 6.
В этом примере в нижнем уравнении стоит «1» перед y .
Найдите y через x .
Подставьте 4 x – 17 вместо y в верхнем уравнении, а затем найдите x .
Замените x на 4 в уравнении y – 4 x = –17 и найдите y .
Решение: x = 4, y = –1.
Проверить решение:
Графический метод
Другой метод решения уравнений состоит в построении каждого уравнения на координатном графике. Координаты пересечения и будут решением системы. Если вы не знакомы с построением координатных графиков, внимательно изучите статьи по координатной геометрии, прежде чем пытаться использовать этот метод.
Пример 8
Решите систему с помощью графика.
Сначала найдите три значения для x и y , которые удовлетворяют каждому уравнению. (Хотя для определения прямой линии необходимы только две точки, нахождение третьей точки является хорошим способом проверки.) Ниже приведены таблицы значений x и y :
(Хотя для определения прямой линии необходимы только две точки, нахождение третьей точки является хорошим способом проверки.) Ниже приведены таблицы значений x и y :
x
и
| 4 | 0
| 2 | –2
| 5 | 1
x
и
| 1 | -1
| 4 | 0
| 7 | 1
Теперь начертите две линии на координатной плоскости, как показано на рис. 1.
Точка пересечения двух прямых (4, 0) является решением системы.
Если прямые параллельны, то они не пересекаются, а значит, у этой системы нет решений.
Рис. 1. График линий х = 4 + y и х – 3 y = 4 с указанием решения.
Пример 9
Решите систему с помощью графика.
Найдите три значения для x и y , которые удовлетворяют каждому уравнению.
3 x + 4 y = 2 6 x + 8 y = 4
Ниже приведены таблицы значений x и 4 y 9002. См. рис. 2.
См. рис. 2.
x
и
| 0 |
| 2 | – 1
| 4 |
x
и
| 0 |
| 2 | – 1
| 4 |
Обратите внимание, что одинаковые точки удовлетворяют каждому уравнению. Эти уравнения представляют одну и ту же прямую.
Следовательно, решение не является единственной точкой. Решением являются все точки на прямой.
Следовательно, решением является любое уравнение прямой, поскольку они оба представляют одну и ту же прямую.
Это похоже на пример, когда это было сделано с использованием метода сложения/вычитания.
Рис. 2. График линий 3 x + 4 y = 2 и 6 x + 8 y = 4 с указанием решения.
Пример 10
Решите систему с помощью графика.
Найдите три значения для x и y , которые удовлетворяют каждому уравнению. См. следующие таблицы значений x и y :
x
и
| 0 | 1
| 2 |
| 4 | -2
x
и
| 0 | 2
| 2 |
| 4 | -1
Обратите внимание, что на рисунке 3 два графика параллельны.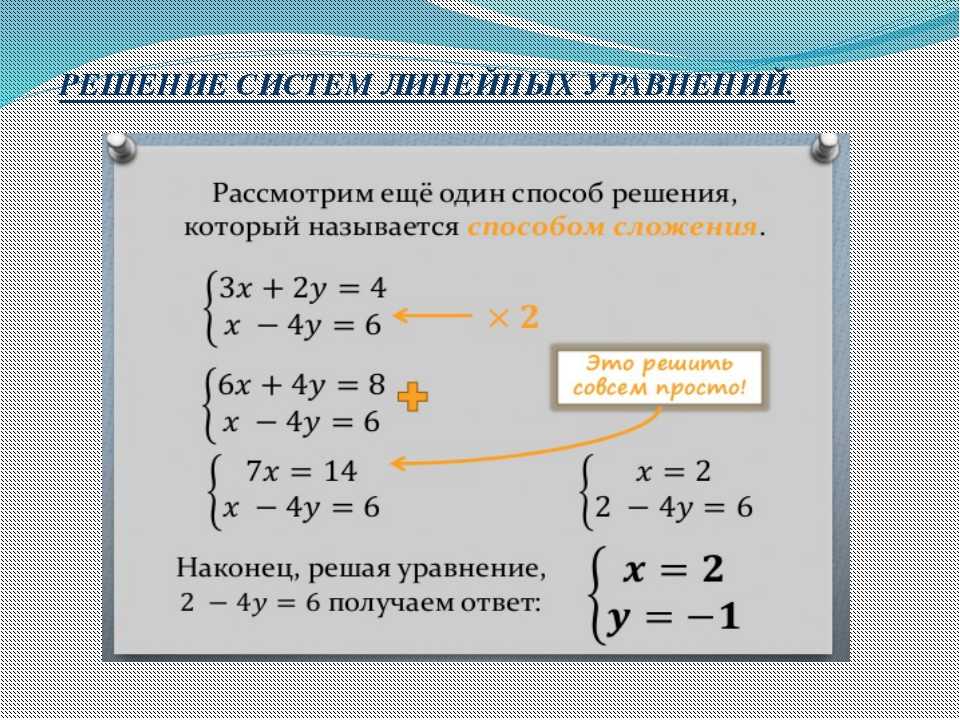 Они никогда не встретятся. Следовательно, для этой системы уравнений решения нет.
Они никогда не встретятся. Следовательно, для этой системы уравнений решения нет.
Для этой системы уравнений не существует решений.
Это похоже на пример, выполненный с использованием метода сложения/вычитания.
Рис. 3. График линий 3 х + 4 у = 4 и 6 х + 8 у = 16, обозначающий решение.
Решение систем уравнений с двумя переменными (Алгебра 2, Как решить систему линейных уравнений) – Mathplanet
Система линейного уравнения состоит из двух или более уравнений, и одно из них ищет общее решение уравнений. В системе линейных уравнений каждому уравнению соответствует прямая линия, и нужно найти точку, в которой две линии пересекаются.
Пример
Решите следующую систему линейных уравнений:
$$\left\{\begin{matrix} y=2x+4\\ y=3x+2\\ \end{matrix}\right .$$
Поскольку мы ищем точку пересечения, мы можем изобразить уравнения:
Здесь мы видим, что прямые пересекаются друг с другом в точке x = 2, y = 8. Это наше решение и мы можем назвать это графическим решением задачи.
Это наше решение и мы можем назвать это графическим решением задачи.
Но как найти решение, если линии никогда не пересекаются? Нельзя, система уравнений не имеет решения.
Правильный ответ можно также получить с помощью метода исключения (также называемого методом сложения или методом линейной комбинации) или методом подстановки.
При использовании метода подстановки мы используем тот факт, что если два выражения y и x имеют одинаковое значение x=y, то x может заменить y или наоборот в другом выражении без изменения значения выражения.
Пример
Решить системы уравнений методом подстановки
$$\left\{\begin{matrix} y=2x+4\\ y=3x+2\\ \end{matrix}\right.$$
Заменим y в верхнем уравнении выражением для второго уравнения:
$$\begin{array}{lcl} 2x+4 & = & 3x+2\\ 4-2 & = & 3x-2x\\ 2 & = & x\\ \end{array }$$
Чтобы определить значение y , мы можем подставить наше значение x в любое из уравнений. Выбираем первое уравнение:
Выбираем первое уравнение:
$$y=2x+4$$
Подставляем x=2 и получаем
$$y=2\cdot 2+4=8$$
Таким образом, мы пришли к точно такому же ответу, как и в графическом решении.
Метод исключения требует, чтобы мы складывали или вычитали уравнения, чтобы исключить x или y , часто нельзя приступить к сложению напрямую, не умножив первое или второе уравнение на некоторое значение.
Пример
$$2x-2y=8$$
$$x+y=1$$
Теперь мы хотим сложить два уравнения, но ни одно из них не даст x или y удаляются. Следовательно, мы должны умножить второе уравнение на 2 с обеих сторон и получить:
$$2x-2y=8$$
$$2x+2y=2$$
Теперь попробуем сложить нашу систему уравнений. Начнем с x -термов слева, затем y -термов и, наконец, с чисел справа:
$$(2x+2x)+(-2y+2y)=8+ 2$$
Члены y теперь исключены, и теперь у нас есть уравнение только с одной переменной:
$$4x=10$$
$$x=\frac{10}{4}=2,5$$
После этого для определения y -значения подставляем x =2,5 в одну уравнений.

 Найдите наименьшее общее кратное этого значения в качестве желаемого числа, которое должно стоять перед каждой буквой.
Найдите наименьшее общее кратное этого значения в качестве желаемого числа, которое должно стоять перед каждой буквой.