Площадь круга: как ее найти по формулам
Поиск площади круга – стандартная задача. Обычно, она задается школьникам в шестом классе, помогает мягко перейти к изучению более сложных примеров из тригонометрии.
В этом материале мы расскажем о том, как найти площадь круга с помощью формулы, обратим внимание на основные определения, отличия которых важно понимать учащемуся. Уже через непродолжительное время тренировок, вы сможете полностью освоить все методы решения задач и получать высокие оценки на уроке.
Важные определения
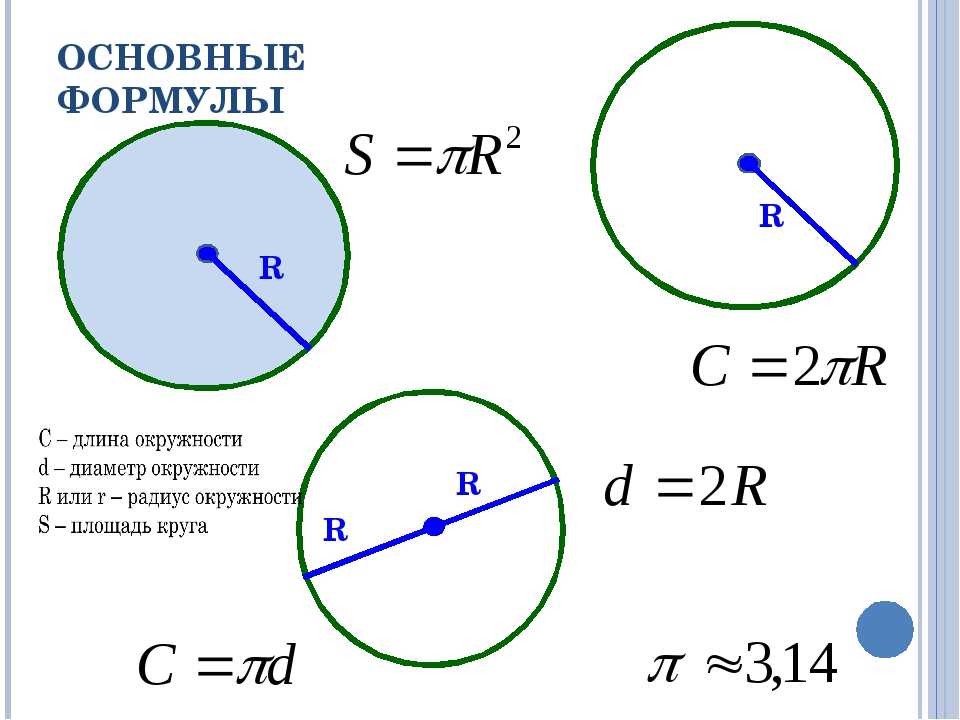
Прежде чем отвечать на вопрос о том, как найти площадь круга по радиусу или диаметру по формуле, нужно установить основные определения. Мы будем пользоваться следующими терминами:
- Круг. Так называют замкнутую плоскую кривую, в которой каждая точка имеет равное удаление от центральной.
- Окружность. Это сразу множество точек, которые располагаются на плоскости. При этом расстояние удаления от центра не будет превышать диаметр.

- Радиус. Расстояние от центра круга до любой его противоположной боковой точки.
- Диаметр. Полное расстояние от двух точек, расположенных на равном удалении друг от друга.
Как найти площадь круга по диаметру: формула
Формула поиска площади для диаметра будет выглядеть так:
S = d2 : 4 × π.
Здесь:
- S – площадь.
- d
- π – константное число, которое в математических расчетах принимается как 3,14.
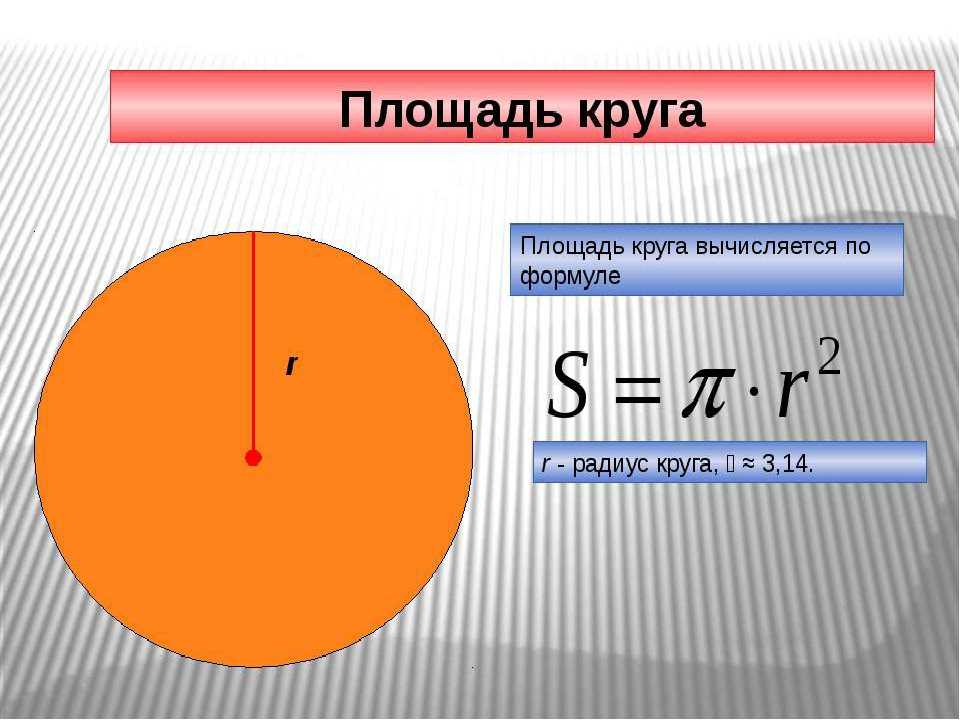
Как найти площадь круга по радиусу: формула
Ищем итоговое значение также по формуле. Это S = π × r2. За число π берем константу 3,14. R – это радиус круга.
Как найти площадь через длину окружности: формула
В математике иногда встречаются задачи, в которых известна длина окружности. В таком случае для решения нужно будет использовать стандартную формулу S = L2 : (4 × π).
Здесь L – это и есть площадь окружности.
Как ускорить процесс обучения: советы специалистов
Есть несколько простых рекомендаций, которые помогают значительно ускорить учебный процесс, помогают быстрее освоиться с тем, как искать площадь круга по разным известным параметрам.
К ним относятся такие, как:
- Убедитесь в том, что ребенок хорошо понимает основные определения. Педагогическая практика показывает, что дети часто путают радиус и диаметр, что приводит к появлению ошибок и выставлению низких оценок учителями.
- В геометрии очень важна наглядность. Все задачи стоит решать исключительно вместе с рисунками круга на бумаге. Это также поможет ребенку значительно быстрее освоиться с использованием циркуля, линейки. Такие навыки сильно помогут в учебе в будущем.
- Не показывайте ученику своего непонимания предмета. Он всегда должен видеть в вас человека, который обладает уверенными знаниями по такому вопросу.
 Не стоит демотивировать его, рассказывать о бесполезности расчетов.
Не стоит демотивировать его, рассказывать о бесполезности расчетов. - Хорошее понимание предмета достигается исключительно через многократное решение задач. Их вы сможете без труда составить своими силами. Все что нужно – ставить условие поиска площади с разными исходными параметрами – длиной окружности, диаметром, радиусом и другими.
- Усложните задачи через введение разных параметров обозначения площади. Есть множество вариантов прописывания площади – это квадратные сантиметры, миллиметры, метры, дециметры и километры. Хорошей математической тренировкой станет перевод разных значений друг в друга. Также можно попробовать посчитать в гектарах. Все это помогает в таких предметах, как геометрия, тригонометрия и математика.
Почему важно тренироваться в решении задач с площадью круга
Мы рассмотрели, как найти площадь круга по формуле. Осталось только ответить на вопрос о том, почему понимание этого вопроса представляет такое большое значение для школьника. Вот лишь несколько важных причин:
- Лучшее понимание геометрических терминов.
 Их
проще всего освоить на практике. Это пригодится при решении значительно более
сложных задач в старших классах.
Их
проще всего освоить на практике. Это пригодится при решении значительно более
сложных задач в старших классах. - Освоение единиц определения площади, решение примеров по переводу величин друг в друга. Это поможет в геометрии и математике. Можно воспользоваться умственным счетом или абакусом, что дополнительно повысит успешность всего учебного процесса.
- Создание базиса для решения комплексных геометрических задач. Они часто направлены на то, чтобы ученик работал с разными фигурами. При этом если пропустить понимание определения площади, радиуса и диаметра круга, длины окружности, в будущем могут возникнуть проблемы, отставание от программы.
Так как в школе дети часто не понимают таких сложных предметов как геометрия до конца, рекомендуем уделить повышенное внимание домашним занятиям. Это нужно делать регулярно и системно, но без сильного давления на школьника, потенциально способного отбить интерес к учебе.
Понравилась статья? Расскажите друзьям:
Читайте также
Рубрика: Образование
Читать все новости
25. 03.2022
03.2022
Подпишитесь на email уведомления
✖
Спасибо, что оставили заявку
Мы скоро свяжемся с вами!
Подпишитесь на группу ВКонтакте
SmartyKidsКак узнать площадь круга если известен диаметр. Площадь круга
– это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом . В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром . Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно : Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.
Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр . Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения .
Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.
Теперь используем данные для примера расчета площади круга по приведенной выше формуле:
Как видим, в результате получаем тот же ответ, что и при первых расчетах.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l
= 8 см. Подставим значение в выведенную формулу:
Итого площадь круга будет равна 5 кв. см.
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a
ее можно найти по теореме Пифагора: отсюда .
После того, как найдем диагональ – мы сможем рассчитать радиус: .
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
В геометрии кругом называется некоторое множество всех точек на плоскости, которые удалены от одной точки, называемой его центром, на расстояние, не большее заданного, называемого его радиусом.
Определение площади круга
При необходимости площадь круга можно вычислить по формуле:
| S | πr 2 | D 2 |
r — радиус круга
D — диаметр круга
S — площадь круга
π — 3.14
Эта геометрическая фигура очень часто встречается как в технике, так и в архитектуре. Конструкторы машин и механизмов разрабатывают различные детали, сечения многих из которых представляют собой именно круг . К примеру, таковыми являются валы, штоки, тяги, цилиндры, оси, поршни и так далее. При изготовлении этих деталей используются заготовки из различных материалов (металлов, древесины, пластических масс), их сечения также представляют собой именно круг . Само собой разумеется, что разработчикам нередко приходится вычислять площадь круга через диаметр или радиус, используя для этой цели несложные математические формулы, открытые еще в глубокой древности.
Именно тогда круглые элементы стали активно и широко использоваться в архитектуре. Один из самых ярки тому примеров – цирк, представляющий собой разновидность строений, предназначенных для проведения в них различных зрелищных мероприятий. Их арены имеют форму круга , а впервые они стали строиться еще во времена античности. Само слово «circus » в переводе с латинского языка означает «круг ». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т. д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить
Архитектурными элементами, которые могут принимать форму круга, являются окна. Конечно, в большинстве случаев они прямоугольные или же квадратные (причем во многом благодаря тому, что это проще как для зодчих, так и для строителей), но в некоторых зданиях можно встретить и круглые окна. Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.
Отнюдь не является редкостью использование круглых элементов для производства мебели, например столов и стульев. Существует даже понятие «круглый стол », которое подразумевает конструктивную дискуссию, в ходе которой происходит всестороннее обсуждение различных важных проблем и вырабатывается пути их решения. Что касается изготовления самих столешниц, имеющих круглую форму, то для их производства применяются специализированные инструменты и оборудование, при условии участия рабочих с довольно высокой квалификацией.
Круг – это видимая совокупность множества точек, которые находятся на одинаковом расстоянии от центра. 2. Другими словами диаметр во 2 степени равен стороне квадрата во 2 степени, умноженной на 2.
2. Другими словами диаметр во 2 степени равен стороне квадрата во 2 степени, умноженной на 2.
Вычислив значение длины диаметра круга, можно узнать и его радиус, после чего воспользоваться одной их формул определения площади круга.
Площадь сектора круга
Сектор – это часть круга, ограниченная 2 радиусами и дугой между ними. Чтобы узнать его площадь, нужно измерить угол сектора. После этого необходимо составить дробь, в числителе которой будет значение угла сектора, а в знаменателе – 360. Чтобы высчитать площадь сектора, значение, полученное в результате деления дроби, нужно умножить на площадь круга, вычисленную по одной из вышеперечисленных формул.
Окружности требуют более аккуратного подхода и встречаются в заданиях B5 гораздо реже. Вместе с тем, общая схема решения даже проще, чем в случае с многоугольниками (см. урок «Площади многоугольников на координатной сетке »).
Все, что требуется в таких заданиях — это найти радиус окружности R
. Затем можно вычислить площадь круга по формуле S
= πR
2 . Из этой формулы также следует, что для решения достаточно найти R
2 .
Из этой формулы также следует, что для решения достаточно найти R
2 .
Чтобы найти указанные величины, достаточно указать на окружности точку, лежащую на пересечении линий сетки. А затем воспользоваться теоремой Пифагора. Рассмотрим конкретные примеры вычисления радиуса:
Задача. Найти радиусы трех окружностей, изображенных на рисунке:
Выполним дополнительные построения в каждой окружности:
В каждом случае точка B выбрана на окружности таким образом, чтобы лежать на пересечении линий сетки. Точка C в окружностях 1 и 3 дополняют фигуру до прямоугольного треугольника. Осталось найти радиусы:
Рассмотрим треугольник ABC в первой окружности. По теореме Пифагора: R 2 = AB 2 = AC 2 + BC 2 = 2 2 + 2 2 = 8.
Для второй окружности все очевидно: R = AB = 2.
Третий случай аналогичен первому. Из треугольника ABC по теореме Пифагора: R 2 = AB 2 = AC 2 + BC 2 = 1 2 + 2 2 = 5.
Теперь мы знаем, как искать радиус окружности (или хотя бы его квадрат). А следовательно, можем найти площадь. Встречаются задачи, где требуется найти площадь сектора, а не всего круга. В таких случаях легко выяснить, какую часть круга составляет этот сектор, и таким образом найти площадь.
А следовательно, можем найти площадь. Встречаются задачи, где требуется найти площадь сектора, а не всего круга. В таких случаях легко выяснить, какую часть круга составляет этот сектор, и таким образом найти площадь.
Задача. Найти площадь S закрашенного сектора. В ответе укажите S /π .
Очевидно, сектор составляет одну четверть круга. Следовательно, S = 0,25 · S круга.
Остается найти S круга — площадь круга. Для этого выполним дополнительное построение:
Треугольник ABC — прямоугольный. По теореме Пифагора имеем: R 2 = AB 2 = AC 2 + BC 2 = 2 2 + 2 2 = 8.
Теперь находим площади круга и сектора: S круга = πR 2 = 8π ; S = 0,25 · S круга = 2π .
Наконец, искомая величина равна S /π = 2.
Площадь сектора при неизвестном радиусе
Это совершенно новый тип задач, ничего подобного в 2010-2011 годах не было. По условию, нам дан круг определенной площади (именно площади, а не радиуса!). Затем внутри этого круга выделяется сектор, площадь которого и требуется найти.
Хорошая новость состоит в том, что подобные задачи — самые легкие из всех задач на площади, которые бывают в ЕГЭ по математике. К тому же, круг и сектор всегда помещается на координатную сетку. Поэтому, чтобы научиться решать такие задачи, просто взгляните на картинку:
Пусть исходный круг имеет площадь S круга = 80. Тогда его можно разделить на два сектора площадью S = 40 каждый (см. 2 шаг). Аналогично, каждый из этих секторов-«половинок» можно снова разделить пополам — получим четыре сектора площадью S = 20 каждый (см. 3 шаг). Наконец, можно разделить каждый из этих секторов еще на два — получим 8 секторов-«ошметков». Площадь каждого из этих «ошметков» составит S = 10.
Обратите внимание: более мелкого разбиения ни в одной задаче ЕГЭ по математике нет! Таким образом, алгоритм решения задачи B-3 следующий:
- Разрезать исходный круг на 8 секторов-«ошметков». Площадь каждого из них составляет ровно 1/8 часть площади всего круга. Например, если по условию круг имеет площадь S круга = 240, то «ошметки» имеют площадь S = 240: 8 = 30;
- Выяснить, сколько «ошметков» помещается в исходном секторе, площадь которого требуется найти.
 Например, если в нашем секторе помещается 3 «ошметка» площадью 30, то площадь искомого сектора равна S
= 3 · 30 = 90. Это и будет ответ.
Например, если в нашем секторе помещается 3 «ошметка» площадью 30, то площадь искомого сектора равна S
= 3 · 30 = 90. Это и будет ответ.
Вот и все! Задача решается практически устно. Если все равно что-то непонятно, купите пиццу и порежьте ее на 8 кусков. Каждый такой кусок будет тем самым сектором-«ошметком», которые можно объединить в более крупные куски.
А теперь разберем примеры из пробного ЕГЭ:
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 40. Найдите площадь заштрихованной фигуры.
Итак, площадь круга равна 40. Разделим его на 8 секторов — каждый площадью S = 40: 5 = 8. Получим:
Очевидно, закрашенный сектор состоит ровно из двух секторов-«ошметков». Следовательно, его площадь равна 2 · 5 = 10. Вот и все решение!
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 64. Найдите площадь заштрихованной фигуры.
Снова разделим весь круг на 8 равных секторов. Очевидно, что площадь одного их них как раз и требуется найти. Следовательно, его площадь равна S
= 64: 8 = 8.
Очевидно, что площадь одного их них как раз и требуется найти. Следовательно, его площадь равна S
= 64: 8 = 8.
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 48. Найдите площадь заштрихованной фигуры.
Опять разделим круг на 8 равных секторов. Площадь каждого из них равна S = 48: 8 = 6. В искомом секторе помещается ровно три сектора-«ошметка» (см. рисунок). Следовательно, площадь искомого сектора равна 3 · 6 = 18.
Калькулятор площади круга
Калькулятор круга
| ||||||||||||
Площадь круга с радиусом 1 равна 3,142 | |
Изображение кружка = 1d = 2C = 6,28 | А = πr 2 = π(d2) 2 А = С 2 4π π = 3,1415A = площадь C = окружность или периметр r = радиус , d = диаметр |
Площадь круга в пересчете на
радиусов :Площадь = π·r 2 = 3,14·1 2 = 3,14 квадратных метров (*)
Площадь круга относительно
диаметра :Площадь = π·(d2) 2 = 3,14·(22) 2 = 3,14·(1) 2 = 3,14 квадратных метров (*)
Площадь круга в пересчете на
окружность :Площадь = С 2 4π = 6,28 2 4π = 39,48(4·3,14) = 39,4812,56 = 3,14 квадратных метров (*)
(*) 3,1415 Примечание: для простоты указанные выше операции были округлены до 2 знаков после запятой, а число π округлено до 3,14.5898 метров, точно или ограничено точностью этого калькулятора (13 знаков после запятой). 
Круг радиусом = 1, или диаметром = 2, или окружностью = 6,283 метра, имеет площадь:
- 3,142E-6 квадратных километров (км²)
- 3,142 квадратных метра (м²)
- 31420 квадратных сантиметров (см²)
- 3142000 квадратных миллиметров (мм²)
- 1,21313E-6 квадратных миль (ми²)
- 3,7578 квадратных ярдов (ярдов²)
- 33,8202 квадратных футов (фут²)
- 790 4870,11 квадратных дюймов
Используйте приведенный ниже калькулятор площади круга, чтобы найти площадь круга по заданному радиусу или другим параметрам. Для расчета площади вам достаточно ввести положительное числовое значение в одно из 3-х полей калькулятора. Вы также можете увидеть в нижней части калькулятора пошаговое решение.
Формула площади круга
Вот три способа нахождения площади круга (формулы):
Формула площади круга в пересчете на радиус
A = πr 2
Формула площади круга в пересчете на радиус диаметр
A = π(d2) 2
Формула площади круга в пересчете на длину окружности
A = C 2 4π
См. ниже некоторые определения, относящиеся к формулам: расстояние вокруг края круга.
ниже некоторые определения, относящиеся к формулам: расстояние вокруг края круга.
Радиус
Радиусом круга является любой из отрезков линии от его центра до периметра. Радиус равен половине диаметра или r = d2.
Диаметр
Диаметром окружности называется любой отрезок прямой линии, проходящий через центр окружности и концы которого лежат на окружности. Диаметр в два раза больше радиуса или d = 2·r.
Греческая буква π
π обозначает число Пи, которое определяется как отношение длины окружности к ее диаметру или π = Cd . Для простоты можно использовать Pi = 3,14 или Pi = 3,1415. Пи — иррациональное число. Первые 100 цифр числа Пи: 3,14159.26535 8979323846 2643383279 5028841971 6939937510 5820974944 5
Примечание. (in²) и так далее…
Окружность часто неправильно пишется как окружность.
Таблица, показывающая соотношение радиусов. Диаметр. Площадь и окружность круга
Примечание. Все значения округлены до двух знаков после запятой.
Все значения округлены до двух знаков после запятой.
| Radius | Diameter | Area | Circumference | ||||
|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.03 | 0.63 | ||||
| 0.15 | 0.3 | 0.07 | 0.94 | ||||
| 0.2 | 0,4 | 0,13 | 1,26 | ||||
| 0,25 | 0,5 | 0,2 | 1,57 | ||||
| 0,3 | 0,6 | 0.28 | 1.88 | ||||
| 0.35 | 0.7 | 0.38 | 2.2 | ||||
| 0.4 | 0.8 | 0.5 | 2.51 | ||||
| 0.45 | 0.9 | 0.64 | 2.83 | ||||
| 0,5 | 1 | 0,79 | 3,14 | ||||
| 0,55 | 1,1 | 0,95 | 3,46 | ||||
| 0,6 | 1.2 | ||||||
| 0,6 | ,10009 | ||||||
| 0,6 | ,2 1. 13 13 | 3.77 | |||||
| 0.65 | 1.3 | 1.33 | 4.08 | ||||
| 0.7 | 1.4 | 1.54 | 4.4 | ||||
| 0.75 | 1.5 | 1.77 | 4.71 | ||||
| 0,8 | 1,6 | 2,01 | 5,03 | ||||
| 0,85 | 1,7 | 2,27 | 5,34 | ||||
| 0,9 | 1,8 | ||||||
| 0,9 | 1,8 | 00092.54 | 5.65 | ||||
| 0.95 | 1.9 | 2.83 | 5.97 | ||||
| 1 | 2 | 3.14 | 6.28 | ||||
| 1.01 | 2.02 | 3.2 | 6.35 | ||||
| 1,02 | 2,04 | 3,27 | 6,41 | ||||
| 1,03 | 2,06 | 3,33 | 6,47 | ||||
| 1,04 | 2,08 97999 | ||||||
| 1,04 | 2,08 97999 | ||||||
| 1,04 | 9000 2,08 97999|||||||
| 1,04 | 9000 2,08 97999|||||||
| 1,04 | 9000 2,0009 3. 4 4 | 6.53 | |||||
| 1.05 | 2.1 | 3.46 | 6.6 | ||||
| 1.06 | 2.12 | 3.53 | 6.66 | ||||
| 1.07 | 2.14 | 3.59 | 6.72 | ||||
| 1,08 | 2,16 | 3,66 | 6.79 | ||||
| 1,09 | 2,18 | 3,73 | 6,85 | ||||
| 1.1 | ,85|||||||
| 1.1 | .0008 2.23.8 | 6.91 | |||||
| 1.10 | 2.2 | 3.8 | 6.91 | ||||
| 1.11 | 2.22 | 3.87 | 6.97 | ||||
| 1.12 | 2.24 | 3.94 | 7.04 | ||||
| 1,13 | 2,26 | 4,01 | 7,1 | ||||
| 1,14 | 2,28 | 4,08 | 7,16 | ||||
| 1.15 | 7,16 | ||||||
| 1,15 | 0009 2. 3 3 | 4.15 | 7.23 | ||||
| 1.16 | 2.32 | 4.23 | 7.29 | ||||
| 1.17 | 2.34 | 4.3 | 7.35 | ||||
| 1.18 | 2.36 | 4.37 | 7.41 | ||||
| 1,19 | 2,38 | 4,45 | 7,48 | ||||
| 1,2 | 2,4 | 4,52 | 7,54 | ||||
| 4,52 | 7,54 | ||||||
| 0008 1.20 | 2.4 | 4.52 | 7.54 | ||||
| 1.21 | 2.42 | 4.6 | 7.6 | ||||
| 1.22 | 2.44 | 4.67 | 7.67 | ||||
| 1.23 | 2.46 | 4.75 | 7,73 | ||||
| 1,24 | 2,48 | 4,83 | 7,79 | ||||
| 1,25 | 2,5 | 4,91 | 7,85 | 4,91 | 7,85 | 0007 | 1. 26 26 | 2.52 | 4.99 | 7.92 |
| 1.27 | 2.54 | 5.06 | 7.98 | ||||
| 1.28 | 2.56 | 5.14 | 8.04 | ||||
| 1.29 | 2.58 | 5,23 | 8.11 | ||||
| 1,3 | 2,6 | 5,31 | 8,17 | ||||
| 1,30 | 2,6 | 5,31 | 8.17 | 2,6 | 5,31 | 8,17 | |
| 1.31 | 2.62 | 5.39 | 8.23 | ||||
| 1.32 | 2.64 | 5.47 | 8.29 | ||||
| 1.33 | 2.66 | 5.55 | 8.36 | ||||
| 1.34 | 2.68 | 5.64 | 8.42 | ||||
| 1,35 | 2,7 | 5,72 | 8,48 | ||||
| 1,36 | 2,72 | 5,81 | 8.54 | 2,72 | 5,81 | 8.54 | 2,72 | 0009
1. 37 37 | 2.74 | 5.89 | 8.61 | ||||
| 1.38 | 2.76 | 5.98 | 8.67 | ||||
| 1.39 | 2.78 | 6.07 | 8.73 | ||||
| 1.4 | 2.8 | 6.15 | 8,8 | ||||
| 1,40 | 2,8 | 6,15 | 8,8 | ||||
| 1,41 | 2,82 | 6,24 | 8,86 | 2,82 | 6,24 | 8,86 | 2,820009 |
| 1.42 | 2.84 | 6.33 | 8.92 | ||||
| 1.43 | 2.86 | 6.42 | 8.98 | ||||
| 1.44 | 2.88 | 6.51 | 9.05 | ||||
| 1.45 | 2.9 | 6.6 | 9.11 | ||||
| 1,46 | 2,92 | 6,69 | 9,17 | ||||
| 1,47 | 2,94 | 6,79 | 2,94 | 6,79 | 0008 9.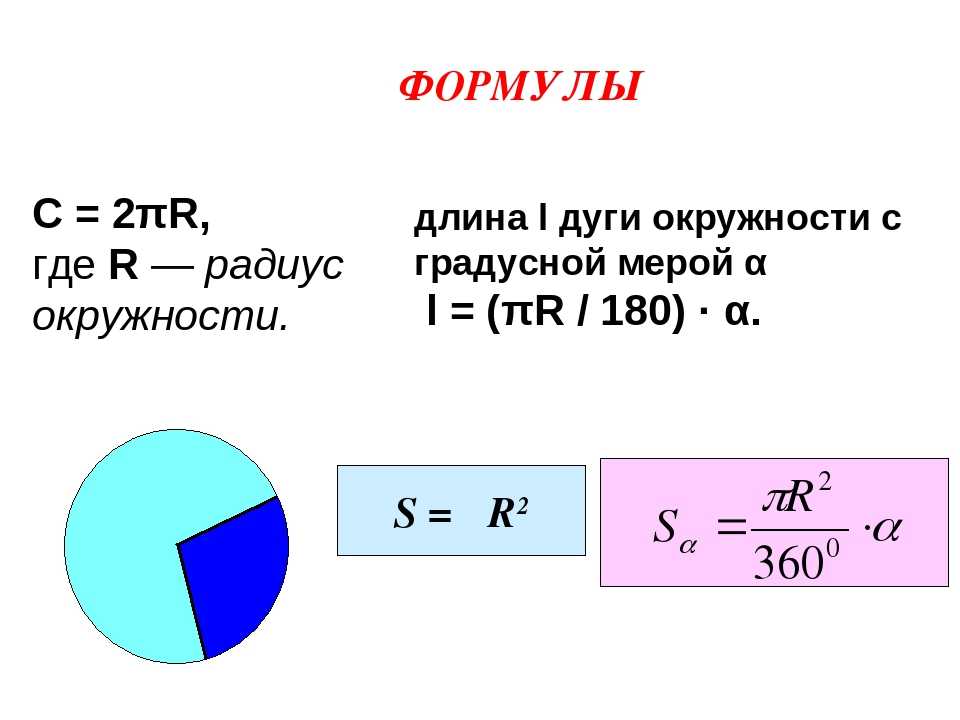 24 24 | ||
| 1.48 | 2.96 | 6.88 | 9.3 | ||||
| 1.49 | 2.98 | 6.97 | 9.36 | ||||
| 1.5 | 3 | 7.07 | 9.42 | ||||
| 1.50 | 3 | 7.07 | 9.42 | ||||
| 1,51 | 3,02 | 7,16 | 9,49 | ||||
| 1,52 | 3,04 | 7.25 | 1,52 | 3,04 | 7.25 | 0009 | 9.55 |
| 1.53 | 3.06 | 7.35 | 9.61 | ||||
| 1.54 | 3.08 | 7.45 | 9.68 | ||||
| 1.55 | 3.1 | 7.54 | 9.74 | ||||
| 1.56 | 3,12 | 7,64 | 9,8 | ||||
| 1,57 | 3,14 | 7,74 | 9,86 | ||||
| 1,58 | 3,1699 9000 | 7.84 | 9.93 | ||||
1. 59 59 | 3.18 | 7.94 | 9.99 | ||||
| 1.6 | 3.2 | 8.04 | 10.05 | ||||
| 1.60 | 3.2 | 8.04 | 10.05 | ||||
| 1,61 | 3,22 | 8.14 | 10.12 | ||||
| 1,62 | 3,24 | 8.24 | 10,18 | ||||
| 1,63 | 3,26 9009 | ||||||
| 1,63 | 3,26 9009 | ||||||
| 1,63 | 3,269 | 00098.34 | 10.24 | ||||
| 1.64 | 3.28 | 8.45 | 10.3 | ||||
| 1.65 | 3.3 | 8.55 | 10.37 | ||||
| 1.66 | 3.32 | 8.65 | 10.43 | ||||
| 1,67 | 3,34 | 8.76 | 10,49 | ||||
| 1,68 | 3,36 | 8,86 | 10,56 | ||||
| 1.69 | 10,56 | ||||||
1. 69 69 | 10,56 | ||||||
| 1.69 | 10,56 | ||||||
| 1.69 | 10,56 | ||||||
| 1.69 | 10,56 | ||||||
| 1.69 | 10,56 | ||||||
| 1,69 | 00093.38 | 8.97 | 10.62 | ||||
| 1.7 | 3.4 | 9.07 | 10.68 | ||||
| 1.70 | 3.4 | 9.07 | 10.68 | ||||
| 1.71 | 3.42 | 9.18 | 10.74 | ||||
| 1,72 | 3,44 | 9.29 | 10,81 | ||||
| 1,73 | 3,46 | 9,4 | 10,87 | ||||
| 9,4 | 10,87 | ||||||
| 0008 1.74 | 3.48 | 9.51 | 10.93 | ||||
| 1.75 | 3.5 | 9.62 | 11 | ||||
| 1.76 | 3.52 | 9.73 | 11.06 | ||||
| 1.77 | 3. 54 54 | 9.84 | 11.12 | ||||
| 1,78 | 3,56 | 9,95 | 11,18 | ||||
| 1,79 | 3,58 | 10,06 | 11,25 | 10,06 | 11,25 | ||
| 1.8 | 3.6 | 10.17 | 11.31 | ||||
| 1.80 | 3.6 | 10.17 | 11.31 | ||||
| 1.81 | 3.62 | 10.29 | 11.37 | ||||
| 1.82 | 3.64 | 10.4 | 11,44 | ||||
| 1,83 | 3,66 | 10,52 | 11,5 | ||||
| 1,84 | 3,68 | 10,63 | 11.56 | ||||
| 1.85 | 3.7 | 10.75 | 11.62 | ||||
| 1.86 | 3.72 | 10.86 | 11.69 | ||||
| 1.87 | 3.74 | 10.98 | 11.75 | ||||
| 1.88 | 3,76 | 11,1 | 11,81 | ||||
| 1,89 | 3,78 | 11,22 | 11,87 | ||||
| 1,9 | 3,8 | ||||||
| 1,9 0009 | 3,8 | ||||||
| 1,9 | 3,8 900 | 11. 34 34 | 11.94 | ||||
| 1.90 | 3.8 | 11.34 | 11.94 | ||||
| 1.91 | 3.82 | 11.46 | 12 | ||||
| 1.92 | 3.84 | 11.58 | 12.06 | ||||
| 1,93 | 3,86 | 11,7 | 12.13 | ||||
| 1,94 | 3,88 | 11,82 | 12.19 | ||||
| 1.95 | 3.9 | 11.94 | 12.25 | ||||
| 1.96 | 3.92 | 12.06 | 12.31 |
| Radius | Diameter | Area | Circumference | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.97 | 3,94 | 12.19 | 12,38 | ||||||||
| 1,98 | 3,96 | 12,31 | 12,44 | ||||||||
| 1,99 | 3.98 | 12.43 | 12.5 | ||||||||
| 2 | 4 | 12. 56 56 | 12.57 | ||||||||
| 2.00 | 4 | 12.56 | 12.57 | ||||||||
| 2.01 | 4.02 | 12.69 | 12.63 | ||||||||
| 2,02 | 4,04 | 12,81 | 12,69 | ||||||||
| 2,03 | 4,06 | 12,94 | 12,75 | ||||||||
| 0008 2.04 | 4.08 | 13.07 | 12.82 | ||||||||
| 2.05 | 4.1 | 13.2 | 12.88 | ||||||||
| 2.06 | 4.12 | 13.32 | 12.94 | ||||||||
| 2.07 | 4.14 | 13.45 | 13,01 | ||||||||
| 2,08 | 4,16 | 13,58 | 13,07 | ||||||||
| 2,09 | 4,18 | 13,72 | 13.13 | 0009 | |||||||
| 2.1 | 4.2 | 13.85 | 13.19 | ||||||||
| 2.10 | 4.2 | 13.85 | 13.19 | ||||||||
2. 11 11 | 4.22 | 13.98 | 13.26 | ||||||||
| 2.12 | 4.24 | 14.11 | 13,32 | ||||||||
| 2,13 | 4,26 | 14.25 | 13,38 | ||||||||
| 2,14 | 4,28 | 14.38 | 2,14 | 4,28 | 14.38 | 2,14 | 4,28 | 14.38 | 2,14 | 000913.45 | |
| 2.15 | 4.3 | 14.51 | 13.51 | ||||||||
| 2.16 | 4.32 | 14.65 | 13.57 | ||||||||
| 2.17 | 4.34 | 14.79 | 13.63 | ||||||||
| 2.18 | 4,36 | 14,92 | 13,7 | ||||||||
| 2,19 | 4,38 | 15,06 | 13,76 | ||||||||
| 2,2 | 4.4 | ||||||||||
| 2,2 | 4.4 | ||||||||||
| 2,2 | 4.4 | 000915.2 | 13.82 | ||||||||
| 2.20 | 4.4 | 15. 2 2 | 13.82 | ||||||||
| 2.21 | 4.42 | 15.34 | 13.89 | ||||||||
| 2.22 | 4.44 | 15.48 | 13.95 | ||||||||
| 2,23 | 4,46 | 15,61 | 14,01 | ||||||||
| 2,24 | 4,48 | 15,76 | 14,07 | ||||||||
| 2,25 | 00094.5 | 15.9 | 14.14 | ||||||||
| 2.26 | 4.52 | 16.04 | 14.2 | ||||||||
| 2.27 | 4.54 | 16.18 | 14.26 | ||||||||
| 2.28 | 4.56 | 16.32 | 14.33 | ||||||||
| 2,29 | 4,58 | 16,47 | 14,39 | ||||||||
| 2,3 | 4,6 | 16,61 | 14,45 | 16,61 | 14,45 | 16,61 | 14,45 | 16,6114,45 | 9000|||
| 2.30 | 4. 6 6 | 16.61 | 14.45 | ||||||||
| 2.31 | 4.62 | 16.76 | 14.51 | ||||||||
| 2.32 | 4.64 | 16.9 | 14.58 | ||||||||
| 2.33 | 4.66 | 17,05 | 14,64 | ||||||||
| 2,34 | 4,68 | 17,19 | 14,7 | ||||||||
| 2,35 | 4,7 | 17,34 | 14,77 | 4,7 | 17,34 | 14,77 | 0009 | ||||
| 2.36 | 4.72 | 17.49 | 14.83 | ||||||||
| 2.37 | 4.74 | 17.64 | 14.89 | ||||||||
| 2.38 | 4.76 | 17.79 | 14.95 | ||||||||
| 2.39 | 4.78 | 17,94 | 15,02 | ||||||||
| 2,4 | 4,8 | 18,09 | 15,08 | ||||||||
| 2,40 | 4,8 | 18.09. | 15.08 | ||||||||
| 2.41 | 4. 82 82 | 18.24 | 15.14 | ||||||||
| 2.42 | 4.84 | 18.39 | 15.2 | ||||||||
| 2.43 | 4.86 | 18.54 | 15.27 | ||||||||
| 2.44 | 4,88 | 18,69 | 15,33 | ||||||||
| 2,45 | 4,9 | 18,85 | 15,39 | ||||||||
| 2,46 | 4.9.39 | ||||||||||
| 2,46 | 4.9.2 | 19 | 15.46 | ||||||||
| 2.47 | 4.94 | 19.16 | 15.52 | ||||||||
| 2.48 | 4.96 | 19.31 | 15.58 | ||||||||
| 2.49 | 4.98 | 19.47 | 15.64 | ||||||||
| 2,5 | 5 | 19,63 | 15,71 | ||||||||
| 2,50 | 5 | 19,63 | 15,71 | ||||||||
| 2,51 | 15,71 | ||||||||||
| 2,51 | 0009 | 5.02 | 19.78 | 15.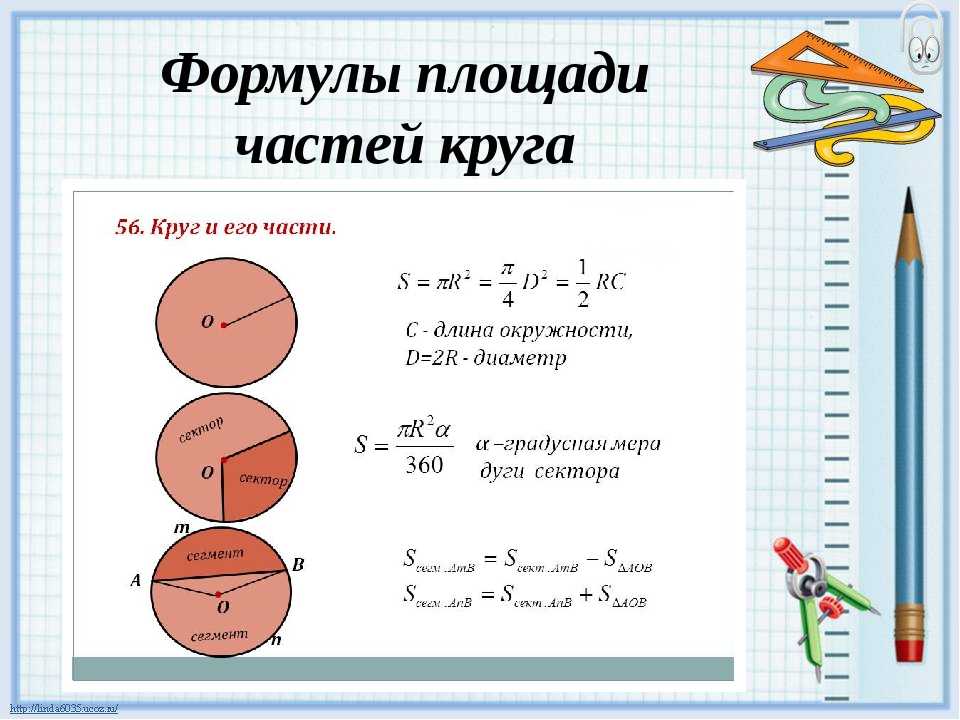 77 77 | |||||||
| 2.52 | 5.04 | 19.94 | 15.83 | ||||||||
| 2.53 | 5.06 | 20.1 | 15.9 | ||||||||
| 2.54 | 5.08 | 20.26 | 15,96 | ||||||||
| 2,55 | 5,1 | 20,42 | 16,02 | ||||||||
| 2,56 | 5,12 | 20,58 | 16.08 | 16,08 | 20,58 | 16,08 | 9000|||||
| 2.57 | 5.14 | 20.74 | 16.15 | ||||||||
| 2.58 | 5.16 | 20.9 | 16.21 | ||||||||
| 2.59 | 5.18 | 21.06 | 16.27 | ||||||||
| 2.6 | 5.2 | 21.23 | 16,34 | ||||||||
| 2,60 | 5,2 | 21,23 | 16,34 | ||||||||
| 2,61 | 5,22 | 21,39 | 16,4 | 0009 | |||||||
2. 62 62 | 5.24 | 21.55 | 16.46 | ||||||||
| 2.63 | 5.26 | 21.72 | 16.52 | ||||||||
| 2.64 | 5.28 | 21.88 | 16.59 | ||||||||
| 2.65 | 5.3 | 22,05 | 16,65 | ||||||||
| 2,66 | 5,32 | 22,22 | 16,71 | ||||||||
| 2,67 | 5.34 | 22,38 | 2,67 | 5.34 | 22,38 | 2,67 | 5,34 | 22,38 | 2,67 | 0009 | 16.78 |
| 2.68 | 5.36 | 22.55 | 16.84 | ||||||||
| 2.69 | 5.38 | 22.72 | 16.9 | ||||||||
| 2.7 | 5.4 | 22.89 | 16.96 | ||||||||
| 2.70 | 5.4 | 22,89 | 16,96 | ||||||||
| 2,71 | 5,42 | 23,06 | 17,03 | ||||||||
| 2,72 | 5,44 9009 | ||||||||||
| 2,72 | . 0009 0009 | 23.23 | 17.09 | ||||||||
| 2.73 | 5.46 | 23.4 | 17.15 | ||||||||
| 2.74 | 5.48 | 23.57 | 17.22 | ||||||||
| 2.75 | 5.5 | 23.75 | 17.28 | ||||||||
| 2,76 | 5,52 | 23,92 | 17,34 | ||||||||
| 2,77 | 5,54 | 24,09 | 17,4 | ||||||||
| 2.78 | 00095.56 | 24.27 | 17.47 | ||||||||
| 2.79 | 5.58 | 24.44 | 17.53 | ||||||||
| 2.8 | 5.6 | 24.62 | 17.59 | ||||||||
| 2.80 | 5.6 | 24.62 | 17,59 | ||||||||
| 2,81 | 5,62 | 24,79 | 17,66 | ||||||||
| 2,82 | 5,64 | 24.97 | 17,72 | 17,72 | 24.97 | 17,72 | 9000|||||
2. 83 83 | 5.66 | 25.15 | 17.78 | ||||||||
| 2.84 | 5.68 | 25.33 | 17.84 | ||||||||
| 2.85 | 5.7 | 25.5 | 17.91 | ||||||||
| 2.86 | 5.72 | 25,68 | 17,97 | ||||||||
| 2,87 | 5,74 | 25,86 | 18,03 | ||||||||
| 2,88 | 5,76 | 26,04 | 18,1 | 5,76 | 26,04 | 18,1 | 0009 | ||||
| 2.89 | 5.78 | 26.23 | 18.16 | ||||||||
| 2.9 | 5.8 | 26.41 | 18.22 | ||||||||
| 2.90 | 5.8 | 26.41 | 18.22 | ||||||||
| 2.91 | 5.82 | 26,59 | 18.28 | ||||||||
| 2,92 | 5,84 | 26,77 | 18,35 | ||||||||
| 2,93 | 5,86 | 26,9.9. | |||||||||
| 5,86 | 26,9,9 0007 2,93 | 5,86 | 26,9,9,9,9,9,9,9,9,9,97 | 2,93 | 6 | 18. 41 41 | |||||
| 2.94 | 5.88 | 27.14 | 18.47 | ||||||||
| 2.95 | 5.9 | 27.33 | 18.53 | ||||||||
| 2.96 | 5.92 | 27.51 | 18.6 | ||||||||
| 2.97 | 5,94 | 27,7 | 18,66 | ||||||||
| 2,98 | 5,96 | 27,88 | 18,72 | ||||||||
| 299 | 5,9,9,72 | ||||||||||
| 299 | 5,9,9,8 | 28.07 | 18.79 | ||||||||
| 3 | 6 | 28.26 | 18.85 | ||||||||
| 3.00 | 6 | 28.26 | 18.85 | ||||||||
| 3.01 | 6.02 | 28.45 | 18.91 | ||||||||
| 3,02 | 6.04 | 28,64 | 18,97 | ||||||||
| 3,03 | 6,06 | 28,83 | 19,04 | ||||||||
| 3,04 | 19,04 | ||||||||||
| 3,04 | 0009 6. 08 08 | 29.02 | 19.1 | ||||||||
| 3.05 | 6.1 | 29.21 | 19.16 | ||||||||
| 3.06 | 6.12 | 29.4 | 19.23 | ||||||||
| 3.07 | 6.14 | 29.59 | 19.29 | ||||||||
| 3,08 | 6.16 | 29,79 | 19,35 | ||||||||
| 3,09 | 6,18 | 29,98 | 19,41 | 29,98 | 19,41 | 29,98 | 19,41 | 9000||||
| 3,1 | 6.2 | 30.18 | 19,48 |
Расчеты круга. 19,3 ярда
- Площадь круга диаметром 6,3 дюйма
- Площадь круга радиусом 10,6
- Площадь круга диаметром 32
- Площадь круга радиусом 6,9сантиметры
- Площадь круга радиусом 5,1 дюйма
- Площадь круга радиусом 16 миль
Отказ от ответственности
Несмотря на то, что мы прилагаем все усилия для обеспечения точности информации, представленной на этом веб-сайте, ни этот веб-сайт, ни его авторы несут ответственность за любые ошибки или упущения. Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.
Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.
Формула площади круга
Площадь круга
- Формула
- Резюме
- Применение
- Примеры
- Пример 1
- Пример 2
- Пример 3
- Объяснение
Формула
Сводка
Площадь круга определяется путем умножения константы круга (тау) на квадрат радиуса круга.
| Выражение | Описание |
|---|---|
| Площадь круга. | |
| Постоянная окружности (тау), где | |
| Радиус окружности. |
Примечание: Этот веб-сайт использует константу (тау) вместо (пи) в качестве постоянной окружности по умолчанию. Подстановку можно использовать для перевода между двумя константами.
Подстановку можно использовать для перевода между двумя константами.
Использование
Площадь круга определяется путем умножения константы круга (тау) на квадрат радиуса круга. Например, чтобы найти площадь круга с радиусом длины, формула:
Площадь круга с радиусом длины равна единицам в квадрате. Это значение можно подставить в выражение, чтобы вычислить площадь, равную приблизительно единицам в квадрате.
Примеры
Площадь радиуса окружности 1
Чтобы вычислить площадь круга при радиусе, равном единице, составьте уравнение для площади круга и подставьте значение радиуса в уравнение.
Установите формулу.
Подставьте радиус вместо переменной .
Вычислите выражение экспоненты.
Вычислите выражение умножения.
Площадь круга равна единицам в квадрате.
Площадь радиуса окружности 2
Чтобы вычислить площадь круга при радиусе, равном единице, составьте уравнение для площади круга и подставьте значение радиуса в уравнение.
Установите формулу.
Подставьте радиус вместо переменной .
Вычислите выражение экспоненты.
Вычислите выражение умножения.
Площадь круга равна единицам в квадрате или приблизительно равна единицам в квадрате.
Площадь радиуса окружности 3
Чтобы вычислить площадь круга при радиусе, равном единице, составьте уравнение для площади круга и подставьте значение радиуса в уравнение.
Установите формулу.
Подставьте радиус вместо переменной .
Вычислите выражение экспоненты.
Вычислите выражение умножения.
Площадь круга равна единицам в квадрате или приблизительно равна единицам в квадрате.
Пояснение
Формула площади круга может быть получена несколькими способами с помощью исчисления [1] или с помощью визуального доказательства, как показано ниже.

 Не стоит демотивировать его, рассказывать о бесполезности расчетов.
Не стоит демотивировать его, рассказывать о бесполезности расчетов. Их
проще всего освоить на практике. Это пригодится при решении значительно более
сложных задач в старших классах.
Их
проще всего освоить на практике. Это пригодится при решении значительно более
сложных задач в старших классах.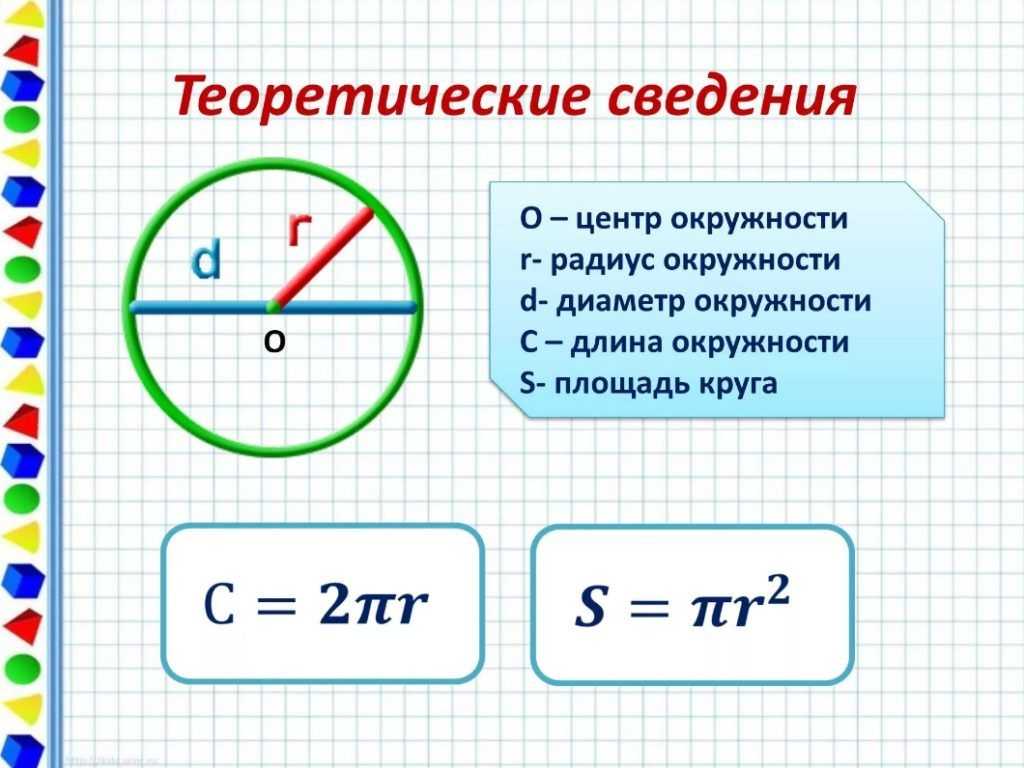 Например, если в нашем секторе помещается 3 «ошметка» площадью 30, то площадь искомого сектора равна S
= 3 · 30 = 90. Это и будет ответ.
Например, если в нашем секторе помещается 3 «ошметка» площадью 30, то площадь искомого сектора равна S
= 3 · 30 = 90. Это и будет ответ.