Нахождение обратной функции – , , .

Взаимно обратные функции, основные определения, свойства, графики

Понятие обратной функции

Допустим, что у нас есть некая функция y=f(x), которая является строго монотонной (убывающей или возрастающей) и непрерывной на области определения x∈a; b; область ее значений y∈c; d, а на интервале c; d при этом у нас будет определена функция x=g(y) с областью значений a; b. Вторая функция также будет непрерывной и строго монотонной. По отношению к y=f(x) она будет обратной функцией. То есть мы можем говорить об обратной функции x=g(y) тогда, когда y=f(x) на заданном интервале будет либо убывать, либо возрастать.

Две этих функции, f и g, будут взаимно обратными.

Yandex.RTB R-A-339285-1

Для чего вообще нам нужно понятие обратных функций?

Это нужно нам для решения уравнений y=f(x), которые записываются как раз с помощью этих выражений.

Нахождение взаимно обратных функций

Допустим, нам нужно найти решение уравнения cos(x)=13. Его решениями будут две точки: x=±arcocs13+2π·k, k∈Z 

Обратными по отношению друг к другу будут, например, функции арккосинуса и косинуса.

Разберем несколько задач на нахождение функций, обратных заданным.

Пример 1

Условие: какая функция будет обратной для y=3x+2?

Решение

Область определений и область значений функции, заданной в условии, – это множество всех действительных чисел. Попробуем решить данное уравнение через x, то есть выразив  x через y.

Мы получим x=13y-23. Это и есть нужная нам обратная функция, но y здесь будет аргументом, а x — функцией. Переставим их, чтобы получить более привычную форму записи:

y=13x-23 

Ответ: функция y=13x-23 будет обратной для y=3x+2.

Обе взаимно обратные функции можно отобразить на графике следующим образом:

Мы видим симметричность обоих графиков относительно y=x. Эта прямая является биссектрисой первого и третьего квадрантов. Получилось доказательство одного из свойств взаимно обратных функций, о котором мы поговорим далее.

Возьмем пример, в котором нужно найти логарифмическую функцию, обратную заданной показательной.

Пример 2

Условие: определите, какая функция будет обратной для y=

zaochnik.com

Определение функции, обратная функция. Видеоурок. Алгебра 10 Класс

На этом уроке мы рассмотрим важнейшие понятия в математике – функция и обратная функция. Мы вспомним, как построить график функции. Кроме того, рассмотрим метод нахождения функции, обратной данной, и решим примеры на нахождение обратной функции и построение ее графика.

Пусть  и  – это два множества.

Функция  – это соответствие, которое каждому элементу из множества  сопоставляет единственный элемент из множества .

Природа элементов множества  и  может быть любая, например числа.

Если даны числовое множество  и правило , позволяющее поставить в соответствие каждому элементу  из множества  определенное число , то говорят, что задана функция   с областью определения .

Областью определения функции  называют множество всех значений , для которых функция имеет смысл.

Множество всех значений функции ,  называют областью значений функции. 

,  

 – независимая переменная (аргумент)

 – зависимая переменная

 – область определения функции

 – область значения функции

 

Графиком функции называется множество всех точек (на координатной плоскости) вида , где .

Примеры

1. ; .

Графиком этой функции является часть гиперболы (см. Рис. 1). Область определения – это проекция графика на ось , область значения – это проекция графика на ось .

Область определения: .

Область значения: .

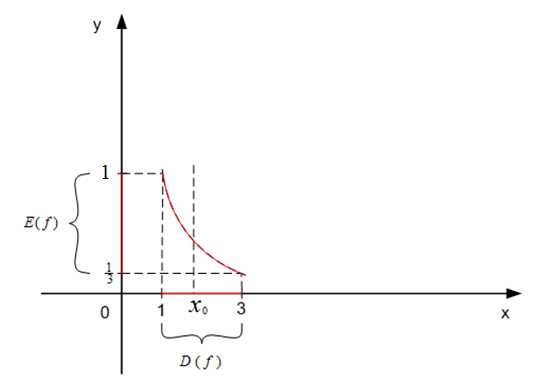
Рис. 1. График функции ;

Любая вертикальная прямая  (если  принадлежит области определения) пересекает график в единственной точке, так как, согласно определению функции, закон  такой, что каждому значению аргумента соответствует только одно значение функции.

2.  (см. Рис. 2).

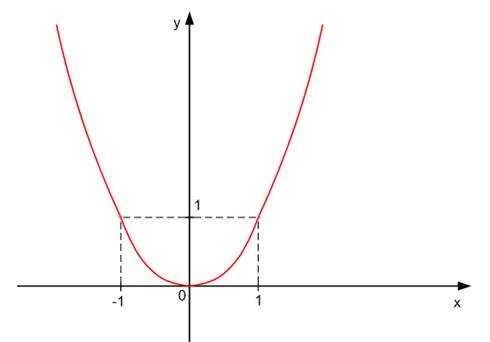
Рис. 2. График функции

Область определения: .

Область значения: .

3. ;  (см. Рис. 3).

Рис. 3. График функции;

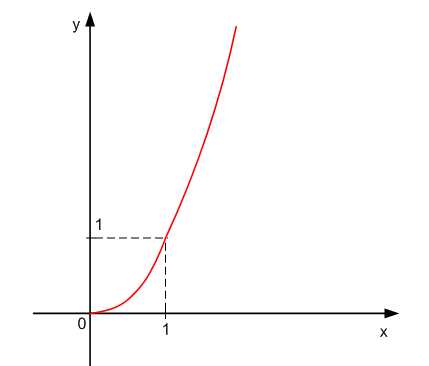
Область определения: .

Область значения: .

4. ;  (см. Рис. 4).

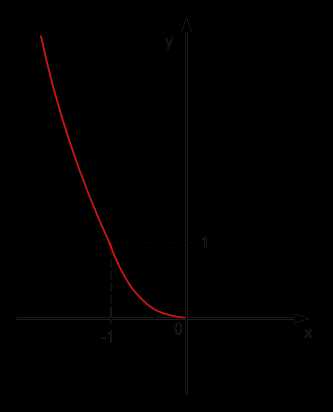
Рис. 4. График функции ;

Область определения: .

Область значения: .

В монотонной функции каждое значение  достигается только при одном значении  (на рисунке 5 показан пример графика монотонно возрастающей функции). То есть уравнение , где , имеет только одно решение ( достигается при единственном значении ).

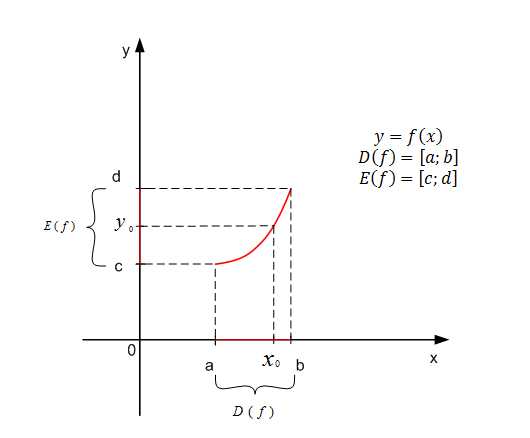
Рис. 5. График монотонной функции

Пусть  – это монотонная функция. Следовательно, каждому  из области значения сопоставляется единственное значение  из области определения. Тем самым задается функция, которая называется обратной, и обозначается . В этом случае независимой переменной является , а зависимой – .

Обратная функция устанавливает взаимно однозначное соответствие между множеством значений и областью определения прямой функции.

 

У каждой монотонной функции есть обратная функция. Однако многие функции кусочно монотонные, обратные функции у них будут существовать только в тех интервалах, где они монотонны.

Например:

1. Функция  (см. Рис. 2) немонотонная,  достигается при  и при , следовательно, на всей области определения для этой функции не существует обратной.

2. Функция ;  (см. Рис. 3) монотонная (возрастающая), например,  достигается только при , следовательно, для нее существует обратная функция.

3. Функция ;  (см. Рис. 4) монотонная (убывающая), например,  достигается только при , следовательно, для нее существует обратная функция.

Графиком обратной функции называется множество всех точек (на координатной плоскости) вида , где .

Графики прямой и обратной функции симметричны относительно прямой

interneturok.ru

Как найти обратную функцию для данной

Обратной функцией называют функцию, обращающую начальную связанность у = f(x) таким образом, что довод х и функция у меняются ролями. То есть х становится функцией от y (х = f(у)). При этом графики взаимно обратных функций у = f (x) и х = f (у) симметричны по отношению к оси ординат в первой и третьей координатных четвертях декартовой системы. Областью определения обратной функции является область значений начальной, а областью значений в свою очередь – область определения заданной функции.

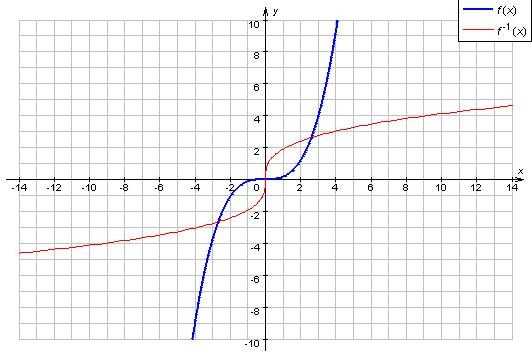
Инструкция

1. В всеобщем случае при нахождении обратной функции для заданной у = f(x) выразите довод х через функцию у. Для этого воспользуйтесь правилами умножения обеих частей равенства на одно и то же значение, переносом многочленов выражений, при этом рассматривайте смену знака. В простом случае рассмотрения показательных функций вида: y = (7/x) + 11, обращение довода х производится элементарно: 7/x = у-11, х = 7*(у-11). Желанная обратная функция имеет вид х = 7*(у-11).

2. Впрочем нередко в функциях применяются трудные степенные и логарифмические выражения, а также тригонометрические функции. В этом случае при нахождении обратной функции необходимо рассматривать знаменитые свойства данных математических выражений.

3. Если в начальной функции довод х стоит под степенью, для приобретения обратной функции возьмите от данного выражения корень с тем же показателем. Скажем, для заданной функции у = 7+ х? обратная будет иметь вид: f(у) = ?у -7.

4. При рассмотрении функции, где довод х представляет собой степень непрерывного числа, примените определение логарифма. Из него следует, что для функции f(х) = ах обратной будет являться f(у) = logаy, причем основание логарифма а – в обоих случаях число, хорошее от нуля. Так же и напротив, рассматривая начальную логарифмическую функцию f(х) = logах, ее обратная функция представляет собой степенное выражение: f(у) = ау.

5. В частном случае изыскания функции, содержащей естественный логарифм ln х либо десятичный lg х, т.е. логарифмы по основанию числа е и 10 соответственно, приобретение обратной функции проводится подобно, только взамен основания а подставляется экспоненциальное число либо число 10. Скажем, f(х) = lg х -> f(у) = 10у и f(х) = ln х -> f(у) = еу.

6. Для тригонометрических функций обратными друг к другу являются следующие пары: – y = cos x -> x = аrccos y;- y = sin x -> x = аrcsin y;- y = tan x -> x = аrctan y.

Обратите внимание!
Следует помнить, что постоянную функцию дозволено обратить лишь на тех интервалах ее значений, где она однообразна.

jprosto.ru

Производная обратной функции | Математика

Если y=f(x) и x=g(y) — пара взаимно обратных функций, и функция y=f(x) имеет производную f'(x), то производная обратной функции g'(x)=1/f'(x).

Таким образом, производные взаимно обратных функций — обратные величины. Формула для производной обратной функции:

   

Примеры. Найти производную обратной функции:

1) y=x²-7lnx.

Имеем:

   

Отсюда

   

   

   

Отсюда 

   

   

Отсюда

   

   

и

   

Примеры для самопроверки. Найти производную обратной функции:

1) y=3x²-5x

   

Показать решение

adminПроизводная

www.matematika.uznateshe.ru

Определение обратной функции

Обратная функция

Не следует путать с Обратная величина.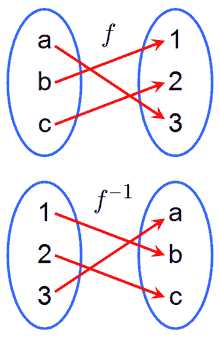 Функция f {\displaystyle f} и обратная ей функция f − 1 {\displaystyle f^{-1}} . Если f ( a ) = 3 {\displaystyle f(a)=3} , то f − 1 ( 3 ) = a {\displaystyle f^{-1}(3)=a}

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x. Обратная функция функции f {\displaystyle f} обычно обозначается f − 1 {\displaystyle f^{-1}} , иногда также используется обозначение f i n v {\displaystyle f^{\mathrm {inv} }} .

Определение

Функция g : Y → X {\displaystyle g:Y\to X} является обратной к функции f : X → Y {\displaystyle f:X\to Y} , если выполнены следующие тождества:

• f ( g ( y ) ) = y {\displaystyle f(g(y))=y} для всех y ∈ Y ; {\displaystyle y\in Y;}
• g ( f ( x ) ) = x {\displaystyle g(f(x))=x} для всех x ∈ X . {\displaystyle x\in X.}

Существование

Чтобы найти обратную функцию, нужно решить уравнение y = f ( x ) {\displaystyle y=f(x)} относительно x {\displaystyle x} . Если оно имеет более чем один корень, то функции, обратной к f {\displaystyle f} не существует. Таким образом, функция f ( x ) {\displaystyle f(x)} обратима на интервале ( a ; b ) {\displaystyle (a;b)} тогда и только тогда, когда на этом интервале она взаимно-однозначна.

Для непрерывной функции F ( y ) {\displaystyle F(y)} выразить y {\displaystyle y} из уравнения x − F ( y ) = 0 {\displaystyle x-F(y)=0} возможно в том и только том случае, когда функция F ( y ) {\displaystyle F(y)} строго монотонна (см. теорема о неявной функции). Тем не менее, непрерывную функцию всегда можно обратить на промежутках её строгой монотонности. Например, x {\displaystyle {\sqrt {x}}} является обратной функцией к x 2 {\displaystyle x^{2}} на [ 0 , + ∞ ) {\displaystyle [0,+\infty )} , хотя на промежутке ( − ∞ , 0 ] {\displaystyle (-\infty ,0]} обратная функция другая: − x {\displaystyle -{\sqrt {x}}} .

Примеры

• Если F : R → R + , F ( x ) = a x {\displaystyle F:\mathbb {R} \to \mathbb {R} _{+},\;F(x)=a^{x}} , где a > 0 , {\displaystyle a>0,} то F − 1 ( x ) = log a ⁡ x . {\displaystyle F^{-1}(x)=\log _{a}x.}
• Если F ( x ) = a x + b , x ∈ R {\displaystyle F(x)=ax+b,\;x\in \mathbb {R} } , где a , b ∈ R {\displaystyle a,b\in \mathbb {R} } фиксированные постоянные и a ≠ 0 {\displaystyle a\neq 0} , то F − 1 ( x ) = x − b a . {\displaystyle F^{-1}(x)={\frac {x-b}{a}}.}
• Если F ( x ) = x n , x ≥ 0 , n ∈ Z {\displaystyle F(x)=x^{n},x\geq 0,n\in \mathbb {Z} } , то F − 1 ( x ) = x n . {\displaystyle F^{-1}(x)={\sqrt[{n}]{x}}.}

Свойства

• Областью определения F − 1 {\displaystyle F^{-1}} является множество Y {\displaystyle Y} , а областью значений — множество X {\displaystyle X} .
• По построению имеем:

y = F ( x ) ⇔ x = F − 1 ( y ) {\displaystyle y=F(x)\Leftrightarrow x=F^{-1}(y)}

или

F ( F − 1 ( y ) ) = y , ∀ y ∈ Y {\displaystyle F\left(F^{-1}(y)\right)=y,\;\forall y\in Y} , F − 1 ( F ( x ) ) = x , ∀ x ∈ X {\displaystyle F^{-1}(F(x))=x,\;\forall x\in X} ,

или короче

F ∘ F − 1 = i d Y {\displaystyle F\circ F^{-1}=\mathrm {id} _{Y}} , F − 1 ∘ F = i d X {\displaystyle F^{-1}\circ F=\mathrm {id} _{X}} ,

где ∘ {\displaystyle \circ } означает композицию функций, а i d X , i d Y {\displaystyle \mathrm {id} _{X},\mathrm {id} _{Y}}  — тождественные отображения на X {\displaystyle X} и Y {\displaystyle Y} соответственно.

• Функция F {\displaystyle F} является обратной к F − 1 {\displaystyle F^{-1}} :

( F − 1 ) − 1 = F {\displaystyle \left(F^{-1}\right)^{-1}=F} .

• Пусть F : X ⊂ R → Y ⊂ R {\displaystyle F:X\subset \mathbb {R} \to Y\subset \mathbb {R} }  — биекция. Пусть F − 1 : Y → X {\displaystyle F^{-1}:Y\to X} её обратная функция. Тогда графики функций y = F ( x ) {\displaystyle y=F(x)} и y = F − 1 ( x ) {\displaystyle y=F^{-1}(x)} симметричны относительно прямой y = x {\displaystyle y=x} .

Разложение в степенной ряд

Обратная функция аналитической функции может быть представлена в виде степенного ряда:

F − 1 ( y ) = ∑ k = 0 ∞ A k ( x 0 ) ( y − f ( x 0 ) ) k k ! , {\displaystyle F^{-1}(y)=\sum _{k=0}^{\infty }A_{k}(x_{0}){\frac {(y-f(x_{0}))^{k}}{k!}},}

где коэффициенты A k {\displaystyle A_{k}} задаются рекурсивной формулой:

A k ( x ) = { A 0 ( x ) = x A n + 1 ( x ) = A n ′ ( x ) F ′ ( x ) {\displaystyle A_{k}(x)={\begin{cases}A_{0}(x)=x\\A_{n+1}(x)={\frac {A_{n}'(x)}{F'(x)}}\end{cases}}}

ru.wikipedia.org>

/ матан коллоквиум / 7.Понятие сложной обратной функции

zna4enie.ru

Как найти функцию, обратную квадратичной функции Как? Так!

Содержимое:

Найти функцию, обратную линейной функции, легко: надо просто сделать «х» зависимой переменной, а затем заменить «х» на «у». Этот процесс значительно усложняется в случае квадратичной функции.

Шаги

1. 1 Выполняйте любые алгебраические операции с обеих сторон функции, чтобы не изменить ее.
2. 2 Перепишите функцию в виде y=a(x-h)²+k. Это не только упростит нахождение обратной функции, но и позволит определить, имеет ли исходная функция обратную. Вы можете сделать это двумя способами:
   • Дополнение до полного квадрата.
     1. Вынесите коэффициент «а» (коэффициент при х²) за скобку, а члены функции разделите на коэффициент «а».
     2. Теперь коэффициент при «х» равен b/а. Разделите его на 2 и получите b/2a, а затем возведите в квадрат: (b/2a)². Полученное значение одновременно прибавьте и вычтите из функции (чтобы не поменять ее значение). Теперь три первых члены в скобках записываются в виде a²+2ab+b², где а = х, b = b/2a (эти величины имеют числовые значения). Эти три первых члена являются полным квадратом.
     3. Первые три члена можно записать в виде (a-b)² или (a+b)² (знак зависит от знака коэффициента при «х» в исходной функции).
     4. Оставшийся член вынесите за скобки и получите: y=a(x-h)²+k.
   • Сравнение коэффициентов.
     1. Слева запишите исходную функцию, а справа – ее желаемый вид (в нашем случае a(x-h)²+k). Это позволит вам найти значения a, h, k, верные при любом значении «х».
     2. Раскройте скобки с правой стороны уравнения (левую часть вообще не трогайте).
     3. Определите коэффициенты при х² и «х».
     4. Сравните коэффициенты при х² и «х» на правой и левой сторонах уравнения – они должны быть равны друг другу. Это приводит к функции вида a(x-h)²+k), в которой вместо «а» подставьте найденное значение. Коэффициент при x⁰ (или 1) на левой стороне уравнения должен быть равен коэффициенту на правой стороне. Сравнивая их, получите уравнение, которое поможет найти значение k.
     5. Используя найденные значения а, h, k, вы можете написать функцию в нужном виде.
3. 3 Убедитесь, что значение h лежит либо на границе области определения, либо вне ее. Значение h – это координата «х» экстремума функции. Если h лежит внутри области определения, то исходная функция не имеет обратной функции. Обратите внимание на знак в скобках: (x—h)²+k. Таким образом, если дано (х + 3), то h = -3 (отрицательное значение).
4. 4 Сделайте (x-h)² зависимым выражением. Для этого вычтите k из обеих сторон уравнения, а затем разделите обе стороны уравнения на «а».
5. 5 Извлеките корень из обеих сторон уравнения. Вы избавитесь от степени. Не забудьте поставить знак +/- на другой стороне уравнения.
6. 6 Определите правильный знак (вы не можете оставить оба знака). Для этого рассмотрите область определения. Если х < определенного значения, то выберите «-». Если х > определенного значения, выберите «+». Теперь сделайте «х» зависимой переменной.
7. 7 Вместо «у» подставьте «х», а вместо «х» подставьте f^-1(x). Вы нашли обратную функцию.

Советы

• Проверьте ответ, вычислив f(х) для некоторого значения «х», а затем подставьте найденное значение в обратную функцию, чтобы найти исходное значение «х». Например, если при х = 3, f(х) = 4, то, подставив 4 в обратную функцию, вы должны получить 3.
• Если возможно, проверьте ответ, построив график обратной функции. Он должен иметь вид графика исходной функции, но симметричный относительно прямой у = х.

Прислал: DarK_Knigt . 2017-11-06 17:28:24

kak-otvet.imysite.ru

Вычисление производной обратной функции.

Определение. Пусть функция $y=f(x)$ непрерывна и строго монотонна в некоторой окрестности точки $x_0,$ и пусть в этой точке существует производная $f'(x_0)\neq 0.$ Тогда обратная функция в точке $y_0=f(x_0)$ имеет производную, которая может быть найдена по формуле $\left(f^{-1}(y_0)\right)’=\frac{1}{f'(x_0)}.$

Примеры.

Найти производные обратных функций  $\left(f^{-1}(y)\right)’.$

1) ${ y=x+x^3 }.$

Решение.

$$\frac{dy}{dx}=1+3 x^2\Rightarrow\frac{dx}{dy}=\frac{1}{1+3x^2}.$$

Ответ: $x’_y=\frac{1}{1+3x^2}.$

 

2) Найти $\left(f^{-1}(0)\right)’,$ $\left(f^{-1}(6/5)\right)’.$

${ y=x+\frac{1}{5}x^5}.$

Решение.

Если $y=0,$ то

$0=x+\frac{1}{5}x^5\Rightarrow 0=x\left(1+\frac{1}{5}x^4\right)\Rightarrow$ $\left[\begin{array}{lcl}x=0\\1+\frac{1}{5}x^4=0\end{array}\right.\Rightarrow$ $\left[\begin{array}{lcl}x=0\\x^4=-5\end{array}\right.\Rightarrow x=0.$ 

Если $y=6/5,$ то $\frac{6}{5}=x+\frac{1}{5}x^5\Rightarrow$ $x=1.$ (Функция имеет единственный корень, поскольку она строго монотонна).

$y’=1+x^4\Rightarrow x’=\frac{1}{1+x^4}.$ Таким образом,
$$x'(0)=\frac{1}{1}=1; \,\, x'(6/5)=\frac{1}{1+1}=\frac{1}{2}.$$

Ответ: $x'(0)=1; \,\, x'(6/5)=\frac{1}{2}.$

 

3) ${ y=2x-\frac{\cos x}{2},\,\, y=-\frac{1}{2}. }$

Решение.

$2x-\frac{\cos x}{2}=-\frac{1}{2},$ следовательно $x=0.$

$y’=2+\frac{\sin x}{2},$ поэтому  $x’=\frac{1}{2+\frac{\sin x}{2}}.$ Таким образом, $x'(-\frac{1}{2})=\frac{1}{2}.$  

Ответ: $x'(-\frac{1}{2})=\frac{1}{2}.$

 

4) ${ y=0,1x+e^{0,1x} ,\,\, y=1.}$

Решение.

$0,1x+e^{0,1x}=1, $ следовательно $x=0.$

$y’=0,1+0,1e^{0,1x},$ поэтому $x’=\frac{1}{0,1+0,1e^{0,1x}}.$
Таким образом, $x'(1)=\frac{1}{\frac{2}{10}}=5.$

Ответ: $x'(1)=5.$

mathportal.net