Квадрат и его свойства, диагонали квадрата, площадь квадрат, теорема
Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.
Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.
Квадрат относится к правильным многоугольникам. У правильного многоугольника все стороны равны и все углы равны.
Перечислим свойства квадрата:
- Все углы квадрата — прямые, все стороны квадрата — равны.
- Диагонали квадрата равны и пересекаются под прямым углом.
- Диагонали квадрата делятся точкой пересечения пополам.
- Диагонали квадрата являются биссектрисами его углов (делят его углы пополам).
- Диагонали квадрата делят его на 4 равных прямоугольных равнобедренных треугольника:
Периметр квадрата P в 4 раза больше его стороны и равен:
Площадь квадрата равна квадрату его стороны: .
Теорема 1. Диагональ квадрата равна произведению его стороны на , то есть
.
Доказательство:
Рассмотрим квадрат ABCD. Проведем диагональ квадрата AC.
Треугольник АВС – прямоугольный с гипотенузой АС. Запишем для треугольника АВС теорему Пифагора:
что и требовалось доказать.
Теорема 2. Радиус вписанной в квадрат окружности равен половине его стороны:
Доказательство:
Пусть окружность с центром в точке О и радиусом r вписана в квадрат АВСD и касается его сторон в точках
P, M, N, K.
Тогда поскольку AB параллельно CD. Через точку О можно провести только одну прямую, перпендикулярную АВ, поэтому точки Р, О и N лежат на одной прямой. Значит, PN – диаметр окружности. Поскольку АРND – прямоугольник, то PN = AD, то есть
, что и требовалось доказать.
Теорема 3. Радиус описанной около квадрата окружности равен половине его диагонали:
Доказательство:
Диагонали квадрата АС и BD равны, пересекаются в точке О и делятся точкой пересечения пополам.
Поэтому OA=OB=OC=OD, т.е. точки A, B, C и D лежат на одной окружности, радиус которой R = d/2 (d=AC=BD). Это и есть описанная около квадрата АВСD окружность.
По теореме
Тогда , что и требовалось доказать.
Заметим, что периметр квадрата тоже можно связать с радиусами вписанной и описанной окружностей:
Четырехугольник является квадратом, если выполняется хотя бы одно из условий:
- Все стороны равны и среди внутренних углов есть прямой угол.
- Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.
Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.
Решение:
Мы знаем, что . Тогда .
Ответ: 2.
Задача 2. Найдите площадь квадрата, если его диагональ равна 1.
Первый способ решения:
Зная связь между стороной и диагональю квадрата (теорема 1), выразим сторону квадрата через его диагональ:
Тогда по формуле площади квадрата:
Второй способ решения:
Воспользуемся формулой для площади ромба:
Ответ: 0,5
Задача 3.
Найдите радиус окружности, описанной около квадрата со стороной, равной .
Решение:
Радиус описанной окружности равен половине диагонали квадрата, поэтому
Ответ: 2.
Задача 4. Найдите сторону квадрата, описанного около окружности радиуса .
Решение:
Диаметр окружности равен стороне квадрата: .
Ответ: 8.
Задача 5. Радиус вписанной в квадрат окружности равен . Найдите диагональ этого квадрата.
Решение:
Сторона квадрата в два раза больше радиуса вписанной окружности:
Диагональ найдем, зная сторону квадрата:
Ответ: 56.
Задача 6. Радиус вписанной в квадрат окружности равен . Найдите радиус окружности, описанной около этого квадрата.
Решение:
Радиус окружности, вписанной в квадрат, равен половине стороны квадрата, а радиус описанной окружности равен половине диагонали квадрата:
Поэтому
Ответ: 22.
Задача 7. Найдите периметр квадрата, если его площадь равна 9.
Решение:
Найдем сторону квадрата:
Периметр квадрата со стороной 3 равен:
Ответ: 12.
Задача 8. Найдите площадь квадрата, в который вписан круг площадью .
Решение:
Площадь круга откуда радиус круга равен 2.
Сторона квадрата в два раза больше радиуса вписанного круга и равна 4. Площадь квадрата равна 16.
Ответ: 16.
Задача 9. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными .
Решение:
Сторону квадрата найдем как диагональ другого квадрата со стороной 2 клеточки. Поскольку длина одной клеточки равна ., то сторона малого квадрата равна . А сторона квадрата ABCD равна
Радиус вписанной окружности в два раза меньше стороны квадрата и равен 2.
Ответ: 2.
Задача 10. Найдите радиус r окружности, вписанной в четырехугольник ABCD.
В ответе укажите .
Решение:
Считаем стороны клеток равными единице. Четырехугольник ABCD — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.
Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, AB.
Она равна . Тогда радиус вписанной окружности равен . В ответ запишем .
Ответ: 5.
Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Квадратu0026nbsp;u0026mdash; определение иu0026nbsp;свойства» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.
Геометрия 7-9 класс. Площадь прямоугольника и квадрата — math200.ru
Skip to contentГеометрия 7-9 класс. Площадь прямоугольника и квадратаadmin2022-12-20T14:14:46+03:00
Скачать файл в формате pdf.
Геометрия 7-9 класс. Площадь прямоугольника и квадрата
| Задача 1. Найдите площадь прямоугольника ABCD, если AB = 7, BC = 3. Ответ ОТВЕТ: 21. | |
| Задача 2. Площадь прямоугольника ABCD равна 36. Найдите длину стороны АВ, если AD = 4. Ответ ОТВЕТ: 9. | |
| Задача 3. Найдите площадь квадрата, если его периметр равен 20. Ответ ОТВЕТ: 25. | |
| Задача 4. Найдите периметр квадрата, если его площадь равна 81. Ответ ОТВЕТ: 36. | |
| Задача 5. Из квадрата со стороной 7 вырезали прямоугольник. Найдите площадь получившейся фигуры, если стороны прямоугольника: 4 и 3. Ответ ОТВЕТ: 37. | |
| Задача 6. Из квадрата со стороной 6 вырезали прямоугольник. Найдите площадь получившейся фигуры, если стороны прямоугольника: 4 и 3. Ответ ОТВЕТ: 24. | |
| Задача 7. На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь. Ответ дайте в квадратных сантиметрах. Ответ ОТВЕТ: 12. | |
| Задача 8. На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь. Ответ дайте в квадратных сантиметрах. Ответ ОТВЕТ: 9. | |
Задача 9. Известно, что в прямоугольнике  Найдите площадь прямоугольника.Ответ ОТВЕТ: 16. | |
| Задача 10. Известно, что в прямоугольнике ABCD сторона АВ в 5 раз больше стороны ВС, а его периметр равен 24. Найдите площадь прямоугольника. Ответ ОТВЕТ: 20. | |
| Задача 11. Дан прямоугольник ABCD периметр которого равен 40. Известно, что AD : DC = 1 : 4. Найдите площадь прямоугольника. Ответ ОТВЕТ: 64. | |
| Задача 12. Дан прямоугольник ABCD площадь которого равен 150. Известно, что AВ : ВC = 2 : 3. Найдите периметр прямоугольника. Ответ ОТВЕТ: 50. | |
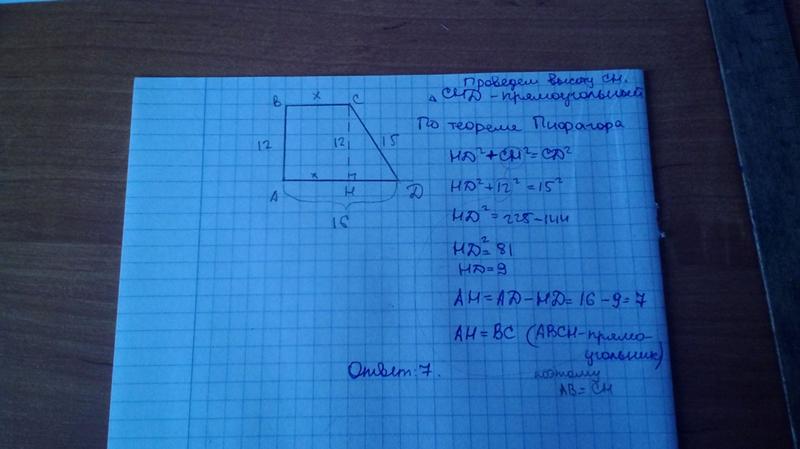
| Задача 13. По данным на рисунке найдите площадь квадрата ABCD, если МС = 30. Ответ ОТВЕТ: 225. | |
Задача 14. По данным на рисунке найдите площадь прямоугольника ABCD, если площадь треугольника AMD равна 37.Ответ ОТВЕТ: 37. | |
| Задача 15. В прямоугольнике ABCD биссектриса BК угла делит сторону AD на отрезки АK = 7, KD = 4. Найдите площадь прямоугольника. Ответ ОТВЕТ: 77. | |
| Задача 16. В прямоугольнике ABCD биссектриса BК угла делит сторону AD на отрезки АK и KD. Известно, что Ответ ОТВЕТ: 204. | |
| Задача 17. Пол комнаты, имеющей форму прямоугольника со сторонами 3,5 м и 4 м, нужно покрыть паркетом прямоугольной формы. Длина каждой дощечки паркета равна 40 см, а ширина 10 см. Сколько потребуется таких дощечек для покрытия пола? Ответ ОТВЕТ: 350. | |
| Задача 18. Сколько потребуется кафельных плиток квадратной формы со стороной 25 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3 м и 2,5 м? Ответ ОТВЕТ: 120. | |
Реклама
Мы Вконтакте
Поддержать нас
Как найти площадь квадрата
Все материалы по математике для старших классов
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по математике для средней школы » Геометрия » Плоская геометрия » Четырехугольники » Площади » Как найти площадь квадрата
ABCD и EFGH — это такие квадраты, что периметр ABCD в 3 раза больше периметра EFGH. Если площадь EFGH равна 25, какова площадь ABCD?
Возможные ответы:
225
75
25
15
5
6 1 Правильный ответ: 6 1 5
Объяснение:
Назначьте переменные таким образом, чтобы
Одна сторона ABCD = a
и одна сторона EFGH = e
Обратите внимание, что все стороны квадрата одинаковы.
Так как периметр есть сумма всех сторон, согласно вопросу:
4а = 3 х 4е = 12е или а = 3е
Из этой области EFGH 25,
e x e = 25, т. е. e = 5
Подставьте a = 3e, т. е. a = 15
Мы еще не закончили. Поскольку нас спросили о площади ABCD, это равно a x a = 225.
Сообщить об ошибке
Квадрат имеет площадь 36. Если все стороны удвоить, какова новая площадь?
Возможные ответы:
132
108
72
144
48
1 Правильный ответ: 900 005 144 Объяснение: Пусть S будет исходной длиной стороны. S * S будет представлять исходную область. Удвоение длины стороны даст вам 2S*2S, упрощение до 4*(S*S), даст новую площадь в 4 раза больше исходной или 144. Сообщить об ошибке Если периметр квадрата равен удвоенному его площадь, какова длина одной из его сторон? Возможные ответы: Правильный ответ: Объяснение: Площадь квадрата по каждой из его сторон: Площадь = S x S Периметр квадрата: Периметр = 4S Итак, если «периметр квадрата равен удвоенному площадь’: 2 x Площадь = Периметр 2 x [S x S] = [4S]; разделить на 2: S x S = 2S; разделить на S: S = 2 Сообщить об ошибке Фредди строит квадратный загон для своей свиньи. Возможные ответы: 3 p 9 p p /6
Он планирует купить x футов ограждения для постройки загона. В результате получится загон площадью p квадратных футов. К сожалению, денег у него хватает только на треть запланированного количества ограждений. Какое выражение представляет собой площадь загона, которую он может построить с этим ограниченным количеством ограждений?4
0004 стр /3
Правильный ответ:
р /9
Объяснение:
Если Фредди использует забор x футов, образуя квадрат, каждая сторона должна быть x /4 фута в длину. Площадь этого квадрата равна ( x /4) 2 = x 2 /16 = p квадратных футов.
Если Фредди использует одну треть из x футов ограждения, образуя квадрат, каждая сторона должна быть x /12 футов в длину.
Площадь этого квадрата равна ( x /12) 2 = x 2 /144 = 1/9 ( x 2 /16) = 1/9 ( P ) = P /9 квадратных футов.
Альтернативный метод:
Масштабный коэффициент между малым периметром и большим периметром = 1 : 3. Поскольку мы сравниваем площадь, двумерное измерение, мы можем возвести масштабный коэффициент в квадрат и увидеть, что отношение площадей равно 1 2 : 3 2 = 1 : 9.
Сообщить об ошибке
Если диагональ квадрата равна , какова площадь квадрата?
Возможные ответы:
Правильный ответ:
Пояснение:
Это равнобедренный прямоугольный треугольник, поэтому диагональ должна быть умножена на длину стороны. Таким образом, одна сторона квадрата измеряет , а площадь равна
Сообщить об ошибке
Квадрат имеет длины сторон .
Стороны второго квадрата равны . Сколько вы можете поместиться в один?
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь равна , площадь равна . Таким образом, вы можете поместить 5,06 в .
Сообщить об ошибке
Периметр квадрата Если квадрат увеличить в три раза, какова новая площадь?
Возможные ответы:
Правильный ответ:
Объяснение:
Периметр квадрата определяется как поэтому длина стороны исходного квадрата равна Сторона нового квадрата увеличивается в 3 раза, чтобы получить
Таким образом, площадь нового квадрата определяется как .
Сообщить об ошибке
Насколько площадь квадрата со стороной 2r больше площади круга с радиусом r? Приблизительно π, используя 22/7.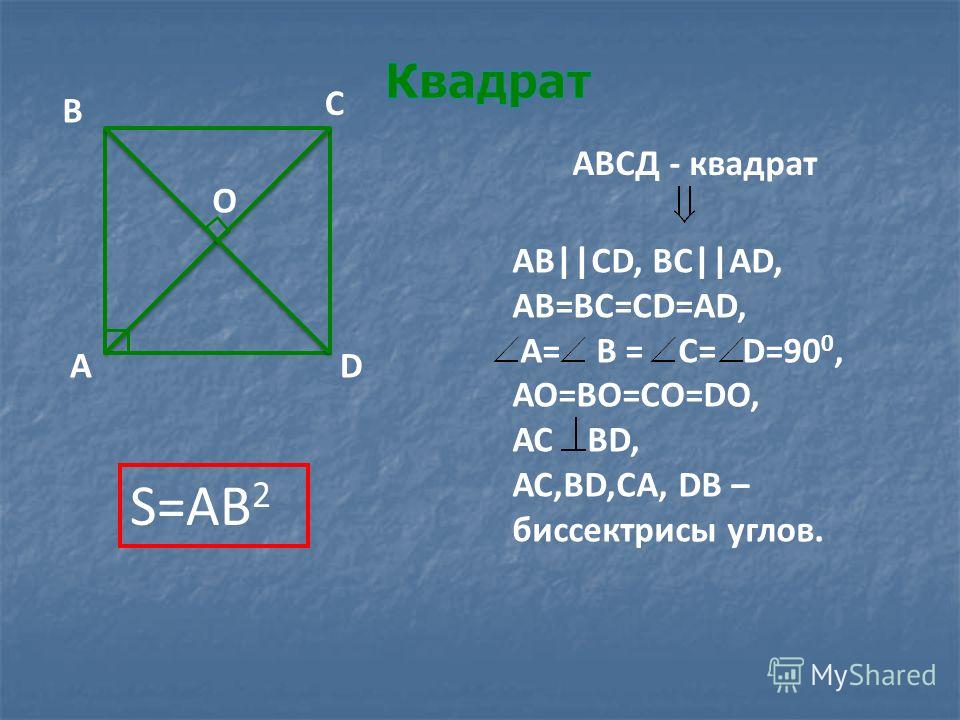
Возможные ответы:
12/14 квадратных единиц
6/7 квадратных единиц
4/7 квадратных единиц
1/7 квадратных единиц
Правильный ответ:
6/7 квадратных единиц
Объяснение:
Площадь круга определяется как A = πr 2 или 22/7r 2
Площадь квадрата определяется как A = s 2 или (2r) 2 = 4r 2
Затем вычтите площадь круга из площади квадрата и получите 6/7 квадратных единиц.
Сообщить об ошибке
Если периметр квадрата равен 44 сантиметрам, какова площадь квадрата в квадратных сантиметрах?
Возможные ответы:
Правильный ответ:
Объяснение:
Так как периметр квадрата равен 44, то каждая сторона равна .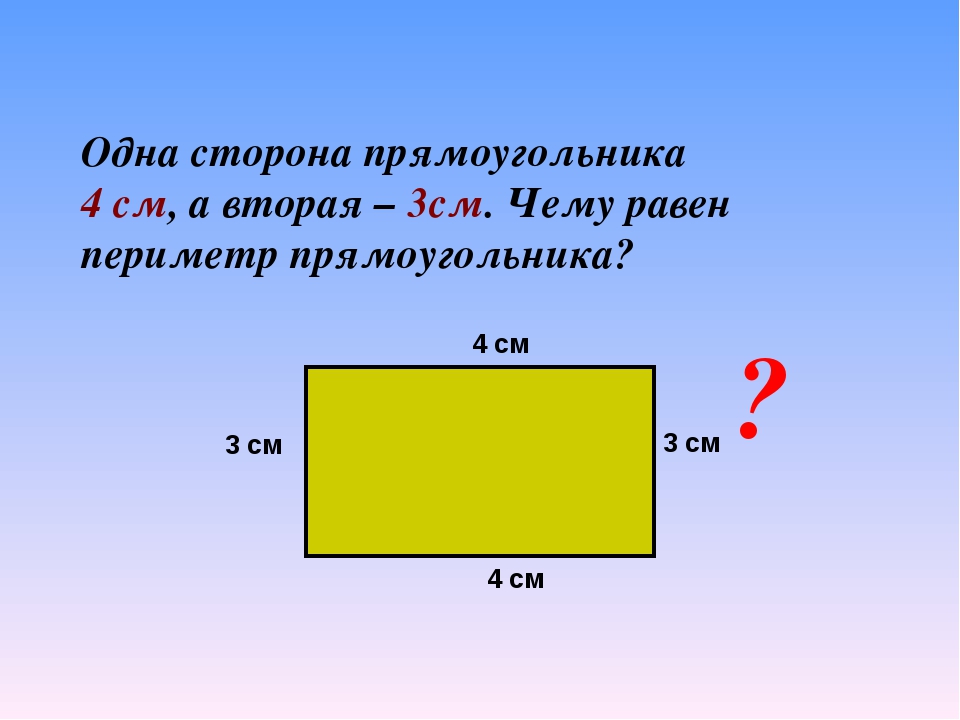
Затем, чтобы найти область, используйте определение, которое
Сообщить об ошибке0004
Дан квадрат , середины каждой стороны которого соединены в новый, меньший квадрат. Во сколько раз площадь большего квадрата больше площади меньшего?
Возможные ответы:
Правильный ответ:
Объяснение:
Предположим, что длина каждой средней точки равна 1. Это означает, что длина каждой стороны большого квадрата равна 2, поэтому площадь большего квадрата равна 4 квадратным единицам.
Чтобы найти площадь меньшего квадрата, сначала найдите длину каждой стороны. Поскольку длина каждой средней точки равна 1, каждая сторона меньшего квадрата равна (используйте либо теорему Пифагора, либо обратите внимание, что эти прямоугольные треугольники являются равнобедренными прямоугольными треугольниками, поэтому их можно использовать).
Тогда площадь меньшего квадрата равна 2 квадратным единицам.
Сравнивая площади двух квадратов, больший квадрат в 2 раза больше меньшего квадрата.
Сообщить об ошибке
92 \ = \ 1 \ \rightarrow \ xy \ = \ \pm 1 \ $ имеет «четырехкратную» симметрию относительно начала координат: если $ \ (x \ , \ y) \ $ — точка на кривой, то $ \ (x \ , \ -y) \ , \ (-x \ , \ y) \ , \ $ и $ \ (-x \ , \ -y) \ \ . \ $ Требование того, что квадрат должен иметь обе вершины и середины его сторон лежат на кривой, означает, что две точки квадрата должны располагаться на каждой «ветви». Это делает невозможным, чтобы стороны квадрата были параллельны осям координат, поскольку либо набор вершин, либо набор средних точек не были бы размещены; это заставляет нас искать решение, в котором квадрат наклонен под некоторым углом к осям. (Вышеупомянутая симметрия также поместит центр квадрата в начало координат, чтобы ответить на Комментарий Эннара .) Затем мы ожидаем решение с одной вершиной на каждой ветви этой «двойной прямоугольной гиперболы» таким образом, что сторона, соединяющая «последовательные» вершины, также пересекает кривую.
Затем у нас есть одна вершина и одна средняя точка на каждой ветви. Изменение знака произведения координат в первом и третьем против во втором и четвертом квадрантах «нарушает» четырехкратную симметрию для квадрата, но мы все еще имеем симметрию относительно начала координат, размещая вершины в $\ \left(X \ , \ \frac{1}{X} \right) \ \ , \ \ \left(-X \ , \ -\frac{1}{X} \right) \ $ на $ \ xy \ = \ +1 \ $ и $ \ \left(\frac{1}{X} \ , \ -X \right) \ \ , \ \ \left(-\frac{1}{X} \ , \ X \ справа) \$ на $\xy\=\-1\\ ; \ $ в этом обозначении мы выбрали $ \ X \ > \ \ frac{1}{X} \ > \ 0 \ \ . \$
Середины сторон, соединяющих последовательные вершины, также «подчиняются» этой «частично нарушенной» симметрии. В более ранней попытке я обнаружил, что использование геометрии квадрата дает только соотношения, которые ничего не говорят о его размере . Оказывается, требование, чтобы середины сторон лежали на ветвях кривой, «задает масштаб» квадрата. Таким образом, мы будем называть эти середины $ \ \left(a \ , \ \frac{1}{a} \right) \ \ , \ \ \left(\frac{1}{a} \ , \ -a \ справа) \ \ ,$ $ \left(-a \ , \ -\frac{1}{a} \right) \ \ , \\ $ и $ \\left(\frac{1}{a} \ , \ -а \право) \ .