Площадь линии: Площадь — линия — Большая Энциклопедия Нефти и Газа, статья, страница 1

Содержание

Площадь — линия — Большая Энциклопедия Нефти и Газа, статья, страница 1

Площадь — линия

Cтраница 1

Площадь линии может быть существенно уменьшена при разветвлении потока на участках охлаждения, что также легко осуществить на роликовом конвейере. Для той же цели используют транспортные тележки, не связанные между собой цепью и перемещающиеся по рельсовому пути. Достоинством роликового конвейера и транспортных тележек является также то, что отдельные их секции приводятся в действие не строго одновременно. В результате резко уменьшаются динамические нагрузки, пере-даваемыена строительные конструкции. [1]

Площадь линии фотоэлектронного спектра данного соединения, ионизованного фотонами, должна быть пропорциональна концентрации этого соединения, так как эффективность ионизации зависит от потока фотонов, сечения ионизации орбитали и количества молекул образца, взаимодействующих с фотонами. Для УФЭС это предположение еще недостаточно проверено. Результаты двух выполненных к настоящему моменту работ [21] вызывают сомнения из-за наличия в них серьезных экспериментальных трудностей. [2]

СБИС, площадь линий связи на кристалле начинает превышать площадь, занимаемую логическими элементами в схеме. В [9, 10] показано, что чем больше степень интеграции СБИС, тем больше часть площади кристалла, приходящаяся на линии связи. В указанных работах делается вывод о том, что без осуществления оптимизации межэлементных связей на кристалле процесс повышения степени интеграции практически будет приостановлен, вследствие достижения физических пределов при распределении площади кристалла. [3]

Таким образом, площадь лоренцевой линии, обрезанной достаточно далеко от точки половинной мощности, очень близка к площади обычной лоренцевой линии. [4]

На участке ABCDEF требуется выделить площадь S линий MN, параллельной АВ. [6]

При частичном загружении q множится на площадь линии влияния, находящейся под нагрузкой. [8]

Равномерно распределенная нагрузка располагается над всей площадью линии влияния одного знака. В к А, соединяются Л и С и проводится DE AC; точка Е располагается на критическом грузе. [9]

Площадь между линией влияния и осью абсцисс дает площадь линии влияния. Отыскание по линии влияния наибольшей величины соответствующего усилия ведется без особого затруднения. [10]

Так как нагр зка расположена па всем пролете, то площади линий влияния надо вычислять на протяжении всего пролета. [11]

Наиболее точный метод определения величин / и / заключается в измерении площади линии резонансного поглощения, наблюдаемой в скоростном спектре. [12]

А если хоть для одного положительного е такой области не удастся найти, тогда площадь линии не равна нулю. [13]

При равномерно распределенной нагрузке д

Вычисление площадей плоских фигур с помощью интеграла

На этом уроке будем учиться вычислять площади плоских фигур, которые называются криволинейными трапециями.

Примеры таких фигур — на рисунке ниже.

С одной стороны, найти площадь плоской фигуры с помощью определённого интеграла предельно просто. Речь идёт о площади фигуры, которую сверху ограничивает некоторая кривая, снизу — ось абсцисс (

Ox), а слева и справа — некоторые прямые. Простота в том, что определённый интеграл функции, которой задана кривая, и есть площадь такой фигуры (криволинейной трапеции).

Но здесь нас подстерегают некоторые важные нюансы, без понимания которых не решить большинство задач на это практическое приложение определённого интеграла. Учтём эти нюансы и будем во всеоружии.

Для вычисления площади фигуры нам понадобятся:

Определённый интеграл от функции, задающей кривую, которая ограничивает криволинейную трапецию сверху. И здесь возникает первый существенный нюанс: криволинейная трапеция может быть ограничена кривой не только сверху, но и снизу. Как действовать в этом случае? Просто, но это важно запомнить: интеграл в этом случае берётся со знаком минус.

Пределы интегрирования a и b, которые находим из уравнений прямых, ограничивающих фигуру слева и справа: x = a, x = b, где a и b — числа.

Отдельно ещё о некоторых нюансах.

Кривая, которая ограничивает криволинейную трапецию сверху (или снизу) должна быть графиком непрерывной и неотрицательной функции y = f(x).

Значения «икса» должны принадлежать отрезку [a, b]. То есть не учитываются такие, например, линии, как разрез гриба, у которого ножка вполне вписывается в этот отрезок, а шляпка намного шире.

Боковые отрезки могут вырождаться в точки. Если вы увидели такую фигуру на чертеже, это не должно вас смущать, так как эта точка всегда имеет своё значение на оси «иксов». А значит с пределами интегрирования всё в порядке.

Теперь можно переходить к формулам и вычислениям. Итак, площадь s криволинейной трапеции может быть вычислена по формуле

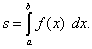(1).

Если же f(x) ≤ 0 (график функции расположен ниже оси Ox), то площадь криволинейной трапеции может быть вычислена по формуле

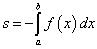. (2)

Есть ещё случаи, когда и верхняя, и нижняя границы фигуры — функции, соответственно y = f(x) и y = φ(x), то площадь такой фигуры вычисляется по формуле

. (3)

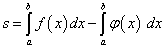
Начнём со случаев, когда площадь фигуры может быть вычислена по формуле (1).

Пример 1. Найти площадь фигуры, ограниченной графиком функции 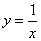, осью абсцисс (Ox) и прямыми x = 1, x = 3.

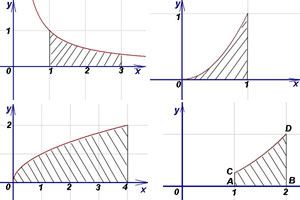
Решение. Так как y = 1/x > 0 на отрезке [1; 3], то площадь криволинейной трапеции находим по формуле (1):

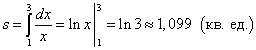Пример 3. Найти площадь фигуры, ограниченной графиком функции 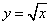, осью абсцисс (Ox) и прямой x = 4.

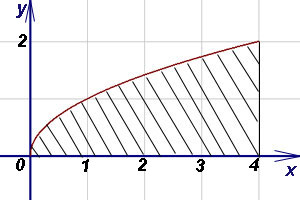Решение. Фигура, соответствующая условию задачи — криволинейная трапеция, у которой левый отрезок выродился в точку. Пределами интегрирования служат 0 и 4. Поскольку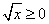

, по формуле (1) находим площадь криволинейной трапеции: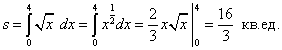

Пример 4. Найти площадь фигуры, ограниченной линиями 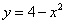, , 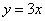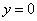и находящейся в 1-й четверти.

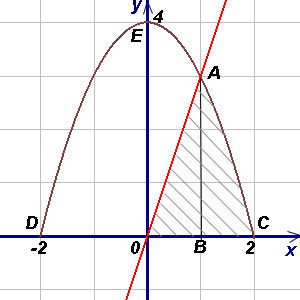
Решение. Чтобы воспользоваться формулой (1), представим площадь фигуры, заданной условиями примера, в виде суммы площадей треугольника OAB и криволинейной трапеции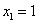

ABC. При вычислении площади треугольника OAB пределами интегрирования служат абсциссы точек O и A, а для фигуры ABC — абсциссы точек A и C (A является точкой пересечения прямой OA и параболы, а C — точкой пересечения параболы с осью Ox). Решая совместно (как систему) уравнения прямой и параболы, получим

(абсциссу точки A) и

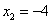(абсциссу другой точки пересечения прямой и параболы, которая для решения не нужна). Аналогично получим

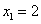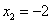(абсциссы точек C и D). Теперь у нас еть всё для нахождения площади фигуры. Находим:

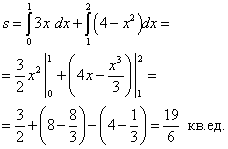
Пример 5. Найти площадь криволинейной трапеции ACDB, если уравнение кривой CD 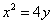и абсциссы A и B соответственно 1 и 2.

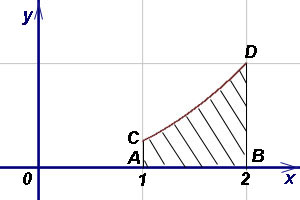
Решение. Выразим данное уравнение кривой через игрек: Площадь криволинейной трапеции находим по формуле (1):

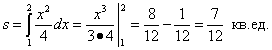Переходим к случаям, когда площадь фигуры может быть вычислена по формуле (2).

Пример 7. Найти площадь, заключённую между осью абсцисс (Ox) и двумя соседними волнами синусоиды.

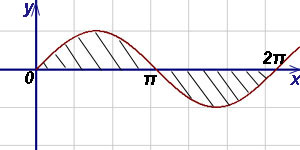
Решение. Площадь данной фигуры можем найти по формуле (2):

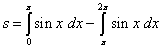Найдём отдельно каждое слагаемое:

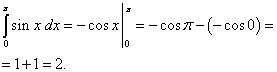Окончательно находим площадь:

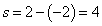Пример 8. Найти площадь фигуры, заключённой между параболой 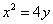и кривой .

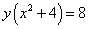Решение. Выразим уравнения линий через игрек:

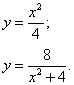
Площадь по формуле (2) получим как

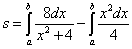где a и b — абсциссы точек A и B. Найдём их, решая совместно уравнения:

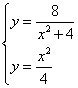
Отсюда

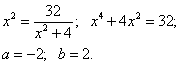
Окончательно находим площадь:

И, наконец, случаи, когда площадь фигуры может быть вычислена по формуле (3).

Начало темы «Интеграл»

1.8. Как вычислить площадь фигуры с помощью определённого интеграла?

Задачка это школьная, но, несмотря на то, почти 100% встретится в вашем курсе высшей математики. Поэтому со всей серьёзностью отнесёмся ко ВСЕМ примерам, и первое, что нужно сделать – это ознакомиться с Приложением Графики функций, чтобы освежить в памяти технику построения элементарных графиков. …Есть? Отлично! Типовая формулировка задания звучит так:

Пример 10
Вычислить площадь фигуры, ограниченной линиями .

И первый важнейший этап решения состоит как раз в построении чертежа. При этом я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций.

В нашей задаче: прямая определяет ось , прямые параллельны оси и парабола симметрична относительно оси , для неё находим несколько опорных точек:

Искомую фигуру желательно штриховать:

Второй этап состоит в том, чтобы правильно составить и правильно вычислить определённый интеграл. На отрезке график функции расположен над осью , поэтому искомая площадь:

Ответ:

После того, как задание выполнено, полезно взглянуть на чертёж
и прикинуть, реалистичный ли получился ответ.

И мы «на глазок» подсчитываем количество заштрихованных клеточек – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получилось, скажем, 20 квадратных единиц, то, очевидно, где-то допущена ошибка – в построенную фигуру 20 клеток явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.

Пример 11
Вычислить площадь фигуры, ограниченной линиями и осью

Быстренько разминаемся (обязательно!) и рассматриваем «зеркальную» ситуацию – когда криволинейная трапеция расположена под осью :

Пример 12
Вычислить площадь фигуры, ограниченной линиями , и координатными осями.

Решение: найдём несколько опорных точек для построения экспоненты:

и выполним чертёж, получая фигуру площадью около двух клеток:

Если криволинейная трапеция расположена не выше оси , то её площадь можно найти по формуле: .
В данном случае:

Ответ: – ну что же, очень и очень похоже на правду.

На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому от простейших школьных задачек мы переходим к более содержательным примерам:

Пример 13
Найти площадь плоской фигуры, ограниченной линиями , .

Решение: сначала нужно выполнить чертеж, при этом нас особо интересуют точки пересечения параболы и прямой , поскольку здесь будут находиться пределы интегрирования. Найти их можно двумя способами. Первый способ – аналитический. Составим и решим уравнение:

таким образом:

Достоинство аналитического способа состоит в его точности, а недостаток – в длительности (и в этом примере нам ещё повезло). Поэтому во многих задачах бывает выгоднее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой».

С прямой всё понятно, а вот для построения параболы удобно найти её вершину, для этого возьмём производную и приравняем её к нулю:
– именно в этой точке и будет находиться вершина. И, в силу симметрии параболы, остальные опорные точки найдём по принципу «влево-вправо»:

Выполним чертеж:

А теперь рабочая формула: если на отрезке некоторая непрерывная функция больше либо равна непрерывной функции , то площадь фигуры, ограниченной графиками этих функций и отрезками прямых , можно найти по формуле:

Здесь уже не надо думать, где расположена фигура – над осью или под осью, а, грубо говоря, важно, какой из двух графиков ВЫШЕ.

В нашем примере очевидно, что на отрезке парабола располагается выше прямой, а поэтому из нужно вычесть

Завершение решения может выглядеть так:

На отрезке : , по соответствующей формуле:

Ответ:

Следует отметить, что простые формулы, рассмотренные в начале параграфа – это частные случаи формулы . Поскольку ось задаётся уравнением , то одна из функций будет нулевой, и в зависимости от того, выше или ниже лежит криволинейная трапеция, мы получим формулу либо

А сейчас пара типовых задач для самостоятельного решения

Пример 14
Найти площадь фигур, ограниченных линиями:

а) , .

б) , ,

Решение с чертежами и краткими комментариями в конце книги

В ходе решения рассматриваемой задачи иногда случается забавный казус. Чертеж выполнен правильно, интеграл решён правильно, но по невнимательности… найдена площадь не той фигуры, именно так несколько раз ошибался ваш покорный слуга. Вот реальный случай из жизни:

Пример 15
Вычислить площадь фигуры, ограниченной линиями

Решение: выполним бесхитростный чертёж,

хитрость которого состоит в том, что искомая площадь заштрихована зелёным цветом (внимательно смотрИте на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована серым цветом! Особое коварство состоит в том, что прямую можно недочертить до оси , и тогда мы вовсе не увидим нужную фигуру.

Этот пример ещё и полезен тем, что в нём площадь фигуры считается с помощью двух определённых интегралов. Действительно:

1) на отрезке над осью

Найти площадь фигуры ограниченной кривыми онлайн

Как найти площадь фигуры ограниченной линиями онлайн

Предлагаем Вашему вниманию онлайн калькулятор для нахождения площади фигуры ограниченной кривыми линиями. Калькулятор в автоматическом режиме составляет интеграл, находит границы интегрирования, а также рисует саму фигуру на координатной плоскости. Как частный случай, калькулятор находит площадь криволинейной трапеции.

1). Как найти площадь криволинейной трапеции онлайн.

Площадь криволинейной трапеции, ограниченной кривой y=f(x) [f(x)≥0], прямыми x=a, x=b и отрезком [a,b] оси Ox находим по формуле

Пример. Найти площадь криволинейной трапеции ограниченной кривой y=2x^2+1 и прямыми x=1,x=2.

Решение. Вставляем в калькулятор функции в виде y=2x^2+1,x=1,x=2, нажимаем «Ok», получаем ответ.

2). Как найти площадь фигуры ограниченной линиями онлайн
Площадь фигуры, ограниченной кривыми y=f₁(x) и y=f₂(x) [f₁(x) ≤ f₂(x)] и прямыми x=a, x=b вычисляется по формуле y=f₁(x) и y=f₂(x) [f₁(x) ≤ f₂(x)] и прямыми x=a, x=b вычисляется по формуле

Пример. Найти площадь фигуры ограниченной линиями y=4x-x^2, y=4-x

Решение. Вставляем функции y=4x-x^2, y=4-x в калькулятор, нажимаем «Ok», получаем ответ.

1. площадь; пространство; участок 2. район; область; зона 3. Ech. членик короны 4. Brack. арея 5. Biv. площадка
area of ablation зона (область) абляции
area of accumulation зона (область) аккумуляции
area of artesian flow площадь артезианских вод
area of dissipation зона (область) абляции
area of distribution ареал обитания; площадь распространения
area of efflux площадь истечения
area of faulting область сбросов
area of foundering площадь проплавления
area of groundwater discharge зона разгрузки подземных вод
area of influence площадь (зона) влияния
area of mountain building (of orogeny) область горообразования
area of sedimentation область осадконакопления; область образования осадочных пород
area of seepage площадь выхода источников
area of stream evaporation площадь испарения потока
area of subsidence площадь опускания, площадь оседания, район осадки
area of well infiltration площадь инфильтрации (просачивания) колодца
abyssal area абиссальная (глубинная) область, абиссальная (глубинная) зона
accumulation area зона (область) аккумуляции
aclinal area аклинальная область, район, не имеющий наклона пластов, площадь горизонтального залегания пласто
alimentation area область питания
ambulacral area амбулакральное поле, амбулакр
apical area апикальная арея
arched area антиклинально построенная площадь
artesian area артезианская площадь
basin area 1. площадь бассейна 2. средняя площадь бассейна; средняя площадь всех бассейнов
basined area резервуарный участок
bearing area опорная площадь, площадь соприкосновения
bow area складчатая зона
cardinal area замочная (кардинальная) арея
catchment area 1. водосборная площадь 2. область питания водоносного горизонта
closely drilled area площадь, густо покрытая скважинами
coastal area прибрежная область
collecting area см. catchment area
compression area область сжатия
contact area поверхность соприкосновения, контактовая зона
crystalline core area кристаллический массив
depression area 1. пониженный участок 2. зона погружения
discharge area область разгрузки
discharge area of groundwater площадь выхода грунтовых вод
disposal area область сброса (вод)
domed area куполообразно построенная площадь
dorsal area дорсальная поверхность (у наутилоидей)
drainage area 1. площадь водосбора, дренируемая площадь, бассейн питания 2. площадь, дренируемая скважиной
drainless area бессточная область
driftless area безвалунная область; внеледниковая область
even-crested summit area район равновысоких вершин
exhausted area истощённая площадь
filled area место отвала грунта, место отвала пустой породы
fold area складчатая область
foundering area площадь проплавления
generating area нагон, разгон (система волн, которая создаётся в открытом океане ветром, дующим с постоянной скоростью и постоянным направлением)
geosynclinal area геосинклинальная область
hinge area пал. замочная площадка
horizontally-projected area площадь в горизон тальной проекции
inclosed area включённый участок
infiltration area площадь просачивания
intake area 1. площадь поглощения 2. область питания
interbasin area внутрибассейновая площадь
interlobate area площадь между двумя лопастями (ледника)
intermountain area межгорная впадина
interstream area междуречье
intertrough area площадь между прогибами
lagoon area лагунная область
land area материковая область
littoral area прибрежная (литоральная) область, побережье
map area площадь картирования
meizoseismal area зона землетрясения максимальной разрушительной силы
minor seismic area второстепенная сейсмическая область, зона землетрясения слабой сейсмичности
neritic area неритовая область
oil (oil-bearing, oil-producing) area нефтеносная площадь
outcrop area площадь распространения
outwash area- безвалунная область накопления осадков
overthrust fault area площадь, перекрытая надвигом
palingenetic area палингенетическая область
polar area полярная область
positive area положительный участок суши
potential area разведочная площадь
pressure area площадь сплошного торошения
primitive area первозданная область
producing area промышленная (продуктивная) площадь
proved area разведанная площадь, площадь с доказанным содержанием ископаемого
recharge area область питания
reflection-free areas зоны отсутствия сейсмических отражений на разрезах MOB
salt dome area район соляных куполов
section area площадь сечения
seepage area площадь выхода источников
seepage area of well площадь инфильтрации (просачивания) колодца
seismic area 1. сейсмическая область 2. зона землетрясения
shield area щит
slipping area площадь сползания
source area область питания, источник сноса
spoil area площадь для отвала
stability area область стабильности
supraembryonic area супраэмбриональный участок
surplus area зона (область) аккумуляции
swampy area болотистая (заболоченная) площадь
unproductive area непродуктивная площадь
* * *
• членик короны, состоящий из одного или более ряда сходных пластинок
площадь+линии+влияния+момента — со всех языков на русский
21 area of influence
площадь [зона] влияния
English-Russian mining dictionary > area of influence
22 площадь влияния скважины
Большой англо-русский и русско-английский словарь > площадь влияния скважины
23 базарная площадь
Большой англо-русский и русско-английский словарь > базарная площадь
24 площадь
Большой англо-русский и русско-английский словарь > площадь
25 по линии
Большой англо-русский и русско-английский словарь > по линии
26 площадь
БНРС > площадь
27 площадь
БНРС > площадь
28 плоскость площадь поверхность
БНРС > плоскость площадь поверхность
29 площадь площадка
БНРС > площадь площадка
30 посевная площадь
БНРС > посевная площадь
31 с со времени с момента в течение
БНРС > с со времени с момента в течение
32 площадь
БФРС > площадь
33 площадь
Большой итальяно-русский словарь > площадь
34 площадь
Якутско-русский словарь > площадь
35 площадь
. площадь;
вӧр площадь — лесная площадь; кӧдза площадь паськаліс — посевная площадь расширилась; площадь тырис йӧзӧн — вся площадь заполнилась народом
Коми-русский словарь > площадь
36 BELOW-THE-LINE (“ниже линии”)
1. Название записей, расположенных ниже горизонтальной линии в счете прибылен и убытков (profit and loss account) компании, которая отделяет отчет о прибылях (убытках) от отчета о распределении прибыли или источниках покрытия убытков. 2. Обозначение расходов на рекламу, за которую не платятся комиссионные рекламному агентству. например прямая рассылка, выставки, реклама, раздаваемая в местах продажи товаров, и свободные образцы рассматриваются как реклама “ниже линии”. 3. Обозначение в национальных счетах движения капитала, а не дохода. Сравни: above-the-line (“выше линии”).
Финансы: англо-русский толковый словарь > BELOW-THE-LINE (“ниже линии”)
37 анализ рабочей нагрузки линии связи
eng.traffic analysis
rus.анализ трафика, рабочей нагрузки линии связи
ukr.аналіз трафіку, робочої нагрузки лінії зв’язку
English-Russian dictionary of information security > анализ рабочей нагрузки линии связи
38 разрыв линии
eng.line disconnect
rus.разрыв линии
ukr.розрив лінії
English-Russian dictionary of information security > разрыв линии
39 чтение с линии связи
eng.line-tap
rus.чтение с линии связи
ukr.читання із лінії зв’язку
English-Russian dictionary of information security > чтение с линии связи
40 площадь

мат. площадь
Кабардинско-русский словарь > площадь
См. также в других словарях:
Молдавская Автономная Советская Социалистическая Республика — Република Аутономэ Советикэ Сочиалистэ Молдовеняскэ (Republica Autonomă Sovietică Socialistă Moldovenească) Молдавська Автономна Радянська Соціалістична Республіка Герб … Википедия
СЕРДЦЕ — СЕРДЦЕ. Содержание: I. Сравнительная анатомия……….. 162 II. Анатомия и гистология……….. 167 III. Сравнительная физиология………. 183 IV. Физиология………………. 188 V. Патофизиология……………. 207 VІ. Физиология, пат.… … Большая медицинская энциклопедия
1: — Терминология 1: : dw Номер дня недели. «1» соответствует понедельнику Определения термина из разных документов: dw DUT Разность между московским и всемирным координированным временем, выраженная целым количеством часов Определения термина из… … Словарь-справочник терминов нормативно-технической документации
Соединённые Штаты Америки — (США) (United States of America, USA). I. Общие сведения США государство в Северной Америке. Площадь 9,4 млн. км2. Население 216 млн. чел. (1976, оценка). Столица г. Вашингтон. В административном отношении территория США … Большая советская энциклопедия
Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора
Япония* — Содержание: I. Физический очерк. 1. Состав, пространство, береговая линия. 2. Орография. 3. Гидрография. 4. Климат. 5. Растительность. 6. Фауна. II. Население. 1. Статистика. 2. Антропология. III. Экономический очерк. 1. Земледелие. 2.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Япония — I КАРТА ЯПОНСКОЙ ИМПЕРИИ. Содержание: I. Физический очерк. 1. Состав, пространство, береговая линия. 2. Орография. 3. Гидрография. 4. Климат. 5. Растительность. 6. Фауна. II. Население. 1. Статистика. 2. Антропология. III. Экономический очерк. 1 … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
время — 3.3.4 время tE (time tE): время нагрева начальным пусковым переменным током IА обмотки ротора или статора от температуры, достигаемой в номинальном режиме работы, до допустимой температуры при максимальной температуре окружающей среды. Источник … Словарь-справочник терминов нормативно-технической документации
Соединённые Штаты Америки — Соединенные Штаты Америки США, гос во в Сев. Америке. Название включает: геогр. термин штаты (от англ, state государство ), так в ряде стран называют самоуправляющиеся территориальные единицы; определение соединенные, т. е. входящие в федерацию,… … Географическая энциклопедия
Япония — гос во в Вост. Азии. В первой половине I тыс. н. э. известна как страна Ямато. Название от этнонима ямато, который относился к союзу племен, живших в центр, части о. Хонсю, и означал люди гор, горцы . В VII в. для страны принимается название… … Географическая энциклопедия
Финляндия — (Finland) История и география Финляндии, население и административно территориальное деление Финляндии Географическое положение и климат Финляндии, Языки и религии Финляндии, экономика и внешняя политика Финляндии, Хельсинки Содержание Содержание … Энциклопедия инвестора
линейная площадь — это … Что такое линейная площадь?
Area 88 — Аниманга Infobox / Название заголовка = Area 88 caption = Рекламное изображение аниме-адаптации 2005 года ja name = エリア 88 ja name trans = Eria Hachi Jū Hachi жанр = Action, Military, RomanceInfobox animanga / Manga title = author = Издатель Kaoru Shintani… Wikipedia
Телефонный код 913 — это код города для телефонных станций, расположенных в Канзасской части столичного округа Канзас-Сити.Код города раньше охватывал весь северный Канзас от линии штата Колорадо до линии штата Миссури, но теперь используется только…… Wikipedia
Линия 2 Orange (Монреальское метро) — Линия 2 Orange / Ligne 2 Orange Панорамный вид на Лайонел Гро… Википедия
Код города 620 — это код города для телефонных станций в большинстве южных районов Канзаса, за исключением города Уичито и его окрестностей.Код города простирается от границы штата Колорадо на западе до границы штата Миссури на востоке.…… Wikipedia
Линия A (Римское метро) — Линия A Обзор Тип Система скоростного транспорта Рим Метро Регион Рим, Италия… Википедия
Браузер линейного режима — отображение немецкой Википедии Автор (ы) оригинала… Википедия
строка — строка1 [līn] n. [ME объединяет OE, шнур, с OFr ligne (оба & LT; L linea, букв., льняная нить, п. использование жен. из линея, из льна и LT; linum, flax)] 1. a) шнур, веревка, проволока, веревка и т.п. б) длинный, тонкий, прочный шнур с крючком, грузило,…… English World Dictionary
Линия 4 — или линия 4 может относиться к: Общественный транспорт 4 (служба метро Нью-Йорка) Линия метро Барселоны 4, линия в сети метро Барселоны, управляемая TMB, линия 4, Пекинское метро, в Пекине, Китай, линия 4 (Метро Будапешта), четвертая линия метро Будапешта… Википедия
Код зоны 785 — это код города для телефонных станций в большей части северного Канзаса.Код города простирается от линии штата Колорадо на западе до линии штата Миссури на востоке, но не включает столичную зону Канзас-Сити. Самый большой город…… Википедия
Код зоны 813 — это телефонный код плана нумерации для города Тампа, Флорида и прилегающих районов, таких как Зефирхиллс и Олдсмар. Описание Код территории 813 охватывает весь округ Хиллсборо, восточные две трети округа Паско и город. из Oldsmar…… Википедия
Линия отхода — это военный термин, используемый для обозначения исходной позиции для атаки на позиции противника.Во время Второй мировой войны в вооруженных силах Великобритании, Канады и Америки использовался термин «линия начала». Линия отправления (LD) когда-то была принята…… Wikipedia
.
Линейные и зональные диаграммы — Руководство по диаграммам Atlas
Закрыть ×
Графики Руководство
Облако
Облако
Версия 19.12 (локальная)
Версия 19.09 (на месте)
Запуск диаграмм MongoDB
Приветственный опыт
Учебники
Визуализация данных заказа
Загрузить пример данных
Создание новой информационной панели
Столбчатая диаграмма
, показывающая общий объем продаж по местоположению магазина
Кольцевая диаграмма с наиболее распространенными тегами для проданных товаров
Сгруппированная столбчатая диаграмма, показывающая наиболее распространенные товары, продаваемые по местоположению магазина
Изменение порядка и размера диаграмм
Диаграмма
, показывающая возрастное распределение клиентов
Визуализация деталей фильма
Загрузить пример данных
Создание новой информационной панели
Столбчатая диаграмма
, показывающая директоров, получивших наибольшее количество наград
Точечная диаграмма номинированных на премию фильмов с рейтингом TomatoMeter
Разместите диаграммы на приборной панели
Панели мониторинга
Управление существующими панелями мониторинга
Разрешения на приборную панель
Обновить данные панели мониторинга
Фильтрация информационных панелей по значениям полей
Взаимодействие с диаграммами на панели инструментов
Источники данных
Управление существующими источниками данных
Разрешения источника данных
Конвейеры источников данных
Таблицы сборки
Общие сведения о каналах кодирования
Создание диаграммы одной серии с несколькими агрегатами
Создание многосерийной диаграммы
Визуализировать встроенные объекты и массивы
Измените свои данные
Расчет новых полей данных
Преобразование типов данных поля
Запуск конвейера агрегирования ваших данных
Результаты диаграммы фильтров
Корзина, сортировка и ограничение данных
Настроить диаграммы
Общие параметры настройки
Опции на уровне поля
Опции оси значений
Параметры геопространственной настройки
Просмотр и экспорт данных диаграммы
Ссылка на здание схемы
Режим выборки
Резервный конвейер агрегации
Типы диаграмм
Столбцы и гистограммы
Графики и диаграммы с областями
Сетка
Тепловая карта
Точечная диаграмма
Круговые диаграммы
Пончиковая диаграмма
Таблица размеров
Текстовые диаграммы
Таблица данных
Изменить порядок столбцов таблицы данных
Сортировка и изменение размера столбцов таблицы данных
Переключение итоговых значений строк и столбцов таблицы данных
Таблица номеров
Облако слов
Геопространственные карты
Карплетная диаграмма
Схемы форм
Геопространственная диаграмма
Геопространственная тепловая карта
Схема встраивания
Встроить диаграммы с iframe
Встроенные диаграммы с помощью SDK для встраивания
Настроить встроенные поставщики аутентификации
Учебники по внедрению
Встроить диаграмму, аутентифицированную с помощью входа в Google
Встроить диаграмму с аутентификацией в области
Внедрить аутентифицированную диаграмму с помощью специального поставщика JWT
Вставить неаутентифицированную диаграмму
Ссылка на SDK для встраивания
Опции встроенных диаграмм
Фильтр встроенных диаграмм
Коды ошибок встроенной диаграммы
Настройки графиков
Графики в Атласе Цены
Примечания к выпуску MongoDB Charts Cloud
Сторонние лицензии
Навигация
Типы диаграмм>
Линия а
.
Линейная диаграмма и диаграмма с областями, что выбрать?
Возможно, вам потребуется рассмотреть вопрос: «Что выбрать?» — линейная диаграмма и диаграмма с областями? при выполнении заданий. Прочтите эту статью, чтобы узнать больше о ключевых факторах и советах.
Что такое линейные диаграммы и диаграммы с областями
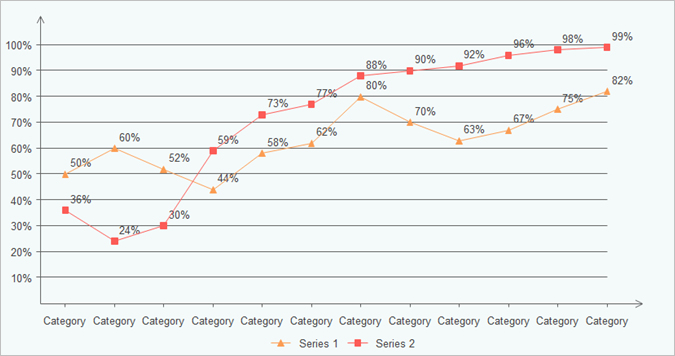
Линейные графики обычно предназначены для обсуждения тенденций за определенное время. Ось Y показывает числовые значения, а ось X представляет некоторые ключевые измерения. Графики четкие и легкие для понимания, поскольку вы можете видеть конкретную тенденцию для отдельной группы данных.На самом деле финансовые менеджеры приветствуют типы линий, чтобы проверить тенденцию к прибыли и некоторые другие бизнес-факторы.

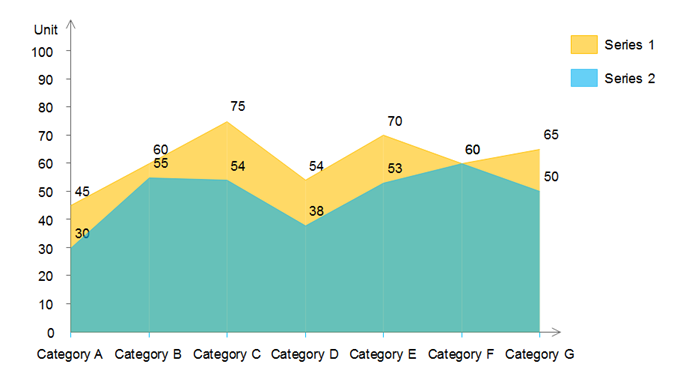
Диаграммы с областями похожи на линейные. Однако пространство между каждой линией и осью X заполнено определенным цветом. Как правило, диаграммы с областями идеально подходят для отображения изменений между различными наборами данных. Диаграммы с областями делятся на две основные категории: диаграммы с накоплением и диаграммы с накоплением 100%.

Ключевые моменты для выбора между линейной диаграммой и диаграммой с областями
Если вы не уверены в использовании линейной диаграммы или диаграммы с областями, просто просмотрите следующие три ключевых момента.
1. Сравнения. Предположим, что ваши задания включают сравнение нескольких значений, тогда вам следует использовать линейную диаграмму вместо типов областей. Диаграммы без теней к областям более эффективны для сравнения разных групп данных, чем закрашенные диаграммы. Вы можете легко показать положительные или отрицательные отношения между двумя или более переменными.

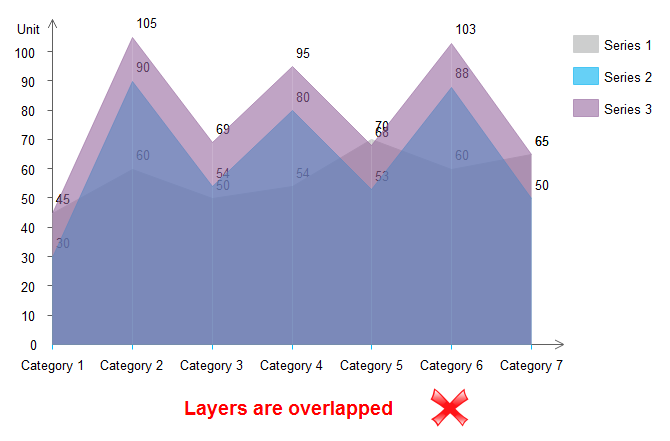
В диаграммах с областями вы обнаружите, что очень сложно четко показать различные группы данных, поскольку верхний уровень скрывает нижние, и это становится еще хуже, особенно когда у вас есть более двух категорий данных.Проблема все еще существует, даже если вы увеличите прозрачность слоев.

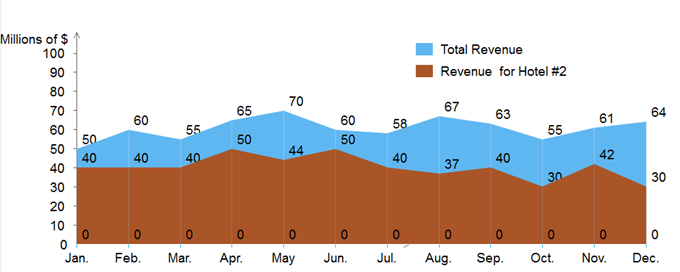
2. Состав между несколькими группами данных. Диаграммы с областями очень подходят для отображения деталей от части к целому. Если ваши цели включают в себя композицию каких-то аспектов, то вам следует выбрать области, а не линейные диаграммы. В этом случае диаграммы с областями могут четко показать, как отдельные части составляют общие части. Для практического примера ниже представьте, что вы хотите быстро получить общее представление о годовом доходе вашего отеля №1, а затем вы можете просто нацелить на синюю цветовую область на приведенной ниже диаграмме.

3. Распределение или тенденция. Предположим, ваша цель — дать читателям понять распределение выбранных вами данных или то, как группа данных работает в течение определенного периода времени, тогда вам следует выбрать линейные диаграммы. Графики хороши для определения общей тенденции и некоторых других связанных деталей в ваших ценностях.

Линейные диаграммы и диаграммы с областями: сводка и дополнительные советы
В заключение, хотя оба этих типа могут использоваться для визуализации данных, они имеют разные цели использования.Лучше выбрать тип области для отношений суммирования для более чем двух различных групп данных и использовать линейные диаграммы для отображения сравнений, распределений или тенденций между непрерывными наборами данных. Кроме того, вы можете попрактиковаться, используя еще несколько советов:
Напоминания о рисовании линейной диаграммы:
Вы можете попробовать сплошные линии вместо прямых.
Убедитесь, что высота вашей индивидуальной линии не выходит за пределы нормы.Поэтому старайтесь не заполнять график на весь экран, вместо этого оставьте место наверху.
Не следует добавлять слишком много строк, чтобы показать свою цель.

Напоминания о рисовании диаграммы с областями:
Не вставляйте слишком много категорий данных (лучше не более пяти групп данных).
Постарайтесь выделить наиболее важную группу данных ваших ресурсов.
Избегайте очень светлых или очень близких цветов для ваших групп данных. Убедитесь, что все ваши детали в таблице не уходят на второй план.

Дополнительные бесплатные шаблоны линейных диаграмм и диаграмм с областями
Следующие бесплатных примеров диаграмм и шаблоны включают основные категории диаграмм для использования в бизнесе и образовании. Не стесняйтесь нажимать на любой из них, чтобы увидеть более подробную информацию.
Какой инструмент построения графиков следует использовать?
Модель Edrawchartmaker позволяет создавать множество различных видов диаграмм, включая столбцы, столбцы, круговые диаграммы, линии, площади, разброс, пауки и датчики.Вы, несомненно, выиграете от других встроенных в диаграмму шаблонов и функций автоматического создания. Более того, вы можете импортировать данные из локальных файлов или одним щелчком мыши установить категорию и номер серии, показать или скрыть легенду и ось, изменить номер отметки оси и интервал категорий и т. Д.

Узнать больше
10 основных типов диаграмм и их использование
Разница между линейной и точечной диаграммами
Как выбрать между столбчатой и круговой диаграммой
Как использовать гистограмму для сравнения данных
.
линейных, площадных и гистограмм | Руководство Kibana [6.8]
Линейные, площади и гистограммыправить
Линейные диаграммы, диаграммы с областями и гистограммы позволяют отображать данные по осям X / Y.
Сначала вам нужно выбрать метрики , которые определяют ось значений.
Метрические агрегаты:
Счетчик
Счетчик Агрегация возвращает необработанное количество элементы в выбранном шаблоне индекса.
Среднее значение
Это агрегирование возвращает средних числовых поле.Выберите поле из раскрывающегося списка.
Сумма
Сумма Агрегация возвращает общую сумму числового поле. Выберите поле из раскрывающегося списка.
мин.
Агрегация мин. возвращает минимальное значение числовое поле. Выберите поле из раскрывающегося списка.
Макс
Агрегация max возвращает максимальное значение числовое поле. Выберите поле из раскрывающегося списка.
Уникальное количество
Мощность Агрегация возвращает количество уникальных значений в поле. Выберите поле из раскрывающегося списка.
Стандартное отклонение
Расширенная статистика агрегирование возвращает стандартное отклонение данных в числовом поле. Выберите поле из раскрывающегося списка.
Top Hit
лучших хитов агрегирование возвращает одно или несколько верхних значений из определенного поля в ваших документах.Выберите поле из раскрывающегося списка, как вы хотите отсортировать документы и выбрать верхние поля и сколько значений должно быть возвращено.
Процентили
процентиль агрегация делит значения в числовом поле в указанные вами процентильные диапазоны. Выберите поле из раскрывающегося списка, затем укажите его. или более диапазонов в полях Percentiles . Щелкните X , чтобы удалить процентильное поле. Нажмите + Добавить , чтобы добавить процентильное поле.
Percentile Рейтинг
Процентиль ранжирует агрегирование возвращает процентильные рейтинги для значений в указанном числовом поле. Выберите числовое поле из раскрывающегося списка, затем укажите одно или несколько значений процентильного ранга в полях Значения . Щелкните X , чтобы удалить поле значений. Щелкните + Добавить , чтобы добавить поле значений.
Агрегации родительских конвейеров:
Для каждого агрегирования родительского конвейера необходимо определить метрику, для которой рассчитывается агрегирование.Это может быть одна из ваших существующих метрик или новая. Вы также можете вкладывать эти агрегаты (например, для производства третьей производной)
Производная
Производная агрегация вычисляет производная от конкретных показателей.
Кумулятивная сумма
Совокупная сумма Агрегация вычисляет кумулятивную сумму указанной метрики в родительской гистограмме
Скользящее среднее
Скользящее среднее Агрегация будет проведите окном по данным и выдайте среднее значение этого окна
Serial Diff
Серийный дифференциал — это метод где значения во временном ряду вычитаются из самого себя в разное время или период
Сводные конвейерные агрегаты:
Как и в случае агрегирования родительского конвейера, вам необходимо указать метрику, для которой будет вычисляться агрегирование одноуровневого конвейера.Вдобавок к этому вам также необходимо предоставить агрегацию сегментов, которая будет определять сегменты, в которых агрегация будет работать
Средний ковш
Ковш в среднем вычисляет (среднее) среднее значение указанной метрики в одноуровневой агрегации
Сумма ведро
Ведро сумм вычисляет сумму значений указанной метрики в одноуровневой агрегации
Мин Ковш
Ковш мин вычисляет минимальное значение указанной метрики в одноуровневой агрегации
Максимальный ковш
Ковш max вычисляет максимальное значение указанной метрики в одноуровневой агрегации
Вы можете добавить агрегирование, нажав кнопку + Добавить метрики .
Введите строку в поле Custom Label , чтобы изменить отображаемую метку.
Блоки Агрегаты определяют, какая информация извлекается из вашего набора данных.
Прежде чем выбрать агрегацию сегментов, укажите, разделяете ли вы срезы в пределах одной диаграммы или на несколько графиков. Разделение на несколько диаграмм должно выполняться перед любыми другими агрегатами. Когда вы разбиваете диаграмму, вы можете изменить если разделения отображаются в строке или столбце, щелкнув Rows | Селектор столбцов .
Ось X этой диаграммы — это ось сегментов . Вы можете определить сегменты для оси X, для области разделения на диаграмму или для разделенных диаграмм.
Ось X этой диаграммы поддерживает следующие агрегаты. Щелкните связанное имя каждой агрегации, чтобы перейти к главному Документация Elasticsearch для этой агрегации.
Гистограмма дат
Гистограмма дат построена на основе числовое поле и упорядочено по дате.Вы можете указать временные рамки для интервалов в секундах, минутах, часах, днях, недели, месяцы или годы. Вы также можете указать настраиваемую рамку интервала, выбрав Custom в качестве интервала и указав число и единицу времени в текстовом поле. Пользовательские единицы времени интервала: с, для секунд, м, для минут, ч
.
No related posts.