Возведение комплексных чисел в степень
Начнем с любимого квадрата.
Пример 9
Возвести в квадрат комплексное число
Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей и перемножить числа по правилу умножения многочленов.
Второй способ состоит в применение известной школьной формулы сокращенного умножения :
Для комплексного числа легко вывести свою формулу сокращенного умножения:
. Аналогичную формулу можно вывести для квадрата разности, а также для куба сумма и куба разности. Но эти формулы более актуальны длязадач комплексного анализа. Что делать, если комплексное число нужно возвести, скажем, в 5-ую, 10-ую или 100-ую степень? Ясно, что в алгебраической форме проделать такой трюк практически невозможно, действительно, подумайте, как вы будете решать пример вроде?
И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра: Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степеньсправедлива формула:
Просто до безобразия.
Пример 10
Дано комплексное число , найти.
Что нужно сделать? Сначала нужно представить данное число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:
Тогда, по формуле Муавра:
Упаси боже, не нужно считать на калькуляторе , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляетрадиан или 360 градусов. Выясним сколько у нас оборотов в аргументе. Для удобства делаем дробь правильной:, после чего становится хорошо видно, что можно убавить один оборот:. Надеюсь всем понятно, чтои– это один и тот же угол.
Таким образом, окончательный ответ запишется так:
Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.
Пример 12
Возвести в степень комплексные числа ,,
Здесь тоже всё просто, главное, помнить знаменитое равенство.
Если мнимая единица возводится в четную степень, то техника решения такова:
Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:
Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями
Рассмотрим пример:
Нельзя извлечь корень? Если речь идет о действительных числах, то действительно нельзя. В комплексных числах извлечь корень – можно! А точнее, два корня:
Действительно ли найденные корни являются решением уравнения ? Выполним проверку:
Что и требовалось проверить.
Часто используется сокращенная запись, оба корня записывают в одну строчку под «одной гребёнкой»: .
Такие корни также называют сопряженными комплексными корнями.
Как извлекать квадратные корни из отрицательных чисел, думаю, всем понятно: ,,,,и т.д. Во всех случаях получаетсядва сопряженных комплексных корня.
Пример 13
Решить квадратное уравнение
Вычислим дискриминант:
Дискриминант отрицателен, и в действительных числах уравнение решения не имеет. Но корень можно извлечь в комплексных числах!
По известным школьным формулам получаем два корня: – сопряженные комплексные корни
Таким образом, уравнение имеет два сопряженных комплексных корня:,
Теперь вы сможете решить любое квадратное уравнение!
И вообще, любое уравнение с многочленом «энной» степени имеет ровнокорней, часть из которых может быть комплексными.
Простой пример для самостоятельного решения:
Пример 14
Найти корни уравнения и разложить квадратный двучлен на множители.
Разложение на множители осуществляется опять же по стандартной школьной формуле.
Возведение в степень комплексного числа, все формулы
Удобнее всего возводить в степень комплексные числа, которые записаны в показательной или тригонометрической форме.
Возведение в степень в показательной форме
Для возведения в степень комплексных чисел в показательной форме верна формула:
Возведение в степень в тригонометрической форме
Обычно комплексные числа принято возводить в степень в тригонометрической форме, для которой верна формула Муавра: .
Данная формула непосредственно следует из формулы Эйлера, связывающей между собой тригонометрические и показательные функции: , поскольку
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Как возвести комплексное число в n-ую степень
Комплексное число имеет три формы записи: алгебраическая форма записи Z=a+bi, показательная и тригонометрическая форма записи
Модулем комплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Модуль комплексного числа a+ bi обозначается |a+ bi | или буквой r и равен:
\(r=|a+bi|= = { \sqrt{a^2+b^2}}\)
Сопряжённые комплексные числа имеют одинаковый модуль.
Аргумент комплексного числа — это угол φ между осью OX и вектором OP, изображающим это комплексное число. Отсюда, tan φ = b / a .
Пусть \(z=a+bi, r=|z|={\sqrt{a^2+b^2}}\) и φ = arg z. Тогда по определению аргумента имеем:
Отсюда получается:
|
z = a + bi = r(cos φ + i sin φ). |
Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.
Записать число \(z=1-{\sqrt3i}\) в тригонометрической форме
Решение:
Найдем модуль этого числа: \(|z|={\sqrt{{1^2}+{(\sqrt3})^2}}={\sqrt {1+3}}=2\)
Аргумент данного числа находится из системы:
Значит, один из аргументов числа \(z=1-{\sqrt3i}\) равен \(-{π\over3}\)
Получаем:
Операции с комплесными числами в тригонометрической форме:
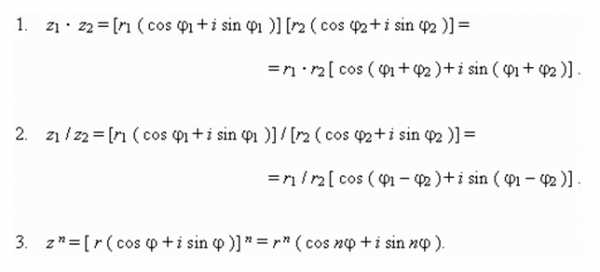
Последняя формула называется формулой Муавра и используется для возведения комплексного числа в n-ую степень.
Автор — Дмитрий Айстраханов
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
myalfaschool.ru
Возведение комплексного числа в натуральную степень
Умножение, деление и возведение в степень выполняются для чисел, представленных в любой форме записи.
Для чисел, представленных в алгебраической форме, возведение в $n$-ю степень осуществляется путем перемножения $n$ одинаковых сомножителей.
Определение 1
Произведением двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое получается перемножением данных чисел по правилам алгебры с учетом того, что $i^{2} =-1$.
Пример 1
Вычислить $n$-ю степень некоторого комплексного числа $z=1+2\cdot i$, где $n=2..4$.
Решение:
По определению операции умножения комплексных чисел в алгебраической форме получим:
Для $n=2$:
\[z^{2} =(1+2\cdot i)\cdot (1+2\cdot i)=1\cdot 1+2\cdot 1\cdot i+1\cdot 2\cdot i+2\cdot 2\cdot i^{2} =1+2i+2i-4=-3+4i\]Для $n=3$:
$z^{3} =z^{2} \cdot (1+2\cdot i)=(-3+4i)\cdot (1+2\cdot i)=-3\cdot 1+4\cdot 1\cdot i-3\cdot 2\cdot i+4\cdot 2\cdot i^{2} =-3+4i-6i-8=-11-2i$
Для $n=4$:
\[\begin{array}{l} {z^{4} =z^{3} \cdot (1+2\cdot i)=(-11-2i)\cdot (1+2\cdot i)=-11\cdot 1-2\cdot 1\cdot i-11\cdot 2\cdot i-2\cdot 2\cdot i^{2} =-11-2i-22i+4=} \\ {=-7-24i} \end{array}\]Определение 2
Произведением двух заданных комплексных чисел $z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )$ и $z_{2} =r_{2} \cdot (\cos \varphi _{2} +i\sin \varphi _{2} )$ является комплексное число, которое определяется равенством
\[z_{1} \cdot z_{2} =r_{1} \cdot r_{2} \cdot [\cos (\varphi _{1} +\varphi _{2} )+i\sin (\varphi _{1} +\varphi _{2} )].\]Замечание 1
Произведением двух заданных комплексных чисел $z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )$ и $z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )$ является комплексное число, которое определяется равенством
\[z_{1} \cdot z_{1} =z_{1}^{2} =r_{1} \cdot r_{1} \cdot [\cos (\varphi _{1} +\varphi _{1} )+i\sin (\varphi _{1} +\varphi _{1} )]=r_{1} ^{2} \cdot (\cos 2\varphi _{1} +i\sin 2\varphi _{1} ).\]Определение 3
Степенью порядка $n$ ($n\in Z_{+} $) комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ является комплексное число, которое определяется равенством
\[z^{n} =r^{n} \cdot (\cos n\varphi +i\sin n\varphi ).\]Данная формула называется формулой Муавра.
Замечание 2
Формулу из определения 3 легко получить из формулы приведенной определении 2 посредством перемножения некоторого комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ на само себя $n$ раз.
Формула Муавра показывает, что возводя некоторое комплексное число в целую положительную степень, необходимо модуль числа возвести в данную степень, а аргумент комплексного числа умножить на показатель степени.
Пример 2
Вычислить степени $z^{3} ,\, \, z^{5} $ данного комплексного числа $z=2\cdot \left(\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} \right)$.
Решение:
Воспользуемся формулой Муавра:
\[z^{n} =r^{n} \cdot (\cos n\varphi +i\sin n\varphi _{1} ).\]Вычисляя $z^{3} $, получим:
\[z^{3} =2^{3} \cdot \left(\cos \left(3\cdot \frac{\pi }{2} \right)+i\cdot \sin \left(3\cdot \frac{\pi }{2} \right)\right)=8\cdot \left(\cos \frac{3\pi }{2} +i\cdot \sin \frac{3\pi }{2} \right).\]Вычисляя $z^{5} $, получим:
\[z^{5} =2^{5} \cdot \left(\cos \left(5\cdot \frac{\pi }{2} \right)+i\cdot \sin \left(5\cdot \frac{\pi }{2} \right)\right)=32\cdot \left(\cos \frac{5\pi }{2} +i\cdot \sin \frac{5\pi }{2} \right)=32\cdot \left(\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} \right).\]При возведении некоторого комплексного числа, представленного в алгебраической форме, в степень с большим показателем необходимо выполнить следующие действия:
- представить число в тригонометрической форме;
- возвести число в степень по формуле Муавра;
- при необходимости перевести число в алгебраическую форму.
Пример 3
Вычислить степени $z^{2} ,\, \, z^{4} $ некоторого комплексного числа $z=\frac{1}{2} +\frac{1}{2} \cdot i$.
Решение:
Представим число в тригонометрической форме:
$z=r\cdot (\cos \varphi +i\sin \varphi )$, где $r=\sqrt{a^{2} +b^{2} } $ и $\varphi =arctg\frac{b}{a} $.
По условию $a=\frac{1}{2} ,b=\frac{1}{2} $.
Вычислим модуль исходного комплексного числа:
\[r=\sqrt{\left(\frac{1}{2} \right)^{2} +\left(\frac{1}{2} \right)^{2} } =\sqrt{\frac{1}{4} +\frac{1}{4} } =\sqrt{\frac{1}{2} } =\frac{\sqrt{2} }{2} .\]Вычислим аргумент исходного комплексного числа:
\[\varphi =\arg z=arctg\frac{1/2}{1/2} =arctg1=\frac{\pi }{4} .\]Подставим полученные значения и получим:
\[z=\frac{\sqrt{2} }{2} \cdot \left(\cos \frac{\pi }{4} +i\sin \frac{\pi }{4} \right).\]Далее воспользуемся формулой Муавра:
\[z^{n} =r^{n} \cdot (\cos n\varphi +i\sin n\varphi ).\]Вычисляя $z^{2} $, получим:
\[z^{2} =\left(\frac{\sqrt{2} }{2} \right)^{2} \cdot \left(\cos \left(2\cdot \frac{\pi }{4} \right)+i\sin \left(2\cdot \frac{\pi }{4} \right)\right)=\frac{1}{2} \cdot \left(\cos \frac{\pi }{2} +i\sin \frac{\pi }{2} \right).\]Запишем ответ в алгебраической форме:
\[z^{2} =\frac{1}{2} \cdot \left(\cos \frac{\pi }{2} +i\sin \frac{\pi }{2} \right)=\frac{1}{2} \cdot \left(0+1\cdot i\right)=0+\frac{1}{2} \cdot i.\]Вычисляя $z^{4} $, получим:
\[z^{4} =\left(\frac{\sqrt{2} }{2} \right)^{4} \cdot \left(\cos \left(4\cdot \frac{\pi }{4} \right)+i\sin \left(4\cdot \frac{\pi }{4} \right)\right)=\frac{1}{4} \cdot \left(\cos \pi +i\sin \pi \right).\]Запишем ответ в алгебраической форме:
\[z^{4} =\frac{1}{4} \cdot \left(\cos \pi +i\sin \pi \right)=\frac{1}{4} \cdot (-1+0\cdot i)=-\frac{1}{4} +0\cdot i.\]При возведении некоторого комплексного числа, представленного в показательной форме, в степень можно воспользоваться следующим свойством:
\[z^{n} =(r\cdot e^{i\cdot \varphi } )^{n} =r^{n} \cdot (e^{i\cdot \varphi } )^{n} =r^{n} \cdot e^{i\cdot \varphi \cdot n} .\]Пример 4
Вычислить степени $z^{3} ,\, \, z^{5} $ данного комплексного числа $z=2\cdot e^{i\cdot \pi } $.
Решение:
Воспользуемся формулой:
\[z^{n} =(r\cdot e^{i\cdot \varphi } )^{n} =r^{n} \cdot e^{i\cdot \varphi \cdot n} .\]Вычисляя $z^{3} $, получим:
\[z^{3} =\left(2\cdot e^{i\cdot \pi } \right)=2^{3} \cdot e^{i\cdot 3\pi } =8\cdot e^{i\cdot 3\pi } =8\cdot e^{(0+i\cdot \pi )+2\pi \cdot i} =8\cdot e^{(0+i\cdot \pi )} =8\cdot e^{i\cdot \pi } .\]Вычисляя $z^{5} $, получим:
\[z^{5} =\left(2\cdot e^{i\cdot \pi } \right)^{5} =2^{5} \cdot e^{i\cdot 5\pi } =32\cdot e^{i\cdot 5\pi } =32\cdot e^{(0+i\cdot 3\pi )+2\pi \cdot i} =32\cdot e^{(0+i\cdot 3\pi )} =32\cdot e^{(0+i\cdot \pi )+2\pi \cdot i} =32\cdot e^{i\cdot \pi } .\]При возведении некоторого комплексного числа, представленного в показательной форме, в степень можно выполнить следующие действия:
- представить число в тригонометрической форме;
- возвести число в степень по формуле Муавра;
- при необходимости перевести число в показательную форму.
Пример 5
Вычислить степени $z^{6} $ данного комплексного числа $z=1\cdot e^{i\cdot \frac{\pi }{6} } $.
Решение:
По условию $r=1,\varphi =\frac{\pi }{6} $.
Подставим полученные значения и получим число в тригонометрической форме:
\[z=1\cdot \left(\cos \frac{\pi }{6} +i\sin \frac{\pi }{6} \right).\]Далее воспользуемся формулой Муавра:
\[z^{n} =r^{n} \cdot (\cos n\varphi +i\sin n\varphi ).\]Вычисляя $z^{6} $, получим:
\[z^{6} =1^{6} \cdot \left(\cos \left(6\cdot \frac{\pi }{6} \right)+i\sin \left(6\cdot \frac{\pi }{6} \right)\right)=1\cdot \left(\cos \pi +i\sin \pi \right).\]Запишем ответ в показательной форме:
\[z^{6} =1\cdot \left(\cos \pi +i\sin \pi \right)=1\cdot e^{i\cdot \pi } .\]Формулу Муавра можно применять при вычислении косинусов и синусов углов, например, $\cos 3\varphi $, $\sin 3\varphi $ и т.д.
При $r=1$ формула Муавра записывается следующим образом:
\[(\cos \varphi +i\sin \varphi )^{n} =\cos n\varphi +i\sin n\varphi .\]Рассмотрим применение формулы Муавра для вычисления тройных углов ($n=3$).
\[(\cos \varphi +i\sin \varphi )^{3} =\cos 3\varphi +i\sin 3\varphi \]\[\cos ^{3} \varphi +i\cdot 3\cos ^{2} \varphi \cdot \sin \varphi -3\cos \varphi \cdot \sin ^{2} \varphi -i\cdot \sin ^{3} \varphi =\cos 3\varphi +i\sin 3\varphi \]По определению равенства двух заданных комплексных числе получим:
\[\cos 3\varphi =\cos ^{3} \varphi -3\cos \varphi \cdot \sin ^{2} \varphi \]и
\[\sin 3\varphi =\sin ^{3} \varphi +3\cos ^{2} \varphi \cdot \sin \varphi .\]spravochnick.ru
Возведение комплексных чисел в степень — Мегаобучалка
Пример 9:
Возвести в квадрат комплексное число
Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей и перемножить числа по правилу умножения многочленов.
Второй способ состоит в применение известной школьной формулы сокращенного умножения :
Для комплексного числа легко вывести свою формулу сокращенного умножения:
. Аналогичную формулу можно вывести для квадрата разности, а также для куба суммы и куба разности. Но эти формулы более актуальны для задач комплексного анализа, поэтому на данном уроке я воздержусь от подробных выкладок.
Что делать, если комплексное число нужно возвести, скажем, в 5-ую, 10-ую или 100-ую степень? В алгебраической форме проделать такой трюк практически невозможно, действительно, подумайте, как вы будете решать пример вроде ?
И здесь на помощь приходит тригонометрическая форма комплексного числа и так называемая формула Муавра: Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степень n справедлива формула:
Пример 10
Дано комплексное число , найти .
Что нужно сделать? Сначала нужно представить данной число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:
. Тогда по формуле Муавра:
Не нужно считать на калькуляторе , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов, но так, чтобы значения синуса и косинуса не изменились. Один оборот составляет радиан или 360 градусов. Смотрим сколько у нас оборотов в аргументе : оборотов, в данном случае можно убавить один оборот: . Надеюсь всем понятно, что и – это один и тот же угол.
Таким образом, окончательный ответ запишется так:
Любители стандартов везде и во всём могут переписать ответ в виде:
(т.е. убавить еще один оборот и получить значение аргумента в стандартном виде).
Хотя – ни в коем случае не ошибка.
Пример 11
Дано комплексное число , найти . Полученный аргумент (угол) упростить, результат представить в алгебраической форме.
Это пример для самостоятельного решения, полное решение и ответ в конце урока.
Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.
Пример 12
Возвести в степень комплексные числа , ,
Здесь тоже всё просто, главное, помнить знаменитое равенство.
Если мнимая единица возводится в четную степень, то техника решения такова:
Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:
Пример 13
Возвести в степень комплексные числа ,
Это пример для самостоятельного решения.
megaobuchalka.ru
Возведение комплексных чисел в степень — МегаЛекции
Начнем со всем любимого квадрата.
Пример 9
Возвести в квадрат комплексное число
Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей и перемножить числа по правилу умножения многочленов.
Второй способ состоит в применение известной школьной формулы сокращенного умножения :
Для комплексного числа легко вывести свою формулу сокращенного умножения:
. Аналогичную формулу можно вывести для квадрата разности, а также для куба сумма и куба разности. Но эти формулы более актуальны длязадач комплексного анализа, поэтому на данном уроке я воздержусь от подробных выкладок.
Что делать, если комплексное число нужно возвести, скажем, в 5-ую, 10-ую или 100-ую степень? Ясно, что в алгебраической форме проделать такой трюк практически невозможно, действительно, подумайте, как вы будете решать пример вроде ?
И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра: Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степень справедлива формула:
Данная формула следует из правила умножения комплексных чисел, представленных в тригонометрической форме: чтобы найти произведение чисел , нужно перемножить их модули и сложить аргументы:
Аналогично для показательной формы: если , то:
Просто до безобразия.
Пример 10
Дано комплексное число , найти .
Что нужно сделать? Сначала нужно представить данное число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:
Тогда, по формуле Муавра:
Упаси боже, не нужно считать на калькуляторе , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляет радиан или 360 градусов. Выясним сколько у нас оборотов в аргументе . Для удобства делаем дробь правильной: , после чего становится хорошо видно, что можно убавить один оборот: . Надеюсь всем понятно, что и – это один и тот же угол.
Таким образом, окончательный ответ запишется так:
Любители стандартов везде и во всём могут переписать ответ в виде:
(т.е. убавить еще один оборот и получить значение аргумента в стандартном виде).
Хотя – ни в коем случае не ошибка.
Пример 11
Дано комплексное число , найти . Полученный аргумент (угол) упростить, результат представить в алгебраической форме.
Это пример для самостоятельного решения, полное решение и ответ в конце урока.
Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.
Пример 12
Возвести в степень комплексные числа , ,
Здесь тоже всё просто, главное, помнить знаменитое равенство.
Если мнимая единица возводится в четную степень, то техника решения такова:
Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:
Пример 13
Возвести в степень комплексные числа ,
Это пример для самостоятельного решения.
Извлечение корней из комплексных чисел.
Квадратное уравнение с комплексными корнями
Наконец-то. Меня всю дорогу подмывало привести этот маленький примерчик:
Нельзя извлечь корень? Если речь идет о действительных числах, то действительно нельзя. В комплексных числах извлечь корень – можно! А точнее, два корня:
Действительно ли найденные корни являются решением уравнения ? Выполним проверку:
Что и требовалось проверить.
Часто используется сокращенная запись, оба корня записывают в одну строчку под «одной гребёнкой»: .
Такие корни также называют сопряженными комплексными корнями.
Как извлекать квадратные корни из отрицательных чисел, думаю, всем понятно: , , , , и т.д. Во всех случаях получается двасопряженных комплексных корня.
О том, как извлечь квадратный корень из комплексного числа с ненулевой мнимой частью, я расскажу чуть позже, а пока нечто знакомое:
Пример 14
Решить квадратное уравнение
Вычислим дискриминант:
Дискриминант отрицателен, и в действительных числах уравнение решения не имеет. Но корень можно извлечь в комплексных числах!
По известным формулам получаем два корня:
– сопряженные комплексные корни
Таким образом, уравнение имеет два сопряженных комплексных корня: ,
Нетрудно понять,что в поле комплексных чисел «школьное» квадратное уравнение всегда при двух корнях! И вообще, любое уравнение вида имеет ровно корней, часть из которых могут быть комплексными.
Простой пример для самостоятельного решения:
Пример 15
Найти корни уравнения и разложить квадратный двучлен на множители.
Разложение на множители осуществляется опять же по стандартной школьной формуле. Но на этом тема не закрыта! Совсем скоро вы будете уверенно решать
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Возведение комплексных чисел в степень
Пример 9:
Возвести в квадрат комплексное число
Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей и перемножить числа по правилу умножения многочленов.
Второй способ состоит в применение известной школьной формулы сокращенного умножения :
Для комплексного числа легко вывести свою формулу сокращенного умножения:
. Аналогичную формулу можно вывести для квадрата разности, а также для куба суммы и куба разности. Но эти формулы более актуальны для задач комплексного анализа, поэтому на данном уроке я воздержусь от подробных выкладок.
Что делать, если комплексное число нужно возвести, скажем, в 5-ую, 10-ую или 100-ую степень? В алгебраической форме проделать такой трюк практически невозможно, действительно, подумайте, как вы будете решать пример вроде ?
И здесь на помощь приходит тригонометрическая форма комплексного числа и так называемая формула Муавра: Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степень n справедлива формула:
Пример 10
Дано комплексное число , найти .
Что нужно сделать? Сначала нужно представить данной число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:
Не нужно считать на калькуляторе , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов, но так, чтобы значения синуса и косинуса не изменились. Один оборот составляет радиан или 360 градусов. Смотрим сколько у нас оборотов в аргументе : оборотов, в данном случае можно убавить один оборот: . Надеюсь всем понятно, что и – это один и тот же угол.
Таким образом, окончательный ответ запишется так:
Любители стандартов везде и во всём могут переписать ответ в виде:
(т.е. убавить еще один оборот и получить значение аргумента в стандартном виде).
Хотя – ни в коем случае не ошибка.
Пример 11
Дано комплексное число , найти . Полученный аргумент (угол) упростить, результат представить в алгебраической форме.
Это пример для самостоятельного решения, полное решение и ответ в конце урока.
Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.
Пример 12
Возвести в степень комплексные числа , ,
Здесь тоже всё просто, главное, помнить знаменитое равенство.
Если мнимая единица возводится в четную степень, то техника решения такова:
Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:
Пример 13
Возвести в степень комплексные числа ,
Это пример для самостоятельного решения.
infopedia.su
