Площадь н угольника формула: Как найти площадь многоугольника — ответ на Uchi.ru

Содержание

Теорема Пика или формула для ленивых: imit_omsu — LiveJournal

: September 23 2019, 12:00

Categories:

Наука
История
Cancel

Каждому из нас нередко приходилось считать площадь решётчатого многоугольника (изображённого, например, на клетчатой бумаге). В основном, это делают ещё по известным со школы формулам. Но в этом случае для каждой фигуры приходится помнить выражение её площади.
Не легче ли использовать одну формулу для всех многоугольников?
— Сказка? — Нет, теорема Пика!

• Названа она в честь Георга Пика (нет, не оружия или покемона), доказавшего её в 1899 году.

Формулировка звучит так:
S

= В + Г / 2 − 1, где S — площадь многоугольника, В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.

• Важное замечание: формула справедлива только для многоугольников, у которых вершины расположены в узлах решетки.

Например, для многоугольника на рисунке, В=7 (красные точки), Г=8 (зелёные точки), поэтому S = 7 + 8/2 — 1 = 10 квадратных единиц.

Докажем теорему Пика:
• Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны a и b. Имеем в этом случае В = (a-1)(b-1), Г = 2a+2b и, по формуле Пика, S = (a-1)(b-1)+a+b-1 = ab .
• Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами

a и b, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат c целочисленных точек.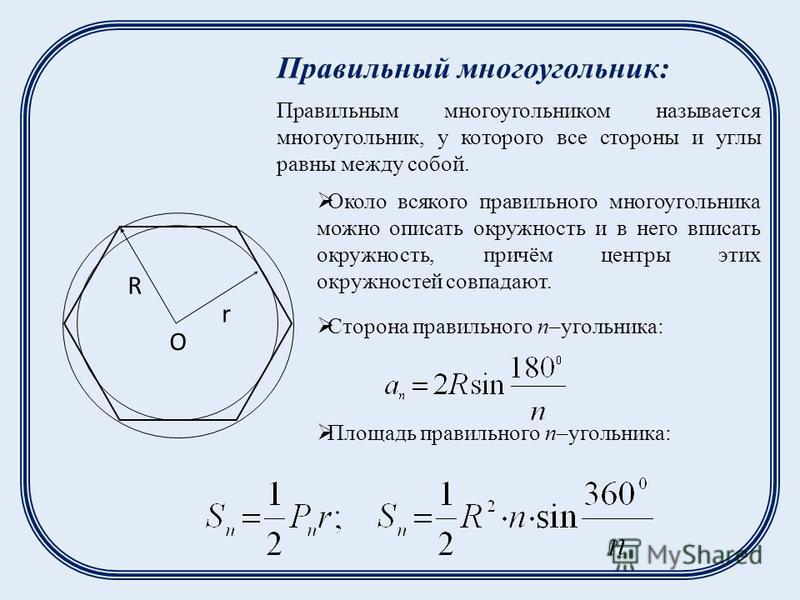

Тогда для этого случая В = ((a-1)(b-1)-c+2)/2, Г = (2a+2b)/2+c-1 и получаем, что S = ab/2.
• Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников (см. рисунок). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.

• Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой многоугольник можно триангулировать, т.е. разбить на треугольники (например, диагоналями). Отсюда по индукции следует, что формула Пика верна для любого многоугольника.

чтд

К сожалению, эта столь простая и красивая формула плохо обобщается на высшие размерности.
Наглядно показал это Рив, предложив в 1957 г. рассмотреть тетраэдр (называемый теперь тетраэдром Рива) со следующими вершинами:
A(0,0,0), B(1,0,0), C(0,1,0), D(1,1,k)
Тогда этот тетраэдр ABCD при любых k не содержит внутри ни одной точки с целочисленными координатами, а на его границе — лежат только четыре точки A, B, C, D. Таким образом, объём и площадь поверхности этого тетраэдра могут быть разными, в то время как число точек внутри и на границе — неизменны; следовательно, формула Пика не допускает обобщений даже на трёхмерный случай.

Тем не менее, некоторое подобное обобщение на пространства большей размерности всё же имеется, — это многочлены Эрхарта, но они весьма сложны, и зависят не только от числа точек внутри и на границе фигуры.

Специально для ЖЖ матфака, Сергей Романов.

ликбез

Площадь многоугольника. Формула Пика

Асанова З.А

Площадь многоугольника.

Формула Пика

«Берем палец и считаем»

В.В.Вавилов

При решении задач на нахождение площади многоугольника на клетчатой бумаге необходимо воображение и знание основных геометрических свойств и формул. Существует множество способов решения задач на клетчатой бумаге.

Если фигура состоит из целых квадратиков, это сделать довольно таки легко. Посчитать квадратики и всё! Сложнее задача, когда многоугольник имеет интересную форму и тогда его надо разбить на простые многоугольники. А если фигура не многоугольник , а например криволинейная трапеция ? Для решения таких задач существует достаточно простой способ с использованием формулы Пика. Ее могут использовать школьники и взрослые при решении реальных ситуаций; учителя, как при проведении уроков по математике, так и на факультативных курсах и дополнительных занятий на повторение.

Формула Пика. Решетки. Узлы

При решении задач на клетчатой бумаге необходимы понятия решетки и узла.

Клетчатая бумага (точнее — ее узлы), на которой мы часто предпочитаем рисовать и чертить, является одним из важнейших примеров точечной решетки на плоскости.

Рассмотрим на плоскости два семейства параллельных прямых, разбивающих плоскость на равные квадраты.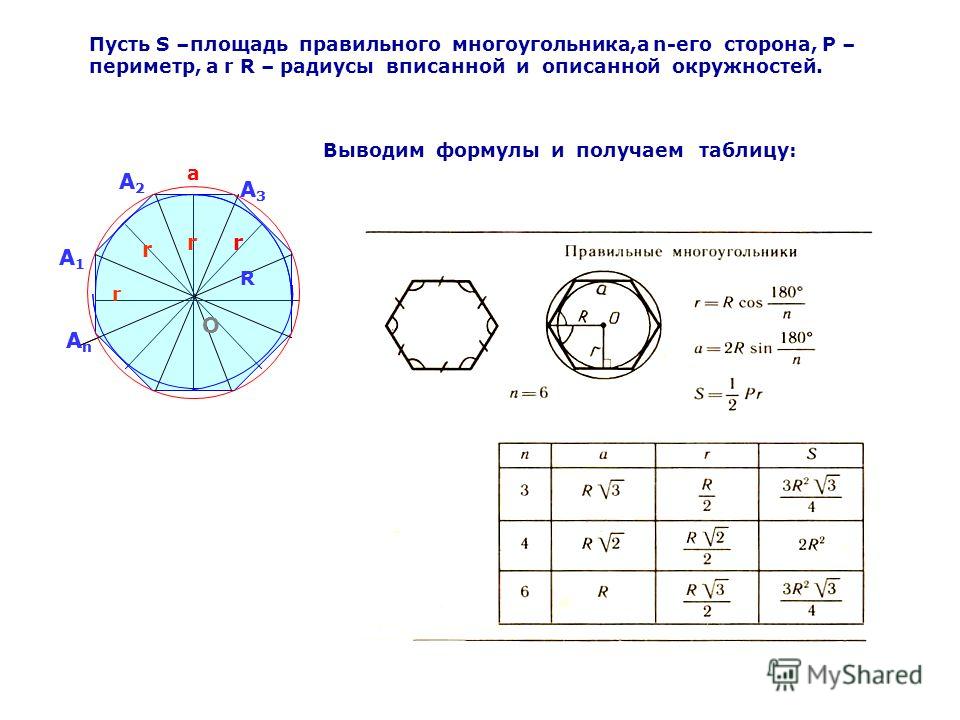

Любой из этих квадратов называется фундаментальным квадратом или квадратом, порождающим решетку. Множество всех точек пересечения этих прямых называется точечной решеткой или просто решеткой, а сами точки – узлами решетки.

Рис.1.

Чтобы оценить площадь многоугольника на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу)

А также, площадь любого многоугольника, нарисованного на клетчатой бумаге, легко посчитать, представив её как сумму или разность площадей прямоугольных треугольников и прямоугольников, стороны которых идут по л иниям сетки, проходящим через вершины нарисованного треугольника. Чтобы вычислить площадь многоугольника, изображенного на рисунке, необходимо достроить его до прямоугольника ABCD, вычислить площадь прямоугольника ABCD, найти площадь заштрихованной фигуры как сумму площадей треугольников и прямоугольников её составляющих, вычесть её из площади прямоугольника.

И хотя многоугольник и выглядит достаточно просто, для вычисления его площади нам придется потрудиться. А если бы многоугольник выглядел более причудливо, как на следующих рисунках?

Оказывается, площади многоугольников, вершины которых расположены в узлах решетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника.

Эта замечательная и простая формула называется формулой Пика:

S = В + — 1

где S– площадь многоугольника,

В – число узлов решетки, расположенных строго внутри многоугольника,

Г – число узлов решетки, расположенных на его границе, включая вершины.

Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах решетки.

Нахождение площадей многоугольников, изображенных на клетчатой бумаге

Приведу несколько примеров из заданий ОГЭ на нахождение площадей многоугольников.

На клетчатой бумаге с клетками размером 1 см х 1 см изображен многоугольник. Найдите его площадь в квадратных сантиметрах
Рисунок	По формуле геометрии	По формуле Пика
	a=6; b=4 S1 = 15: 2 = 2,5. S2=55:2 = 12,5 S = 2,5 + 12,5 = 15(см2)	Г=12,B=10 . S=10+ -1=15(см2)
	S1= b=1/2 7 3,5 S2= b=1/2 7 2=7 S3= b=1/2 4 1=2 S4= b=1/2 5 1=2,5 S5=a²=1²=1 Sкв.= a²=7²=49 S=49-3,5-7-2-2,51=33(см²)	Г=4;В=32. S=32+ -1=33см²
	S=a S= =36 см2	Г=18, В=28 S=28+ -1=36см2
	S1= b=1/2 3 6=9 S2= b=1/2 6 6=18 S3= b=1/2 3 6=9 S=9+18+9=36см²	Г=18;В=28. S=28+ -1=36см²

S1= b=1/2 2 4=4

S2= =1/2 4 4=8

S3= =1/2 8 2=8

S4= =1/2 4 1=2

Sпр.= b=6 8=48

S5=48-4-8-8-2=26см²

Г=18;В=18.

S=18+ -1=26см²

Геометрические задачи с практическим содержанием.

Поможет нам формула Пика и для решения геометрических задач с практическим содержанием.

Задача 1. Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м .

Решение. Найдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика:

S = В + — 1

В = 8, Г = 7. S = 8 + 7/2 – 1 = 10,5 (см²)

1 см² — 200² м²; S = 40000 · 10,5 = 420 000 (м²)

Ответ: 420 000 м²

Задача 2. Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м.

Решение. Найдём S площадь четырёхугольника изображенного на клетчатой бумаге по формуле Пика: S = В + — 1

В = 7, Г = 4. S = 7 + 4/2 – 1 = 8 (см²)

1 см² — 200² м²; S = 40000 · 8 = 320 000 (м²)

Ответ: 320 000 м²

Задача 3. Вершины квадрата соединены с серединами его сторон, как показано на рис 5. Найдите площадь закрашенного восьмиугольника, если стороны квадрата равны 12.

Решение: По формуле Пика: S= В + Г /2 – 1. В = 21,

Г = 8, S = 21 + 8 / 2 – 1 = 24 (кв.ед.)

Ответ: 24 кв.ед.

Рассмотренные задания имеют различный уровень трудности – от простых до олимпиадных. Каждый может найти среди них задачи посильного уровня сложности, отталкиваясь от которых, можно будет переходить к решению более трудных. Такой способ нахождения площадей многоугольников, изображенных на клетчатой бумаге, можно использовать на ОГЭ для решения задач на ОГЭ и ЕГЭ.

Литература

Свободная энциклопедия Википедия, статья «Формула Пика», URL: https://ru.wikipedia.org/wiki/%D0%A4%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D0%B0_%D0%9F%D0%B8%D0%BA%D0%B0

Свободная энциклопедия Википедия, статья «Пик, Георг», URL: https://ru.wikipedia.org/wiki/%D0%9F%D0%B8%D0%BA,_%D0%93%D0%B5%D0%BE%D1%80%D0%B3

Научно-популярный физико-математический журнал «Квант», Н. Б.Васильев, статья «Вокруг формулы Пика», URL:http://kvant.ras.ru/1974/12/vokrug_formuly_pika.htm

Математика, которая мне нравится [электронный ресурс], статья «Георг Александр Пик (1859-1942)», URL: http://hijos.ru/2011/12/30/georg-aleksandr-pik-1859-1942/

{\circ} \right)$. Квадрат — это особый вид прямоугольника (равносторонний) и особый вид параллелограмма (равносторонний и равноугольный).

Какова площадь квадрата?

Площадь квадрата – это мера занимаемой им площади или поверхности. Рассмотрим квадрат длины $6$ единиц, т. е. квадрат, у которого длина всех ребер (сторон) равна $6$ единиц.

Далее разделим этот квадрат на несколько маленьких квадратов со стороной $1$.

9{2}$.

Как вычислить площадь квадрата по сторонам?

Площадь квадрата равна квадрату его длины. Для нахождения площади квадрата используются следующие шаги:

Шаг 1: Запишите длину квадрата

Шаг 2: Подставляем значение длины квадрата в формулу

Шаг 4: Упростите выражение в формуле, чтобы получить площадь в квадратных единицах

Примеры

9{2}$

Количество плиток = $\frac {250000}{625} = 400$

Следовательно, чтобы покрыть квадратный двор длиной $5 м$, необходимо количество квадратных плиток длиной $25 см$, равное $400$. {2}$ 9{2}$

Количество плиток = $\frac {25}{0,0625} = 400$

Следовательно, чтобы покрыть квадратный двор длиной $5 м$, необходимо количество квадратных плиток длиной $25 см$, равное $400$.

10 Известные математики

Формула площади квадрата с использованием диагонали

Вы также можете найти площадь квадрата, если известна длина его диагонали. В этом случае вы используете теорему Пифагора, чтобы найти площадь квадрата.

Рассмотрим квадрат со стороной $s$ и диагональю $d$. 9{2}$.