Определение
Высота параллелограмма — это перпендикуляр, проведенный из вершины параллелограмма к стороне (или к продолжению стороны), не содержащей эту вершину.
Например, высота \(BK\) падает на сторону \(AD\), а высота \(BH\) — на продолжение стороны \(CD\):
Теорема: площадь параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена эта высота.
Доказательство
Проведем перпендикуляры \(AB’\) и \(DC’\), как показано на рисунке. Заметим,что эти перпендикуляры равны высоте параллелограмма \(ABCD\).
Тогда \(AB’C’D\) – прямоугольник, следовательно, \(S_{AB’C’D}=AB’\cdot AD\).
Заметим, что прямоугольные треугольники \(ABB’\) и \(DCC’\) равны. Таким образом,
\(S_{ABCD}=S_{ABC’D}+S_{DCC’}=S_{ABC’D}+S_{ABB’}=S_{AB’C’D}=AB’\cdot
AD.
\[{\Large{\text{Площадь треугольника}}}\]
Определение
Будем называть сторону, к которой в треугольнике проведена высота, основанием треугольника.
Теорема
Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию.
Доказательство
Пусть \(S\) – площадь треугольника \(ABC\). Примем сторону \(AB\) за основание треугольника и проведём высоту \(CH\). Докажем, что \[S = \dfrac{1}{2}AB\cdot CH.\] Достроим треугольник \(ABC\) до параллелограмма \(ABDC\) так, как показано на рисунке:
Треугольники \(ABC\) и \(DCB\) равны по трем сторонам (\(BC\) – их общая сторона, \(AB = CD\) и \(AC = BD\) как противоположные стороны параллелограмма \(ABDC\)), поэтому их площади равны. Следовательно, площадь \(S\) треугольника \(ABC\) равна половине площади параллелограмма \(ABDC\), то есть \(S = \dfrac{1}{2}AB\cdot CH\).
Теорема
Если два треугольника \(\triangle ABC\) и \(\triangle A_1B_1C_1\) имеют равные высоты, то их площади относятся как основания, к которым эти высоты проведены.
Следствие
Медиана треугольника делит его на два треугольника, равных по площади.
Теорема
Если два треугольника \(\triangle ABC\) и \(\triangle A_2B_2C_2\) имеют по равному углу, то их площади относятся как произведения сторон, образующих этот угол.
Доказательство
Пусть \(\angle A=\angle A_2\). Совместим эти углы так, как показано на рисунке (точка \(A\) совместилась с точкой \(A_2\)):
Проведем высоты \(BH\) и \(C_2K\).
Треугольники \(AB_2C_2\) и \(ABC_2\) имеют одинаковую высоту \(C_2K\), следовательно: \[\dfrac{S_{AB_2C_2}}{S_{ABC_2}}=\dfrac{AB_2}{AB}\]
Треугольники \(ABC_2\) и \(ABC\) имеют одинаковую высоту \(BH\), следовательно: \[\dfrac{S_{ABC_2}}{S_{ABC}}=\dfrac{AC_2}{AC}\]
Перемножая последние два равенства, получим: \[\dfrac{S_{AB_2C_2}}{S_{ABC}}=\dfrac{AB_2\cdot AC_2}{AB\cdot AC} \qquad \text{ или } \qquad \dfrac{S_{A_2B_2C_2}}{S_{ABC}}=\dfrac{A_2B_2\cdot A_2C_2}{AB\cdot AC}\]
Теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:
Верно и обратное: если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других двух сторон, то такой треугольник прямоугольный.
Теорема
Площадь прямоугольного треугольника равна половине произведения катетов.
Теорема: формула Герона
Пусть \(p\) – полупериметр треугольника, \(a\), \(b\), \(c\) – длины его сторон, тогда его площадь равна \[S_{\triangle}=\sqrt{p(p — a)(p — b)(p — c)}\]
\[{\Large{\text{Площадь ромба и трапеции}}}\]
Замечание
Т.к. ромб является параллелограммом, то для него верна та же формула, т.е. площадь ромба равна произведению высоты и стороны, к которой проведена эта высота.
Теорема
Площадь выпуклого четырехугольника, диагонали которого перпендикулярны, равна половине произведения диагоналей.
Доказательство
Рассмотрим четырехугольник \(ABCD\). Обозначим \(AO=a, CO=b, BO=x, DO=y\):
Заметим, что данный четырехугольник составлен из четырех прямоугольных треугольников, следовательно, его площадь равна сумме площадей этих треугольников:
\(\begin{multline*} S_{ABCD}=\frac12ax+\frac12xb+\frac12by+\frac12ay=\frac12(ax+xb+by+ay)=\\ \frac12((a+b)x+(a+b)y)=\frac12(a+b)(x+y)\end{multline*}\)
Следствие: площадь ромба
Площадь ромба равна половине произведения его диагоналей: \[S_{\text{ромб}}=\dfrac12 d_1\cdot d_2\]
Определение
Высота трапеции – это перпендикуляр, проведенный из вершины одного основания к другому основанию.
Теорема: площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту.
Доказательство
Рассмотрим трапецию \(ABCD\) с основаниями \(BC\) и \(AD\). Проведем \(CD’\parallel AB\), как показано на рисунке:
Тогда \(ABCD’\) – параллелограмм.
Проведем также \(BH’\perp AD, CH\perp AD\) (\(BH’=CH\) – высоты трапеции).
Тогда \(S_{ABCD’}=BH’\cdot AD’=BH’\cdot BC, \quad S_{CDD’}=\dfrac12CH\cdot D’D\)
Т.к. трапеция состоит из параллелограмма \(ABCD’\) и треугольника \(CDD’\), то ее площадь равна сумме площадей параллелограмма и треугольника, то есть:
\[S_{ABCD}=S_{ABCD’}+S_{CDD’}=BH’\cdot BC+\dfrac12CH\cdot D’D=\dfrac12CH\left(2BC+D’D\right)=\] \[=\dfrac12 CH\left(BC+AD’+D’D\right)=\dfrac12 CH\left(BC+AD\right)\]
Расчет стороны многоугольника. Калькулятор расчета площади земельного участка неправильной формы. Указываем все данные в метрах
Среда программирования:
Visual Studio 2013
В данном примере строится многоугольник по количеству сторон n , координатам центра многоугольника и расстоянию R от центра многоугольника до его стороны.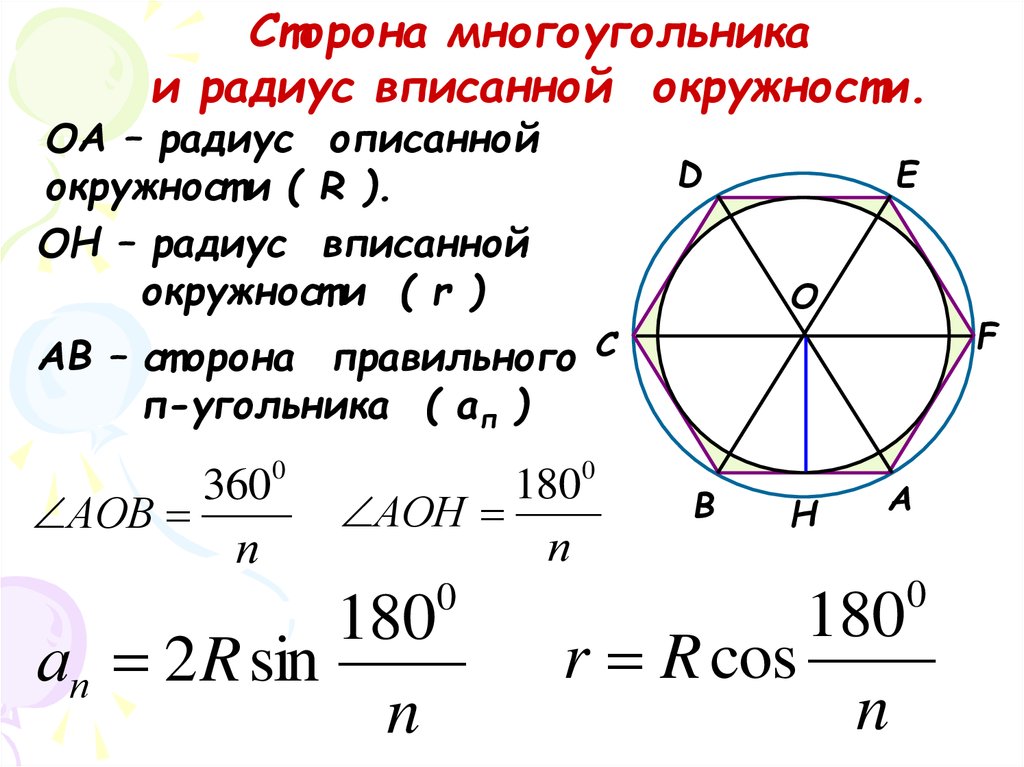
Все эти данные вводятся пользователем и начинают обрабатываться по нажатию кнопки «Построить». Программа позволяет рисовать на одной форме многоугольники с различными параметрами.
Функция button1_Click
Код программы:
using
System
;
using
System.Collections.Generic
;
using
System.ComponentModel
;
using
System.Data
;
using
System.Drawing
;
using
System.Linq
;
using
System.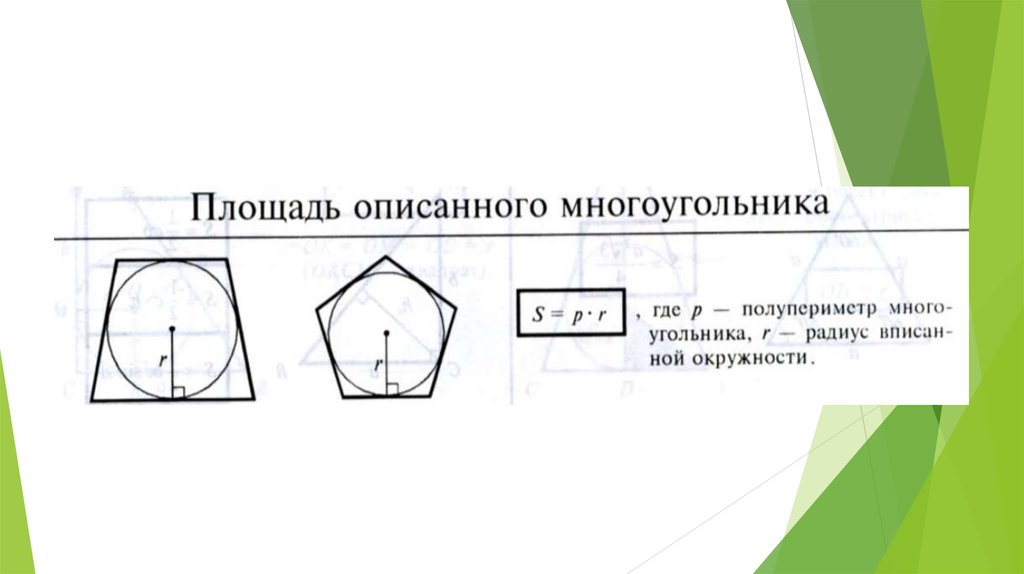
Text
;
using
System.Threading.Tasks
;
using
System.Windows.Forms
;
namespace
pravilnyy_mnogougolnik
{
public
partial
class
Form1 :
Form
{
public
Form1()
{
InitializeComponent()
;
}
int
n;
//количество сторон
int
R;
//расстояние от центра до стороны
Point Cntr;
//центр
Point
p;
//массив точек будущего многоугольника
//создаём массив точек нашего многоугольника
private
void
lineAngle(double
angle)
{
double
z =
0
;
int
i=
0
;
while
(inew
Point[
n +
1
]
;
lineAngle((double
)
(360.0
/
(double
)
n)
)
;
int
i =
n;
Graphics g =
pictureBox2.
CreateGraphics
()
;
while
(i >
0
)
{
g.
DrawLine
(new
Pen(Color.
Black
, 2
)
, p[
i]
, p[
i —
1
]
)
;
i =
i —
1
;
}
}
}
//оставляем нарисованный многоугольник, обнуляем входные значения для нового ввода
private
void
button2_Click(object
sender, EventArgs e)
{
textBox4.
Text
=
«0»
;
textBox5.
Text
=
«0»
;
textBox6.
Text
=
«0»
;
textBox7.
Text
=
«0»
;
label10.
Text
=
«»
;
}
//стираем всё нарисованное, не обнуляя последние входные данные
private
void
button3_Click(object
sender, EventArgs e)
{
pictureBox2.
Данный онлайн калькулятор помогает произвести расчет, определение и вычисление площади земельного участка в онлайн режиме. Представленная программа способна правильно подсказать, как выполнить расчет площади земельных участков неправильной формы.
Важно! Важ участок должен приблизительно вписываться в окружность. Иначе расчеты будут не совсем точными.
Указываем все данные в метрах
A B, D A, C D, B C — Размер каждой стороны делянки.
Согласно введен данным, наша программа в онлайн режиме выполнить расчет и определить, площадь земельных угодий в квадратных метрах, сотках, акрах и гектарах.
Методика определения размеров участка ручным методом
Чтобы правильно выполнить расчет площади делянок, не нужно использовать сложные инструменты. Мы берем деревянные колышки или металлические прутья и устанавливаем их в углах нашего участка. Далее при помощи измерительной рулетки определяем ширину и длину делянки.
Далее переходим к расчету площади делянки. При правильной форме участка, можно использовать геометрическую формулу определения площади (S) прямоугольника. Согласно этой формуле, нужно выполнить умножение ширины (20) на длину (40) , то есть произведение длин двух сторон. В нашем случае S=800 м².
После того, как мы определили нашу площадь, мы можем определить количество соток на земельном участке. Согласно общепринятым данным, в одной сотке – 100 м². Далее при помощи простой арифметики, мы разделим наш параметр S на 100. Готовый результат и станет равен размеру делянки в сотках. Для нашего примера, этот результат – 8. Таким образом, получаем, что площадь участка составляет восемь соток.
В том случае, когда территория угодий очень большая, то лучше всего выполнять все измерения в других единицах – в гектарах.
Согласно общепринятым единицам измерения – 1 Га = 100 соток. К примеру, если наша земельная делянка согласно полученным измерениям составляем 10 000 м², то в этом случае его площадь равна 1 гектару или 100 соткам.
Если Ваш участок неправильной формы, то в этом случае количество соток напрямую зависит от площади. Именно по этой причине при помощи онлайн калькулятора Вы сможете правильно рассчитать параметр S делянки, и после этого разделив полученный результат на 100. Таким образом, Вы получите расчеты в сотках. Такой метод предоставляет возможность измерять делянки сложных форм, что весьма удобно.
Общие данные
Расчет площади земельных участков базируется на классических расчетах, которые выполняются согласно общепринятым геодезическим формулам.
Всего доступно несколько методов для расчета площади земельных угодий – механический (рассчитывается по плану при помощи мерных палеток), графический (определяется по проекту) и аналитический (при помощи формулы площади по измеренным линиям границ).
На сегодняшний день самым точным способом заслуженно считается – аналитический. Используя данный метод, ошибки при расчетах, как правило, появляются из-за погрешностей на местности измеренных линий. Данный способ является также и достаточно сложным, если границы криволинейные или количество углом на делянке больше десяти.
Немного проще по расчетам является графическим способ. Его лучше всего использовать в том случае, когда границы участка представлены в виде ломанной линии, с небольшим количеством поворотов.
И самый доступный и простой способ, и наиболее популярный, но и в тоже время самой большой погрешностью – механический способ. Используя данный метод, Вы сможете легко и быстро выполнить расчет площади земельных угодий простой или сложной формы.
Среди серьезных недостатков механического или графического способа, выделяют следующее, кроме погрешностей при измерении участка, при расчетах добавляется погрешность из-за деформации бумаги или погрешность при составлении планов.
Конвертер единиц расстояния и длины Конвертер единиц площади Присоединяйтесь © 2011-2017 Довжик Михаил Копирование материалов запрещено. В онлайн калькуляте можно использовать величины в одинаквых единицах измерения! Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади. Дополнительные возможности калькулятора вычисления площади четырехугольника
- Между полями для ввода можно перемещаться нажимая клавиши «вправо» и «влево» на клавиатуре.
Теория. Площадь четырехугольника Четырёхугольник — геометрическая фигура, состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Четырёхугольник называется выпуклым, если отрезок соединяющий любые две точки этого четырехугольника, будет находиться внутри него.
Как узнать площадь многоугольника?
Формула определения площади определяется путем взятия каждого ребра многоугольника АВ, и вычисления площади треугольника АВО с вершиной в начале координат О, через координаты вершин.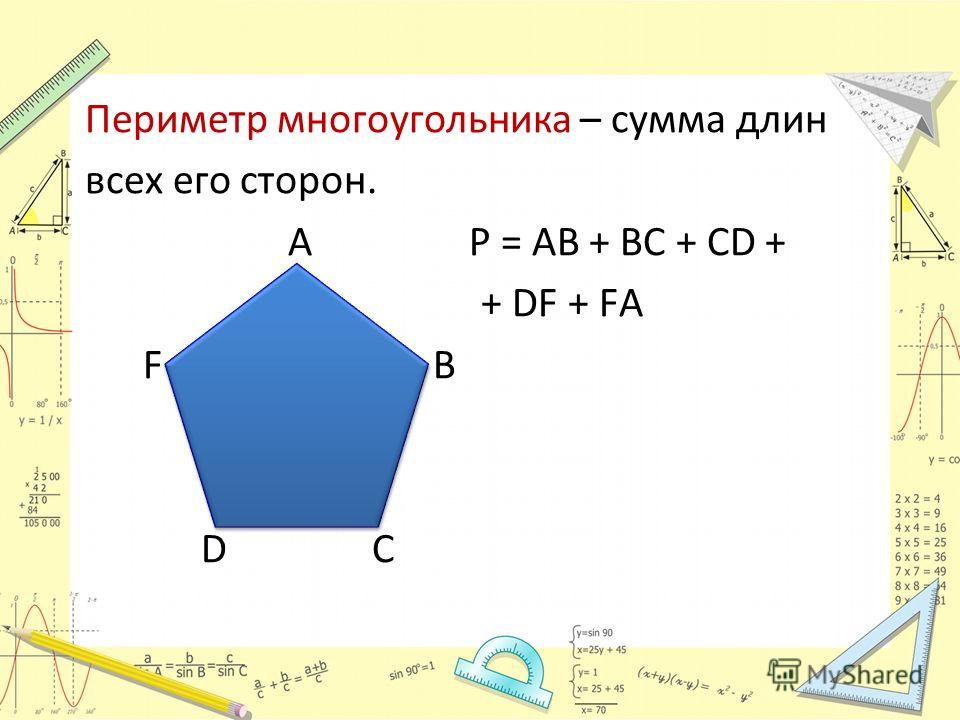
При обходе вокруг многоугольника, образуются треугольники, включающие внутреннюю часть многоугольника и расположенные снаружи его. Разница между суммой этих площадей и есть площадь самого многоугольника.
Поэтому формула называется формулой геодезиста, так как «картограф» находится в начале координат; если он обходит участок против часовой стрелки, площадь добавляется если она слева и вычитается если она справа с точки зрения из начала координат. Формула площади действительна для любого самонепересекающегося (простого) многоугольника, который может быть выпуклым или вогнутым. Содержание
- 1 Определение
- 2 Примеры
- 3 Более сложный пример
- 4 Объяснение названия
- 5 См.
Площадь многоугольника
Внимание
Это может быть:
- треугольник;
- четырехугольник;
- пяти- или шестиугольник и так далее.
Такая фигура непременно будет характеризоваться двумя положениями:
- Смежные стороны не принадлежат одной прямой.
- У несмежных отсутствуют общие точки, то есть они не пересекаются.
Чтобы понять, какие вершины являются соседними, потребуется посмотреть, принадлежат ли они одной стороне. Если да, то соседние. В противном случае их можно будет соединить отрезком, который необходимо назвать диагональю. Их можно провести только в многоугольниках, у которых больше трех вершин.
Какие их виды существуют? Многоугольник, у которого больше четырех углов, может быть выпуклым или вогнутым. Отличие последнего в том, что некоторые его вершины могут лежать по разные стороны от прямой, проведенной через произвольную сторону многоугольника.
Как найти площадь правильного и неправильного шестиугольника?
- Зная длину стороны, умножим её на 6 и получим периметр шестиугольника:10 см х 6 = 60 см
- Подставим полученные результаты в нашу формулу: Площадь = 1/2*периметр*апофему Площадь = ½*60см*5√3 Решаем: Теперь осталось упростить ответ, чтобы избавиться от квадратных корней, а полученный результат укажем в квадратных сантиметрах: ½ * 60 см * 5√3 см =30 * 5√3 см =150 √3 см =259.
8 см² Видео о том, как найти площадь правильного шестиугольника Существует несколько вариантов определения площади неправильного шестиугольника:- Метод трапеции.
- Метод расчета площади неправильных многоугольников при помощи оси координат.
- Метод разбивания шестиугольника на другие фигуры.
В зависимости от исходных данных, которые вам будут известны, подбирается подходящий метод.
Важно
Некоторые неправильные шестиугольники состоят из двух параллелограммов. Для определения площади параллелограмма следует умножить его длину на ширину и затем сложить две уже известные площади. Видео о том, как найти площадь многоугольника Равносторонний шестиугольник имеет шесть равных сторон и является правильным шестиугольником.
Площадь равностороннего шестиугольника равняется 6 площадям треугольников, на которые разбита правильная шестиугольная фигура. Все треугольники в шестиугольнике правильной формы равны, поэтому для нахождения площади такого шестиугольника достаточно будет знать площадь хотя бы одного треугольника.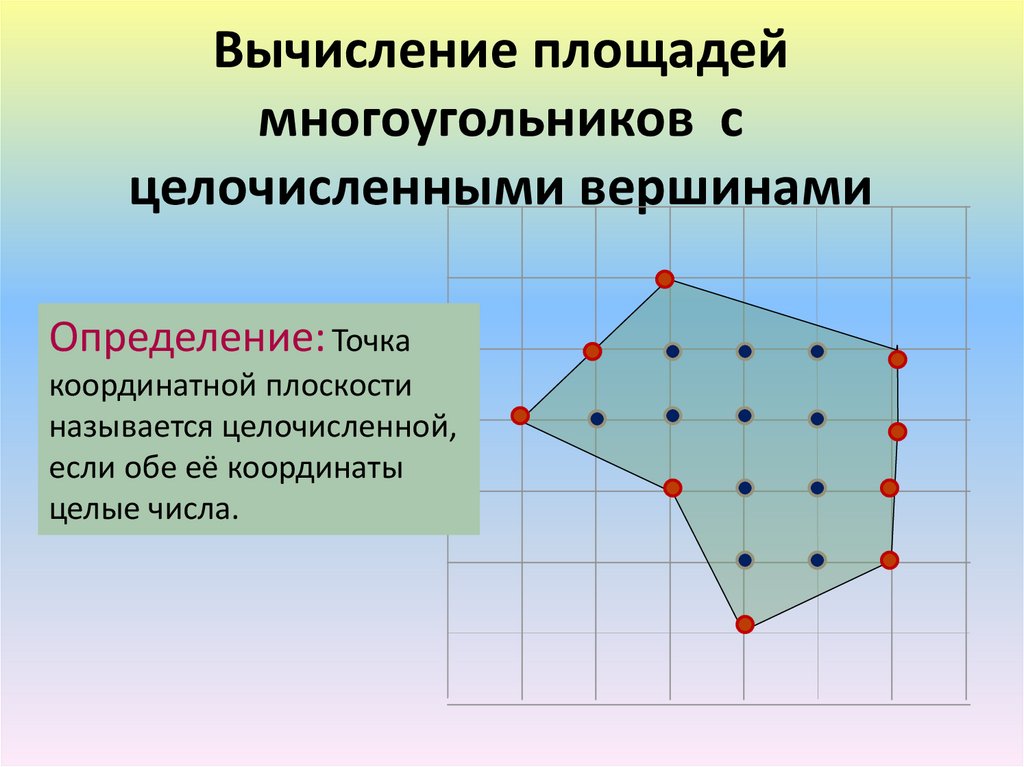
Для нахождения площади равностороннего шестиугольника используется, конечно же, формула площади правильного шестиугольника, описанная выше.
404 not found
Украшение жилища, одежды, рисование картин способствовало процессу формирования и накопления сведений в области геометрии, которые люди тех времён добывали опытным путем, по крупицам и передавали из поколения в поколение. Сегодня знания геометрии необходимы и закройщику, и строителю, и архитектору и каждому простому человеку в быту. Поэтому нужно учиться рассчитывать площадь различных фигур, и помнить, что каждая из формул может пригодиться впоследствии на практике, в том числе, и формула правильного шестиугольника.
Шестиугольником называется такая многоугольная фигура, общее количество углов которой равно шести. Правильным шестиугольником называют шестиугольную фигуру, которая имеет равные стороны. Углы у правильного шестиугольника также между собой равны.
В повседневной жизни мы часто можем встретить предметы, имеющие форму правильного шестиугольника.
Калькулятор площади неправильного многоугольника по сторонам
Вам понадобится
- — рулетка;
- — электронный дальномер;
- — лист бумаги и карандаш;
- — калькулятор.
Инструкция 1 Если вам нужна общая площадь квартиры или отдельной комнаты, просто прочтите технический паспорт на квартиру или дом, там указан метраж каждого помещения и общий метраж квартиры. 2 Для измерения площади прямоугольной или квадратной комнаты возьмите рулетку или электронный дальномер и измерьте длину стен. При измерении расстояний дальномером обязательно следите за перпендикулярностью направления луча, иначе результаты замеров могут быть искажены. 3 Затем полученную длину (в метрах) комнаты умножьте на ширину (в метрах). Полученное значение и будет площадью пола, она измеряется в квадратных метрах.
Формула площади гаусса
Если требуется посчитать площадь пола более сложной конструкции, например, пятиугольной комнаты или комнаты с круглой аркой, схематично начертите эскиз на листе бумаги.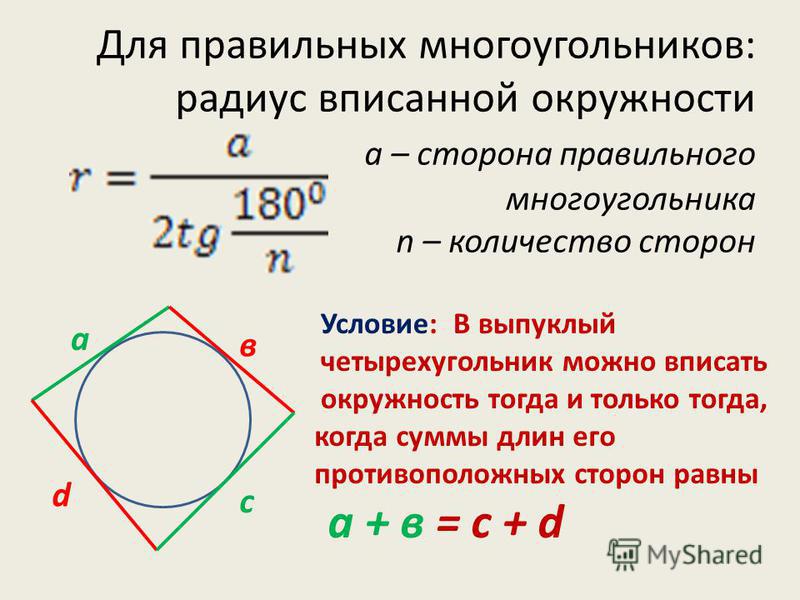
Затем разделите сложную форму на несколько простых, например, на квадрат и треугольник или прямоугольник и полукруг. Измерьте при помощи рулетки или дальномера величину всех сторон получившихся фигур (для круга необходимо узнать диаметр) и занесите результаты на ваш чертеж.
5 Теперь посчитайте площадь каждой фигуры по отдельности. Площадь прямоугольников и квадратов высчитывайте перемножением сторон. Для расчета площади круга диаметр разделите пополам и возведите в квадрат (умножьте его на самого себя), затем умножьте полученное значение на 3,14.
Если вам нужна только половина круга, разделите полученную площадь пополам. Чтобы рассчитать площадь треугольника, найдите Р, для этого сумму всех сторон поделите на 2.
Формула расчета площади неправильного многоугольника
Если точки пронумерованы последовательно в направлении против часовой стрелки, то детерминанты в формуле выше положительны и модуль в ней может быть опущен; если они пронумерованы в направлении по часовой стрелке, детерминанты будут отрицательными.
Это происходит потому, что формула может рассматриваться как частный случай теоремы Грина. Для применения формулы необходимо знать координаты вершин многоугольника в декартовой плоскости.
Для примера возьмём треугольник с координатами {(2, 1), (4, 5), (7, 8)}. Возьмём первую х -координату первой вершины и умножим её на y -координату второй вершины, а затем умножим х второй вершины на y третьей. Повторим эту процедуру для всех вершин. Результат может быть определен по следующей формуле: A tri.
Формула расчета площади неправильного четырехугольника
A} _{\text{tri.}}={1 \over 2}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3}|} где xi и yi обозначают соответствующую координату. Эту формулу можно получить, раскрыв скобки в общей формуле для случая n = 3. По этой формуле можно обнаружить, что площадь треугольника равна половине суммы 10 + 32 + 7 − 4 − 35 − 16, что даёт 3. Число переменных в формуле зависит от числа сторон многоугольника. Например, в формуле для площади пятиугольника будут использоваться переменные до x5 и y5: A pent.
= 1 2 | x 1 y 2 + x 2 y 3 + x 3 y 4 + x 4 y 5 + x 5 y 1 − x 2 y 1 − x 3 y 2 − x 4 y 3 − x 5 y 4 − x 1 y 5 | {\displaystyle \mathbf {A} _{\text{pent.}}={1 \over 2}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{5}+x_{5}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{5}y_{4}-x_{1}y_{5}|} A для четырехугольника — переменные до x4 и y4: A quad.
Сторона многоугольника — введение, названия многоугольников, примеры и часто задаваемые вопросы
Многоугольник — это любая геометрическая форма, которая классифицируется по количеству сторон и заключена в несколько прямых сторон. Однако многоугольник считается правильным, если все его стороны имеют одинаковую длину. Например, 3-сторонний многоугольник — это треугольник, 8-сторонний многоугольник — это восьмиугольник, а 11-сторонний многоугольник называется 11-угольником или шестнадцатеричным. Количество сторон правильного многоугольника можно вычислить с помощью внутренних и внешних углов.
Например, шестиугольник — это шестиугольник, а треугольник — трехугольник.
Внутренние и внешние углы, которые представляют собой внутренние и внешние углы, образованные соединяющимися сторонами многоугольника, могут использоваться для вычисления количества сторон правильного многоугольника.
Вычтите внутренний угол из 180, чтобы получить внешний угол. Например, если внутренний угол равен 165, вычитание этого значения из 180 даст вам 15.
Разделите 360 на разность углов и 180 градусов. 360 разделить на 15 = 24, что в данном случае является количеством сторон многоугольника.
Чтобы рассчитать количество сторон многоугольника, разделите 360 на величину внешнего угла. Например, если внешний угол равен 60 градусам, то деление 360 на 60 равно 6, то есть количеству сторон многоугольника.
Names of Polygons
Number of Sides of a Polygon | Polygon Shape |
3 sided polygon | Triangle |
4 sided polygon | Square, Rectangle, Quadrilaterals— Parallelogram, Rhombus, Kite, Dart |
5 sided polygon | Pentagon |
6-сторонний многоугольник | Шестиугольник |
7-сторонний многоугольник | Семиугольник |
8 sided polygon | Octagon |
9 sided polygon | Nonagon |
10 sided polygon | Decagon |
11 sided polygon | Hendecagon |
12-сторонний многоугольник | Dodecagon |
20-сторонний многоугольник | Icosagon |
100 sided polygon | Hectagon |
n sides (infinite number of sides) | N-gon |
Convex and Вогнутые многоугольники
Выпуклый многоугольник замыкается во внутреннем пространстве, не создавая «вмятины».
Ни один из внутренних углов не направлен внутрь. В геометрической математике у вас может быть 4-сторонний многоугольник, который направлен наружу во всех направлениях, как воздушный змей, или у вас могут быть одинаковые четыре стороны, так что две из них направлены внутрь, создавая дротик. Дротик вогнутый, а воздушный змей выпуклый.
Каждый внутренний угол выпуклого многоугольника меньше 180°. Вогнутый многоугольник имеет минимум один угол больше 180°. Представьте шестиугольник в форме галстука-бабочки (6 сторон). Он будет состоять из двух внутренних углов больше 180°.
(Изображение скоро будет загружено)
Простые и сложные многоугольники
Простые многоугольники не содержат самопересекающихся сторон. Сложные многоугольники, также известные как самопересекающиеся многоугольники, содержат стороны, которые пересекаются друг с другом. Примером сложного многоугольника является классическая звезда.
Большинство людей могут очень быстро нарисовать звезду на листе бумаги, но некоторые называют ее пентаграммой, сложным многоугольником или многоугольником, делящимся пополам.
Семейство сложных многоугольников в форме звезды обычно имеет префикс греческого числа и использует суффикс -gram: пентаграмма, гексаграмма, гептаграмма, октаграмма и т. д.
Градусы в многоугольниках: как их найти
Многоугольник — это замкнутый двумерный объект, состоящий из трех или более связанных сегментов прямой. Многоугольники включают треугольники, трапеции и восьмиугольники, и это лишь некоторые из них. Многоугольники часто классифицируют на основе количества сторон, углов и относительных размеров сторон. Многоугольники также могут быть классифицированы как правильные и неправильные. Правильные многоугольники имеют равные длины сторон и равные углы. В правильных многоугольниках можно вычислить градусы углов, но это не обязательно в случае неправильных многоугольников.
Стороны многоугольника умножаются на количество сторон. Сумма всех градусов внутреннего угла равна (n — 2) 180. Вычтите 2 из числа сторон и умножьте на 180 в этом вычислении). Сумма градусов для восьмиугольника, например, составляет (8-2) 180. В сумме это составляет 1080.
Разделите полученную на шаге 1 сумму на количество сторон, если многоугольник правильный (все стороны и углы равны). Это степень каждого из углов многоугольника. В обычном восьмиугольнике, например, каждый угол имеет степень 135:1. Разделите 1080 на восемь, чтобы получить ответ.
Чтобы определить меру внешнего угла правильного многоугольника, умножьте угол из шага 2 на 180 минус градус. Это градус внешнего угла каждого многоугольника. Поскольку угол в этом примере равен 135 градусам, значение дополнительного угла равно 45 градусам.
Решенные примеры для формы многоугольника
Пример:
1.
Найдите внутренний угол правильного восьмиугольника?
Решение:
Правильный восьмиугольник состоит из 8 сторон, таким образом:
Внешний угол восьмиугольника =\[ \frac{360°}{8} = 45° \]
Внутренний угол восьмиугольника = 180° − 45° = 135°
Или мы могли бы также использовать формулу для определить внутренний угол восьмиугольника:
Внутренний угол = \[ \frac{(n−2) \times 180° }{n} \]
= \[ \frac{(8−2) \times 180° {8} \]
= \[ \frac{6 \times 180° }{8} \]
= 135°
Таким образом, внутренний угол восьмиугольника равен 135°
Пример:
2. Определить внутренний и внешний углы правильного шестиугольника?
Решение:
Правильный шестиугольник состоит из 6 сторон, таким образом:
Внешний угол шестиугольника = \[\frac{360°}{6} = 60°\]
Внутренний угол шестиугольника = 180° − 60° = 120°
Забавные факты
Внутренний и внешний углы многоугольника — это соответственно внутренние и внешние углы, образованные соединяющимися сторонами многоугольника.
Чтобы быть многоугольником, форма должна быть плоской, описанной в пространстве и создаваться с использованием только прямых сторон.
Многоугольники с равными углами и сторонами правильные; а все остальные нерегулярны.
Многоугольники, у которых все внутренние углы меньше 180°, являются выпуклыми
Многоугольники, у которых минимум один внутренний угол больше 180°, являются вогнутыми.
Простые многоугольники не пересекают стороны
Сложные многоугольники имеют стороны, делящиеся пополам.
Вы можете видеть многоугольники вокруг себя!
Заключение
Многоугольники можно изучать и классифицировать по-разному.
Вы видите, что многоугольники могут быть правильными или неправильными, вогнутыми или выпуклыми, простыми или сложными. Когда вы сталкиваетесь с незнакомым многоугольником, вы можете просто определить его свойства и правильно классифицировать.
полигонов
Многоугольник – это плоская фигура с прямыми сторонами.
Это многоугольник?
Многоугольники — это двумерные фигуры. Они состоят из прямых линий, а форма «замкнутая» (все линии соединяются вверх).
| Полигон (прямые стороны) | Не Многоугольник (имеет кривую) | Не a Полигон (открытый, не закрытый) |
Полигон происходит от греческого. Poly- означает «много», а -gon означает «угол».
Типы полигонов
Обычные или нестандартные
У правильного многоугольника все углы равны и все стороны равны, в противном случае он неправильный
| Обычный | Нестандартный |
Вогнутая или выпуклая
Выпуклый многоугольник не имеет углов, направленных внутрь.
Точнее, внутренний угол не может быть больше 180°.
Если какой-либо внутренний угол больше 180°, то многоугольник является вогнутым . ( Подумайте: в вогнутой части есть «пещера» )
| Выпуклая | Подбарабанье |
Простой или сложный
Простой многоугольник имеет только одну границу и не пересекает сам себя. Сложный полигон пересекает сам себя! Многие правила о многоугольниках не работают, когда они сложные.
| Простой многоугольник (это пятиугольник) | Комплексный полигон (он же Пентагон) |
Другие примеры
| Неправильный шестигранник | Вогнутый восьмиугольник | Сложный многоугольник («Звездный многоугольник», в данном случае — пентаграмма) |
Играй с ними!
Попробуйте интерактивные многоугольники.
.. сделайте их правильными, вогнутыми или сложными.
Имена полигонов
| Если это правильный многоугольник … | |||
| Имя | стороны | Форма | Внутренний уголок |
|---|---|---|---|
| Треугольник (или треугольник) | 3 | 60° | |
| Четырехугольник (или Тетрагон) | 4 | 90° | |
| Пентагон | 5 | 108° | |
| Шестигранник | 6 | 120° | |
| Семиугольник (или Септагон) | 7 | 128,571° | |
| Октагон | 8 | 135° | |
| Нонагон (или Эннеагон) | 9 | 140° | |
| Декагон | 10 | 144° | |
| Hendecagon (или Undecagon) | 11 | 147,273° | |
| Додекагон | 12 | 150° | |
| Трискайдекагон | 13 | 152,308° | |
| Тетракайдекагон | 14 | 154,286° | |
| Пятиугольник | 15 | 156° | |
| Шестигранник | 16 | 157,5° | |
| Семидесятиугольник | 17 | 158,824° | |
| Октакайдекагон | 18 | 160° | |
| Эннеадекагон | 19 | 161,053° | |
| Икосагон | 20 | 162° | |
| Триаконтагон | 30 | 168° | |
| Тетраконтагон | 40 | 171° | |
| Пятиугольник | 50 | 172,8° | |
| Шестиугольник | 60 | 174° | |
| Гептаконтагон | 70 | 174,857° | |
| Октаконтагон | 80 | 175,5° | |
| Эннеаконтагон | 90 | 176° | |
| Шестиугольник | 100 | 176,4° | |
| Чилиагон | 1000 | 179,64° | |
| Мириагон | 10 000 | 179,964° | |
| Мегагон | 1 000 000 | ~180° | |
| Гуголгон | 10 100 | ~180° | |
| н-угольник | нет | ( n −2) × 180 ° / n | |
Вы можете делать имена, используя этот метод:
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример: 62-сторонний многоугольник представляет собой Hexacontadigon | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
..
д.. НО, для многоугольников с 13 или более сторонами можно (и проще) написать « 13-угольник «, « 14-угольник » .