Как найти площадь равнобедренного треугольника? Ответ на webmath.ru
Содержание:
- Формула
- Примеры вычисления площади равнобедренного треугольника
Формула
Чтобы найти площадь равнобедренного треугольника (рис. 1), необходимо вычислить произведение половины основания этого треугольника на его высоту:
$$\mathrm{S}_{\Delta}=\frac{1}{2} a h_{a}$$
Напомним, что треугольник называется равнобедренным, если его две стороны равны. Равные стороны называются боковыми сторонами рассматриваемого треугольника, а третья сторона — основанием.
Примеры вычисления площади равнобедренного треугольника
Пример
Задание. Найти площадь равнобедренного треугольника $ABC$, если известно, что его основание равно 4 м, а высота, проведенная к этому основанию — 6 м.
Решение. Искомая площадь равна произведению высоты на основание, деленному на два:
$\mathrm{S}_{\Delta A B C}=\frac{4 \cdot 6}{2}=\frac{24}{2}=12$ (м2)
 {2}}=\sqrt{25-16}=\sqrt{9}=3$ (cм)
{2}}=\sqrt{25-16}=\sqrt{9}=3$ (cм)
А тогда искомая площадь
$\mathrm{S}_{\Delta A B C}=\frac{1}{2} A C \cdot B H=\frac{8 \cdot 3}{2}=4 \cdot 3=12$ (см2)
Ответ. $\mathrm{S}_{\Delta A B C}=12$ (см2)
Остались вопросы?
Здесь вы найдете ответы.
Площадь равнобедренного треугольника с прямым углом составляет 16 см кв. Каким образом можно вычислить длину гипотенузы данной треугольной фигуры?
Обозначим через х катет имеющегося равнобедренного треугольника, имеющего прямой угол. В этом случае его площадь будет представлять собой ½ длины его катета, возведенную в квадратную степень. Это значит, что квадрат катета равен двум площадям треугольника (2S). В нашем случае это:
2S = 2*16 = 32 см кв.
Для того чтобы найти длину катета, нужно извлечь корень квадратный из числа 32:
х = 4*√2 см.
Теперь можно высчитать длину гипотенузы, которая будет равна:
х / sin45 = 8 см.
Ответ: Длина гипотенузы равна 8 см.
Имеется равнобедренный треугольник площадью 192 см кв. Его основание составляет 32 см. Как можно вычислить периметр данной треугольной фигуры?
Дан треугольник АВС, в котором АВ=ВС и АС=32 см.
Проведем к основанию треугольника высоту ВН, также являющуюся медианой.
Площадь треугольника равна половине произведения длины его основания на высоту:
S=АС*ВН/2
Из этой формулы можно выразить ВН:
ВН=2S/АС=2*192/32=12 см.
Известно, что в равнобедренном треугольнике две стороны равны:
АВ=ВС=√(ВН²+(АС/2)²)=√(144+256)=20 см.
Теперь можно высчитать периметр (Р) треугольника АВС, который будет равен сумме длин его сторон:
Р=2АВ+АС=40+32=72 см.
Ответ: Периметр равнобедренного треугольника АВС равен 72 см.
Длина гипотенузы равнобедренного треугольника, имеющего прямой угол, составляет 12 см. Как найти площадь данного треугольника?
Обозначим буквой х катет имеющегося треугольника. Тогда по теореме
Пифагора:
Тогда по теореме
Пифагора:
12²=x² + x², что равно 144=2х²
Отсюда находим значение х:
x²=72, x=√72
Зная длину катета равнобедренного треугольника, можно найти его площадь (S):
S = √72 * √72/2 = 36 см кв.
Ответ: Площадь треугольника равна 36 см кв.
Дан равнобедренный треугольник, угол в основании которого составляет 25 градусов. Площадь данной фигуры равна 16 см кв. Есть еще один равнобедренный треугольник с углом 130 градусов и площадью 4з см кв. Чему будет равно отношение оснований этих двух треугольных фигур?
Разберемся с первым из треугольников. Так как он является равнобедренным, то оба угла при его основании будут равны. Зная о том, что сумма всех углов треугольника равна 180 градусом, мы можем найти третий угол треугольника, находящийся при его вершине:
180-25-25=130 градусов.
Переходим ко второму треугольнику. Известно, что угол при его вершине
равен 230 градусом. Исходя из этого можно рассчитать величины его углов,
расположенных в основании фигуры:
Исходя из этого можно рассчитать величины его углов,
расположенных в основании фигуры:
(180-130)/2=25 градусов.
Очевидно, что треугольники являются подобными на основании равенства углов.
Следует определить коэффициент подобия двух треугольных фигур. Квадрат коэффициента подобия будет равен отношению площадей треугольников:
49/16=kˆ2
Отсюда выражаем k:
k=7/4
Коэффициент подобия представляет собой отношение основания первой подобной треугольной фигуры ко второй. Это значит, что:
С/c=k = 7/4
Ответ: Отношение оснований двух треугольников равно 7/4.
Чему равна площадь равнобедренного треугольника с прямым углом при условии, что длина его гипотенузы составляет с?
Площадь (S) треугольника с прямым углом составляет ½ часть произведения
его катетов. Принимая во внимание тот факт, что треугольник является
равнобедренным, можно утверждать, что длины его катетов равны. Их можно
обозначить через х. В этом случае формулу для расчета площади треугольника
можно записать в следующем виде:
Их можно
обозначить через х. В этом случае формулу для расчета площади треугольника
можно записать в следующем виде:
S=½x*x=½x²
Согласно теореме Пифагора, действительной для прямоугольного треугольника:
с²=х²+х²=2x²
x²=½c²
Подставим в формулу площади получившееся равенство:
S=½*½с²=¼с² см.кв.
Ответ: Площадь равнобедренного треугольника равна ¼с² см кв.
Как можно рассчитать площадь равнобедренного треугольника, если длина его высоты и основания – величины известные?
Площадь (S) любой треугольной фигуры рассчитывается путем деления пополам произведения длины его основания (с) и высоты (h):
S = ½ c*h
Как найти площадь равнобедренного треугольника?
Площадь каждого треугольника, в том числе и равнобедренного, рассчитывается как половина, взятая от произведения длины высоты треугольника и его основания. Формула имеет следующий вид:
S=1/2 *a*h
Пусть а = 150 см.
Проводим высоту к основанию треугольника. Она же будет являться и медианой по той причине, что треугольник равнобедренный. В результате образовался треугольник с прямым углом и гипотенузой, длина которой равна 85 см. Один из катетов треугольника равен h, а второй рассчитывается как а/2:
150/2=75 см.
Теперь можно рассчитать длину второго катета (на основании теоремы Пифагора):
h=√85²-75²=√7225-5625=√1600=40 см.
Когда все необходимые для расчета площади треугольника величины известны, можно найти ее значение:
S=1/2 *a*h=1/2 *150*40=3000 см.
Как можно найти площадь треугольника при условии, что он является равнобедренным, и его периметр равен 100 см, а основание – 48 см?
Вычислим длину боковой стороны равнобедренного треугольника, отняв от его периметра длину основания и разделив полученное число на 2:
(100-48):2=26 см.
Тогда площадь равнобедренного треугольника с заданными параметрами будет равна:
S=b/4*√(4a²-b²)=12*√(2704-2304)=12*20=240 cм кв.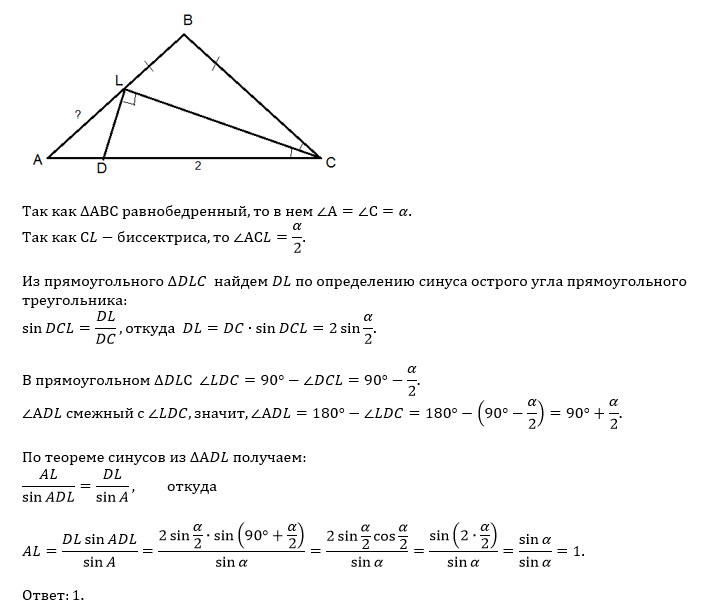
Чему равна площадь равнобедренного треугольника, длины сторон которого составляют 10 см и 12 см (сумма длин его катетов)?
К основанию равнобедренного треугольника проведем высоту, делящую его на две равные треугольные фигуры, каждая из которых имеет угол 90 градусов и катет длиной 12/2 = 6 см. Гипотенуза подобных треугольников имеет длину 10 см.
В случае с прямоугольным треугольником может быть применима теорема Пифагора, которая поможет найти катет, являющийся высотой треугольника:
h² = 10² — 6² = 64 см
Избавимся от квадратов:
h = 8 см.
Тогда площадь треугольника будет равна:
S = 12 * 8 : 2 = 48 см кв.
Как рассчитать площадь равнобедренного треугольника, если известно о том, что длина его гипотенузы составляет 44 см?
Введем условные обозначения, согласно которым х – это длина одного из
катетов равнобедренного треугольника. В этом случае длина второго катета
тоже будет равна х.
х²+ х² = 44²
2х² = 1936
Отсюда можем найти значение х:
x=√968
Найдя длину катета равнобедренного треугольника, можно вычислить его площадь (S), равную ½ произведения длин его катетов:
S = √968*√968/2 = 484 см кв.
Каким образом возможно высчитать площадь равнобедренного треугольника через стороны и длину его основания?
Располагая сведениями о длине основания (b) и стороны (a) треугольной фигуры с равными катетами, возможно рассчитать площадь (S) этой фигуры. С этой целью следует пользоваться приведенной ниже формулой:
S = b/4×√ 4× a²-b².
Возможно ли определить площадь равнобедренного треугольника через его боковые стороны и образованный ими угол?
Информация о длине боковых сторон (а) треугольной фигуры с катетами равной
длины и размере угла (α), который образован этими катетами, позволит
определить площадь этой фигуры.
S = 1/2a2 * sin(α).
Как можно высчитать площадь равнобедренного треугольника при условии, что известна длина его основания и угол?
Для расчета площади треугольной фигуры с катетами равной длины, при условии, что известна их длина (а), основание (b) и угол, который образован основанием и одним из катетов(α), используется следующая формула:
S = ½ * a * b * sin(α)
Длина основания равнобедренного треугольника превышает длину его боковой стороны на 3 см. Периметр данной треугольной фигуры равен 30 см. Как можно высчитать длину основания данного равнобедренного треугольника?
Примем неизвестную длину основания равнобедренного треугольника за х. В данном случае длина каждой из боковых сторон, которые в равнобедренном треугольнике равны, будет составлять (х-3). Известно, что периметр (Р) треугольника равен 30 см. Тогда:
Р = 3х-6 = 30 см.
Отсюда можно вывести х:
х = (30+6)/3 = 12 см.
Ответ: Длина основания равна 12 см.
Высота, проведенная в равнобедренном треугольнике, равна 15 см. Длина основания данной фигуры превышает длину его боковой стороны на 15 см. Как найти основание равнобедренного треугольника в этом случае?
Примем х за длину основания равнобедренного треугольника. Тогда длина его боковой стороны будет составлять (х-15). Высота, проведенная в треугольнике с прямым углом, также представляет собой его медиану, которая делит его на две равных треугольных фигуры. Следует рассмотреть одну из образовавшихся треугольных фигур. Для начала вычислим ее основания, используя теорему Пифагора:
с2 = а2 + b2 = (15)²+(0,5x)²=(x-15)²
Из этого получается:
225-x²-30x+225-0,25x²
0=0,75x²-30x
x(0,75x-30)=0
x¹=0 см.
x=40 см.
Очевидно, что сторона треугольной фигуры не может иметь длину, равную 0см.
Поэтому можно сделать вывод о том, что ее длина составляет 40 см.
По какой формуле можно высчитать площадь равнобедренного треугольника?
Для ответа на поставленный вопрос следует провести высоту из вершины того угла равнобедренного треугольника, который является противоположным его основанию. После этого длину проведенной высоты (а) нужно умножить на длину основания фигуры (b), а затем разделить полученное значение на два. Формула расчета площади треугольной фигуры, которая является равнобедренной, выглядит следующим образом:
S=a*b/2, или S=1/2a* b.
В равнобедренном треугольнике к его основанию проведена высота, длина которой равна 1,2 см. Длина самого основания фигуры составляет 3,2 см. Как рассчитать длину боковой стороны этого равнобедренного треугольника?
Вычислим половину длины основания данного равнобедренного треугольника:
3,2/2 = 1,6 см.
Имеется треугольник с прямым углом и катетами, длины которых равны 1,2 см
и 1,6 см. Требуется определить длину его гипотенузы. Ее можно вычислить,
используя теорему Пифагора:
Ее можно вычислить,
используя теорему Пифагора:
с²=а²+в²
с² = 1,2² + 1,6² = 1,44 + 2,56 = 4
Осталось только извлечь корень квадратный из 4:
с=√4=2 см.
Ответ: Длина боковой стороны равнобедренного треугольника равна 2 см.
Один из углов равнобедренного треугольника является тупым. Одна сторона данной фигуры составляет 14 см, а другая – 8 см. Чему равно основание треугольника с двумя равными сторонами?
Известно, что углы, расположенные у основания равнобедренного треугольника, всегда являются острыми, иначе сумма всех трех углов превышала бы 180 градусов. Исходя из этого, можно сделать вывод о том, что тупой угол расположен у вершины данной треугольной фигуры.
Доказанным фактом является то, что та сторона фигуры, которая расположена
напротив тупого угла, имеет большую длину, чем сторона, лежащая против
острого угла треугольника. Это позволяет утверждать, что длина основания
данного треугольника больше длины его боковой стороны. По причине того,
что треугольная фигура является равнобедренной, и известны длины двух ее
сторон (8 см и 14 см), можно говорить о том, что неизвестная сторона будет
составлять 8 см или 14 см. Если предположить, что длина неизвестной
стороны равна 14 см, тогда длина основания будет составлять 8 см, что
невозможно, так как противоречит утверждению о расположении больших сторон
напротив тупых углов. Это означает, что длина третьей стороны треугольника
равна 8 см, а основание в данном случае составляет 14 см.
По причине того,
что треугольная фигура является равнобедренной, и известны длины двух ее
сторон (8 см и 14 см), можно говорить о том, что неизвестная сторона будет
составлять 8 см или 14 см. Если предположить, что длина неизвестной
стороны равна 14 см, тогда длина основания будет составлять 8 см, что
невозможно, так как противоречит утверждению о расположении больших сторон
напротив тупых углов. Это означает, что длина третьей стороны треугольника
равна 8 см, а основание в данном случае составляет 14 см.
Равнобедренный треугольник имеет сторону длиной 29 см. Высота, проведенная в нем, составляет 21 см. Чему равно основание треугольника с указанными параметрами?
Для решения данной задачи следует воспользоваться теоремой Пифагора:
с²=а²+в²
Отсюда можно выразить квадрат длины неизвестной стороны, который будет равен разности квадратов известной стороны и высоты:
29²-21² = 400.
Для того чтобы узнать длину основания равнобедренного треугольника, нужно извлечь корень квадратный из числа 400, а затем умножить полученное число на 2:
√400*2 = 20*2 = 40 см.
Ответ: Длина основания равнобедренного треугольника равна 40 см.
Читать дальше: как найти площадь равностороннего треугольника.
Площадь равнобедренного треугольника со стороной а. Как находить площадь треугольника (формулы)
Словари. Энциклопедии. История. Литература. Русский язык » Энциклопедия » Площадь равнобедренного треугольника со стороной а. Как находить площадь треугольника (формулы)
В зависимости от вида треугольника выделяют сразу несколько вариантов нахождения его площади. К примеру, для вычисления площади прямоугольного треугольника используется формула S= a * b / 2, где а и b — это его катеты. Если же требуется узнать площадь равнобедренного треугольника, то необходимо делить на два произведение его основания и высоты. То есть, S= b*h / 2, где b – это основание треугольника, а h – его высота.
Далее, может понадобиться расчет площади равнобедренного прямоугольного треугольника. Здесь приходит на помощь следующая формула: S= a* а / 2, где катеты «а» и «а» – обязательно должны быть с одинаковыми значениями. 2) высчитываем длину неизвестного катета, затем используем ее для расчета площади треугольника.
2) высчитываем длину неизвестного катета, затем используем ее для расчета площади треугольника.
Как находить площадь равнобедренного треугольника
Площадь равнобедренного треугольника можно очень легко и быстро найти по формуле S= b*h / 2, но, при отсутствии одного из показателей, задача значительно усложняется. Ведь необходимо выполнять дополнительные действия.
Возможные варианты задач:
- Дано: длина одной из боковых сторон и длина основания. Находим через теорему Пифагора высоту, то есть длину второго катеты. При условии, что длина основания, разделенная на два, является катетом, а изначально известная боковая сторона – гипотенузой.

- Дано: основание и угол между боковой стороной и основанием. Вычисляем по формуле h=c*ctg(B)/2 высоту (не забываем сторону «c» разделить на два).
- Дано: высота и угол, который был образован основанием и боковой стороной: применяем формулу c=h*tg(B)*2 для нахождения высоты, и полученный результат умножаем на два. Далее вычисляем площадь.
- Известна: длина боковой стороны и угол, который образовался между ним и высотой. Решение: используем формулы — c=a*sin(C)*2 и h=a*cos(C) для нахождения основания и высоты, после чего считаем площадь.
Как найти площадь равнобедренного прямоугольного треугольника
Если все данные известны, то по стандартной формуле S= a* a / 2 вычисляем площадь равнобедренного прямоугольного треугольника, если же в задаче не указаны некоторые показатели, то выполняются дополнительные действия.
Например: нам не известны длины обеих сторон (мы помним, что в равнобедренном прямоугольном треугольнике они равны), но дана длинна гипотенузы. 2, где R — радиус окружности.
2, где R — радиус окружности.
Математика — это удивительная наука. Однако такая мысль приходит только тогда, когда ее понимаешь. Чтобы этого достичь, нужно решать задачи и примеры, чертить схемы и рисунки, доказывать теоремы.
Путь к пониманию геометрии лежит через решение задач. Отличным примером могут служить задания, в которых нужно найти площадь равнобедренного треугольника.
Что такое равнобедренный треугольник, и в чем его отличие от других?
Чтобы не пугаться терминов «высота», «площадь», «основания», «равнобедренного треугольника» и прочих, потребуется начать с теоретических основ.
Сначала о треугольнике. Это плоская фигура, которая образована из трех точек — вершин, в свою очередь, соединенных отрезками. Если два из них оказываются равны друг другу, то треугольник становится равнобедренным. Эти стороны получили название боковых, а оставшаяся стала основанием.
Существует частный случай равнобедренного треугольника — равносторонний, когда и третья сторона равна двум боковым.
Свойства фигуры
Они оказываются верными помощниками в решении задач, которые требуют найти площадь равнобедренного треугольника. Поэтому знать и помнить о них необходимо.
- Первое из них: углы равнобедренного треугольника, одна сторона которых — основание, всегда равны друг другу.
- Важным является и свойство о дополнительных построениях. Проведенные к непарной стороне высота, медиана и биссектриса совпадают.
- Эти же отрезки, проведенные из углов при основании треугольника, попарно равны. Это тоже часто облегчает поиск решения.
- Два равных угла в нем всегда имеют значение меньше чем 90º.
- И последнее: вписанная и описанная окружности строятся так, что их центры лежат на высоте к основанию треугольника, а значит медиане и биссектрисе.
Как в задаче распознать равнобедренный треугольник?
Если при решении задания встает вопрос о том, как найти площадь равнобедренного треугольника, то сначала нужно понять, что он относится к этой группе. А в этом помогут определенные признаки.
А в этом помогут определенные признаки.
- Равны два угла или две стороны треугольника.
- Биссектриса является еще и медианой.
- Высота треугольника оказывается медианой или биссектрисой.
- Равны две высоты, медианы или биссектрисы фигуры.
Обозначения величин, принятые в рассматриваемых формулах
Для упрощения того, как находить площадь равнобедренного треугольника по формулам, введена замена его элементов на буквы.
Внимание! Важно не путать «а» с «А» и «в» с «В». Это разные величины.
Формулы, которыми можно воспользоваться в разных задачах
Известны длины сторон, и требуется найти площадь равнобедренного треугольника.
В этом случае нужно возвести в квадрат оба значения. То число, которое получилось от изменения боковой стороны, умножить на 4 и вычесть из него второе. Из полученной разности извлечь квадратный корень. Длину основания разделить на 4. Два числа перемножить. Если записать эти действия буквами, то получится такая формула:
Пусть она будет записана под №1.
Найти по значениям сторон площадь равнобедренного треугольника. Формула, которая кому-то может показаться проще, чем первая.
Первым действием нужно найти половину основания. Потом найти сумму и разность этого числа с боковой стороной. Два последних значения перемножить и извлечь квадратный корень. Последним действием умножить все на половину основания. Буквенное равенство будет выглядеть так:
Это формула №2.
Способ найти площадь равнобедренного треугольника, если известны основание и высота к нему.
Одна из самых коротких формул. В ней нужно перемножить обе данные величины и разделить их на 2. Вот как она будет записана:
Номер этой формулы — 3.
В задании известны стороны треугольника и значение угла, лежащего между основанием и боковой стороной.
Здесь, для того чтобы узнать, чему будет равна площадь равнобедренного треугольника, формула будет состоять из нескольких множителей. Первый из них — это значение синуса угла. Второй равен произведению боковой стороны на основание. Третий — дробь ½. Общая математическая запись:
Второй равен произведению боковой стороны на основание. Третий — дробь ½. Общая математическая запись:
Порядковый номер формулы — 4.
В задаче даны: боковая сторона равнобедренного треугольника и угол, лежащий между его боковыми сторонами.
Как и в предыдущем случае, площадь находится по трем множителям. Первый равен значению синуса угла, указанного в условии. Второй — это квадрат стороны. И последний также равен половине единицы. В итоге формула запишется так:
Ее номер — 5.
Формула, которая позволяет найти площадь равнобедренного треугольника, если известны его основание и угол, лежащий напротив него.
Сначала нужно вычислить тангенс половины известного угла. Полученное число умножить на 4. Возвести в квадрат длину боковой стороны, которое потом разделить на предыдущее значение. Таким образом, получится такая формула:
Номер последней формулы — 6.
Примеры задач
Первая задача: известно, что основание равнобедренного треугольника равно 10 см, а его высота — 5 см. Нужно определить его площадь.
Нужно определить его площадь.
Для ее решения логично выбрать формулу под номером 3. В ней все известно. Подставить числа и сосчитать. Получится, что площадь равна 10 * 5 / 2. То есть 25 см 2 .
Вторая задача: в равнобедренном треугольнике даны боковая сторона и основание, которые равны соответственно 5 и 8 см. Найти его площадь.Первый способ. По формуле №1. При возведении в квадрат основания получается число 64, а учетверенный квадрат боковой стороны — 100. После вычитания из второго первого получится 36. Из него прекрасно извлекается корень, который равен 6. Основание, поделенное на 4, равно 2. Итоговое значение определится как произведение 2 и 6, то есть 12. Это ответ: искомая площадь равна 12 см 2 .
Второй способ. По формуле №2. Половина основания равна 4. Сумма боковой стороны и найденного числа дает 9, их же разность — 1. После умножения получается 9. Извлечение квадратного корня дает 3. И последнее действие, умножение 3 на 4, что дает те же 12 см 2 .
Решая задачи по геометрии и определяя, как найти площадь равнобедренного треугольника, можно получить неоценимый опыт. Чем больше различных вариантов заданий выполнено, тем проще найти ответ в новой ситуации. Поэтому регулярное и самостоятельное выполнение всех заданий — это путь к успешному усвоению материала.
Чем больше различных вариантов заданий выполнено, тем проще найти ответ в новой ситуации. Поэтому регулярное и самостоятельное выполнение всех заданий — это путь к успешному усвоению материала.
Встаёт не только перед школьниками или студентами, но и в реальной, практической жизни. Например, во время строительства возникает необходимость отделки фасадной части, находящейся под крышей. Как вычислить количество нужного материала?
Часто с подобными задачами сталкиваются мастера, которые работают с тканью или кожей. Ведь многие детали, которые предстоит выкроить мастеру, имеют как раз форму равнобедренного треугольника.
Итак, существует несколько способов, помогающих найти площадь равнобедренного треугольника. Первый — вычисление её по основанию и высоте.
Для решения нам необходимо построить для наглядности треугольник MNP с основанием MN и высотой PO. Теперь кое-что достроим в чертеже: из точки P провести линию, параллельную основанию, а из точки M — линию, параллельную высоте. Точку пересечения назовём Q. Чтобы узнать, как найти площадь равнобедренного треугольника, нужно рассмотреть полученный четырёхугольник MOPQ, в котором боковая сторона данного нам треугольника MP является уже его диагональю.
Точку пересечения назовём Q. Чтобы узнать, как найти площадь равнобедренного треугольника, нужно рассмотреть полученный четырёхугольник MOPQ, в котором боковая сторона данного нам треугольника MP является уже его диагональю.
Докажем сначала, что это прямоугольник. Так как мы строили его сами, то знаем, что стороны MO и OQ параллельны. И стороны QM и OP тоже параллельны. Угол POM прямой, значит и угол OPQ тоже прямой. Следовательно, получившийся чётырёхугольник является прямоугольником. Найти его площадь не составит труда, она равна произведению PO на OM. OM — это половина основания данного треугольника MPN. Отсюда вытекает, что площадь построенного нами прямоугольника равна полупроизведению высоты прямоугольного треугольника на его основание.
Вторым этапом поставленной перед нами задачи, как определить площадь треугольника, является доказательство того факта, что полученный нами прямоугольник по площади соответствует данному равнобедренному треугольнику, то есть, что площадь треугольника также равна полупроизведению основания и высоты.
Сравним для начала треугольник PON и PMQ. Они оба прямоугольны, так как прямой угол в одном из них образован высотой, а прямой угол в другом является углом прямоугольника. Гипотенузы в них являются сторонами равнобедренного треугольника, следовательно, также равны. Катеты PO и QM также равны как параллельные стороны прямоугольника. Значит, и площадь треугольника PON , и треугольника PMQ равны между собой.
Площадь прямоугольника QPOM равна площадям треугольников PQM и MOP в сумме. Заменив надстроенный треугольник QPM треугольником PON, получаем в сумме данный нам для вывода теоремы треугольник. Теперь мы знаем, как найти площадь равнобедренного треугольника по основанию и высоте — вычислить их полупроизведение.
Но можно узнать, как найти площадь равнобедренного треугольника по основанию и боковой стороне. Здесь также существует два варианта: теорема Герона и Пифагора. Рассмотрим решение с применением теоремы Пифагора. Для примера возьмём тот же PMN с высотой PO.
В прямоугольном треугольнике POM MP — гипотенуза. Её квадрат равен сумме квадратов PO и OM. А так как OM — половина основания, которое нам известно, то мы легко может найти OM и возвести число в квадрат. Произведя вычитание из квадрата гипотенузы полученное число, узнаем, чему равен квадрат другого катета, который в равнобедренном треугольнике является высотой. Найдя из разности и узнав высоту прямоугольного треугольника, можно дать ответ на поставленное перед нами задание.
Её квадрат равен сумме квадратов PO и OM. А так как OM — половина основания, которое нам известно, то мы легко может найти OM и возвести число в квадрат. Произведя вычитание из квадрата гипотенузы полученное число, узнаем, чему равен квадрат другого катета, который в равнобедренном треугольнике является высотой. Найдя из разности и узнав высоту прямоугольного треугольника, можно дать ответ на поставленное перед нами задание.
Нужно просто перемножить высоту на основание и полученный результат разделить напополам. Почему именно так следует поступать, мы объяснили в первом варианте доказательства.
Бывает, что нужно произвести вычисления по боковой стороне и углу. Тогда находим высоту и основание, используя формулу с синусами и косинусами, и, опять же, перемножаем их и делим результат пополам.
Буквенные обозначения сторон и углов на приведенном рисунке соответствуют обозначениям, которые указаны в формулах. Таким образом, это поможет Вам сопоставить их с элементами равнобедренного треугольника. Из условия задачи определите, какие элементы известны, найдите на чертеже их обозначения и подберите подходящую формулу.
Из условия задачи определите, какие элементы известны, найдите на чертеже их обозначения и подберите подходящую формулу.
Формула площади равнобедренного треугольника
Далее приведены формулы нахождения площади равнобедренного треугольника : через стороны, боковую сторону и угол между ними, через боковую сторону, основание и угол при вершине, через сторону основания и угол при основании и т.д. Просто найдите наиболее подходящую на рисунке слева. Для самых любопытных в тексте справа поясняется, почему формула явяляется правильной и как именно с ее помощью находится площадь.
- можно найти, зная его сторону и основание . Данное выражение было получено путем упрощения более общей, универсальной формулы. Если за основу взять формулу Герона, а затем принять во внимание, что две стороны треугольника равны меду собой, то выражение упрощается до формулы, представленной на картинке.
Пример использования такой формулы приведен на примере решения задачи ниже.
- Вторая формула позволяет найти его площадь через боковые стороны и угол между ними — это половина квадрата боковой стороны, умноженная на синус угла между боковыми сторонами
Если мысленно опустить высоту на боковую сторону равнобедренного треугольника, заметим, что ее длина будет равна a * sin β. Поскольку длина боковой стороны нам известна, высота, опущенная на нее теперь известна, половина их произведения и будет равна площади данного равнобедренного треугольника (Пояснение: полное произведение дает площадь прямоугольника, что очевидно. Высота делит этот прямоугольник на два малых прямоугольника, при этом стороны треугольника являются их диагоналями, которые делят их ровно пополам. Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту). См. также Формулу 5 - Третья формула показывает нахождение площади через боковую сторону, основание и угол при вершине .
Строго говоря, зная один из углов равнобедренного треугольника, можно найти и остальные, поэтому применение данной или предыдущей формулы — вопрос вкуса (кстати, поэтому можно запомнить только одну из них).
У третьей формулы также есть еще одна интересная особенность — произведение a sin α даст нам длину высоты, опущенной на основание. В результате мы получим простую и очевидную формулу 5. - Площадь равнобедренного треугольника можно также найти через сторону основания и угол при основании (углы при основании равны) как квадрат основания, деленный на четыре тангенса половины угла, образованного его боковыми сторонами. Если присмотреться внимательнее, то станет очевидно, что половина основания (b/2) умноженная на tg(β/2) даст нам высоту треугольника. Поскольку высота в равнобедренном треугольнике является, одновременно, биссектрисой и медианой, то tg(β/2) — это отношение половины основания (b/2) к высоте — tg(β/2) = (b/2)/h. Откуда h = b / (2 tg(β/2)). В итоге формула снова будет сведена к более простой Формуле 5, которая вполне очевидна.
- Разумеется, площадь равнобедренного треугольника можно найти, опустив высоту из вершины на основание, в результате чего получится два прямоугольных треугольника.
 Далее — все очевидно. Половина произведения высоты на основание и есть искомая площадь. Пример использования данной формуле см. в задаче ниже (2-й способ решения)
Далее — все очевидно. Половина произведения высоты на основание и есть искомая площадь. Пример использования данной формуле см. в задаче ниже (2-й способ решения) - Эта формула получается, если попытаться найти площадь равнобедренного треугольника с помощью теоремы Пифагора . Для этого выразим высоту из предыдущей формулы, которая одновременно, является катетом прямоугольного треугольника, образованного боковой стороной, половиной его основания и высотой, через теорему Пифагора. Боковая сторона является гипотенузой, поэтому из квадрата боковой стороны (а) вычтем квадрат второго катета. Поскольку он равен половине основания (b/2) то его квадрат будет равен b 2 /4. Извлечение корня из данного выражения и даст нам высоту. Что и видно в Формуле 6. Если числитель и знаменатель умножить на два, а потом двойку числителя внести под знак корня, получим второй вариант той же самой формулы, который написан через знак «равно».
Кстати, самые сообразительные могут увидеть, что если в Формуле 1 раскрыть скобки, то она превратиться в Формулу 6. Или наоборот, разность квадратов двух чисел, разложенная на множители, даст нам исходную, первую.
Или наоборот, разность квадратов двух чисел, разложенная на множители, даст нам исходную, первую.
Обозначения , которые были применены в формулах на рисунке:
a — длина одной из двух равных сторон треугольника
b — длина основания
α — величина одного из двух равных углов при основании
β — величина угла между равными сторонами треугольника и противолежащего его основанию
h — длина высоты, опущенная из вершины равнобедренного треугольника на основание
Важно . Обратите внимание на обозначения переменных! Не перепутайте α и β, а также a и b !
Примечание . Это часть урока с задачами по геометрии (раздел площадь равнобедренного треугольника). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение .
Задача
Боковая сторона равнобедренного треугольника равна 13 см, а основание равно 10 см. Найдите площадь равнобедренного треугольника.1-й способ . Применим формулу Герона. Поскольку треугольник равнобедренный, то она примет более простой вид (см. формулу 1 в списке формул выше):
где а — длина боковых сторон, а b — длина основания.
Подставив значения длин сторон треугольника из условия задачи, получим:
S = 1/2 * 10 * √ ((13 + 5)(13 — 5)) = 5 √ (18 * 8) = 60 см 2
2-й способ
. Применим теорему Пифагора
Предположим, что мы не помним формулу, использованную в первом способе решения. Поэтому опустим из вершины B на основание AC высоту BK.
Поскольку высота равнобедренного треугольника делит его основание пополам, то длина половины основания будет равна
AK = AC / 2 = 10 / 2 = 5 см.
Высота с половиной основания и стороной равнобедренного треугольника образует прямоугольный треугольник ABK. В этом треугольнике нам известна гипотенуза AB и катет AK. Выразим длину второго катета через теорему Пифагора.
В этом треугольнике нам известна гипотенуза AB и катет AK. Выразим длину второго катета через теорему Пифагора.
Равнобедренный прямоугольный треугольник: определение, площадь, периметр, примеры
Что такое равнобедренный прямоугольный треугольник?
Равнобедренный прямоугольный треугольник — это прямоугольный треугольник, у которого длина основания и высоты (катетов) равна . Это тип особого равнобедренного треугольника, в котором один внутренний угол является прямым, а остальные два угла, таким образом, конгруэнтны, поскольку углы, противоположные равным сторонам, равны.
Также известен под названием прямоугольный равнобедренный треугольник или прямоугольный равнобедренный треугольник.
Если объединить эти два свойства вместе, получится равнобедренный прямоугольный треугольник.
Равнобедренный прямоугольный треугольник: Определение
Равнобедренный прямоугольный треугольник — это тип прямоугольного треугольника, стороны которого (основание и высота) равны по длине.
Поскольку две стороны прямоугольного треугольника равны по размеру, соответствующие углы также равны. Следовательно, в равнобедренном прямоугольном треугольнике две стороны и два острых угла равны. 9{\circ}$.
Родственные игры
Гипотенуза равнобедренного прямоугольного треугольника
Гипотенуза прямоугольного треугольника — это самая длинная сторона треугольника, противоположная прямому углу.
Он ровно в $√2$ умножен на длину конгруэнтных сторон треугольника. Если длина каждой из равных сторон равна x единицам, то длина гипотенузы равнобедренного прямоугольного треугольника будет равна $\sqrt{2x}$ единицам.
Это свойство выводится с помощью теоремы Пифагора. Вот прямоугольный треугольник, $\Delta PQR$: 9{2}}$
$Hypotenuse= \sqrt{2}x$
Мы можем использовать полученный выше результат без применения каждый раз теоремы Пифагора. Длина гипотенузы равнобедренного прямоугольного треугольника всегда будет равна $√2$, умноженной на длину равных сторон треугольника.
Формулы равнобедренного прямоугольного треугольника
Мы только что обсудили формулу для нахождения гипотенузы равнобедренного прямоугольного треугольника. Оно определяется как
Гипотенуза $= \sqrt{2} \times$ Длина конгруэнтных сторон 9{2}}{2}$, где «x» равно длине конгруэнтной стороны.
Периметр равнобедренного прямоугольного треугольника
Периметр треугольника $=$ Сумма длин всех его сторон
Периметр равнобедренного прямоугольного треугольника $\Delta PQR = PQ + QR + PR$
$PQ = QR = x $ единиц
$PR = h$ единиц
Периметр формулы равнобедренного прямоугольного треугольника $= x + x + h = (2x + h)$ единиц.
Следовательно, периметр формулы равнобедренного прямоугольного треугольника равен $2x + h$, где «x» представляет собой длину конгруэнтных сторон, а «h» равен длине гипотенузы. 9{\circ}$.

Интересные факты!
- Так как две стороны равнобедренного прямоугольного треугольника равны, то и углы равны. И оба угла равны 45 градусов.
- Прямой угол всегда является самым большим углом в прямоугольном треугольнике.
- В прямоугольном треугольнике не может быть тупых углов.
Заключение
В этой статье мы исследовали свойства равнобедренного прямоугольного треугольника. Давайте решим несколько практических задач для лучшего понимания.
Решенные примеры на равнобедренном прямоугольном треугольнике
1. Каждая сторона равнобедренного прямоугольного треугольника равна 5 единицам. Вычислите длину его гипотенузы.
Решение:
Мы знаем, что формула для вычисления гипотенузы равнобедренного прямоугольного треугольника:
Гипотенуза $= \sqrt{2\; x}$
где «x» — длина конгруэнтной стороны.
Длина равных сторон равна 5 единицам.
Следовательно, гипотенуза будет равна $\sqrt{2 \times 5} = 7,071$ единиц.
2. Длина основания равнобедренного прямоугольного треугольника равна 10 единицам. Чему будет равна площадь этого треугольника?
Решение:
Мы знаем, что формула для вычисления площади равнобедренного прямоугольного треугольника: 9{2} = 72 \times 2 = 144$
$x = \sqrt{144}$
$x = 12$ единиц.
Следовательно, мера основания равнобедренного прямоугольного треугольника площадью 72 квадратных единицы равна 12 единицам.
4. Высота прямоугольного равнобедренного треугольника равна 8 единицам. Каков будет его периметр?
Решение:
Периметр равнобедренного прямоугольного треугольника $= (2x + h)$ единиц.
x равна длине конгруэнтной стороны
ч — мера гипотенузы.
Высота этого равнобедренного прямоугольного треугольника равна 8 единицам.
Здесь,
$Гипотенуза = \sqrt{2x}$
$h = \sqrt{2 \times 8} = 11,3137$ единиц
$Периметр = 2x + h = (2 \times 8) + 11,3137 = 27,3137 $ единиц.
5. Периметр равнобедренного прямоугольного треугольника равен $10 + 5\sqrt{2}$ единиц. Если неконгруэнтная сторона равна $5\sqrt{2}$ единиц, то найдите меру конгруэнтных сторон.
Решение:
Мы знаем, что формула для вычисления периметра равнобедренного прямоугольного треугольника: $(2x + h)$ единиц.
Где x равно длине конгруэнтной стороны, а h — мера гипотенузы.
$Периметр = 10 + 5\sqrt{2}$ единиц
Гипотенуза $= 5\sqrt{2}$ единиц
Поместим это в приведенную выше формулу:
$10 + 5\sqrt{2} = 2x + 5\sqrt{2}$
$10 = 2x$
$x = 5$ единиц.
Следовательно, конгруэнтная сторона равна 5 единицам.
Практические задачи на равнобедренный прямоугольный треугольник
1Каждая сторона равнобедренного прямоугольного треугольника равна 7 единицам.
 {2}}{2} = \frac{1}{2}$ кв. ед. 5
{2}}{2} = \frac{1}{2}$ кв. ед. 5Гипотеноза правого треугольника Isosceles, равные стороны которых даны x единиц
$ \ sqrt {3x} $ UNITS
$ \ SQRT {2x} $ UNITS
$ 2x $ UNITS
$. x$ единиц
Правильный ответ: $\sqrt{2x}$ единиц
Гипотенуза равнобедренного прямоугольного треугольника равна $\sqrt{2x}$, где x представляет длину конгруэнтных сторон.
Часто задаваемые вопросы о равнобедренном прямоугольном треугольнике
Все ли треугольники равнобедренные прямоугольные 9{\circ}$. Это связано с тем, что один угол должен быть прямым (90 градусов), и, следовательно, два других угла должны быть равны, так как противоположные стороны равны.
Какие бывают треугольники по длине сторон?
- Равнобедренный треугольник: две стороны равны.

- Равносторонний треугольник: все стороны равны.
- Разносторонний треугольник: все стороны разной длины.
Что такое остроугольный треугольник?
Треугольник, все углы которого меньше 90 градусов, называется остроугольным.
Что такое тупоугольный треугольник?
Треугольник, один из углов которого выходит за пределы 90 градусов, называется тупоугольным.
Какие три типа равнобедренных треугольников существуют?
Равнобедренные треугольники можно разделить на три типа: 1) остроугольный равнобедренный треугольник, 2) тупоугольный равнобедренный треугольник и 3) прямоугольный равнобедренный треугольник.
Равнобедренный прямоугольный треугольник — формула, свойства, площадь, примеры
Равнобедренный треугольник определяется как треугольник, две стороны которого имеют одинаковую меру. Равнобедренный треугольник с прямым углом известен как равнобедренный прямоугольный треугольник . Мы будем изучать свойства и формулы равнобедренного прямоугольного треугольника вместе с примерами в этой статье.
Мы будем изучать свойства и формулы равнобедренного прямоугольного треугольника вместе с примерами в этой статье.
| 1. | Что такое равнобедренный прямоугольный треугольник? |
| 2. | Свойства равнобедренного прямоугольного треугольника |
| 3. | Формула равнобедренного прямоугольного треугольника |
| 4. | Часто задаваемые вопросы о равнобедренном прямоугольном треугольнике |
Что такое равнобедренный прямоугольный треугольник?
Равнобедренный прямоугольный треугольник определяется как прямоугольный треугольник с равными основанием и высотой, которые также известны как катеты треугольника. Это особый равнобедренный треугольник, в котором один угол прямой, а два других равны, так как углы лежат против равных сторон. Он также известен как прямоугольный равнобедренный треугольник или прямоугольный равнобедренный треугольник. Площадь равнобедренного прямоугольного треугольника определяется общей формулой площади треугольника, где основание и высота являются двумя равными сторонами треугольника. Давайте посмотрим на изображение равнобедренного прямоугольного треугольника, показанное ниже. Если конгруэнтные стороны измеряют x единиц каждая, то гипотенуза или неравная сторона треугольника будет измеряться x√2 единицами.
Площадь равнобедренного прямоугольного треугольника определяется общей формулой площади треугольника, где основание и высота являются двумя равными сторонами треугольника. Давайте посмотрим на изображение равнобедренного прямоугольного треугольника, показанное ниже. Если конгруэнтные стороны измеряют x единиц каждая, то гипотенуза или неравная сторона треугольника будет измеряться x√2 единицами.
Гипотенуза прямоугольного равнобедренного треугольника
Гипотенуза прямоугольного равнобедренного треугольника — это сторона, противоположная углу в 90 градусов. Это в √2 раза больше длины равной стороны треугольника. Итак, если измерение каждой из равных сторон равно х единиц, то длина гипотенузы равнобедренного прямоугольного треугольника равна х√2 единиц. Он выводится с использованием теоремы Пифагора, которую вы узнаете в следующем разделе.
Свойства равнобедренного прямоугольного треугольника
Равнобедренный прямоугольный треугольник обладает почти такими же свойствами, что и равнобедренный треугольник. Давайте посмотрим на список свойств, за которыми следует равнобедренный прямоугольный треугольник.
Давайте посмотрим на список свойств, за которыми следует равнобедренный прямоугольный треугольник.
- Один угол равен 90º.
- Стороны этого треугольника перпендикулярны друг другу, которые также известны как основание и высота.
- Два других угла равнобедренного прямоугольного треугольника острые и равны по 45° каждый.
- Сумма всех внутренних углов равна 180°.
- Высота, проведенная из прямого угла, является серединным перпендикуляром к гипотенузе (противоположная сторона).
- Площадь равнобедренного прямоугольного треугольника выражается как (1/2) × основание × высота в квадратных единицах.
Формула равнобедренного прямоугольного треугольника
Равнобедренный прямоугольный треугольник следует теореме Пифагора, чтобы дать отношение между гипотенузой и равными сторонами. Давайте посмотрим на диаграмму ниже, чтобы понять формулу равнобедренного прямоугольного треугольника.
В ∆PQR,
PQ = QR = x единиц [Равносторонние]
PR = l единиц [гипотенуза]
Используя теорему Пифагора, 90 247
Гипотенуза 2 = Сторона 2 + Сторона 2
PR 2 = PQ 2 + QR 2
л 2 = х 2 + х 2
л 2 = 2x 2
Таким образом, l = x√2 единиц
Периметр равнобедренного прямоугольного треугольника Формула
Периметр равнобедренного прямоугольного треугольника определяется как сумма всех трех сторон.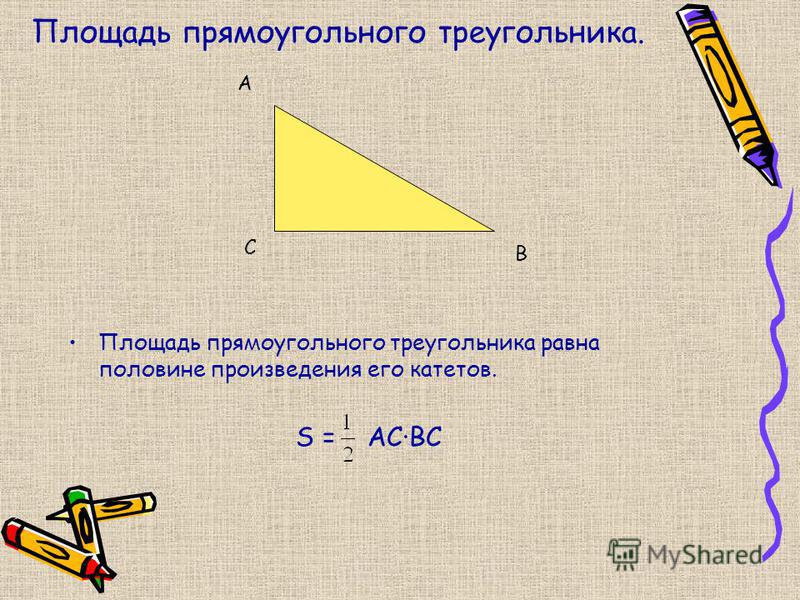 В показанном выше ∆PQR с длинами сторон PQ = QR = x единиц и PR = l единиц формула периметра равнобедренного прямоугольного треугольника определяется как PQ + QR + PR = x + x + l = (2x + l) единиц.
В показанном выше ∆PQR с длинами сторон PQ = QR = x единиц и PR = l единиц формула периметра равнобедренного прямоугольного треугольника определяется как PQ + QR + PR = x + x + l = (2x + l) единиц.
Таким образом, периметр формулы равнобедренного прямоугольного треугольника равен 2x + l, где x представляет собой конгруэнтную длину стороны, а l представляет собой длину гипотенузы.
Площадь равнобедренного прямоугольного треугольника
Площадь равнобедренного прямоугольного треугольника вычисляется по общей формуле площади треугольника: (1/2) × основание × высота. В показанном выше ∆PQR с длинами сторон PQ = QR = x, где PQ представляет высоту, а QR представляет собой основание, формула площади равнобедренного прямоугольного треугольника определяется как 1/2 × PQ × QR = x 2 /2 квадратных шт.
Таким образом, формула площади равнобедренного прямоугольного треугольника равна x 2 /2, где x представляет собой конгруэнтную длину стороны.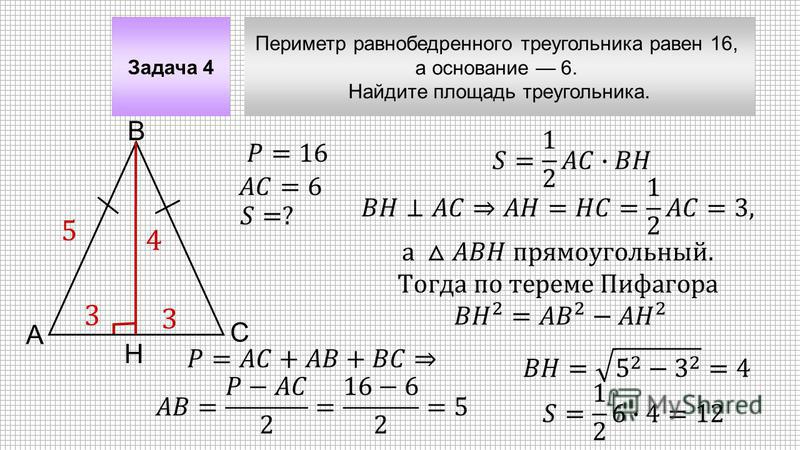
Статьи по теме
Проверьте эти статьи, связанные с понятием равнобедренного прямоугольного треугольника в геометрии.
- Острый лестничный треугольник
- Правый разносторонний треугольник
- Равнобедренный тупоугольный треугольник
Примеры равнобедренного прямоугольного треугольника
Пример 1: Каждая сторона равнобедренного прямоугольного треугольника равна 8 единицам. Найдите площадь.
Решение: Для равнобедренного прямоугольного треугольника формула площади равна x 2 /2, где x длина конгруэнтных сторон.
Здесь x = 8 единиц
Таким образом, Площадь = 8 2 /2 = 32 квадратных единицы
Следовательно, требуемая площадь равна 32 квадратных единиц.
Пример 2: Периметр равнобедренного прямоугольного треугольника равен 10 + 5√2. Если неконгруэнтная сторона равна 5√2 единицам, то найдите меру конгруэнтных сторон.

Решение: Для прямоугольного равнобедренного треугольника формула периметра равна 2x + l, где x — длина конгруэнтной стороны, а l — длина гипотенузы.
Здесь l = 5√2 единиц, периметр = 10 + 5√2 единиц
Используя формулу,
2x + l = 10 + 5√2
2x = 10 [Так как l = 5√2]
Таким образом, x = 5 единиц
Следовательно, длина каждой конгруэнтной стороны равна 5 единицам.
Пример 3: Если площадь равнобедренного прямоугольного треугольника составляет 200 квадратных дюймов, найдите длины равных сторон.
Решение: Формула площади прямоугольного равнобедренного треугольника: x 2 /2 квадратных единиц, где x — длина каждой равной стороны. Подставляя заданное значение площади, получаем
200 = x 2 /2
400 = x 2
x = 20
Следовательно, длина каждой конгруэнтной стороны равна 20 дюймам.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по равнобедренному прямоугольному треугольнику
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о равнобедренном прямоугольном треугольнике
Что такое равнобедренный прямоугольный треугольник?
Равнобедренный прямоугольный треугольник определяется как треугольник с двумя равными сторонами, известными как катеты, прямым углом и двумя острыми углами, которые конгруэнтны друг другу.
Могут ли равнобедренные треугольники быть правильными?
Да, любой равнобедренный треугольник, один угол которого равен 90°, а два других угла конгруэнтны друг другу (по 45° каждый), может быть равнобедренным прямоугольным треугольником.
Как найти гипотенузу равнобедренного прямоугольного треугольника?
Гипотенуза равнобедренного прямоугольного треугольника — это наибольшая сторона треугольника, лежащая против прямого угла. Если мера каждой из равных сторон равна «a» единиц, то длина гипотенузы равна a√2 единиц.
Если мера каждой из равных сторон равна «a» единиц, то длина гипотенузы равна a√2 единиц.
Как найти площадь равнобедренного прямоугольного треугольника?
Площадь равнобедренного прямоугольного треугольника находится по формуле сторона 2 /2, где сторона представляет собой конгруэнтную длину стороны. Например, площадь равнобедренного прямоугольного треугольника со стороной, равной 4 единицам, равна 4 2 /2 = 8 квадратных единиц.
Какие углы равнобедренного прямоугольного треугольника?
Углы равнобедренного прямоугольного треугольника равны 90°, 45° и 45°.
Какой наименьший угол в равнобедренном прямоугольном треугольнике?
Три угла равнобедренного прямоугольного треугольника равны 90°, 45° и 45°. Итак, наименьший угол равен 45°.
Как найти периметр равнобедренного прямоугольного треугольника?
Периметр равнобедренного прямоугольного треугольника находится путем сложения всех трех сторон треугольника.



 Далее — все очевидно. Половина произведения высоты на основание и есть искомая площадь. Пример использования данной формуле см. в задаче ниже (2-й способ решения)
Далее — все очевидно. Половина произведения высоты на основание и есть искомая площадь. Пример использования данной формуле см. в задаче ниже (2-й способ решения) Или наоборот, разность квадратов двух чисел, разложенная на множители, даст нам исходную, первую.
Или наоборот, разность квадратов двух чисел, разложенная на множители, даст нам исходную, первую.
