Площадь разностороннего четырехугольника: Площадь неправильного четырехугольника | Калькулятор + Формулы

Содержание

Сумма углов четырехугольника — свойства и следствия

Перейти к содержанию

Search for:

Главная » геометрия

Обновлено 01.02.2022

Свойства

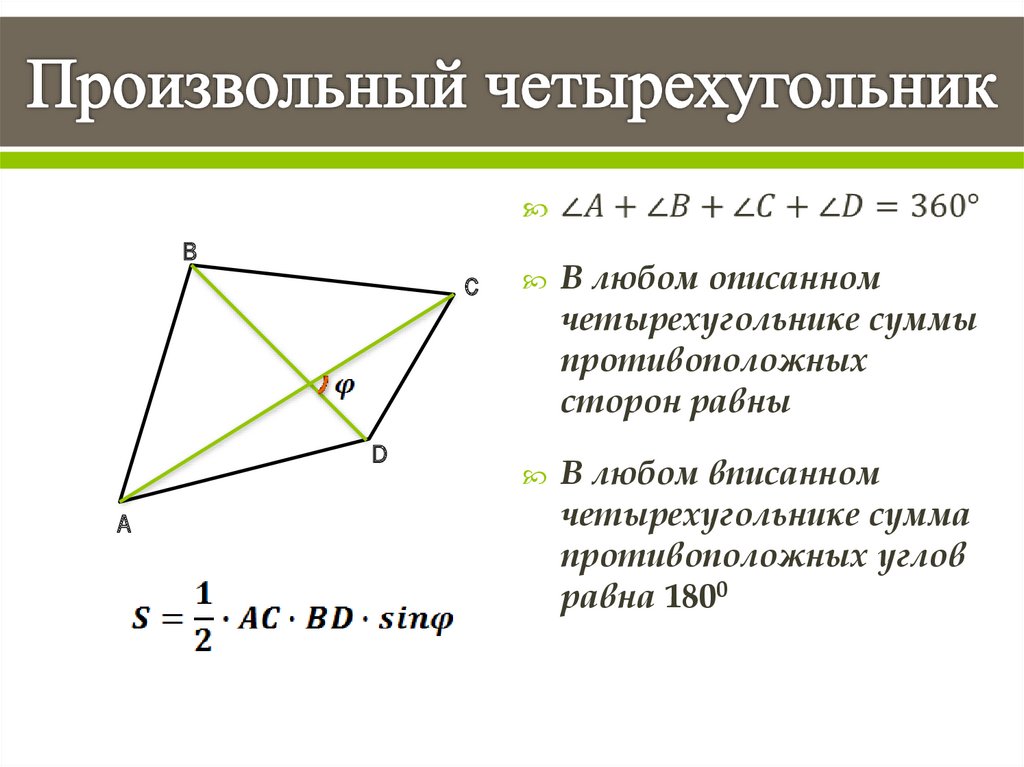
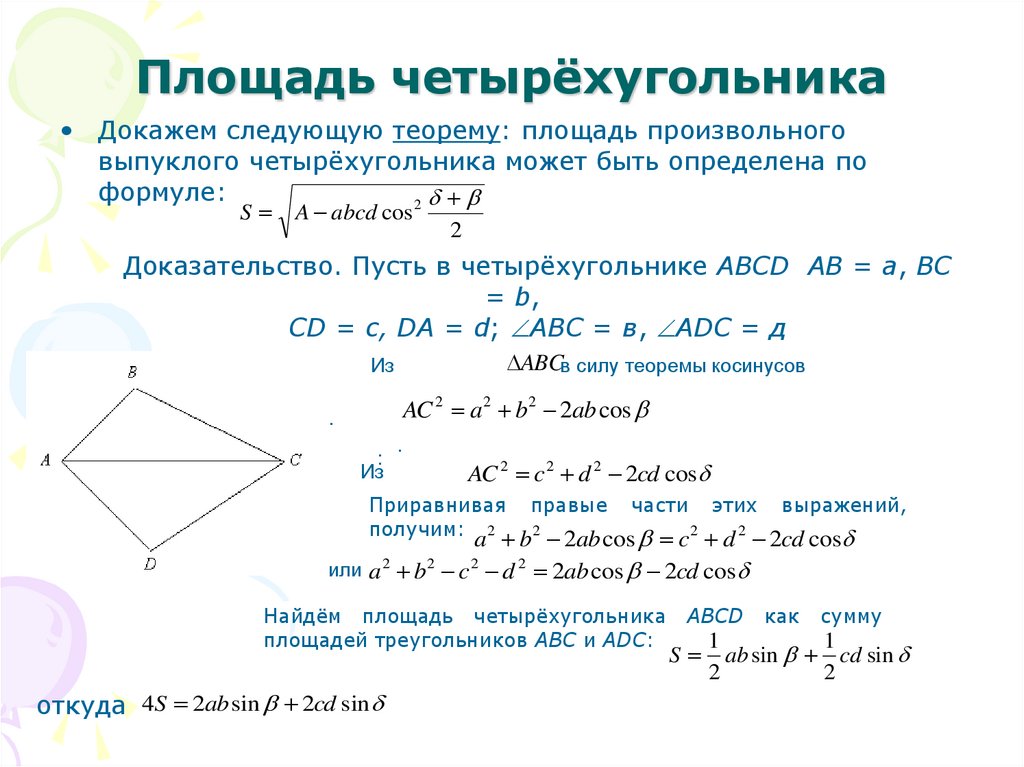
Сумма углов четырехугольника равна 360°.
∠A + ∠B + ∠C + ∠D = 360°.
Если четырехугольник правильный, то каждый угол по 90°
и этот четырехугольник является квадратом.
∠A = ∠B = ∠C = ∠D, ⇒ ∠A = ∠B = ∠C = ∠D = 90°,
ABCD — квадрат.
Сумма противоположных углов четырехугольника равна 180°,
если около четырехугольника описана окружность.
∠A + ∠С = ∠В + ∠D = 180°.
Такие четырехугольники называют вписанными.
Если сумма трех углов четырехугольника равна 270°,
то четвертый угол прямой — 90°.
∠A + ∠B + ∠С = 270°, ⇒ ∠D = 90°(прямой угол).
Виды четырехугольников: квадрат, прямоугольник,
параллелограмм, ромб, трапеция.
Это все виды четырехугольников,
которые изучаются в школьном
курсе по геометрии.
Сумма внутренних углов любого четырехугольника равна 360°.
α + β + γ + δ = 360°.
Все углы вписанного четырёхугольника являются вписанными
в окружность, а также, равны половине дуг, на которые опираются.
◡ABC = 180°, ⇒ ∠ADC = 90°.
◡BCD = 180°, ⇒ ∠BAD = 90°.
Формула суммы углов четырехугольника:
∠A + ∠B + ∠C + ∠D = (n-2) · 180°,
где n — количество сторон четырехугольника.
Сумма трех углов четырехугольника равна 300°,
значит четвертый угол равен 60 градусам.

Сумма внешних и внутренних углов четырехугольника равна 720°.
Все углы имеют одинаковую градусную меру — 90°,
только у квадрата и у прямоугольника.
Сумма углов четырехугольника равна сумме углов фигур,
из которых состоит четырехугольник.
∠DCA + ∠ADC + ∠CAD + ∠ACB + ∠CBA + ∠BAC = 360°.

Следствия

Если в четырехугольнике известны три угла,
но неизвестен четвертый угол, то его можно найти,
так: вычесть из 360 сумму всех трех известных углов,
так мы найдем четвертый угол.
∠A = 360° — (∠B + ∠C + ∠D).
Если три угла четырехугольника равны
90 градусов, то четвертый угол равен тоже 90.
Чтобы на рисунке измерить углы,
и найти их градусную меру, нужно
воспользоваться транспортиром.
Сумма углов четырехугольника
не может быть равна 180 градусам.
∠A + ∠B + ∠C + ∠D ≠ 180°.
Чтобы найти сумму углов
четырехугольника, нужно сложить все углы.
Сумма двух углов четырехугольника равна 180 градусам,
только, в том случае, если этот четырехугольник вписан в окружность.

Геометрия Калькулятор | Геометрия Расчет

Геометрия

2D геометрия

Рамка

Площадь кадра

Площадь кадра
Площадь рамы с учетом внутренней длины, внутренней ширины и толщины

Площадь кадра с учетом внутренней длины, внутренней ширины и диагонали вершины
Площадь рамы с учетом внутренней длины, внешней ширины и толщины
Площадь кадра с учетом внутренней длины, внешней ширины и диагонали вершины
Площадь рамы с учетом внешней длины, внутренней ширины и толщины
Площадь кадра с учетом внешней длины, внутренней ширины и диагонали вершины
Площадь рамы с учетом внешней длины, внешней ширины и толщины
Площадь кадра с учетом внешней длины, внешней ширины и диагонали вершины

Равнобедренная трапеция

Центральная медиана равнобедренной трапеции

Центральная медиана равнобедренной трапеции с учетом площади и высоты
Центральная медиана равнобедренной трапеции с учетом площади, бокового края и острого угла
Центральная медиана равнобедренной трапеции с учетом обоих оснований
Центральная медиана равнобедренной трапеции с учетом высоты, диагонали и тупого угла между диагоналями

Центральная медиана равнобедренной трапеции с учетом высоты, бокового края и длинного основания
Центральная медиана равнобедренной трапеции с учетом высоты, бокового края и короткого основания
Центральная медиана равнобедренной трапеции с учетом высоты, короткого основания и острого угла

Диагональ равнобедренной трапеции

Диагональ равнобедренной трапеции
Диагональ равнобедренной трапеции через площадь и острый угол между диагоналями
Диагональ равнобедренной трапеции с учетом высоты и основания
Диагональ равнобедренной трапеции с учетом высоты и центральной медианы
Диагональ равнобедренной трапеции по высоте, длинному основанию и острому углу
Диагональ равнобедренной трапеции по высоте, длинному основанию и боковому краю
Диагональ равнобедренной трапеции с учетом высоты, короткого основания и острого угла

Диагональ равнобедренной трапеции по длинному основанию, боковому краю и острому углу
Диагональ равнобедренной трапеции с длинным основанием, боковым краем и тупым углом
Диагональ равнобедренной трапеции с учетом короткого основания, бокового края и острого угла
Диагональ равнобедренной трапеции с учетом короткого основания, бокового края и тупого угла

L Форма

Площадь L-образной формы

Площадь L-образной формы
Площадь L-образной формы с учетом длинной внутренней, короткой внешней и короткой внутренней сторон
Площадь L-образной формы с заданными длинными внутренними, короткими внешними сторонами и шириной
Площадь L-образной формы с учетом длинной внешней, длинной внутренней и короткой внутренней сторон
Площадь L-образной формы с учетом длинной внешней, длинной внутренней и короткой внешней сторон
Площадь L-образной формы с учетом длинной внешней, короткой внутренней и короткой внешней сторон

Площадь L-образной формы с заданными длинными, короткими внутренними сторонами и шириной
Площадь L-образной формы с заданными длинными, короткими внешними сторонами и шириной

Прямоугольный шестиугольник

Площадь прямоугольного шестиугольника

Площадь прямоугольного шестиугольника
Площадь прямоугольного шестиугольника по диагонали, внутренней длине, внутренней ширине и короткой ширине
Площадь прямоугольного шестиугольника по диагонали, внутренней длине, короткой длине и внутренней ширине
Площадь прямоугольного шестиугольника по диагонали, внутренней длине, короткой длине и ширине
Площадь прямоугольного шестиугольника по диагонали, внутренней длине, ширине и короткой ширине
Площадь прямоугольного шестиугольника по диагонали, длине, внутренней ширине и короткой ширине
Площадь прямоугольного шестиугольника по диагонали, длине, короткой длине и внутренней ширине
Площадь прямоугольного шестиугольника по диагонали, длине, короткой длине и ширине
Площадь прямоугольного шестиугольника по диагонали, длине, ширине и короткой ширине
Площадь прямоугольного шестиугольника с учетом внутренней длины, малой длины, внутренней ширины и малой ширины
Площадь прямоугольного шестиугольника с учетом внутренней длины, малой длины, ширины и внутренней ширины
Площадь прямоугольного шестиугольника с учетом внутренней длины, малой длины, ширины и малой ширины
Площадь прямоугольного шестиугольника при заданной длине, внутренней длине, внутренней ширине и короткой ширине
Площадь прямоугольного шестиугольника по заданной длине, внутренней длине, ширине и короткой ширине
Площадь прямоугольного шестиугольника с заданной длиной, малой длиной, шириной и внутренней шириной
Площадь прямоугольного шестиугольника с заданной длиной, малой длиной, шириной и малой шириной

Площадь прямоугольного шестиугольника по периметру, внутренней длине, ширине и внутренней ширине
Площадь прямоугольного шестиугольника по периметру, внутренней длине, ширине и короткой ширине
Площадь прямоугольного шестиугольника по периметру, длине, внутренней длине и внутренней ширине
Площадь прямоугольного шестиугольника по периметру, длине, внутренней длине и короткой ширине
Площадь прямоугольного шестиугольника по периметру, длине, короткой длине и внутренней ширине
Площадь прямоугольного шестиугольника с учетом периметра, длины, малой длины и малой ширины
Площадь прямоугольного шестиугольника по периметру, короткой длине, ширине и внутренней ширине
Площадь прямоугольного шестиугольника по периметру, короткой длине, ширине и короткой ширине

Диагональ прямоугольного шестиугольника

Диагональ прямоугольного шестиугольника

Диагональ прямоугольного шестиугольника с заданной длиной, внутренней длиной и малой шириной
Диагональ прямоугольного шестиугольника с заданными длиной, внутренней длиной, шириной и внутренней шириной
Диагональ прямоугольного шестиугольника по периметру, внутренней длине, ширине и внутренней ширине
Диагональ прямоугольного шестиугольника с учетом периметра, длины, внутренней длины и внутренней ширины
Диагональ прямоугольного шестиугольника с учетом малой длины, ширины и внутренней ширины

Длина прямоугольного шестиугольника

Длина прямоугольного шестиугольника
Длина прямоугольного шестиугольника с учетом площади, внутренней длины, внутренней ширины и короткой ширины
Длина прямоугольного шестиугольника с учетом площади, внутренней длины, ширины и внутренней ширины
Длина прямоугольного шестиугольника с учетом площади, внутренней длины, ширины и короткой ширины

Длина прямоугольного шестиугольника с учетом площади, периметра, малой длины и малой ширины
Длина прямоугольного шестиугольника с учетом площади, малой длины, внутренней ширины и малой ширины
Длина прямоугольного шестиугольника с учетом площади, малой длины, ширины и внутренней ширины
Длина прямоугольного шестиугольника с учетом площади, малой длины, ширины и малой ширины
Длина прямоугольного шестиугольника с учетом площади, ширины, внутренней длины и внутренней ширины
Длина прямоугольного шестиугольника по диагонали, внутренней длине и короткой ширине
Длина прямоугольного шестиугольника по диагонали, внутренней длине, ширине и внутренней ширине
Длина прямоугольного шестиугольника по периметру и ширине

Внутренняя длина прямоугольного шестиугольника

Внутренняя длина прямоугольного шестиугольника
Внутренняя длина прямоугольного шестиугольника с учетом площади, длины, внутренней и короткой ширины
Внутренняя длина прямоугольного шестиугольника с учетом площади, длины, ширины и внутренней ширины
Внутренняя длина прямоугольного шестиугольника с учетом площади, длины, ширины и малой ширины
Внутренняя длина прямоугольного шестиугольника с учетом площади, периметра, длины и внутренней ширины
Внутренняя длина прямоугольного шестиугольника с учетом площади, периметра, длины и малой ширины
Внутренняя длина прямоугольного шестиугольника с учетом площади, малой длины, внутренней ширины и малой ширины
Внутренняя длина прямоугольного шестиугольника с учетом площади, малой длины, ширины и внутренней ширины
Внутренняя длина прямоугольного шестиугольника с учетом площади, малой длины, ширины и малой ширины
Внутренняя длина прямоугольного шестиугольника по диагонали, длине и ширине
Внутренняя длина прямоугольного шестиугольника по диагонали, длине, ширине и внутренней ширине
Внутренняя длина прямоугольного шестиугольника по периметру, диагонали, длине и внутренней ширине

Короткая длина прямоугольного шестиугольника

Короткая длина прямоугольного шестиугольника
Короткая длина прямоугольного шестиугольника с учетом площади, внутренней длины, внутренней и короткой ширины
Короткая длина прямоугольного шестиугольника с учетом площади, внутренней длины, ширины и внутренней ширины
Короткая длина прямоугольного шестиугольника с учетом площади, внутренней длины, ширины и малой ширины
Короткая длина прямоугольного шестиугольника с учетом площади, длины, внутренней ширины и короткой ширины
Короткая длина прямоугольного шестиугольника с учетом площади, длины, ширины и внутренней ширины
Короткая длина прямоугольного шестиугольника с учетом площади, длины, ширины и короткой ширины
Короткая длина прямоугольного шестиугольника с учетом площади, периметра, длины и внутренней ширины
Короткая длина прямоугольного шестиугольника с учетом площади, периметра, длины и малой ширины
Короткая длина прямоугольного шестиугольника с учетом диагонали и малой ширины
Короткая длина прямоугольного шестиугольника с учетом диагонали, ширины и внутренней ширины
Короткая длина прямоугольного шестиугольника с учетом периметра, диагонали, длины и внутренней ширины

Ширина прямоугольного шестиугольника

Ширина прямоугольного шестиугольника
Ширина прямоугольного шестиугольника с учетом площади, внутренней длины, короткой длины и внутренней ширины
Ширина прямоугольного шестиугольника с учетом площади, внутренней длины, малой длины и малой ширины
Ширина прямоугольного шестиугольника с учетом площади, длины, внутренней длины и внутренней ширины
Ширина прямоугольного шестиугольника с учетом площади, длины, внутренней длины и короткой ширины
Ширина прямоугольного шестиугольника с учетом площади, длины, внутренней длины и ширины
Ширина прямоугольного шестиугольника с учетом площади, длины, малой длины и внутренней ширины
Ширина прямоугольного шестиугольника с учетом площади, длины, малой длины и малой ширины
Ширина прямоугольного шестиугольника с учетом площади, периметра, малой длины и малой ширины
Ширина прямоугольного шестиугольника по диагонали, длине, внутренней длине и внутренней ширине
Ширина прямоугольного шестиугольника по диагонали, короткой длине и внутренней ширине
Ширина прямоугольного шестиугольника по периметру и длине

Внутренняя ширина прямоугольного шестиугольника

Внутренняя ширина прямоугольного шестиугольника
Внутренняя ширина прямоугольного шестиугольника с учетом площади, внутренней длины, малой длины и малой ширины
Внутренняя ширина прямоугольного шестиугольника с учетом площади, внутренней длины, малой длины и ширины
Внутренняя ширина прямоугольного шестиугольника с учетом площади, длины, внутренней длины и малой ширины
Внутренняя ширина прямоугольного шестиугольника с учетом площади, длины, внутренней длины и ширины
Внутренняя ширина прямоугольного шестиугольника с учетом площади, длины, малой длины и малой ширины
Внутренняя ширина прямоугольного шестиугольника с учетом площади, длины, малой длины и ширины
Внутренняя ширина прямоугольного шестиугольника с учетом площади, длины, ширины и внутренней длины
Внутренняя ширина прямоугольного шестиугольника с учетом площади, периметра, внутренней длины и ширины
Внутренняя ширина прямоугольного шестиугольника с учетом площади, периметра, малой длины и ширины
Внутренняя ширина прямоугольного шестиугольника по диагонали, длине, внутренней длине и ширине
Внутренняя ширина прямоугольного шестиугольника по диагонали, короткой длине и ширине
Внутренняя ширина прямоугольного шестиугольника по периметру, диагонали, внутренней длине и ширине

Короткая ширина прямоугольного шестиугольника

Короткая ширина прямоугольного шестиугольника
Короткая ширина прямоугольного шестиугольника с учетом площади, внутренней длины, короткой длины и внутренней ширины
Короткая ширина прямоугольного шестиугольника с учетом площади, внутренней длины, малой длины и ширины
Короткая ширина прямоугольного шестиугольника с учетом площади, длины, внутренней длины и внутренней ширины
Короткая ширина прямоугольного шестиугольника с учетом площади, длины, внутренней длины и ширины
Короткая ширина прямоугольного шестиугольника с учетом площади, длины, малой длины и внутренней ширины
Короткая ширина прямоугольного шестиугольника с учетом площади, длины, малой длины и ширины
Короткая ширина прямоугольного шестиугольника с учетом площади, периметра, внутренней длины и ширины
Короткая ширина прямоугольного шестиугольника с учетом площади, периметра, короткой длины и ширины
Короткая ширина прямоугольного шестиугольника с учетом диагонали и малой длины
Короткая ширина прямоугольного шестиугольника с учетом диагонали, длины и внутренней длины
Короткая ширина прямоугольного шестиугольника по периметру, диагонали, внутренней длине и ширине

Правая трапеция

Основание правой трапеции

Короткое основание правой трапеции

Короткое основание правой трапеции
Короткое основание прямой трапеции по обеим сторонам и длинному основанию
Короткое основание правильной трапеции с учетом центральной медианы и длинного основания
Короткое основание прямой трапеции с учетом диагоналей, прямого угла, угла между диагоналями, длинного основания
Короткое основание прямой трапеции с прямым углом, длинным основанием и острым углом
Короткое основание прямой трапеции с учетом наклонной стороны, длинного основания и острого угла

Т-образная форма

Площадь Т-образной формы

Площадь Т-образной формы
Площадь Т-образной формы с учетом всех сторон, кроме толщины балки
Площадь Т-образной формы с учетом всех сторон, кроме длины вала
Площадь Т-образной формы с учетом плеча, длины вала, ширины луча и толщины вала
Площадь Т-образной формы с учетом длины луча и вала, толщины и высоты
Площадь Т-образной формы с учетом длины балки, толщины, длины плеча и вала

Трапеция

Inradius трапеции
X Координата центра тяжести трапеции

Диагональ трапеции

Длинная диагональ трапеции

Длинная диагональ трапеции
Длинная диагональ трапеции со всеми сторонами
Длинная диагональ трапеции с учетом площади, короткой диагонали и угла между диагоналями
Длинная диагональ трапеции с учетом высоты, длинного основания и большего острого угла
Длинная диагональ трапеции при заданной высоте, длинном основании и коротком катете
Длинная диагональ трапеции с учетом высоты, медианы, короткой диагонали и угла между диагоналями
Длинная диагональ трапеции с учетом высоты, короткого основания и меньшего острого угла
Длинная диагональ трапеции с учетом высоты, короткой диагонали, обоих оснований и угла стороны между диагоналями
Длинная диагональ трапеции с коротким основанием, длинным катетом и большим острым углом
Длинная диагональ трапеции по короткой диагонали и всем сторонам

Короткая диагональ трапеции

Короткая диагональ трапеции
Короткая диагональ трапеции со всеми сторонами
Короткая диагональ трапеции с учетом площади, длинной диагонали и угла между диагоналями
Короткая диагональ трапеции при заданной высоте, длинном основании и длинном катете
Короткая диагональ трапеции с учетом высоты, длинного основания и меньшего острого угла
Короткая диагональ трапеции с заданной высотой, длинной диагональю, обоими основаниями и углом стороны между диагоналями
Короткая диагональ трапеции с учетом высоты, медианы, длинной диагонали и угла между диагоналями.
Короткая диагональ трапеции с учетом высоты, короткого основания и большего острого угла
Короткая диагональ трапеции по длинной диагонали и всем сторонам
Короткая диагональ трапеции с учетом короткого основания, короткого катета и меньшего тупого угла

Стороны трапеции

Длинное основание трапеции

Длинное основание трапеции
Длинное основание трапеции с учетом центральной медианы и короткого основания
Длинное основание трапеции с учетом высоты, обеих диагоналей, короткого основания и угла между диагоналями.
Длинное основание трапеции по высоте, короткому основанию и обоим острым углам
Длинное основание трапеции с учетом короткого основания, длинного катета и обоих острых углов
Длинное основание трапеции с учетом короткого основания, короткого катета и обоих острых углов

Короткое основание трапеции

Короткое основание трапеции
Короткое основание трапеции с учетом центральной медианы и длинного основания
Короткое основание трапеции с учетом высоты, обеих диагоналей, длинного основания и угла между диагоналями.
Короткое основание трапеции по высоте, длинному основанию и обоим острым углам
Короткое основание трапеции по длинному основанию, длинному катету и обоим острым углам
Короткое основание трапеции, учитывая длинное основание, короткую ногу и оба острых угла.

3D геометрия

Цилиндр, разрезанный пополам по диагонали

Высота цилиндра, разрезанного пополам по диагонали

Высота цилиндра, разделенного по диагонали вдвое, с учетом площади боковой поверхности
Высота цилиндра, разделенного по диагонали вдвое, с учетом пространственной диагонали
Высота цилиндра, разделенного по диагонали вдвое, с учетом общей площади поверхности
Высота цилиндра, разделенного по диагонали вдвое, при заданном объеме

Пространственная диагональ диагонально разделенного пополам цилиндра

Пространственная диагональ диагонально разделенного пополам цилиндра
Пространственная диагональ цилиндра, разделенного пополам по диагонали, с учетом площади боковой поверхности и высоты
Пространственная диагональ цилиндра, разделенного по диагонали вдвое, с учетом площади боковой поверхности и радиуса
Пространственная диагональ цилиндра, разделенного по диагонали вдвое, при заданных объеме и высоте
Пространственная диагональ цилиндра, разделенного по диагонали вдвое, с учетом объема и радиуса

Площадь поверхности цилиндра, разделенного по диагонали вдвое

Площадь боковой поверхности цилиндра, разделенного по диагонали вдвое

Площадь боковой поверхности цилиндра, разделенного по диагонали вдвое
Площадь боковой поверхности цилиндра, разделенного пополам по диагонали, с учетом пространственной диагонали и высоты
Площадь боковой поверхности цилиндра, разделенного по диагонали вдвое, при заданной пространственной диагонали и радиусе
Площадь боковой поверхности цилиндра, разделенного по диагонали вдвое, при заданной общей площади поверхности
Площадь боковой поверхности цилиндра, разделенного по диагонали пополам, при заданных объеме и высоте
Площадь боковой поверхности цилиндра, разделенного пополам по диагонали, при заданных объеме и радиусе

Общая площадь поверхности цилиндра, разделенного по диагонали вдвое

Общая площадь поверхности цилиндра, разделенного по диагонали вдвое
Общая площадь поверхности цилиндра, разделенного пополам по диагонали, с учетом площади боковой поверхности и высоты
Общая площадь поверхности цилиндра, разделенного пополам по диагонали, с учетом площади боковой поверхности и радиуса
Общая площадь поверхности цилиндра, разделенного пополам по диагонали, с учетом пространственной диагонали
Общая площадь поверхности цилиндра, разделенного пополам по диагонали, с учетом пространственной диагонали и высоты
Общая площадь поверхности цилиндра, разделенного пополам по диагонали, с учетом пространственной диагонали и радиуса
Общая площадь поверхности разделенного по диагонали цилиндра с учетом объема и высоты
Общая площадь поверхности цилиндра, разделенного по диагонали вдвое, с учетом объема и радиуса

Отношение поверхности к объему цилиндра, разделенного по диагонали вдвое

Отношение поверхности к объему цилиндра, разделенного пополам по диагонали, с учетом площади боковой поверхности и высоты
Отношение поверхности к объему цилиндра, разделенного пополам по диагонали, с учетом площади боковой поверхности и радиуса
Отношение поверхности к объему цилиндра, разделенного по диагонали вдвое, при заданной пространственной диагонали
Отношение поверхности к объему цилиндра, разделенного по диагонали вдвое, с учетом пространственной диагонали и высоты
Отношение поверхности к объему цилиндра, разделенного по диагонали вдвое, с учетом пространственной диагонали и радиуса
Отношение поверхности к объему цилиндра, разделенного пополам по диагонали, с учетом общей площади поверхности
Отношение поверхности к объему цилиндра, разделенного по диагонали вдвое, с учетом общей площади поверхности и радиуса
Отношение поверхности к объему цилиндра, разделенного по диагонали вдвое, с учетом объема и высоты
Отношение поверхности к объему цилиндра, разделенного по диагонали вдвое, с учетом объема и радиуса

Объем цилиндра, разрезанного по диагонали пополам

Объем цилиндра, разделенного по диагонали вдвое
Объем цилиндра, разделенного пополам по диагонали, с учетом площади боковой поверхности и высоты
Объем цилиндра, разделенного по диагонали вдвое, с учетом площади боковой поверхности и радиуса
Объем цилиндра, разделенного пополам по диагонали, с учетом пространственной диагонали и высоты
Объем цилиндра, разделенного по диагонали вдвое, с учетом общей площади поверхности
Объем цилиндра, разделенного по диагонали вдвое, с учетом общей площади поверхности и отношения поверхности к объему

Рампа

Ширина рампы

Ширина рампы
Ширина пандуса с учетом общей площади поверхности, прилегающей стороны и гипотенузы
Ширина пандуса с учетом общей площади поверхности, смежной стороны и противоположной стороны
Ширина пандуса с учетом общей площади поверхности, противоположной стороны и гипотенузы
Ширина рампы с учетом объема, гипотенузы и прилегающей стороны
Ширина рампы с учетом объема, гипотенузы и противоположной стороны

Copied!

Неправильные четырехугольники | Площадь, определение и видео

Написано

Малкольм МакКинси

11 января 2023

Проверка по факту

Пол Маццола

Определение четырехстороннего награда

. Напомним, квадратный квадроцик ) — двумерная плоская фигура, состоящая из четырех отрезков, ограничивающих пространство. Поскольку определение настолько широкое, многие распространенные формы являются четырехугольниками:

Squares
Rectangles
Trapezoids
Parallelograms
Kites
Rhombuses

Regular quadrilaterals

Of the long list, only a square is a regular quadrilateral . Правильные многоугольники имеют равные стороны и углы. Легко видеть, что прямоугольник может иметь четыре внутренних угла 90° , но не обязательно иметь четыре стороны одинаковой длины.

Неправильные четырехугольники

Что такое неправильный четырехугольник ? К неправильным четырехугольникам относятся: прямоугольник, трапеция, параллелограмм, воздушный змей и ромб. Они симметричны, но не обязаны иметь конгруэнтные стороны или углы. Однако не отчаивайтесь, потому что некоторые из них, как и квадрат, поддаются формулам площади.

Кроме симметричных неправильных четырехугольников могут существовать и другие неправильные четырехугольники без симметрии, всего четыре неравные стороны:

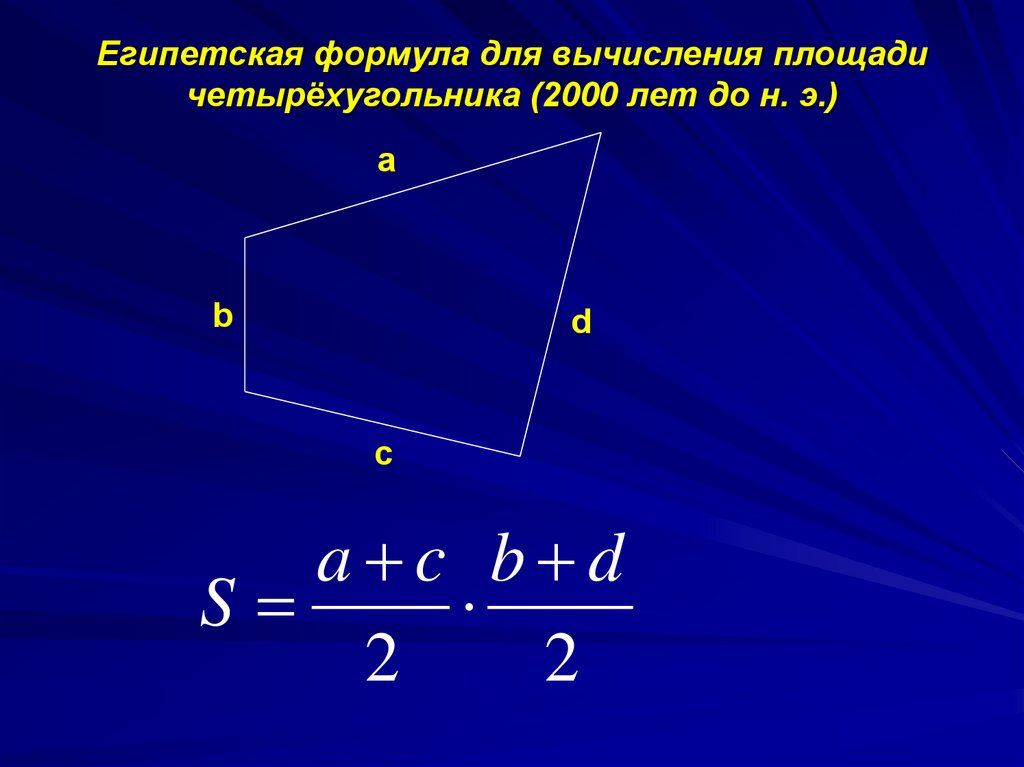
Неправильный четырехугольник

Площадь неправильного четырехугольника

Вычислить площадь (в квадратных единицах) для квадрата и прямоугольника легко:

Если у вас есть квадрат со стороной 17 см длиной, площадь равна 289 квадратных см . Если у вас есть прямоугольник с двумя сторонами 17 см и двумя сторонами 34 см , площадь равна 17×34=57817\умножить на 34=57817×34=578 квадратных см .

Вычисление площади большинства других неправильных четырехугольников может оказаться сложной задачей. Площадь параллелограмма или ромба, например, равна его высота (или высота), а не длина его короткой стороны, умноженное на его основание . Для трапеции вам нужно найти среднее двух оснований и умножить это значение на высоту трапеции .

Воздушный змей , который имеет две смежные короткие стороны и две смежные длинные стороны, имеет формулу площади, основанную на его диагоналях, d1 и d2 :

Площадь очень

неправильных четырехугольников 9 из предыдущего примера5 9 неправильного четырехугольника, MATH показывает, что четыре стороны не гарантируют симметричную форму. Чтобы найти площадь таких неправильных четырехугольников, следуйте трехэтапной стратегии:

Разделите четырехугольник на два треугольника, построив диагональ, не нарушающую известный внутренний угол
Вычислите площадь каждого треугольника, используя формулы
Складываем площади двух треугольников

Для нашего четырехугольника MATH , соединение вершины A с вершиной H разбивает фигуру на △MAH\треугольник MAH△MAH и △ATH\треугольник ATH△ATH. Вы не знаете высоты h любого из треугольников, поэтому вы не можете вычислить площадь, используя 12bh\frac{1}{2}bh31bh.

Вместо этого проявите творческий подход (математика полна творчества), строя один факт на другом. В нашем четырехугольнике MATH , если мы знаем один угол, мы можем использовать эти четыре шага, чтобы найти общую площадь:

Знание, которое включает угол T — 120 ° , вы можете использовать боковой стороны , чтобы найти область △ Ath \ Triangle Ath △ Ath
ATH\треугольник ATH△ATH, вы можете использовать Закон косинусов для вычисления неизвестной длины диагонали AH
Зная длину диагонали AH , вы можете использовать Формула для вычисления площади △MAH\треугольника MAH△MAH
Зная площади двух треугольников, сложите их, чтобы получить площадь неправильного четырехугольника

Обратите внимание, что вы должны работать последовательно, и вы должны есть некоторые основные факты, чтобы начать. Вы должны знать длины сторон неправильного четырехугольника и величину одного из углов. Давайте пройдемся по каждому шагу.

Использовать сторона-угол-сторона

Учитывая длины двух сторон AT и TH и их угол T , используйте тригонометрическую функцию A=12AT×TH×sin⁡(T)A=\frac{1}{2}AT\times TH\times \sin\left(T\right)A=21AT×TH×sin(T) для вычисления площади △ATH\треугольника ATH△ATH:

Используйте закон косинусов

Теперь мы знаем площадь △ ATH\треугольник ATH△ATH, но мы знаем а не длину диагонали AH . Мы будем использовать Закон косинусов:

Этот закон позволяет вычислить неизвестную длину. Мы должны переделать формулу, используя наши определенные метки, имея в виду, что в нашем △ATH\треугольнике ATH△ATH стороны могут быть обозначены строчными версиями их противоположных углов:

Сторона AT может быть помечена h
Боковая сторона TH может быть маркирована a
0049 AH может быть помечен T

У нас теперь приблизительно длины боковой AH AS 13. 747 CM , так что мы можем использовать HERON. сечение нашего четырехугольника.

Используйте формулу Герона

Формула Герона зависит от знания полупериметра или половины периметра треугольника. Для нашего △MAH\треугольника MAH△MAH три стороны имеют размер:

MA = 7 cm
AH = 13.747 cm
HM = 14 cm

The semiperimeter, s , половина суммы сторон:

Вот Формула Герона , где a , b и 9004 — длины трех сторон:

Подставьте значение s , чтобы получить площадь:

Наконец, у нас есть площади двух наших треугольников. Сложите их, и вы получите общую площадь неправильного четырехугольника:

С точностью до тысячных квадратных см мы получим площадь четырехугольника МАТЕМАТИКА !

Итоги урока

Теперь, когда вы полностью проработали урок, вы можете различать четырехугольники, различать правильные и неправильные четырехугольники, а также вспоминать и объяснять отличительные свойства правильных и неправильных четырехугольников. Теперь вы также можете применять длину на ширину в качестве формулы для вычисления площади правильных и некоторых неправильных четырехугольников, и, когда формула длины на ширину неприменима, находить площадь неправильных четырехугольников с помощью других стратегий, в том числе с использованием закона косинусов и формулы Герона.

Формула четырехугольника — объяснение, типы, примеры решения

Обычно существует 5 формул, которые можно использовать для вычисления площади 7 наиболее распространенных типов четырехугольников. Обычно существует всего 5 формул, хотя некоторые из них имеют вариации и могут применяться для двойного назначения — например, вы можете рассчитать площадь воздушного змея по формуле ромба и наоборот. Однако, прежде чем начать знать все формулы четырехугольника, важно понять типы четырехугольников и их свойства

Ниже приведены все типы фигур, которые известны как четырехугольники. Вы можете легко нарисовать гораздо больше четырехугольников, и мы даже можем узнать многие из них вокруг нас.

(Изображение будет загружено в ближайшее время)

Типы четырехугольников и их свойства с формулами

Прямоугольник

Четырехугольник, у которого противоположные стороны параллельны и равны, называется прямоугольником.

Свойства прямоугольника:

Все углы прямые. 9{2}} \]
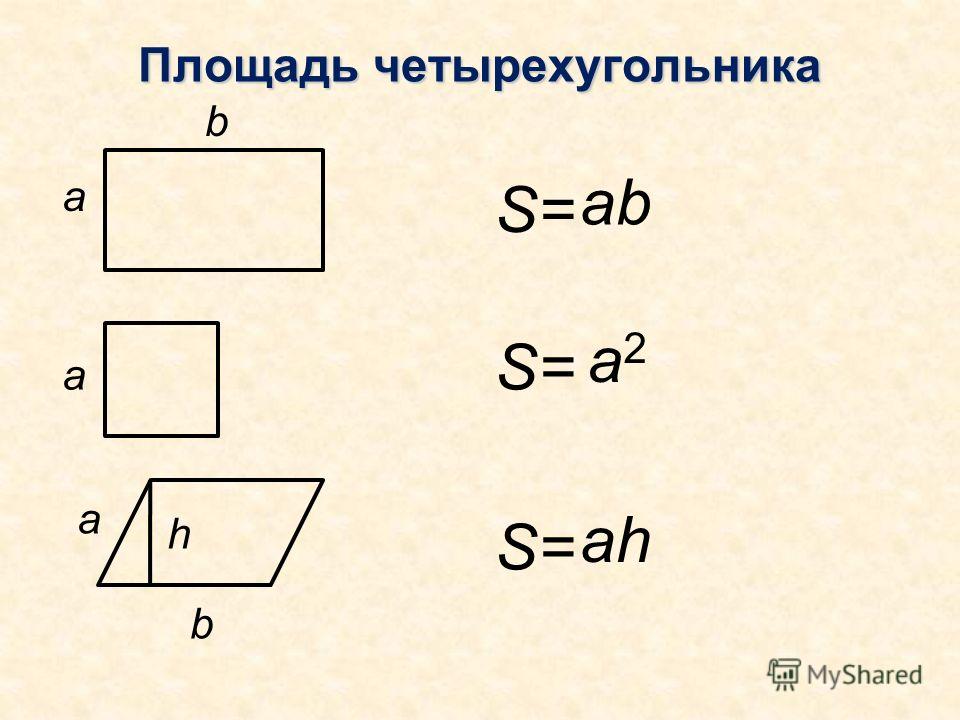
Площадь прямоугольника = L × B
Периметр прямоугольника = 2 (L+B)

Speectes 9003

9005
SOVERESTER OF THAP параллелограмм, у которого все стороны равны, называется квадратом.
Свойства квадратов:
Все стороны и углы равны друг другу
Противоположные стороны параллельны
Диагонали равны
Диагонали перпендикулярны и пересекают друг друга.
Важные формулы для квадратов:
Если мы предположим, что длина квадрата равна L, тогда
Длина диагонали = L √2
Площадь квадрата = L×L.
Периметр квадрата = 4L
Ромб
Четырехугольник, все четыре стороны которого равны по длине, является ромбом. Иногда его также называют равносторонним четырехугольником из-за его характеристики эквивалентности длины.
Свойства ромба:
Все стороны имеют одинаковую длину
Противоположные углы равны
Диагонали перпендикулярны и пересекают друг друга.
Смежные углы составляют дополнительные углы (например, ∠m + ∠n = 180°).
Важные формулы для ромба:
Если мы предположим, что длины ромба равны L и m, n — длина его диагоналей, тогда
Трапеция
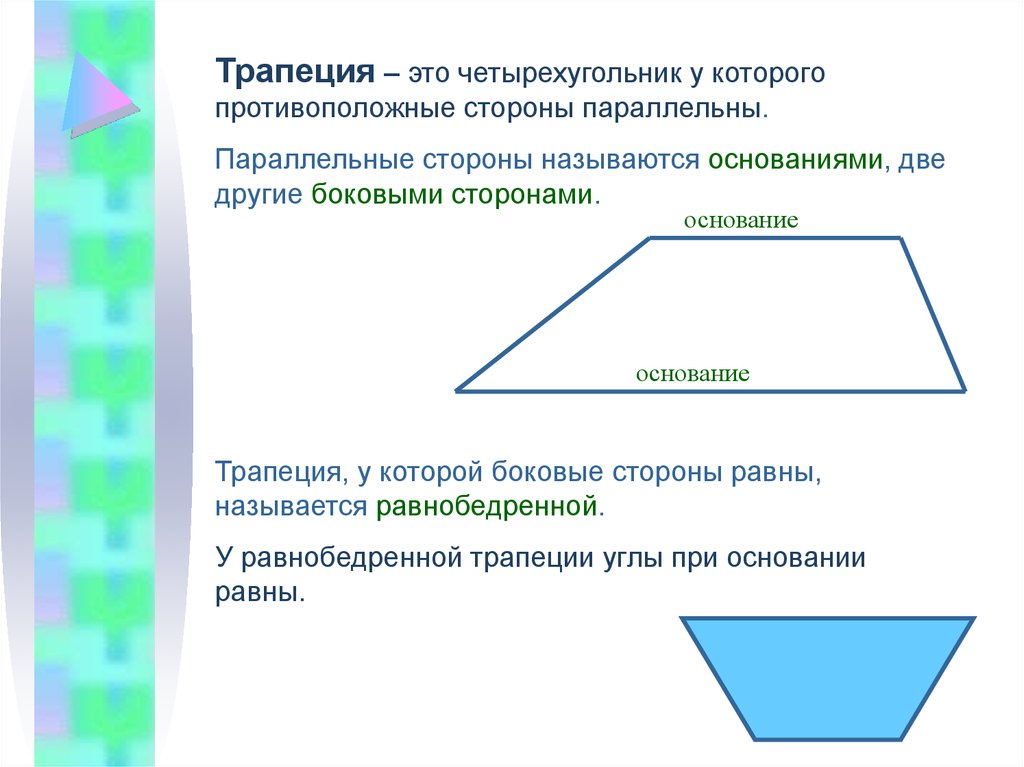
Выпуклый четырехугольник с минимум одной парой параллельных сторон называется трапецией на английском языке и называется трапецией на американском и канадском языках
Свойства трапеции:
Важные формулы для трапеции :
Площадь трапеции MNOP = (M+N)/2 h {M и N — параллельные стороны}
Периметр трапеции = M + N +O + P трапеция = 1/2 х сумма параллельных сторон х высота
Площадь медианы трапеции = 1/2 x сумма параллельных сторон
Напоминание: медиана – это линия, которая находится на равном расстоянии от параллельных сторон).
Равнобедренная трапеция
Четырехугольник, у которого только одна пара противоположных сторон параллельна друг другу, а остальные пары сторон равны, то это равнобедренная трапеция.
Свойства равнобедренной трапеции:
Две пары смежных углов являются дополнительными, т.е. в сумме дают 180 градусов.
Можно вписать в круг.
Диагонали образуют пару конгруэнтных треугольников с равными сторонами в основании
Сумма четырех внешних и четырех внутренних углов равна 4 прямым углам.
Крошку конуса получаем вращением равнобедренной трапеции вокруг вертикальной оси, соединяющей середины параллельных сторон
Важная формула равнобедренной трапеции:
Решенные примеры
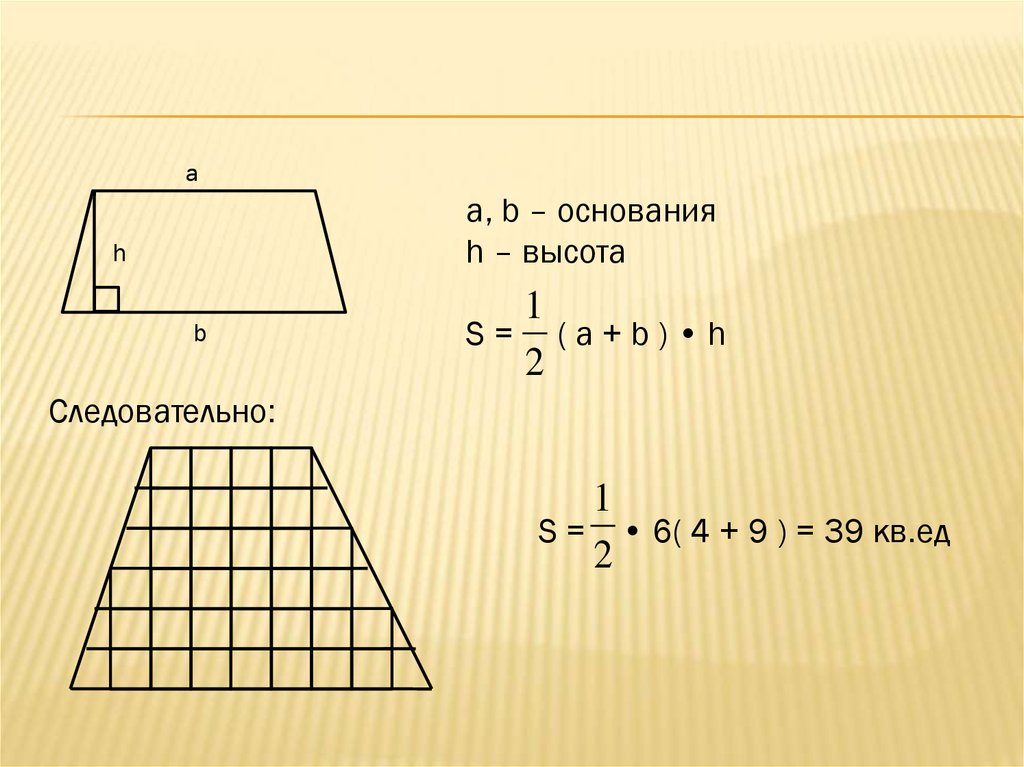
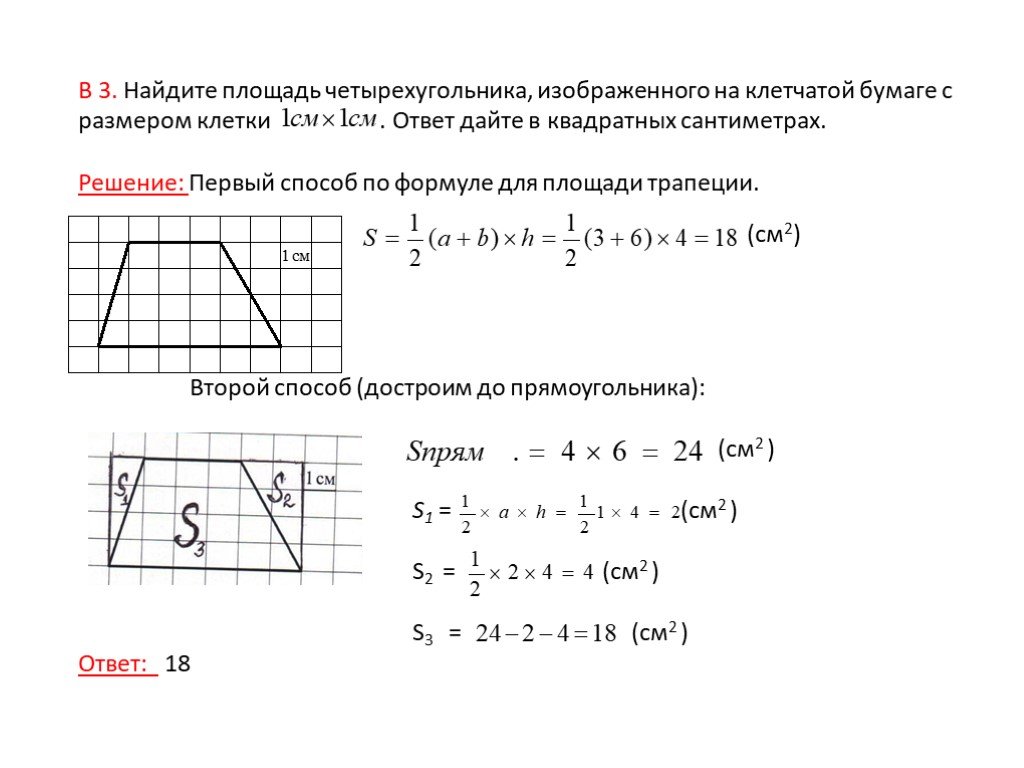
Пример 1. Найдите площадь трапеции, используя длину и высоту ее оснований. У вас есть трапеция с одним основанием 8 см, другим основанием 12 см, а линия высоты, соединяющая их, имеет длину 4 см.
Решение:
Учитывая длину трапеции, а также высоту обоих оснований, мы будем использовать следующую формулу:
Площадь = (Основание1 + Основание2)/2 × высота
или
A = (м + n) / 2 × h
Теперь посчитаем и составим уравнение
Вы можете рассчитать его площадь следующим образом: (8 + 12)/2 × 4 = (20)/2 × 4 = 40 см
Пример 2: Найдите площадь воздушного змея, используя следующие измерения. Воздушный змей имеет диагонали длиной 18 метров и 6 метров, тогда какова его площадь?
Решение:
Применим формулу диагонали ромба, чтобы найти площадь воздушного змея, поскольку ромб — это особый вид воздушного змея, все длины которого имеют одинаковую меру.
No related posts.