Матрица зачем нужна в математике: Математика онлайн

Содержание

Зачем нужна математика в программировании?

Доклад на тему: “Зачем нужна
математика в программирование?”
Выполнил: Цыс Максим. Группа: 20ПКС-1
Учитель: Ходырева Ирина Сергеевна
План
1) Математика в программирование.
2) Области математики
3) Логика
4) Комбинаторика
5) Теория вероятностей
6)Теория вероятностей в играх
7) Математическая статистика
8) Линейная алгебра
9) Алгебра для игр
10) Теория графов
11) Теория сложности
12) Итоги
Области математики
Многие интересуются, можно ли стать программистом, не зная математики.
Разумеется, можно. Программист — это не тот человек, который идеально решает
уравнения и возводит числа в степень, а тот, который знает несколько языков
программирования и способен создавать программы. Математические знания
решают то, насколько человек будет компетентен в своей сфере работы. Изучать
приведенные в статье разделы математики до самых глубин не нужно. Достаточно
знать основы и свободно в них разбираться. Если понадобятся более углубленные
знания, их всегда можно получить из интернета.
Какие разделы математики нужны программисту? Речь идет в основном о
дискретной. Важно разбираться в логике, комбинаторике, теории вероятности,
математической статистике, линейной алгебре, теории графов и сложности. Как
видим, все они развивают человека и рассчитаны на улучшение гибкости
мышления. Далее рассмотрим каждую дисциплину отдельно.
Логика
Математик и программист – профессии, которые взаимосвязаны. Математику
программирование, можно сказать, не нужно. Программисту разбираться во
многих математических понятиях очень важно. Рассмотрим, чем полезна логика.
Компьютер состоит из материальных деталей и программного обеспечения. Все
они не могут работать без математической логики. Сейчас она используется
широко во время применения различных языков программирования, позволяя
делать программы максимально удобными и нересурсозатратными. Что собой
представляет утилита? Это последовательная система, которая выполняет
команды, вшитые в нее или же поступающие с устройств ввода-вывода. Если
рассматривать понятие «программа» более детально, то можно заметить участие
логики во всем этом процессе.
В 30-х годах 19 века появились первые идеи вычислительной машины. Тогда
логика стала одной из фундаментальных структур. Сам математический
раздел начал стремительно развиваться в начале 20 века. Исследования,
которые тогда были проведены, положили начало всем языка
программирования, основанным на алгоритмическом выполнении команд.
На сегодняшний момент этот раздел изучается для того, чтобы программист
мог самостоятельно разрабатывать программы, не опираясь на созданные
шаблоны. Однако успешное освоение логики будет развивать нестандартное
мышление, которое является важным для любого программиста. В принципе,
все сферы точной науки должны быть направлены именно на эту цель.
Именно такую играет роль математика. В профессии программиста она
является неотъемлемой частью.
Комбинаторика
Что собой представляет данный раздел математики? Он учит вычислять
количество возможных комбинаций для достижения целей. В отличие от
вышеописанной логики, комбинаторика используется повсеместно. Нужно
отметить, что она является негласной «матерью» тоже же теории графов.
Последняя использовалась для создания сетевых протоколов, но об этом
немного ниже. Все глубже вникая в создание различных утилит, становится
понятно, зачем программисту математика. Именно благодаря этой науке
информационные технологии так быстро и успешно развиваются. Если бы не
она, то вряд ли мы могли бы увидеть компьютеры, маршрутизаторы,
телефоны и так далее. Ведь для них нужна прошивка.
Также нужно отметить, что комбинаторика используется для
работы маршрутизации в сетях. Искусственные нейронные сети
также созданы на ее основе. Благодаря этому разделу
математики происходит разработка искусственного интеллекта.
Комбинаторика является неотъемлемой и в криптографии.
Следует отметить, что этот раздел математики требует развитого
мышления, в чем помогает изучение логики. Как уже становится
понятно, эти разделы связаны между собой и тесно
переплетены. Именно поэтому их объединяют воедино под
названием «дискретная математика».
Теория вероятностей
Те программисты, которые работают аналитиками данных, должны хорошо
разбираться в теории вероятностей. Почему? Чтобы машинные методы работы не
казались «волшебством», нужно разбираться в математической статистике. Она
базируется на теории вероятностей.
Этот раздел математики можно разделить на две части. Первая дискретная,
вторая непрерывная. Начинающих программистов, не любящих точную науку,
можно огорчить, так как оба этих подраздела математики в профессии
программиста пригодятся. Дискретная теория разработана для явлений, которые
описываются с определенным количеством возможных вариантов. Речь идет,
например, о монетках или игральных костях. Непрерывная базируется на
явлениях, которые распределены в круге или на отрезке, то есть на плотном
множестве.
Теория вероятностей в играх
Если программист собирается разрабатывать игры, а не сидеть в аналитическом отделе
компании, ему все равно придется разобраться с теорией вероятности. Чтобы было понятно,
зачем это нужно, рассмотрим простой случай. К примеру, объектом разработки является
шутер. Механика стрельбы – практически главный элемент в таком программном проекте. Те
шутеры, где оружие стреляет максимально точно, вряд ли понравится большинству игрокам.
Поэтому следует добавлять разброс. Сделать точки максимально рандомными не следует. Это
повлечет за собой проблемы с точной настройкой и нарушит игровой баланс. Если
использовать знания из теории вероятности, то можно взять случайные показатели, а по их
распределению сделать анализ того, как будет работать то или иное оружие с заданным
разбросом. Так можно откорректировать игру.
Разбирая, какая роль математики в профессии программиста, относительно теории вероятности
следует сказать, что благодаря этой науке создаются нейросети, биржевые торговые роботы,
крипто-анализ и алгоритмы шифрования. Кроме того, машинное обучение – сфера, где
использована математическая статистика и теория вероятности. Без них не обойтись.
Математическая статистика
Следует отметить, что статистика и теория вероятности взаимосвязаны. Первый раздел
базируется на втором. Как правило, в вузах они изучаются обязательно. Сначала преподаются
вероятности, потом уже благодаря полученным данным можно выучить статистику.
Используется этот раздел также часто, как и теория вероятности. Он нужен практически в тех
же сферах.
Математическая статистика – важная наука для любого программиста. Чтобы разобраться с ней,
нужно иметь гибкое мышление и быть усидчивым. Мало просто походить на курсы,
позаниматься с репетитором. Этого будет достаточно, чтобы выучить основы и базу. Чтобы
действительно начать разбираться в этой теме – нет. В программировании она играет огромную
роль. Именно благодаря статистике создаются динамические программы. Не всегда можно
знать конечную цифру в выполняемом цикле, так как все данные вводятся с клавиатуры. Здесь
поможет именно статистика. В любых неоднозначных задачах следует прибегать к помощи
этого раздела математики. Для программистов она — как волшебная палочка. Главное — уметь ею
пользоваться.
Линейная алгебра
Этот раздел математики поможет освоить языки программирования.
Важные темы: матрицы и векторы, а также базовые операции над
матрицами. Почему они так важны? В любом языке
программирования при выполнении сложной задачи создается
матрица значений. Она работает таким же образом, как и в
математике. Чтобы уметь правильно оперировать функциями языка
программирования, нужно как следует подучить математику.
Алгебра для игр
Этот раздел математики для программистов будет полезен, если они
собираются разрабатывать игры. Тогда стоит подучить дополнительно темы
про векторы. Если в приложении есть экранные кнопки, можно обращаться к
камере и ее направлению, но в любом случае придется воспользоваться
знаниями из линейной алгебры. Вектор нужен для того, чтобы запоминать
местоположение, направление и скорость объекта. Для движения машинки
или другого персонажа придется использовать сложение векторов. Для
стрельбы оружия понадобятся знания о том, как вычитать векторы. Этот же
раздел математики необходим в играх, где происходят взрывы. Чтобы
рассчитать расстояния между ними и персонажем, а также подсчитать
ущерб, следует уметь рассчитать вектор, который находится между ними.
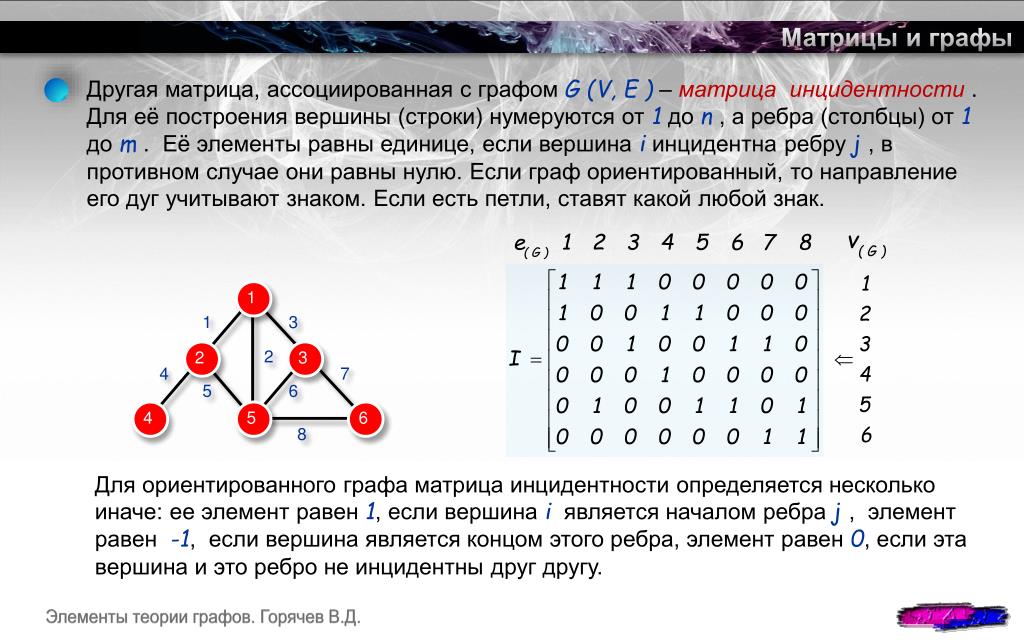
Теория графов
Специальности математик и программист связаны, как уже было сказано ранее. При этом любой
успешный знаток точной науки сможет, подучив программирование, создавать программы. Что
касаемо теории графов, то ее следует знать поверхностно. Она нужна для того, чтобы понимать,
как устроены те или иные детали, программы и так далее. Благодаря данному разделу
математики реализуются алгоритмы поиска решений. Речь идет, например, о кратчайшем пути
по маршруту, расположении дорожек на микросхеме, поиске победной игровой стратегии.
Кроме того, нередко для работы с программой и ее отладкой необходимо использовать AST.
Если программист не понимает основ графов, то ему будет легко запутаться в git. Для анализа и
разрешения различных задач тоже понадобится этот раздел дискретной математики. Для
нахождения путей и определения цикличностей, которые используются не так уж редко
(социальные сети, навигаторы, абстракции в компьютерных играх), используется теория графов.
Изучать в этом разделе советуем графы и все, что с ними связано (вершины, ребра, подграфы).
Также нужно обратить внимание на пути, циклы и маршруты. Следует разобраться с тем, какие
операции могут совершаться над графами.
Теория сложности
Рассматривая,
какие
нужно
изучать
разделы
математики
программистам, советы опытных айтишников о теории сложности
никак нельзя обойти стороной. Этот раздел математики необходим для
того, чтобы описывать базовые и простые элементы, которые в
дальнейшем влияют на систему в целом и помогают решать сложные
задачи. Чтобы с ними не возникало проблем, следует изучать
логарифмы и экспоненту. Нередко в работе используются знания из
понятия арифметической суммы. Скорость роста алгоритмов и их
анализ тоже понадобятся.
Итоги
В докладе дан ответ на вопрос, какая математика нужна
программисту. Без нее не получится составить программу, которая не
будет занимать всю оперативную память и одновременно решать
сложные задачи. В вузах преподают все из перечисленных разделов
математики. При обучении стоит обратить внимание именно на них,
а не отдавать предпочтение дифференциальным уравнениям,
сложным интегралам и так далее. Математика для программистов
очень важна не столько для написания программ, сколько для
понимания машинных методов, нейронных систем.
Список литературы
1)
https://fb.ru/article/426683/matematika-dlya-programmista
2)
https://ami.nstu.ru/entrant/proceed/why_math.php
3)
Википедия
4)
https://www.youtube.com/watch?v=2A_l9aKVNqM

«Зачем искать определитель матрицы, в чем смысл? Где конкретно это может понадобиться в реальной жизни?» — Яндекс Кью

Чем полезны матрицы?

Я работаю в области прикладной математики, поэтому дам вам точку зрения прикладного математика.

Я делаю числовые PDE. По сути, я беру дифференциальное уравнение (уравнение, решением которого является не число, а функция, и оно включает функцию и ее производные) и вместо аналитического решения пытаюсь найти приближенное значение решение в некоторых точках (подумайте о сетке точек). Это немного глубже, чем это, но это не главное. Дело в том, что в конце концов мне приходится решать линейную систему уравнений, которая обычно имеет огромный размер (порядка миллионов). Я бы сказал, что нужно решить довольно большое количество уравнений.

Где вступают в игру матрицы? Ну, как вы знаете (а может и нет, я не знаю), линейную систему можно рассматривать в матрично-векторной форме как

$$\text{A}\underline{x}=\underline{b}$$ где $\underline{x}$ содержит неизвестные, A — коэффициенты уравнений, а $\underline{b}$ содержит значения правых частей уравнений. Например, для системы

$$\begin{cases}2x_1+x_2=3\\4x_1-x_2=1\end{cases}$$ у нас есть

$$\text{A}=\left[ \begin{массив}{cc} 2 и 1\\ 4 и -1 \конец{массив} \right],\qquad \underline{x}= \left[\begin{массив}{с} х_1\\ х_2 \конец{массив} \right]\qquad \underline{b}= \left[\begin{массив}{с} 3\\ 1 \конец{массив} \справа]$$

Для того, что я сказал до сих пор, в этом контексте матрицы выглядят просто как причудливый и компактный способ записать систему уравнений, простые таблицы чисел.

Однако для быстрого решения этой системы недостаточно использовать калькулятор с большой оперативной памятью и/или высокой тактовой частотой (ЦП). Конечно, чем мощнее калькулятор, тем быстрее вы получите решение. Но иногда ускорение все же может означать

дней (или больше), если вы решите проблему неправильным образом, даже если вы находитесь на Blue Gene.

Итак, чтобы уменьшить вычислительные затраты, вы должны придумать хороший алгоритм, умную идею. Но для этого вам нужно использовать какое-то свойство или некоторую структуру вашей линейной системы. Эти свойства каким-то образом закодированы в коэффициентах матрицы A. Поэтому изучение матриц и их свойств имеет решающее значение для повышения эффективности линейных решателей. Признание того, что матрица обладает определенным свойством, может иметь решающее значение для разработки быстрого алгоритма или даже для доказательства того, что решение существует или что решение обладает каким-то хорошим свойством.

Например, рассмотрим линейную систему

$$\left[\begin{array}{cccc} 2 и -1 и 0 и 0\\ -1 и 2 и -1 и 0\\ 0 и -1 и 2 и -1\\ 0 и 0 и -1 и 2 \конец{массив} \правильно] \оставил[ \начать{массив}{с} х_1\\ х_2\\ х_3\\ х_4 \конец{массив} \право]= \оставил[ \начать{массив}{с} 1\\ 1\\ 1\\ 1 \конец{массив} \право]$$ что соответствует (в форме уравнения)

$$\begin{case} 2x_1-x_2=1\\ -x_1+2x_2-x_3=1\\ -x_2+2x_3-x_4=1\\ -x_3+2x_4=1 \end{case}$$

Просто бегло взглянув на матрицу, я могу утверждать, что эта система имеет решение и, более того, решение неотрицательно (имеется в виду, что все компоненты решения неотрицательны). Я почти уверен, что вы не сможете сделать такой вывод, просто взглянув на систему, не пытаясь ее решить. Я также могу утверждать, что для решения этой системы вам нужно всего 25 операций (одна операция — это сложение/вычитание/деление/умножение). Если вы построите большую систему с тем же шаблоном (2 по диагонали, -1 по верхней и нижней диагонали) и поместите правую часть только с положительными элементами, я все еще могу утверждать, что решение существует и оно положительное, а число операций, необходимых для ее решения, составляет всего $8n-7$, где $n$ — размер системы.

Кроме того, люди уже указали другие области, где матрицы являются важными кирпичиками и играют важную роль. Я надеюсь, что эта тема дала вам представление о том, почему стоит изучать матрицы. =)

линейная алгебра — Почему исторически мы умножаем матрицы именно так?

Вот ответ, прямо отражающий историческую перспективу из статьи Мемуары по теории матриц Автор Кейли, 1857 г. Эта статья доступна здесь.

Этой статье приписывают «первое абстрактное определение матрицы» и «алгебру матриц, определяющую сложение, умножение, скалярное умножение и инверсию» (источник).

В данной статье используются нестандартные обозначения. Я постараюсь поместить его в более «современную» (но все же нестандартную) нотацию. Основная часть содержания этого поста будет со страниц 20-21.

Чтобы ввести обозначения, $$ (X,Y,Z)= \left( \begin{array}{ccc} а и б и в \\ а’&б’&в’\\ a» & b» & c» \end{array} \right)(x,y,z)$$

будет представлять набор линейных функций $(ax + by + cz, a’z + b ‘y + c’z, a»z + b»y + c»z)$, которые тогда называются $(X,Y,Z)$.

Кэли определяет сложение и скалярное умножение, а затем переходит к матричному умножению или «композиции». Он специально хочет решить проблему:

$$(X,Y,Z)= \left( \begin{array}{ccc} а и б и в \\ а’&б’&в’\\ a» & b» & c» \end{array} \right)(x,y,z) \quad \text{где} \quad (x,y,z)= \left( \begin{array {cc} \альфа и \бета и \гамма\\ \альфа’ и \бета’ и \гамма’ \\ \alpha» & \beta» & \gamma» \\ \end{array} \right)(\xi,\eta,\zeta)$$

Теперь он хочет представить $(X,Y,Z)$ в терминах $(\xi,\eta,\zeta)$. Он делает это, создавая другую матрицу, которая удовлетворяет уравнению:

$$(X,Y,Z)= \left( \begin{array}{ccc} А и В и С \\ А ‘и В’ и С’ \\ A» & B» & C» \\ \end{array} \right)(\xi,\eta,\zeta)$$

Он продолжает писать, что значение, которое мы получаем, равно:

$$ \begin{выравнивание}\left(\begin{массив}{ccc} А и В и С \\ А ‘и В’ и С’ \\ A» & B» & C» \\ \end{массив} \right) &= \left( \begin{массив}{ccc} а и б и в \\ а’&б’&в’\\ a» & b» & c» \end{массив} \right)\left( \begin{массив}{ccc} \альфа и \бета и \гамма\\ \альфа’ и \бета’ и \гамма’ \\ \alpha» & \beta» & \gamma» \\ \end{массив} \right)\\[0,25 см] &= \left( \begin{массив}{ccc} a\alpha+b\alpha’ + c\alpha» & a\beta+b\beta’ + c\beta» & a\gamma+b\gamma’ + c\gamma» \\ a’\alpha+b’\alpha’ + c’\alpha» & a’\beta+b’\beta’ + c’\beta» & a’\gamma+b’\gamma’ + c’\ гамма» \\ a»\alpha+b»\alpha’ + c»\alpha» & a»\beta+b»\beta’ + c»\beta» & a»\gamma+b’ ‘\gamma’ + c»\gamma»\end{массив} \right)\end{align}$$

Это стандартное определение умножения матриц.

Зачем нужна математика в программировании?

«Зачем искать определитель матрицы, в чем смысл? Где конкретно это может понадобиться в реальной жизни?» — Яндекс Кью

Чем полезны матрицы?

линейная алгебра — Почему исторически мы умножаем матрицы именно так?

Добавить комментарий Отменить ответ