Синус 36: Mathway | Популярные задачи

alexxlab / / Разное

Содержание

Mathway | Популярные задачи

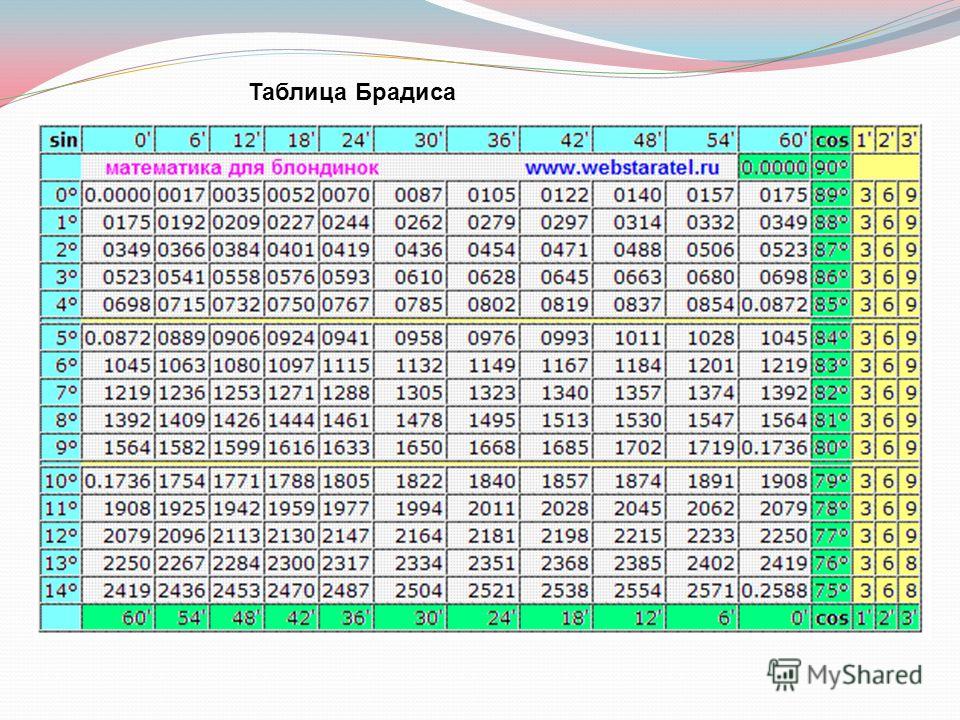
1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значение
cos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значение sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значение csc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значение
sin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99
Найти точное значение		arcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Пещеристый синус — e-Anatomy — IMAIOS

 ПОДПИСАТЬСЯ

ПОДПИСАТЬСЯ

Анатомия человека 2

Анатомия человека 1

  • Анатомия человека 2
  • Анатомия человека 1

Sinus cavernosus

Определение

English

Определение этой анатомической структуры пока отсутствует

Определение на:

English

Я даю согласие на уступку прав, связанных с моим участием в проекте, в соответствии с Правила и условия пользования сайтом.


Я даю согласие на уступку прав, связанных с моим участием в проекте, в соответствии с Правила и условия пользования сайтом.


Галерея

Анатомическая иерархия

Человеческое тело > Systemata integrantia > Сердечно-сосудистая система > Venae systemicae > Venae craniales > Синусы твердой мозговой оболочки > Нижний каменистый синус > Пещеристый синус

Основные структуры:

  • Клиновидно-теменной синус
  • Sinus intercavernosi
  • Plexus venosus basilaris

Системная анатомия > Сердечно-сосудистая система > Вены > Верхняя полая вена > Плечеголовная вена > Внутренняя яремная вена > Синусы твердой мозговой оболочки > Пещеристый синус

Основные структуры:

  • Передний межпещеристый синус
  • Задний межпещеристый синус

Сравнительная анатомия животных

  • Кавернозный синус

Переводы

Заметили ошибку?

Не стесняйтесь предложить поправку, свою версию перевода или решение по улучшению контента.

Сообщить об ошибке

Ваши комментарии помогают нам улучшить содержимое сайта. Не стесняйтесь предлагать поправки. Мы их внимательно рассмотрим.

Пожалуйста, опишите ошибку

Показать больше

Показать меньше

IMAIOS и некоторые третьи лица используют файлы cookie или подобные технологии, в частности для измерения аудитории. Файлы cookie позволяют нам анализировать и сохранять такую информацию, как характеристики вашего устройства и определенные персональные данные (например, IP-адреса, данные о навигации, использовании и местонахождении, уникальные идентификаторы). Эти данные обрабатываются в следующих целях: анализ и улучшение опыта пользователя и/или нашего контента, продуктов и сервисов, измерение и анализ аудитории, взаимодействие с социальными сетями, отображение персонализированного контента, измерение производительности и привлекательности контента. Для получения дополнительной информации ознакомьтесь с нашей политикой конфиденциальности: privacy policy.

Вы можете дать, отозвать или отказаться от согласия на обработку данных в любое время, воспользовавшись нашим инструментом для настройки файлов cookie. Если вы не согласны с использованием данных технологий, это будет расцениваться как отказ от имеющего правомерный интерес хранения любых файлов cookie. Чтобы дать согласие на использование этих технологий, нажмите кнопку «Принять все файлы cookie».

Аналитические файлы сookie

Эти файлы cookiе предназначены для измерения аудитории: статистика посещаемости сайта позволяет улучшить качество его работы.

  • Google Analytics

Sin 36 градусов — Найти значение Sin 36 градусов

LearnPracticeDownload

Значение sin 36 градусов равно 0,5877852. . . . Sin 36 градусов в радианах записывается как sin (36° × π/180°), т. е. sin (π/5) или sin (0,628318…). В этой статье мы обсудим способы нахождения значения sin 36 градусов на примерах.

  • Sin 36°: 0,5877852. . .
  • Sin 36° в дробях: √(10 — 2√5)/4
  • Sin (-36 градусов): -0,5877852. . .
  • Sin 36° в радианах: sin (π/5) или sin (0,6283185 . . .)

Каково значение греха 36 градусов?

Значение sin 36 градусов в десятичной системе равно 0,587785252. . .. Sin 36 градусов также можно выразить с помощью эквивалента заданного угла (36 градусов) в радианах (0,62831 . . .).

Используя преобразование градусов в радианы, мы знаем, что θ в радианах = θ в градусах × (pi/180°)
⇒ 36 градусов = 36° × (π/180°) рад = π/5 или 0,6283. . .
∴ sin 36° = sin(0,6283) = √(10 — 2√5)/4 или 0,5877852. . .

Объяснение:

Для sin 36 градусов угол 36° лежит между 0° и 90° (первый квадрант). Поскольку функция синуса положительна в первом квадранте, значение sin 36° = √(10 — 2√5)/4 или 0,5877852. . .
Поскольку функция синуса является периодической функцией, мы можем представить sin 36° как sin 36 градусов = sin(36° + n × 360°), n ∈ Z.
⇒ sin 36° = sin 396° = sin 756° и так далее.
Примечание: Поскольку синус является нечетной функцией, значение sin(-36°) = -sin(36°).

Методы нахождения значения Sin 36 градусов

Функция синуса положительна в 1-м квадранте. Значение sin 36° равно 0,58778. . .. Мы можем найти значение sin 36 градусов по:

  • Используя тригонометрические функции
  • Использование единичного круга

Sin 36° в терминах тригонометрических функций

Используя формулы тригонометрии, мы можем представить sin 36 градусов как:

  • ± √(1-cos²(36°))
  • ± тангенс 36°/√(1 + тангенс²(36°))
  • ± 1/√(1 + раскладушка²(36°))
  • ± √(сек²(36°) — 1)/сек 36°
  • 1/косек 36°

Примечание. Поскольку 36° лежит в 1-м квадранте, конечное значение sin 36° будет положительным.

Мы можем использовать тригонометрические тождества для представления sin 36° как

  • sin(180° — 36°) = sin 144°
  • -sin(180° + 36°) = -sin 216°
  • cos(90° — 36°) = cos 54°
  • -cos(90° + 36°) = -cos 126°

Sin 36 градусов с помощью единичной окружности

Чтобы найти значение sin 36 градусов с помощью единичной окружности:

  • Поверните ‘r’ против часовой стрелки, чтобы образовать угол 36° с положительной осью x.
  • Грех в 36 градусов равен координате y (0,5878) точки пересечения (0,809, 0,5878) единичной окружности и r.

Следовательно, значение sin 36° = y = 0,5878 (приблизительно)

☛ Также проверьте:

  • sin 10 градусов
  • грех 120 градусов
  • грех 150 градусов
  • грех 73 градуса
  • грех 165 градусов
  • грех 200 градусов

Примеры использования Sin 36 градусов

  1. Пример 1: Найдите значение sin 36°, если cosec 36° равно 1,7013.

    Решение:

    Поскольку sin 36° = 1/csc 36°
    ⇒ sin 36° = 1/1,7013 = 0,5878

  2. Пример 2: Используя значение sin 36°, найдите: (1-cos²(36°)).

    Решение:

    Мы знаем, (1-cos²(36°)) = (sin²(36°)) = 0,3455
    ⇒ (1-cos²(36°)) = 0,3455

  3. Пример 3. Найдите значение 5 sin(36°)/7 cos(54°).

    Решение:

    Используя тригонометрические тождества, мы знаем, что sin(36°) = cos(90° — 36°) = cos 54°.
    ⇒ sin(36°) = cos(54°)
    ⇒ Значение 5 sin(36°)/7 cos(54°) = 5/7

перейти к слайдуперейти к слайдуперейти к слайду

 

Готовы увидеть мир глазами математика?

Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.

Запишитесь на бесплатный пробный урок

Часто задаваемые вопросы о Sin 36 Degrees

Что такое Sin 36 Degrees?

Sin 36 градусов — значение тригонометрической функции синуса для угла, равного 36 градусам. Значение sin 36° равно √(10 — 2√5)/4 или 0,5878 (приблизительно).

Каково значение Sin 36 градусов в терминах Tan 36°?

Мы знаем, что, используя тригонометрические тождества, мы можем записать sin 36° как tan 36°/√(1 + tan²(36°)). Здесь значение тангенса 36° равно 0,726542.

Каково значение Sin 36° в терминах Sec 36°?

Поскольку функцию синуса можно представить с помощью функции секанса, мы можем записать sin 36° как √(sec²(36°) — 1)/sec 36°. Значение sec 36° равно 1,236068.

Как найти значение греха 36 градусов?

Значение sin 36 градусов можно рассчитать, построив угол 36° с осью x и затем найдя координаты соответствующей точки (0,809, 0,5878) на единичной окружности. Значение sin 36° равно координате y (0,5878).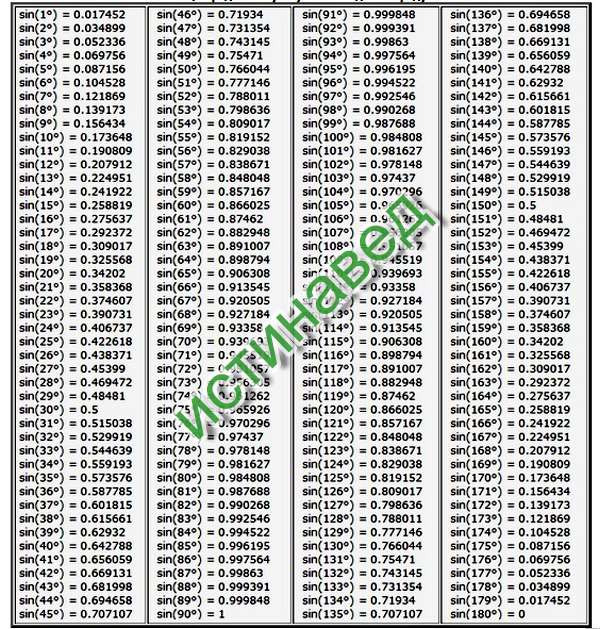 ∴ sin 36° = 0,5878.

Как найти Sin 36° с точки зрения других тригонометрических функций?

Используя формулу тригонометрии, значение sin 36° может быть выражено через другие тригонометрические функции следующим образом:

  • ± √(1-cos²(36°))
  • ± тангенс 36°/√(1 + тангенс²(36°))
  • ± 1/√(1 + раскладушка²(36°))
  • ± √(сек²(36°) — 1)/сек 36°
  • 1/косек 36°

☛ Также проверьте: таблица тригонометрии

 

Скачать БЕСПЛАТНЫЕ учебные материалы

Тригонометрия

Рабочие листы по математике и
наглядная программа

Калькулятор — sin(36) — Solumath1s

Sin, расчет онлайн

Резюме:

Тригонометрическая функция sin для вычисления синуса угла в радианах, градусов или градианов.

sin online

Описание:

Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить синус , косинус и касательная угла через одноименные функции.

Синус тригонометрической функции отметил грех , позволяет вычислить синус угла онлайн , можно использовать разные угловые единицы: градус, градус и радианы, которые по умолчанию являются угловыми единицами.

  1. Расчет синуса

    2. Вычисление синуса угла в радианах

    Калькулятор синуса позволяет через функцию sin вычислить онлайн синус синус угла в радианах, сначала нужно выберите нужную единицу, нажав на кнопку параметров расчетного модуля. После этого можно приступать к расчетам.

    Чтобы вычислить синус онлайн от `pi/6`, введите sin(`pi/6`), после вычисления результат `1/2` возвращается.

    Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.

    Вычислить синус угла в градусах

    Чтобы вычислить синус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

    Чтобы вычислить синус 90, введите sin(90). результат 1 возвращается.

    Вычислить синус угла в градусах

    Чтобы вычислить синус угла в градианах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

    Чтобы вычислить синус 50, введите sin(50), после вычисления, возвращается результат `sqrt(2)/2`.

    Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.

  2. Таблица специальных синусоидальных значений

    3. Синус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот таблица значений общего синуса :

    sin(`2*pi`) `0`
    sin(`pi`) `0`
    sin(`pi/2`) `1`
    sin(`pi/4`) `sqrt(2)/2` 79

    9 902 `pi/3`)

    		 `sqrt(3)/2`
    sin(`pi/6`) `1/2`
    sin(`2*pi/3`) `sqrt(3)/2`
    sin(`3*pi/4`) `sqrt(2)/2`
    sin(`5*pi/6`) ` 1/2`
    sin(`0`) `0`
    sin(`-2*pi`) `0`
    sin(`-pi`) `0`
    sin(``) sin(`pi/2`) 1`
    sin(`-pi/4`) `-sqrt(2)/2`
    sin(`-pi/3`) `-sqrt(3)/2`
    sin(`-pi/6`) `-1/2`
    sin(`-2*pi/3`) `-sqrt(3)/2`72
  3. 72
    		4.  sin(`-3*pi/4`) `-sqrt(2)/2`
    sin(`-5*pi/6`) `-1/2`

  4. Основные свойства

    5. `AA x в RR, k в ZZ`,

  • `sin(-x)= -sin(x)`
  • `sin(x+2*k*pi)=sin(x)`
  • `sin(pi-x)=sin(x) `
  • `sin(pi+x)=-sin(x)`
  • `sin(pi/2-x)=cos(x)`
  • `sin(pi/2+x)=cos(x) `

  • Производная синуса

    • Производная синуса равна cos(x).

  • Первообразная синуса

    • Первообразная синуса равна -cos(x).

  • Свойства функции синуса

    • Функция sine является нечетной функцией, для каждого действительного x `sin(-x)=-sin(x)`. Следствием для кривой, представляющей синусоидальную функцию, является то, что она допускает начало отсчета как точку симметрии.

  • Уравнение с синусом

    • Калькулятор имеет решатель, который позволяет решать уравнение с синусом формы cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `грех(х)=1/2` или же `2*sin(x)=sqrt(2)` с этапами расчета.

    Синтаксис:

    sin(x), где x — мера угла в градусах, радианах или градах.

    Примеры:

    sin(`0`), возвращает 0

    Производный синус:

    можно использовать калькулятор производной, который позволяет вычислить производную функции синуса

    производная sin(x) is производная(`sin(x)`)=`cos(x)`

    Первообразная синуса :

    Калькулятор первообразной позволяет вычислить первообразную функции синуса.

    Первопроизводная sin(x) является первообразной(`sin(x)`)=`-cos(x)`

    Предел синуса :

    Калькулятор предела позволяет вычислить пределы функции синуса.

    Предел sin(x) равен limit(`sin(x)`)

    Обратная функция синуса :

    обратная функция синуса представляет собой функцию арксинуса, отмеченную арксинусом.

    Графический синус :

    Графический калькулятор может отображать синусоидальную функцию в заданном интервале.

    Свойство функции синуса:

    Функция синуса является нечетной функцией.

    Расчет онлайн с синусом

    См. также

    Список связанных калькуляторов:

    • Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
    • Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
    • Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
    • Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
    • Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
    • Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
    • Котангенс: котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
    • Тригонометрическое расширение: expand_trigo.

      No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *