Площадь сечения круга через диаметр – —

Определение величины

Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.

По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.

На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».

С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.

Область применения

Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:

1. Определение объемов емкостей.
2. Решение задач по сопротивлению материалов и электротехнике.
3. Расчет количества материалов при проектировании, строительстве и ремонте.
4. Ведение поливного земледелия.

Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.

Круг имеет ряд характеристик:

• радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
• диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
• длина окружности (C/c/L/l).

Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).

Способы расчета

Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.

Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.

При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.

Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).

Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

1. Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
2. Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
3. Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.

Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».

tokar.guru

Формула площади круга

В геометрии кругом называется некоторое множество всех точек на плоскости, которые удалены от одной точки, называемой его центром, на расстояние, не большее заданного, называемого его радиусом. При этом внешней границей круга является окружность, а в том случае, если длина радиуса равна нулю, круг вырождается в точку.

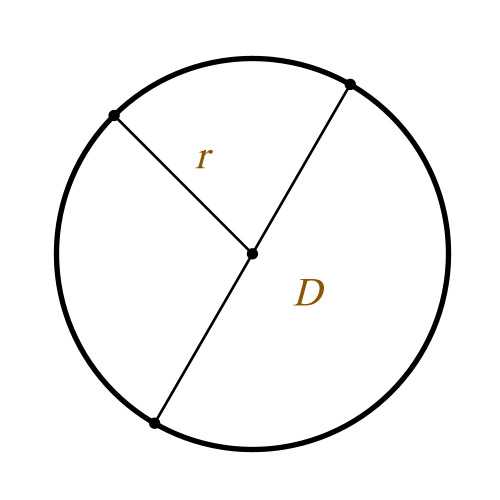
Определение площади круга

 

 

При необходимости площадь круга можно вычислить по формуле:

 

r – радиус круга

D – диаметр круга

S – площадь круга

π – 3.14

Эта геометрическая фигура очень часто встречается как в технике, так и в архитектуре. Конструкторы машин и механизмов разрабатывают различные детали, сечения многих из которых представляют собой именно круг

. К примеру, таковыми являются валы, штоки, тяги, цилиндры, оси, поршни и так далее. При изготовлении этих деталей используются заготовки из различных материалов (металлов, древесины, пластических масс), их сечения также представляют собой именно круг. Само собой разумеется, что разработчикам нередко приходится вычислять площадь круга через диаметр или радиус, используя для этой цели несложные математические формулы, открытые еще в глубокой древности.

Именно тогда круглые элементы стали активно и широко использоваться в архитектуре. Один из самых ярки тому примеров – цирк, представляющий собой разновидность строений, предназначенных для проведения в них различных зрелищных мероприятий. Их арены имеют форму круга, а впервые они стали строиться еще во времена античности. Само слово «circus» в переводе с латинского языка означает «круг». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т. д. Стандартный диаметр цирковой арены составляет

13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить площадь круга через диаметр, то получится, что для цирковой арены эта величина составляет 113,04 квадратных метра.

Архитектурными элементами, которые могут принимать форму круга, являются окна. Конечно, в большинстве случаев они прямоугольные или же квадратные (причем во многом благодаря тому, что это проще как для зодчих, так и для строителей), но в некоторых зданиях можно встретить и круглые окна. Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.

Отнюдь не является редкостью использование круглых элементов для производства мебели, например столов и стульев. Существует даже понятие «

круглый стол», которое подразумевает конструктивную дискуссию, в ходе которой происходит всестороннее обсуждение различных важных проблем и вырабатывается пути их решения. Что касается изготовления самих столешниц, имеющих круглую форму, то для их производства применяются специализированные инструменты и оборудование, при условии участия рабочих с довольно высокой квалификацией.

simple-math.ru

Таблица Брадиса — ПЛОЩАДЬ КРУГА ДИАМЕТРА D

Площадь круга диаметра D  (Таблица Брадиса 7)

Таблица брадиса 7, построенная подобно таблице 6, позволяет находить площадь круга по данному значению его диаметра, а также находить диаметр круга по данному значению его площади

 

Если диаметр круга увеличить (уменьшить) в 10, 100, 1000 и т. д. раз, то площадь круга увеличится (уменьшится) в 102= 100, в 1002=10 000, в 1000а=1 000 000 и т. д. раз. 

d	0	1	2	3	4	5	6	7	8	9	1	2	3	4	5
1,00	0,7854	,7870	,7885	,7901	,7917	,7933	,7949	,7964	,7980	,7996	2	3	5	6	8
1,01	0,8012	,8028	,8044	,8060	,8075	,8091	,8107	,8123	,8139	,8155	2	3	5	6	8
1,02	0,8171	,8187	,8203	,8219	,8235	,8252	,8268	,8284	,8300	,8316	2	3	5	6	8
1,03	0,8332	,8343	,8365	,8381	,8397	,8413	,8430	,8446	,8462	,8479	2	3	5	7	8
1,04	0,8495	,8511	,8528	,8544	,8560	,8577	,8593	,8610	,8626	,8643	2	3	5	7	8
1,05	0,8659	,8676	,8692	,8709	,8725	,8742	,8758	,8775	,8791	,8808	2	3	5	7	8
1,06	0,8825	,8841	,8858	,8875	,8891	,8908	,8925	,8942	,8958	,8975	2	3	5	7	8
1,07	0,8992	,9009	,9026	,9043	,9059	,9076	,9093	,9110	,9127	,9144	2	3	5	7	8
1,08	0,9161	,9178	,9195′	,9212	,9229	,9246	,9263	,9280	,9297	,9314	2	3	5	7	9
1,09	0,9331	,9348	,9366	,9383	,9400	,9417	,9434	,9452	,9469	,9486	2	3	5	7	9
1,10	0,9503	,9521	,9538	,9555	,9573	,9590	,9607	,9625	,9642	,9659	2	3	5	7	9
1,11	0,9677	,9694	,9712	,9729	,9747	,9764	,9782	,9799	,9817	,9834	2	4	5	7	9
1,12	0,9852	,9870	,9887	,9905	,9923	,9940	,9958	,9976	,9993	1,0011	2	4	5	7	9
1,1				1,003	1,021	1,039	1,057	1,075	1,094	1,112	2	4	5	7	9
1,2	1,131	1,150	1,169	1,188	1,208	1,227	1,247	1,267	1,287	1,307	2	4	6	8	10
1,3	1,327	1,348	1,368	1,389	1,410	1 431	1,453	1,474	1,496	1,517	2	4	6	8	11
1,4	1,539	1,561	1,584	1,606	1,629	1,651	1,674	1,697	1,720	1,744	2	5	7	9	11
1,5	1,767	1,791	1,815	1,839	1,863	1,887	1,911	1,936	1,961	1,986	2	5	7	10	12
1,6	2.011	2,036	2.061	2,087	2,112	2,138	2,164	2,190	2,217	2,243	3	5	8	10	13
1,7	2,270	2,297	2,324	2,351	2,378	2,405	2,433	2,461	2,488	2,516	3	5	8	11	14
1,8	2,545	2,573	2,602	2,630	2,659	2,688	2,717	2,746	2,776	2,806	3	6	9	12	15
1,9	2,835	2,865	3,895	2,926	2,956	2,986	3,017	3,048	3,079	3,110	3	6	9	12	15
2,0	3,142	3,173	3,205	3,237	3,269	3,301	3,333	3,365	3,398	3,431	3	6	10	13	16
2,1	3.464	3,497	3,530	3,563	3,597	3,631	3.664	3,698	3,733	3,767	3	7	10	14	17
2.2	3,801	3,836	3,871	3,906	3,941	3,976	4,011	4,047	4,083	4,119	4	7	11	14	18
2,3	4,155	4,191	4,227	4.264	4,301	4,337	4,374	4,412	4,449	4,486	4	7	11	15	18
2,4	4,524	4,562	4,600	4,638	4,676	4,714	4,753	4,792	4,831	4,870	4	8	12	15	19
2,5	4,909	4,948	4,988	5,027	5,067	5,107	5,147	5,187	5,228	5,269	4	8	12	16	20
2,6	5,309	5,350	5,391	5,433	5,474	5,515	5,557	5,599	5,641	5,683	4	8	12	17	21
2,7	5,726	5,768	5,811	5,853	5,896	5,940	5,983	6,026	6,070	6,114	4	9	13	17	22
2,8	6,158	6,202	6,246	6,290	6,335	6,379	6,424	6,469	6,514	6,560	4	9	13	18	22
2,9	6,605	6,651	6,697	6,743	6,789	6,835	6,881	6,928	6,975	7,022	5	9	14	19	23
d	0	1	2	3	4	5	6	7	8	9	1	2	3	4	5

 

Если диаметр круга увеличить (уменьшить) в 10, 100, 1000 и т. д. раз, то площадь круга увеличится (уменьшится) в 102= 100, в 1002=10 000, в 1000а=1 000 000 и т. д. раз.

d	0	1	2	3	4	5	6	7	8	9	1	2	3	4	5
3,0	7,069	7,116	7,163	7,211	7,258	7,306	7,354	7,402	7,451	7,499	5	10	14	19	24
3,1	7,548	7,596	7,645	7,694	7,744	7,793	7,843	7,892	7,942	7,992	5	10	15	20	25
3,2	8,042	8,093	8,143	8,194	8,245	8,296	8,347	8,398	8,450	8,501	5	10	15	20	26
3,3	8,553	8,605	8,657	8,709	8,762	8,814	8,867	8,920	8,973	9,026	5	10	16	21	26
3,4	9,079	9,133	9,186	9,240	9,294	9,348	9,402	9,457	9,511	9,566	5	11	16	22	27
3,5	9,621	9,676	9,731	9,787	9,842	9,898	9,954				6	11	17	22	28
3,5								10,01	10,07	10,12	1	1	2	2	3
3,6	10,18	10,24	10,29	10,35	10,41	10,46	10,52	10,58	10,64	10,69	1	1	2	2	3
3,7	10,75	10,81	10,87	10,93	10,99	11,04	11,10	11,16	11,22	11,28	1	1	2	2	3
3,8	11,34	11,40	11,46	11,52	11,58	11,64	11,70	11,76	11,82	11,88	1	1	2	2	3
3,9	11,95	12,01	12,07	12,13	12,19	12,25	12,32	Й-,38	12,44	12,50	1	1	2	2	3
4,0	12,57	12,63	12,69	12,76	12,82	12,88	12,95	13,01	13,07	13,14	1	1	2	3	3
4,1	13,20	13,27	13,33	13,40	13,46	13,53	13,59	13,66	13,72	13,79	1	1	2	3	3
4,2	13,85	13,92	13,99	14,05	14,12	14,19	14,25	14,32	14,39	14,45	1	1	2	3	3
4,3	14,52	14,59	14,66	14,73	14,79	14,86	14,93	15,00	15,07	15,14	1	1	2	3	3
4,4	15,21	15,27	15,34	15,41	15,48	15,55	15,62	15,69	15,76	15,83	1	1	2	3	3
4,5	15,90	15,98	16,05	16,12	16,19	16,26	16,33	16,40	16,47	16,55	1	1	2	3	4
4,6	16,62	16,69	16,76	16,84	16,91	16,98	17,06	17,13	17,20	17,28	1	1	2	3	4
4,7	17,35	17,42	17,50	17,57	17,65	17,72	17,80	17,87	17,95	18,02	1	1	2	3	4
4,8	18,10	18,17	18,25	18,32	18,40	18,47	18,55	18,63	18,70	18,78	1	2	2	3	4
4,9	18,86	18,93	19,01	19,09	19,17	19,24	19,32	19,40	19,48	19,56	1	2	2	3	4
5,0	19,63	19,71	19,79	19,87	19,95	20,03	20,11	20,19	20,27	20,35	1	2	2	3	4
5,1	20,43	20,51	20,59	20,67	20,75	20,83	20,91	20,99	21,07	21,16	1	2	2	3	4
5,2	21,24′	21,32	21,40	21,48	21,57	21,65	21,73	21,81	21,90	21,98	1	2	2	3	4
5,3	22,06	22,15	22,23	22,31	22,40	22,48	22,56	22,65	22,73	22,82	1	2	3	3	4
5,4	22,90	22,99	23,07	23,16	23,24	23,33	23,41	23,50	23,59	23,67	1	2	3	3	4
5,5	23,76	23,84	23,93	24,02	24,11	24,19	24,28	24,37	24,45	24,54	1	2	3	3	4
5,6	24,63	24,72	24,81	24,89	24,98	25,07	25,16	25,25	25,34	25,43	1	2	3	4	4
5,7	25,52	25,61	25,70	25,79	25,88	25,97	26,06	26,15	26,24	26,33	1	2	3	4	5
5,8	26,42	26,51	26,60	26,69	26,79	26,88	26,97	27,06	27,15	27,25	1	2	3	4	5
5,9	27,34	27,43	27,53	27,62	27,71	27,81	27,90	27,99	28,09	28,18	1	2	3	4	5
6,0	28,27	28,37	28,46	28,56	28,65	28,75	28,84	28,94	29,03	29,13	1	2	3	4	5
6,1	29,22	29,32	29,42	29,51	29,61	29,71	29,80	29,90	30,00	30,09	1	2	3	4	5
6,2	30,19	30,29	30,39	30,48	30,58	30,68	30,78	30,88	30,97	31,07	1	2	3	4	5
6,3	31,17	31,27	31,37	31,47	31,57	31,67	31,77	31,87	31,97	32,07	1	2	3	4	5
6,4	32,17	32,27	32,37	32,47	32,57	32,67	32,78	32,88	32,98	33,08	1	2	3	4	5
d	0	1	2	3	4	5	6	7	8	9	1	2	3	4	5

Если диаметр круга увеличить (уменьшить) в 10, 100, 1000 и т. д. раз, то площадь круга увеличится (уменьшится) в 102= 100, в 1002=10 000, в 1000а=1 000 000 и т. д. раз.

d	0	1	2	3	4	5	6	7	8	9	1	2	5	4	5
6,5	33,18	33,29	33,39	33,49	33,59	33,70	33,80	33,90	34,00	34,11	1	2	3	4	5
6,6	34,21	34,32	34,42	34,52	34,63	34,73	34,84	34,94	35,05	35,15	1	2	3	4	5
6,7	35,26	35,36	35,47	35,57	35,68	35,78	35,89	36,00	36,10	36,21	1	2	3	4	5
6,8	36,32	36,42	36,53	36,64	36,75	36,85	36,96	37,07	37,18	37,28	1	2	3	4	5
6,9	37,39	37,50	37,61	37,72	37,83	37,94	38,05	38,16	38,26	38,37	1	2	3	4	5
7,0	38,48	38,59	38,70	38,82	38,93	39,04	39,15	39,26	39,37	39,48	1	2	3	4	6
7,1	39,59	39,70	39,82	39,93	40,04	40,15	40,26	40,38	40,49	40,60	1	2	3	4	6
7,2	40,72	40,83	40,94	41,C6	41,17	41,28	41,40	41,51	41,62	41,74	1	2	3	5	6
7,3	41,85	41,97	42,08	42,20	42,31	42.43	42,54	42,66	42,78	42,89	1	2	3	5	6
7,4	43,01	43,12	43,24	43,36	43,47	43,59	43,71	43,83	43,94	44,06	1	2	4	5	6
7,5	44,18	44,30	44,41	44,53	44,65	44,77	44,89	45,01	45,13	45,25	1	2	4	5	6
7,6	45,36	45,48	45,60	45,72	45,84	45,96	46,08	46,20	46,32	46,45	1	2	4	5	6
7,7	46,57	46,69	46,81	46,93	47,05	47,17	47,29	47,42	47,54	47,66	1	2	4	5	6
7,8	47,78	47,91	48,03	48,15	48,27	48,40	48,52	48,65	48,77	48,89	1	2	4	5	6
7,9	49,02	49,14	49,27	49,39	49,51	49,64	49,76	49,89	50,01	50,14	1	2	4	5	6
8,0	50,27	50,39	50,52	50,64	50,77	50,90	51,02	51,15	51,28	51,40	1	3	4	5	6
8,1	51,53	51,66	51,78	51,91	52,04	52,17	52,30	52,42	52,55	52,68	1	3	4	5	6
8,2	52,81	52,94	53,07	53,20	53,33	53,46	53,59	53,72	53,85	53,98	1	3	4	5	6
8,3	54,11	54,24	54,37	54,50	54,63	54.76	54,89	55,02	55,15	55,29	1	3	4	5	7
8,4	55,42	55,55	55,68	55,81	55,95	56,08	56,21	56,35	56,48	56,61	1	3	4	5	7
8,5	56,75	56,88	57,01	57,15	57,28	57,41	57,55	57,68	57,82	57,95	1	3	4	5	7
8,6	58,09	58,22	58,36	58,49	58,63	58,77	58,90	59,04	59,17	59,31	1	3	4	5	7
8,7	59,45	59,58	59,72	59,86	59,99	60,13	60,27	60,41	60,55	60,68	1	3	4	5	7
8,8	60,82	60,96	61,10	61,24	61,38	61.51	61,65	61,79	61,93	62,07	1	3	,4	6	7
8,9	62,21	62,35	62,49	62,63	62.77	62,91	63,05	63,19	63,33	63,48	1	3	4	6	7
9,0	63,62	63,76	63,90	64,04	64,18	64,33	64,47	64,61	64,75	64,90	1	3	4	6	7
9,1	65,04	65,18	65,33	65,47	65,61	65,76	65,90	66,04	66,19	66,33	1	3	4	6	7
9,2	66,48	66,62	66,77	66,91	67,06	67,20	67,35	67,49	67,64	67,78	1	3	4	6	7
9,3	67,93	68,08	68,22	68,37	68,51	68,66	68.81	68,96	69,10	69,25	1	3	4	6	7
9,4	69,40	69,55	69,69	69,84	69,99	70,14	70,29	70,44	70,58	70,73	1	3	4	6	7
9,5	70,88	71,03	71,18	71,33	71,48	71,63	71,78	71,93	72,03	72,23	1	3	5	6	7
9,6	72,38	72,53	72,68	72,84	72,99	73,14	73,29	73,44	73,59	73,75	2	3	5	б	8
9,7	73,90	74,05	74,20	74,36	74,51	74.66	74,82	74,97	75,12	75,28	2	3	5	6	8
9,8	75,43	75,58	75,74	75,89	76,05	76,20	76,36	76,51	76,67	76,82	2	3	5	6	8
9,9	76,98	77,13	77,29	77,44	77,60	77,76	77,91	78,07	78,23	78,38	2	3	5	6	8
10,0	78,54										2	3	5	6	8
d	0	1	2	3	4	5	6	7	8	9	1	2	3	4	3

Если диаметр круга увеличить (уменьшить) в 10, 100, 1000 и т. д. раз, то площадь круга увеличится (уменьшится) в 102= 100, в 1002=10 000, в 1000а=1 000 000 и т. д. раз.

_______________

Источник информации: Брадис В.М. Четырехзначные математические таблицы: Для средней школы. / В.М. Брадис . — 57-е изд., — М.: Просвещение, 1990.

infotables.ru

Сопромат.in.ua: Площадь сечения некоторых фигур

Приведены формулы вычисления площади некоторых фигур, которые вы можете вычислить непосредственно на этой странице.

Фигура	Формула вычисления площади	Примечания	Вычислить площадь
Квадрат	$$a^2$$	a длина стороны квадрата.
Равносторонний треугольник	$$\frac{\sqrt{3}}{4}a^2$$	a – длина одной из сторон
Треугольник	$$\sqrt{s(s-a)(s-b)(s-c)}$$	где s = 1/2 (a + b + c), a,b,c – длины сторон треугольника
	$$\frac{1}{2}b\cdot h_b$$	где b – длина стороны треугольника hb – высота, проведённая на сторону b
	$$\frac{1}{2} a b \sin \gamma $$	где a и b – длина сторон треугольника [math]\gamma[/math] – угол между ними в °
Правильный шестиугольник	$$\frac{3\sqrt{3}}{2}s^2$$	s – сторона шестиугольника
Правильный восьмиугольник	$$2\left(1+\sqrt{2}\right)s^2$$	s – сторона восьмиугольника R – радиус описанной окружности $$s={R\over\sqrt{1+{\sqrt{2}/2}}} ≈ {R\over 1.3066}$$
Прямоугольник	$$a\cdot b$$	a и b стороны прямоугольника (длина и ширина)
Параллелограмм	$$b\cdot h$$	b – длина одной из основ параллелограмма h – высота параллелограмма
Трапеция	$$\frac{a+b}{2}\cdot h $$	a и b длины параллельных сторон, а h – высота (расстояние между параллельными сторонами)
Правильный многоугольник (это многоугольник, у которого все углы и все стороны равны между собой)	$$\frac{ns^2} {4 \cdot \tan(\pi/n)} $$	s -длина стороны, а n число сторон.
Круг	$$\pi r^2 \text{   или  } \frac{\pi d^2}{4} $$	r – радиус, а d – диаметр
Эллипс	$$\pi ab $$	a и b – большая и малая полуоси эллипса, соответственно.
Сектор (часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга)	$$\frac{1}{2} r^2 \theta $$	r и [math]\theta[/math] – радиус и угол (в радианах), соответственно
	$$\frac{1}{2} r^2 \frac{\theta \pi}{180} $$	r и [math]\theta[/math] – радиус и угол (в ° ), соответственно

sopromat.in.ua

No related posts.