Площадь трапеции правильной: Все формулы площади трапеции и калькулятор онлайн

Содержание

Площадь равнобедренной трапеции | Треугольники

Площадь равнобедренной трапеции можно найти с помощью любой из формул для нахождения площади трапеции в общем случае. Благодаря свойствам равнобедренной трапеции некоторые из этих формул могут быть упрощены.

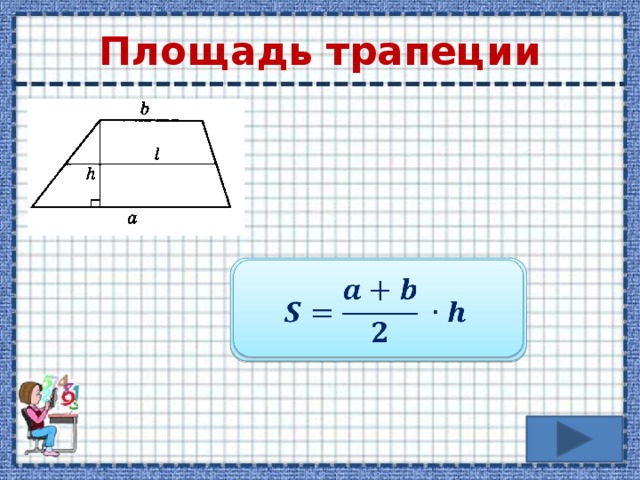
I Площадь трапеции равна произведению полусуммы оснований на высоту.

Как и для случая произвольной трапеции, площадь равнобедренной трапеции ABCD, AD∥BC, AB=CD,

Если AD=a, BC=b, BF=h, то формула площади трапеции принимает вид

II. Площадь трапеции равна произведению её средней линии на высоту.

Это верно, в частности, для равнобедренной трапеции.

Если MN — средняя линия трапеции ABCD, BF — её высота, то площадь трапеции равна

Если MN=m, BF=h, то

III. Площадь трапеции равна половине произведения её диагоналей на синус угла между ними.

Поскольку диагонали равнобедренной трапеции равны, площадь равнобедренной трапеции равна половине произведения квадрата её диагонали на синус угла между диагоналями.

Для равнобедренной трапеции ABCD

AD∥BC, AB=CD, AC∩BD=O,

Если AC=d, ∠COD=φ

VI. Площадь равнобедренной трапеции с перпендикулярными диагоналями.

1) Если диагонали равнобедренной трапеции перпендикулярны, так как sin 90º=1, предыдущая формула принимает вид:

2) Площадь равнобедренной трапеции, диагонали которой перпендикулярна, равна квадрату её высоты.

В равнобедренной трапеции ABCD

AD∥BC, AB=CD, AC∩BD=O, проведем высоту FK через точку пересечения диагоналей.

Прямоугольные треугольники AOD и BOC — равнобедренные (с основаниями AD и BC). Поэтому их высоты OK и OF являются также медианами. Следовательно, по свойству медианы, проведенной к гипотенузе

Таким образом, формула для нахождения площади равнобедренной трапеции с перпендикулярными диагоналями:

V. Площадь трапеции равна произведению её полупериметра на радиус вписанной окружности.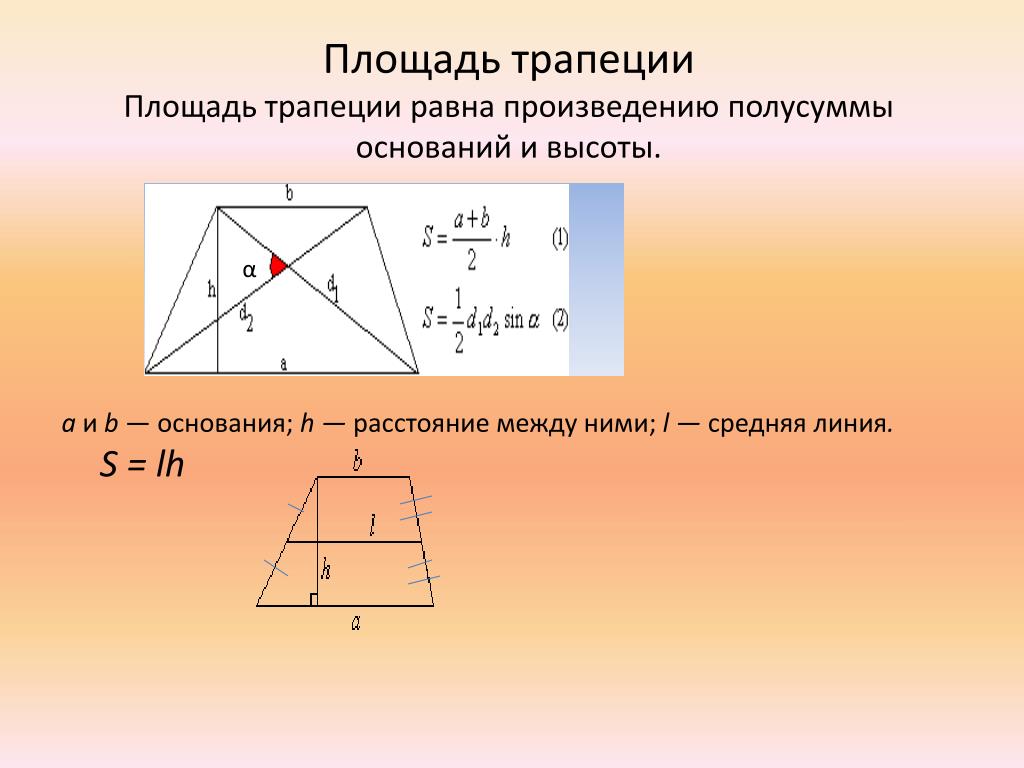

Так как в трапецию ABCD можно вписать окружность, то

AD+BC=AB+CD, то есть p=AD+BC или p=AB+CD=2AB.

Таким образом, площадь равнобедренной трапеции, в которую можно вписать окружность, равна произведению суммы оснований на радиус окружности.

Если обозначить основания трапеции AD=a, BC=b, то

Также площадь равнобедренной трапеции, в которую можно вписать окружность, равна удвоенному произведению боковой стороны на радиус окружности.

Если обозначить боковые стороны AB=CD=c, то формула площади трапеции в этом случае

Так как высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями, то площадь равнобедренной трапеции, в которую можно вписать окружность, равна произведению среднего арифметического и среднего геометрического её оснований:

Все формулы площади равнобедренной трапеции

1. Формула площади равнобедренной трапеции через стороны и угол

а — нижнее основание

b — верхнее основание

с — равные боковые стороны

α — угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S ):

Формула площади равнобедренной трапеции через стороны и угол, (S ):

2. Формулы площади равнобедренной трапеции если в нее вписана окружность

R — радиус вписанной окружности

D — диаметр вписанной окружности

O — центр вписанной окружности

H — высота трапеции

α, β — углы трапеции

а — нижнее основание

b — верхнее основание

Формула площади равнобедренной трапеции через радиус вписанной окружности, (S ):

СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

R — радиус вписанной окружности

m — средняя линия

O — центр вписанной окружности

c — боковые стороны

а — нижнее основание

b — верхнее основание

Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию (S

СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции

α, β — углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

c — боковая сторона

m — средняя линия трапеции

α, β — углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (

S ):

5. Формула площади равнобедренной трапеции через основания и высоту

a — нижнее основание

b — верхнее основание

h — высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S ):

Подробности: Автор: Administrator; Опубликовано: 14 августа 2013; Обновлено: 13 августа 2021

Калькулятор площади правой трапеции

Автор: Gabriela Diaz

Отзыв от Luciano Mino

Последнее обновление: 02 февраля 2023 г.

Содержание:

Что такое правильная трапеция?
Как найти площадь правильной трапеции
Как использовать калькулятор площади правильной трапеции
Другие калькуляторы площади трапеции
Часто задаваемые вопросы

Добро пожаловать в калькулятор площади правильной трапеции , 900 22, где вы сможете вычислить площадь любой правильной трапеции в мгновение ока! 😉
Здесь мы также узнаем:

Что такое прямая трапеция ; и
Как самостоятельно найти площадь правильной трапеции , даже если сначала не известна ее высота.

Начнем?

Что такое прямая трапеция?

Прямоугольная трапеция является частным случаем трапеции, четырехсторонней геометрии, по крайней мере, с одной парой противоположных сторон, параллельных друг другу. Эти параллельные стороны, также известные как основания, обозначены на изображении ниже как aaa и bbb.

В конкретном случае прямоугольной трапеции одна из двух оставшихся сторон, ccc на рисунке , перпендикулярна параллельным сторонам aaa и bbb, образуя между ними углы 90° (прямые углы).

Как найти площадь прямой трапеции

Чтобы найти площадь правильной трапеции , используйте формулу:

A = (a + b) x h/2 .
Где:
А – Площадь трапеции;
а и б – Основания нижние и верхние; и
h – Высота.
Это означает, что если вы знаете все эти измерения, вы сможете вычислить площадь вашей правой трапеции напрямую.
Но что, если вы не знаете высоту h ? Сможете ли вы еще вычислить площадь? Вот тут и приходит на помощь старая добрая тригонометрия!
Глядя на изображение, мы видим прямоугольный треугольник, формирующийся из высоты h , разность оснований (а - б) и стороны d .
Отсюда, если знаете:
две стороны (a - b) и d ; или
Одна сторона и один угол прямоугольного треугольника, все готово!
Если вы знаете две стороны , вычисление h вращается вокруг теоремы Пифагора как:
h = √(d² - (a - b)²)
С другой стороны, если у вас есть одна сторона и один угол , вы можете получить значение h с помощью функции арксинуса (инверсия синуса) как:
h = arcsin(δ ) * д
или…
h = arcsin(γ - π/2) * d
💡 Вы можете узнать больше о тригонометрической функции арксинуса с помощью нашего калькулятора арксинуса. Чтобы узнать о других тригонометрических функциях, воспользуйтесь нашим калькулятором тригонометрии!
Как использовать калькулятор площади правой трапеции
Чтобы использовать калькулятор площади правой трапеции:
Введите основания a и b . Например, предположим, что a = 10 и b = 6 .
Введите значение высоты h . В нашем примере предположим, что ч = 4 .
Калькулятор отобразит результат для площади в последней строке. Для нашего расчета мы получаем А = 32 . Вот и все! 😀
💡 Не знаете значение высоты h ? Нажмите кнопку Расширенный режим , чтобы получить значение площади путем ввода углов и наклонной стороны.
Другие калькуляторы трапеций
Теперь, когда вы научились вычислять площадь правильной трапеции, почему бы не прочитать о площади неправильной трапеции или не расширить свои знания о трапециях с помощью нашего калькулятора трапеций.
Чтобы узнать о конкретных темах, касающихся трапеций, мы рекомендуем другие наши инструменты:

Калькулятор трапеций
Калькулятор площади трапеции
Калькулятор периметра трапеции
Калькулятор стороны трапеции
Калькулятор угла трапеции
Калькулятор высоты трапеции
Средняя часть калькулятора трапеций
Калькулятор равнобедренной трапеции
Калькулятор площади равнобедренной трапеции
Калькулятор правой трапеции
Калькулятор площади неправильной трапеции
Часто задаваемые вопросы
Может ли трапеция иметь ровно один прямой угол?
Нет, трапеция не может иметь только один прямой угол.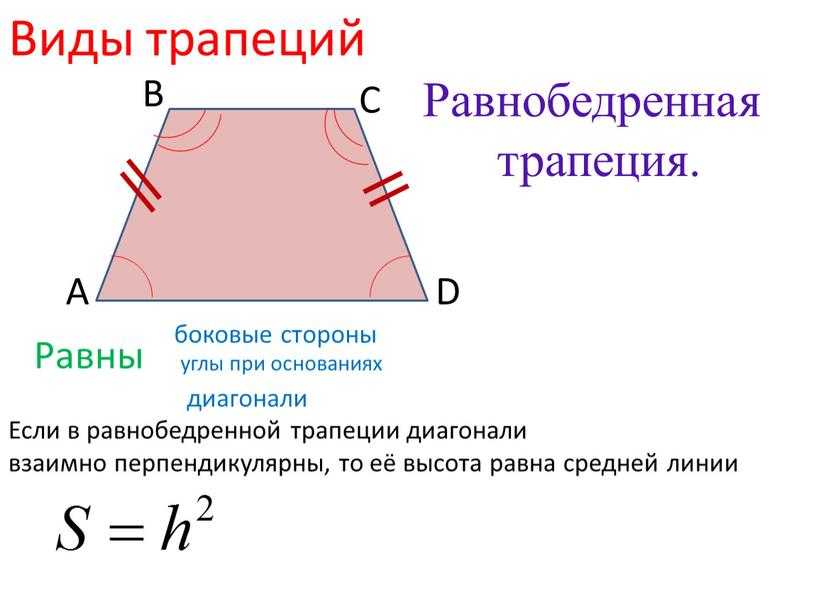 Минимальное количество прямых углов трапеции равно двум. Эта конфигурация известна как правильная трапеция. Следующее количество прямых углов равно четырем; это случай прямоугольника.
Как найти высоту прямой трапеции?
Чтобы найти высоту прямой трапеции вы можете встретить один из следующих случаев:
Если известны основания a и b , а также наклонная сторона d , используйте формулу Пифа теорема Гора: h = √(d² - (a - b)²) .
Зная наклонную сторону d и острый угол δ , используйте: h = arcsin(δ) x d .
Если знать наклонную сторону d и тупой угол γ используйте: h = arcsin(γ - π/2) x d .
Габриэла Диаз
a (основание)
b (основание)
h (высота)
Площадь (A)
Проверьте 23 похожих калькулятора 2D-геометрии 📏
ПлощадьПлощадь прямоугольникаПлощадь полумесяца… 20 подробнее
Площадь трапеции — формула, примеры, определение, вывод
Площадь трапеции — это количество единичных квадратов, которые могут быть вписаны в нее, и измеряется в квадратных единицах (например, см ² , м ² , в ² и т. д.). Например, если внутрь трапеции можно поместить 15 единичных квадратов длиной 1 см каждый, то ее площадь будет равна 15 см ² . Трапеция — это тип четырехугольника с одной парой параллельных сторон (которые известны как основания). Это означает, что другая пара сторон может быть непараллельной (известной как ноги). Не всегда возможно нарисовать единичные квадраты и измерить площадь трапеции. Итак, давайте узнаем о формуле для нахождения площади трапеции на этой странице.

1. Какова площадь трапеции?
2. Площадь трапеции Формула
3. Площадь трапеции без высоты
4. Как вывести формулу площади трапеции?
5. Калькулятор площади трапеции
6. Часто задаваемые вопросы по площади трапеции
Какова площадь трапеции?
Площадь трапеции равна площади, занимаемой ее сторонами.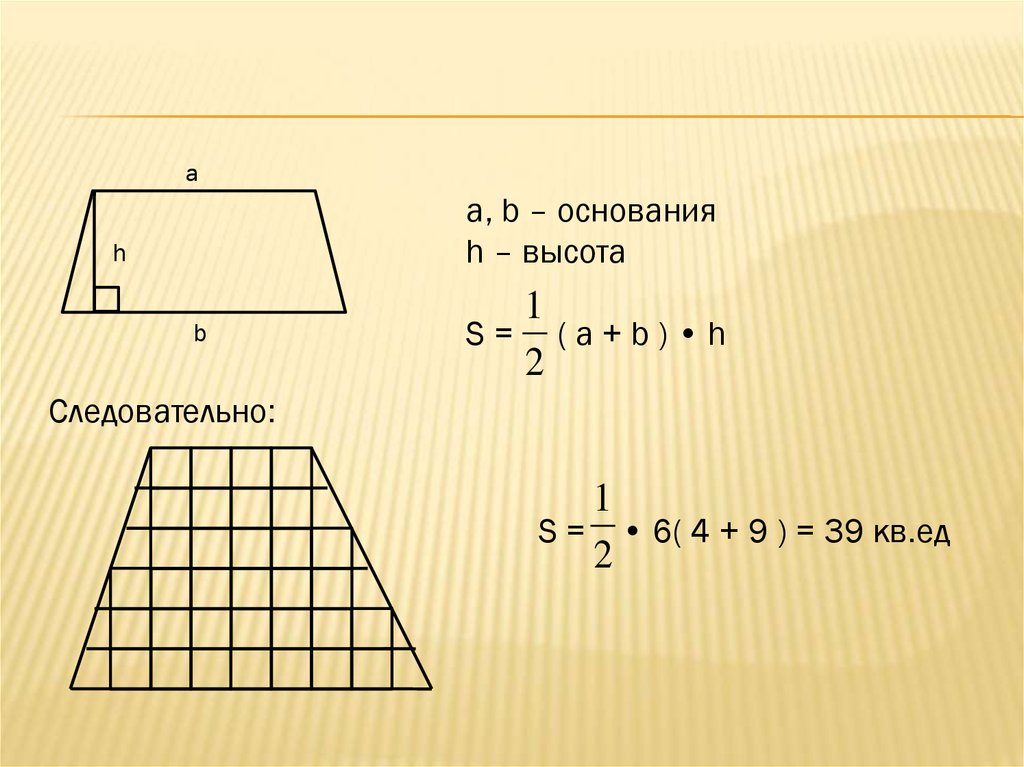 Здесь следует отметить интересный момент: если мы знаем длины всех сторон, мы можем просто разделить трапецию на более мелкие многоугольники, такие как треугольники и прямоугольники, найти их площади и сложить их, чтобы получить площадь трапеции. Однако есть прямая формула, которая используется для нахождения площади трапеции, если известны определенные размеры.

Формула площади трапеции
Площадь трапеции можно вычислить, если известны длины ее параллельных сторон и расстояние (высота) между ними. Формула площади трапеции выражается следующим образом:
A = ½ (a + b) h
, где (A) — площадь трапеции, «a» и «b» — основания. (параллельные стороны), а «h» — высота (перпендикулярное расстояние между a и b)

Пример:
Найдите площадь трапеции, параллельные стороны которой равны 32 см и 12 см соответственно, а высота равна 5 см.
Решение:
Основания даны как, a = 32 см; б = 12 см; высота h = 5 см.
Площадь трапеции = A = ½ (a + b) h
A = ½ (32 + 12) × (5) = ½ (44) × (5) = 110 см ² .
Площадь трапеции без высоты
Зная все стороны трапеции и не зная высоту, можно найти площадь трапеции. В этом случае нам сначала нужно вычислить высоту трапеции. Давайте разберемся в этом с помощью примера.
Пример: Найдите площадь трапеции, у которой основания (параллельные стороны) равны 6 и 14 единицам соответственно, а непараллельные стороны (катеты) равны 5 единицам каждая.
Решение: Вычислим площадь трапеции, используя следующие шаги.
Шаг 1: Мы знаем, что площадь трапеции = ½ (a + b) h; где h — высота трапеции, которая в данном случае не приводится; a = 6 единиц, b = 14 единиц, непараллельные стороны (ножки) = по 5 единиц.
Шаг 2: Итак, если мы найдем высоту трапеции, мы сможем вычислить площадь. Если мы начертим высоту трапеции с обеих сторон, мы увидим, что трапеция разбита на прямоугольник ABQP и 2 прямоугольных треугольника, ADP и BQC.
Шаг 3: Поскольку прямоугольник имеет равные противоположные стороны, это означает, что AP = BQ, и известно, что стороны AD = BC = 5 единиц. Итак, высоты AP и BQ можно вычислить по теореме Пифагора.
Шаг 4: Теперь найдем длину DP и QC. Поскольку ABQP — прямоугольник, AB = PQ и DC = 14 единиц. Это означает, что PQ = 6 единиц, а оставшуюся общую длину DP + QC можно рассчитать следующим образом. DC — PQ = 14 — 6 = 8. Итак, 8 ÷ 2 = 4 единицы. Следовательно, DP = QC = 4 ед.
Шаг 5: Теперь можно вычислить высоту трапеции по теореме Пифагора. Взяв прямоугольный треугольник ADP, мы знаем, что AD = 5 единиц, DP = 4 единицы, поэтому AP = √(AD ² — DP ² ) = √(5 ² — 4 ² ) = √(25 — 16) = √9 = 3 единицы. Поскольку ABQP — прямоугольник, у которого противоположные стороны равны, AP = BQ = 3 единицы.
Шаг 6: Теперь, когда мы знаем все размеры трапеции, включая высоту, мы можем вычислить ее площадь по формуле: площадь трапеции = ½ (a + b) h; где h = 3 ед. , a = 6 ед., b = 14 ед. После подстановки значений в формулу получаем, площадь трапеции = ½ (a + b) h = ½ (6 + 14) × 3 = ½ × 20 × 3 = 30 ед. ² .
Как вывести формулу площади трапеции?
Мы можем доказать формулу площади трапеции, используя здесь треугольник. Взяв трапецию с основаниями «а» и «b» и высотой «h», докажем формулу.
Шаг 1: Разделите одну из ножек на две равные части и вырежьте треугольную часть трапеции, как показано на рисунке.
Шаг 3: Прикрепите его снизу, как показано, так, чтобы получился большой треугольник.
Шаг 4: Таким образом, трапеция преобразуется в треугольник. Даже после того, как мы присоединим его таким образом, мы знаем, что площади трапеции и нового большого треугольника остаются прежними. Мы также можем видеть, что основание нового большого треугольника равно (a + b), а высота треугольника равна h.
Шаг 5: Итак, можно сказать, что площадь трапеции = площади треугольника
Шаг 6: Это можно записать как площадь трапеции = ½ × основание × высота = ½ (a + b) h
Итак, мы доказали формулу нахождения площади трапеции.
Калькулятор площади трапеции
Площадь трапеции — это количество единичных квадратов, которые могут в нее поместиться. Калькулятор площади трапеции — это онлайн-инструмент, который помогает найти площадь трапеции. Если доступны определенные параметры, такие как значение основания или высоты, мы можем напрямую ввести входные данные и рассчитать площадь. Попробуйте калькулятор площади трапеции Куэмата и рассчитайте площадь трапеции за несколько секунд. Для большей практики проверьте площадь листа трапеции и решите задачи с помощью калькулятора.
☛ Статьи по теме
Площадь равностороннего треугольника
Площадь квадрата
Площадь параллелограмма
Площадь прямоугольника
Площадь ромба
Район Пентагона
Площадь круга
Cuemath — одна из ведущих мировых платформ для обучения математике, предлагающая онлайн-уроки по математике в режиме реального времени один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.

Площадь трапеции Примеры
Пример 1: Если одно из оснований трапеции равно 8 единицам, высота 12 единиц, а площадь 108 квадратных единиц, найдите длину другого основания.
Решение:
Одно из оснований равно «а» = 8 единиц.
Пусть другое основание будет ‘b’.
Площадь трапеции A = 108 квадратных единиц.
Его высота ‘h’ = 12 единиц.
Подставить все эти значения в область формулы трапеции,
A = ½ (a + b) h
108 = ½ (8 + b) × (12)
108 = 6 (8 + b)
Разделение обе стороны на 6,
18 = 8 + b
b = 10
Ответ: Длина другого основания данной трапеции = 10 единиц.
Пример 2: Найдите площадь равнобедренной трапеции, у которой длина каждого катета равна 8 единицам, а основания равны 13 единицам и 17 единицам соответственно.
Решение:
Базы a = 13 единиц и b = 17 единиц. Предположим, что его высота равна h.
Данную трапецию можно разделить на два конгруэнтных прямоугольных треугольника и прямоугольник следующим образом:
Из рисунка выше
x + x + 13 = 17
2x + 13 = 17
900 02 2x = 4
x = 2
Используя теорему Пифагора,
x ² + h ² = 8 ²
2 ² + h ² = 64
4 + h ² = 64
h ² = 60
h = √60 = √4 × √15 = 2√15
Площадь
A = ½ (a + b) h
A = ½ (13 + 17) × (2√15) = 30√15 = 116,18 квадратных единиц
Ответ: Площадь данной трапеции трапеция = 116,18 квадратных единиц.
Пример 3: Найдите площадь трапеции, основания которой равны 7 единицам и 9единиц, а высота равна 5 единицам.
Решение: Площадь трапеции = ½ (a + b) h; где a = 7, b = 9, h = 5.
Подставив эти значения в формулу, получим:
A = ½ (a + b) h
A = ½ (7 + 9) × 5
A = ½ × 16 × 5 = 40 единиц ²
Следовательно, площадь трапеции равна 40 квадратных единиц.
перейти к слайдуперейти к слайдуперейти к слайду
Развивайте логическое мышление и укрепляйте его уверенность!
Благодаря гибкому учебному плану Куэмат выходит за рамки традиционных методов обучения. Мы делаем математику увлекательной. Проверьте, как!
Записаться на бесплатный пробный урок
Практические вопросы по площади трапеции

перейти к слайдуперейти к слайду
Часто задаваемые вопросы по площади трапеции
Что такое площадь трапеции в математике?
Площадь трапеции — это количество единичных квадратов, которые могут в нее поместиться. Мы знаем, что трапеция — это четырехугольник, у которого одна пара противоположных сторон параллельна. Площадь трапеции рассчитывается по формуле Площадь трапеции = ½ (a + b) h, где «a» и «b» — основания (параллельные стороны), а «h» — перпендикулярная высота. Он представлен в квадратных единицах.
Как найти площадь трапеции?
Площадь трапеции находится по формуле A = ½ (a + b) h, где «a» и «b» — основания (параллельные стороны), а «h» — высота (перпендикулярное расстояние между основания) трапеции.
Почему площадь трапеции равна ½ (a + b) h?
Формулу площади трапеции можно легко доказать. Рассмотрим трапецию с основаниями «а» и «b» и высотой «h». Мы можем отрезать от трапеции треугольную часть и прикрепить ее внизу, чтобы вся трапеция превратилась в треугольник. Тогда полученный треугольник имеет основание (a + b) и высоту h. Применяя формулу площади треугольника, площадь трапеции (или треугольника) = ½ (a + b) h. Для получения дополнительной информации вы можете обратиться к статье Как вывести формулу площади трапеции? раздел этой страницы.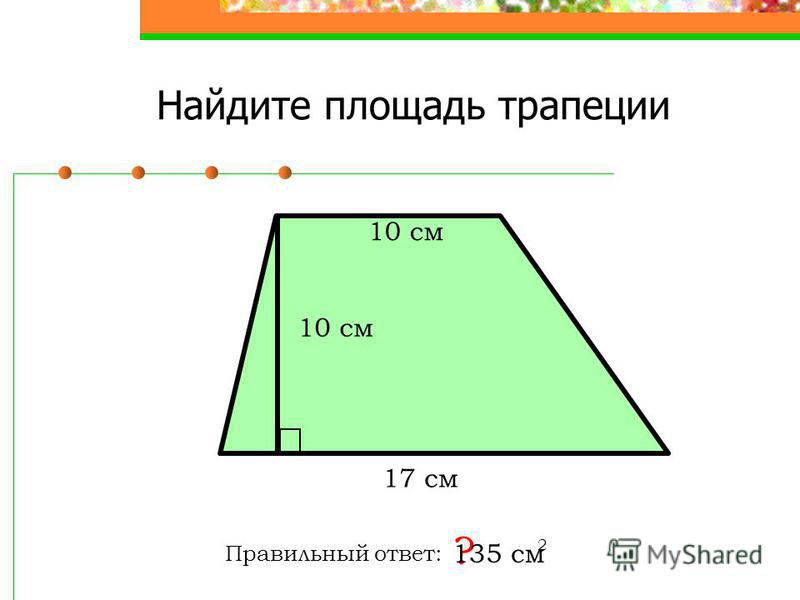
Как найти недостающее основание трапеции, если известна площадь?
Мы знаем, что площадь трапеции с основаниями «a» и «b» и высотой «h» равна A = ½ (a + b) h. Если одно из оснований (скажем, «а»), высота и площадь заданы, то мы просто подставим эти значения в приведенную выше формулу и решим ее для отсутствующего основания (а) следующим образом:
A = ½ (a + b) h
Умножение обеих частей на 2,
2A = (a + b) h
Разделение обеих частей на h,
2A/h = a + b
Вычитание b с обеих сторон,
a = (2A/h) — b
Как найти высоту трапеции с площадью и основанием?
Если площадь и основания трапеции известны, то мы можем вычислить ее высоту по формуле Площадь трапеции = ½ (a + b) h; где «а» и «b» — основания, а «h» — высота. Другими словами, мы можем найти высоту трапеции, подставив заданные значения площади и двух оснований.
Как найти площадь равнобедренной трапеции без высоты?
Если высота трапеции не известна и известны все ее стороны, то мы можем разделить трапецию на два конгруэнтных прямоугольных треугольника и прямоугольник.
No related posts.