Десятичные дроби. Классы десятичных дробей. «Альфа-школа».
Десятичные дроби — это вид дроби, в которой \(m\) – простое число, а \(n\) в какой-либо степени \(10\). Рассмотрим примеры: \(\frac{1}{10},\frac{1}{100},\frac{1}{1000}\)- в десятой, в сотой и в тысячной части соответственно. Дробь семь пятидесятых \(\frac{7}{50}\) можно записать в виде десятичного числа, умножив числитель и знаменатель на \(2\), получаем \(\frac{14}{100}\), то есть \(0,14\), \(\frac{6}{1000}\) произносится как шесть тысячных и записывается в десятичном виде как \(0,006\).
Дробь четыре пятых \(\frac{4}{5}\) можно написать как восемь десятых \(\frac{8}{10}\).
По каким правилам обыкновенная дробь переводится в десятичную?
- \(\frac{1}{5}=0,2\)
- \(\frac{2}{5}=0,4\)
- \(\frac{3}{5}=0,6\)
Первый способ.
Чтобы перевести дробь в десятичную нужно числитель и знаменатель умножить на одно и то же число, чтобы в знаменателе получилось \(10,100,1000,10 000\) и т.
Второй способ.
Второй способ более сложный, но применяется чаще первого. Для его использования, нужно вспомнить деление уголком:
- Десятичная дробь не поменяет свое значение, если у нее отнять справа несколько нулей, если они есть;
- Десятичная дробь не поменяет свое значение, если к ней прибавить справа несколько нулей;
- Дробь со знаменателем \(10\) в степени n можно записать в виде десятичной дроби;
- Дробная и целая часть разделяется запятой;
- Если дробь содержит конечное число цифр, то дробь называется конечной;
- Если дробь имеет бесконечное число цифр, то дробь называется бесконечной;
Пример бесконечной дроби:
- Повторяющиеся цифры после запятой, называется периодом этой бесконечной десятичной дроби;
- Бесконечные десятичные дроби существуют двух видов: периодические и непериодические дроби;
Можно ли перевести любую дробь в конечную десятичную?
- Если знаменатель обыкновенной дроби раскладывается на простые множители
\(2\) и \(5\), то она является конечной:
- Если знаменатель обыкновенной дроби, раскладывается на простые множители не только на \(2\) и \(5\),
то она является бесконечной.
Десятичные дроби применяются в единицах измерения длины.
\(1\) км \(=1000\) м \(=10000\) дм \(=100000\)см \(=1000000\) мм
\(1\) мм -\(1\) одна миллионная км,\(0,000001\)
\(1\) см — \(1\) стотысячная км, \(0,00001\)
\(1\) дм — \(1\) десятитысячная км \(0,0001\)
\(1\) м — \(1\) одна тысячная км \(0,001\)
Задача:
Решение:
1)убираем ноль с правой части, получаем \(2,25\)
2) в одном км — \(1000\) м значит делим на \(1000 :0,00225\) км
Ответ: \(0,00225\) км.
Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Перевод десятичной дроби в обыкновенную и наоборот: правило, примеры
Бывает, что для удобства расчетов нужно перевести обыкновенную дробь в десятичную и наоборот.
О том, как это делать, мы поговорим в данной статье. Разберем правила перевода обыкновенных дробей в десятичные и обратно, а также приведем примеры.
Перевод обыкновенных дробей в десятичные
Мы будем рассматривать перевод обыкновенных дробей в десятичные, придерживаясь определенной последовательности. Во первых, рассмотрим, как в десятичные переводятся обыкновенные дроби со знаменателем, кратным 10: 10, 100, 1000 и т.д.Дроби с такими знаменателями, по сути, являются, более громоздкой записью десятичных дробей.
Далее мы рассмотрим, как переводить в десятичные дроби обыкновенные дроби с любым, не только кратным 10, знаменателем. Отметим, что при обращении обыкновенных дробей в десятичные получаются не только конечные десятичные, но и бесконечные периодические десятичные дроби.
Приступим!
Перевод обыкновенных дробей со знаменателями 10, 100, 1000 и т.д. в десятичные дроби
Первым делом, скажем, что некоторые дроби нуждаются в определенной подготовке перед обращением в десятичный вид.
В чем она заключается? Перед цифрой, стоящей в числителе, необходимо дописать столько нулей, чтобы количество цифр числителя стало равно числу нулей в знаменателе. Например, для дроби 3100 число 0 необходимо один раз дописать слева от 3 в числителе. Дробь 610, согласно изложенному выше правилу, не нуждается в доработке.
Рассмотрим еще один пример, после чего сформулируем правило, которым особенно удобно пользоваться на первых порах, пока опыта в обращении дробей не так много. Так, дробь 1610000 после дописывания нулей в числителе будет иметь вид 001510000.
Как перевести обыкновенную дробь со знаменателем 10, 100, 1000 и т.д. в десятичную?
Правило перевода обыкновенных правильных дробей в десятичные- Записываем 0 и ставим после него запятую.
- Записываем число из числителя, которое получилось после дописывания нулей.
Теперь перейдем к примерам.
Пример 1. Перевод обыкновенных дробей в десятичныеПереведем обыкновенную дробь 39100 в десятичную.
Сначала смотрим на дробь и видим, что никаких подготовительных действий проводить не нужно — количество цифр в числителе совпадает с количеством нулей в знаменателе.
Следуя правилу, записываем 0, ставим после него десятичную запятую и записываем число из числителя. Получаем десятичную дробь 0,39.
Разберем решение еще одного примера по этой теме.
Пример 2. Перевод обыкновенных дробей в десятичныеЗапишем дробь 10510000000 в виде десятичной дроби.
Количество нулей в знаменателе равно 7, а в числителе только три цифры. Допишем перед числом в числителе еще 4 нуля:
000010510000000
Теперь записываем 0, ставим после него десятичную запятую и записываем число из числителя. Получаем десятичную дробь 0,0000105.
Рассмотренные во всех примерах дроби — обыкновенные правильные дроби. Но как перевести неправильную обыкновенную дробь в десятичную? Сразу скажем, что необходимость в подготовке с дописыванием нулей для таких дробей отпадает. Сформулируем правило.
- Записываем число, которое находится в числителе.
- Десятичной запятой отделяем столько цифр справа, сколько нулей есть в знаменателе исходной обыкновенной дроби.
Ниже приведем пример на использование этого правила.
Пример 3. Перевод обыкновенных дробей в десятичныеПереведем дробь 56888038009100000 из обыкновенной неправильной в десятичную.
Сначала запишем число из числителя:
56888038009
Теперь справа отделим десятичной запятой пять цифр (количество нулей в знаменателе — пять). Получим:
568880,38009
Следующий вопрос, который закономерно возникает: как перевести в десятичную дробь смешанное число, если знаменателем его дробной части является число 10, 100, 1000 и т.д. Для обращения в десятичную дробь такого числа можно воспользоваться следующим правилом.
- Выполняем подготовку дробной части числа, если это необходимо.
- Записываем целую часть исходного числа и ставим после него запятую.
- Записываем число из числителя дробной части вместе с дописанными нулями.
Обратимся к примеру.
Пример 4. Перевод смешанных чисел в десятичные дробиПереведем смешанное число 231710000 в десятичную дробь.
В дробной части имеем выражение 1710000. Выполним его подготовку и допишем слева от числителя еще два нуля. Получим: 001710000.
Теперь записываем целую часть числа и ставим после него запятую: 23,..
После запятой записываем число из числителя вместе с нулями. Получаем результат:
231710000=23,0017
Перевод обыкновенных дробей в конечные и бесконечные периодические дроби
Конечно, можно переводить в десятичные дроби и обыкновенные дроби со знаменателем, не равным 10, 100, 1000 и т.д.
Часто дробь можно легко привести к новому знаменателю, а затем уже воспользоваться правилом, изложенным в первом пункте данной статьи. Например, достаточно умножить числитель и знаменатель дроби 25 на 2, и мы получим дробь 410, которая легко приводится к десятичному виду 0,4.
Однако такой способ перевода обыкновенной дроби в десятичную удается использовать не всегда. Ниже рассмотрим, как поступать, если применить рассмотренный способ невозможно.
Принципиально новый способ обращения обыкновенной дроби в десятичную сводится к делению числителя на знаменатель столбиком. Эта операция очень похожа на деление натуральных чисел столбиком, но имеет свои особенности.
Числитель при делении представляется в виде десятичной дроби — справа от последней цифры числителя ставится запятая и дописываются нули. В получившемся частном десятичная запятая ставится тогда, когда заканчивается деление целой части числителя. Как именно работает этот способ, станет понятно после рассмотрения примеров.
Переведем обыкновенную дробь 6214 в десятичный вид.
Представим число 621 из числителя в виде десятичной дроби, добавив после запятой несколько нулей. 621=621,00
Теперь разделим столбиком 621,00 на 4. Первые три шага деления будут такими же, как при делении натуральных чисел, и мы получим.
Когда мы добрались до десятичной запятой в делимом, а остаток отличен от нуля, ставим в частном десятичную запятую, и продолжаем делить, не обращая более внимания на запятую в делимом.
В итоге мы получаем десятичную дробь 155,25, которая и является результатом обращения обыкновенной дроби 6214
6214=155,25
Рассмотрим решение еще одного примера, чтобы закрепить материал.
Пример 6. Перевод обыкновенных дробей в десятичныеОбратим обыкновенную дробь 21800.
Для этого в столбик разделим дробь 21,000 на 800. Деление целой части закончится на первом же шаге, поэтому сразу после него ставим в частном десятичную запятую и продолжаем деление, не обращая внимания на запятую в делимом до того момента, пока не получим остаток, равный нулю.
В результате мы получили: 21800=0,02625.
Но как быть, если при делении мы так и не получим в остатке 0. В таких случаях деление можно продолжать бесконечно долго. Однако, начиная с определенного шага, остатки будут периодически повторяться.
Соответственно, будут повторяться и цифры в частном. Это значит, что обыкновенная дробь переводится в десятичную бесконечную периодическую дробь. Проиллюстрируем сказанное на примере.
Обратим обыкновенную дробь 1944 в десятичную. Для этого выполним деление столбиком.
Мы видим, что при делении повторяются остатки 8 и 36. При этом в частном повторяются цифры 1 и 8. Это и есть период в десятичной дроби. При записи эти цифры берутся в скобки.
Таким образом, исходная обыкновенная дробь переведена в бесконечную периодическую десятичную дробь.
1944=0,43(18).
Пусть перед нами несократимая обыкновенная дробь. К какому виду она приведется? Какие обыкновенные дроби переводятся в конечные десятичные, а какие — в бесконечные периодические?
Во первых, скажем, что если дробь удается привести к одному из знаменателей 10, 100, 1000.., то она будет иметь вид конечной десятичной дроби. Чтобы дробь приводилась к одному из таких знаменателей, ее знаменатель должен быть делителем хотя бы одного из чисел 10, 100, 1000 и т.
д. Из правил разложения чисел на простые множители следует, что делитель чисел 10, 100, 1000 и т.д. должен, при разложении на простые множители, содержать лишь числа 2 и 5.
Подытожим сказанное:
- Обыкновенную дробь можно привести к виду конечной десятичной дроби, если ее знаменатель можно разложить на простые множители 2 и 5.
- Если кроме чисел 2 и 5 в разложении знаменателя присутствуют другие простые числа, дробь приводится к виду бесконечной периодической десятичной дроби.
Приведем пример.
Пример 8. Перевод обыкновенных дробей в десятичныеКакая из данных дробей 4720, 712, 2156, 3117 переводится в конечную десятичную дробь, а какая — только в периодическую. Дадим ответ на этот вопрос, не выполняя непосредственно перевода обыкновенной дроби в десятичную.
Дробь 4720, как легко заметить, умножением числителя и знаменателя на 5 приводится к новому знаменателю 100.
4720=235100. Отсюда делаем вывод, что данная дробь переводится в конечную десятичную дробь.
Разложение знаменателя дроби 712 на множители дает 12=2·2·3. Так как простой множитель 3 отличен от 2 и от 5, данная дробь не может быть представлена в виде конечной десятичной дроби, а будет иметь вид бесконечной периодической дроби.
Дробь 2156, во-первых, нужно сократить. После сокращения на 7 получим несократимую дробь 38, разложение знаменателя которой на множители дает 8=2·2·2. Следовательно, это конечная десятичная дробь.
В случае с дробью 3117 разложение знаменателя на множители представляет собой само простое число 17. Соответственно, эту дробь можно обратить в бесконечную периодическую десятичную дробь.
Обыкновенную дробь нельзя перевести в бесконечную и непериодическую десятичную дробь
Выше мы говорили только о конечных и бесконечных периодических дробях. Но может ли какая-либо обыкновенная дробь быть обращена в вид бесконечной непериодической дроби?
Отвечаем: нет!
Важно!При переводе бесконечной дроби в десятичную получается либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь.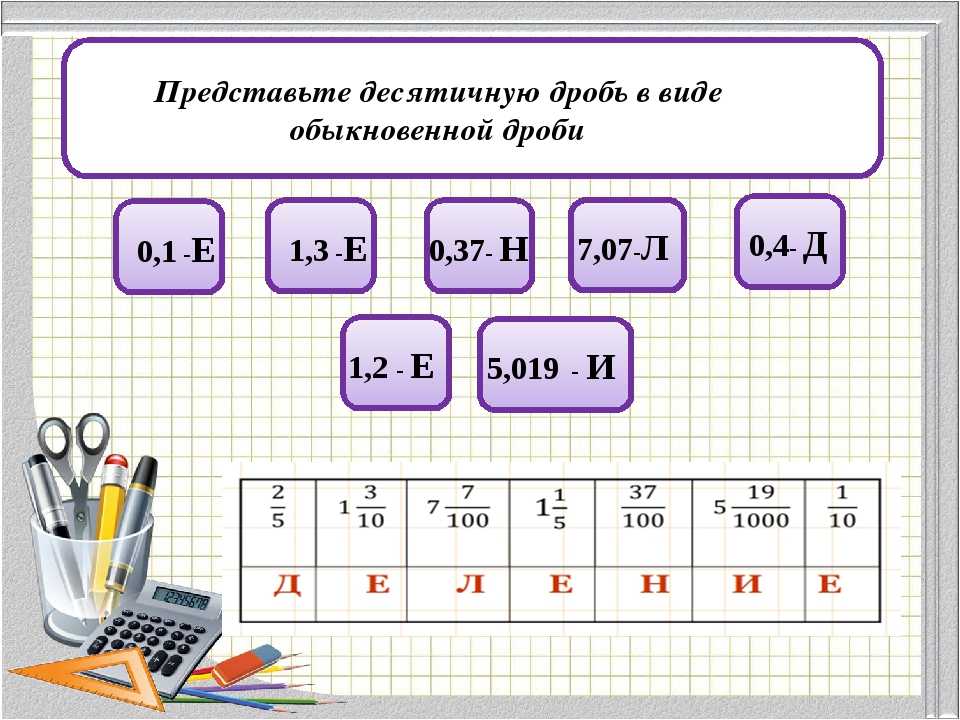
Остаток от деления всегда меньше делителя. Другими словами, согласно теореме о делимости, если мы делим какое-то натуральное число на число q, то остаток деления в любом случае не может быть больше, чем q-1. После окончания деления возможна одна из следующих ситуаций:
- Мы получаем в остатке 0, и на этом деление заканчивается.
- Мы получаем остаток, который при последующем делении повторяется, в результате мы имеем бесконечную периодическую дробь.
Иных вариантов при обращении обыкновенной дроби в десятичную не может быть. Скажем также, что длина периода (количество цифр) в бесконечной периодической дроби всегда меньше, чем число цифр в знаменателе соответствующей обыкновенной дроби.
Перевод десятичных дробей в обыкновенные дроби
Теперь пришло время рассмотреть обратный процесс перевода десятичной дроби в обыкновенную. Сформулируем правило перевода, которое включает три этапа. Как перевести десятичную дробь в обыкновенную?
Правило перевода десятичных дробей в обыкновенные дроби- В числитель записываем число из исходной десятичной дроби, отбросив запятую и все нули слева, если они есть.
- В знаменатель записываем единицу и за ней столько нулей, сколько цифр есть в исходной десятичной дроби после запятой.
- При необходимости сокращаем полученную обыкновенную дробь.
Рассмотрим применение данного правила на примерах.
Пример 8. Перевод десятичных дробей в обыкновенныеПредставим число 3,025 в виде обыкновенной дроби.
- В числитель записываем саму десятичную дробь, отбросив запятую: 3025.
- В знаменателе пишем единицу, а после нее три нуля — именно столько цифр содержится в исходной дроби после запятой: 30251000.
- Полученную дробь 30251000 можно сократить на 25, в результате чего мы получим: 30251000=12140.
Переведем дробь 0,0017 из десятичных в обыкновенные.
- В числителе запишем дробь 0,0017, отбросив запятую и нули слева. Получится 17.
- В знаменатель записываем единицу, а после нее пишем четыре нуля: 1710000. Данная дробь несократима.
Если в десятичной дроби есть целая часть, то такую дробь можно сразу перевести в смешанное число. Как это сделать?
Сформулируем еще одно правило.
Правило перевода десятичных дробей в смешанные числа.- Число, стоящее в дроби до запятой, записываем как целая часть смешанного числа.
- В числителе записываем число, стоящее в дроби после запятой, отбросив нули слева, если они есть.
- В знаменателе дробной части дописываем единицу и столько нулей, сколько цифр есть в дробной части после запятой.
Обратимся к примеру
Пример 10. Перевод десятичной дроби в смешанное числоПредставим дробь 155,06005 в виде смешанного числа.
- Записываем число 155, как целую часть.
- В числителе записываем цифры после запятой, отбросив нуль.
- В знаменателе записываем единицу и пять нулей
Поучаем смешанное число: 1556005100000
Дробную часть можно сократить на 5. Сокращаем, и получаем финальный результат:
155,06005=155120120000
Перевод бесконечных периодических десятичных дробей в обыкновенные дроби
Разберем на примерах, как осуществлять перевод периодических десятичных дробей в обыкновенные.
Прежде чем начать, уточним: любую периодическую десятичную дробь можно перевести в обыкновенную.
Самый простой случай — период дроби равен нулю. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.
Пример 11. Перевод периодической десятичной дроби в обыкновеннуюОбратим периодическую дробь 3,75(0).
Отбросив нули справа, получим конечную десятичную дробь 3,75.
Обращая данную дробь в обыкновенную по алгоритму, разобранному в предыдущих пунктах, получаем:
3,75(0)=3,75=375100=154.
Как быть, если период дроби отличен от нуля? Периодическую часть следует рассматривать как сумму членов геометрический прогрессии, которая убывает. Поясним это на примере:
0,(74)=0,74+0,0074+0,000074+0,00000074+..
Для суммы членов бесконечной убывающей геометрической прогрессии существует формула. Если первый член прогрессии равен b, а знаменатель q таков, что 0<q<1, то сумма равна b1-q.
Рассмотрим несколько примеров с применением данной формулы.
Пример 12. Перевод периодической десятичной дроби в обыкновеннуюПусть у нас есть периодическая дробь 0,(8) и нам нужно перевести ее в обыкновенную.
Запишем:
0,(8)=0,8+0,08+0,008+..
Здесь мы имеем бесконечную убывающую геометрическую прогрессию с первым членом 0,8 и знаменателем 0,1.
Применим формулу:
0,(8)=0,8+0,08+0,008+..=0,81-0,1=0,80,9=89
Это и есть искомая обыкновенная дробь.
Для закрепления материала рассмотрим еще один пример.
Пример 13. Перевод периодической десятичной дроби в обыкновеннуюОбратим дробь 0,43(18).
Сначала записываем дробь в виде бесконечной суммы:
0,43(18)=0,43+(0,0018+0,000018+0,00000018..)
Рассмотрим слагаемые в скобках. Эту геометрическую прогрессию можно представить в следующем виде:
0,0018+0,000018+0,00000018..=0,00181-0,01=0,00180,99=189900.
Полученное прибавляем к конечной дроби 0,43=43100 и получаем результат:
0,43(18)=43100+189900
После сложения данных дробей и сокращения получим окончательный ответ:
0,43(18)=1944
В завершение данной статьи скажем, что непериодические бесконечный десятичные дроби нельзя перевести в вид обыкновенных дробей.
Что такое 4/5 в виде десятичной дроби? (Преобразовать 4/5 в десятичную)
Преобразование 4/5 в десятичную, возможно, является одним из самых простых вычислений, которые вы можете сделать. В этом (очень коротком) руководстве мы покажем вам, как превратить любую дробь в десятичную менее чем за 3 секунды! Вот так!
Хотите быстро узнать или показать учащимся, как преобразовать 4/5 в десятичную дробь? Включи это очень быстрое и веселое видео прямо сейчас!
Прежде всего, если вы не знаете, что такое числитель и знаменатель в дроби, нам нужно повторить это:
4 (числитель) / 5 (знаменатель)
Вот небольшой секрет, с помощью которого можно мгновенно преобразовать любую дробь в десятичную: Просто разделите числитель на знаменатель:
= 4/5
= 4 ÷ 5
= 0,8
3
Вот буквально все! 4/5 в десятичном виде равно 0,8. Хотел бы я рассказать вам больше о преобразовании дроби в десятичную, но это действительно так просто, и мне больше нечего об этом сказать.
Если вы хотите потренироваться, возьмите ручку и блокнот и попробуйте самостоятельно вычислить некоторые дроби в десятичном формате. Если вы действительно чувствуете себя ленивым , вы можете вместо этого использовать наш калькулятор ниже!
Почему вы хотите преобразовать 4/5 в десятичную дробь?
Отличный вопрос. У нас есть много расчетов на этом сайте о преобразовании дроби в десятичную, но зачем вам вообще это нужно?
Ну, во-первых, это просто хороший способ представить дробь в лучшем виде, который позволяет вам выполнять с ними обычные арифметические действия (такие как сложение, вычитание, деление и умножение).
В реальной жизни мы в основном имеем дело с десятичными дробями (например, с валютой), и, поскольку наш мозг с юных лет приучают понимать и сравнивать десятичные дроби чаще, чем дроби, проще понимать и сравнивать дроби, если они сначала преобразовать в десятичную!
Вот небольшой пример из реальной жизни преобразования дроби в десятичную при использовании количества.
Допустим, вы готовите, и обычно вы можете видеть, сколько ингредиента осталось в упаковке. Однако электронные весы измеряют вес в десятичных дробях, а не в долях оставшегося ингредиента. Это делает преобразование между дробями и десятичными дробями полезным навыком в кулинарии.
Надеюсь, это руководство помогло вам понять, как преобразовать дробь в десятичное число. Теперь вы можете идти вперед и преобразовывать дроби в десятичные столько, сколько пожелает ваше маленькое сердце!
Процитируйте, дайте ссылку или ссылку на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
«Что такое 4/5 в виде десятичной дроби?».
VisualFractions.com . По состоянию на 23 апреля 2023 г. http://visualfractions.com/calculator/fraction-as-decimal/what-is-4-5-as-a-decimal/.«Что такое 4/5 в виде десятичной дроби?». VisualFractions.com , http://visualfractions.com/calculator/fraction-as-decimal/what-is-4-5-as-a-decimal/. По состоянию на 23 апреля 2023 г.
Что такое 4/5 в виде десятичной дроби?. VisualFractions.com. Получено с http://visualfractions.com/calculator/fraction-as-decimal/what-is-4-5-as-a-decimal/.
VisualFractions.com . По состоянию на 23 апреля 2023 г. http://visualfractions.com/calculator/fraction-as-decimal/what-is-4-5-as-a-decimal/.Калькулятор преобразования дроби в десятичную дробь
Дробь в виде десятичной дроби
Введите числитель и знаменатель
Расчет следующей дроби в десятичную дробь
- Что такое 4/6 в виде десятичной дроби?
Случайные дроби в десятичные числа
Если вы добрались до этого конца страницы, значит, вы ДЕЙСТВИТЕЛЬНО любите преобразовывать дроби в десятичные? Ниже приведена куча случайно сгенерированных вычислений для вашего удовольствия от десятичной любви:
Что такое 945/952 в виде десятичного числа
Что такое 257/954 в виде десятичного числа
Что такое 308/668 в виде десятичного числа
Что такое 258/366 в виде десятичного числа
Что такое 119/631 в виде десятичного числа
3
3
3 229/772 в виде десятичного числа
Что такое 514/905 в виде десятичного числа
Что такое 813/848 в виде десятичного числа
Что такое 826/997 в виде десятичного числа
Что такое 848/885 в виде десятичного числа
3 274/392 в виде десятичного числа
Что такое 299/413 в виде десятичного числа
Что такое 9
Что такое десятичное число 67/997
Что такое 64/463
Что такое десятичное число 942/964
Что такое 922/940 в виде десятичного числа
Что такое 979/981 в виде десятичного числа
Что такое 741/944 в виде десятичного числа
Что такое 217/790 в виде десятичного числа
Что такое 38/372 в виде десятичного числа
03
03 905/973 в виде десятичного числа
Что такое 508/930 в виде десятичного числа
Что такое 789/932 в виде десятичного числа
Что такое 796/872 в виде десятичного числа
Что такое 112/234 в виде десятичного числа
Что такое 371/752 в виде десятичного числа
Что такое 439/758 в виде десятичного числа Что такое
23
/755 в виде десятичного числа
Что такое 37/170 в виде десятичного числа
Что такое 415/951 в виде десятичного числа
Что такое 12/663 в виде десятичного числа
Что такое 402/535 в виде десятичного числа
2 /498 в виде десятичного числа
Что такое 129/141 в виде десятичного числа
Что такое 516/777 в виде десятичного числа
Что такое десятичное число 797/905?
Что такое десятичное число 840/967?
Что такое десятичное число 699/809?
Что такое десятичное число 260/483?
Десятичное число 803/999
Десятичное число 702/967
Десятичное число 379/389
Десятичное число 549/792
Десятичное число 549/794
Что такое 452/581 в виде десятичного числа
Что такое 903/928 в виде десятичного числа
Десятичное число 306/778
Десятичное число 119/924
Десятичное число 868/989
Десятичное число 111/300
Десятичное число 4 182/7
Десятичное число 707/810
Десятичное число 452/867
Десятичное число 386/540
Десятичное число 381/623
Десятичное число 26
Что такое 464/661 в виде десятичного числа
Что такое 21/547 в виде десятичного числа
Что такое десятичное число 840/964?
Что такое десятичное число 933/942?
Что такое десятичное число 668/925?
Что такое десятичное число 424/486?
Что такое десятичное число 964/969?
Что такое десятичное число 568/905?
Что такое десятичное число 534/715?
Что такое десятичное число 545/912?
Что такое 490/911 в виде десятичного числа
Что такое 449/548 в виде десятичного числа
Что такое десятичное число 267/619?
Что такое десятичное число 596/721?
Что такое десятичное число 592/763?
Что такое десятичное число 892/916?
Десятичное число 420/696
Десятичное число 629/999
Десятичное число 213/432
Десятичное число 403/744
Десятичное число 56
Что такое 794/972 в виде десятичного числа
Что такое 731/994 в виде десятичного числа
Десятичное число 167/673
Десятичное число 796/849
Десятичное число 608/690
Десятичное число 833/913
Десятичное число 418/98
Десятичное число 271/733
Десятичное число 791/880
Десятичное число 226/863
Десятичное число 868/907
Десятичное число 96/7
Что такое 327/582 в виде десятичного числа
Что такое 984/985 в виде десятичного числа
Десятичное число 147/450
Десятичное число 922/998
Десятичное число 480/736
Десятичное число 337/562 Конвертер десятичных чисел
Главная›Конвертация›Преобразование чисел›Дробь в десятичную
Калькулятор фракций Упрощение дробей Преобразователь дробей
От DecimalFractionPercent
До Десятичная дробьПроцент
Введите дробь
Десятичный результат
Расчет
Преобразователь десятичной дроби в дробную ►
Как преобразовать дробь в десятичную
Метод №1
Разложить знаменатель до степени 10.
Пример №1
35
6000023
2
по умножив числитель на 2 и знаменатель на 2:
| 3 | = | 3×2 | = | 6 | = | 0,6 |
| 5 | 5×2 | 10 |
Пример #2
34
расширяется до
75100
путем умножения числителя на 25 и знаменателя на 25:
| 3 | = | 3×25 | = | 75 | = | 0,75 |
| 4 | 4×25 | 100 |
Пример №3
58
расширяется до
6251000
путем умножения числителя на 125 и знаменателя на 125:
| 5 | = | 5×125 | = | 625 | = | 0,625 |
| 8 | 8×125 | 1000 |
Метод №2
- Разделите числитель дроби на знаменатель с помощью калькулятора.
- Для смешанных чисел добавьте целое число.
Пример №1
25
= 2÷5 = 0,4
Пример №2
1
25
= 1+2÷5 = 1+2÷5 #3 900 1,4
Метод 002 Используйте длинное деление, чтобы разделить числитель дроби через знаменатель дроби.Пример
Вычислить 3/4 делением 3 на 4 в длинном ряду:
| 0,75 | |
| 4 | 3 |
| 0 | |
| 30 | |
| 28 | |
| 20 | |
| 20 | |
| 0 |
Таблица перевода дроби в десятичную дробь
| Дробь | Десятичный |
|---|---|
| 1/2 | 0,5 |
| 1/3 | 0,33333333 |
| 2/3 | 0,66666667 |
| 1/4 | 0,25 |
| 2/4 | 0,5 |
| 3/4 | 0,75 |
| 1/5 | 0,2 |
| 2/5 | 0,4 |
| 3/5 | 0,6 |
| 4/5 | 0,8 |
| 1/6 | 0,16666667 |
| 2/6 | 0,33333333 |
| 3/6 | 0,5 |
| 4/6 | 0,66666667 |
| 5/6 | 0,83333333 |
| 1/7 | 0,14285714 |
| 2/7 | 0,28571429 |
| 3/7 | 0,42857143 |
| 4/7 | 0,57142858 |
| 5/7 | 0,71428571 |
| 6/7 | 0,85714286 |
| 1/8 | 0,125 |
| 2/8 | 0,25 |
| 3/8 | 0,375 |
| 4/8 | 0,5 |
| 5/8 | 0,625 |
| 6/8 | 0,75 |
| 7/8 | 0,875 |
| 1/9 | 0,11111111 |
| 2/9 | 0,22222222 |
| 3/9 | 0,33333333 |
| 4/9 | 0,44444444 |
| 5/9 | 0,55555556 |
| 6/9 | 0,66666667 |
| 7/9 | 0,77777778 |
| 8/9 | 0,88888889 |
| 1/10 | 0,1 |
| 2/10 | 0,2 |
| 3/10 | 0,3 |
| 4/10 | 0,4 |
| 5/10 | 0,5 |
| 6/10 | 0,6 |
| 7/10 | 0,7 |
| 8/10 | 0,8 |
| 9/10 | 0,9 |
| 1/11 | 0,009 |
| 2/11 | 0,18181818 |
| 3/11 | 0,27272727 |
| 4/11 | 0,36363636 |
| 5/11 | 0,45454545 |
| 6/11 | 0,54545454 |
| 7/11 | 0,63636363 |
| 8/11 | 0,72727272 |
| 9/11 | 0,81818181 |
| 11/10 | 0,091 |
Преобразование десятичной дроби ►
См.
