Краткий курс высшей математики
Краткий курс высшей математики
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. МЕТОД КООРДИНАТ. ПОНЯТИЕ ФУНКЦИИ § 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КООРДИНАТЫ ТОЧКИ НА ПРЯМОЙ 2. Геометрическое изображение действительных чисел. Координаты точки на прямой 3. Абсолютная величина действительного числа  Расстояние между двумя точками на прямой§ 2. КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ 2. Расстояние между двумя точками на плоскости 3. Деление отрезка в данном отношении 4. Координаты точки в пространстве 5. Расстояние между двумя точками в пространстве § 3. УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ 2. Полярные координаты 3. Зависимость между декартовыми и полярными координатами § 4. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ 2. Понятие функции 3. График функции 4. Способы задания функций 5. Основные элементарные функции и их графики 6. Сложные функции. Элементарные функции 7. Целые и дробно-рациональные функции 8. Функции четные и нечетные. Периодические функции § 5. УРАВНЕНИЕ ЛИНИИ 2. Нахождение уравнения линии по ее геометрическим свойствам § 6 ПРЕОБРАЗОВАНИЕ КООРДИНАТ 2. Поворот осей координат ГЛАВА II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ § 1. ПРЯМАЯ 2. Уравнение прямой с угловым коэффициентом 3. Уравнение прямой, параллельной оси ординат 4.  Общее уравнение прямой и его частные случаи5. Точка пересечения прямых. Построение прямой по ее уравнению 6. Вычисление угла между двумя прямыми. Условия параллельности и перпендикулярности двух прямых 7. Уравнение прямой, проходящей через данную точку в заданном направлении 8. Пучок прямых 9. Уравнение прямой, проходящей через две данные точки 10. Расстояние от точки до прямой § 2. КРИВЫЕ ВТОРОГО ПОРЯДКА 2. Окружность 3. Эллипс 4. Гипербола 5. Парабола 6. Окружность, эллипс, гипербола и парабола как конические сечения 7. Упрощение уравнения кривой второго порядка. График квадратного трехчлена 8. Уравнение равносторонней гиперболы, асимптоты которой приняты за оси координат 9. График дробно-линейной функции 10. Преобразование уравнения кривой второго порядка, не содержащего члена с произведением координат § 1. ЭЛЕМЕНТЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ 2. Определитель третьего порядка 3.  Понятие об определителях высших порядков§ 2. СИСТЕМЫ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ 2. Однородная система двух уравнений первой степени с тремя неизвестными 3. Система трех уравнений первой степени с тремя неизвестными 4. Однородная система трех уравнений первой степени с тремя неизвестными § 3. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ 2. Линейные операции над векторами 4. Проекция вектора на ось и составляются вектора по оси 5. Разложение вектора на составляющие по осям координат 6. Направляющие косинусы вектора 7. Условие коллинеарности двух векторов 8. Скалярное произведение 9. Выражение скалярного произведения через проекции перемножаемых векторов 10. Косинус угла между двумя векторами 11. Векторное произведение 12. Выражение векторного произведения через проекции перемножаемых векторов 13. Смешанное произведение трех векторов 14. Геометрический смысл смешанного произведения 15. Условие компланарности трех векторов § 4. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ 2.  Равенство матриц. Действия над матрицами3. Обратная матрица 4. Матричная запись и матричное решение системы уравнений первой степени § 5. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ 2. Преобразование координат 3. Приведение квадратичной формы к каноническому виду 4. Упрощение общего уравнения кривой второго порядка ГЛАВА IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ § 1. ПЛОСКОСТЬ 2. Нормальный вектор плоскости. Уравнение плоскости, проходящей через данную точку 3. Общее уравнение плоскости и его частные случаи 5. Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей 6. Точка пересечения трех плоскостей § 2. ПРЯМАЯ В ПРОСТРАНСТВЕ 2. Общие уравнения прямой 3. Векторное уравнение прямой. Параметрические уравнения прямой 4. Канонические уравнения прямой 5. Уравнения прямой, проходящей через две точки 6. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых § 3.  Прямая и плоскость в пространстве2. Точка пересечения прямой с плоскостью 3. Расстояние от точки до плоскости 4. Пучок плоскостей § 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА 2. Цилиндрические поверхности 3. Конические поверхности 4. Поверхность вращения 6. Гиперболоиды 7. Параболоиды ГЛАВА V. ТЕОРИЯ ПРЕДЕЛОВ § 1. ПРЕДЕЛ ФУНКЦИИ 2. Предел функции при х -> -оо 3. Предел функции при х->х0 4. Бесконечно малые функции. Ограниченные функции 5. Бесконечно большие функции и их связь с бесконечно малыми функциями 6. Основные теоремы о пределах 7. Предел функции при x -> 0 8. Последовательность. Число e 9. Натуральные логарифмы 10. Сравнение бесконечно малых функций § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 2. Операции над непрерывными функциями. Непрерывность элементарных функций 3. Свойства функций, непрерывных на сегменте 4. Понятие об обратной функции 5. Обратные тригонометрические функции 6. Показательная и логарифмическая функции 7.  Понятие о гиперболических функцияхГЛАВА VI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ 1. Приращение аргумента и приращение функции 2. Определение непрерывности функции с помощью понятии приращения аргумента и приращения функции 3. Задачи, приводящие к понятию производной 5. Дифференцируемость функции 6. Геометрический смысл производной 7. Производные некоторых основных элементарных функций 8. Основные правила дифференцирования 9. Производная обратной функции 10. Производные обратных тригонометрических функций 11. Производная сложной функции § 12. Производные гиперболических функций 13. Производная степенной функции с любым показателем 14. Сводная таблица формул дифференцирования 15. Неявные функции и их дифференцирование 16. Уравнения касательной а нормали к кривой 17. Графическое дифференцирование § 2. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ 1. Нахождение производных высших порядков 2.  Механический смысл второй производной§ 3. ДИФФЕРЕНЦИАЛ ФУНКЦИИ 2. Производная как отношение дифференциалов 3. Дифференциал суммы, произведения и частного функций 4. Дифференциал сложной функции. Инвариантность формы дифференциала 5. Применение дифференциала к приближенным вычислениям 6. Дифференциалы высших порядков § 4. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ, И ИХ ДИФФЕРЕНЦИРОВАНИЕ 2. Дифференцирование функций, заданных параметрически § 5. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА 2. Векторная функция скалярного аргумента и ее производная 3. Уравнения касательной прямой и нормальной плоскости к пространственной кривой 4. Механический смысл первой и второй производных векторной функции скалярного аргумента § 6. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ 2. Теорема Ролля 3. Теорема Лагранжа 4. Правило Лопиталя § 7. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ 2. Максимум и минимум функции 3. Достаточный признак существования экстремума, основанный на знаке второй производной 4.  5. Применение теории максимума и минимума к решению задач 6. Выпуклость и вогнутость графика функции. Точки перегиба 7. Асимптоты графика функции 8. Общая схема исследования функции и построение ее графика § 8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 2. Уточнение найденных значений корней методом хорд и касательных § 9. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА ГЛАВА VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА 2. Геометрический смысл неопределенного интеграла 3. Таблица основных интегралов 4. Основные свойства неопределенного интеграла § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 2. Интегрирование методом замены переменной 3. Интегрирование по частям § 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Рациональные дроби. Выделение правильной рациональной дроби 3. Интегрирование простейших рациональных дробей 4. Разложение правильной рациональной дроби на простейшие дроби 5.  Метод неопределенных коэффициентов6. Интегрирование рациональных дробей § 4. Интегрирование тригонометрических функций 2. Рациональные функции двух переменных 3. Интегралы вида § 5. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Интеграл вида 3. Интегралы видов 4. Интегралы вида § 6. ОБЩИЕ ЗАМЕЧАНИЯ О МЕТОДАХ ИНТЕГРИРОВАНИЯ. ИНТЕГРАЛЫ, НЕ БЕРУЩИЕСЯ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ 2. Понятие об интегралах, не берущихся в элементарных функциях ГЛАВА VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ОПРЕДЕЛЕННОМУ ИНТЕГРАЛУ 2. Задача о работе переменной силы § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 2. Свойства определенного интеграла 3. Производная интеграла по переменной верхней границе 4. Формула Ньютона—Лейбница 5. Замена переменной в определенном интеграле 6. Интегрирование по частям в определенном интеграле 2. Вычисление площади в полярных координатах 3.  Вычисление объема тела по известным поперечным сечениям4. Объем тела вращения 5. Длина дуги кривой 6. Дифференциал дуги 7. Площадь поверхности вращения 8. Общие замечания о решении задач методом интегральных сумм § 4. КРИВИЗНА ПЛОСКОЙ КРИВОЙ 2. Вычисление кривизны 3. Радиус кривизны. Круг кривизны. Центр кривизны 4. Эволюта и эвольвента § 5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2. Интегралы от разрывных функций 3. Признаки сходимости несобственных интегралов § 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 2. Метод трапеций 3. Метод параболических трапеций (метод Симпсона) ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. График функции двух переменных 3. Функции трех и большего числа переменных § 2. Предел функции нескольких переменных. Непрерывность функции. Точки разрыва 2. Непрерывность функции нескольких переменных 3. Понятие области 4.  Точки разрыва5. Свойства функций, непрерывных в ограниченной замкнутой области § 3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ 2. Геометрический смысл частных производных функции двух переменных 3. Частные производные высших порядков § 4. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. Полный дифференциал функции 3. Приложение полного дифференциала к приближенным вычислениям § 5. Дифференцирование сложных и неявных функций 2. Инвариантность формы полного дифференциала 3. Дифференцирование неявных функций § 6. СКАЛЯРНОЕ ПОЛЕ 2. Производная по направлению 3. Градиент 4. Касательная плоскость а нормаль к поверхности 5. Геометрический смысл полного дифференциала функции двух переменных § 7. ЭКСТРЕМУМ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ 2. Наибольшее и наименьшее значения функции двух переменных ГЛАВА X. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ § 1. ДВОЙНОЙ ИНТЕГРАЛ 2. Двойной интеграл. Теорема существования 3. Свойства двойного интеграла 4.  Вычисление двойного интеграла в декартовых координатах5. Вычисление двойного интеграла в полярных координатах 6. Приложения двойного интеграла § 2. ТРОЙНОЙ ИНТЕГРАЛ 2. Тройной интеграл и его свойства 3. Вычисление тройного интеграла в декартовых координатах 4. Вычисление тройного интеграла в цилиндрических координатах 5. Приложения тройного интеграла § 3. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 2. Задача о работе. Криволинейный интеграл 3. Вычисление криволинейного интеграла 4. Формула Остроградского — Грина 5. Независимость криволинейного интеграла от пути интегрирования 6. Отыскание первообразной по полному дифференциалу 7. Криволинейный интеграл по длине дуги ГЛАВА XI. РЯДЫ § 1. ЧИСЛОВЫЕ РЯДЫ 2. Геометрическая прогрессия 3. Простейшие свойства числовых рядов 4. Необходимый признак сходимости ряда 5. Достаточные признаки сходимости знакоположительных рядов 6. Знакопеременные ряды 7. Остаток ряда и его оценка § 2.  ФУНКЦИОНАЛЬНЫЕ РЯДЫ2. Правильно сходящиеся функциональные ряды и их свойства § 3. СТЕПЕННЫЕ РЯДЫ 2. Свойства степенных рядов 3. Ряды по степеням разности х-а 4. Разложение функций в степенные ряды. Ряд Тейлора 5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена § 4. ПРИЛОЖЕНИЕ РЯДОВ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ 2. Приближенное вычисление интегралов § 5. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. СТЕПЕННЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ 2. Числовые ряды с комплексными членами 3. Степенные ряды в комплексной области § 6. РЯДЫ ФУРЬЕ 2. Ряд Фурье 3. Сходимость ряда Фурье 4. Ряды Фурье для четных и нечетных функций 5. Разложение в ряд Фурье функций с периодом 2l ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 2. Дифференциальные уравнения первого порядка 3. Уравнения с разделяющимися переменными 4. Однородные уравнения 5. Линейные уравнения 6. Уравнение в полных дифференциалах 7.  Особые решения8. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2. Простейшие уравнения второго порядка, допускающие понижение порядка 3. Понятие о дифференциальных уравнениях высших порядков § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2. Линейные однородные дифференциальные уравнения второго порядка 3. Линейные неоднородные дифференциальные уравнения второго порядка 4. Метод вариации произвольных постоянных § 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 2. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 3. Приложение линейных дифференциальных уравнений второго порядка к изучению механических и электрических колебаний § 5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ 2. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами § 6.  ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ§ 7. ПОНЯТИЕ О СИСТЕМАХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 2. Системы линейных дифференциальных уравнений с постоянными коэффициентами ПРИЛОЖЕНИЕ 1. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА ПРИЛОЖЕНИЕ 2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ |
Производная определённого интеграла : Чулан (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
| wolf.ram |
| ||
04/06/10 |
| ||
| |||
Проинтеграля и потом продифференциаля. А если не топорно, что с таким делают?| profrotter |
| |||
16/02/11 |
| |||
| ||||
..| chessar |
| ||
03/12/08 |
| ||
| |||
wolf. ram |
| ||
04/06/10 |
| ||
| |||
| profrotter |
| |||
16/02/11 |
| |||
| ||||
06.2011, 21:20 wolf. ram |
| ||
04/06/10 |
| ||
| |||
| gris |
| |||
13/08/08 |
| |||
| ||||
06.2011, 22:25 | chessar |
| ||
03/12/08 |
| ||
| |||
06.2011, 08:20 | profrotter |
| |||
16/02/11 |
| |||
| ||||
06.2011, 14:48 
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 9 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Видео-вопрос: Нахождение производной функции, заданной интегралом, где ее пределы содержат переменную
Стенограмма видео
Нахождение производной функции
𝑔 от 𝑥 равно определенному интегралу от трех 𝑥 до четырех 𝑥 от 𝑢 в квадрате
минус три все разделить на 𝑢 в квадрате плюс пять относительно 𝑢.
Нам дана функция 𝑔 от 𝑥. И мы видим, что это определенная интеграл, где оба предела интегрирования являются функциями из 𝑥. И нас просят найти производная этой функции. Поскольку мы пытаемся различать функцию, где пределы интегрирования являются функциями от 𝑥, попробуем сделать это с помощью основной теоремы исчисления.
Начнем с того, что вспомним
следующую часть основной теоремы исчисления. Если строчная 𝑓 является непрерывной
функция на отрезке от 𝑎 до 𝑏, и у нас есть заглавная 𝐹 из 𝑥 — это
определенный интеграл от 𝑎 до 𝑥 строчной 𝑓 от 𝑢 относительно 𝑢, то
заглавное 𝐹 простое число 𝑥 будет равно строчному 𝑓 числа 𝑥 для всех значений 𝑥 в
открытый интервал от 𝑎 до 𝑏. Иными словами, эта часть
Основная теорема исчисления дает нам способ дифференцировать функцию, определенную
по интегралу.
Однако функция, которую мы запрашиваем дифференцировать в вопросе 𝑔 от 𝑥, сильно отличается от нашего определения столица 𝐹 из 𝑥. Во-первых, нижняя граница интегрирование должно быть константой. Однако нам дается это как функция в 𝑥. У нас похожая история верхний предел интегрирования. Это должно быть 𝑥, но мы задана функция из 𝑥. Тем не менее, мы можем обойти оба эти проблемы, используя то, что мы знаем об определенных интегралах и цепочке правило.
Первое, что нам понадобится
вспоминать — одно из наших правил для определенных интегралов. Чтобы обойти проблему не
имея постоянный предел интегрирования, мы собираемся разделить нашу определенную
интеграл на два определенных интеграла. Мы знаем следующее правило для
определенные интегралы. Интеграл от 𝑎 до 𝑏 от 𝑓 от
𝑢 по 𝑢 равно интегралу от 𝑐 до 𝑏 от 𝑓 от 𝑢 с
относительно 𝑢 плюс интеграл от 𝑎 до 𝑐 от 𝑓 от 𝑢 относительно 𝑢.
Но есть несколько важных
информацию об этом правиле, которую нам необходимо уточнить.
Наиболее важным из них является это
будет истинным только в том случае, если наша функция 𝑓 интегрируема во всех этих областях
интеграция. В частности, наша функция 𝑓 должна
быть интегрируемой на отрезке от 𝑏 до 𝑐 и на отрезке от 𝑐
к 𝑎. Мы хотим использовать это, чтобы переписать наш
функция 𝑔 от 𝑥. Таким образом, используя верхний предел
интегрирование в виде четырех 𝑥, нижний предел интегрирования в виде трех 𝑥 и наша функция
строчная буква 𝑓 из 𝑢 как 𝑢 в квадрате минус три разделить на 𝑢 в квадрате плюс пять, мы
получил бы интеграл от 𝑐 до четырех 𝑥 от 𝑢 в квадрате минус три, деленные на 𝑢
квадрат плюс пять относительно 𝑢 плюс интеграл от трех 𝑥 до 𝑐 от 𝑢
в квадрате минус три все разделить на 𝑢 в квадрате плюс пять по отношению к 𝑢.
Но помните, нам также нужны наши функция должна быть интегрируемой в обеих этих областях интеграции. В частности, нам нужно выбрать значение константы 𝑐. В этом случае мы могли бы фактически выбрать любое значение константы 𝑐. Чтобы объяснить почему, давайте посмотрим в нашем подынтегральном выражении. Наше подынтегральное выражение есть частное два многочлена. значит рационально функция. И мы знаем, что рациональные функции будут быть непрерывными во всей своей области. А если функция непрерывна на интервал, то он также интегрируем на этом интервале. Итак, все, что нам нужно сделать, это проверить домен нашей функции в нижнем регистре 𝑓 из 𝑢. Это рациональная функция, поэтому будет определено для всех значений 𝑢, за исключением случаев, когда его знаменатель равен нуль.
А если решить знаменатель 𝑢
квадрат плюс пять равен нулю, мы увидим, что мы не получаем реальных решений.
Таким образом, наш подынтегральная функция определена для всех
реальные значения 𝑢. Это означает, что это непрерывно для всех
действительные значения 𝑢, что означает, что он интегрируем на любом интервале. Так что в этом случае мы действительно можем
выберите любое значение 𝑐. Однако это не всегда будет
случай. В этом случае мы выберем 𝑐
равен нулю. Теперь мы разделили это на два
определенные интегралы, каждый из которых ближе к использованию фундаментальной
теорема исчисления.
Еще немного
манипуляции, которые нам необходимо проделать, прежде чем мы сможем использовать фундаментальную теорему
исчисление. Во втором интеграле мы хотим
поменять местами наши пределы интегрирования. Помните, мы можем сделать это,
умножение всего интеграла на отрицательный. При этом мы переписали наш
второй интеграл как отрицательный, умноженный на определенный интеграл от нуля до трех 𝑥 от
𝑢 в квадрате минус три, все разделить на 𝑢 в квадрате плюс пять по отношению к 𝑢.
И вот мы почти готовы к использованию фундаментальная теорема исчисления для вычисления этих определенных интегралов. Единственная проблема — это наш верхний предел интегрирования является функцией в 𝑥 вместо 𝑥. И есть два способа получить вокруг этой проблемы. Во-первых, мы могли бы использовать замена 𝑣 из 𝑥 равна четырем 𝑥. Тогда мы можем дифференцировать наш первый интеграл с помощью цепного правила. Мы могли бы сделать то же самое с нашим второй интеграл, установив 𝑣 из 𝑥 равным трем 𝑥, а затем оценив его производную с помощью цепного правила. И это сработает. Однако мы можем сделать это и в общий случай с основной теоремой исчисления.
Имеем, если 𝑣 из 𝑥 является
дифференцируемая функция, то с помощью цепного правила мы получаем, если строчная 𝑓 является
непрерывная функция на отрезке от 𝑎 до 𝑏, а заглавная 𝐹 в 𝑥 — это
определенный интеграл от 𝑎 до 𝑣 от 𝑥 строчных 𝑓 от 𝑢 относительно 𝑢, то
заглавная 𝐹 простая из 𝑥 будет равна строчной 𝑓, оцениваемой как 𝑣 из 𝑥, умноженной на d𝑣
на d𝑥, пока 𝑣 из 𝑥 находится в открытом интервале от 𝑎 до 𝑏.
Таким образом, мы смогли переписать наш
версия фундаментальной теоремы исчисления, если 𝑣 из 𝑥 является
дифференцируемая функция только с помощью цепного правила.
И теперь мы можем видеть оба наших определенные интегралы имеют такой вид. Мы установим 𝑣 один из 𝑥 равным четырем 𝑥 и 𝑣 два из 𝑥 будут тремя 𝑥. Обычно мы устанавливаем наше значение 𝑎 равно нулю в обоих случаях, а затем проверить интервалы, на которых наша интегральная функция является непрерывным. Это связано с тем, что для использования фундаментальная теорема исчисления, нам нужно проверить, где находится наше подынтегральное выражение непрерывный. Однако мы уже показали, что наша подынтегральная функция непрерывна для всех действительных значений. Следовательно, он будет непрерывным на любой закрытый интервал.
Теперь мы готовы найти
выражение для 𝑔 простого числа 𝑥.
Мы будем различать каждый из наших
интегралы отдельно. Чтобы продифференцировать наш первый интеграл
используя фундаментальную теорему исчисления, нам нужно проверить, что 𝑣 одно из 𝑥
является дифференцируемым. И это линейная функция, поэтому мы
знать, что оно дифференцируемо. Это означает, что мы можем использовать это, и мы
получить 𝑓 оценивается в 𝑣 один из 𝑥 раз d𝑣 один на d𝑥. И у нас такая же история
второй интеграл. На этот раз 𝑣 двое из 𝑥 будут
три 𝑥, которая также является линейной функцией, поэтому она дифференцируема. Это означает, что нам нужно вычесть 𝑓
оценивается в 𝑣 два раза из 𝑥 d𝑣 два раза d𝑥.
Итак, мы нашли выражение для
𝑔 премьера 𝑥. И мы действительно можем оценить все
эти выражения. Начнем с замены в нашем
выражения для 𝑣 одного из 𝑥 и 𝑣 двух из 𝑥. Это дает нам 𝑔 простое число 𝑥 равно
равно строчной 𝑓, оцененной в четыре 𝑥, умноженной на производную от четырех 𝑥 с
относительно 𝑥 минус строчная 𝑓 оценивается как три 𝑥, умноженные на производную
из трех 𝑥 относительно 𝑥.
И помните, из фундаментального
Теорема исчисления, строчная буква 𝑓 будет нашим подынтегральным выражением. Итак, теперь мы готовы найти
выражение для 𝑔 простого числа 𝑥.
Во-первых, чтобы найти 𝑓 оценивается в четыре 𝑥, мы подставляем 𝑢 равно четырем 𝑥 в наше подынтегральное выражение, что дает нам четыре 𝑥 всего в квадрате минус три все разделить на четыре 𝑥 все в квадрате плюс пять. Далее нам нужно умножить это на производная четырех 𝑥 по 𝑥. Конечно, это линейка. функция, поэтому мы знаем, что производная от нее по 𝑥 будет коэффициент 𝑥, который равен четырем. И мы можем сделать то же самое для найти выражение для нашего второго члена.
Чтобы найти 𝑓 оценивается в три 𝑥,
мы подставляем 𝑢 равно трем 𝑥 в наше подынтегральное выражение, что дает нам три 𝑥 всего
в квадрате минус три все разделить на три 𝑥 все в квадрате плюс пять.
И, конечно же, нам нужно умножить
это производная от трех 𝑥 по 𝑥, которая, как мы знаем, равна трем. Наконец, мы упростим это
выражение путем оценки всех наших показателей и умножения на наши
коэффициенты. И, делая это, мы получаем наш окончательный
отвечать. 𝑔 простое число 𝑥 равно четырем
умножить на 16𝑥 в квадрате минус три, все разделить на 16𝑥 в квадрате плюс пять минус три
умножить на девять 𝑥 в квадрате минус три, все разделить на девять 𝑥 в квадрате плюс пять.
Производная интегральной формулы
Производная — это термин, который относится к чему-либо, происходящему или основанному на другой вещи. Его можно использовать в прямом или переносном смысле. Неотъемлемая часть любого уравнения, производная может использоваться для вычисления изменения функции в заданные моменты времени. Его также можно использовать как инструмент для оптимизации и стабильности. Вот несколько примеров производных в действии: — В спорте производная используется для определения того, насколько быстро игрок ускоряется, замедляется или поворачивает.
— В финансах деривативы используются для хеджирования рисков. – В инженерии производные могут помочь стабилизировать конструкции во время землетрясений или других стихийных бедствий.
Производная интеграла — это функция, описывающая изменение значения интеграла во времени. Производную можно рассматривать как «спидометр» для подынтегральной функции, говорящий нам, как быстро она движется во времени.
Производные важны для решения задач, связанных с интегралами. Например, если мы хотим найти площадь под кривой, нам нужно найти ее производную. А для решения задач, связанных с производными, нам нужно знать некоторые основные свойства производных.
Существуют три основных свойства производных:
1) Производные аддитивны: если две производные существуют и дифференцируемы в данной точке, то их сумма также дифференцируема в этой точке. Это называется цепным правилом.
2) Производные дистрибутивны: если y — функция, а x — переменная, то dy/dx = (y(x+d)/y(x))*d, где d — любое число, отличное от 0.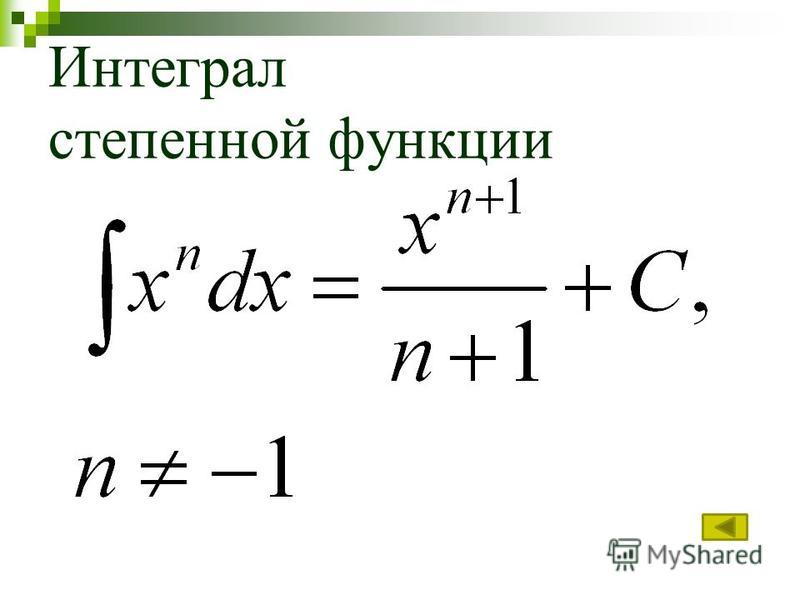
Это свойство позволяет нам интегрировать функции по произвольным интервалам, используя частичные дроби.
3) Производные являются обратными: для данной функции f(x) существует обратная функция f-1(x) такая, что f(x) = f-1(x)(f (x-1)+f — 2(х)) . Другими словами, обращение всех производных по x возвращает нам исходную функцию.
Что такое производная интеграла?Интеграл — это математическая функция, которая имеет дело с изменениями в заданной площади или объеме. Его можно использовать для расчета скорости изменения, производной и интеграла различных переменных. Производная интеграла — это скорость изменения в определенной точке пространства или времени. Его можно рассчитать с помощью следующего уравнения:
, где «dx» — изменение значения «x», «dy» — изменение значения «y», а «dv» — изменение значения «v». Производные для разных переменных можно комбинировать для создания более сложных уравнений. Например, если мы хотим найти производную для функции, которая принимает два разных значения, мы должны использовать следующее уравнение:
Второе уравнение исходит из рассмотрения функций как скоростей, то есть во сколько раз их входные данные изменяются на единицу.
время. Это позволяет нам объединить несколько производных вместе в одно уравнение, с которым становится намного проще работать.
Производные интегралов сложно вычислить, но они могут помочь понять свойства исходной функции. В этой статье мы рассмотрим некоторые распространенные проблемы с производными и их решения.
Сначала начнем с простого примера: вычисляем производную функции в точке x0. Для этого нам нужно найти наклон линии, соединяющей x0 и график функции в этой точке. Мы можем сделать это, найдя точку пересечения по оси y линии (x0 + h) на графике, а затем используя эту информацию для вычисления расстояния h от x0.
Чтобы усложнить задачу, давайте рассмотрим уравнение, описывающее кривую. Например, рассмотрим y = mx + c. Это уравнение определяет кривую на плоскости, называемую линейным уравнением. Наклон этой линии равен m, и он говорит нам, насколько круто линия спускается от x1 к x2. Его также можно рассматривать как указание на то, насколько изменяется y на каждую единицу изменения x с 1 на 2.
Теперь давайте посмотрим на другое уравнение, описывающее кривую: y = f(x). Это уравнение определяет кривую траекторию, называемую функциональным уравнением. Наклон этой линии также равен f(), и он говорит нам, насколько изменяется y на каждую единицу изменения x от 0 до 1. Обратите внимание, что этот наклон не всегда равен 9.0005
Что такое производная?Производная — это математическая функция, представляющая изменение значения переменной во времени. Производные можно использовать для расчета скорости изменений, прогнозирования будущих значений и анализа поведения систем.
Существует несколько различных типов деривативов, каждый из которых имеет свои особенности использования. Наиболее распространенными производными являются те, которые представляют скорость изменения: наклон и точка пересечения. Наклон представляет собой изменение y с течением времени как функцию x, а точка пересечения представляет собой точку, в которой кривая пересекает ноль (или x=0).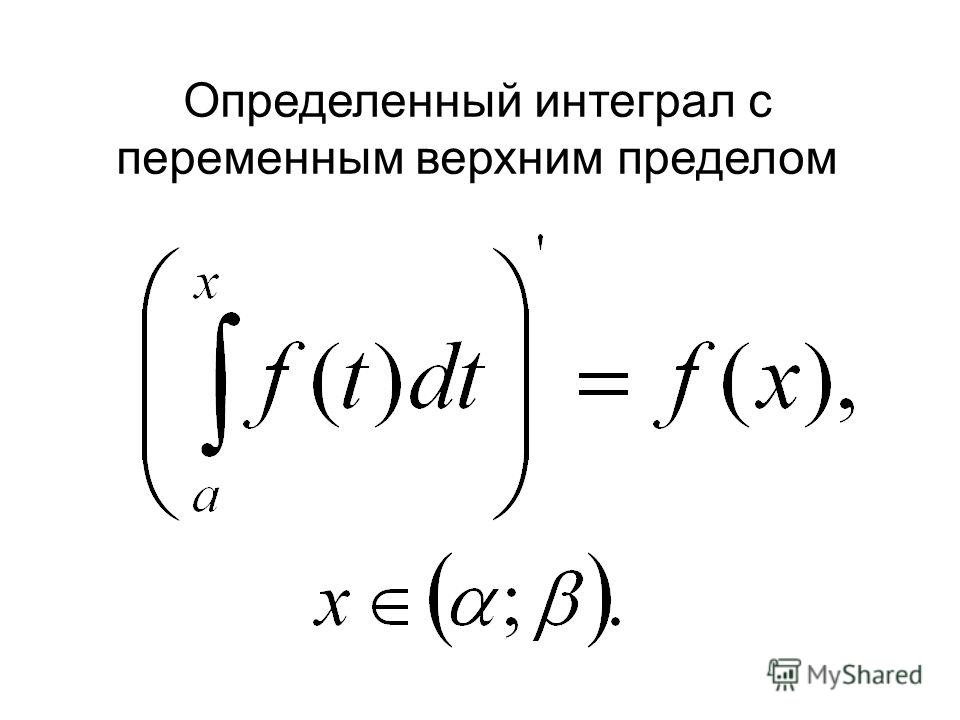
Другие производные включают ПРОИЗВОДНЫЕ ИНТЕГРАЛА, ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ 9.0005
В исчислении интеграл — это математическая операция, позволяющая вычислять площади под кривыми. Интеграл принимает два входа: начальную точку (x 0 ) и конечную точку (x). Он вычисляет площадь под кривой между этими точками, используя простые алгебраические формулы.
Самый распространенный тип интеграла известен как непрерывный интеграл. Это означает, что его можно применить к любой кривой, а не только к прямым линиям. Непрерывные интегралы играют важную роль в физике и технике, потому что они позволяют нам вычислять такие вещи, как полная энергия или объем во времени.
Однако существует еще один вид интеграла, называемый производной. Производная — это просто другое название среднего — это то, что мы используем, когда хотим рассчитать, как что-то меняется с течением времени.
Типы производных
Существует много типов производных, но здесь мы рассмотрим только два: линейный и нелинейный.
Линейные производные легче всего понять, поэтому мы начнем с них. Линейная производная — это функция, которая принимает один вход (x) и выдает другой (y), где выход зависит только от входа, а не от каких-либо других переменных. Примером линейной производной является y = x2. Чтобы вычислить линейную производную, вы просто подставляете входные данные и используете оператор производной (d):
Анализ данных
Нелинейные производные немного сложнее, но они могут быть очень полезны при анализе данных. Нелинейная производная — это функция, которая принимает один вход (x) и выдает другой (y), где выход зависит не только от входа, но и от других переменных, называемых производными от x по y. Примером нелинейной производной является y = f(x). Чтобы вычислить нелинейную производную, сначала нужно найти все производные от x по y. Затем используйте эти производные, чтобы изобразить их на графике, подобном этому:
Когда у вас есть график, вы можете использовать его, чтобы узнать, как изменение одной переменной влияет на другую переменную.
Интеграл — это математическая функция, которая принимает входные данные и возвращает значение с течением времени. Существует множество различных типов интегралов, но наиболее распространенным является неопределенный интеграл. Неопределенный интеграл — это функция, которая принимает неопределенные входные данные и вычисляет результат за неопределенное количество шагов.
Основная идея вычисления неопределенного интеграла состоит в том, чтобы найти сумму всех бесконечных рядов, возникающих из заданной функции. Эту сумму может быть очень сложно вычислить, поэтому важно понимать, как дифференцировать неопределенные интегралы. Дифференцирование неопределенного интеграла включает в себя разбиение функции на более мелкие части, решение соответствующих частных производных, а затем объединение этих результатов для получения окончательного ответа.
Дифференцировать неопределенный интеграл может быть сложно, но с практикой это становится намного проще.
И если вы когда-нибудь столкнетесь с проблемой, связанной с дифференциацией, не волнуйтесь — существует множество онлайн-ресурсов, которые могут вам помочь.
Производная определенного интеграла — это концепция исчисления, которая позволяет вычислять скорости изменения или производные. Его можно рассматривать как наклон графика, изображающего скорость, с которой функция изменяется во времени. Производные широко используются в инженерных и научных расчетах и могут дать представление о проблемах, которые в противном случае было бы трудно решить.
Чтобы вычислить производную интеграла, нам сначала нужно найти исходную функцию и ее производную. Мы делаем это, подставляя нашу исходную функцию в уравнение под интегралом:
Теперь, поскольку наша подынтегральная функция является функцией, мы можем интегрировать обе части, чтобы получить нашу производную:
Мы также можем записать эту информацию в полярной форме, чтобы с ней было легче работать:
Теперь, когда у нас есть наша производная, мы необходимо использовать его в нашем расчете скорости изменения.
Для этого нам нужно преобразовать его обратно в декартовы координаты (x-, y-):
Затем нам нужно найти, как быстро меняется каждая переменная в любой заданный момент времени:
Наконец, мы можем сложить их. по всем точкам пространства (или времени) и получаем нашу скорость изменения для каждой переменной:
Существует несколько производных интеграла, которые могут быть полезны при решении задач. Наиболее распространенными производными являются секанс, тангенс и косеканс. Эти производные можно использовать для нахождения решений линейных уравнений с одной или двумя переменными. Кроме того, эти производные также можно использовать для нахождения пределов и точек перегиба.
Сеанс получается из интеграла путем взятия производной по x:
Тангенс получается из интеграла путем взятия производной по y:
Косеканс получается из интеграла путем взятия производной по x и y:
Когда оба предела имеют переменные В исчислении производные являются важными инструментами для управления функциями.
Производные интеграла можно использовать для нахождения наклона функции в определенной точке или для нахождения максимального или минимального значения функции в наборе точек. В этой статье мы рассмотрим два распространенных примера: вывод производной уравнения и поиск производной функционала.
Вывод производной уравнения
Чтобы вывести производную уравнения, нам сначала нужно определить аллювиальные термины и термины в квадратных скобках. Аллювиальные термины — это термины, которые представляют изменение величины (т. Е. Они увеличиваются или уменьшаются), в то время как заключенные в скобки термины — это просто термины, которые содержат как аллювиальные, так и интегративные термины (т. Е. Они оба увеличиваются или уменьшаются). Чтобы определить, какой термин есть какой, мы используем следующее правило: если термин аллювиальный (не содержащий интегративного термина), то он заключается в скобки; в противном случае он является интегративным. Вот пример:
y = 4x + 7
В этом уравнении есть три аллювиальных члена (y = 4x + 7), один заключенный в квадратные скобки член (y = 3x + 6) и один интегральный член (y = x + 3).
Чтобы определить, какой термин есть какой, мы используем следующее правило: если термин аллювиальный (не содержащий интегративного термина), то он заключается в скобки; в противном случае он является интегративным. Вот
Когда один из пределов является константой, производная становится алгебраической функцией. В этом случае производные могут быть представлены частными производными и первообразными. Частные производные обозначаются греческими буквами дельта (?), мю (?) и сигма (?), а первообразные обозначаются буквой гамма (?). Эти символы могут быть сокращены как d(?), m(?) и s(?).
Основной принцип при работе с деривативами заключается в том, чтобы сначала определить предел, когда он приближается к определенному значению. Это можно сделать путем дифференциации или интеграции. Если функция задана в двух точках пространства, то предел ее производной в этих точках можно найти дифференцированием. Если функция задана в нескольких точках пространства, то предел ее производной в этих точках можно найти с помощью интегрирования.