Средняя линия треугольника ABC: определение, свойства, признак, длина
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Что такое средняя линия треугольника
В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала.
- Определение средней линии треугольника
- Свойства средней линии треугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Признак средней линии треугольника
- Пример задачи
Определение средней линии треугольника
Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.
- KL – средняя линия треугольника ABC
- K – середина стороны AB: AK = KB
- L – середина стороны BC: BL = LC
Свойства средней линии треугольника
Свойство 1
Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.
На рисунке выше:
- KL параллельна AC
- KL = 1/2 ⋅ AC
Свойство 2
Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.
На рисунке выше:
- △KBL ∼ △ABC (подобие по пропорциональности всех сторон)
- Стороны △KBL в два раза меньше соответствующих сторон △ABC:
AB = 2KB, BC = 2BL, AC = 2KL. - S△ABC = 4 ⋅ S△KBL
Свойство 3
В любом треугольнике можно провести три средние линии.
KL, KM и ML – средние линии треугольника ABC.
- KL || AC, KL = 1/2 ⋅ AC
- KM || BC, KM = 1/2 ⋅ BC
- ML || AB, ML = 1/2 ⋅ AB
Свойство 4
Три средние линии треугольника делят его на 4 равных по площади треугольника.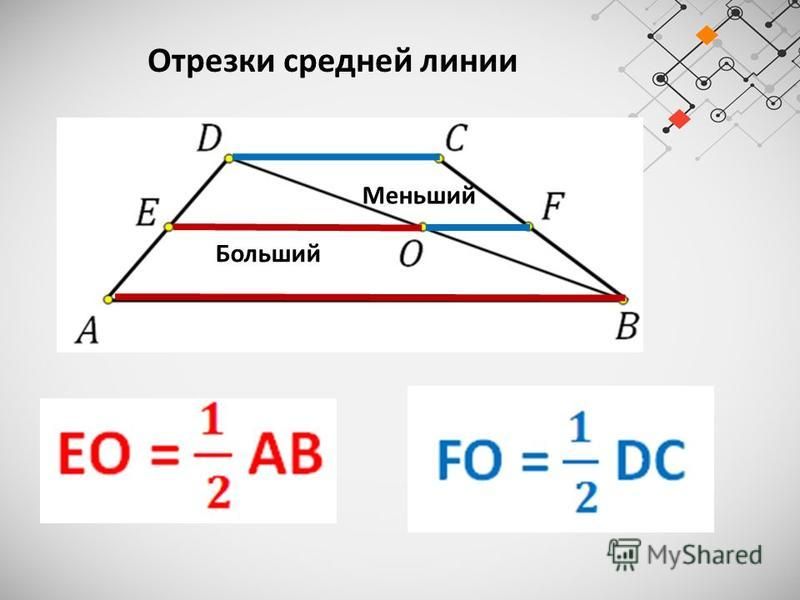
S1 = S2 = S3 = S4
Признак средней линии треугольника
Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.
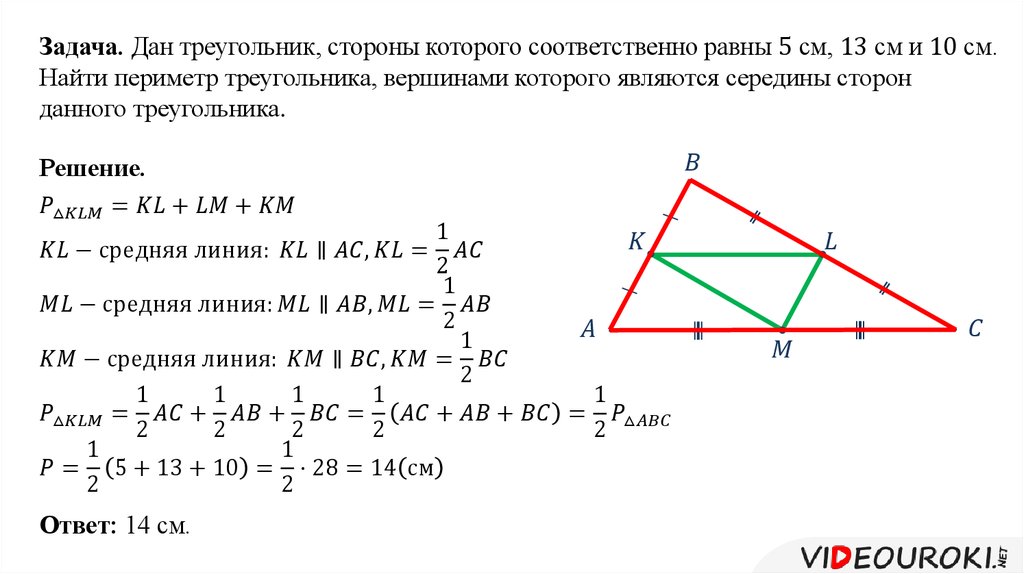
Пример задачи
Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.
Решение
Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.
Мы можем найти гипотенузу, воспользовавшись теоремой Пифагора.
BC2 = AB2 + AC2 = 62 + 82 = 100.
BC = 10.
Таким образом, средняя линия LM = 1/2 ⋅ BC = 1/2 ⋅ 10 = 5.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Боковое ребро правильной треугольной призмы равно 9 см,а диагональ боковой грани равна 15 см. Найти площадь боковой и полной поверхности
призмы
Найти площадь боковой и полной поверхности
призмы
Решено
На предприятии работают несколько сотрудников, зарплата каждого составляет целое число тугриков (разные сотрудники могут иметь разную зарплату). Инкассаторы привезли на предприятие 100 монет по 1
В варианте олимпиады 7 задач, каждая оценивается в 8 баллов (за задачу можно получить целое число от 0 до 8 баллов включительно). По результатам
Докажите что если на рисунке углы С и D прямые и MD=KC,то треугол MKC = треугол KMD
Медиана равностороннего треугольника равна 13√3.Найдите его сторону. Решение плиз
Пользуйтесь нашим приложением
Билет № 10
Теорема о средней линии трапеции.
Формулы площади треугольника. Запись, вывод одной из них.
Вопрос № 1 Теорема о средней линии трапеции
Трапецией называется четырёхугольник, у которого
две стороны параллельны, а две другие
стороны не параллельны.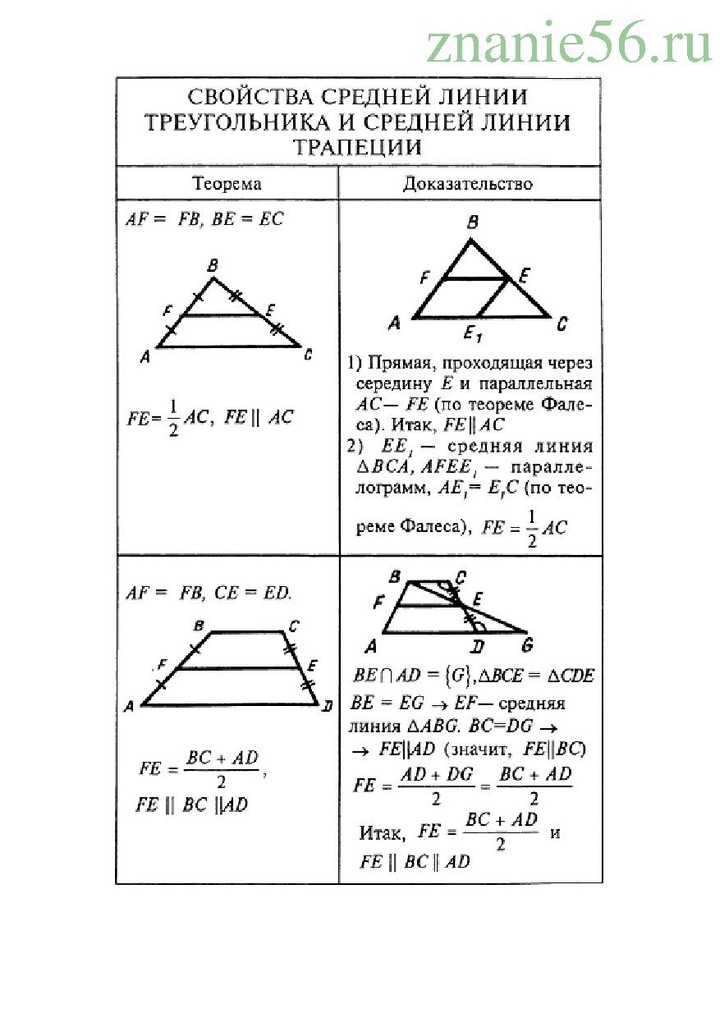 Параллельные
стороны трапеции называются её основаниями, а
непараллельные стороны — боковыми сторонами.
Параллельные
стороны трапеции называются её основаниями, а
непараллельные стороны — боковыми сторонами.
На рисунке ABCD — трапеция, ВС || AD, ВС и AD — основания, АВ Ц CD, АВ и CD — боковые стороны.
Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.
B C
Дано: ABCD — трапеция, ВС || AD, MN — средняя линия.
Доказать: MN
|| ВС, MN
|| AD,
MN = 2 (BC + AD).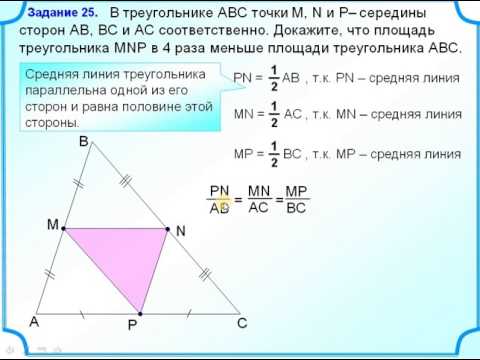
A
Доказательство
По правилу многоугольника сложения нескольких векторов
MN = MB + BC + CN и MN = MA + AD + DN. Сложив эти равенства, получим
2mN = (MB+MA)+ (BC + ~AD)+ (CN + DN ).
По условию теоремы MN — средняя линия трапеции, поэтому M и N — середины сторон АВ и CD, а MB и MA, CNиDN — противоположные векторы. Так как сумма противоположных векторов равна нулевому вектору, то MB + MA = 0 и CN + DN = 0. Следовательно, 2MN = BC + AD, отсюда MN =1 (BC + AD).
Так
как BC
tt
AD ,
то MN
tt
BC
и MN
tt
AD,
а длина вектора
BC + AD равна
BC + AD. Отсюда следует, что
MN
||
ВС,
MN
||
AD
и
MN =1 (BC
+ AD).
Отсюда следует, что
MN
||
ВС,
MN
||
AD
и
MN =1 (BC
+ AD).
Итак, средняя линия трапеции параллельна основаниям и равна их полусумме.
Ч.т.д.
Вопрос № 2
Формулы площади треугольника. Запись, вывод одной из них
Одну из сторон треугольника часто называют его основанием. Если основание выбрано, то под словом «высота» подразумевают высоту треугольника, проведенную к основанию.
Теорема. Площадь треугольника равна половине произведения его основания на высоту.
a
Рис. 1 C D
Дано: D АВС, АВ = а, СН = h.
Доказать: SDАВС = 2ah.
Доказательство
Достроим
треугольник АВС до
параллелограмма ABDC так, как показано на рисунке 1.
Итак, площадь треугольника равна половине произведения его основания на высоту.
Ч.т.д.
SA = 1 aha =1 bhb = 1 chc2 2 2
a
Площадь прямоугольного треугольника
Sa
b
Площадь прямоугольного треугольника равна половине произведения его катетов.
ab
A(bcosC;b sinC )
Теорема. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Дано: А АВС, ВС = а, АС = b.
Доказать: S = —ab sin C.
Доказательство
Введем
прямоугольную систему координат так,
чтобы точка С совпала
с началом координат, точка В лежала
на положительной полуоси Ох, а точка А имела
положительную ординату, тогда вершины
треугольника будут иметь координаты С (0; 0), В (а; 0), A(bcosC; bsinC).
Площадь данного треугольника можно вычислить по формуле S = — ah, где h — высота треугольника. Но h равна ординате точки А, т.е. h = b sin C. Следовательно, S = 1 ab sin C.
2
Итак, площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Ч.т.д.
Формула Герона
S = V p (p —a Xp —b )(p —c),
где а, b, с — стороны треугольника,
р — полупериметр треугольника,
Р
= 2 (а + b + с).
a
Площадь равностороннего треугольника
S
где а — сторона треугольника.
Средняя линия треугольника — свойства, признаки и формулы » Kupuk.net
Одним из важных понятий, с помощью которого легко решается целый класс задач по геометрии, является средняя линия треугольника.
Разберём данное понятие, рассмотрим свойства, и научимся правильно решать задачи на эту тему.
Определение и признаки средней линии треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.
Отрезок, у которого один из концов совпадает с серединой одной из сторон, другой находится на второй стороне, проведённый параллельно третьей стороне, является средней линией треугольника.
Доказательство следует из теоремы Фалеса.
Теорема о средней линии треугольника
Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.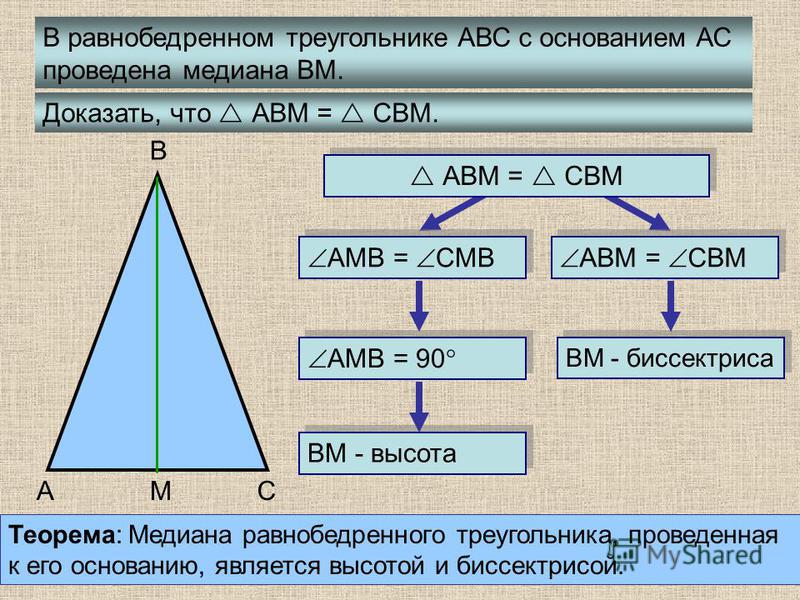
Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.
Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.
По определению, MN – средняя линия ΔABC.
Необходимо доказать, что MN II AC, MN = ½AC.
Доказательства
Первый способ
Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.
Следовательно, MN II AC.
Пусть NP II AB.
Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.
Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.
Доказано.
Второй способ
Рассматриваются треугольники MBN и ABC. В них угол B является общим,
По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.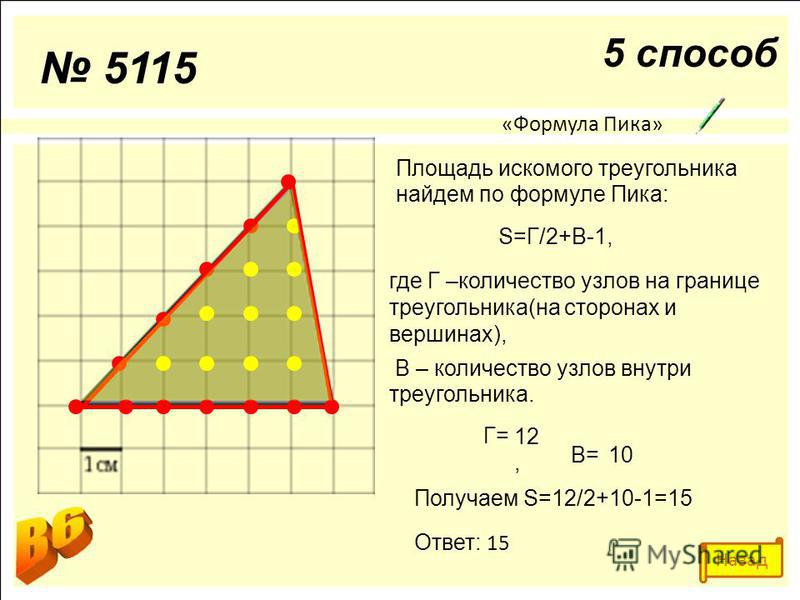
Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.
Формула MN = ½AC следует из условий
поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.
Доказано.
Третий способ
Рассматривается сумма векторов
Поскольку в результате образуется замкнутая ломаная, то
Отсюда следует, что
Так как
то
Из последнего равенства следуют условия теоремы.
Доказано.
Следствия из теоремы с доказательствами
Следствие №1
Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.
Доказательство.
По определению стороны AB и BC делятся пополам, поэтому
Согласно теореме,
Из третьего признака подобия вытекает рассматриваемое свойство.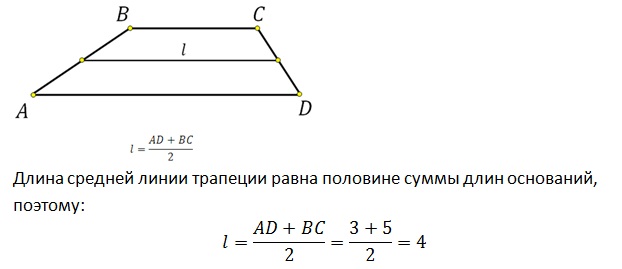
Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как
Доказано.
Следствие №2
Три средних линии треугольника разбивают его на четыре равных треугольника, подобные заданному, с коэффициентом подобия ½.
Доказательство.
Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.
Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.
Таким образом: ∠BNM = ∠BCA = ∠MPA.
Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.
Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.
Равенство остальных пар треугольников доказывается аналогично.
По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½. Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.
Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.
Доказано.
Свойства средней линии треугольника
Теорема и следствия из неё составляют основные свойства средней линии треугольника.
Согласно второму утверждению, вид большого треугольника такой же, как и у маленьких. То есть для равностороннего и равнобедренного треугольников средние линии отсекают равносторонние и равнобедренные треугольники.
Высоты тупоугольного треугольника, проведённые к тупому углу из вершин острых, располагаются вне треугольника. Поэтому часто рассматривают не саму среднюю линию, а её продолжение. Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.
Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.
Биссектриса угла треугольника точкой пересечения со средней линией также делится пополам.
Средняя линия прямоугольного треугольника
Для прямоугольного треугольника две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе.
Остроугольный разносторонний треугольник не имеет средних линий, обладающих подобными характеристиками.
Пример решения задачи
Доказать, что середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.
Решение.
Проводя диагональ четырёхугольника, получают разбиение на два треугольника, в каждом из которых построена средняя линия, параллельная по основной теореме диагонали, как основанию.
Так как две прямые, параллельные третьей, параллельны между собой, то противолежащие стороны образованного средними линиями четырёхугольника параллельны.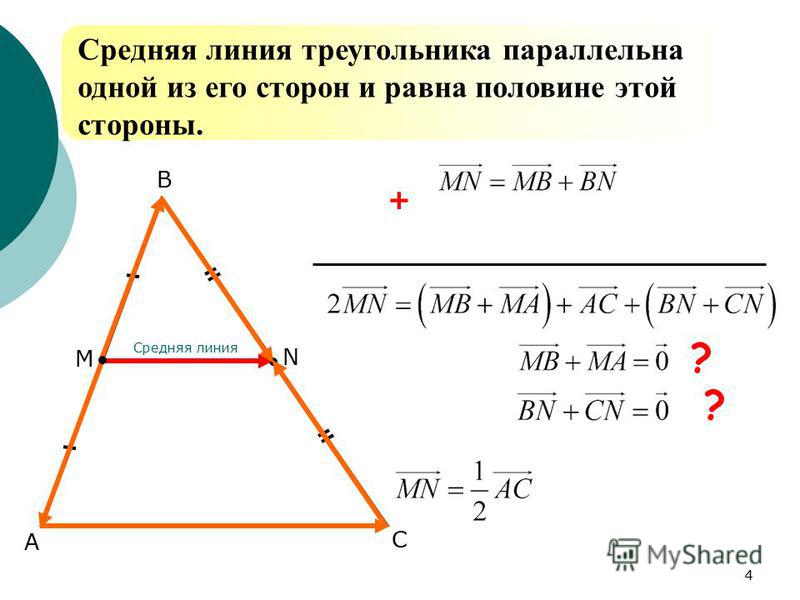
Аналогично доказывается параллельность двух других сторон нового четырёхугольника. По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.
Доказано.
Как найти площадь через среднюю линию треугольника
Главная » Компьютеры
На чтение 4 мин Просмотров 1. 6к. Опубликовано
6к. Опубликовано
Содержание
- Содержание
- Средняя линия треугольника [ править | править код ]
- Свойства [ править | править код ]
- Признаки [ править | править код ]
- Средняя линия четырёхугольника [ править | править код ]
- Свойства [ править | править код ]
- Средняя линия трапеции [ править | править код ]
Средняя линия фигур в планиметрии — отрезок, соединяющий середины двух сторон данной фигуры. Понятие употребляется для следующих фигур: треугольник, четырёхугольник, трапеция.
Содержание
Средняя линия треугольника [ править | править код ]
Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника [1] .
Свойства [ править | править код ]
- средняя линия треугольника параллельна основанию и равна его половине.
- средняя линия отсекает треугольник, подобный и гомотетичный исходному с коэффициентом 1/2; его площадь равна одной четвёртой площади исходного треугольника.

- три средние линии делят исходный треугольник на четыре равных треугольника. Центральный из этих треугольников называется дополнительным или серединным треугольником.
Признаки [ править | править код ]
- Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок – средняя линия.
Средняя линия четырёхугольника [ править | править код ]
Средняя линия четырёхугольника — отрезок, соединяющий середины противолежащих сторон четырёхугольника.
Свойства [ править | править код ]
Первая линия соединяет 2 противоположные стороны. Вторая соединяет 2 другие противоположные стороны. Третья соединяет центры двух диагоналей (не во всех четырёхугольниках диагонали пунктом пересечения делятся пополам).
- Если в выпуклом четырёхугольнике средняя линия образует равные углы с диагоналями четырёхугольника, то диагонали равны.
- Длина средней линии четырёхугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.

- Середины сторон произвольного четырёхугольника — вершины параллелограмма. Его площадь равна половине площади четырёхугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона;
- Последний пункт означает следующее: В выпуклом четырёхугольнике можно провести четыре средние линии второго рода. Средние линии второго рода – четыре отрезка внутри четырёхугольника, проходящие через середины его смежных сторон параллельно диагоналям. Четыре средние линии второго рода выпуклого четырёхугольника разрезают его на четыре треугольника и один центральный четырёхугольник. Этот центральный четырёхугольник является параллелограммом Вариньона.
- Точка пересечения средних линий четырёхугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является центроидом вершин четырёхугольника.
- В произвольном четырёхугольнике вектор средней линии равен полусумме векторов оснований.

Средняя линия трапеции [ править | править код ]
Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции. Отрезок, соединяющий середины оснований трапеции, называют второй средней линией трапеции.
Она рассчитывается по формуле: E F = A D + B C 2 <displaystyle EF=<frac <2>>> , где AD и BC — основания трапеции.
07.06.2019
5 июня Что порешать по физике
30 мая Решения вчерашних ЕГЭ по математике
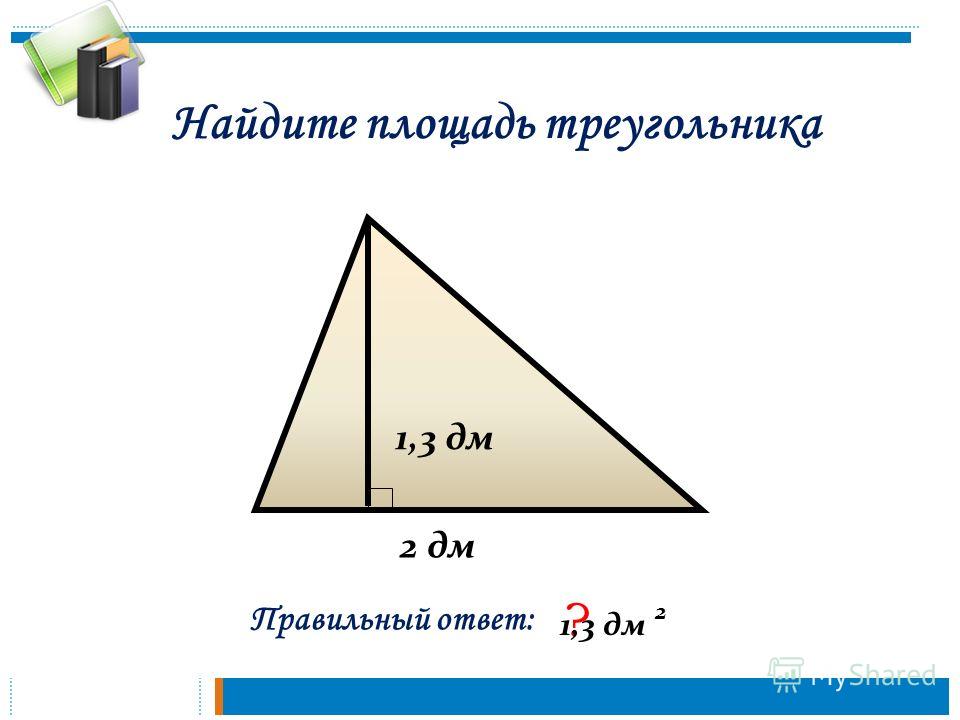
Площадь треугольника ABC равна 176, DE — средняя линия. Найдите площадь треугольника CDE.
Средняя линия отсекает от треугольника подобный ему с коэффициентом подобия Площади подобных фигур относятся как квадрат коэффициента подобия. Тогда
Выясним, как связаны средняя линия треугольника и его площадь.
I. Площадь треугольника равна половине произведения основания на высоту, проведённую к этой стороне:
Поскольку средняя линия треугольника, соединяющая середины двух сторон, равна половине третьей стороны:
то можно найти площадь треугольника через его среднюю линию:
Площадь треугольника равна произведению средней линии и высоты, перпендикулярной этой средней линии.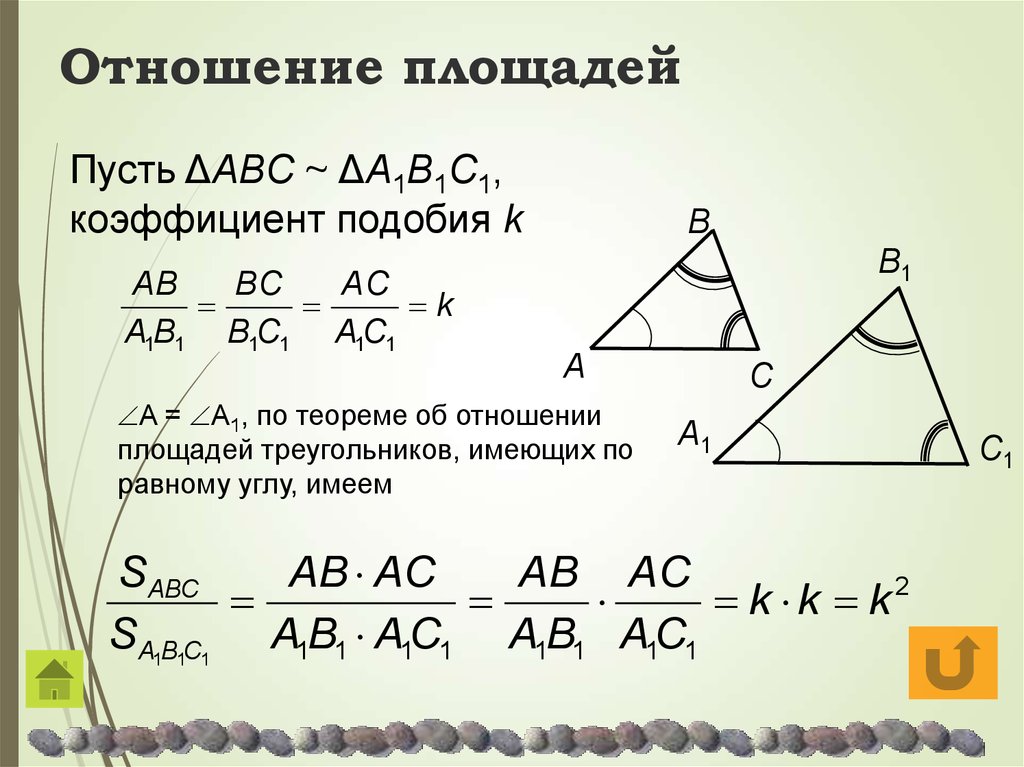
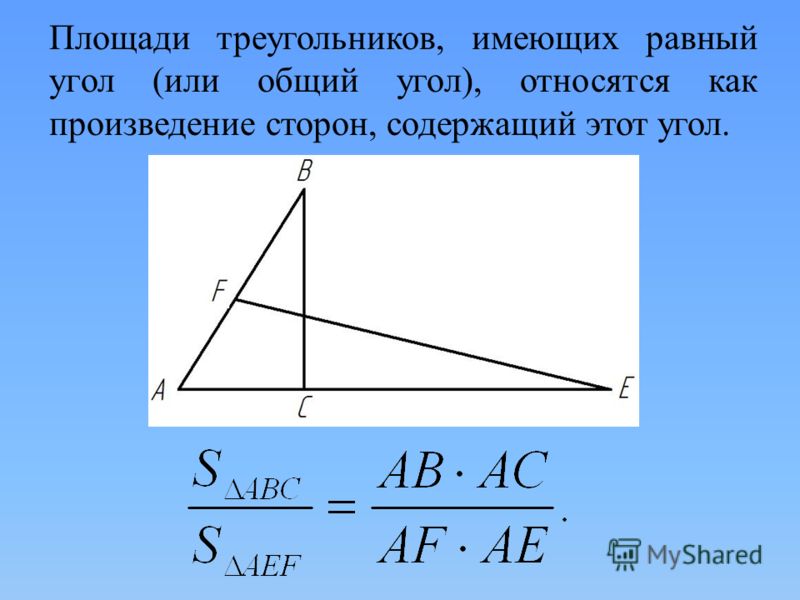
II.Прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от него подобный треугольник.
Если MN- средняя линия треугольника ABC и MN параллельна AC, то треугольники ABC и MBN подобны.
Так как площади подобных треугольников относятся как квадраты их соответствующих сторон, то
Средняя линия треугольника отсекает от него треугольник, площадь которого равна четверти площади исходного треугольника.
Например, если площадь треугольника ABC равна 40 см², то средняя линия MN, параллельная стороне AC, делит его площадь на части:
Площадь трапеции AMNC составляет три четверти площади треугольника ABC
или может быть найденакак разность площадей треугольников ABC и MBC.
ГДЗ по геометрии 8 класс Смирнов, Туяков Решебник
Повторение курса геометрии 7 класса
Глава 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
Глава 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Глава 3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Глава 4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
§1.
 Ломаные
Ломаные1 2 3 4 5 6 7 8 9 10 11 12
§2.
 Многоугольник
Многоугольник1 2 3 4 5 6 7 8 9 10 11 12 13 14
§3.
 Сумма углов выпуклого многоугольника
Сумма углов выпуклого многоугольника1 2 3 4 5 6 7 8 9 10 11 12 13
§4.
 Параллелограмм
Параллелограмм1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
§5.
 Признаки параллелограмма
Признаки параллелограмма1 2 3 4 5 6 7 8 9 10 11 12 13 14
§6.
 Прямоугольник
Прямоугольник1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
§7.
 Ромб, квадрат
Ромб, квадрат1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
§8.
 Средняя линия треугольника
Средняя линия треугольника1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
§9.
 Трапеция
Трапеция1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
§10.
 Средняя линия трапеции
Средняя линия трапеции1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
§11.
 Теорема Фалеса. Пропорциональные отрезки
Теорема Фалеса. Пропорциональные отрезки1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
§12.
 Замечательные точки треугольника
Замечательные точки треугольника1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
§13.
 Тригонометрические функции острого угла
Тригонометрические функции острого угла1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
§14.
 Теорема Пифагора
Теорема Пифагора1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39
§15.
 Тригонометрические тождества
Тригонометрические тождества1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
§16.
 Решение прямоугольных треугольников
Решение прямоугольных треугольников1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41
§17.
 Тригонометрические функции прямого и тупого углов
Тригонометрические функции прямого и тупого углов1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
§18.
 Практические задачи на нахождение расстояний и углов
Практические задачи на нахождение расстояний и углов1 2 3 4 5 6 7 8 9 10 11 12 13 14
§19.
 Понятие площади. Площадь прямоугольника
Понятие площади. Площадь прямоугольника1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
§20.
 Площадь параллелограмма
Площадь параллелограмма1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
§21.
 Площадь треугольника
Площадь треугольника1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
§22.
 Площадь трапеции
Площадь трапеции1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
§23.
 Площадь многоугольника
Площадь многоугольника1 2 3 4 5 6 7 8 9 10
§24.
 Равновелнкость и равносоставленность
Равновелнкость и равносоставленность1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
§25.
 Координаты точек
Координаты точек1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
§26.
 Расстояние между двумя точками. Уравнение окружности
Расстояние между двумя точками. Уравнение окружности1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
§27.
 Уравнение прямой
Уравнение прямой1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
§28.
 Аналитическое задание фигур на плоскости
Аналитическое задание фигур на плоскости1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Повторение курса геометрии 8 класса
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114
Вопросы
§1 §2 §3 §4 §5 §6 §7 §8 §9 §10 §11 §12 §13 §14 §15 §16 §17 §19 §20 §21 §22 §23 §24 §25 §26 §27 §28
Проверь себя
Глава 1 Глава 2 Глава 3 Глава 4
Навыки работы с простейшими геометрическими фигурами школьники получают уже в младших классах, изучая курс общей математики начальной школы. Но тогда они осваивали очень простые и достаточно интересные темы. А сейчас начинается сложная и кропотливая работа с предметом. Необходимо доказывать не всегда понятные теоремы и запоминать аксиомы. Очень часто необходим совет – как понять и закрепить нюансы каждой темы. Именно для помощи в выполнении этой важной задачи и разработан персональный онлайн-репетитор.
Но тогда они осваивали очень простые и достаточно интересные темы. А сейчас начинается сложная и кропотливая работа с предметом. Необходимо доказывать не всегда понятные теоремы и запоминать аксиомы. Очень часто необходим совет – как понять и закрепить нюансы каждой темы. Именно для помощи в выполнении этой важной задачи и разработан персональный онлайн-репетитор.
Решебник по геометрии за 8 класс Смирнов поможет понять предмет
Геометрия – наука очень требовательная. Ученик должен досконально разбираться в теории, уметь применять многочисленные формулы (которые, к тому же, надо запомнить), потребуется чертёжный навык, хорошие способности к расчётам, а самое сложное – умение мыслить пространственно, разбираясь в двухмерных и трёхмерных проекциях. Безусловно, нередко возникают проблемы с такой трудной наукой не только у гуманитариев, но у любителей точных наук. Поэтому невозможно переоценить огромную поддержку виртуального консультанта, в качестве которого и выступает сборник готовых домашних заданий по геометрии для учащихся восьмых классов средних школ.
Основные плюсы решебника по геометрии для 8 класса 8 класс Смирнов В. А., Туяков Е. А.
Преимущества ГДЗ следующие:
- В решебнике пошагово показан алгоритм выполнения задач на основе аксиом и теорем.
- Ко всем ответам прилагаются изображения, что в разы упрощает понимание задания.
- Добавлены различные схемы и правила для лучшего усвоения.
Если вы родители восьмиклассника, и понимаете, что школьник сильно отстаёт по программе, не понимает учителя или репетитора, то можете обратиться за помощью к решебнику. ГДЗ с лёгкостью поможет ребенку в следующем: выполнение домашней работы по геометрии, подготовка к предстоящей контрольной и понимание школьного материала. Благодаря решебнику, ученик сможет решить задания на уроке и дома самостоятельно. В пособие включены готовые ответы и пояснения к темам об элементарных математических операциях, рассматриваются геометрические тела. Сверяя свои ответы с теми, которые приведены в пособии, ребенок станет более самостоятельным, научится выявлять ошибки и своевременно исправлять их.
Плюсы ГДЗ для родителей
Решебник существенно экономит время мам и пап, помогая вместе с ребенком понять геометрию быстро и легко. Взрослые могут дольше заниматься домашними делами, или же просто отдыхать после трудового дня. Сборник помогают быстрее проверять уроки, предоставляя взрослым возможность проводить как можно большее количество времени в кругу своей семьи.
Середина треугольника — Cuemath
Замкнутая фигура, состоящая из трех отрезков, образует форму треугольника.
Давайте познакомимся с миром треугольников
Треугольник состоит из множества частей. Например, углы, стороны, медиана, середина, середина и т. Д. Вот занятие для вас. Теперь вы можете визуализировать различные типы треугольников в математике на основе их сторон и углов. Попробуйте изменить положение вершин, чтобы понять связь между сторонами и углами треугольника.
В последней части этой главы мы обсудим середину и средние сегменты треугольника.
Для любых двух точек, скажем, \(A\) и \(C\), середина — это точка \(B\), расположенная посередине между точками \(A\) и \(B\).
Заметим, что точка \(B\) равноудалена от \(A\) и \(C\).
Средняя точка существует только для линейного сегмента.
Линия, соединяющая среднюю точку, называется серединой.
В этом мини-уроке мы исследуем мир середины треугольника, находя ответы на такие вопросы, как что такое середина треугольника, теорема о середине треугольника и доказательство с помощью интерактивных вопросов.
Итак, приступим!
План урока| 1. | Что такое середина треугольника? |
| 2. | Важные примечания о средней линии треугольника |
| 3. | Решенные примеры на средней линии треугольника |
| 4. | Интерактивные вопросы о середине треугольника |
| 5. | Сложный вопрос о средней части треугольника |
Средняя линия треугольника – это отрезок, соединяющий середины или центр двух противоположных или смежных сторон треугольника
На приведенном выше рисунке D – это середина AB и E — середина AC.
Здесь DE — средняя линия треугольника ABC.
Теорема о середине треугольника
Теорема о середине сегмента утверждает, что отрезок, соединяющий середины любых двух сторон треугольника, параллелен третьей стороне треугольника и составляет ее половину.
В треугольнике ABC имеем
\(AD=DB\) и \(AE=EC\)
Тогда по теореме о средней линии \dfrac{1}{2}\ до н.э.\)
Аналогично,
\(AD=DB\) и \(BF=FC\)
Тогда по теореме о срединном отрезке
\(DF∥AC\) и \(DF=\dfrac{1}{2 }\ AC\)
Аналогично,
\(AE=EC\) и \(BF=FC\)
Тогда по теореме о середине отрезка
\(EF∥AB\) и \(EF=\dfrac {1}{2}\ AB\)
Доказательство средней линии треугольника
В предыдущем разделе мы видели треугольник \(ABC\) с \(D,\) \(E,\) и \(F\) как три середины.
Нам нужно доказать две вещи, чтобы оправдать доказательство теоремы о середине треугольника:
- \(DE∥BC\)
- \(DE=\dfrac{1}{2}\ BC\)
Дано: D и E — середины отрезков AB и AC
Чтобы доказать, \(DE∥BC\) и \(DE=\dfrac{1}{2}\ BC\), нам нужно нарисуйте линию, параллельную AB, и встретите E, полученную в точке F.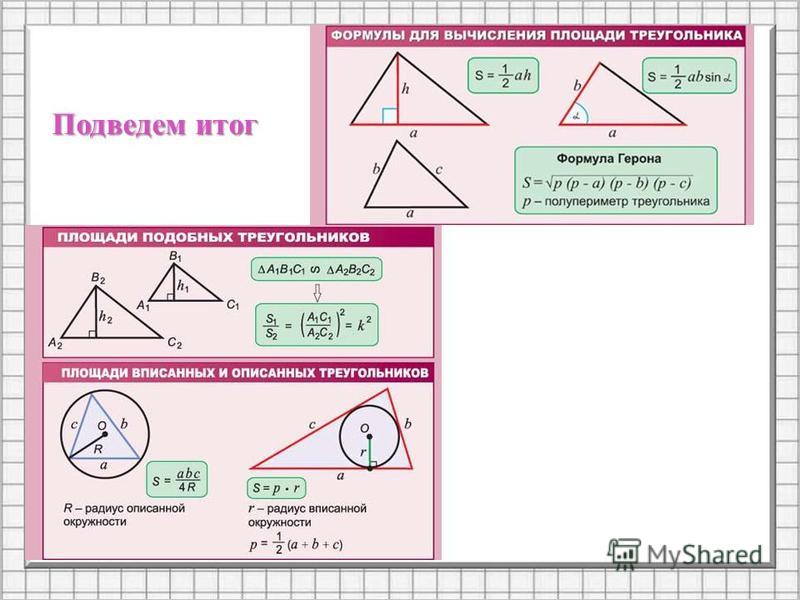
В \(\bigtriangleup{ADE}\) и \(\bigtriangleup{CFE}\)
\(\begin{align} AE &=EC\text{ (E — середина AC)}\\\ \angle{1} &=\angle{2}\text{ (Вертикально противоположные углы)}\\\ \angle{3} &=\angle{4}\text { (Альтернативные углы)}\end{выравнивание}\)
По конгруэнтности треугольника по AAS имеем,
\(\bigtriangleup{ADE} \cong \bigtriangleup{CFE}\)
По CPCT имеем,
\(DE=FE\)
\(AD= CF\)
D — середина AB
\(AD=BD\)
\(BD=CF\)
DBCF — параллелограмм,
\(DF || BC\) и \(DF = BC\)
\(DE || BC\) и \(DF = BC\)
\(DE=\dfrac{1}{2}DF\)
так как, DF = BC
\( DE=\dfrac{1}{2}BC\)
Отсюда доказано
Средняя часть формулы треугольника| Средняя часть \(=\) \(\dfrac{1}{2}\times\) Основание треугольника |
Что является обратной теоремой о средней линии треугольника?
Теорема, обратная теореме о срединном отрезке, определяется следующим образом: когда отрезок соединяет две середины двух противоположных сторон треугольника и параллелен третьей стороне треугольника и составляет ее половину, то он является средним отрезком треугольника.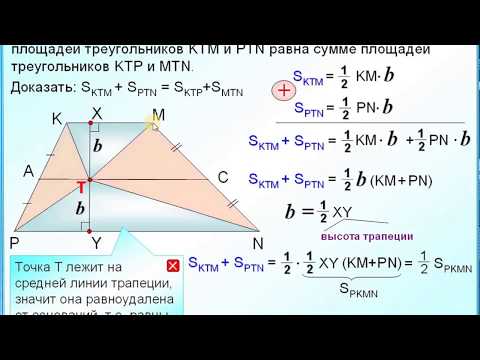 .
.
В треугольнике ABC имеем
\(DE∥BC\) и \(DE=\dfrac{1}{2}\ BC\)
Тогда согласно обратной теореме о середине треугольника
\(AD=DB\) и \(AE=EC\)
\(DE\) является средней линией треугольника \(ABC\)
Доказательство обратной теоремы о средней линии треугольника
В предыдущем разделе мы видели \(\bigtriangleup{ABC}\), где \(D ,\) \(E,\) и \(F\) как три середины.
Чтобы обосновать доказательство обратной теоремы о середине треугольника, нам нужно доказать любую из перечисленных ниже вещей:
- \(DE\) является средней частью треугольника \(\bigtriangleup{ABC}\)
- \(AD=DB\) и \(AE=EC\)
У нас есть D как середина AB, тогда \(AD = DB\) и \(DE||BC\)
\(AB\) \(=\) \(AD + DB\) \ (=\) \(DB + DB\) \(=\) \(2DB\)
DBCF — параллелограмм.
\(DE||BC\) и \(BD||CF\)
Противоположные стороны параллелограмма равны.
\(BD=CF\)
\(DA=CF\)
В \(\bigtriangleup{ADE}\) и \(\bigtriangleup{CFE}\)
\(\begin{align}\angle{1} &=\angle{2}\text{ (вертикально противоположные углы)}\\\ \angle{3} &=\angle{4}\text{ (альтернативный углов)}\\\ DA &=CF\end{align}\)
Согласно конгруэнтности треугольника по AAS,
\(\bigtriangleup{ADE} \cong \bigtriangleup{CFE}\)
По CPCT мы have
\(AE=EC\)
E — середина AC и DF.
Следовательно, DE является средней частью \(\bigtriangleup{ABC}\).
Важные примечания
а) Отрезок, проходящий через середину, всегда параллелен одной стороне треугольника.
б) Середина \(=\) \(\dfrac{1}{2}\) длина третьей стороны треугольника.
в) Треугольник может иметь не более трех средних сегментов.
г) Середина отрезка теоремы треугольника также известна как теорема о средней точке.
Чтобы лучше понять среднюю часть треугольника, давайте рассмотрим несколько примеров решения.
| Пример 1 |
На данном рисунке H и M — середины треугольника EFG. Помогите Джейми доказать \(HM||FG\) для следующих двух случаев.
а) EH = 6, FH = 9, EM = 2 и GM = 3
б) EH = 16, FH = 12, EM = 4 и GM = 3
Решение
а) Имеем EH = 6, FH = 9, EM = 2 и GM = 3
\dfrac{EH}{FH}=\dfrac{6}{9}=\dfrac{2}{3}\)
\(\dfrac{EM}{GM}= \dfrac{EH}{FH}=\dfrac{2}{3}\)
б) Имеем EH = 16, FH = 12, EM = 4, и GM = 3
\(\dfrac{EH}{FH}=\dfrac{16}{12}=\dfrac{4}{3}\)
\(\dfrac{EM}{GM}= \ dfrac{EH}{FH}=\dfrac{4}{3}\)
HM делит EF и EG треугольника EFG в равных отношениях.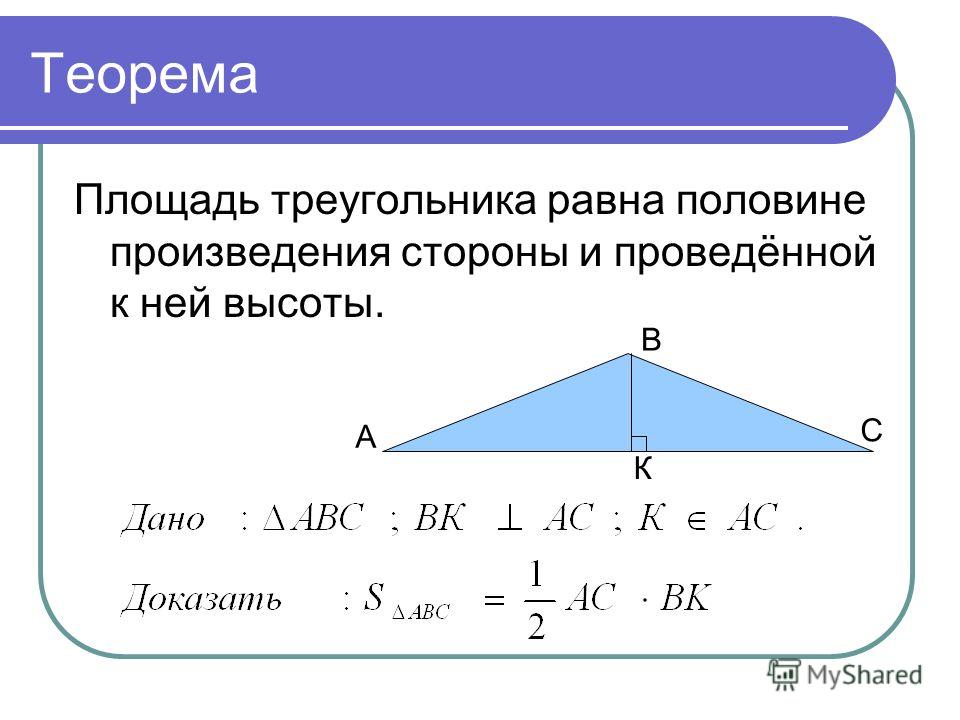
Следовательно, HM — средняя линия треугольника EFG.
\(\следовательно\) \(HM || FG\) |
| Пример 2 |
Помогите Рону найти значение x и значение отрезка AB, учитывая, что A и B являются серединами треугольника PQR.
Решение
У нас есть две середины A и B.
36 &=2(9х)\\\
х &=2\\\
АВ &=18\конец{выравнивание}\)
| \(\следовательно\) Значение x равно 2 Значение AB равно 18 | .
Интерактивные вопросы
Вот несколько упражнений для практики. Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат. а) Рассмотрим треугольник ABC, и пусть D — любая точка на BC. Пусть X и Y — середины сторон AB и AC. Покажите, что XY делит AD пополам. б) Рассмотрите параллелограмм ABCD. E и F — середины отрезков AB и CD соответственно. Докажите, что отрезки AF и EC пересекают диагональ BD пополам. Мини-урок был посвящен захватывающей концепции середины треугольника. Математическое путешествие по средней части треугольника начинается с того, что ученик уже знает, и продолжается творческим созданием новой концепции в умах молодых людей. Сделано таким образом, что это не только понятно и легко для понимания, но и останется с ними навсегда. В этом заключается магия Cuemath. В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов! Благодаря интерактивному и увлекательному подходу «обучение-преподавание-обучение» учителя изучают тему со всех сторон. Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, мы в Cuemath верим в логическое мышление и разумный подход к обучению. Середина треугольника – это отрезок, соединяющий середины или центры двух противоположных или смежных сторон треугольника. В треугольнике может быть 3 середины. На приведенном выше рисунке D — это середина AB, E — середина AC, а F — середина BC. Здесь DE, DF и EF — три средние линии треугольника ABC. Мы можем найти среднюю часть треугольника, используя формулу средней части треугольника, Средняя часть \(=\) \(\dfrac{1}{2}\times\) Основание треугольника. Теорема о средней точке утверждает, что отрезок прямой, соединяющий середины любых двух сторон треугольника, параллелен третьей стороне и равен половине третьей стороны. Теорема о средней точке утверждает, что DE будет параллелен ВС и равен ровно половине ВС. Средняя линия треугольника, соединяющая середины двух сторон, составляет половину длины стороны, которой она параллельна. Отрезок, соединяющий две середины сторон треугольника, называется средним отрезком . \(\overline{DF}\) — это середина между \(\overline{AB}\) и \(\overline{BC}\). Засечки показывают, что \(D\) и \(F\) являются средними точками. \(\overline{AD}\cong \overline{DB}\) и \(\overline{BF}\cong \overline{FC}\). У каждого треугольника есть три середины. Существуют два важных свойства средних сегментов, которые в совокупности составляют Теорему о средних сегментах . Теорема о среднем сегменте утверждает, что средний сегмент, соединяющий середины двух сторон треугольника, параллелен третьей стороне треугольника, а длина этого среднего сегмента составляет половину длины третьей стороны. Таким образом, если \(\overline{DF}\) является средним отрезком \(\Delta ABC\), то \(DF=\dfrac{1}{2}AC=AE=EC\) и \(\overline{ DF} \parallel \overline{AC}\). Обратите внимание, что здесь есть две важные идеи. Во-первых, середина параллельна стороне треугольника. Другая состоит в том, что средний сегмент всегда составляет половину длины этой стороны. Что, если бы вам дали \(\Delta FGH\) и сказали, что \(\overline{JK}\) это его середина? Как можно найти длину \(JK\), зная длину третьей стороны треугольника \(FH\)? Пример \(\PageIndex{1}\) Найдите значение \(x\) и AB. \(A\) и \(B\) являются серединами. Решение \(AB=34\div 2=17\). Чтобы найти \(x\), установите \(3x−1\) равным 17. \(\begin{align*} 3x−1&=17 \\ 3x&=18 \\ x&=6\end{align* }\) Пример \(\PageIndex{2}\) Верно или неверно: если линия проходит через две стороны треугольника и параллельна третьей стороне, то она является средней линией. Решение Это утверждение неверно. Линия, проходящая через две стороны треугольника, является средней линией только в том случае, если она проходит через середины двух сторон треугольника. Пример \(\PageIndex{3}\) Вершинами \(\Delta LMN\) являются \(L(4,5),\: M(−2,−7)\:and\: N( −8,3)\). Найдите середины всех трех сторон, обозначьте их O, P и Q. Затем начертите треугольник, отметьте середины и нарисуйте средние сегменты. Решение Чтобы решить эту задачу, используйте формулу средних точек 3 раза, чтобы найти все средние точки. Напомним, что формула средней точки имеет вид \(\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\right)\). \(L\) и \(M=\left(\dfrac{4+(-2)}{2}, \dfrac{5+(-7)}{2}\right)=(1,- 1),\: точка\: O\) \(M\) и \(N=\left(\dfrac{−2+(−8)}{2},\dfrac{−7+3}{ 2}\right)=(−5,−2),\: точка\: P\) \(L\) и \(N=\left(\dfrac{4+(−8))}{2} , \dfrac{5+3}{2}\right)=(−2,4),\: точка\: Q\) Пример \(\PageIndex{4}\) Отметить все конгруэнтных сегментов на \(\Delta ABC\) со средними точками \(D\), \(E\ ) и \(F\). Решение Нарисовав все три средние сегмента, мы получим: Кроме того, это означает, что четыре меньших треугольника конгруэнтны по SSS. Теперь отметьте все параллельные прямые на \(\Delta ABC\) с серединами \(D\), \(E\) и \(F\). Пример \(\PageIndex{5}\) \(M\), \(N\) и \(O\) — середины сторон \(\Delta \(x\)YZ\) . Решение Найдите \(MN\), \(XY\) и периметр \(\Delta \(x\)YZ\). Используйте теорему о средней линии: \(MN=OZ=5\) \(XY=2(ON)=2\cdot 4=8\) Сложите три стороны \(\Delta XYZ \) найти периметр. \(XY+YZ+XZ=2\cdot 4+2\cdot 3+2\cdot 5=8+6+10=24\) Помните: отсутствие отрезка над MN означает длину или расстояние. Определите, является ли каждое утверждение истинным или ложным. R, S, T и U являются серединами сторон \(\Delta XPO\) и \(\Delta YPO\) В вопросах 9-15 найдите указанную(ые) переменную(ые). Вы можете предположить, что все отрезки внутри треугольника являются средними отрезками. Координатная геометрия Учитывая вершины \(\Delta ABC\) ниже, найдите середины каждой стороны. Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 5.1. 100003
100003
Часто задаваемые вопросы (FAQ) 1. Что такое средняя линия треугольника?
2. Как найти среднюю линию треугольника?
3. Что такое теорема о средней точке?
 Рассмотрим произвольный треугольник \(\bigtriangleup{ABC}\). Пусть D и E — середины сторон AB и AC. Предположим, что вы соединяете D и E:
Рассмотрим произвольный треугольник \(\bigtriangleup{ABC}\). Пусть D и E — середины сторон AB и AC. Предположим, что вы соединяете D и E: 4.19: Теорема о среднем отрезке — K12 LibreTexts




Обзор

 \(\Delta ABC\) образуется путем соединения середины \(\Delta XYZ\).
\(\Delta ABC\) образуется путем соединения середины \(\Delta XYZ\). Обзор (ответы)
Ресурсы
youtube.com/embed/P5SEb7xpTjE?vq=hd1080″ frameborder=»0″ allowfullscreen=»true»> Словарь
Срок Определение средний сегмент Средняя линия соединяет середины двух сторон треугольника или непараллельные стороны трапеции. Конгруэнтность Конгруэнтные фигуры одинаковы по размеру, форме и размеру. Формула средней точки Формула средней точки говорит, что для конечных точек \((x_1,y_1)\) и \((x_2,y_2)\) средняя точка равна (\dfrac{x_1+x_2}{2}, \frac{y_1+y_2} {2})\).
Дополнительные ресурсы
Видео: Определение неизвестных значений с использованием свойств средних сегментов треугольника
Задания: Теорема о средних сегментах Вопросы для обсуждения
Учебные пособия: Биссектрисы, медианы, высоты Учебное пособие
Практика: Теорема о среднем отрезке
Реальный мир: Теорема о среднем отрезке
Эта страница под названием 4. 19: Теорема о середине сегмента распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
19: Теорема о середине сегмента распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
ПОД ЛИЦЕНЗИЕЙ
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- СК12
- Лицензия
- СК-12
- Программа OER или Publisher
- СК-12
- Показать оглавление
- нет
- Теги
- источник@https://www.
 ck12.org/c/geometry
ck12.org/c/geometry
- источник@https://www.
Передний треугольник шеи — Подразделы
- 1 Границы
- 2 Содержание
- 3 Подразделы
- 3.1 Сонный треугольник
- 0129
- 3.2 Подподбородочный треугольник
- 3.3 Поднижнечелюстной треугольник
- 3.4 Мышечный треугольник
- 3.1 Сонный треугольник
Передний треугольник расположен на передней части шеи.
В этой статье мы рассмотрим анатомию переднего треугольника шеи – его границы, содержимое и подразделения.
Примечание: важно отметить, что все треугольники, упомянутые здесь, являются парными; они расположены как на левой, так и на правой стороне шеи.
Границы
Передний треугольник расположен на передней поверхности шеи. Ограничена:
- Сверху – нижний край нижней челюсти (челюстная кость).
- Латерально – передний край грудино-ключично-сосцевидной мышцы.

- Медиально – сагиттальная линия вниз по средней линии шеи.
Покрывающая фасция покрывает крышу треугольника, а висцеральная фасция покрывает дно. Его можно разделить на четыре треугольника, которые подробно описаны далее в этой главе.
Автор: TeachMeSeries Ltd (2022)
Рис. 1.0. Границы переднего треугольника шеи.
Содержимое
Содержимое переднего треугольника включает мышцы, нервы, артерии, вены и лимфатические узлы.
Мышцы этой части шеи различаются по расположению относительно подъязычной кости. Надподъязычные мышцы расположены выше подъязычной кости, а подподъязычные — снизу.
В переднем треугольнике имеется несколько важных сосудистых структур. общая сонная артерия разветвляется внутри треугольника на наружную и внутреннюю сонную ветви. В этой области также можно найти внутреннюю яремную вену, которая отвечает за венозный отток головы и шеи.
Многочисленные черепных нервов расположены в переднем треугольнике. Некоторые проходят прямо, а другие дают ответвления, которые иннервируют некоторые другие структуры внутри треугольника. К черепным нервам в переднем треугольнике относятся лицевой [VII], языкоглоточный [IX], блуждающий [X], добавочный [XI] и подъязычный [XII] нервы.
| Надподъязычные мышцы | Подъязычные мышцы |
|
|
TeachMeSeries Ltd (2022)
Рис. 2. Экстракраниальный анатомический ход подъязычного нерва через передний треугольник шеи.
Подразделы
Передний треугольник подразделяется подъязычной костью, надподъязычной и подподъязычной мышцами на четыре треугольника.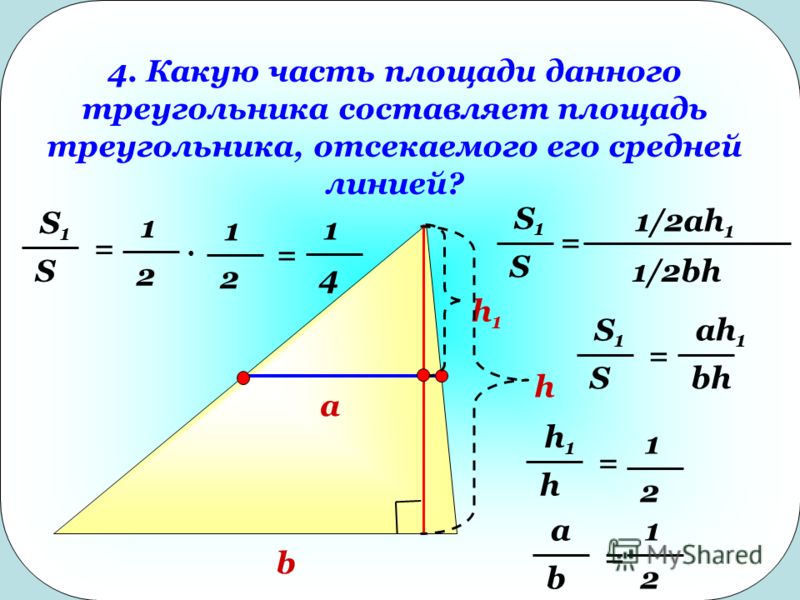
Сонный треугольник
Сонный треугольник шеи имеет следующие границы:
- Верхняя – заднее брюшко двубрюшной мышцы.
- Латеральный – медиальный край грудино-ключично-сосцевидной мышцы.
- Нижняя – верхнее брюшко лопаточно-подъязычной мышцы.
Основным содержимым сонного треугольника являются общая сонная артерия (которая разветвляется внутри сонного треугольника на наружную и внутреннюю сонные артерии), внутренняя яремная вена и подъязычный и блуждающие нервы .
By TeachMeSeries Ltd (2022)
Рис. 3. Сонный треугольник шеи
Клиническая значимость: Медицинское использование каротидного треугольника
В сонном треугольнике многие сосуды и нервы относительно поверхностный , доступ к которому возможен хирургическим путем. Сонные артерии, внутренняя яремная вена, блуждающий и подъязычный нервы являются частыми мишенями этого хирургического доступа.
Сонный треугольник также содержит каротидный синус — расширенную часть общей сонной и внутренней сонной артерий. Он содержит специфические сенсорные клетки, называемые барорецепторами . Барорецепторы обнаруживают растяжение как меру артериального давления. языкоглоточный нерв передает эту информацию в мозг, и она используется для регулирования артериального давления.
У некоторых людей барорецепторы сверхчувствительны к растяжению. У этих пациентов внешнее давление на каротидный синус может вызвать замедление сердечного ритма и снижение артериального давления. Мозг становится недостаточно перфузированным , что приводит к обморокам. У таких пациентов не рекомендуется проверять пульс на сонном треугольнике.
Субментальный треугольник
подбородочный треугольник на шее расположен под подбородком. Он содержит подбородочные лимфатические узлы , которые фильтруют лимфу, оттекающую от дна рта и частей языка.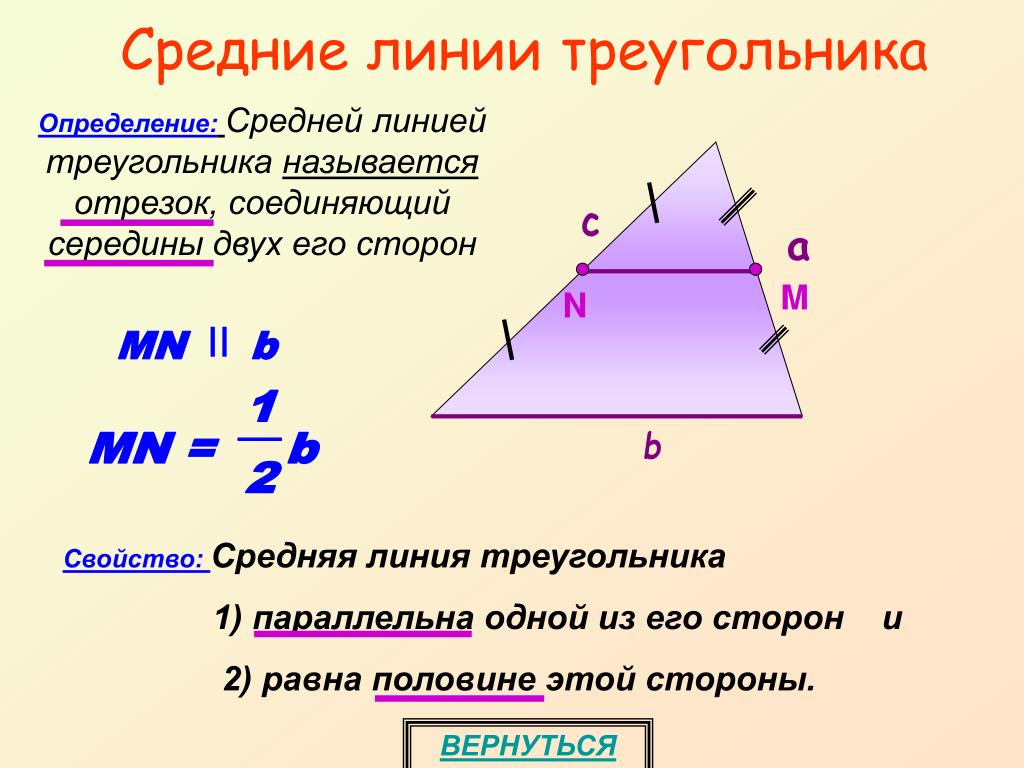
Ограничен:
- Книзу – подъязычная кость.
- Медиально – средняя линия шеи.
- Латерально – переднее брюшко двубрюшного
Пол подбородочного треугольника образован челюстно-подъязычная мышца , идущая от нижней челюсти к подъязычной кости.
Автор: TeachMeSeries Ltd (2022)
Рис. 4. Подподбородочный треугольник шеи.
Поднижнечелюстной треугольник
Поднижнечелюстной треугольник расположен под телом нижней челюсти . Он содержит поднижнечелюстную железу (слюнную) и лимфатические узлы. Лицевая артерия и вена также проходят через эту область.
Границами поднижнечелюстного треугольника являются:
- Сверху – тело нижней челюсти.
- Спереди – переднее брюшко двубрюшной мышцы.
- Сзади – заднее брюшко двубрюшной мышцы.


 ..
.. 03.17
03.17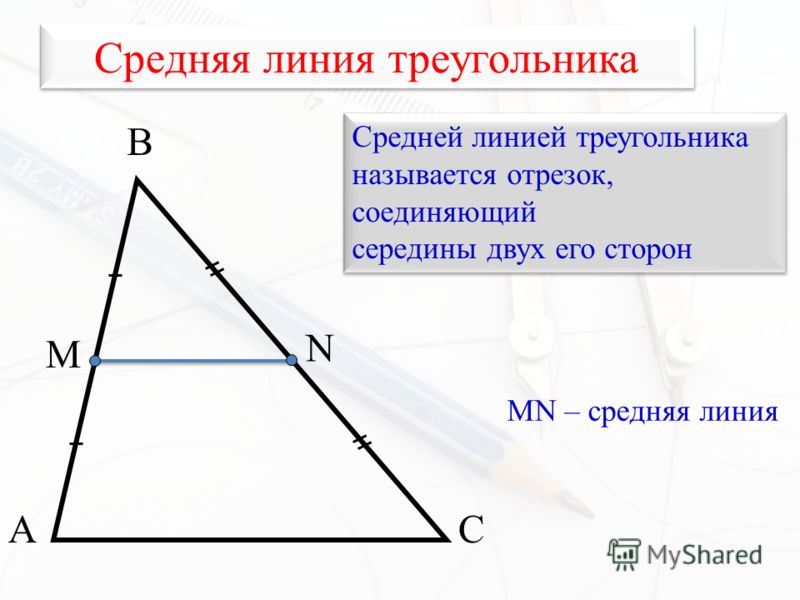


 ck12.org/c/geometry
ck12.org/c/geometry
