Конкретный смысл действия умножение. Название чисел при умножении
Та-ак, надо хорошенечко всё подсчитать. Вот малыш обрадуется!
Ой, здравствуйте, ребята! Вы знаете, ко мне должен приехать в гости мой маленький двоюродный брат. Вот он на фотографии. Братец очень любит играть с кубиками. И вот к его приезду я решил соорудить стенку из кубиков. Но, так как братец тоже является математическим знаком, он не терпит никакого беспорядка. Поэтому стеночка должна быть идеальная во всех отношениях. Вот я и пытаюсь подсчитать, сколько кубиков мне необходимо для построения такой стенки.
Пусть в основании стенки будет находиться 5 красных кубиков. Чтобы стеночка была идеально ровная и красивая, на красные поставлю 5 зелёных кубиков, потом ещё 5 жёлтых кубиков, а сверху — 5 синих кубиков. Ах, какая симпатичная стеночка получилась - ровненькая, просто идеальная.
Я
думаю, малыш захочет построить ещё одну такую же, но у меня кубики закончились.
Здесь использовали сочетательное свойство сложения. Получили, что нужно купить 20 кубиков. Хотя, вы обратили внимание, что действие какое-то длинноватое получилось. Но, самое интересное, слагаемые-то все одинаковые. А, вспомнил! Для таких случаев есть специальное действие. Его-то и выполняет мой маленький братец. Ведь его имя — Умножение. И действие, которым можно заменить сумму одинаковых слагаемых тоже называется умножением.
Итак, посмотрите на стеночку и на записанное числовое выражение. В каждом ярусе стенки по 5 кубиков — 5 красных, 5 зелёных, 5 жёлтых, 5 синих. Таких ярусов — 4.
То
есть, можно сказать, в этой стенке по пять кубиков четыре раза. И сейчас
между числами 5 и 4 мы поставим точку. Но не внизу, как в конце предложения, а
точно в центре клеточки, которая пропущена между числами 5 и 4.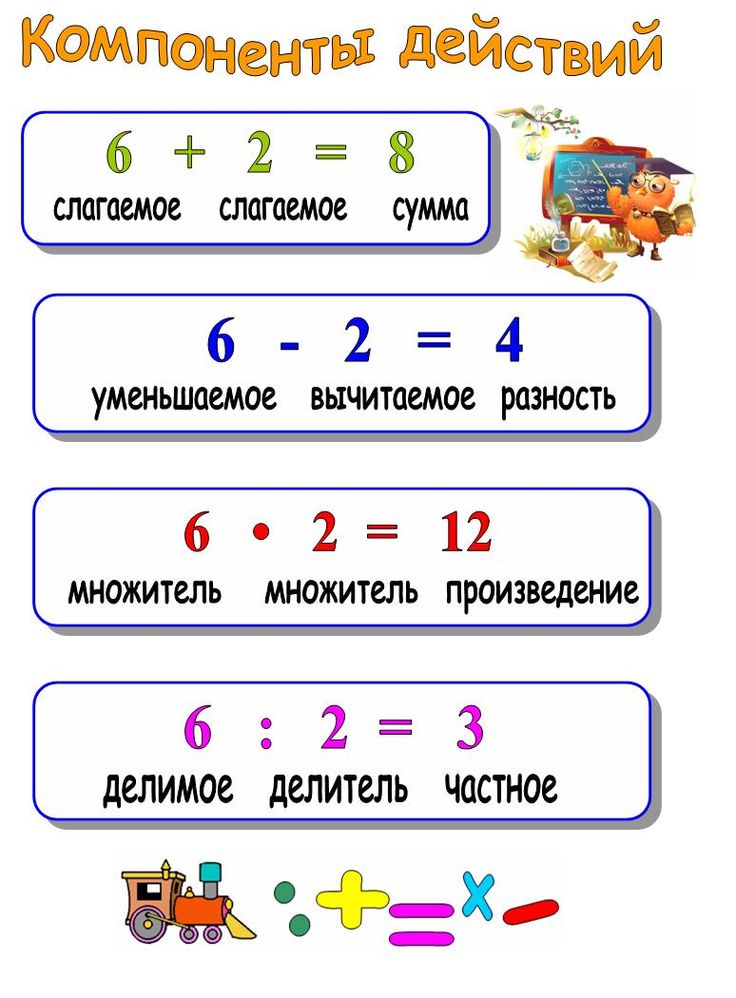
Правда, знак очень похож на моего двоюродного братца? Хотя, мой братик очень любит переодеваться, и иногда надевает вот такой костюмчик * или вот такой ´. Но пока он носит только костюмчик-точку.
Но вернёмся к нашему действию умножения. Что же мы сделали? Мы сумму одинаковых слагаемых заменили действием умножения. То есть, вместо трёх действий у нас получилось только одно, вместо четырёх чисел в числовом выражении только два. Первое число показывает, какие должны были быть слагаемые, а второе — сколько таких слагаемых. Ну, как вам экономия времени и бумаги?
А вот посмотрите на это числовое выражение:
Ну, ничего себе, выраженьице! Целых 6 одинаковых слагаемых. Ну, понятно, получается 18. Все слагаемые
А теперь посчитаем,
сколько троек — их 6, поэтому второе число — 6. Между ними ставлю знак
умножения — точку. Получилось новое числовое выражение:Его можно прочитать так: По три берём шесть раз. Или так: Шесть умножить на три. А иногда даже так: Шестью три.
Кстати, а знаете, как называются числа в действии умножения?
Вот когда числа складываются, мы их называем так: слагаемое + слагаемое = сумма. Действие сложение, а числа в нём — слагаемые. А вот в действии умножения числа называются множители! Первый множитель × второй множитель. Действие умножения, и числа в нём — множители. А вот результат действия умножения называется длинным и очень важным словом — произведение.
А теперь посмотрите вот на такую запись:
Давайте
попробуем сделать наоборот — умножение заменим сложением. В этом выражении
первый множитель — 6. Он показывает, какие числа складываются.
Второй множитель
— 2. Он показывает, сколько таких слагаемых. Это значит, по шесть надо взять
два раза. Поэтому действие умножения мы можем заменить вот таким действием
сложения:
А если заменить вот такое выражение:
Это значит, что по два надо взять пять раз. Первый множитель — 2. Это число показывает, какие будут слагаемые. Второй множитель — 5, показывает, сколько таких слагаемых. Получается вот такая запись:
Вот сравните, как выглядит сложение пяти одинаковых чисел, и как выглядит умножение. А результат один и тот же.
Я думаю, вы догадались, что нельзя. Ведь здесь нет одинаковых слагаемых. Все слагаемые разные. Так что, не всегда вместо сложения можно использовать действие умножения, а только в тех случаях, когда слагаемые одинаковые. Значит, и я вам ещё очень даже пригожусь.
Ну как, ребята, вы запомнили?
· сумму одинаковых слагаемых можно заменить умножением;
· знак умножения — точка;
Запись действия умножения можно прочитать так:
· 2 умножить на 7;
· по два взять семь раз;
А иногда можно услышать и такое:
· дважды семь;
· семью два;
· числа в действии умножения называются множителями, а результат умножения - произведением;
Действие
умножение тесно связано со сложением.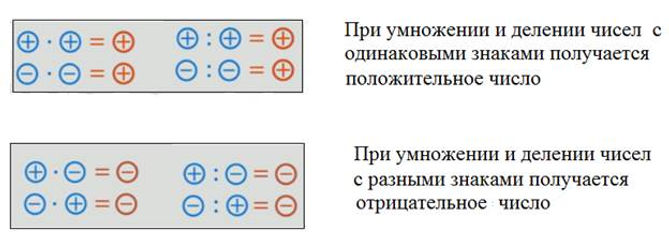
При этом:
· первый множитель показывает, какие числа складываются;
· второй множитель показывает, сколько одинаковых чисел складывается.
Ну, вроде бы все готово, надо только сходить за вторым комплектом кубиков. Я поскорее пойду за кубиками для маленького брата. До свидания, ребята!
Что такое «асимметричная криптография» — Разработка на vc.ru
Привет! Это команда Eppie. Подробнее о нашем проекте бессерверной электронной почты можно почитать в этой статье. А здесь поговорим подробнее о криптографии.
155 просмотров
Асимметричная криптография сейчас у всех на слуху благодаря бурному развитию Web3. Но мало кто понимает, как она на самом деле работает. Попробуем это исправить. Если вы давно хотели составить себе хотя бы поверхностное представление о современной криптографии, но Википедия не помогла — это статья для вас.
Будет немного формул, но текст рассчитан на читателей, владеющих математикой на уровне общеобразовательной школы, не сложнее.
Наш криптограф считает необходимым добавить, что в статье допущены упрощения, и даже некоторые неточности. Более формальное описание было бы длиннее и сложнее для восприятия.
Самый простой шифр
Чтобы объяснить, что такое асимметричная криптография, начнем с симметричной.
Договоримся, что все виды данных в компьютере — текст, цвет, звук и все содержимое вашего профиля в Google — представлены числами. Шифрование в компьютере — это преобразование одного числа в другое с помощью математической операции. Например:
9 + 4 = 13
Можно сказать, что мы зашифровали число 9, прибавив к нему число 4 (оно в криптографии называется ключом) . Теперь можно произвести над шифром (13) обратную операцию, и мы получим исходный текст (9):
13 – 4 = 9
Самая примитивная схема шифрования — «шифр Цезаря» — устроена похожим образом: каждая буква в тексте смещаются на k позиций в алфавите. Так, если ключ k = 4, то «а» преобразуется в «д», «б» — в «е», и далее по кругу.
Последние буквы в алфавите сдвигаются в начало, поэтому «я» с ключом 4 превратится в «г». Один участник переписки прибавляет k к каждой букве в сообщении, чтобы его зашифровать. Второй — расшифровывает его, отнимая от каждой буквы то же число. Таким образом слово «яблоко», зашифрованное методом Цезаря с ключом 4 превратится в «гептот».
«Шифр Цезаря»
Чтобы понимать друг друга, обе стороны должны владеть одним и тем же ключом. Поэтому такой способ шифрования называется симметричным. Момент передачи ключа — его самое слабое звено. В конце концов шифрование придумано для обмена секретной информацией по незащищенному каналу. Представьте: вы Цезарь, и вам нужно послать гонца с секретным сообщением к вашему генералу у стен Карфагена. Если вы уверены в преданности гонца, и в том, что по дороге его не перехватят враги — может быть, вам и не нужно шифрование. Если же у вас нет безопасного способа доставить сообщение, значит сообщение нужно зашифровать.
Но встает вопрос: как передать ключ? Этот вопрос не потерял своей актуальности с появлением телеграфа, телефона и интернета. С античности и до изобретения асимметричной криптографии в 70-х годах XX века хорошего решения у нас не было. Передача ключей шифрования была дорогим и сложным в организации мероприятием.
В асимметричных криптографических алгоритмах для шифрования и расшифровки используют разные ключи. У каждого участника свой секретный ключ, известный только ему. Их не нужно (и нельзя) передавать. Это исключает возможность перехвата.
Криптограф уточняет, что симметричное шифрование используют и сейчас. Не только когда бухгалтерия присылает вам по почте архив вместе с паролем в теме письма. Но в том числе и в сочетании с асимметричными протоколами. Например, можно создать совместный ключ асимметричным способом, и использовать его потом для симметричного шифрования. Ниже мы как раз подробно разберем такой протокол.
Еще немного арифметики
Вернемся к нашему уравнению.
9 + 4 = 13
Если мы знаем результат (13), одну из переменных (4) и операцию (+) , мы можем вычислить вторую, неизвестную, переменную с помощью обратной операции.
x + 4 = 13
x = 13 – 4
x = 9
Чтобы асимметричная криптография работала, нам нужно «защитить» x. То есть использовать такую математическую операцию, для которой не существует эффективного алгоритма вычисления неизвестной переменной, даже когда остальные значения известны. Для этого мы можем использовать, например, модульную арифметику.
Будем складывать по модулю N. Если сумма превышает N, результат будет равен разнице суммы и модуля. Допустим, модуль равен 12.
(9 + 4) mod 12 = 13 – 12 = 1
Наглядный пример такой операции — движение стрелки по циферблату. Когда стрелка доходит до последнего элемента (11 часов) , счет продолжается с нуля.
Циферблат как пример сложения по модулю
Несколько примечаний от криптографа:
— В криптографии используются не любые операции по модулю, а «вычисления в конечной группе».
По определению конечной группы оба слагаемых и результат всегда принадлежат группе.
— Не любое множество может считаться конечной группой — должны выполняться некоторые обязательные условия, но мы не будем их разбирать, чтобы не усложнять объяснение.
— В примере с часами нужно допустить, что стрелка всегда указывает на целое значение и никогда не оказывается между. В данном случае группа состоит из 12 элементов от 0 до 11 и N = 12.
— Строго говоря, сумма по модулю равна не разнице суммы и модуля, а остатку от деления суммы на значение модуля. Ниже, когда перейдем к умножению, это будет иметь значение.
По определению конечной группы оба слагаемых и результат всегда принадлежат группе. Теперь, чтобы найти (расшифровать) неизвестное слагаемое, нужно знать сумму по модулю, одно из слагаемых и значение модуля. Зная эти три параметра, мы все еще можем вычислить неизвестное слагаемое.
(9 + x) mod 12 = 1
(9 + x) — 12n = 1
где n показывает, сколько раз стрелка пересекла нулевую отметку. Если сумма двух чисел меньше 12, то стрелка не успела сделать полный круг, и n = 0.
В нашем случае сумма равна 13, и n = 1. Поскольку оба слагаемых в конечной группе меньше модуля, n может принять всего два значения.
В первом случае x = -8, и это не может быть правильным ответом по условию (-8 нет на циферблате) , во втором x = 4, и это правильный ответ. Проверить два значения n несложно.
Теперь попробуем умножение. В конечной группе с умножением N должно быть простым числом. Поэтому пусть N = 11, а в качестве множителей возьмем 6 и 9.
(6 ⋅ 9) mod 11 = 54 mod 11 = 10
(11 помещается в 54 целиком 4 раза, а остаток — 10)
Пусть 9 — неизвестная величина. Чтобы ее вычислить, нужно решить уравнение:
(6 x) mod 11 = 10
Выше мы упомянули, что 10 — остаток от деления произведения на модуль. Это можно выразить вот так:
6x — 11n = 10
x = (10 + 11n) /6
В группе с умножением n может принимать значения от 0 до N-2. Будем подставлять все варианты n по очереди, пока x не окажется положительным целым числом, принадлежащим группе.
1024, подбор такого ключа на самом мощном современном компьютере займет миллиарды лет, и считается на практике невозможным.
Возведение в степень в конечной группе — это такое математическое преобразование, которое нельзя «провернуть обратно», чтобы получить исходные значения.
Еще одна важная особенность конечных групп, которая нам понадобится — ассоциативность, или, как учат в школе, «результат не зависит от расстановки скобок»:
((a b) c) mod N = (a (b c)) mod N
Давайте посмотрим, как это работает на реальном примере — в протоколе генерации совместного ключа Диффи-Хеллмана.
Обмен ключами по протоколу Diffie-Hellman
Итак, Алиса и Боб (традиционные имена в описании криптографических алгоритмов) хотят создать совместный (симметричный) ключ шифрования с таким условием, чтобы Ева (злоумышленник) могла полностью подслушать их разговор, но не могла воспроизвести ключ.
Боб звонит Алисе, и они договариваются о конечной группе с модулем N.
ba mod N
Схема генерации совместного ключа по протоколу Диффи-Хеллмана
Теперь у Алисы и Боба есть совместный секретный ключ K. Это ключ для симметричного шифрования, но он был создан «асимметричным способом». При его генерации каждый использовал свой приватный ключ и публичный ключ собеседника. И Ева, владея всей публичной информацией, не может воспроизвести совместный секретный ключ шифрования.
Где используется асимметричная криптография?
Асимметричная криптография защищает вас прямо сейчас. Посмотрите на адресную строку браузера: префикс https (в отличие от устаревшего http) значит, что данные, передаваемые между вашим компьютером и сервером VC.ru, зашифрованы, а ключ шифрования был получен по протоколу Диффи-Хеллмана, о котором мы только что рассказали.
Технология цифровой подписи, которой вы пользуетесь при подаче налоговой декларации в электронном виде, тоже основана на приемах асимметричной криптографии.
Эти приемы можно использовать и в качестве альтернативы парольной аутентификации. Это распространено в криптовалютах и других Web3 сервисах. Например, механизм шифрования в децентрализованной почте или мессенджере упрощенно мог бы выглядеть так: публичный ключ пользователя — и есть его почтовый адрес в децентрализованной сети. Каждое письмо шифруются с помощью пары ключей — приватного ключа отправителя и публичного ключа (адреса) получателя. Получатель в свою очередь расшифровывает письмо с помощью публичного ключа отправителя и своего приватного.
Пример шифрования почты в децентрализованной сети
Криптограф подчеркивает, что это упрощенная схема. Она не устойчива к некоторым видам атак, например, к атаке типа Man In The Middle, когда Ева вклинивается между Алисой и Бобом, и обращается к Алисе от имени Боба, а к Бобу — от имени Алисы. Чтобы защититься от атак такого типа, Алиса и Боб должны подписывать свои сообщения — но это тема для отдельной статьи.
В такой схеме, в отличие от парольной аутентификации, вам не нужно доказывать системе, что почтовый адрес принадлежит вам. В системе нет элемента, который принимает решение об аутентификации пользователя. Право доступа к почтовому ящику дает вам не сервер (которого не существует) а приватный ключ, который хранится только у вас. Он дает вам, единственному в мире, возможность расшифровать отправленные вам письма. Ваши ключи — ваши письма.
Если вас заинтересовал этот материал, подписывайтесь на наш блог и задавайте вопросы в комментариях. И, конечно, записывайтесь на бета-тест Eppie.
Видео-урок: свойства сложения и умножения
На примерах узнайте о коммутативных, ассоциативных и тождественных свойствах и о том, как они применяются к операциям сложения и умножения. Также посмотрите, как свойство дистрибутива применяется к добавлениям в скобках в продукте.
Стенограмма видео
Каковы свойства сложения и умножения? Свойства — это утверждения, которые верны для всех чисел.
Во-первых, коммутативные свойства. Начнем с коммутативного свойства сложения. Коммутативное свойство сложения гласит, что порядок сложения двух чисел не меняет их суммы. Переменное представление этого 𝑎 плюс 𝑏 — это то же самое, что сказать 𝑏 плюс 𝑎. Или четыре плюс три — это то же самое, что три плюс четыре. Порядок здесь не имеет значения. Свойство коммутативности можно применить и к умножению.
Посмотрите на изменения, которые произошли на экране. Коммутативное свойство умножения гласит, что порядок умножения двух чисел не меняет их произведения. В этом случае 𝑎 умножить на 𝑏 равно 𝑏 умножить на 𝑎. Например, пять раз четыре равно четыре раза пять. Один из способов запомнить свойство коммутативности — подумать о слове «коммутировать». Слово коммутировать и слово коммутативное относится к обмену, замещению и обмену. Здесь с коммутативным свойством мы конкретно говорим о том, когда мы меняем порядок, в котором мы складываем или умножаем. И в этом случае не меняет значение в зависимости от заказа.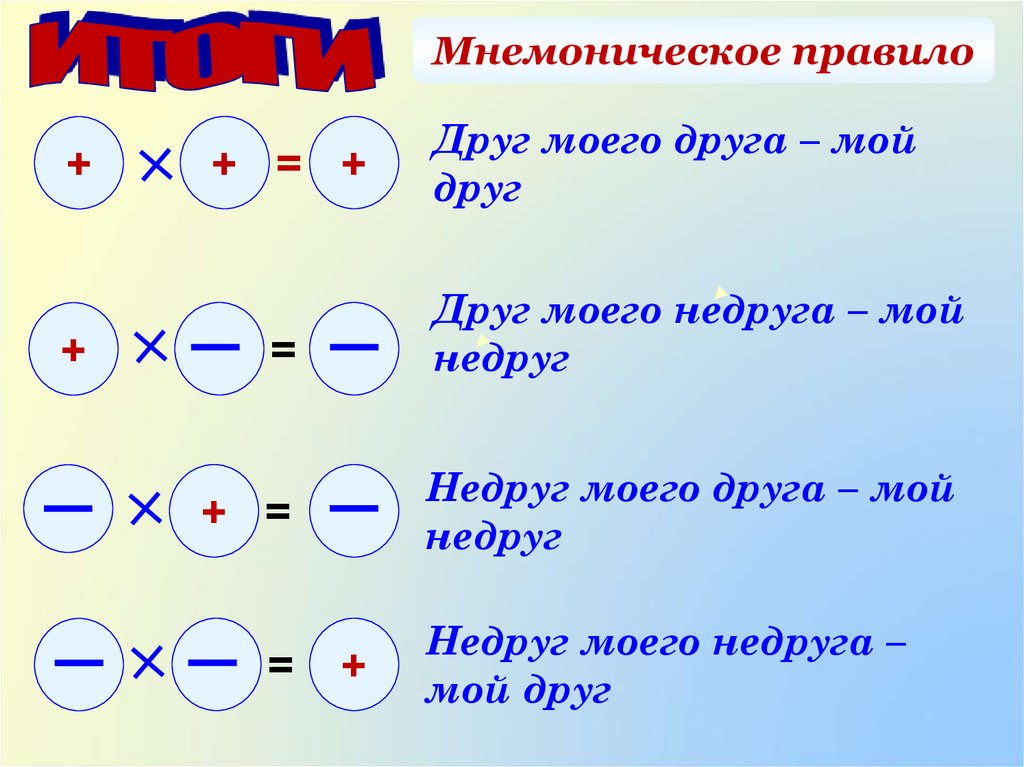
Далее, ассоциативное свойство. И снова начнем с сложения. Ассоциативное свойство сложения гласит, что способ группировки трех чисел при их сложении не меняет их суммы. Вот как это выглядит с переменными. 𝑎 плюс 𝑏 плюс 𝑐 равно 𝑎 плюс 𝑏 плюс 𝑐. Это означает, что если мы сначала сложим 𝑏 и 𝑐 вместе, а затем добавим 𝑎, эта сумма будет такой же, как если бы мы сначала сложили 𝑎 и 𝑏, а затем добавили 𝑐. В этом случае один плюс два плюс три равно один плюс два плюс три. Один плюс пять равно три плюс три. Это свойство можно применить и к умножению. Обратите внимание на изменения здесь. Ассоциативное свойство умножения гласит, что то, как сгруппированы три числа при их умножении, не меняет их произведения. Если мы сначала умножим 𝑏 и 𝑐, а затем возьмем это значение и умножим его на 𝑎, мы получим тот же продукт, как если бы мы умножили 𝑎 и 𝑏, а затем это значение на 𝑐.
Мы можем вспомнить ассоциативное свойство слова «ассоциировать». Ассоциация имеет дело с группировками. То, как группируются три числа при их сложении или умножении, не меняет ни их суммы, ни их произведения.
И третье в нашем списке — свойства идентичности. Начиная со свойства идентичности сложения, это свойство утверждает, что сумма слагаемого и нуля является слагаемым. 𝑎 плюс ноль равно 𝑎. Семь плюс ноль будет семь. Переходя к тождественному свойству умножения, давайте внимательно посмотрим на все изменения. Свойство идентичности умножения говорит, что произведение фактора и один является этим фактором. В нашем примере 𝑎 умножить на один равно 𝑎. Обратите внимание, что тождественное свойство умножения умножает множитель на единицу.
Давайте рассмотрим эти свойства рядом. Когда мы добавляем ноль к любому значению, мы собираемся получить то же самое значение обратно. И когда мы умножаем на единицу, происходит то же самое. Вы можете вспомнить свойство идентичности, подумав о том, что смотрите в зеркало. 𝑎 выглядит так же после добавления нуля. 𝑎 также выглядит одинаково после умножения на единицу. Наше последнее свойство немного отличается. Распределительное свойство показывает нам, как мы сочетаем сложение и умножение.
Распределительное свойство говорит об этом. Чтобы умножить сумму на число, умножьте каждое слагаемое суммы на число за скобками. Это много слов. Давайте посмотрим, как это выглядит. Начнем с примера, в котором используются числа.
Свойство говорит нам умножить сумму на число. Вот наша сумма, а вот число. Нам нужно умножить каждое слагаемое суммы. Четыре и шесть являются слагаемыми суммы. И мы умножаем это на число за скобками, в данном случае на три. Если вы решите обе части уравнения, вы получите тридцать равно тридцати. Свойство распределения помогает нам взять эту тройку и распределить ее между четырьмя и шестью, двумя слагаемыми суммы. Алгебраическое представление дистрибутивного свойства или представление с переменными будет выглядеть так. 𝑎 умножить на 𝑏 плюс 𝑐 равно 𝑎 умножить на 𝑏 плюс 𝑎 умножить на 𝑐. Здесь мы берем 𝑎 и распределяем его между слагаемым 𝑏 и слагаемым 𝑐. Это верно и в обратном порядке. Это верно и в обратном порядке.
В этом примере мы хотим убрать 𝑎, поместить его за скобки и сначала добавить 𝑏 и 𝑐.
Вот этот пример с цифрами. Пять раз два плюс пять раз три — это то же самое, что сказать пять раз пять или пять раз два плюс три. Вот диаграмма, которая поможет вам обобщить все различные свойства. Эти свойства лягут в основу решения всевозможных уравнений.
математика — Исторические корни обоснования правила умножения отрицательных чисел
В качестве дополнительного вопроса по поводу : Кто записал минус, умноженный на минус, равно плюсу? и к: Исторически, как люди определяли умножение для отрицательных чисел?, может быть интересно проследить первое «современное» обоснование для правила:
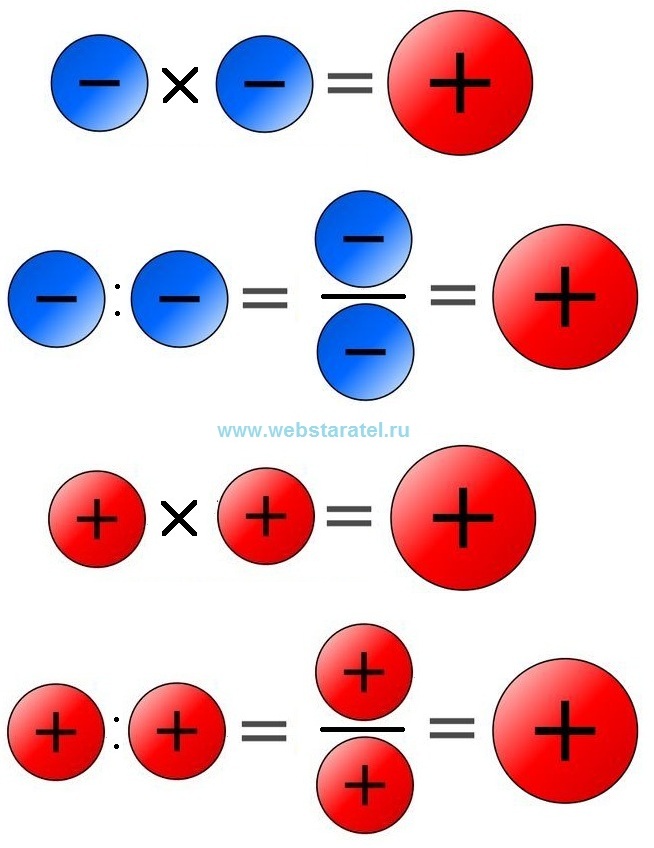
« минус , умноженное на минус , дает плюс ».
Если интуитивно понятно, что «если у вас есть долг в размере 3 долларов США на людей по 3 доллара, то у вас есть долг в размере 9 долларов$» (мы можем оправдать это сокращением умножения на повторение суммы ) не так просто представить долг в 3$ «минус» 3$ людям.
Для (отрицательной) ссылки см.
- Исаак Ньютон, Универсальная арифметика: или Трактат об арифметической композиции и разрешении, к которому добавлен метод доктора Галлея арифметического нахождения корней уравнений (латинская рукопись: Arithmetica Universalis (отредактировано и опубликовано Уильямом Уистоном, преемником Ньютона) Лукасовским профессором математики в Кембриджском университете в 1707 г. на основе конспектов лекций Ньютона) 9.0047
См. стр. 3:
Количество либо утвердительно, либо больше нуля; или отрицательный, или меньше, чем ничего. Таким образом, в гуманитарных делах Имущество или Запасы можно назвать утвердительными Товарами, а Долги отрицательными . […] Отрицательное количество обозначается знаком $-$ ; Знак $+$ ставится перед утвердительным […].
В совокупности количеств примечание $+$ означает, что количество, к которому оно предшествует, должно быть добавлено, а примечание $-$ — что оно должно быть вычтено.
И мы обычно выражаем эти Заметки словами Плюс (или больше ) и Минус (или меньше ). Таким образом, $2+3$, или на $2$ больше $3$, обозначает сумму чисел $2$ и $3$, то есть $5$. А $5-3$ или $5$ меньше $3$ обозначают разницу, которая возникает при вычитании $3$ из $5$, то есть $2$. [ Обратите внимание на четкое различие между двумя употреблениями знаков $+$ и $-$ .]См. стр. 16:
Простые алгебраические термины умножаются путем умножения чисел на числа и видов на виды, а произведение становится утвердительным, если оба множителя утвердительные, или оба отрицательными: и отрицательными, если иначе. Таким образом, $2a$ в $3b$ или $-2a$ в $-3b$ дают $6ab$ или $6ba$; ибо неважно, в каком порядке они расположены. Таким образом, также $2a$ на $- 3b$ или $- 2a$ на $3b$ дают $- 6ab$.
Полезные «постньютоновские» ссылки:
- Уильям Джейкоб с’Гравесанде, Элементы универсальной математики или алгебры (1728 г. — латинский оригинал: 1727 г.), стр. 9:
— латинский оригинал: 1727 г.), стр. 9:, если знаки множимого и множителя знакомы (или совпадают), произведение будет утвердительным, но отрицательным, если они разные.
Объяснение случая минус умножить на дается с точки зрения «симметрии», за которой следует интуитивно понятный пример:
В этом Случае отнимается отрицательное Количество, благодаря которому исчезает Отрицание. Таким образом, забрать Долг — значит заплатить по нему [курсив наш].
Полезно сравнить с полностью «алгебраическим» объяснением одного из самых блестящих последователей Ньютона:
- Колин МакЛорин, «Трактат об алгебре» (посмертно: 1748 — 3-е изд. 1771), стр. 13:
По определению $+a-a=0$; следовательно, если мы умножим $+a-a$ на $n$, произведение должно быть равно нулю или равно $0$, потому что множитель $a-a$ равен $0$. […] Следовательно, $-a$, умноженное на $+n$, дает $-na$.
