Уравнения с дробями 4 класс: 4 класс, уравнение, решение уравнений, примеры и задачи

Содержание

Урок математики по теме «Деление дробей в уравнениях»

Форма урока: объяснение нового материала.

Цели урока:

Обучающая: выработать навыки учащихся умножать и делить обыкновенные дроби, решать и оформлять задачи на уравнения.
Воспитательная: воспитывать самостоятельность, аккуратность
Развивающая: развивать внимание, математическую речь, вычислительные навыки учащихся, интерес к математике.

Ожидаемые результаты: дети научаться решать задачи и уравнения на дроби.

Этапы урока	Время (мин)	Слайды
Организационный момент.	2	Слайд 1
Устная работа и повторение ранее изученного	8	Слайды 2, 3, 4, 5,6
Формирование новых знаний и умений	10	Слайды 7, 8
Физкультминутка	2	Слайды 9, 10
Закрепление нового материала	5	Слайд 11
Проверка знаний (с/р)	10	Слайд 12
Постановка домашнего задания	1	Слайд 13
Подведение итогов урока	2

ХОД УРОКА

I. Организационный этап

– Здравствуйте, мы проведем сегодня урок по теме «Деление дробей в уравнених». Откройте тетради, запишите число, классная работа и тему урока.
Целью нашего урока является закрепление и проверка умений умножать и делить обыкновенные дроби, а также повторить навыки решения задач и уравнений.

II. Устный опрос учащихся

Чтобы умным в жизни стать
Надо дроби изучать

1) Переведите смешанную дробь в неправильную (Приложение 1, слайд 3)

2) Выделите целую часть (Приложение 1, слайд 4)

3) Умножьте дроби (Приложение 1, слайд 5)

– Повторим правило умножения двух дробей: Чтобы умножить дробь на дробь нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе знаменателем.

4) Выполните деление (в тетрадях с последующей взаимопроверкой, сосед у соседа) (Приложение 1, слайд 6)

– Повторим правило деления двух дробей: Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.

III. Формирование новых знаний и умений

– При изучении темы деление большое значение имеет умение решать уравнения. Рассмотрим пример и запишем его в тетрадь. (Приложение 1, слайд 7)

– Чтобы решить уравнение необходимо определить какой компонент в уравнении является неизвестным.
– Какой?
– 1 множитель
– Правильно! Чтобы найти неизвестный множитель, что нужно сделать?

– Чтобы найти неизвестный множитель необходимо произведение разделить на известный множитель.
– Находим корень уравнения, выполняя деление. Выполним проверку и запишем ответ.

– А теперь давайте проверим ваше умение решать задачи.

№ 597 (Приложение 1, слайд 7)

– Сколько всего прошел лыжник ? (26 км)
– Сколько километров прошел в первый день? (неизвестно)
– Сколько километров прошел во второй день? (неизвестно)
– Какую величину, с какой сравнивают?
– Что возьмем за х?
– Как найти дробь от числа?
– Сколько километров прошел за два дня?
– Как найти?
– Составим уравнение.

– 14 км лыжник прошел во второй день

26 – 14 = 12 км лыжник прошел в первый день.

№ 598 (Приложение 1, слайд 8)

– Вспомним что такое 1% (одна сотая)
– Какой дробью запишем 75% (75/100 = 3/4)
– Сколько грибов собрала белка? (неизвестно)
– Сколько грибов собрал бельчонок? (неизвестно)
– Какую величину, с какой сравнивают?
– Что обозначим за икс?
– Как найти дробь от числа?
– Сколько собрали вместе белка и бельчонок?
– Составим уравнение.

200 грибов собрала белка
350 – 200 = 150 грибов собрал бельчонок

IV. Физкультминутка

– Встаем и выполняем несколько упражнений.

А теперь, ребята, встали,
Быстро руки вверх подняли,
В стороны, вперёд, назад
Повернулись вправо, влево,
Тихо сели, вновь за дело.

V. Закрепление нового материала

№ 594

– Сколько собрал Митя?
– Сколько собрал Коля?
– Какую величину, с какой сравнивают?
– Что обозначим за икс?
– Как найти дробь от числа?
– Сколько собрали вместе мальчики?

28 грибов собрал Митя

64 – 28 = 36 грибов собрал Коля

VI. «Математический выбор»

Уравнения, оцениваемые в 3 балла: Уравнения, оцениваемые в 5 баллов:

1)                                                                      1)

2)                                                                       2)

3)                                                                    3)

4)                                                                  4)

Уравнения, оцениваемые в 6 баллов:

1)

2)

3)

4)

Оценки: 5 – 12 баллов; 4 – 9 баллов; 3 – 6 баллов.

Каждый выбирает себе уравнения по «плечу».
Учитель во время работы оценивает учеников.

VII. Итог урока

– С каким настроением вы сегодня работали на уроке?
– Какая задача для вас была самой интересной?
– Ребята чему мы научились на сегодняшнем уроке?
– Как найти часть от числа?
– Как найти неизвестный множитель?

Оценки за урок.

VIII. Домашнее задание

– С листов решить любые три уравнения, из тех которые не решали в классе.

«Дроби». Математика 4 класс — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

«Дроби».
Математика
4 класс
Ц ЕЛИ :
закрепить знание понятий «дроби»правильные и неправильные; смешанные
числа;
повторить свойства сложения и

вычитания дробей
формирование умений решать
составные задачи на нахождение третьей
части;
развивать речь, внимание, память;
навыки устных и письменных вычислений,
самоанализа.
ДЕВИЗ УРОКА.
«
Начнешь в учении
с малого,
постигнешь и
большее».
А КТУАЛИЗАЦИЯ
ЗНАНИЙ .
1 7 5 2 16 7 13 4 9
6 9 6 9 9 6
6 9
Тема: «Дроби»
Т ЕМА «Д РОБИ »
План.
1. Виды дробей.
2. Сложение и вычитание
дробей.
3. Решение задач.
Д РОБИ .
1 числитель
знаменатель
6
Сколько частей
взяли.
На сколько
частей
разделили.

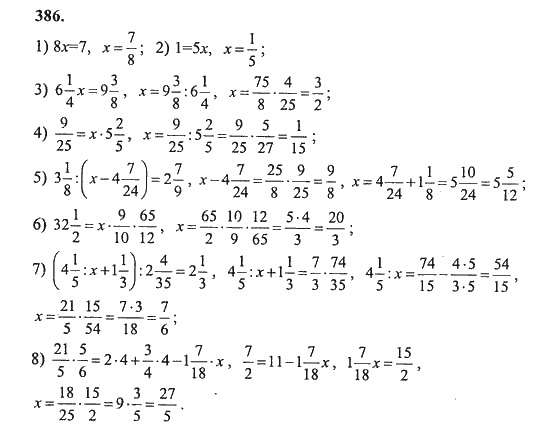
К ЛАССИФИКАЦИЯ ДРОБЕЙ .
правильные
неправильные
1
5
2
4
7
9
16
7
6
6
9
6
9
9
9
6
Числитель
меньше
знаменателя
Числитель
больше
знаменателя
К ЛАССИФИКАЦИЯ
ДРОБЕЙ
Дроби
со знаменателем 6

со знаменателем 9
*
РАБОТА
ПО ВАРИАНТАМ .
Вариант1: расположить дроби со
знаменателем 6 в порядке возрастания;
Вариант2: расположить дроби со
знаменателем 9 в порядке убывания.
Проверка:
1в. 1; 4;
6
6
5; 7
6
6
2в. 16;
9
9;
7; 2
9
9
9
Д РОБИ .
правильные
неправильные
смешанные
Уровень А – составить выражение с дробями на сложение
и вычитание по схеме:
а
n
в
n
а
n
в
n
Уровень В – составить выражение в несколько действий с
дробями по схеме
а
n
в
n
с
n
а
n
Уровень С – составить уравнение с дробями.
а х в
n
n
а х в
n
n
в
n
с
n
с
n
При сложении дробей с одинаковыми
знаменателями, числители
складываются, а знаменатели остаются
без изменения.

При вычитании дробей с одинаковыми
знаменателями, из числителя первой
дроби вычесть числитель второй дроби,
знаменатель остается без изменения.
С ЛОЖЕНИЕ И ВЫЧИТАНИЕ
ДРОБЕЙ .
а + в = а+в
n n
n
а–в =а-в
n n
n
Р ЕШЕНИЕ
ЗАДАЧ .
Длина трех рек России Волги,
Дуная и Днепра составляет 8100км.
Длина реки Волги составляет -4\9всей
длины, длина Дуная составляет 1\3
всей длины. Какова длина Днепра?
1 СПОСОБ :
План решения задачи:
1) : х
2) : х
3) — :
Проверка
1) 8100: 9х4
2) 8100:3 х1
3)8100- 3600 -2700
2
СПОСОБ :
8100 – (8100:9х4 + 8100:3х1)= 1800(км)
Вывод: При решении задачи на
нахождение третьей части, нужно из целого
вычесть первую часть, а потом – вторую. Или
из целого вычесть сумму двух частей.
.
Г ЕНИЙ СОСТОИТ ИЗ
1% ВДОХНОВЕНИЯ И 99% ПОТЕНИЯ .
Словарная работа:
Гений – высшая творческая
способность. (Человек,
обладающий такой
способностью).

Вдохновение – творческий
подъем, прилив творческих сил.
И ТОГ
УРОКА .
— Назовите тему урока.
-Что мы повторили?
— Что понравилось ? Что нового для себя открыли?
Д\З : по выбору:
1)тренажер
2) по учебнику
3) Составить и решить задачу с дробями

English Русский Правила

Рабочие листы для дробей

Половины, трети и четверти

Откройте дверь к пониманию дробей для младших школьников до 3-го класса с помощью наших листов для половин, третей и четвертей! Удобные для детей иллюстрации, увлекательные упражнения и практические занятия позволяют детям впитывать все, что касается половинок, третей и четвертей.

Визуальные модели дробей

Помогите учащимся 3-х и 4-х классов понять дроби как равные части целого, используя фигуры, реальные объекты, кусочки пиццы и множество визуальных моделей дробей! Они определяют правильные дроби, единичные дроби, смешанные числа и многое другое.

Определение дробей

Хотите, чтобы ребенок научился определять дроби в один миг? Приложите все усилия, чтобы найти числители и знаменатели, заполнить таблицу, составив дроби, и многое другое с помощью этих динамических рабочих листов в формате PDF.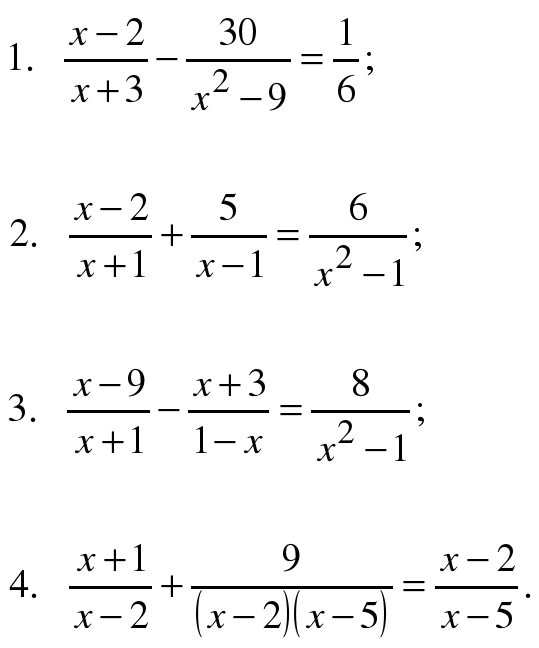

Типы дробей

Какой дробью является 1/4? Да, это единичная дробь. Определите правильную дробь, неправильную дробь, смешанное число, единичную дробь, например дроби, в отличие от дробей, как профессионал, с этими печатными листами дробей.

Упрощение дроби

Сократите правильную дробь, неправильную дробь и смешанные числа до наименьшего члена.

Преобразование неправильных дробей в смешанные числа

Что легче интерпретировать, 1 1/4 или 5/4? Некоторым учащимся может быть сложнее работать со смешанными числами, чем с неправильными дробями, для других неправильные дроби могут показаться более легкими. Подготовьтесь к преобразованию между ними с помощью этих рабочих листов в формате PDF!

Эквивалентная дробь

Интерактивные рабочие листы, в которых используются полосы дробей, круговая модель, визуальная графика и многое другое.

Дроби на числовой прямой

Эти рабочие листы с дробями на числовой прямой помогают детям визуально понимать дроби.

Сложение дробей

Сложение одинаковых, непохожих, правильных, неправильных и смешанных дробей. Включены специальные дроби, такие как единица и обратная дробь.

Вычитание дробей

Бесплатные рабочие листы по вычитанию включают в себя все типы дробей, построенные с различными уровнями навыков.

Умножение дробей

Распознавание умножения дробей на целые числа с использованием повторного сложения, массивов, моделей числовых рядов, равных групп и моделей площадей; выполнять умножение двух и трех дробей, умножение дробей на смешанные числа и т. д.; решить ряд задач на умножение дробей.

Деление дробей

Подключитесь к нашим печатным листам деления дробей и попрактикуйтесь в делении дробей на целые числа, дроби на дроби, смешанного числа на дроби и т. д.!

Проблемы со словами на дроби

Узнайте, как дроби применяются и используются в реальной жизни, выполняя эти задачи со словами.

Сравнение дробей

Изучите наши листы сравнения дробей, чтобы без труда сравнить две дроби с одинаковыми и разными знаменателями. Благодаря большому количеству моделей и упражнений, эти PDF-файлы являются отличным учебным пособием для детей.

Сравнение смешанных чисел

Что больше, 1 2/5 или 2 5/6? Сравните такие смешанные числа мгновенно и безошибочно с помощью наших рабочих таблиц сравнения смешанных чисел!

Упорядочивание дробей

Расположите дроби в возрастающем или убывающем порядке.

Округление дробей

Округление дробей до ближайшего целого числа или до ближайшей половины. Числовые строки также включены.

Оценка дробей

Оценить сумму, разность, произведение и частное с дробями.

Рабочие листы «Преобразование дробей в десятичные числа»

Поддержите знания ребенка, связанные с преобразованием дробей в десятичные числа, включив множество увлекательных упражнений и стремительно повышая их силу!

Преобразование между дробями, десятичными знаками и процентами Рабочие листы

Помогите учащимся сделать большой прорыв в выполнении преобразования между процентами, десятичными знаками и дробями. Обширный набор упражнений направлен на улучшение при проверке их понимания темы.

Иллюстративная математика

класс 4

4 класс

4.ОА. 4 класс — Операции и алгебраическое мышление

4.ОА.А. Используйте четыре операции с целыми числами для решения задач.

Сравнение роста, вариант 1
Сравнение роста, вариант 2

4.ОА.А.1. Интерпретируйте уравнение умножения как сравнение, например, интерпретируйте $35 = 5 \times 7$ как утверждение, что 35 в 5 раз больше, чем 7, и в 7 раз больше, чем 5. Представьте вербальные утверждения мультипликативных сравнений в виде уравнений умножения.

Тысячи и миллионы четвероклассников
Находящиеся под угрозой исчезновения

4.ОА.А.2. Умножьте или разделите, чтобы решить текстовые задачи, включающие мультипликативное сравнение, например, используя рисунки и уравнения с символом неизвестного числа для представления проблемы, отличая мультипликативное сравнение от аддитивного сравнения.

Сравнение привлеченных денег

4.ОА.А.3. Решите многошаговые словесные задачи, поставленные с целыми числами и имеющие ответы с целыми числами, используя четыре операции, включая задачи, в которых необходимо интерпретировать остатки. Представьте эти проблемы, используя уравнения с буквой, обозначающей неизвестную величину. Оцените обоснованность ответов, используя вычисления в уме и стратегии оценки, включая округление.

Билеты на карнавал
Сад Карла

4.ОА.Б. Знакомство с множителями и множителями.

Идентификация множественных
Кратные числа 3, 6 и 7
Числа в таблице умножения

4.ОА.Б.4. Найдите все пары множителей для целого числа в диапазоне от 1 до 100. Признать, что целое число является кратным каждого из его делителей. Определить, является ли заданное целое число в диапазоне от 1 до 100 кратным заданному однозначному числу.

Игра в шкафчик

4.ОА.С. Создавайте и анализируйте шаблоны.

Кратные числа 3, 6 и 7

4.ОА.С.5. Создайте шаблон числа или формы, который следует заданному правилу. Определите очевидные особенности шаблона, которые не были явными в самом правиле. Например, учитывая правило «Добавить 3» и начальный номер 1, создайте термины в результирующей последовательности и обратите внимание, что термины чередуются между нечетными и четными числами. Неформально объясните, почему числа будут продолжать чередоваться таким образом.

Двойной плюс один
Кратность девяти

4.НБТ. 4 класс — Числа и операции с основанием десять

4.НБТ.А. Обобщить понимание разряда для многозначных целых чисел.

Какой у меня номер?

4.

Тысячи и миллионы четвероклассников
Находящиеся под угрозой исчезновения

4.НБТ.А.2. Читать и писать многозначные целые числа, используя числа с основанием десять, имена чисел и расширенную форму. Сравните два многозначных числа на основе значений цифр в каждом разряде, используя символы $>$, = и $

Заказ 4-значных номеров

4.НБТ.А.3. Используйте понимание разрядности для округления многозначных целых чисел до любого места.

Округление в числовой строке
Округление до ближайшей 1000
Округление до ближайших 100 и 1000

4.НБТ.Б. Используйте понимание позиционного значения и свойства операций для выполнения многоразрядной арифметики.

Перегруппировывать или не перегруппировывать

4.НБТ.Б.5. Умножьте целое число до четырех цифр на однозначное целое число и умножьте два двузначных числа, используя стратегии, основанные на разрядности и свойствах операций. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.

Тысячи и миллионы четвероклассников

4.НБТ.Б.6. Находите целые числа в частных и остатках с до четырехзначными делителями и однозначными делителями, используя стратегии, основанные на разрядном значении, свойствах операций и/или взаимосвязи между умножением и делением. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.

Стратегия ментального подразделения

4.НФ. 4 класс — Числа и операции — Дроби

4.НФ.А. Расширьте понимание дробной эквивалентности и порядка.

Деньги в копилку
Забеги

4.НФ.А.1. Объясните, почему дробь $a/b$ эквивалентна дроби $(n \times a)/(n \times b)$, используя визуальные модели дробей, обращая внимание на то, как количество и размер частей различаются, несмотря на то, что сами две фракции имеют одинаковый размер. Используйте этот принцип для распознавания и создания эквивалентных дробей.

Объяснение эквивалентности дробей с помощью изображений
Дроби и прямоугольники

4.НФ.А.2. Сравните две дроби с разными числителями и разными знаменателями, например, создав общие знаменатели или числители, или сравнив с эталонной дробью, такой как 1/2. Признайте, что сравнения допустимы только тогда, когда две дроби относятся к одному и тому же целому. Запишите результаты сравнений символами $>$, = или $

Сравнение дробей с использованием игры эталонов
Удвоение числителей и знаменателей
Список дробей в возрастающем размере
Использование контрольных показателей для сравнения дробей

4.

Сравнение двух разных пицц

4.NF.B.3. Под дробью $a/b$, где $a > 1$, понимается сумма дробей $1/b$.

Запись смешанного числа в виде эквивалентной дроби

4.NF.B.3.а. Понимать сложение и вычитание дробей как соединение и разделение частей, относящихся к одному и тому же целому.

Сравнение сумм единичных дробей

4.NF.B.3.б. Разложите дробь на сумму дробей с одинаковым знаменателем более чем одним способом, записывая каждое разложение уравнением. Обоснуйте разложения, например, с помощью визуальной дробной модели. Примеры: $\frac38 = \frac18 + \frac18 + \frac18$; $\frac38 = \frac18 + \frac28$; $2 \frac18 = 1 + 1 + \frac18 = \frac88 + \frac88 + \frac18.$

Делаем 22 семнадцатых разными способами

4.NF.B.3.c. Складывать и вычитать смешанные числа с одинаковыми знаменателями, например, заменяя каждое смешанное число эквивалентной дробью и/или используя свойства операций и отношения между сложением и вычитанием.

Идеальный удар Синтии
Персики
Пластиковые строительные блоки
Запись смешанного числа в виде эквивалентной дроби

4.NF.B.3.d. Решайте текстовые задачи, включающие сложение и вычитание дробей, относящихся к одному и тому же целому и имеющих одинаковые знаменатели, например, используя визуальные модели дробей и уравнения для представления задачи.

Пока нет задач, иллюстрирующих этот стандарт.

4.NF.B.4. Применяйте и расширяйте прежнее понимание умножения, чтобы умножить дробь на целое число.

Расширение умножения целых чисел на дроби

4.NF.B.4.а. Под дробью $a/b$ следует понимать кратное $1/b$. Например, используйте модель визуальной дроби, чтобы представить $5/4$ как произведение $5 \times (1/4)$, записав вывод уравнением $5/4 = 5 \times (1/4).$

Пока нет задач, иллюстрирующих этот стандарт.

4.NF.B.4.b. Понимайте кратное $a/b$ как кратное $1/b$ и используйте это понимание, чтобы умножить дробь на целое число. Например, используйте модель визуальной дроби, чтобы выразить $3 \times (2/5)$ как $6 \times (1/5)$, распознав этот продукт как $6/5$. (Вообще, $n \times (a/b) = (n \times a)/b.$)

Пока нет задач, иллюстрирующих этот стандарт.

4.NF.B.4.c. Решайте текстовые задачи, связанные с умножением дроби на целое число, например, используя визуальные модели дробей и уравнения для представления задачи. Например, если каждый человек на вечеринке съест 3/8 фунта ростбифа, а на вечеринке будет 5 человек, сколько фунтов ростбифа потребуется? Между какими двумя целыми числами лежит ваш ответ?

Сахар в шести банках газировки

4.Н.Ф.К. Понимать десятичную запись дробей и сравнивать десятичные дроби.

4.NF.C.5. Выразите дробь со знаменателем 10 в виде эквивалентной дроби со знаменателем 100 и используйте эту технику, чтобы сложить две дроби со знаменателями 10 и 100 соответственно.

Добавление десятых и сотых
Даймс и Пенни
Расширенные дроби и десятичные дроби
Эквивалентность дроби
Сколько десятых и сотых?

4.NF.C.6. Используйте десятичную запись для дробей со знаменателем 10 или 100. Например, перепишите $0,62$ как $62/100$; описать длину как $0,62$ метра; найдите $0,62$ на диаграмме с числовыми линиями.

Даймс и Пенни
Расширенные дроби и десятичные дроби
Сколько десятых и сотых?

4.NF.C.7. Сравните два десятичных знака с сотыми, рассуждая об их размере. Признайте, что сравнения действительны только тогда, когда два десятичных знака относятся к одному и тому же целому. Запишите результаты сравнений символами $>$, = или $

Использование значения места

4.МД. 4 класс — Измерения и данные

4.МД.А. Решайте задачи, связанные с измерением и преобразованием измерений из большей единицы в меньшую.

4.МД.А.1. Знать относительные размеры единиц измерения в пределах одной системы единиц, в том числе км, м, см; кг, г; фунт, унция; л, мл; ч, мин, сек. В рамках единой системы измерения выражайте измерения в большей единице через меньшую. Запишите эквиваленты измерений в таблицу из двух столбцов. Например, известно, что 1 фут в 12 раз длиннее 1 дюйма. Выразите длину змеи длиной 4 фута как 48 дюймов. Создайте таблицу преобразования для футов и дюймов, перечислив пары чисел $(1, 12)$, $( 2, 24)$, $(3, 36)$, …

Кто самый высокий?

4.МД.А.2. Используйте четыре операции для решения текстовых задач, связанных с расстояниями, интервалами времени, объемами жидкостей, массами объектов и деньгами, включая задачи с простыми дробями или десятичными знаками, а также задачи, требующие выражения измерений, выраженных в более крупной единице, через меньшую единицу.

Марджи покупает яблоки

4.МД.А.3. Применяйте формулы площади и периметра для прямоугольников в реальных и математических задачах. Например, найдите ширину прямоугольной комнаты, зная площадь пола и длину, рассматривая формулу площади как уравнение умножения с неизвестным коэффициентом.

Сад Карла

4.МД.Б. Представлять и интерпретировать данные.

4.МД.Б.4. Создайте линейный график для отображения набора данных измерений в долях единицы $(1/2, 1/4, 1/8)$. Решайте задачи на сложение и вычитание дробей, используя информацию, представленную в виде линейных графиков. Например, по линейному графику найдите и интерпретируйте разницу в длине между самым длинным и самым коротким экземпляром в коллекции насекомых.

Диаметр кнопки

4.

4.МД.С.5. Распознавать углы как геометрические фигуры, которые образуются там, где два луча имеют общую конечную точку, и понимать принципы измерения углов:

Пока нет задач, иллюстрирующих этот стандарт.

4.MD.C.5.а. Угол измеряется по отношению к окружности с центром в общей конечной точке лучей, принимая во внимание долю дуги окружности между точками, где два луча пересекают окружность. Угол, который проходит через 1/360 окружности, называется «углом в один градус» и может использоваться для измерения углов.

Пока нет задач, иллюстрирующих этот стандарт.

4.MD.C.5.b. Угол, который проходит через $n$ углов в один градус, называется угловой мерой, равной $n$ градусам.

Пока нет задач, иллюстрирующих этот стандарт.

4.МД.

Измерение углов

4.МД.С.7. Признать угловую меру аддитивной. Когда угол разлагается на непересекающиеся части, угловая мера целого равна сумме угловых мер частей. Решите задачи на сложение и вычитание, чтобы найти неизвестные углы на диаграмме в реальном мире, и математические задачи, например, используя уравнение с символом для неизвестной меры угла.

Нахождение неизвестного угла
Измерение углов

4.Г. 4 класс — Геометрия

4.Г.А. Рисуйте и идентифицируйте линии и углы, а также классифицируйте фигуры по свойствам их линий и углов.

4.Г.А.1. Рисовать точки, прямые, отрезки, лучи, углы (прямые, острые, тупые), перпендикулярные и параллельные прямые. Определите их на двумерных фигурах.

Измерение углов
Геометрия букв
В чем смысл?