По диаметру вычислить окружность: Длина окружности. Площадь круга — урок. Математика, 6 класс.

Формула для измерения длины окружности

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Арабян  М.Н. 1

---

1Муниципальное бюджетное образовательное учреждение «Березовская средняя школа»

Мамонова  В.М. 1

---

1Муниципальное бюджетное образовательное учреждение «Березовская средняя школа»

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Геометрия – одна из самых древних наук, она возникла очень давно, ещё до нашей эры. В переводе с греческого слово «геометрия» означает «землемерие».

Геометрия – наука о пространстве, точнее – наука о формах, размерах и границах тех частей пространства, которые в нем занимают вещественные тела; раздел математики, изучающий пространственные отношения и их обобщения.

В школе предмет «Геометрия» изучается с 7 класса и, по мнению многих учащихся, является одним из самых сложных школьных предметов.

Что же геометрия означает в нашей жизни? Кое – кто, возможно, считает, что различные замысловатые линии, фигуры, поверхности можно встретить только в книгах ученых математиков. Однако стоит посмотреть вокруг, и можно увидеть, что многие предметы имеют форму, похожую на уже знакомые геометрические фигуры. Оказывается их много. Просто это не всегда бросается в глаза.

Геометрия – древнейшая наука и первые расчеты производились более тысячи лет назад. Древние люди составляли на стенах пещер орнаменты из треугольников, ромбов, кругов. Со временем человек научился использовать свойства фигур в практической жизни.

Многие вещи, окружающие нас, напоминают окружность, например, обруч, кольцо, тарелка. Арбуз, глобус, мячи – похожи на шар. Предметов, имеющих форму цилиндра и конуса в окружающем нас мире очень много: трубы, кастрюли, бочки, стаканы, консервные банки.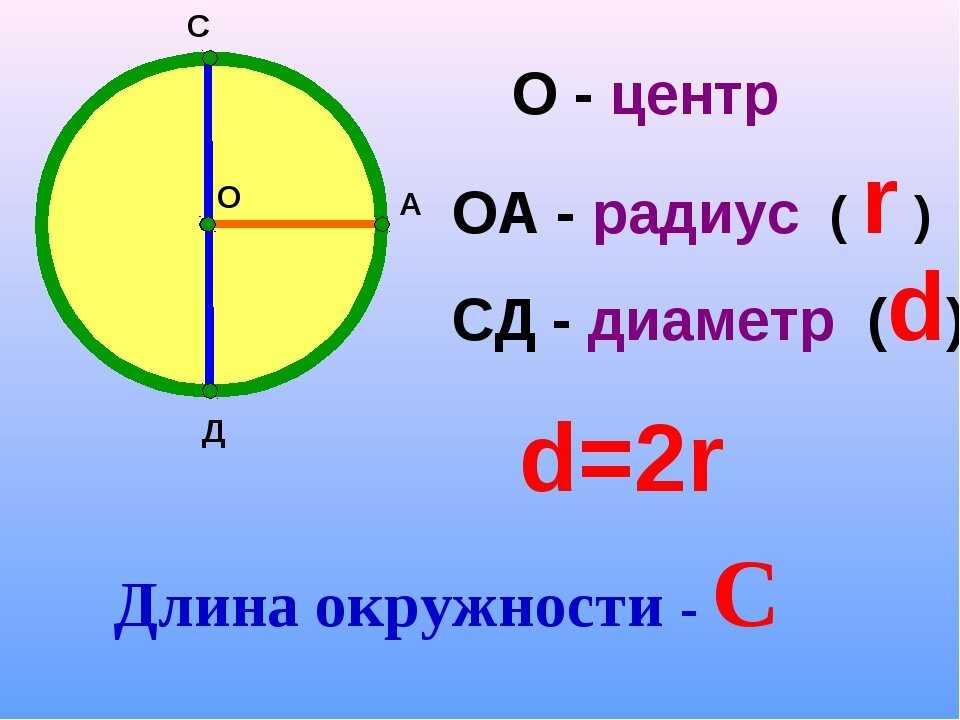

В современной архитектуре смело используются самые разные геометрические формы. Многие жилые дома украшаются колоннами. Геометрические фигуры различной формы можно увидеть в постройке соборов и конструкциях мостов.

По улице движутся автомобили, трамваи, автобусы, мотоциклы и велосипеды. Их колеса с геометрической точки зрения – круги. Сложную форму имеет корпус подводной лодки. Корпус космического спутника состоит из цилиндра.

Сложную форму имеют и детали машин – гайки, винты, зубчатые колеса.

В природе много замечательных геометрических форм. Необыкновенно красивы и разнообразны многоугольники, созданные природой. Кристаллы горного хрусталя напоминают отточенный карандаш. Кристалл соли имеет форму куба, кристаллы алмаза имеют форму правильного восьмигранника – октаэдра. Кто из нас не любовался в зимний солнечный день искристыми снежинками? Каждая снежинка – это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной.

Снежинки – это одна из самых красивых геометрических фигур. Обычная горошина, капельки росы – имеют форму шара.

Многих животных природа наделила талантом строить себе дома в форме геометрических тел. Птицы строят гнёзда в форме полушара. Но самые искусные геометры – пчелы. Они строят соты из шестиугольников.

Из всего сказанного можно сделать вывод: геометрия нужна не только для того чтобы называть части строений или формы окружающего нас мира, с помощью геометрии можно решить многие задачи, ответить на многие вопросы.

Цель: вывести формулу длины окружности.

Задачи: изучить окружность, её элементы, показать связь между ними. Гипотеза: формулу длины окружности можно вывести практическим путем.

Методы исследования:

• Изучение литературы по данной теме.
• Практическая работа на измерение длины окружности.
• Анализ, сравнение, сопоставление.

Глава 1. Что такое окружность?

Окружность – замкнутая, плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.

Круг – часть плоскости, ограниченная окружностью.

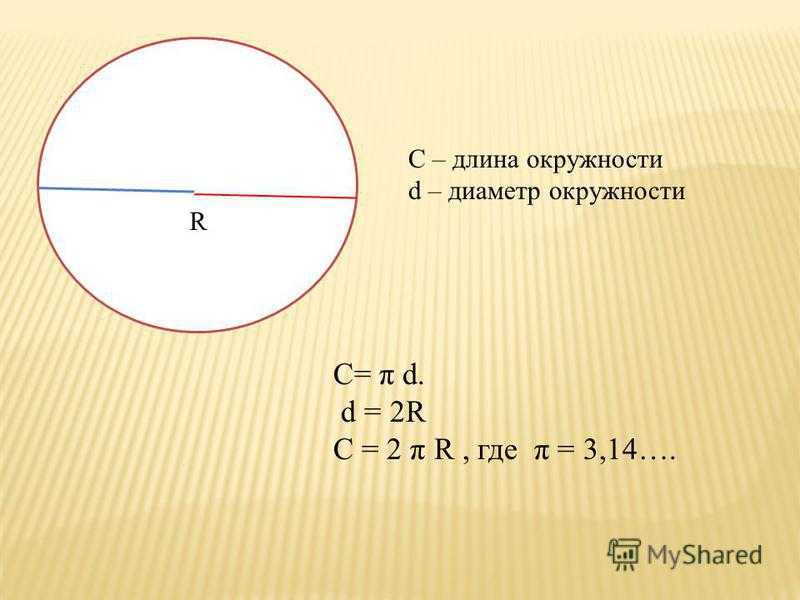
Радиус – отрезок прямой, соединяющий центр окружности с какой – либо её точкой, а также длина этого отрезка. Обычно обозначается R.

Диаметр – отрезок прямой, соединяющий пару наиболее удаленных друг от друга точек окружности, а также длина этого отрезка. Диаметр всегда проходит через центр окружности. Обычно обозначается d или Ø. Диаметр равен удвоенному радиусу окружности: d = 2R, R = d/2.

Отношение длины окружности к её диаметру одинаково для всех окружностей. Это отношение есть трансцендентное число, обозначаемое греческой буквой пи: _…

Длина окружности: C = 2πR= πd

Радиус окружности: R = C/2π

Диаметр окружности: d = C/π

Площадь круга: S = πR² = πd²/4

Радиус круга: R = _{(S/π), где — корень квадратный.}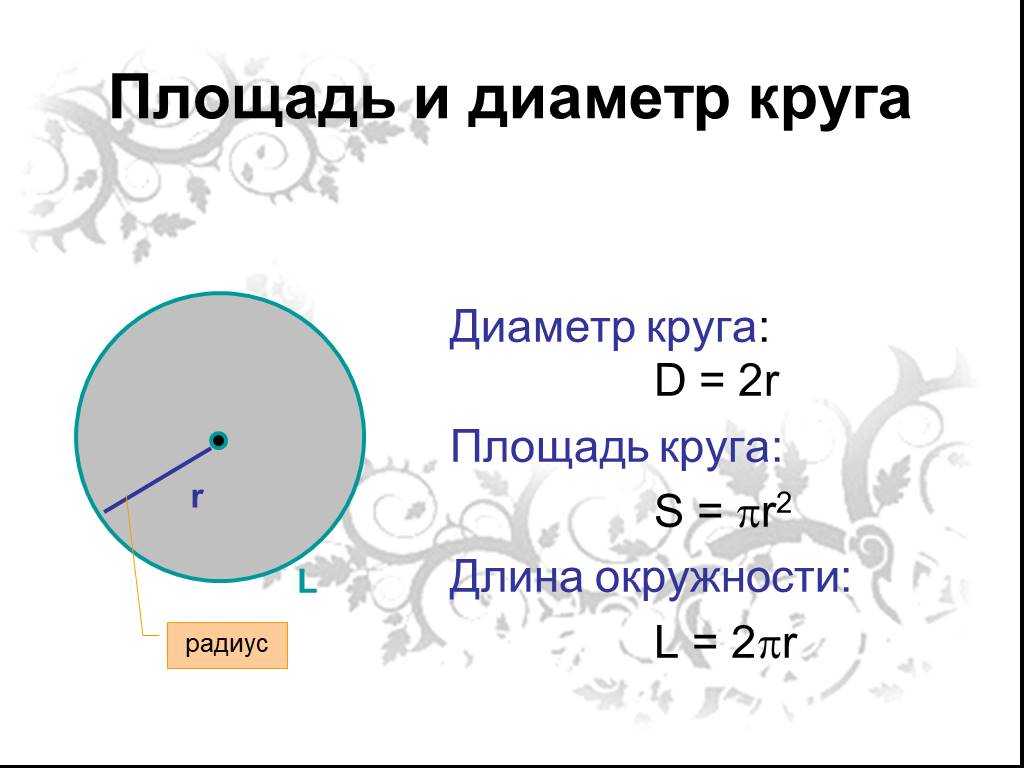

Диаметр круга: d = 2_(S/π)

Круг Окружность

Исторические сведения

В древней Греции круг и окружность считались венцом совершенства. Действительно, в каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности сделало возможным возникновение колеса, поскольку ось и втулка колеса должны все время быть в соприкосновении. Но ещё до колеса люди использовали круглые бревна – катки для перевозки тяжестей. Рисунки на стенах египетских пирамид рассказывают нам, что именно так доставлялись огромные камни на строительство этих пирамид.

Глава 2. Вывод формулы длины окружности

Как же можно вывести формулу для вычисления длины окружности? Самое простое, что приходит на ум – это измерить с помощью нити длину предметов, имеющих форму круга или окружности. Так как у любой окружности и у круга имеется диаметр, то вполне возможно его измерить.

Итак, для измерений необходимы предметы цилиндрической формы, такие как: кружка, термос, кастрюля; и предметы, имеющие непосредственно форму круга, например циферблат часов и барометр бытовой.

Первый этап работы заключается в измерении с помощью нити длины окружности выбранных предметов. Затем нужно длину нити измерить с помощью линейки. На втором этапе подобным образом можно измерить диаметры данных предметов. Должна же существовать какая – то связь между длиной окружности и её диаметром.

Измерение длины окружности с помощью нити и линейки.

Измерение диаметра окружности с помощью нити и линейки.

В результате проведённых измерений были получены следующие результаты:

Кружка для чая: C = 22 см, d = 7 см.

Термос: C = 43 см, d = 13,7см.

Кастрюля: C = 64 см, d = 20,5см.

Циферблат часов: C = 70 см, d = 22,6 см.

Барометр бытовой: C = 47,4 см, d = 15,1 см.

Нетрудно увидеть, что длина окружности каждого предмета больше её диаметра в несколько раз.

Что же получится, если посчитать, во сколько раз длина окружности больше диаметра в каждом случае? Для вычислений можно воспользоваться калькулятором.

C/d = 22 см / 7 см = 3,14285 _3,14

C/d = 43 см / 13, 7 см = 3,13868 _3,14

C/d = 64 см / 20,5 см = 3,13725 _3,14

C/d = 71 см / 22,6 см = 3,14159 _3,14

C/d = 47,4см / 15,1 см = 3,13907 _3,14

Как видно из полученных вычислений, отношение длины окружности к диаметру, если округлить его до сотых долей, является одним и тем же числом C/d_{3,14. Таким образом, получается, что если длину окружности любого размера разделить на её диаметр, то это отношение всегда будет приближаться к числу 3,14.}

Отношение длины окружности к её диаметру одинаково для всех окружностей.

Это есть известное число π

3,14. Т. е. C/d = π, отсюда следует, что C = πd.

d = 2r, где r – радиус окружности, тогда C = 2πr.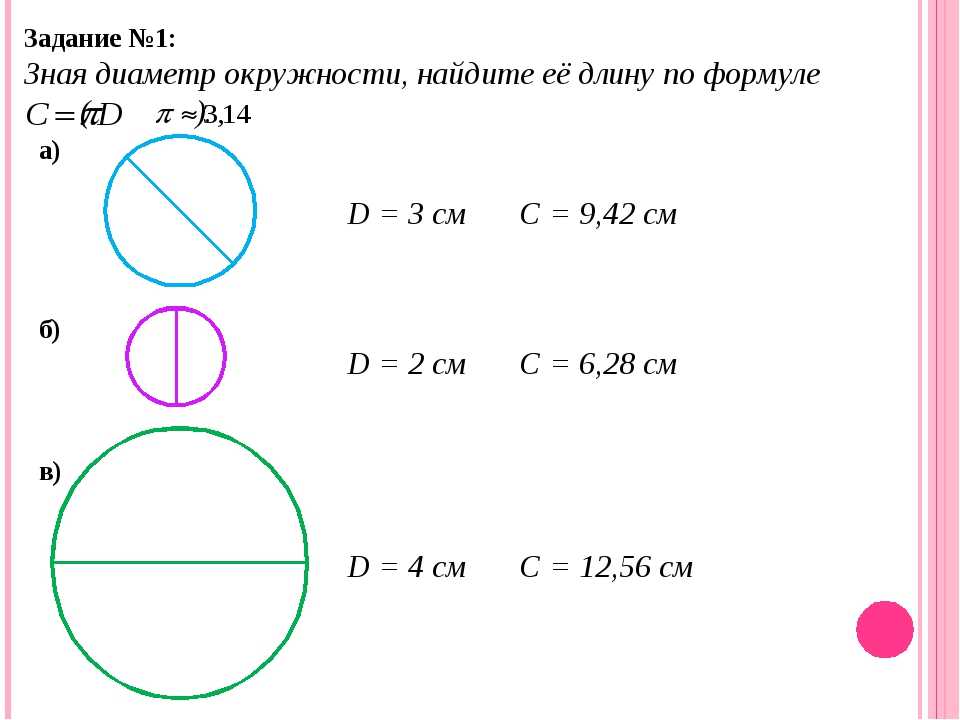

Заключение

В ходе исследовательской работы с помощью измерений и вычислений мы вывели формулу для вычисления длины окружности:

C = 2πr

Определили, как с помощью эксперимента получить известное число

π = 3,14

Литература

1. Геометрия. 7-9 классы: учебник для общеобразовательных учреждений / [Л.А. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. ]. – М. Просвещение, 2016г. – 384 с.:ил.
2. Красота математики М. Давыдов г. Н.Новгород 2007г.
3. http://ru.wikipedia.org/wiki/. [Электронный ресурс].

Просмотров работы: 505

Отношение длины окружности к диаметру

Рассматривая процесс нахождения длины окружности, можно заметить, что число, на которое нужно умножить диаметр, чтобы получить длину окружности, не зависит от величины самого диаметра, так что если мы нашли, что длина какой-нибудь окружности равна её диаметру, умноженному на некоторое число, то и длина всякой другой окружности будет равна её диаметру, умноженному на то же самое число.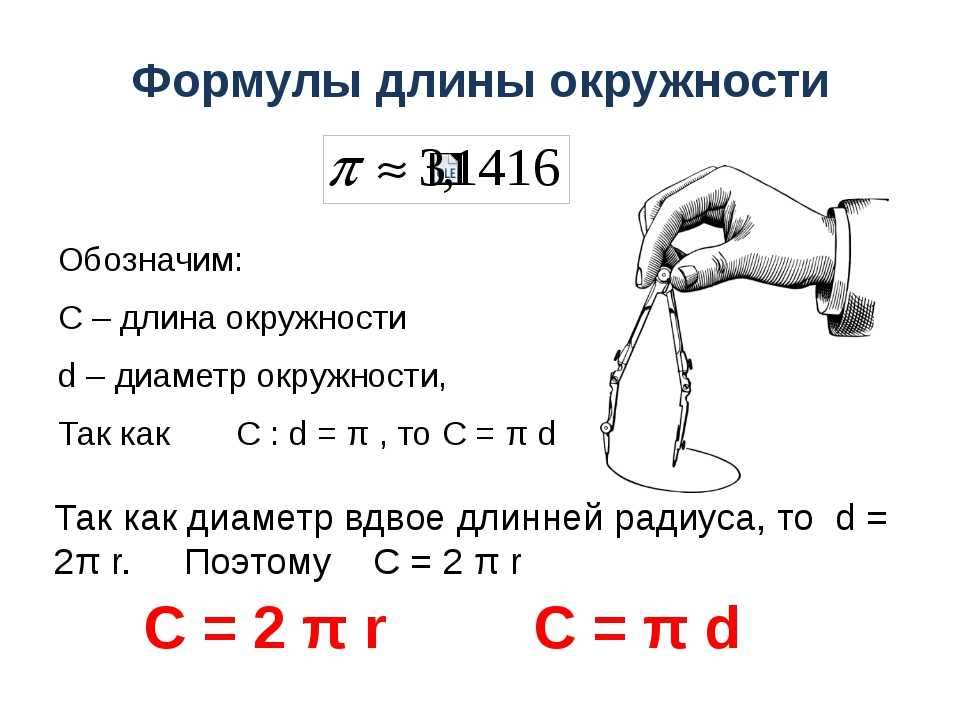

В самом деле, возьмём две окружности: одну радиуса R, другую радиуса r. Длину первой окружности обозначим через С, длину второй — через c. Впишем в каждую из них правильный многоугольник с одним и тем же числом сторон и будем удваивать число сторон каждого из этих многоугольников.

Обозначим через Р_n переменный периметр правильного многоугольника, вписанного в первую окружность, и через

р_n переменный периметр правильного многоугольника с тем же числом сторон, вписанного во вторую окружность.

На основании формулы P_n = 2Rn • sin ^180°/_n, мы можем написать:

$$ \frac{P_n}{2R} = \frac{p_n}{2r} $$

Переменный периметр Р_n имеет пределом длину С первой окружности. Переменный периметр р_n имеет пределом длину c второй окружности. А потому из равенства \(\frac{P_n}{2R} = \frac{p_n}{2r}\) вытекает ^C/_2R = ^c/_2r .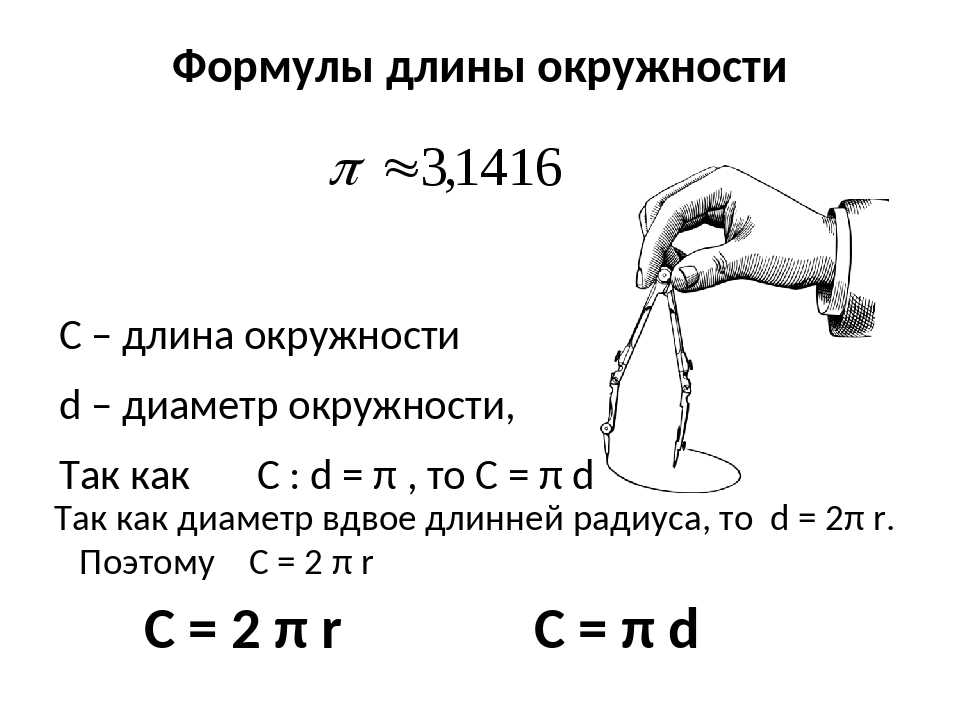

Таким образом, мы можем сказать, что отношение длины окружности к её диаметру есть число постоянное для всех окружностей.

Это постоянное число принято обозначать греческой буквой π. Обозначение это введено, по всей вероятности, в XVII столетии. Буква π (пи) есть начальная буква греческого слова περιφερεια (окружность).

Мы можем, таким образом, для длины С окружности написать такую формулу:

С = 2R • π, или С = 2πR.

Доказано, что число π является числом иррациональным, и, значит, оно не может быть выражено точно никаким рациональным числом. Но его приближённые значения можно находить различными способами с какой угодно точностью. Приняв периметр вписанного 96-угольника за приближённую длину окружности, мы получим для π приближённое значение 3,14 с недостатком и с точностью до 0, 01. Эта точность для практических целей часто бывает достаточна. Для более точных вычислений можно брать

π ≈ 3,14159.

При решении геометрических задач часто встречается число, обратное числу π, т.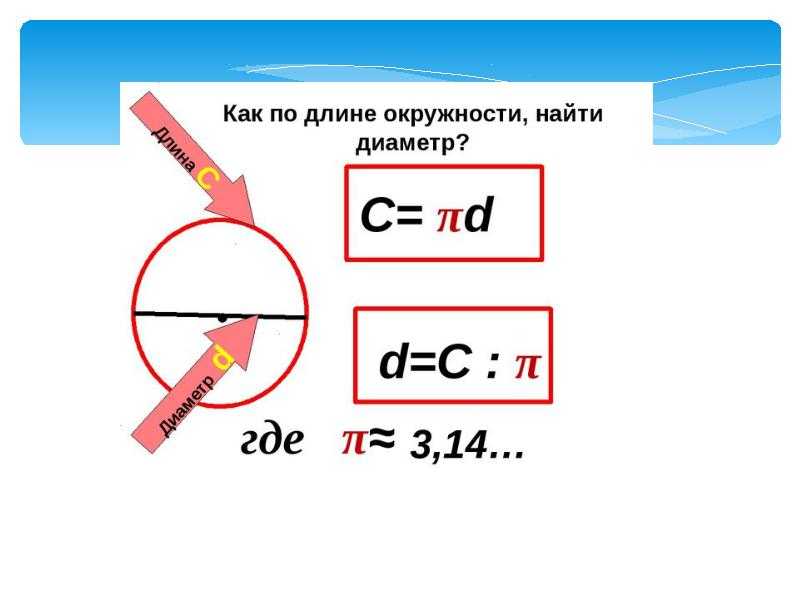 е. равное дроби ¹/_π. Полезно запомнить несколько цифр этого числа:

¹/_π = 0,3183098 …

Длина окружности есть 2πR, значит, длина дуги в 1° равна ^2πR/₃₆₀ = ^πR/₁₈₀; следовательно, длина s дуги, содержащей n°, выразится так:

s = ^πRn/₁₈₀

Если дуга выражена в минутах (’) или в секундах («), то длина её определяется соответственно формулами:

s = ^πRn/_180•60 или s = ^πRn/_{180•60•60},

где n — число минут или секунд.

Задача. Вычислить с точностью до 1 мм радиус такой окружности, дуга которой, содержащая 81°21’ 36″, равна 0,452 м.

Обратив 81°21’ 36″ в секунды, получим число 292 896. Из уравнения

0, 452 = ^πR•292896/_{180•60•60}

находим:

R = ^{0,452•180•60•60}/_292896π = ¹/_π = 0,318 (м)

Задача. Определить число градусов дуги, длина которой равна радиусу.

Заменив в формуле, определяющей длину дуги в n°, величину s на R, получим уравнение:

R = ^πRn/₁₈₀, или 1 = ^πn/₁₈₀,

откуда

n° = ^180°/_π = 180° • ¹/_π = 180° • 0,3183098 = 57°295764 = 57°17’ 44″,8.

Заметим, что дуга, равная радиусу, называется радианом.

1 угловой радиан это — центральный угол, опирающийся на такую дугу окружности, длина которой равна радиусу этой окружности.

Следовательно:

1(радиан) \(\approx\) 57°17’ 45″

$$ 1° = \frac{2\pi}{360°}\approx 0,017 (радиана) $$

Радианы специального обозначения не имеют. Угол равный α радианов обозначается просто α.

Переход от одного измерения к другому производится по формулам:

$$ \alpha° = \frac{180°}{\pi}\alpha \\ \alpha = \frac{\pi}{180°}\alpha° $$

2$ имеет диаметр $18\text{ см}$, можно ли найти длину окружности без использования или введения иррациональной константы Pi ($\pi=3,1415926535\ldots)$ вообще, и если можно, как?

Чтобы найти площадь $254,34$, я использовал $\pi$ как $3,14$ в сокращении. Формула, которую вы даете, должна позволить мне найти окружность как $ 56,52 \ text {cm} $ (так как это также использует $ \ pi $ как 3,14)

Извините! В вопросе ошибка!

• геометрия
• круги

$\endgroup$

10

$\begingroup$

Рассмотрим правильный многоугольник с $n$ сторонами, как показано на рисунке ниже.

Пусть диаметр многоугольника, как показано, равен $d$, а сторона многоугольника равна $a$. Тогда площадь треугольника, как показано на рисунке, равна $$T = \dfrac12 \times a \times \dfrac{d}2 = \dfrac{ad}4$$ Периметр многоугольника равен $$P = na,$$, а площадь многоугольника равна $$A = nT = \dfrac{nad}4.$$ Отсюда получаем, что $$A = \dfrac{Pd} 4$$ Устремляя число сторон $n$ к бесконечности, многоугольник «стремится» к окружности, и мы получаем, что $$\text{Площадь круга} = \dfrac{\text{Диаметр}\times \text{диаметр}}4$$ или наоборот $$\text{Окружность} = \dfrac{4 \times \text{Площадь круга}}{\text{диаметр}}$$ Как видите, $\pi$ нигде не нужно. 92 = 254,34$$ $$C = 2\pi r$$ $$d = 2r = 18$$

, где $A$ — площадь, $r$ — радиус, $C$ — длина окружности, а $d$ — диаметр. Мы пытаемся найти выражение во втором; если мы посмотрим на первую формулу, там почти , но в ней отсутствует множитель 2 (легко решить) и есть дополнительный множитель $r$. Но если мы разделим выражение первой формулы на выражение третьей формулы, то получим

$$\frac{254,34}{18} = A/d = \frac{\pi r}{2}$$

Почти готово! Теперь нам нужно просто умножить на 4:92=2A/r=4A/d$, где $d$ — диаметр.

$\endgroup$

2

$\begingroup$

Я удивлен, что никто еще не дал этот ответ, поэтому: $$C=\tau r=\frac{\tau}{2}d$$ Так что нет, $\pi$ не нужно 😉

$\endgroup$

2

$\begingroup$

Соотношение между площадью круга и его окружностью можно увидеть, разрезав его по своему вкусу в виде луковицы или пиццы.

$\endgroup$

$\begingroup$

Думаю, этот ответ тоже может помочь.

Предположим, вы априори знаете, что единственный способ получить то, что вы хотите, либо с помощью алгоритмов, которые аппроксимируют площадь A многоугольника круга с n сторонами.

Если вам нужен алгоритм, в котором не упоминается иррациональная константа $\pi$, то у вас может быть дюжина алгоритмов, которые обеспечивают площадь $A>0$ круга путем аппроксимации площадей $A_{n_k}$ polignos $ n_k$ сторон. Здесь $k$ указывает на $k$-й шаг алгоритма. В общем случае все эти алгоритмы представляют собой алгоритм, описанный ниже.

Концептуальный алгоритм

1. Инициализация: Установите $k = 0$ и один (или несколько, если хотите) полигно $P_{n_k}$ с $n_k$ сторонами. Число $\epsilon> 0$, площадь $A>0$ круга.

2. Интерактивный шаг: некоторая эффективная процедура, которая получает полигно $P_{n_{k +1}}$ с помощью полигноса из предыдущего шага, которая составляет последовательность $ A_k $ областей полигноза $P_{n_{k}} $ сходится.

   No related posts.