Предел 0 бесконечность: Неопределенности пределов

Раскрытие неопределенностей при вычислении пределов

С данной статьи начинаем цепочку публикаций, которые научат Вас находить особенности в границах, классифицировать неопределенности и применять правильную методику раскрытия. Дело заключается в том, что разработано много правил и приемов, которые позволяют по виду заданной функции или последовательности быстро сориентироваться как находить предел. Однако при изучении теоретического материала или на практических занятиях Вам или на этом не отмечают, или Ваши мысли гуляют за пределами аудитории.
Для охвата всего материала мы собрали много примеров из студенческой практики, модулей, контрольных, заказов и попытаемся здесь разъяснить, как и в каких случаях применять приведенные алгоритмы.

 

Пример 1. Вычислить предел последовательности:

Решение: При подстановке бесконечности получим неопределенность вида бесконечность разделить на бесконечность (∞/∞). Разделим числитель и знаменатель на переменную в наибольшей степени и сократим на нее. В результате избавимся от неопределенности, а слагаемые что останутся, будут стремиться к нулю при больших номерах последовательности

Все числа, что останутся и укажут куда стремится предел.

 

Пример 2. Вычислить предел последовательности:

Решение: При прямой подстановке бесконечно большого номера получим неопределенность бесконечность минус бесконечность (∞-∞).
Правило раскрытия такого типа неопределенности хорошо расписано в литературе и заключается в умножении и разделении неопределенности на множитель, сопряженный к ней.
Как правило, такие примеры содержат корни и чтобы их лишиться используем умножение на сопряженный множитель, что приводит к разности квадратов или кубов, в то время в знаменателе (или числителе) получим выражение с корнем, которое не содержит неопределенности.
Далее из числителя и знаменателя выделяем доминирующий множитель и упрощаем на него.
Все числа, что останутся и составят предел последовательности.
На языке формул этому отвечает запись

 

 

Пример 3. Найти предел функции:

Решение: При подстановке x=3 получим неопределенность 0/0.
Это означает, что и числитель и знаменатель содержат особенность.
Для раскрытия неопределенности выделим в числителе (x-3), а знаменатель умножим и разделим на сопряженное выражение .
В результате получим множитель (x-3), на который упрощаем дробь. Далее предел вычисляется методом подстановки переменной

 

Пример 4. Найти предел функции:

Решение: Задание для большинства студентов чрезвычайно сложное, а все потому что необходимо свести неопределенность типа 0/0 до известных случаев.
В результате преобразования функций получим выражения вида ln(1+x)/x, tan(x)/x, sin(x)/x при переменной стремящейся к нулю.
Далее выделяем первую замечательный предел и ее следствие, затем расписываем через произведение известных пределов.
Все остальное сводится к произведению единиц и отдельного множителя, который и является пределом заданной функции.

Внимательно разберите приведенный пример, он Вас многому научит.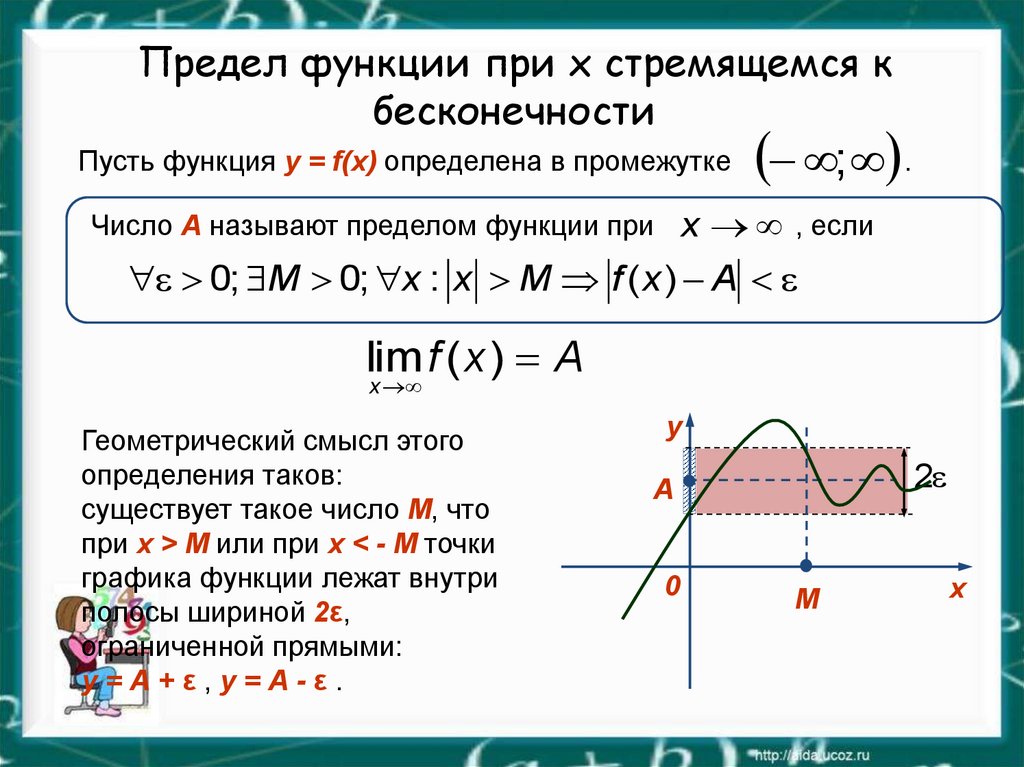 ∞). Для ее раскрытия и в функции в скобках, и в дроби, что является показателем выделяем часть, что вносит особенность (х-3).
Далее, для упрощения манипуляций с выражениями делаем замену переменных x-3=t, новая переменная при этом стремится к нулю.
После этого выделяем второй замечательный предел и ищем лимит показателя, что остался.

На этом разбор распространенных примеров, которые распространены в учебной практике не завершается.
В соседней публикации будут проанализированы новые алгоритмы вычислений, и примеры пределов функций та последовательностей, которые помогут Вам быстрее освоить теоретический материал и подготовиться к контрольной, модулю, экзамене.

0 бесконечность

Вы искали 0 бесконечность? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 0 в степени 0 неопределенность, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «0 бесконечность».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 0 бесконечность,0 в степени 0 неопределенность,0 в степени бесконечность,0 в степени бесконечность неопределенность,0 делить на 0 предел,0 делить на бесконечность,0 делить на бесконечность равно,0 на 0 бесконечность на бесконечность,0 на 0 предел,0 на 0 равно бесконечность,0 на бесконечность делить,0 на бесконечность делить на,0 на бесконечность умножить на бесконечность,0 разделить на бесконечность,0 умножить на бесконечность,1 умножить на бесконечность,бесконечность 0,бесконечность в 0 степени,бесконечность в нулевой степени,бесконечность в степени,бесконечность в степени 0,бесконечность в степени бесконечность пределы,бесконечность в степени бесконечность раскрытие неопределенности,бесконечность в степени минус бесконечность равно,бесконечность в степени ноль,бесконечность деленная на бесконечность равно,бесконечность делить на 0,бесконечность делить на 0 равно,бесконечность делить на бесконечность минус бесконечность,бесконечность делить на бесконечность предел,бесконечность делить на бесконечность равно,бесконечность делить на бесконечность равно бесконечность,бесконечность делить на минус бесконечность равно,бесконечность делить на ноль,бесконечность делить на ноль равно бесконечность,бесконечность минус бесконечность делить на бесконечность,бесконечность минус бесконечность неопределенность,бесконечность на бесконечность неопределенность,бесконечность на бесконечность предел,бесконечность на бесконечность равно,бесконечность на ноль,бесконечность на ноль неопределенность,бесконечность на ноль предел,бесконечность на ноль равно бесконечность,бесконечность равно 0,бесконечность разделить на 0,бесконечность разделить на бесконечность равно,бесконечность разделить на ноль,бесконечность умножить на 0,бесконечность умножить на 1,бесконечность умножить на бесконечность равно,бесконечность умножить на ноль,деление бесконечность на бесконечность,делить на 0 бесконечность,делить на 0 равно бесконечность,как раскрыть неопределенность бесконечность в степени бесконечность,минус бесконечность делить на бесконечность,минус бесконечность делить на бесконечность равно,неопределенность 0 в степени 0,неопределенность 0 в степени бесконечность,неопределенность 0 на 0,неопределенность 0 на бесконечность,неопределенность 1 в степени бесконечность как раскрыть,неопределенность бесконечность в степени 0,неопределенность бесконечность в степени бесконечность,неопределенность бесконечность на 0,неопределенность бесконечность на бесконечность,неопределенность бесконечность на ноль,неопределенность бесконечность умножить на бесконечность,неопределенность бесконечность умножить на ноль,неопределенность вида,неопределенность вида бесконечность в степени бесконечность,неопределенность вида бесконечность минус бесконечность,неопределенность вида бесконечность на бесконечность,неопределенность вида бесконечность умножить на бесконечность,неопределенность ноль на бесконечность,неопределенность ноль на ноль,неопределенность ноль умножить на бесконечность,неопределенность ноль умножить на ноль,ноль в степени бесконечность,ноль делить на бесконечность равно,ноль делить на ноль предел,ноль на бесконечность,ноль на бесконечность неопределенность,ноль на бесконечность предел,ноль на бесконечность умножить на бесконечность,ноль на ноль предел,ноль на ноль пределы,ноль на ноль равно бесконечность,ноль разделить на бесконечность,предел 0 делить на 0,предел 0 на 0,предел бесконечность в степени бесконечность,предел бесконечность делить на бесконечность,предел бесконечность на бесконечность,предел бесконечность на ноль,предел неопределенность бесконечность на бесконечность,предел ноль делить на ноль,предел ноль на бесконечность,предел ноль на ноль,пределы бесконечность в степени бесконечность,пределы бесконечность на бесконечность,пределы ноль на ноль,разделить бесконечность на ноль,раскрытие неопределенностей вида бесконечность на бесконечность,раскрытие неопределенности 1 в степени бесконечность,раскрытие неопределенности бесконечность в степени бесконечность,раскрытие неопределенности бесконечность на бесконечность,таблица неопределенностей,число в степени бесконечность равно,что будет если бесконечность разделить на бесконечность.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 0 бесконечность. Просто введите задачу в окошко и нажмите «решить» здесь (например, 0 в степени бесконечность).

Решить задачу 0 бесконечность вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

предел при делении нуля на бесконечность

Задавать вопрос

спросил 7 лет, 2 месяца назад

Изменено 5 лет, 6 месяцев назад

Просмотрено 58 тысяч раз

$\begingroup$

У меня есть случай, когда

$$\lim_{x\стрелка вправо\infty}=\frac{f\left(x\right)}{h\left(x\right)}$$

Я знаю, что $ \lim_{x\rightarrow\infty} f(x)=0$ и $\lim_{x\rightarrow\infty} h(x)=\infty$

Итак, при и у меня есть $\frac{0}{ \infty}$.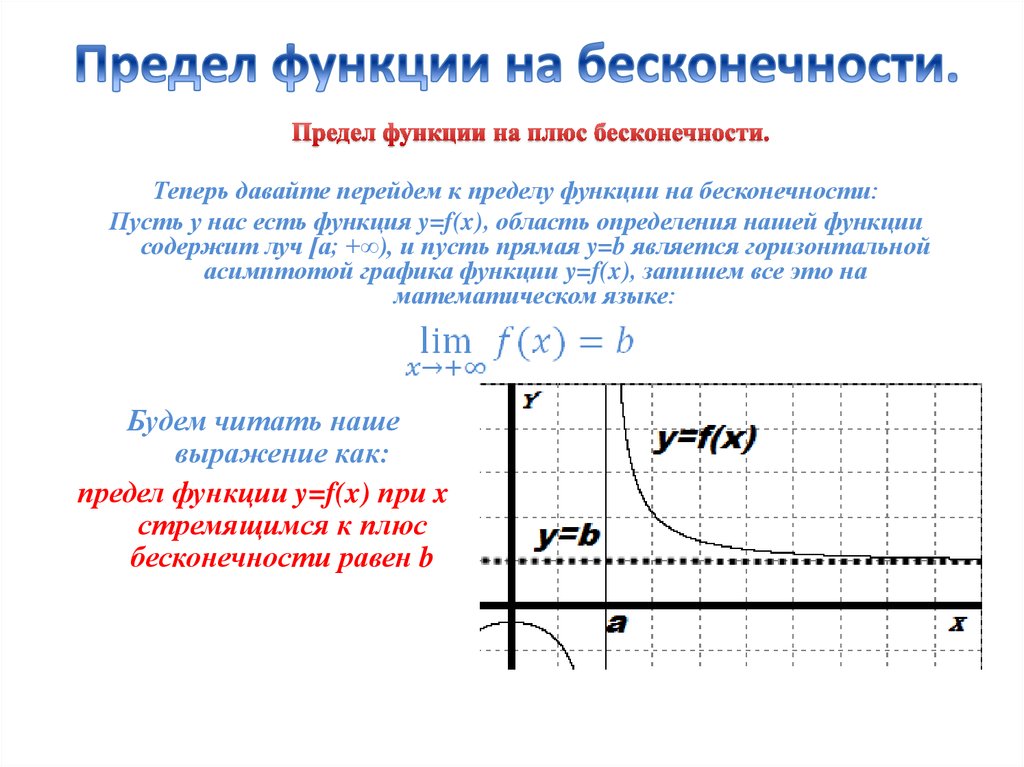

Я знаю, что бесконечность не является реальным числом, но я не уверен, что предел не определен. (Кроме того, в Интернете есть люди, которые говорят противоречивые вещи)

Я очень хорошо знаю, что правило Хопиталя невозможно использовать.

Я предполагаю, что: Поскольку мы знаем, что $\lim_{x\rightarrow\infty}\frac{1}{\infty}=0$, мы можем просто написать $\lim_{x\стрелка вправо\infty} \frac{1}{\infty}=0$

$$\lim_{x\стрелка вправо\infty} \frac{1-0}{\infty}=0$$

$$\lim_{x\rightarrow\infty} \frac{1}{\infty}-\frac{0}{\infty}=0$$

Итак, в данном случае $\frac{0}{ \infty}=0$.

Каким может быть ответ и его объяснение?

• пределы

$\endgroup$

1

$\begingroup$

$\frac{0}{\infty}$ не является неопределенной формой. Напротив, эти пределы говорят вам, что предел всего частного равен $0$.

Это может быть легче увидеть, если вы перепишете на $$ \lim_{x\to\infty} f(x)\frac1{h(x)} $$ где $\lim_{x\to\infty} f(x) = 0 $ и $\lim_{x\to\infty} \frac1{h(x)}=0 $, а произведение двух функций, имеющих лимит $0$ наверняка также имеет лимит $0$.

$\endgroup$

3

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

9y$ сходится к 0 при $|c|<1$, расходится к бесконечности при $c>1$, колеблется без сходимости при $c \leq -1$ и неопределенно при $c=1$.