По двум сторонам и углу между ними это какой признак: Первый признак равенства треугольников — урок. Геометрия, 7 класс.

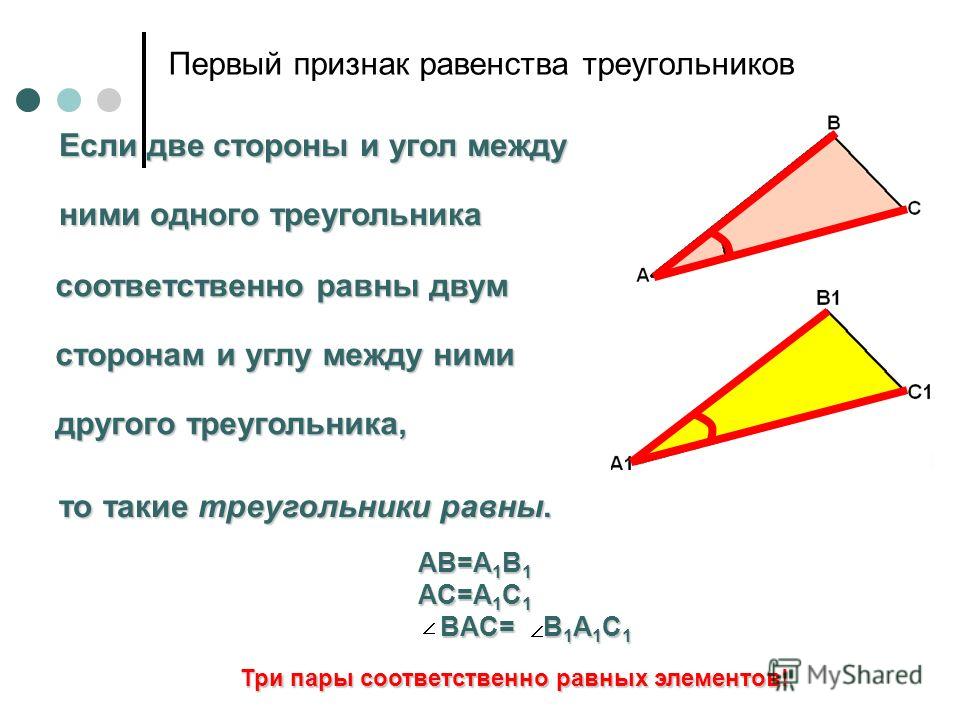
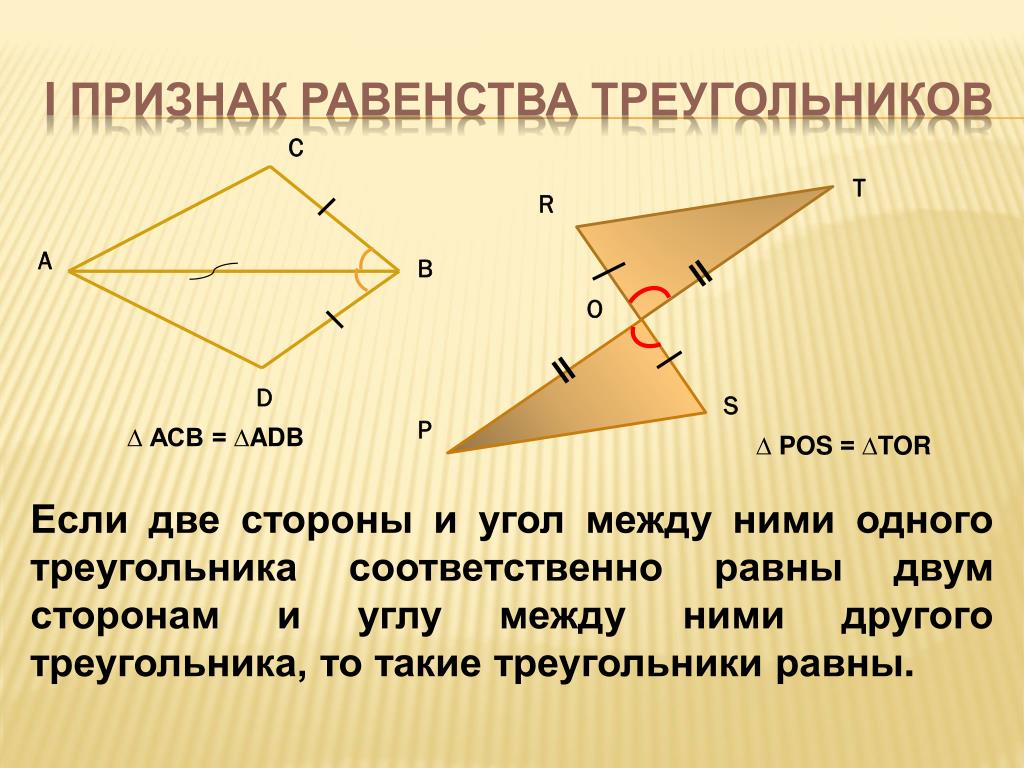
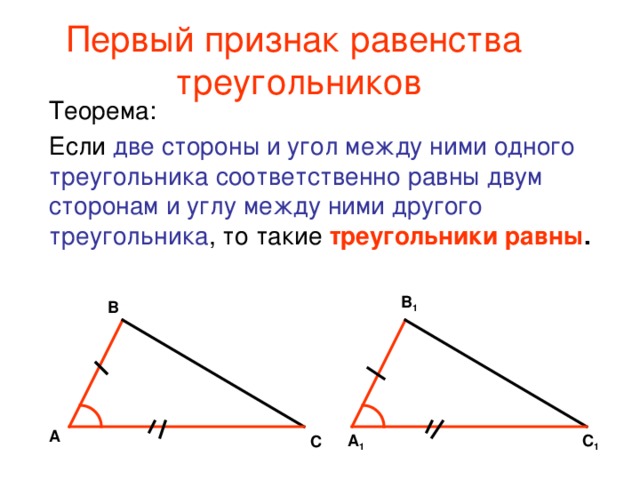
Признак равенства треугольников по двум сторонам и углу между ними

Признак равенства

треугольников по

двум сторонам и

углу между ними

В 1

В

С 1

С

А

А 1

Первый признак равенства треугольников

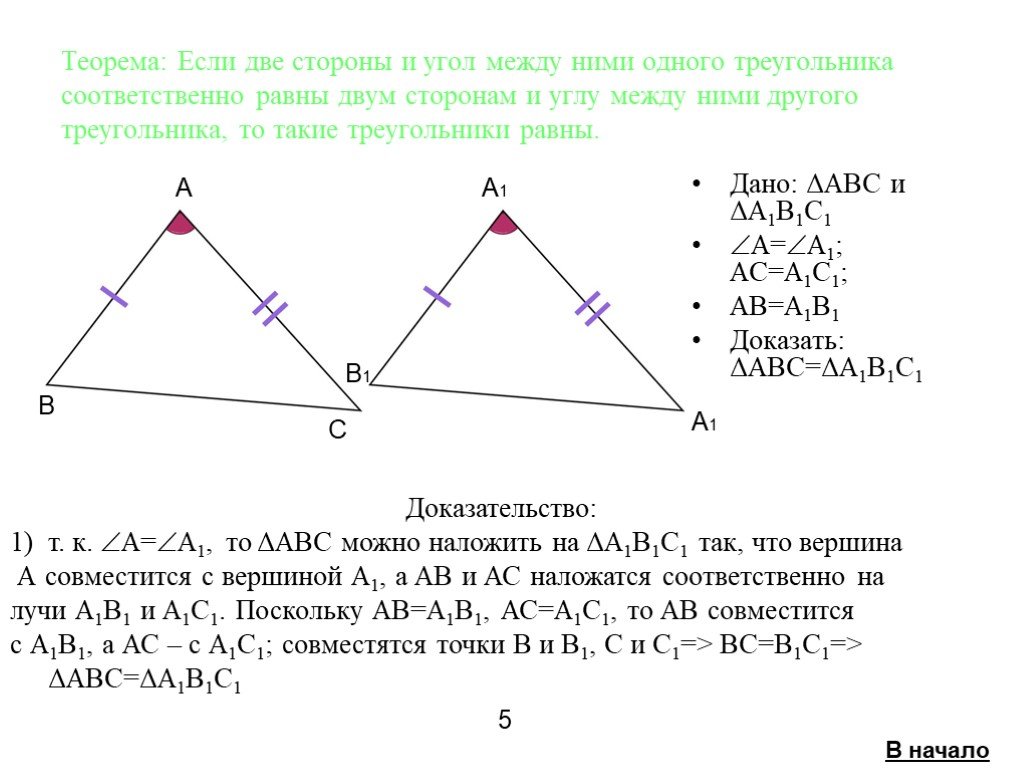
Теорема:

Если две стороны и угол между ними одного

треугольника, соответственно равны двум

сторонам и углу между ними другого треугольника,

то такие треугольники равны.

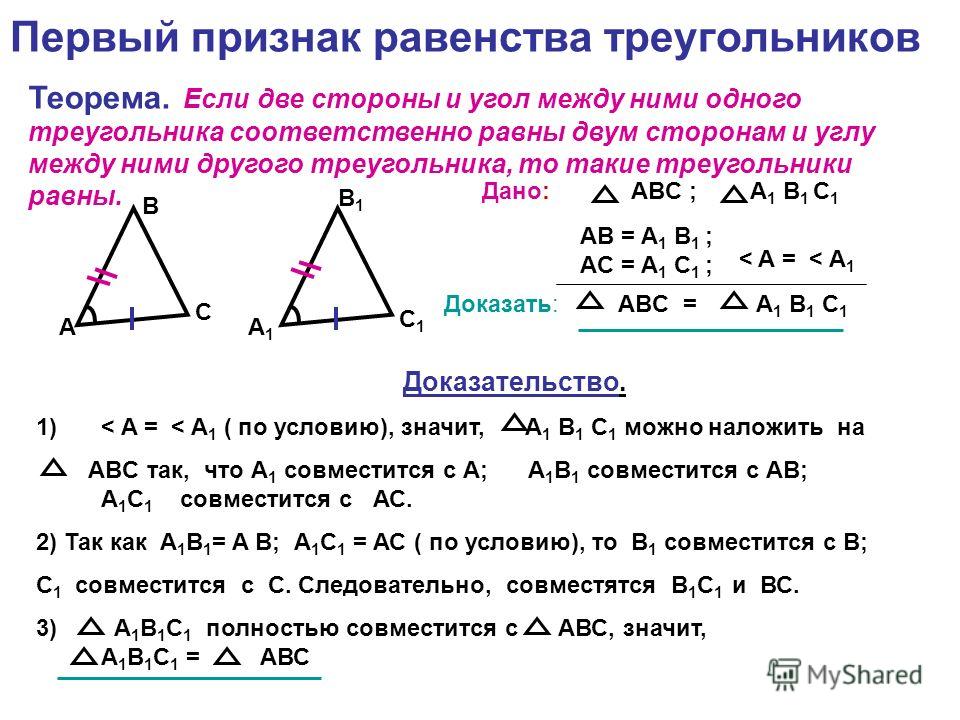
Дано:  АВС,  А 1 В 1 С 1 ,

 А=  А 1

АС=А 1 С 1 ,

АВ=А 1 В 1 ,

Доказать:  АВС=  А 1 В 1 С 1

В

В 1

С

С 1

А 1

А

В

В 1

С

С 1

А 1

А

Доказательство.

(метод наложения)

Т.к.  А=  А 1, то  АВС можно наложить на  А 1 В 1 С 1 так, что луч АВ совместится с лучом А 1 В 1 и луч АС совместится с лучом А 1 С 1 .

1.

В 1

В

С 1

А

С

А 1

2.

Т.к. АВ=А 1 В 1 , то

сторона АВ совместится со стороной А 1 В 1

(точка В совместится с точкой В 1 ).

В 1

В

А 1

А

С 1

С

3.

Т.к. АС=А 1 С 1 , то

сторона АС совместится со стороной А 1 С 1

(точка С совместится с точкой С 1 ).

В 1

В

1

В

С 1

С 1

С

А 1

А

А 1

Т. к. концы отрезков ВС и В 1 С 1 совместились,

4.

то сторона ВС совместится со стороной В 1 С 1.

5.

 АВС совместился с  А 1 В 1 С 1 ,

значит  АВС=  А 1 В 1 С 1 .

Ч.

Т.

Д.

В 1

В

В

А

С 1

С

А 1

С

Докажите, что треугольники равны.

1.

а)

 K=  L,

KM=LN,

KO=LP

 KMO=  LNP

б)

 1=  2,

AB=AD,

AC — общая

 ABC=  ADC

в)

 1=  2,

RS=PQ,

RQ — общая

 QRS=  QRP

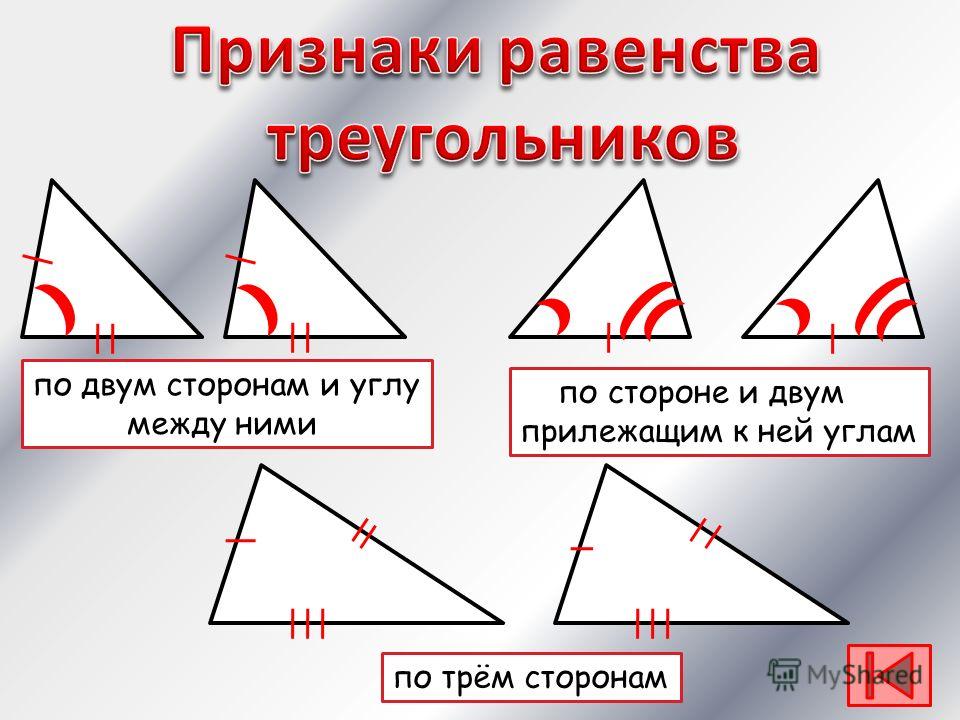
2. Дополните условия так, чтобы

треугольники были равны по первому

признаку равенства треугольников.

Дано:  ABC,  CDE, С- середина АD и BE.

Доказать:  ABC=  CDE.

B

C

D

A

E

Домашнее задание:

Глава II, §1, п. 14-15 читать,

выучить записи в тетради.

Спасибо за внимание!!!

Равенство Треугольников

Главная » геометрия

Обновлено 28.02.2022

Содержание

1. Первый признак равенства треугольников
2. Второй признак равенства треугольников
3. Третий признак равенства треугольников
4. Итог

Первый признак равенства треугольников

По двум сторонам и углу между ними.

Формулировка первого признака
равенства треугольников:

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника,
то такие треугольники равны.

Доказательство первого признака
равенства треугольников:

1. Рассмотрим △ABC и △FHE, в которых AC = FE, AB = HE, ∠A = ∠E. Докажем, что △ABC = △FHE.
2. ∠A = ∠E, значит △ABC можно наложить на △FHE так, что вершина A совместится с вершиной E.
   
3. AC = FE и AB = HE, значит стороны AC и FE, а также стороны AB и HE можно наложить друг на друга так, что они совместятся:
   AC совместится с FE, AB совместится с HE.
4. Итак, △ABC и △FHE полностью совместятся, значит они равны —
   ч.т.д.

Второй признак равенства треугольников

По стороне и двум прилежащим к ней углам.

Формулировка второго признака
равенства треугольников:

Если сторона и прилежащие к ней два угла одного треугольника соответственно равны стороне
и прилежащим к ней двум углам другого треугольника то такие треугольники равны.

Доказательство второго признака
равенства треугольников:

1. Рассмотрим △ABC и △FHE, в которых AC = FE, ∠С = ∠F, ∠A = ∠E. Докажем, что △ABC = △FHE.
2. AC = FE, значит△ABC можно наложить на△FHE так, что сторона AC совместится со стороной FE.
   
3. ∠С = ∠F и ∠A = ∠E, можно наложить друг на друга так, что они совместятся:
   ∠С совместится с ∠F, ∠A совместится с∠E.
   
4. Итак, △ABC и △FHE полностью совместятся, значит они равны — ч.т.д.

Третий признак равенства треугольников

По трем сторонам.

Формулировка третьего признака
равенства треугольников:

Если три стороны одного треугольника соответственно равны трём сторонам
другого треугольника, то такие треугольники равны.

Доказательство третьего признака равенства
треугольников:

1. Рассмотрим △ABC и △FHE, в которых AC = FE, AB = HE, BC = FH. Докажем, что △ABC = △FHE.
2. AC = FE, AB = HE, BC = FH, значит эти стороны можно наложить друг на друга так, что они совместятся:
   AC совместится с FE, AB совместится с HE, BC совместится с FH.
3. Итак, △ABC и △FHE полностью совместятся, значит они равны — ч.т.д.

Итог

Равенство треугольников можно доказать с помощью трех признаков:

1. По двум сторонам и углу между ними.
2. По стороне и двум прилежащим к ней углам.
3. По трем сторонам.

Решение треугольников SAS

«SAS» означает «сторона, угол, сторона»

« SAS » — это когда мы знаем две стороны и угол между ними.

Решение треугольника SAS

• использовать закон косинусов для вычисления неизвестной стороны,
• затем используйте закон синусов, чтобы найти меньший из двух других углов,
• , а затем прибавьте к трем углам 180°, чтобы найти последний угол.

Пример 1

В этом треугольнике мы знаем:

• угол А = 49°
• б = 5
• и с = 7

 

Чтобы решить треугольник, нам нужно найти сторону a и углы B и C .

Используйте закон косинусов, чтобы найти сторону a сначала:

a ² = b ² + c ² − 2bc cosA

a ² = 5 ² + 7 ² − 2 × 5 × 7 × cos(49°)

a ² = 25 + 49 − 70 × cos(49°)

a6 2 − 70 × 0,6560…

а ²

= 74 − 45,924… = 28,075…

а = √28,075…

а = 5,298…

7 до а = 9004 2 знака после запятой

 

Теперь воспользуемся законом синусов, чтобы найти меньший из двух других углов.

Почему меньший угол? Поскольку функция обратного синуса дает ответы менее 90° даже для углов больше 90°. Выбирая меньший угол (у треугольника не может быть двух углов больше 90°), мы избегаем этой проблемы.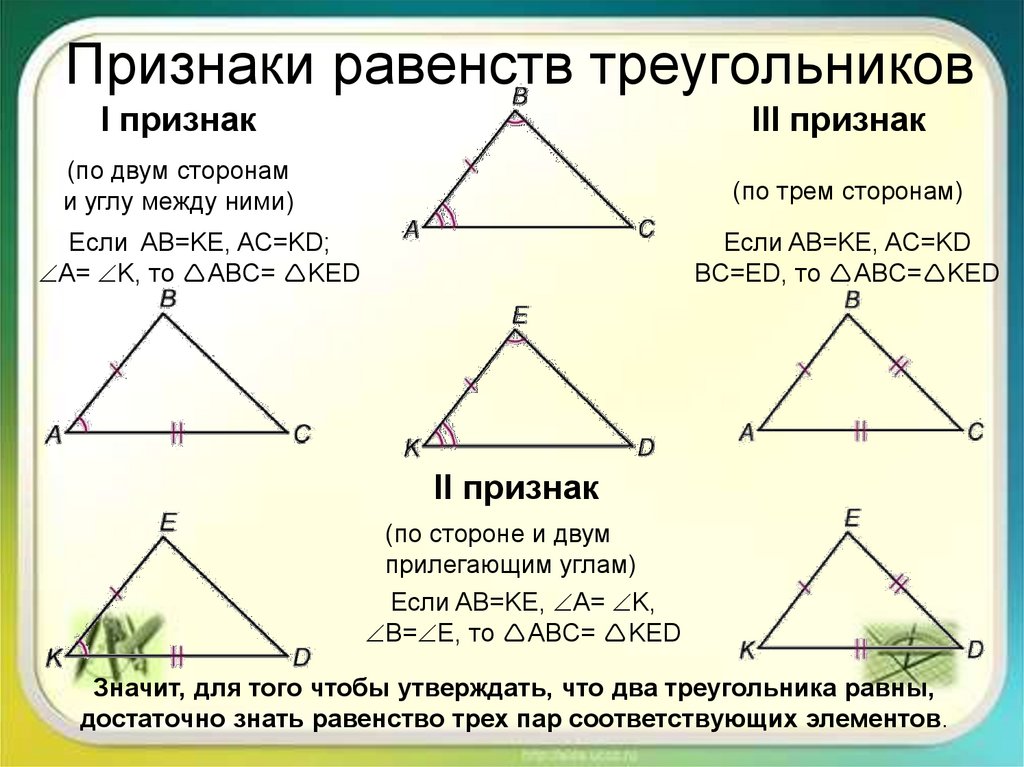 Примечание: меньший угол обращен к более короткой стороне.

 

Выберите угол B:

sin B / b = sin A / a

sin B / 5 = sin(49°) / 5,298…

Вы заметили, что мы не использовали a = 5.30 . Это число округляется до 2 знаков после запятой. Гораздо лучше использовать неокругленное число 5,298… которое все еще должно быть в нашем калькуляторе с момента последнего расчета.

sin B = (sin(49°) × 5) / 5,298…

sin B = 0,7122…

B = sin ^-1 (0,7122…)

B = 45,4° с точностью до одного десятичного знака

 

Теперь находим угол C, который легко найти, используя формулу «углы треугольника прибавляют 180°»:

C = 180° − 49° − 45,4° до одного знака после запятой

 

Теперь мы полностью решили треугольник, т.е. нашли все его углы и стороны.

 

Пример 2

Это также треугольник SAS.

Прежде всего, мы найдем R , используя Закон косинатов:

R ² = P ² + Q ² — 2PQ COS R

R ² = 6,9 ² + 2. 6666 2 = 6,9 ² + 2.66. ² — 2 х 6,9 х 2,6 х cos(117°)

r ² = 47,61 + 6,76 — 35,88 х cos(117°)

r ^{2 х 2 х 2 х 2 х )}

р ² = 54,37 + 16,289… = 70,659…

r = √70,659…

r = 8,405… = 8,41 до 2 знаков после запятой

 

Теперь о законе синусов.

Выбрать меньший угол? Мы не должны! Угол R больше 90°, поэтому углы P и Q должны быть меньше 90°.

 

sin P / p = sin R / r

sin P / 6,9 = sin(117°) / 8,405…

sin P = (sin(117°) × 6,9) / 8,405…

sin P = 0,7313…

P = sin ^-1 (0,7313…)

P = 47,0° с точностью до одного десятичного знака

 

Теперь найдем угол Q, используя формулу «углы треугольника прибавить к 180°05»:

 

Q = 180° − 117° − 47,0°

Q = 16,0° с точностью до одного десятичного знака

Для овладения этим навыком требуется много практики, поэтому попробуйте ответить на эти вопросы:

265, 3961, 1546, 266, 1547, 1548, 1562, 2374, 2375, 3962

геометрия — две стороны и угол между ними вопрос треугольника.

спросил 10 лет, 8 месяцев назад

Изменено 3 года, 6 месяцев назад

Просмотрено 31к раз

$\begingroup$

Можно ли найти третью сторону треугольника, если известны длины двух других и угол между известными сторонами? треугольник не равносторонний.

мы используем камеру kinect, и мы можем найти расстояние от камеры до начала линии и расстояние до конца линии, мы можем рассчитать угол между двумя линиями, зная максимальный вертикальный и горизонтальный угол но можно ли рассчитать длину линии на земле? проблема в том, что камера не будет точно над линией, поэтому треугольник, который мы получим, не будет равносторонним.

• геометрия
• треугольники

$\endgroup$

1

$\begingroup$

Как насчет закона косинусов?

Рассмотрим следующий треугольник $\triangle ABC$, $ \color{maroon} {\text{poly 1}}$ внизу, со сторонами $\color{maroon}{\overline{AB}=c}$ и $ \color{maroon}{\overline{AC}=b}$ известен.