Подобие по 2 углам: Признаки подобия треугольников — урок. Геометрия, 8 класс.

Признаки подобия треугольников — презентация онлайн

Похожие презентации:

Признаки подобия треугольников. (Упражнение 10. 8 класс)

Второй и третий признаки подобия треугольников

ІІ и ІІІ признаки подобия треугольников

2 и 3 признаки подобия треугольников

Подобные треугольники

Второй и третий признаки подобия треугольников

Первый признак подобия треугольников

Подобие треугольников

Второй признак равенства треугольников. Урок 2

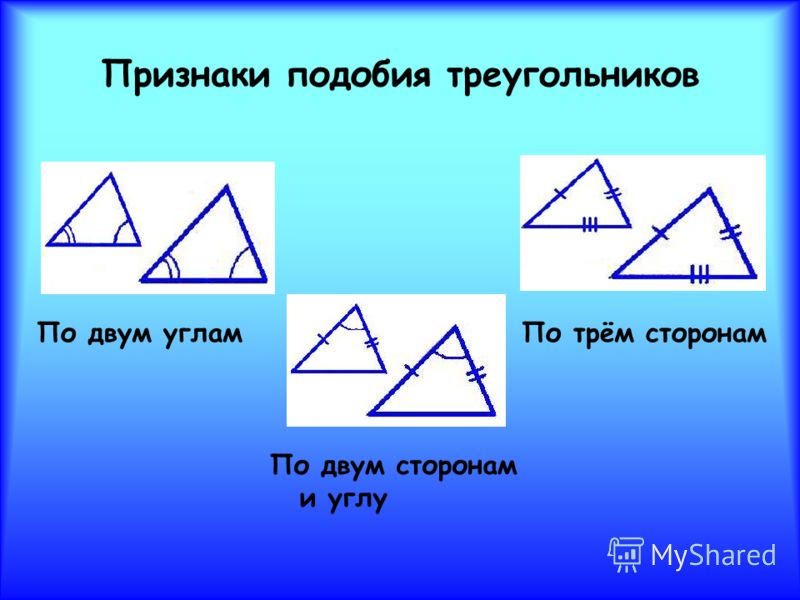
Признаки подобия треугольников

I
признак подобия треугольников. Если два угла одного
треугольника соответственно равны двум углам другого,
то такие треугольники подобны.
С
Дано: ABC,
А1В1С1, А А1 , В В1,
Доказать:
А
В
ABC
А1В1С1
Доказательство:
С1
1). С 180 А В
0
С1 1800 А1 В1
С С1
А1
В1
А А1 ,
2).
С
А
С С1
AB AC
S ABC
S A1B1C1 A1 B1 A1C1
СA CВ
S ABC
S A1B1C1 С1 А1 С1 В1
AB AC
СА СВ

A1 B1 A1C1 С1 А1 С1 В1
В
С1
AB
СВ
A1 B1 С1 В1
А1
В1
3).
С
А
А А1 ,
AB AC
S ABC
A1 B1 A1C1
S A1B1C1
В В1 ,
ВA CВ
S ABC
S A1B1C1 В1 А1 С1 В1
AB AC
ВА СВ
A1 B1 A1C1 В1 А1 С1 В1
В
С1
AС
СВ
A1С1 С1 В1
А1
В1
4).
С
А
Было дано
А А1 ,
Мы доказали, что
В
AB
СВ
A1 B1 С1 В1
В В1 ,
С С1
и
AС
СВ
A1С1 С1 В1
тогда
С1
СВ
AB AС
A1 B1 A1С1 С1 В1
Треугольники подобны по
определению.
А1
В1
II
признак подобия треугольников. Если две стороны
одного треугольника пропорциональны двум сторонам
другого треугольника и углы, заключенные между этими
сторонами, равны, то такие треугольники подобны.
АВ
АС
Дано: ABC, А1В1С1, А А1 ,
А1 В1 А1С1
Доказать:
ABC
А1В1С1
Доказательство: докажем, что В В1 и применим 1
признак подобия треугольников
С1
А1
С
В1
А
В
С
С1
В1
А1
В
А
1
2
1). Рассмотрим ABC2, у которого
1= А1,
2= В1.
ABC2
А1В1С1
по двум углам
АВ
АС2
Тогда
А1 В1 А1С1
АВ
АС
по условию
А1 В1 А1С1
С2
АС = АС2
С
С1
В1
А1
В
А
1
2
2).
ABC = АВС2
В = 2,
=
по двум сторонам и углу
между ними
2= В1
С2
III
признак подобия треугольников. Если три стороны
одного треугольника пропорциональны трем сторонам
другого, то такие треугольники подобны.
Дано: ABC,
Доказать:
А1В1С1,
ABC
Доказательство:
АВ
ВС
АС
А1 В1 В1С1 А1С1
А1В1С1
докажем, что А А1 и применим
2 признак подобия треугольников
С
С1
А1
В1 А
В
С
С1
В1
А1
В
А
1
2
1). Рассмотрим ABC2, у которого
1= А1,
2= В1.
ABC2
А1В1С1
Тогда
по двум углам
АВ ВС 2 АС2
А1 В1 В1С1 А1С1
АВ
ВС
АС
по условию
А1 В1 В1С1 А1С1
АС = АС2
С2
ВС = ВС2
С
С1
В1
А1
В
А
1
2
2).
ABC = АВС2
А = 1,
=
по трем сторонам
1= А1
С2

English     Русский Правила

8 класс. Геометрия. Подобные треугольники. Практические приложения подобия треугольников. — Практические приложения подобия треугольников.

Комментарии преподавателя

Прак­ти­че­ские при­ло­же­ния по­до­бия тре­уголь­ни­ков

По­вто­рим ос­нов­ные по­ня­тия, свя­зан­ные с по­до­би­ем тре­уголь­ни­ков.

Опре­де­ле­ние. Два тре­уголь­ни­ка на­зы­ва­ют­ся по­доб­ны­ми, ес­ли­их углы по­пар­но равны, а сто­ро­ны, ле­жа­щие на­про­тив со­от­вет­ствен­ных углов, про­пор­ци­о­наль­ны (см. Рис. 1).

.

Рис. 1

Таким об­ра­зом, сто­ро­ны боль­ше­го тре­уголь­ни­ка можно вы­ра­зить через сто­ро­ны ма­ло­го тре­уголь­ни­ка таким об­ра­зом: .

При­зна­ки по­до­бия тре­уголь­ни­ков.

1. Пер­вый при­знак по­до­бия тре­уголь­ни­ков (по двум углам). Если два угла од­но­го тре­уголь­ни­ка равны двум углам дру­го­го тре­уголь­ни­ка, то такие тре­уголь­ни­ки по­доб­ны.

 

2. Вто­рой при­знак по­до­бия тре­уголь­ни­ков (по двум сто­ро­нам и углу между ними). Если две сто­ро­ны од­но­го тре­уголь­ни­ка про­пор­ци­о­наль­ны двум сто­ро­нам дру­го­го тре­уголь­ни­ка и углы между этими сто­ро­на­ми равны, то такие тре­уголь­ни­ки по­доб­ны.

 

3. Тре­тий при­знак по­до­бия тре­уголь­ни­ков (по трем сто­ро­нам). Если три сто­ро­ны од­но­го тре­уголь­ни­ка про­пор­ци­о­наль­ны трем сто­ро­нам дру­го­го тре­уголь­ни­ка, то такие тре­уголь­ни­ки по­доб­ны.

 

При­мер 1. Опре­де­лить вы­со­ту де­ре­ва () и рас­сто­я­ние до его вер­ши­ны (), не за­ле­зая на него (см. Рис. 2).

Ре­ше­ние. Для опре­де­ле­ния ис­ко­мых ве­ли­чин ис­поль­зу­ем шест  из­вест­ной длины с вра­ща­ю­щей­ся план­кой на конце, ко­то­рый уста­нав­ли­ва­ем так, чтобы точки  ле­жа­ли на одной пря­мой. Ис­поль­зо­ва­ние вспо­мо­га­тель­но­го шеста необ­хо­ди­мо для уста­нов­ле­ния факта по­до­бия тре­уголь­ни­ков  и вы­чис­ле­ния ис­ко­мых сто­рон с по­мо­щью ко­эф­фи­ци­ен­та по­до­бия.

Тре­уголь­ни­ки  по пер­во­му при­зна­ку по­до­бия, т.к. у них угол  общий и они пря­мо­уголь­ные, т.е. имеют еще по пря­мо­му углу.

Рис. 2

Сле­до­ва­тель­но, по опре­де­ле­нию по­доб­ных тре­уголь­ни­ков , где  вы­со­та шеста,  рас­сто­я­ние от точки  до шеста,  по тео­ре­ме Пи­фа­го­ра.

Ответ. , где .

При­мер 2. Опре­де­лить рас­сто­я­ние от точки  до недо­ступ­ной точки  (см. Рис. 3).

Ре­ше­ние.

Рис. 3

Вы­би­ра­ем на мест­но­сти удоб­ную точку  и за­ме­ря­ем углы . По этим углам можно по­стро­ить дру­гой мень­ший тре­уголь­ник , ко­то­рый будет по­доб­ным к тре­уголь­ни­ку  по пер­во­му при­зна­ку по­до­бия. В по­стро­ен­ном, на­при­мер, на бу­ма­ге тре­уголь­ни­ке  можно вы­пол­нить любые из­ме­ре­ния. Из­ме­рим длину сто­рон  и . Затем из­ме­рим на мест­но­сти рас­сто­я­ние от ука­зан­ной точки  до вы­бран­ной точки : .

За­пи­шем со­от­но­ше­ние сто­рон по­доб­ных тре­уголь­ни­ков :

.

Ответ. .

Рас­смот­рим ана­ло­гич­ную за­да­чу, но уже с рас­че­та­ми, в ко­то­рых важно уметь вы­брать удоб­ный ко­эф­фи­ци­ент по­до­бия.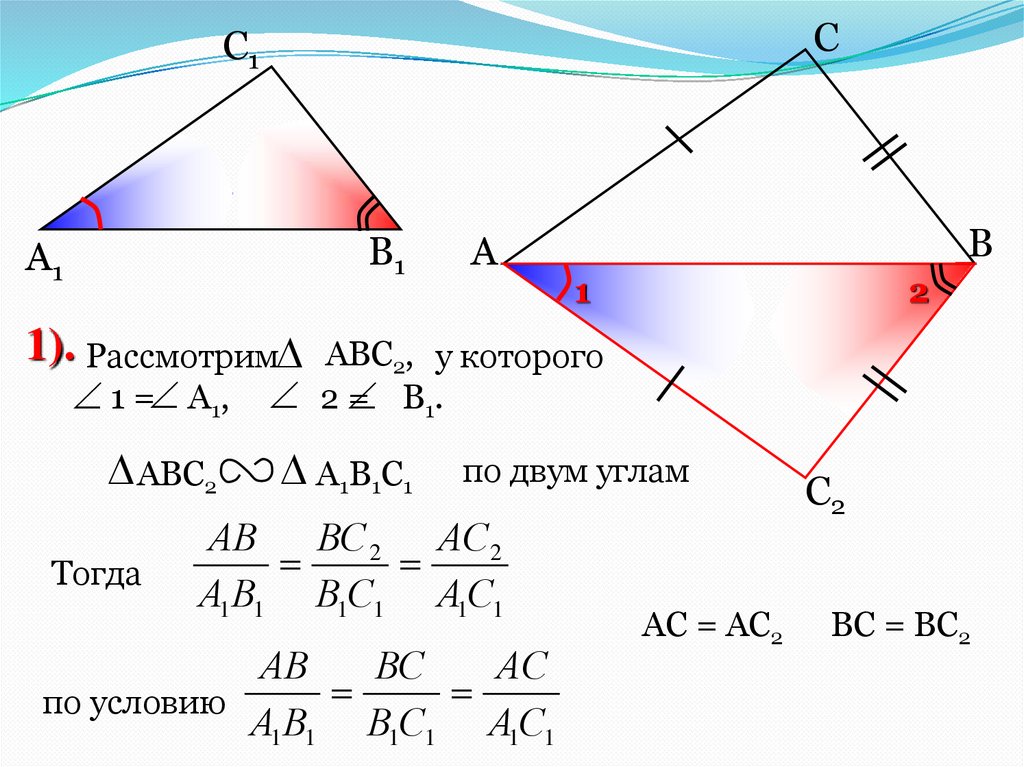

При­мер 3. Опре­де­лить рас­сто­я­ние в мет­рах от точки  до недо­ступ­ной точки , если  (см. Рис. 3).

Ре­ше­ние. По­стро­им умень­шен­ный по­доб­ный тре­уголь­ник  так, чтобы , т.е. тогда ко­эф­фи­ци­ент по­до­бия будет равен удоб­но­му для даль­ней­ших вы­чис­ле­ний числу . За­ме­ря­ем .

По­сколь­ку, как ука­за­но ранее, .

Ответ. 200 м.

При­мер 4. По­стро­ить тре­уголь­ник по двум углам и бис­сек­три­се при вер­шине тре­тье­го угла.

По­стро­е­ние. Дано:  бис­сек­три­са тре­тье­го угла (см. Рис. 4).

Рис. 4

Вы­бе­рем про­из­воль­ный от­ре­зок  и стро­им на нем тре­уголь­ник  по сто­роне и двум углам . В по­стро­ен­ном тре­уголь­ни­ке про­во­дим бис­сек­три­су из угла , и если она не сов­па­ла с ука­зан­ной в усло­вии бис­сек­три­сой, то стро­им . Затем через точку  про­во­дим пря­мую  до пе­ре­се­че­ния с про­дол­же­ни­я­ми сто­рон  и  тре­уголь­ни­ка . Ис­ко­мый тре­уголь­ник  по­стро­ен. Углы  как со­от­вет­ствен­ные при па­рал­лель­ных пря­мых,  необ­хо­ди­мая бис­сек­три­са (см. Рис. 5).

Рис. 5

По­стро­е­но.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/8-klass/podobnye-treugolniki/prakticheskie-prilozheniya-podobiya-treugolnikov

http://www.youtube.com/watch?v=BiI7bp4DP1o

http://istudy.su/wp-content/uploads/2015/09/9_Podobie-treugolnikov.jpg

http://u.900igr.net/zip/4f253519402fc80180e2e7788897eaca.zip

http://u.900igr.net/zip/fbe99e0a6c821bee79b37640f9f6da53.zip

http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/103-test-po-geometrii-8-klass-tema-primenenie-podobiya-pri-reshenii-zadach-variant-1.html

http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/104-test-po-geometrii-8-klass-tema-primenenie-podobiya-pri-reshenii-zadach-variant-2.html

С++ — Как выполнить сравнение двух изображений по их углам с помощью opencv?

спросил 4 года 11 месяцев назад

Изменено 4 года, 11 месяцев назад

Просмотрено 274 раза

Я новичок в Opencv, я хочу сравнить два изображения по их угловым функциям, а не по другим, я пробовал SURF, SIFT, ORB .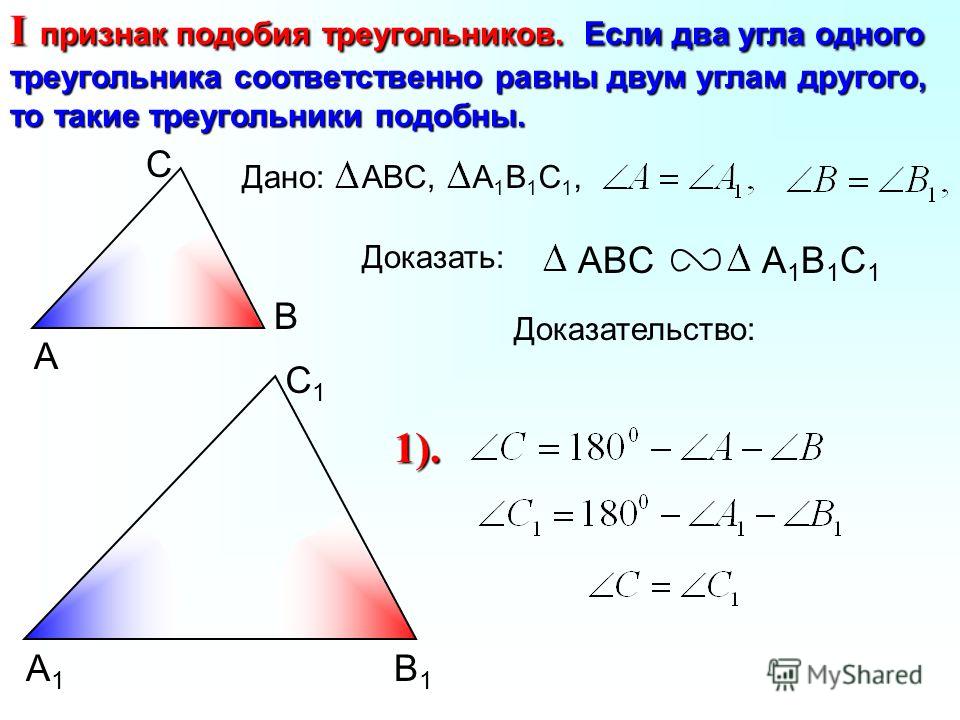

.., но они мне не подходят, может кто-нибудь дать мне какое-то предложение по этому поводу ? например, изображение ниже image1 и image2 похожи, потому что у них много одинаковых углов (хотя это не точно), но image3 не похоже на 1 и 2, спасибо.

• С++
• opencv
• компьютерное зрение

1

Здесь можно попробовать многое, и другие могут предложить вам другие решения, но вот мое:

Используйте алгоритм Minutiae (алгоритм, используемый для идентификации отпечатков пальцев). В алгоритме minutiae извлекается набор общих признаков, таких как:

Они называются Minutiae. Как видите, эти функции очень похожи на углы ваших изображений. Я предлагаю вам следующую процедуру:

1) Найдите углы (Вы уже это сделали)

2) Присвойте каждому углу класс деталей (например, один из классов изображения). Вы можете сделать это с помощью алгоритма локального бинарного шаблона или просто следовать обычному рецепту из алгоритма отпечатка пальца (см.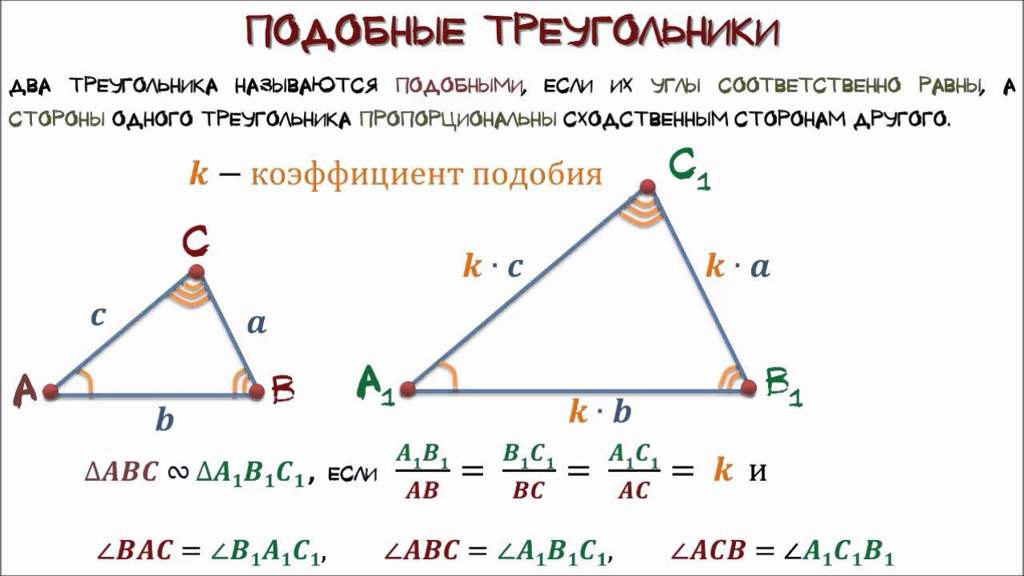

ссылку в конце или поиск в Google).

3) Чтобы вычислить сходство, просто проголосуйте. Например, предположим, что изображение (я назову его А) имеет 4 детали типа а) и две детали типа Е). Чтобы вычислить сходство в новом изображении, мне придется вычислить эти детали в новом изображении. Затем посмотрите, сколько элементов в классе имеют оба изображения. Вы можете добавить столько функций или мелочей, сколько хотите, чтобы сделать ваш алгоритм более надежным (а также сложным).

В любом случае, вы можете посмотреть в Google алгоритм распознавания отпечатков пальцев Minutiae (является одним из самых известных алгоритмов обработки цифровых изображений). Вот один из нескольких слайдов, которые вы можете найти, объясняя алгоритм

https://is.muni.cz/el/1433/jaro2008/PV204/um/finger/MinutiaeBasedFpMatching.pdf

Просто позаботьтесь об изменении основного алгоритма чтобы удовлетворить ваши потребности

Надеюсь, это поможет

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Алгоритм

— Вычисление сходства 2-х наборов выпуклых многоугольников?

спросил 2 года 9 месяцев назад

Изменено 1 год, 6 месяцев назад

Просмотрено 755 раз

Я сгенерировал 2 набора выпуклых многоугольников с помощью разных алгоритмов. Каждый многоугольник в каждом наборе описывается массивом координат [n_points, xy_coords], поэтому квадрат описывается массивом [4,2], а пятиугольник со скругленными углами имеет [80,2], а дополнительные 75 точек составляют используется для описания кривизны.

Моя цель — определить, насколько похожи два набора геометрий.

Может ли кто-нибудь порекомендовать какие-либо способы сделать это?

На данный момент мне попалось:

• Расстояние Хэмминга
• Расстояние Хаусдорфа

Я хотел бы знать, какие другие надежные меры подобия для 2D полигонов. В идеале метод должен быть надежным для выпуклых многоугольников и давать меру сходства между большими наборами (10 000+ каждый).

• алгоритм
• геометрия
• подобие

8

Как я понял, вы ищете алгоритмы подобия формы или анализа формы. Здесь вы найдете более надежные методы: https://www. cs.princeton.edu/courses/archive/spr00/cs59.8b/лекции/полигонподобие/полигонподобие.pdf и https://student.cs.uwaterloo.ca/~cs763/Projects/phil.pdf

1. Функция поворота;
2. Сопоставление графиков;
3. Подпись формы.

Предполагая, что оба многоугольника выровнены, центрированы и выпуклы, вы можете попытаться оценить сходство, вычислив отношение площади меньшего многоугольника к площади выпуклой оболочки обоих многоугольников.

Отношение = Мин.(Площадь(A), Площадь(B)) / Площадь(Выпукл.Оболочка(A, B))

Отношение будет равно 1, если оба многоугольника равны, и 0, если они сильно различаются, как точка и квадрат.

Площадь многоугольника может быть вычислена за время O(N). См. Площадь многоугольника. Выпуклая оболочка может быть вычислена за O (N log N). См. Вычисление выпуклой оболочки. Его можно ускорить до O(N) путем сортировки слиянием уже отсортированных вершин обоих полигонов и применения второго этапа алгоритма сканирования Грэма.