Найти уравнение горизонтальных касательных к графику функции. Уравнение касательной к графику функции — Гипермаркет знаний
В этой статье мы разберем все типы задач на нахождение
Вспомним геометрический смысл производной : если к графику функции в точке проведена касательная, то коэффициент наклона касательной (равный тангенсу угла между касательной и положительным направлением оси ) равен производной функции в точке .
Возьмем на касательной произвольную точку с координатами :
И рассмотрим прямоугольный треугольник :
В этом треугольнике
Отсюда
Это и есть уравнение касательной, проведенной к графику функции в точке .
Чтобы написать уравнение касательной, нам достаточно знать уравнение функции и точку, в которой проведена касательная. Тогда мы сможем найти и .
Есть три основных типа задач на составление уравнения касательной.
1. Дана точка касания
2. Дан коэффициент наклона касательной, то есть значение производной функции в точке .
3. Даны координаты точки, через которую проведена касательная, но которая не является точкой касания.
Рассмотрим каждый тип задач.
1 . Написать уравнение касательной к графику функции в точке .
.
б) Найдем значение производной в точке . Сначала найдем производную функции
Подставим найденные значения в уравнение касательной:
Раскроем скобки в правой части уравнения. Получим:
Ответ: .
2 . Найти абсциссы точек, в которых касательные к графику функции параллельны оси абсцисс.
Если касательная параллельна оси абсцисс, следовательно угол между касательной и положительным направлением оси равен нулю, следовательно тангенс угла наклона касательной равен нулю. Значит, значение производной функции в точках касания равно нулю.
а) Найдем производную функции .
б) Приравняем производную к нулю и найдем значения , в которых касательная параллельна оси :
Приравняем каждый множитель к нулю, получим:
Ответ: 0;3;5
3
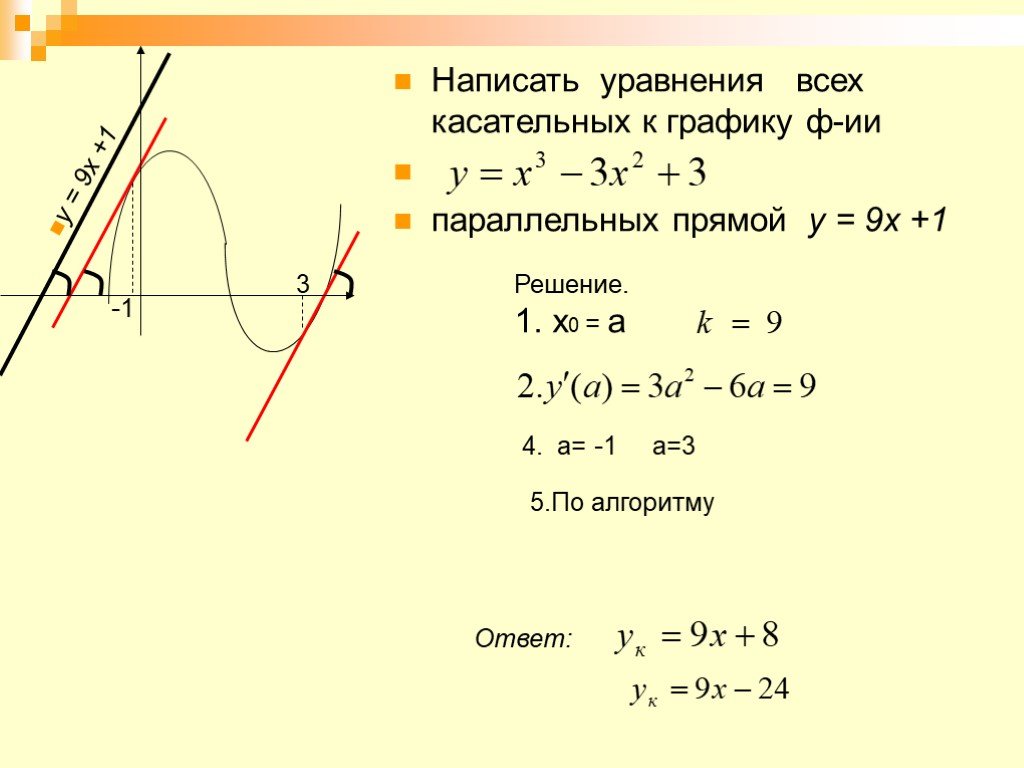
.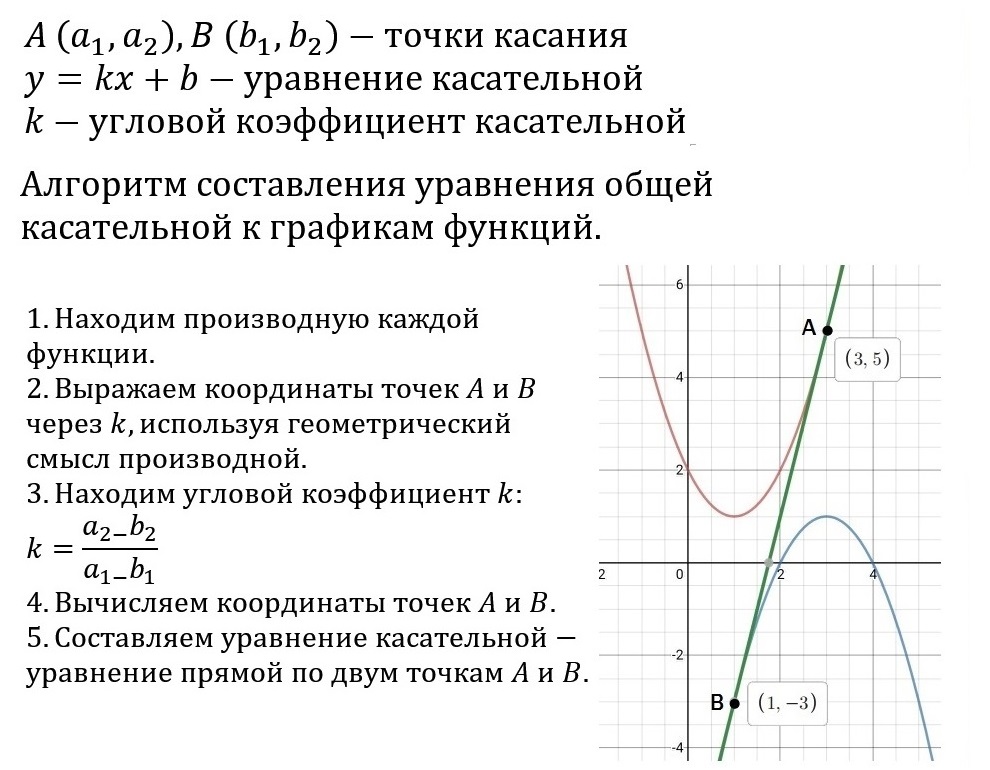 Написать уравнения касательных к графику функции , параллельных прямой .
Написать уравнения касательных к графику функции , параллельных прямой .
Касательная параллельна прямой . Коэффициент наклона этой прямой равен -1. Так как касательная параллельна этой прямой, следовательно, коэффициент наклона касательной тоже равен -1. То есть мы знаем коэффициент наклона касательной , а, тем самым, значение производной в точке касания .
Это второй тип задач на нахождение уравнения касательной.
Итак, у нас дана функция и значение производной в точке касания.
а) Найдем точки, в которых производная функции равна -1.
Сначала найдем уравнение производной.
Приравняем производную к числу -1.
Найдем значение функции в точке .
(по условию)
.
б) Найдем уравнение касательной к графику функции в точке .
Найдем значение функции в точке .
(по условию).
Подставим эти значения в уравнение касательной:
.
Ответ:
4
. 2}»>. Мы получили под корнем отрицательное число, равенство не верно, и точка не принадлежит графику функции и не является точкой касания.
2}»>. Мы получили под корнем отрицательное число, равенство не верно, и точка не принадлежит графику функции и не является точкой касания.
Это последний тип задач на нахождение уравнения касательной. Первым делом нам нужно найти абсциссу точки касания .
Найдем значение .
Пусть — точка касания. Точка принадлежит касательной к графику функции . Если мы подставим координаты этой точки в уравнение касательной, то получим верное равенство:
.
Значение функции в точке равно .
Найдем значение производной функции в точке .
Сначала найдем производную функции . Это .
Производная в точке равна .
Подставим выражения для и в уравнение касательной. Получим уравнение относительно :
Решим это уравнение.
Сократим числитель и знаменатель дроби на 2:
Приведем правую часть уравнения к общему знаменателю. Получим:
Упростим числитель дроби и умножим обе части на — это выражение строго больше нуля. 2} {8-3x_0>=0} }}{ }»>
2} {8-3x_0>=0} }}{ }»>
Решим первое уравнение.
Решим квадратное уравнение, получим
Второй корень не удовлетворяет условию title=»8-3x_0>=0″>, следовательно, у нас только одна точка касания и её абсцисса равна .
Напишем уравнение касательной к кривой в точке . Для этого подставим значение в уравнение — мы его уже записывали.
Ответ:
.
У = f(х) и если в этой точке к графику функции можно провести касательную, не перпендикулярную к оси абсцисс, то угловой коэффициент касательной равен f»(а). Мы этим уже несколько раз пользовались. Например, в § 33 было установлено, что график функции у = sin х(синусоида) в начале координат образует с осью абсцисс угол 45° (точнее, касательная к графику в начале координат составляет с положительным направлением оси х угол 45°), а в примере 5 § 33 были найдены точки на графике заданной
 В этом параграфе мы выработаем алгоритм составления уравнения касательной.к графику любой функции.
В этом параграфе мы выработаем алгоритм составления уравнения касательной.к графику любой функции.Пусть даны функция у = f(х) и точка М (а; f(а)), а также известно, что существует f»(а). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид у = кх+m, поэтому задача состоит в отыскании значений коэффициентов к и m.
С угловым коэффициентом к проблем нет: мы знаем, что к = f»(а). Для вычисления значения т воспользуемся тем, что искомая прямая проходит через точку М(а; f (а)). Это значит, что, если подставить координаты точки М в уравнение прямой, получим верное равенство: f(а) = ка+m, откуда находим, что m = f(а) — ка.
Осталось подставить найденные значения коэффициентов кит в уравнение прямой:
Нами получено уравнение касательной к графику функции у = f(х) в точке х=а.
Если, скажем,
Подставив в уравнение (1) найденные значения а = 1, f(а) = 1 f»(а) = 2, получим: у = 1+2(х-f), т. е. у = 2х-1.
е. у = 2х-1.
Сравните этот результат с тем, что был получен в примере 2 из § 33. Естественно, получилось то же самое.
Именно поэтому мы и провели тангенсоиду в § 15 (см. рис. 62) через начало координат под углом 45° к оси абсцисс.
Решая эти достаточно простые примеры, мы фактически пользовались определенным алгоритмом, который заложен в формуле (1). Сделаем этот алгоритм явным.
АЛГОРИТМ СОСТАВЛЕНИЯ УРАВНЕНИЯ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ у = f(x)
1) Обозначить абсциссу точки касания буквой а.
2) Вычислить 1 (а).
3) Найти f»(х) и вычислить f»(а).
4) Подставить найденные числа а, f(а), (а) в формулу (1).
Пример 1. Составить уравнение касательной к графику функции в точке х = 1.
Воспользуемся алгоритмом, учитывая, что в данном примере
На рис.
Чертеж подтверждает приведенные выкладки: действительно, прямая у = 2-х касается гиперболы в точке(1; 1).
Ответ: у =2- х.
Пример 2. К графику функции провести касательную так, чтобы она была параллельна прямой у =4х — 5.
Уточним формулировку задачи. Требование «провести касательную» обычно означает «составить уравнение касательной». Это логично, ибо если человек смог составить уравнение касательной, то вряд ли он будет испытывать затруднения с построением на координатной плоскости прямой по ее уравнению.
Воспользуемся алгоритмом составления уравнения касательной, учитывая, что в данном примере Но в отличие от предыдущего примера здесь имеется неясность: не указана явно абсцисса точки касания.
Начнем рассуждать так. Искомая касательная должна быть параллельна прямой у = 4х-5. Две прямые параллельны тогда и только тогда, когда равны их угловые коэффициенты. Значит, угловой коэффициент касательной должен быть равен угловому коэффициенту заданной прямой: Таким образом, значение а мы можем найти из уравнения f»(а)= 4.
Имеем:
Из уравнения Значит, имеются две касательные, удовлетворяющие условию задачи: одна в точке с абсциссой 2, другая в точке с абсциссой -2.
Теперь можно действовать по алгоритму.
Пример 3. Из точки (0; 1) провести касательную к графику функции
Воспользуемся алгоритмом составления уравнения касательной, учитывая, что в данном примере Заметим, что и здесь, как в примере 2, не указана явно абсцисса точки касания. Тем не менее действуем по алгоритму.
По условию касательная проходит через точку (0; 1). Подставив в уравнение (2) значения х = 0, у = 1, получим:
Как видите, в этом примере только на четвертом шаге алгоритма нам удалось найти абсциссу точки касания. Подставив значение а =4 в уравнение (2), получим:
На рис. 127 представлена геометрическая иллюстрация рассмотренного примера: построен график функции
В § 32 мы отметили, что для функции у = f(х), имеющей производную в фиксированной точке х, справедливо приближенное равенство:
Для удобства дальнейших рассуждений изменим обозначения: вместо х будем писать а, вместо будем писать х и соответственно вместо будем писать х-а. Тогда написанное выше приближенное равенство примет вид:
Тогда написанное выше приближенное равенство примет вид:
А теперь взгляните на рис. 128. К графику функции у = f(х) проведена касательная в точке М (а; f (а)). Отмечена точка х на оси абсцисс близко от а. Ясно, что f(х) — ордината графика функции в указанной точке х. А что такое f(а) + f»(а) (х-а)? Это ордината касательной, соответствующая той же точке х — см. формулу (1). В чем же смысл приближенного равенства (3)? В том, что для вычисления приближенного значения функции берут значение ординаты касательной.
Пример 4. Найти приближенное значение числового выражения 1,02 7 .
Речь идет об отыскании значения функции у = х 7 в точке х = 1,02. Воспользуемся формулой (3), учтя, что в данном примере
В итоге получаем:
Если мы воспользуемся калькулятором, то получим: 1,02 7 = 1,148685667…
Как видите, точность приближения вполне приемлема.
Ответ: 1,02 7 =1,14.
А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн , Математика в школе скачать
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие
Совершенствование учебников и уроковисправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки
Пусть дана функция f , которая в некоторой точке x 0 имеет конечную производную f (x 0).
Тогда прямая, проходящая через точку (x 0 ; f (x 0)), имеющая угловой коэффициент f ’(x 0), называется касательной.
А что будет, если производная в точке x 0 не существует? Возможны два варианта:
- Касательная к графику тоже не существует. Классический пример — функция y = |x | в точке (0; 0).
- Касательная становится вертикальной. Это верно, к примеру, для функции y = arcsin x в точке (1; π /2).
Всякая невертикальная прямая задается уравнением вида y = kx + b , где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x 0 , достаточно знать значение функции и производной в этой точке.
Итак, пусть дана функция y = f (x ), которая имеет производную y = f ’(x ) на отрезке . Тогда в любой точке x 0 ∈ (a ; b ) к графику этой функции можно провести касательную, которая задается уравнением:
y = f ’(x 0) · (x − x 0) + f (x 0)
Здесь f
’(x
0) — значение производной в точке x
0 , а f
(x
0) — значение самой функции.
Задача. Дана функция y = x 3 . Составить уравнение касательной к графику этой функции в точке x 0 = 2.
Уравнение касательной: y = f ’(x 0) · (x − x 0) + f (x 0). Точка x 0 = 2 нам дана, а вот значения f (x 0) и f ’(x 0) придется вычислять.
Для начала найдем значение функции. Тут все легко: f
(x
0) = f
(2) = 2 3 = 8;
Теперь найдем производную: f
’(x
) = (x
3)’ = 3x
2 ;
Подставляем в производную x
0 = 2: f
’(x
0) = f
’(2) = 3 · 2 2 = 12;
Итого получаем: y
= 12 · (x
− 2) + 8 = 12x
− 24 + 8 = 12x
− 16.
Это и есть уравнение касательной.
Задача. Составить уравнение касательной к графику функции f (x ) = 2sin x + 5 в точке x 0 = π /2.
В этот раз не будем подробно расписывать каждое действие — укажем лишь ключевые шаги. Имеем:
f
(x
0) = f
(π
/2) = 2sin (π
/2) + 5 = 2 + 5 = 7;
f
’(x
) = (2sin x
+ 5)’ = 2cos x
;
f
’(x
0) = f
’(π
/2) = 2cos (π
/2) = 0;
Уравнение касательной:
y = 0 · (x − π /2) + 7 ⇒ y = 7
В последнем случае прямая оказалась горизонтальной, т. к. ее угловой коэффициент k
= 0. Ничего страшного в этом нет — просто мы наткнулись на точку экстремума.
к. ее угловой коэффициент k
= 0. Ничего страшного в этом нет — просто мы наткнулись на точку экстремума.
Касательная – это прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка (рис.1).
Другое определение : это предельное положение секущей при Δx →0.
Пояснение : Возьмем прямую, пересекающую кривую в двух точках: А и b (см.рисунок). Это секущая. Будем поворачивать ее по часовой стрелке до тех пор, пока она не обретет только одну общую точку с кривой. Так мы получим касательную.
Строгое определение касательной:
Касательная к графику функции f , дифференцируемой в точке x о , — это прямая, проходящая через точку (x о ; f (x о )) и имеющая угловой коэффициент f ′(x о ).
Угловой коэффициент имеет прямая вида y = kx + b . Коэффициент k и является угловым коэффициентом этой прямой.
Угловой коэффициент равен тангенсу острого угла, образуемого этой прямой с осью абсцисс:
|
Здесь угол α – это угол между прямой y = kx + b и положительным (то есть против часовой стрелки) направлением оси абсцисс. Он называется углом наклона прямой (рис.1 и 2).
Если угол наклона прямой y = kx + b острый, то угловой коэффициент является положительным числом. График возрастает (рис.1).
Если угол наклона прямой y = kx + b тупой, то угловой коэффициент является отрицательным числом. График убывает (рис.2).
Если прямая параллельна оси абсцисс, то угол наклона прямой равен нулю. В этом случае угловой коэффициент прямой тоже равен нулю (так как тангенс нуля есть ноль). Уравнение прямой будет иметь вид y = b (рис.3).
Если угол наклона прямой равен 90º (π/2), то есть она перпендикулярна оси абсцисс, то прямая задается равенством x = c , где c – некоторое действительное число (рис. 4).
4).
Уравнение касательной к графику функции y = f (x ) в точке x о :
Пример
: Найдем уравнение касательной к графику функции f (x ) = x 3 – 2x 2 + 1 в точке с абсциссой 2.
Решение .
Следуем алгоритму.
1) Точка касания x о равна 2. Вычислим f (x о ):
f (x о ) = f (2) = 2 3 – 2 ∙ 2 2 + 1 = 8 – 8 + 1 = 1
2) Находим f ′(x ). Для этого применяем формулы дифференцирования, изложенные в предыдущем разделе. Согласно этим формулам, х 2 = 2х , а х 3 = 3х 2 . Значит:
f ′(x ) = 3х 2 – 2 ∙ 2х = 3х 2 – 4х .
Теперь, используя полученное значение f ′(x ), вычислим f ′(x о ):
f ′(x о ) = f ′(2) = 3 ∙ 2 2 – 4 ∙ 2 = 12 – 8 = 4.
3) Итак, у нас есть все необходимые данные: x о = 2, f (x о ) = 1, f ′(x о ) = 4. Подставляем эти числа в уравнение касательной и находим окончательное решение:
Подставляем эти числа в уравнение касательной и находим окончательное решение:
у = f (x о ) + f ′(x о ) (x – x о ) = 1 + 4 ∙ (х – 2) = 1 + 4х – 8 = –7 + 4х = 4х – 7.
Ответ : у = 4х – 7.
4.1.3 Уравнение касательной к графику функции
Видеоурок: Уравнение касательной к графику функции
Лекция: Уравнение касательной к графику функции
Если некоторая прямая проходит через точку с координатами (х0; f (х0)), а угол наклона данной прямой равен производной функции в данной токе, то такую прямую называют касательной к графику.
Обратите внимание, если не существует производной графика в данной точке, то и не может существовать касательной, или же данная касательная перпендикулярна к оси ОХ. Второй случай можно наблюдать в результате проведения касательной для графика функции арксинуса.
Итак, давайте рассмотрим задание касательной. Мы знаем, что для задания любой прямой, необходимо воспользоваться формулой y = kx + b.
Коэффициент k показывает, под каким углом будет располагаться прямая относительно оси ОХ. Если данный коэффициент больше нуля, то угол наклона между касательной и осью ОХ острый, если же коэффициент отрицательный, то угол между осью ОХ и касательной тупой.
Но давайте возвратимся к тому, что такое угловой коэффициент и как он находится. С прошлых вопросов мы помним, что угловой коэффициент – это производная функции в некоторой точке х0.
Чтобы задать уравнение касательной, необходимо воспользоваться формулой:
Итак, давайте рассмотрим подробнее, для этого необходимо провести аналогию между первоначальным уравнением прямой и уравнением касательной.
Отсюда следует, что для нахождения коэффициента k, необходимо найти производную в рассматриваемой точке.
Давайте найдем уравнение прямой для функции у = х3 в точке х0 = 3.
1. Находим производную данной функции:
y’ = 3x2.
2. Как уже было сказано ранее, коэффициент – это производная функции в некоторой точке, поэтому
y'(3) = 3* 32 = 27.
3. Как видно из уравнения касательной, нам так же необходимо найти и значение функции в рассматриваемой точке f(x0):
f(3) = 33 = 27.
Совершенно случайно получилось так, что значение производной в точке совпало со значением функции в заданной точке. Обратите внимание, что это просто совпадения и НЕ обязательно y’ = f(x0).
4. Теперь давайте составим уравнение касательной по заданной формуле:
у = 27 * (х – 3) + 27.
Чтобы получить конечно уравнение, необходимо сделать некоторые преобразования:
у = 27 * (х – 3) + 27 = 27х – 81 + 27 = 27х — 54.
То есть уравнение касательной:
у = 27х — 54.
Найти уравнение касательной достаточно просто, главное не запутаться в формуле. Для этого её необходимо просто выучить.
- Вконтакте
- Сайт
Как вычислить касательную функции – x-engineer.org
Касательная к функции в точке – это линия, которая соприкасается с графическим представлением функции только в этой конкретной точке.
Касательная касается функции (графика) только в указанной точке. Другими словами, касательная едва касается функции (графика).
Другими словами, касательная едва касается функции (графика).
Линия, которая пересекает (пересекает) график функции, называется секанс .
Изображение: Тангенс и секанс к графику функции
В приведенном выше примере красная линия — это тангенс. Она касается функции f(x) в точке P(x 1 , y 1 ) . Синяя линия — это секанс, и, как вы видите, она пересекает функцию f(x) в двух точках.
Учитывая функцию f(x) и точку P 1 (x 1 , y 1 ) , как вычислить тангенс? Нахождение касательной означает нахождение уравнения прямой, касательной к функции 9{3}=1\]
Мы знаем, что:
\[y_{1}=f(x_{1})\]
Это означает, что результат вычисления функции в точке x 1 — это координата y 1 . Теперь мы определили точку P 1 (1, 1) . 1. Изображение: График кубической функции с точкой касания Шаг 2 : Определите две точки P 0 и P 2 , слева и справа от P 1. Выберем точку P 0 при x 0 = 0,6 и P 2 при x 90 2 2 Эти точки должны быть равномерно распределены слева и справа от P 1 9{3}=-0,744\\ Теперь мы определили точку P 2 (1,4,-0,744) . Давайте теперь обновим наш график функции точками P 0 и P 2 и их координатами. Изображение: График кубической функции с точкой касания и двумя точками смещения Шаг 4 . Определив две точки, мы можем легко провести прямую линию между ними. Также с помощью координат двух точек мы можем рассчитать наклон линии. В нашем случае у нас будет две линии: одна между точками P 0 и P 1 , а вторая между P 1 и P 2 . Для обеих линий мы можем вычислить их наклон. Обычным обозначением уклона линии является буква м . Для первой линии уклон м 0 рассчитывается как: \[ \begin{equation*} \begin{split} Для второй линии уклон м 2 рассчитывается как: \[ \begin{equation*} \begin{split} Ниже приведено графическое представление двух линий и функции f(x) . Обе линии являются секущей нашей функции f(x) . Изображение: График кубической функции с точкой касания и двумя секущими Шаг 5 . Вычислить наклон касательной в точке P 1 (1, 1) Наклон касательной в точке P 1 будет средним арифметическим наклонов двух секущих . Такой метод расчета возможен, потому что мы выбрали точки x 0 и x 2 на равном расстоянии от x 1 . \[ \begin{equation*} \begin{split} Шаг 6 (последний шаг) . Рассчитаем уравнение касательной в точке P 1 . Теперь, когда мы знаем координаты точки касания P1 и значение наклона, мы можем легко вычислить уравнение касательной: \[ \begin{equation*} \begin{split} Имея уравнение касательной, мы можем изобразить на одном графике функцию f(x) и касательную y(x) . Изображение: График квадратичной функции с точкой касания и линией касания \[f(x)=10 \cdot \sqrt{2 \cdot x} + 3 \cdot x + 2\] Изображение: График функции квадратного корня с точкой касания и линией касания Примените тот же метод к своей функции и дайте нам результат! Если у вас есть какие-либо вопросы или замечания относительно этого урока, пожалуйста, используйте форму комментариев ниже. Не забудьте поставить лайк, поделиться и подписаться! Калькулятор касательной плоскости — найти уравнение (шаг за шагом) функция с 2 или 3 переменными по заданным координатам. Калькулятор касательной плоскости | Лучшие шаги полного решения — Voovers www. Мгновенно рассчитайте уравнение касательной плоскости и просмотрите этапы решения, чтобы проверить свою работу с помощью Калькулятора касательной плоскости Voovers. Почему мы изучаем… · Как найти уравнение… Ähnliche Fragen Что такое уравнение касательной плоскости в трех измерениях? Какая формула для касательной плоскости? Калькулятор касательной плоскости к поверхности — Math34.pro math34.pro › tangent_plane Касательная плоскость к калькулятору поверхности. Затем показано, как построить касательную плоскость к точке на поверхности, используя эти аппроксимированные градиенты. Уравнение плоскости по трем точкам — Онлайн-калькулятор Keisan — CASIO keisan.casio.com › exec › system Вычисляет уравнение плоскости по трем точкам. … это позволило нам прогнозировать цены поставщиков на основе трех оценок затрат, охватывающих две переменные. Исчисление III. tutorial.math.lamar.edu › классы › calciii › TangentP… 16.11.2022 · В этом разделе формально определите, что такое касательная плоскость к поверхности и как мы используем частные производные, чтобы найти уравнения … Калькулятор касательной — — Symbolab www.symbolab.com › … › Приложения для производных Калькулятор свободной касательной — найдите уравнение касательная с заданной точкой или точкой пересечения шаг за шагом. Определение уравнения касательной плоскости — YouTube www.youtube.com › смотреть 04.02.2011 · В этом видео показано, как определить уравнение касательной плоскости к поверхности, заданной … Calc III: Поиск уравнений касательной плоскости и нормали — YouTube www.youtube.com › смотреть 26.02.2018 · Ваш браузер не может это воспроизвести видео. Построим график функции f(x) для x = 0 … 2 и точки P 1 с координатами x 1 и y 1
Построим график функции f(x) для x = 0 … 2 и точки P 1 с координатами x 1 и y 1
y_{2}&=-0,744
\end{split} \end{equation*} \] Вычислить наклоны линий, определенных между точками P 0 -P 1 и P 1 -P 2
Вычислить наклоны линий, определенных между точками P 0 -P 1 и P 1 -P 2
м_{0}&=\frac{y_{1}-y_ {0}}{x_{1}-x_{0}}=\frac{1-1,784}{1-0,6}=-1,96\\
м_{0}&=-1,96
\end{split} \end {уравнение*} \]
м_{2}&=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-0,744-1}{1,4-1}=-4,36\\
m_{2}&=-4. 36
36
\end{split} \end{equation*} \]
м_{1}&=\frac{m_{0}+m_{2}}{2}=\frac{-1,96-4,36}{2} =-3,16\\
м_{1}&=-3,16
\end{split} \end{equation*} \]
y(x ) &= y_{1} + m_1 \cdot (x – x_1)\\
y(x) & = 1 – 3,16 \cdot (x – 1)
\end{split} \end{equation*} \] 2 + 2 \cdot x + 1\]
2 + 2 \cdot x + 1\] tangent-plane-calculator-3-variables — Googlesuche 92у при (х,у)=(3,2). естественный язык; Математический ввод. Используйте режим математического ввода, чтобы напрямую вводить математические обозначения из учебника.
 voovers.com › Исчисление
voovers.com › Исчисление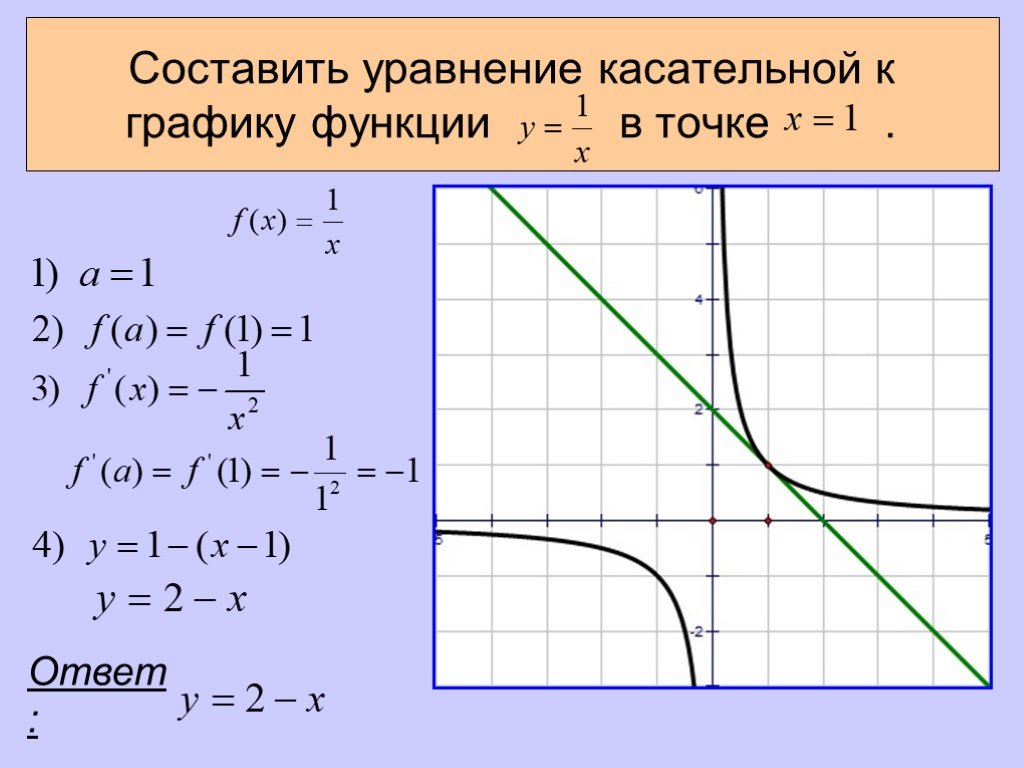 Касательные плоскости и линейные приближения
Касательные плоскости и линейные приближения
Dauer: 10:08
Прислан: 04.02.2011

 Тогда прямая, проходящая через точку (x
0 ; f
(x
0)), имеющая угловой коэффициент f
’(x
0), называется касательной.
Тогда прямая, проходящая через точку (x
0 ; f
(x
0)), имеющая угловой коэффициент f
’(x
0), называется касательной.